Cluster-Based Bagging of Constrained Mixed-Effects Models for High Spatiotemporal Resolution Nitrogen Oxides Prediction over Large Regions

Abstract

Background

Accurate estimation of nitrogen dioxide (NO₂) and nitrogen oxide (NO_x) concentrations at high spatiotemporal resolutions is crucial for improving evaluation of their health effects, particularly with respect to short-term exposures and acute health outcomes. For estimation over large regions like California, high spatial density field campaign measurements can be combined with more sparse routine monitoring network measurements to capture spatiotemporal variability of NO₂ and NO_x concentrations. However, monitors in spatially dense field sampling are often highly clustered and their uneven distribution creates a challenge for such combined use. Furthermore, heterogeneities due to seasonal patterns of meteorology and source mixtures between sub-regions (e.g. southern vs. northern California) need to be addressed.

Objectives

In this study, we aim to develop highly accurate and adaptive machine learning models to predict high-resolution NO₂ and NO_x concentrations over large geographic regions using measurements from different sources that contain samples with heterogeneous spatiotemporal distributions and clustering patterns.

Methods

We used a comprehensive Kruskal-K-means method to cluster the measurement samples from multiple heterogeneous sources. Spatiotemporal cluster-based bootstrap aggregating (bagging) of the base mixed-effects models was then applied, leveraging the clusters to obtain balanced and less correlated training samples for less bias and improvement in generalization. Further, we used the machine learning technique of grid search to find the optimal interaction of temporal basis functions and the scale of spatial effects, which, together with spatiotemporal covariates, adequately captured spatiotemporal variability in NO₂ and NO_x at the state and local levels.

Results

We found an optimal combination of four temporal basis functions and 200 m scale spatial effects for the base mixed-effects models. With the cluster-based bagging of the base models, we obtained robust predictions with an ensemble cross validation R² of 0.88 for both NO₂ and NO_x [RMSE (RMSEIQR): 3.62 ppb (0.28) and 9.63 ppb (0.37) respectively]. In independent tests of random sampling, our models achieved similarly strong performance (R² of 0.87–0.90; RMSE of 3.97–9.69 ppb; RMSEIQR of 0.21–0.27), illustrating minimal over-fitting.

Conclusions

Our approach has important implications for fusing data from highly clustered and heterogeneous measurement samples from multiple data sources to produce highly accurate concentration estimates of air pollutants such as NO₂ and NO_x at high resolution over a large region.

1. Introduction

Several studies have shown that nitrogen dioxide (NO₂), a criteria air pollutant, has adverse acute and chronic effects on human health [1, 2]. Acute NO₂ exposure has been shown to cause airway inflammation, and chronic exposure can decrease lung function and further increase response to allergens [3]. Furthermore, nitrogen oxides (NO_x) emissions contribute to the formation of fine particles (PM) and ground-level ozone [4], both of which are associated with adverse health effects [5, 6]. By increasing accuracy of air pollution exposure estimation, health effect estimation bias will be reduced [7]. While state and local government agencies in the United States have operated routine NO_x monitoring networks over the past four decades with relatively wide spatial coverage, the sparse distributions of such monitoring efforts limit highly resolved spatial and temporal exposure modeling efforts at the broad community to narrow neighborhood scale. Therefore, measurements from various field sampling campaigns are often used to supplement routine monitoring data in order to capture finer-scale spatial variability. However, field sampling locations are often highly clustered due to sampling convenience within narrow geographic regions, and limitations in funding, feasibility, temporality, and study goals of these field campaigns. Further, these field sampling campaign clusters may also differ substantially in size due to similar reasons. These factors result in potentially significant heterogeneity in the signals being captured between and within clusters, for example, emission sources, meteorological factors, concentration range and spatial and temporal variability of air pollutants. In addition, there could be a wide range of differences in the measurement methods (e.g. instruments, sampling time and duration) and intended sampling campaign objectives, leading to complex data harmonization that is needed for modeling. Disregarding sample clustering, uneven distributions and inherent variability in measurement data sources when building exposure models could result in unbalanced model training and therefore introduce bias in exposure predictions and further health risk models that rely on such predictions.

Spatiotemporal exposure models that aim to model regional or broad geographic areas that encompass both rural and urban locations over hundreds to thousands of kilometers must be able to capture both complex local variability and larger spatial patterns in pollutant concentrations over time. Several standard statistical methods have been used to estimate NO₂ concentrations and assess exposures within and across regions in health studies, ranging from nearest monitor or time period approaches and multiple linear regression, to non-linear methods such as generalized additive models and geospatial models such as kriging [8–11]. Most of these early approaches estimate long-term average concentrations (high spatial variability, limited temporal variability) with model R² values ranging from 0.44 to 0.87.

Traditional LUR models [12, 13], LUR models with meteorology [14, 15], LUR models with chemical transport model outputs [16], and spatiotemporal models with kriging [17–19] have been developed to estimate NO₂ and NO_x concentrations, but such models are subject to limited temporal resolution and overall performance [cross validation (CV) R²: 0.52–0.84; few reported R² of independent test]. More sophisticated methods such as hybrid models [20] merging land-use, satellite based and chemical transport models with monitoring data, partial least squares plus universal kriging [21], mixed effects models [22, 23] with geographical weighted regression (GWR) [24], geographically and temporally weighted regression [25, 26], machine learning methods such as neural networks [27] and random forest [28] have been used to estimate concentrations of particulate matter less than 2.5μm in aerodynamic diameter (PM_2.5) at high spatial (100 m to 1000 m) and temporal (hourly, daily, biweekly or monthly) resolutions. However, for NO₂ and NO_x, there are a very limited number of studies employing sophisticated spatiotemporal models such as machine learning methods to estimate concentrations at high spatiotemporal resolution with robust prediction performance, which might be more important for these pollutants due to finer spatial heterogeneity compared to PM_2.5. Our earlier work on NO₂ and NO_x resulted in model performance with cross-validation R² up to 0.87 [29], but our model was specific to the southern California region with limited generalizability to broader regions. Differences in training data ranges and variances between the original modeling region and the new modeling region may alter the associations between covariates and true NO_x concentrations. Further, atmospheric processes are complex and are influenced by multiple factors (e.g. meteorology, topography, co-pollutants) likely varying across regions. Therefore, some models that perform well in one region may not transfer effectively when applied in another region or larger regions.

The bootstrap machine learning approach uses re-sampling with replacement to obtain different samples and train different models or learners. Compared with the traditional approach of generating single models, the ensemble learning with bootstrap aggregation (bagging) can reduce sampling variance and obtain more stable solutions [30, 31]. However, despite a heterogeneous measurement error structure across sampling sources within a large geographic region, regular bagging uses random samples without consideration of sampling source, which can limit the models’ ability to capture the true variability of air pollutant concentrations to be estimated, thus lowering the models prediction performance. Further, for highly clustered samples that are typical for NO₂ and NO_x monitoring data across large regions like California, with significant variance of concentrations between clusters, regular bagging does not consider the clustered nature of the data and may result in highly correlated individual models making the ensemble learning less efficient.

In this study, we demonstrate that enhanced machine learning techniques can overcome these challenges and improve results obtained in a constrained mixed-effects modeling framework with ensemble learning [29] to predict NO₂ and NO_x concentrations at high spatial and temporal resolution for the entire state of California (CA). We designed an approach of cluster-based bagging, where natural clusters within sampling locations and time were identified and extracted using an optimal clustering method to enhance the bootstrap phase. In this approach, we considered balance between clusters and heterogeneity within clusters for the samples from multiple sources to minimize the sampling bias and decrease the correlation among the ensemble models, thus potentially boosting the ensemble learning.

We demonstrate that, by using a grid search machine learning method, we can obtain an optimal combination of the number of temporal basis functions and scale of spatial effects for modeling, in addition to other spatiotemporal covariates, that produces fine temporal and spatial estimates of NO₂ and NO_x concentrations over a large region and for a long time period. As a case study, we estimated 22 years (1992–2013) of biweekly NO₂ and NO_x concentrations at high spatial resolution over the entire State of California. Finally, we conducted vigorous model validation using ensemble learning cross validation and site-based, 10-fold CV, as well as independent tests using completely separate source of validation data.

2. Materials

2.1. Study domain

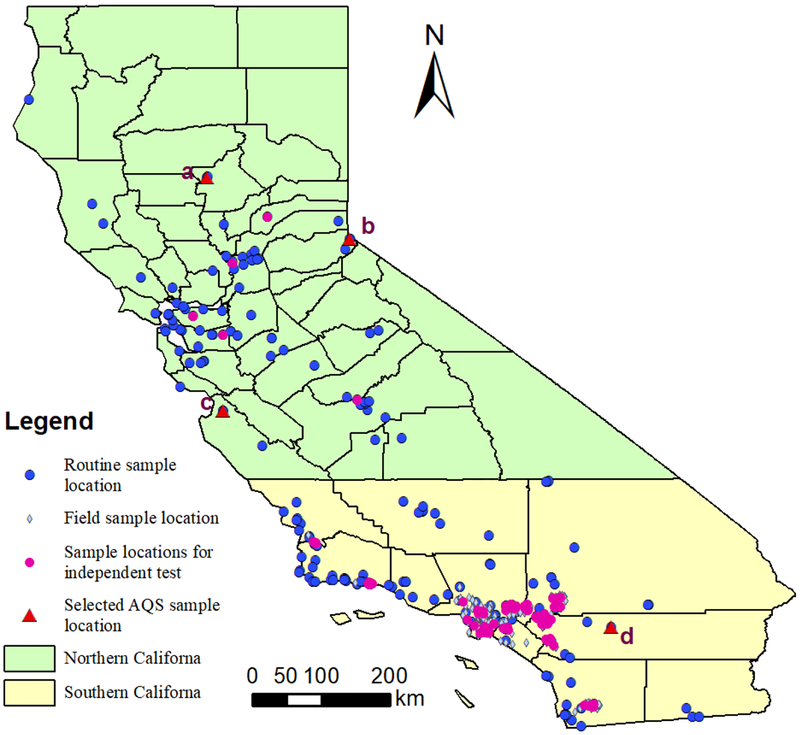
The study region that covers the entire state of California, including locations of the training and test sample data, is shown in Figure 1 [four locations (flagged as a, b, c and d) selected for presentation of the simulated time series in Figure 7].

Figure 1.

Study region with training and independent test sample locations [four routine AQS monitoring locations, a (468 Manzanita Av., Chico, CA), b (3377 Tahoe Blvd., South Lake Tahoe, CA), c (II-1270 Natividad Rd., Salinas, CA) and d (6078 Adobe Rd., Twentynine Palms, CA) selected for the long-term time series plots of the observed, predicted and simulated concentrations in Figure 7]

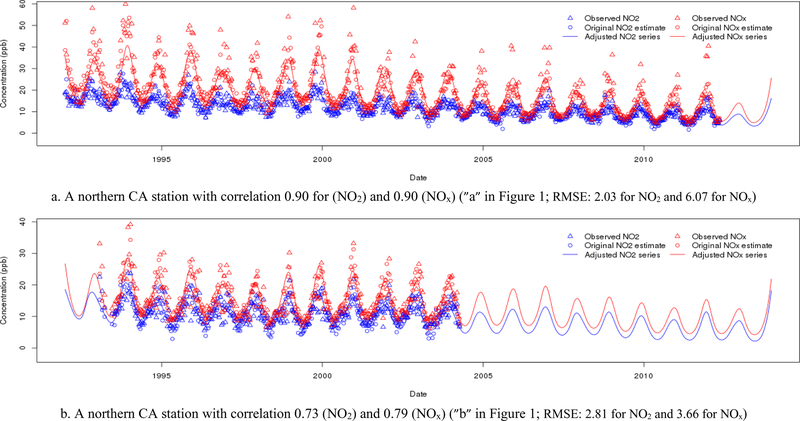
Figure 7.

Plots of the observed, predicted and simulated concentrations for the four AQS monitoring stations in California (for specific locations, see Figure 1)

2.2. NO₂ and NO_x measurements

Concentrations of NO₂ and NO_x were acquired from two sources (1513 sampling locations in total): (1) the U.S. Environmental Protection Agency Air Quality System (AQS), which provided long-term hourly measurements from 193 routine AQS monitoring stations operated by the California Air Resources Board (CARB) and other governmental agencies (1992–2013), and (2) special sampling campaigns where weekly or biweekly intensive field measurements were collected by the University of Southern California (1104 sampling locations in 12 southern California communities, 2005–2009), University of California, Los Angeles (184 sampling locations in Los Angeles County, 2006–2007), and University of California, Irvine (32 sampling locations in south Los Angeles County and Orange County, 2009), respectively. All AQS monitors used the Federal Reference Method (FRM), and the weekly and biweekly field measurements used passive diffusion-based Ogawa samplers to measure NO₂ and NO_x concentrations. The passive measurements were systematically adjusted to be consistent with the continuous FRM NO_x and NO₂ measurements. We then aggregated hourly and weekly concentrations to biweekly averages (average concentrations in a biweekly time series starting from 01/01/1992 and ending on 12/18/2013), as in our previous study [29]. To address the differences in timing of the weekly and bi-weekly field campaigns, we estimated the ratios of average concentrations during the sampling period and the target time period of estimation (e.g. biweekly) based on the nearest AQS routine monitoring station samples, that were in turn used to adjust the differences.

2.3. Spatiotemporal covariates, basis functions and Thiessen polygons

Temporal basis functions and Thiessen polygons capture temporal and spatial patterns, respectively. Temporal basis functions were extracted using iterative singular value decomposition [32] to the AQS NO₂ and NO_x data and were embedded into the modeling framework to characterize regional seasonal patterns, and Thiessen polygons were utilized to model spatial patterns not explained by the aforementioned spatial covariates [29]. In addition, we included spatially-and temporally- varying covariates, such as traffic, meteorology and geographic factors. Specifically, these covariates included: traffic-related NO_x (ppb) modeled by CALINE4 dispersion model to capture local traffic emissions (on freeways and on non-freeways), traffic density in circular buffers from 300 m to 5000 m radius (distance-decayed average number of vehicles per day), distance to major roadways (m); gridded (4 km) minimum and maximum air temperature (°C), specific humidity (grams of vapor per kilogram of air), precipitation (millimeters of rain per square meter in 1 h), wind speed (m/second); gridded (1 km) elevation (m); and distance to the shoreline (m), and population density in a 300 m buffer (number of persons per square mile).

3. Modeling Approach

For statewide estimation of NO₂ and NO_x concentrations, we developed new models based on the three-stage modeling framework previously developed for southern CA [29]. This included single mixed-effects models to account for spatiotemporal variability of concentrations (Stage 1), ensemble machine learning to reduce the uncertainty in point estimates of location- and time- specific samples (Stage 2), and constrained optimization to simulate the long-term continuous time series estimates of concentrations (Stage 3). In the new modeling framework (Supplementary Figure S1), we include cluster-based bagging to enhance the ensemble machine learning stage (Section 3.1) where comprehensive clustering algorithms (Section 3.1.1) are used to extract natural spatiotemporal clusters that subsequently serve as stratifying and exclusion factors (Section 3.1.2) in bootstrap. This results in a more balanced spatiotemporal distribution of samples that decreases the bias in training samples. Further, a cluster-based exclusion method is used to de-correlate the predictions of ensemble models, consequently reducing the errors in predictions. The modeling framework also includes a grid search (Section 3.2), which facilitates finding the optimal combination of temporal basis functions (Section 3.2.1) and scale of spatial effects (Section 3.2.2) that characterizes temporal and spatial variability of NO₂ and NO_x regionally across CA (Section 3.2.3). To evaluate the new approach, we conducted cross-validation (Section 3.3.1) and two independent tests with data not used in the modeling framework (Section 3.3.2).

3.1. Cluster-based Bagging

3.1.1. Clustering method for the samples

With inherent heterogeneity and multiplicity in the distribution of the samples from different NO₂ and NO_x monitoring sources, we apply a clustering approach that combines the Kruskal algorithm and K-means to obtain optimal spatiotemporal clusters for the training samples.

The classic K-means algorithm intends to partition samples into a pre-selected number of clusters, K, in which each sample belongs to the cluster with the nearest mean. Supplementary Section 1.1 provides more details on the K-means algorithm. Given the number of monitoring sites and their complex spatiotemporal distribution, it is impractical to set a reasonable number of clusters a priori. Thus, we introduce the Kruskal algorithm, which is a single-linkage density-based algorithm that detects naturally-shaped clusters according to the shortest intercluster distance [34]. Compared with K-means, this algorithm has several advantages: no need for pre-selected numbers of clusters, high computing efficiency, and no distributional assumptions. The input parameter for the Kruskal algorithm is the minimum intercluster distance to consider points to form a cluster. This distance can be first determined and then adjusted by inspection upon the possible distance between potential clustered sampling locations. For more details about the Kruskal algorithm, please refer to Supplementary Section 1.2.

Kruskal is a variant of single linkage agglomerative clustering with sub-optimal solution for the single-link samples [33], while K-Means can deal well with the clusters of single-link samples if such samples exist. Thus, we combine both methods to compensate their respective shortcoming (pre-selected number of clusters and single-link samples) to obtain optimal clusters. In the comprehensive Kruskal-K-Mean method, we used Kruskal to find the potential clusters and then used K-means to solve single-link samples (see Supplementary Section 1.3 for details).

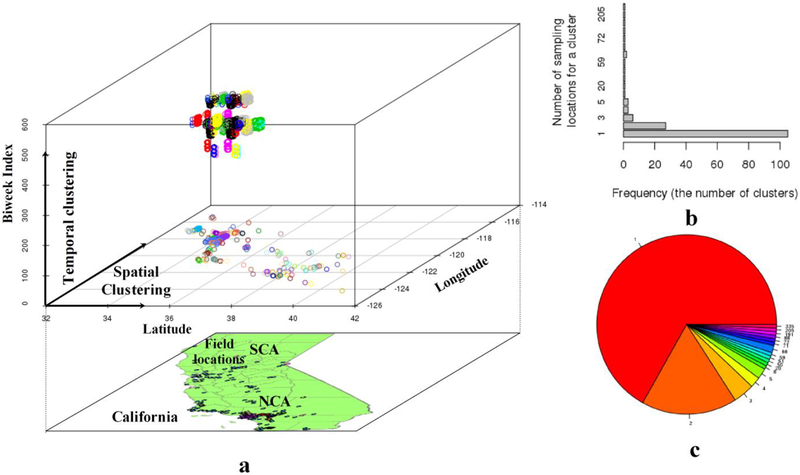
To perform spatiotemporal clustering of NO₂ and NO_x samples, we applied the Kruskal-K-Mean method to conduct spatial clustering at first and then temporal clustering within each resultant spatial cluster (see Supplementary Section 1.4 for details). With the sequential spatial to temporal clustering (Figure 2-a), we do not need to define a complex spatiotemporal distance and corresponding threshold. Temporal clustering of the samples was mostly due to the limited number of sampling periods from the field campaigns (for each field campaign, sampling concentrated in several periods). Most routine monitoring stations had no temporal clusters due to continuous sampling over time. This approach of moving from spatial to temporal clustering can be used for most practical applications.

Figure 2.

Spatiotemporal clustering (spatial→temporal) (a), frequency bar plot (b) and pie chart (c) for the number of sampling locations for a cluster

3.1.2. Cluster-based bagging

With optimal spatiotemporal clusters obtained, we leveraged cluster-based stratification and exclusion bootstrap to reduce bias and error in ensemble predictions based on the training samples.

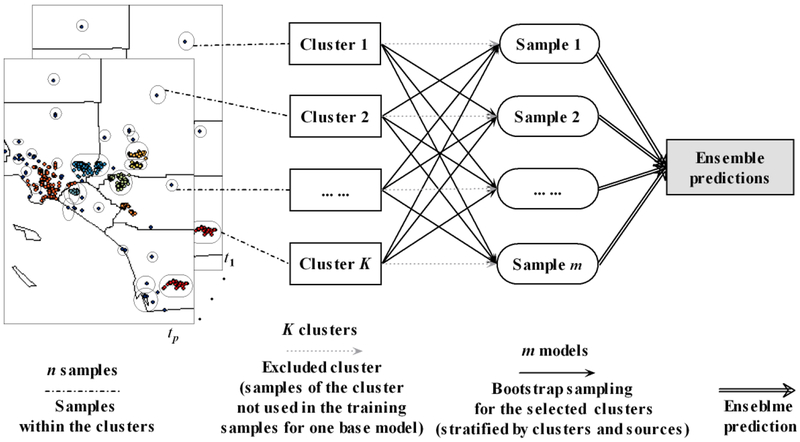
Bagging proceeded whereby all samples within a selected cluster were removed and stratified bootstrap was conducted on the samples of the remaining K-1 clusters to get the training samples for one mixed-effects base model. Assume that the total number of samples is n with K-1 clusters (one cluster excluded), then about 63.2% of the samples within each remaining cluster are drawn within each bootstrap. Therefore, we obtain about 63.2% of n-n_k (n_k: number of samples within the excluded k^th cluster) samples for each base model. Excluding the samples within a cluster is to minimize the similarity between the testing and training data in space and time, and reduce the correlation between individual models to boost the ensemble predictions. The mathematical explanation for lower expected square errors for less related models in ensemble learning was provided in Supplementary Section 2. By excluding the samples from the selected cluster for each base model, the predictions by the base models may become less correlated to boost generalization in ensemble prediction.

Further, we employed the clusters and sampling sources (routine monitoring source versus field measurement campaigns) as stratifying factors in bootstrap to obtain balanced samples (evenly distributed across the selected clusters) to reduce bias in the training samples. Figure 3 shows the sampling framework of cluster-based bagging and we can generalize this as the n-K-m framework using three digits (n samples, K clusters, and m base models).

Figure 3.

n-K-m sampling framework of spatiotemporal cluster-based bagging

3.2. Grid search for optimal solutions

In our modeling framework (Supplementary Figure S1), a base model is a mixed-effects spatiotemporal model that contains temporal basis functions to capture regional temporal variability of NO₂ and NO_x, spatial effects based on Thiessen polygons to capture spatial autocorrelation, and aforementioned spatial and temporal covariates. Together these model components accounted for a considerable amount of local spatial and spatiotemporal variability in NO₂ and NO_x concentrations, as demonstrated in our previous southern California models [29]. When this framework is extended to large regions, it is necessary to extend the temporal basis functions to better represent temporal variability of concentrations over whole region, and re-define the spatial scale of spatial effects to capture spatial variability within and across sub-regions of the larger domain. Above all, the interaction between temporal and spatial effects is also important in order to obtain an optimal solution for the base models.

3.2.1. Temporal basis functions to represent regional patterns of temporal variability

As variants of principal components, temporal basis functions were used to characterize temporal processes for each target region and temporally varying target variable (e.g. meteorological parameters and NO₂ or NO_x concentrations that have seasonal patterns) [17]. It has been found that the first two basis functions [29] sufficiently capture the major temporal variability of NO₂ and NO_x for a region like southern California. However, this does not sufficiently capture heterogeneity in seasonal patterns due to interregional differences in temporal variability across all of California in this study. To address this, we included additional temporal basis functions to characterize multi-regional temporal patterns. We also compared the temporal basis functions for different regions (urban vs. rural region; southern vs. northern California) and pollutants (NO₂ vs. NO_x) to inform interregional difference in temporal patterns.

3.2.2. Scale of spatial effect by Thiessen polygons

Spatial effects were modeled based on Thiessen polygons constructed around the sampling locations. The method based on Thiessen polygons are derived from the triangular irregular networks modeling idea in the community of spatial data analysis [35, 36]. Because the nodes (similar to the monitoring stations, sampling locations, or centroid location of one cluster in our case study) in the network can be placed irregularly over a surface, triangular irregular networks can have a higher resolution in areas where a surface is highly variable or where more detail is desired (like urban areas where emission sources and dispersion processes can be complex) and a lower resolution in areas that are less variable (like rural areas where the variability in sources and concentrations might be lower). As an extreme case, each sampling location is covered by its own polygon; however, this would result in longer training time and potential over-fitting. Thus, an optimal set of Thiessen polygons was constructed based on an aggregate distance that simultaneously captured small-scale spatial variability while reducing potential over-fitting. In our earlier work [29], we used K-means to a pre-selected number of clusters to generate the central nodes to derive Thiessen polygons by Voronoi decomposition [37]. In this study, we use the aggregate distance between clusters from the Kruskal-K-means method (Section 3.1.1) to initialize the spatial scale of Thiessen polygons, which further informs spatial random effects in the models.

3.2.3. Grid search for optimal interaction of temporal basis functions and spatial effect

Grid search is a machine learning technique used to find the optimal solution through exhaustive search of a manually specified subset in the space of a model’s hyperparameters [38, 39]. A hyperparameter is a parameter whose value needs to be set before learning and different values may have a different influence on the results. Model performance metrics such as cross validation (CV) RMSE or R² can be used to guide the grid search and obtain an optimal solution. Different from the search for an optimal solution of a single parameter, grid search can test the effect of interactions (combinations) of different hyperparameters on model performance when the combination of respective optimal solutions of hyperparameters does not relate to the global optimal solution. Using empirical knowledge to constrain the ranges of the hyperparameters, we can shrink the grid spaces to improve efficiency of the search.

For this study, grid search was used to find the optimal interaction between the number of temporal basis functions and the scale of spatial effects (aggregating distance for generation of Thiessen polygons). The grid table consisted of different combinations of two superparameters [temporal basis functions (1 to 10) and aggregate distances (from 100 m to 800 m by steps of 100 m)]. Thus, the size of our search space is 8×10=80. The R² and RMSE of the ensemble predictions were used as the performance metric in the grid search.

3.3. Model Validation

3.3.1. Cross validation

To evaluate location- and time- specific point estimates from the cluster-based ensemble predictions, we used performance metrics including CV R², RMSE, and normalized RMSE by the inter-quartile (IQR) (RMSEIQR) of the observed values [RMSEIQR=RMSE/IQR(y)]. RMSE is scale-dependent and cannot be compared across the datasets with different concentration scales. RMSEIQR is a relatively objective metric to compare the models across different concentration scales and is less sensitive to extreme values (outliers) than RMSE [40]. We evaluated these metrics (R², RMSE and RMSEIQR) for the entire state of CA, southern versus northern CA, and routine versus field NO₂ and NO_x measurements. We also examined residual plots for potential over- or under-estimation, normality and heteroscedasticity.

A site-based 10-fold cross validation (CV) was conducted to evaluate model performance. For this CV, all samples from 10% of the sampling sites were removed from the training dataset. Samples from the remaining 90% of the sampling sites were employed to train the model which in turn was used to predict the values for the 10% of sampling sites removed. This procedure was iterated until the samples for all the monitoring sites from AQS and field campaigns were predicted. Then, the performance metrics were evaluated for all the point estimates. R² in the site-based 10-fold CV was used in the grid search to find the optimal solution.

On average, a sample is selected 63.2% of the time when using stratified bootstrap aggregation. The trained model was used to make predictions for the samples not selected in each bootstrap set. Then the averages of these predictions were calculated to obtain the ensemble predictions. The result of the ensemble predictions represents 36.8% cross validation (called ensemble cross validation), close to 3 fold CV. The same performance metrics are evaluated using the performance-metric (the reciprocal of RMSE) weighted averages based on the outputs from multiple ensemble learning models.

Constrained optimization [29] was used to simulate the time series of biweekly NO₂ and NO_x concentrations based on the temporal basis functions and ensemble point estimates. We also evaluated the Pearson’s correlation coefficient between the simulated series of biweekly averages of NO₂ and NO_x by constrained optimization, and the observed values at each AQS monitoring station in California. Correlations from all AQS monitoring sites were then summarized to have a comprehensive evaluation of the model performance in simulation of time series.

3.3.2. Independent test of model performance

Given the possibility of obtaining overly optimistic CV R² when using random test and training data selection techniques in the cross-validation [41], we also conducted two independent tests of model performance.

For the first test, we randomly selected about 10% of the sampling locations stratified by the cluster id and source [AQS vs. each field campaign data (USC, UCI and UCLA)] as an independent test dataset. Thus, we named this as independent tests of random sampling. Figure 1 shows spatial locations of these test samples (shown as black cross). Models were developed excluding the independent testing samples entirely. Specifically, in the samples of independent test, we obtained 126 sampling locations [5 AQS locations in northern California, and 121 locations (4 from AQS, 105 from USC, 1 from UCI and 11 from UCLA) in southern California] from 1,511 sampling locations. We calculated R², RMSE and normalized RMSE of NO₂ and NO_x for each cluster and the population respectively. The scatter plots of observed vs. predicted concentrations and residuals were also examined.

For the second test, we removed all 49 UCI samples from the field campaigns to conduct model evaluation (and kept the UCLA and USC samples in model training). This test aims to examine the generalization of the models to the independent UCI samples not from the population of the training samples.

4. Results

4.1. Summary of measured concentrations and covariates

In total, we examined 56,961 biweekly NO₂ and NO_x concentrations obtained from 1,511 monitoring sites in California, among which 78 AQS sites were from northern California, 113 AQS sites were from southern California, and 1,320 were from the special field campaigns (Table 1 and Figure 1). Over the study period (1992–2013), California had a mean NO₂ concentration of 16.0 ppb (IQR: 12.8 ppb) and NO_x concentration of 28.8 ppb (IQR: 26.0 ppb). On average, southern California concentrations were almost double those of northern California [NO₂: 23.4 ppb (IQR: 16.2 ppb) vs. 13.4 ppb (IQR: 8.7 ppb); NO_x: 45.4 ppb (IQR: 31.1 ppb) vs. 23.5 ppb (IQR: 18.9 ppb), respectively]. The distribution of covariates demonstrated different mean levels by region (Supplementary Figure S2): northern California had lower CALINE4 NO_x, traffic density, air temperature, annual mean concentrations, and population density, but higher wind speed [42].

Table 1.

Summary of NO₂ and NO_x measurements for the training and test samples

Source	#Monitoring locations	Distribution of monitoring locations (number of biweekly periods with valid data)				Mean concentration (ppb)		Standard deviation (ppb)		Correlation between NO2 and NOx
		≤100	(100,280]	(280,400]	>400	NO2	NOx	NO2	NOx
Southern California AQSa	113	21	31	17	44	24.5	46.8	11.9	31.7	0.82
Southern California Non-AQS	1320	1320				17.2	37.6	9.2	23.5	0.85
Southern California Total	1433	1341	13	17	44	23.4	45.4	11.7	31.2	0.82
Northern California AQS	78	24	16	8	30	13.4	23.5	6.45	18.1	0.89
California Total	1511	1365	29	25	74	16.0	28.8	10.3	27.4	0.87

Note:

^a.AQS: EPA’s Air Quality System archive of quality-assured routinely collected measurement data.

For the independent test, we removed 2,523 biweekly samples of 126 sampling locations: 258 from 117 field campaign sites and 2265 from 9 AQS routine monitoring stations), leaving 54,438 samples to train the models. The independent test sample had mean NO₂ (NO_x) of 15.19 (33.11) ppb with standard deviation of 12.31 (27.08) ppb, respectively.

4.2. Distribution and statistics of spatial and temporal clusters

For spatial clustering, we set up the initial minimum intercluster distances as 6 km according to visual inspection on the possible distance for the highly clustered samples (Supplementary Figure S3). Sensitivity analysis, changing the minimum distance ±2 km around 6 km, showed no changes in the clusters. For temporal clustering, we examined the temporal separation between the samples from the field campaigns and set up the minimum intercluster distance as 5 biweeks. In total, 131 spatial clusters (partially shown in Supplementary Figure S4) were identified with a total intra-cluster variance equal to 732 km. Among these clusters, 2 had a sample size >200, 1 of 191, 7 between 50 and 100, 10 between 10 and 50, and 121 smaller than 10. There are 83 clusters with just one sampling location (mostly from routine AQS monitoring stations in suburban and rural areas). Based on the results of spatial clustering, temporal clustering was in turn conducted (mainly for the samples from the field campaigns, concentrated in two periods for UCI and UCLA, and in three periods for USC). In total, we extracted 157 spatiotemporal clusters (Figure 2-b and c for statistics). Since the samples within each spatiotemporal cluster needed to be excluded at least once from the training dataset of a base model in our framework, we needed at least 157 base models to be trained given 157 clusters extracted. We selected 157 as the number of base models based on sensitivity test that showed little improvement for more models.

4.3. Grid search results for temporal basis functions and aggregate distance of Thiessen polygons

4.3.1. Overall results

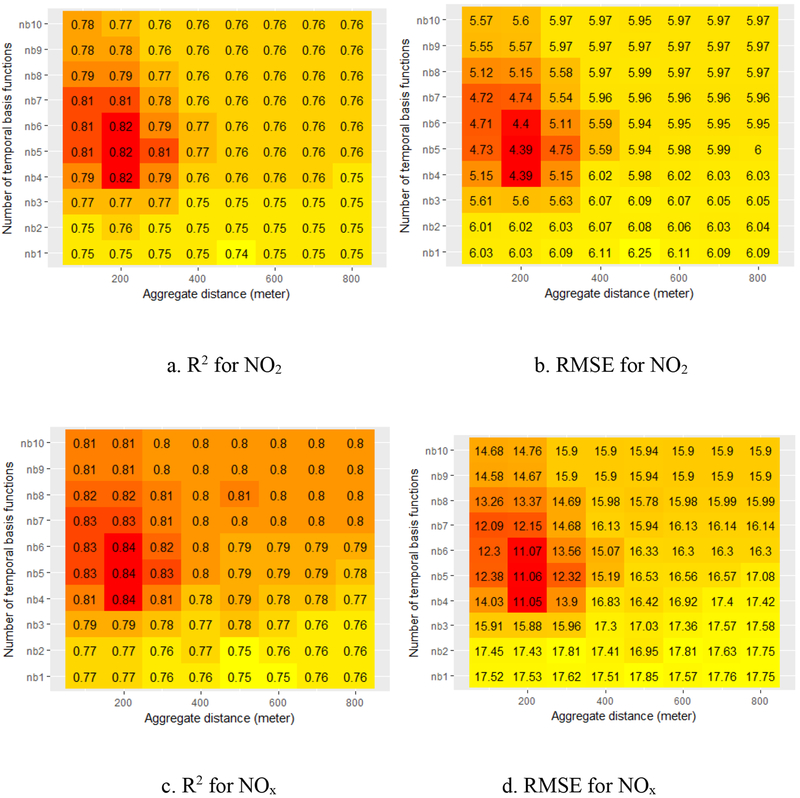
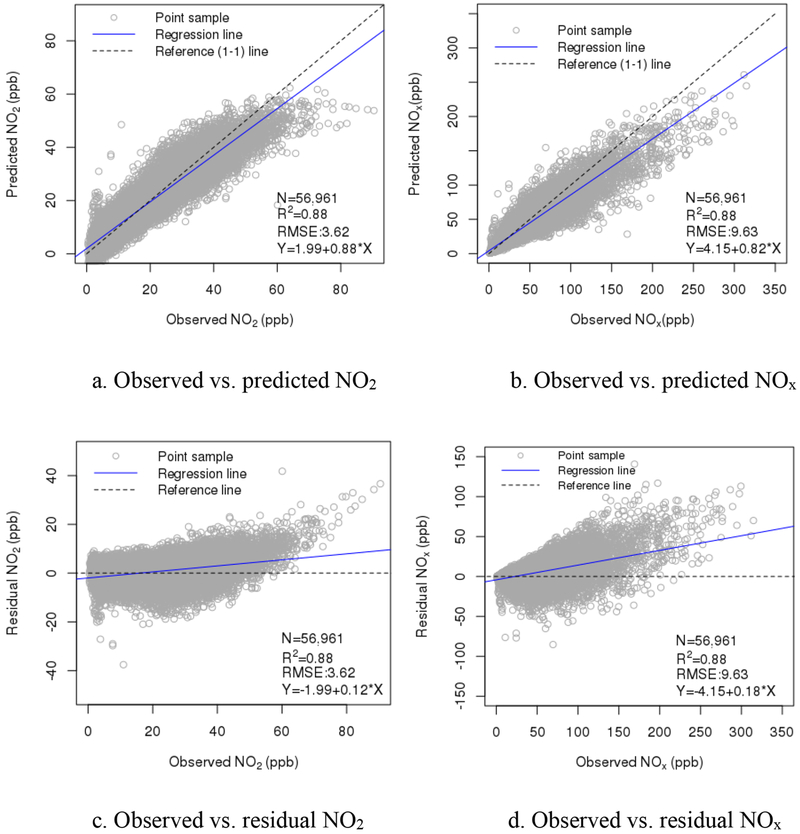
By grid search we obtained an optimal solution, which included an interaction of 4–6 temporal basis functions with a spatial effect at an aggregate distance of 200 m [Figure 4 summarizing model performance as a function of the input superparameters (number of temporal basis functions vs. choice of aggregation distance in constructing spatial effects)]. For computing efficiency and to minimize overfitting, we used 4 temporal basis functions in the final models. For this optimal solution, the ensemble cross validation resulted in an CV R² of 0.88 for both NO₂ and NO_x with RMSE (RMSEIQR) of 3.62 ppb (0.28) for NO₂ and 9.63 ppb (0.37) for NO_x (Table 2; Figure 5), which is better than our previous southern CA only models. The site-based 10-fold cross validation (Table 3) resulted in a total R² of 0.82 for NO₂ and 0.84 for NO_x with a total RMSE (RMSEIQR) of 4.39 ppb (0.34) for NO₂ and 11.05 ppb (0.43) for NO_x for CA. Table 3 also presents the results for northern (R²: 0.78 for NO₂, 0.80 for NO_x) vs. southern (R²: 0.82 for NO₂, 0.84 for NO_x) CA and the AQS (R²: 0.82 for NO₂, 0.84 for NO_x) vs. non AQS field sampling locations(R²: 0.78 for NO₂, 0.81 for NO_x) (See Supplementary Figure S5 for residual plots). The statistics (Supplementary Table S1) and histograms (Supplementary Figure S6) of the ensemble prediction residuals show a normal distribution with a mean close to 0 and absolute skewness <1. Based on residuals plots (Supplementary Figure S7), we found less than 0.1% samples with extreme values (outliers) of underestimation (for high observed values) or overestimation (for low observed values).

Figure 4.

Variation of the models’ performance (R²: a and c; RMSE: b and d) in grid search with different combinations of the number of temporal basis functions (used to capture regional temporal variability) and aggregate distance for spatial effect modeling (to capture spatial variability at regional level).

Table 2.

Stratified ensemble cross validation statistics

Region	Pollutant	Sample size	CVa R2	CV RMSE	CV RMSEIQR
California	NO2	56,961	0.88	3.62 ppb	0.28
	NOx	56,961	0.88	9.63 ppb	0.37
Northern California AQSb	NO2	21,037	0.84	2.56 ppb	0.29
	NOx	21,037	0.84	7.11 ppb	0.38
Southern California AQS	NO2	33,800	0.88	4.10 ppb	0.25
	NOx	33,800	0.88	10.81 ppb	0.35
AQS	NO2	54,837	0.88	3.59 ppb	0.28
	NOx	54,837	0.88	9.56 ppb	0.37
Non AQS	NO2	2,124	0.77	4.42 ppb	0.29
	NOx	2,124	0.81	10.06 ppb	0.36

Note:

^a.CV: cross validation;

^b.AQS: EPA’s Air Quality System archive of quality-assured routinely collected measurement data.

Figure 5.

Plots of the observed vs. predicted NO₂ (a) and NO_x (b) as well as the residual plots of NO₂ (c) and NO_x (d) by the ensemble validation

Table 3.

Site- and region- based 10-fold cross validation statistics

Region	Pollutant	Sample size	CVa R2	CV RMSE	CV RMSEIQR
California	NO2	56,961	0.82	4.39 ppb	0.34
	NOx	56,961	0.84	11.05 ppb	0.43
Northern California AQSb	NO2	21,037	0.78	3.08 ppb	0.36
	NOx	21,037	0.80	8.01 ppb	0.42
Southern California AQS	NO2	33,800	0.82	5.04 ppb	0.31
	NOx	33,800	0.84	12.62 ppb	0.40
AQS	NO2	54,837	0.82	3.39 ppb	0.27
	NOx	54,837	0.84	11. 09 ppb	0.43
Non AQS	NO2	2,124	0.78	4.31 ppb	0.28
	NOx	2,124	0.81	10.34 ppb	0.37

Note:

^a.CV: cross validation;

^b.AQS: EPA’s Air Quality System archive of quality-assured routinely collected measurement data.

When comparing northern and southern California, the latter had higher variance of concentrations (Table 1) and a higher proportion of the training samples. This was beneficial for learning the parameters since more samples from higher variable regions like southern California could help train the models to better capture such variability. Further, our results showed better predictions for southern California (R²: 0.88, RMSEIQR: 0.25–0.35) than northern California (R²: 0.84, RMSEIQR: 0.29–0.38) even though northern California had lower absolute RMSE (2.56–7.11 ppb vs. 4.10–10.81 ppb). In addition, the small difference (0.04 for R² and 0.03–0.04 for RMSEIQR) in ensemble cross validation between northern and southern California demonstrated that our models worked similarly well in both regions.

4.3.2. Temporal basis functions

Temporal basis functions were compared separately for urban vs. rural sites (Supplementary Figure S8: a–d), southern vs. northern CA (Supplementary Figure S9 and S10), and southern and northern CA vs. the whole CA (Supplementary Figure S8: e–h). The first four temporal basis function patterns were compared in Supplementary Figure S11. For the first temporal basis function, the rural and urban sites showed similar patterns with small differences. The second basis function for the rural sites appeared more irregular, potentially due to random fluctuations caused by the smaller sample size in rural areas. Similarly, the patterns captured by the first temporal basis function were similar between northern and southern California, but the second basis function was quite different. Likewise, the third basis functions showed similar seasonal patterns across regions, while the fourth basis function is more erratic and different across regions.

4.3.3. Thiessen polygons for spatial effects

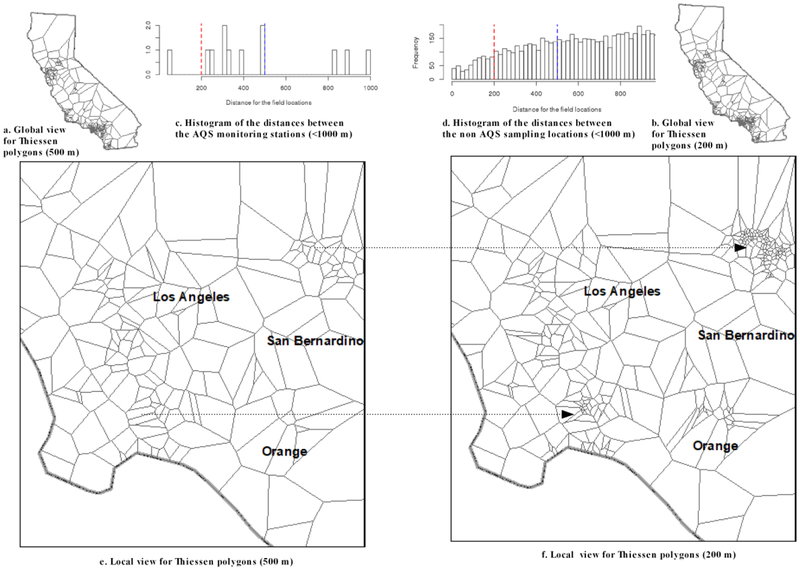
As an indicator for the spatial resolution of Thiessen polygons and the scale of spatial effects, the aggregate distance (100 m to 800 m) showed little impact on the routine AQS monitoring locations since most of these locations were sparsely distributed (Supplementary Figure S12). For the purpose of illustration, Figure 6 displays the enlarged Thiessen polygons for two typical aggregate distances: one for the optimal solution: 200 meters; the other for a coarse resolution: 500 meters. An aggregate distance of 200 m generated smaller polygons on the dense non-AQS field sampling locations, which were highly clustered, compared to an aggregate distance of 500 m (Figure 6 c vs. d; Supplementary Figures S3 and S12). The differences at the local scale were apparent in zoomed maps of the Thiessen polygons for the aggregate distances of 500 m vs. 200 (Figure 6 e vs. f). The increase in the number of Thiessen polygons had the most influence on the sub-regions where the dense field sampling campaigns were located. The total configuration of the polygons was relatively stable with micro-scale changes in highly clustered regions (Figure 6). Our results also illustrate this, with larger R² for highly clustered field samples while the total R² almost did not change. We also found that the extreme case of one Thiessen polygon per sampling point (roughly an aggregate distance of 50 m) resulted in over-fitting, lowering the model performance for the field locations in the ensemble cross validation by 3–4% in R².

Figure 6.

Thiessen polygons by aggregate distances of 500 m (a, e) vs. 200 m (b, f), and histograms of the distances between the AQS (c) and non AQS (d) locations for California

4.4. Simulation of time series by constrained optimization

We applied the location- and time- specific point estimates of ensemble predictions with constrained optimization [29] to derive complete time series for a target location. The validation and independent test results of the AQS monitoring locations showed that the simulated series captured the temporal trends of the concentrations well: the mean (0.92 for NO₂; 0.95 for NO_x) and median (0.93 for NO₂; 0.96 for NO_x). Pearson’s correlations between the estimated and simulated concentrations (Supplementary Figure S13) were high. Figure 7 represents the simulated time series of NO₂ and NO_x for the four representative routine AQS monitoring locations (flagged as a-d in Figure 1). For the purpose of comparison, Supplementary Figure S14 shows the simulated time series of NO₂ and NO_x for two other AQS locations with lower correlations of simulated to observed values. The comparison with the observed values showed that the simulated concentrations captured the seasonal and long-term time trends of NO₂ and NO_x well. For the field sample locations, the total correlations ranged from 0.70 to 0.95 (NO₂) and 0.88 to 0.97 (NO_x) with means of 0.90 (NO₂) and 0.95 (NO_x).

4.5. Independent tests

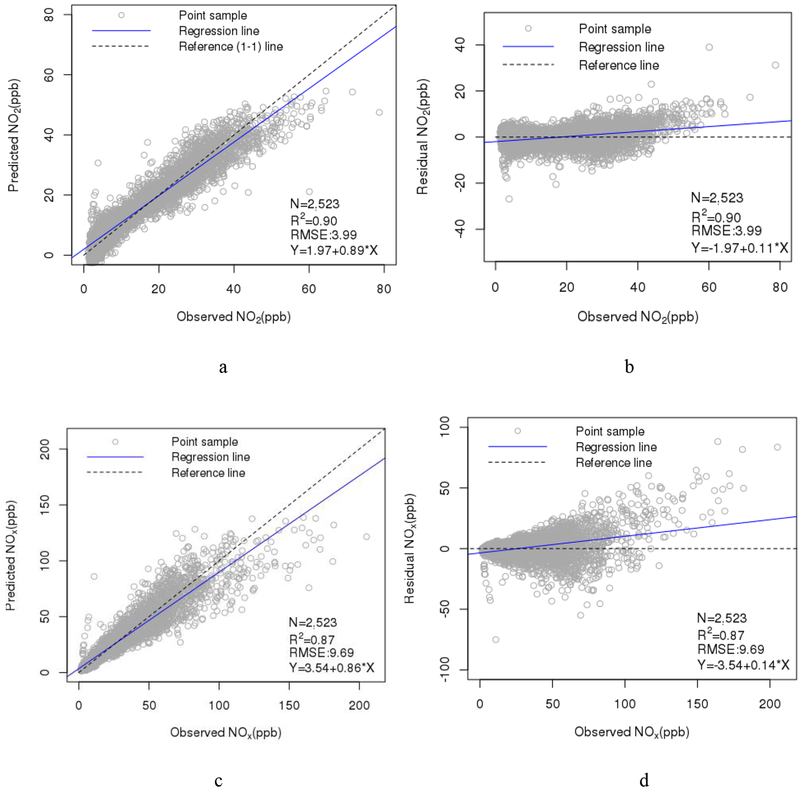
Our models achieved an R² of 0.90 (NO₂) and 0.87 (NO_x), and RMSE (RMSEIQR) of 3.97 ppb (0.21) for NO₂ and 9.69 ppb (0.27) for NO_x in the independent test of random sampling. The scatters of the observed vs. predicted and residual concentrations are shown in Figure 8. These results are more accurate (R²) than our previously published independent test results. We also computed R² and RMSE for the samples of each spatial cluster in the independent test (Supplementary Figure S15). The results showed that at some locations there was low R² but most of their RMSEs were not high. There is a slight difference in R² between the ensemble training (R²: 0.88) and independent test results (R²: 0.87–0.90), also illustrating no or very slight over-fitting of our models in prediction.

Figure 8.

Plots of the observed vs. predicted (a and c) and residual (b and d) NO₂ and NO_x for the independent tests

The independent test of the UCI samples showed our models were able to capture the observed NO₂ (correlation: 0.85; RMSE: 4.8 ppb; RMSEIQR: 0.36) and NO_x (correlation: 0.83; RMSE 13.15 ppb; RMSEIQR: 0.41) even with the test samples not from the population of the training samples.

5. Discussion

For accurate estimation of NO₂ and NO_x concentrations at high resolution in large geographic regions, fusing samples from multiple sources can generate broader spatial and temporal coverage of samples, but highly clustered samples from multiple field campaigns and their inherent heterogeneity creates a challenge for their combined use. In this study, we developed a clustering-enhanced ensemble machine learning approach to obtain high-resolution predictions of NO₂ and NO_x concentration over a large region such as California. The results show that we can achieve state-of-the-art accuracy (CV R²: 0.88; independent test R²: 0.87–0.90). To deal with the challenge of fusing sparsely distributed routine samples and highly spatiotemporal clustered field samples from multiple sources within a single model, cluster-based bagging decreased the correlation between different training models as well as the overall expected squared errors in ensemble predictions. Furthermore, grid search enabled us to find the optimal combination of temporal basis functions and scale of spatial effects, together with other spatial and spatiotemporal covariates. This improved the generalizability of the mixed-effects models by capturing spatiotemporal variability of concentrations at both the regional and local scales. In independent tests of random sampling we obtained similar results as with the ensemble CV, illustrating minimal over-fitting and bias in our models and highlighting the advantages of our method over other methods of NO₂ and NO_x prediction.

Although our approach achieved R² of 0.87–0.90 in ensemble cross validation and independent test of random sampling, we did observe slight over-estimation of low values and under- estimation of high values (as shown in Figure 5-c and d), even though the proportion of such errors is very small. A further check showed abnormally low or high values in some covariates for these samples (e.g. low traffic density for high observed NO₂ and NO_x concentrations and vice versa) , which inhibited the models from estimating concentrations well in these scenarios. Despite our attempt to use high quality covariate data, these covariate datasets are subject to different level of uncertainties, which result in uncertainties in model estimates, especially for extreme values. The machine learning regression models like ours aim to predict expected values rather than precisely observed values, which may fluctuate substantially from short-term perturbation of local meteorology and emission sources that cannot be captured by available data. Thus there are always differences between observed and expected values, and such differences are particularly evident at very low and very high observed values, due to a common limitation of statistical models that rely on the covariates values averaged over two week or even longer time period (e.g. traffic) therefore unable to capture short-term extreme values well. In our study, a small number of outliers with over-estimation of low values and under-estimation of high values have little impact on the overall model performance [43, 44].

While ensemble machine learning like bootstrap aggregating has been used to reduce the errors in individual models, simple random sampling does not deal appropriately with highly clustered samples without biasing training samples and may result in correlated base models. The n-K-m cluster-based bagging approach developed in this study is an example of how unbiased clustered samples can improve the training by stratification and exclusion, boost the power of regression models and reduce potential for over-fitting [30, 31]. Less correlated base models can reduce the squared error of the ensemble predictions. This approach is easy to implement and effective. Sensitivity analysis shows an improvement of about 5% in R² over regular bagging.

Furthermore, heterogeneity in the samples between different sub-regions might create the difficulty of generalizing sub-regional models over a diverse domain due to changes in the application assumptions inherent in the models trained. Two national PM_2.5 models [27, 28] also demonstrated the difference in accuracy between at national and sub-regional levels. Adjustment for existing covariates or addition of new covariates that reflect regional characteristics may be useful to account for variability of NO₂ and NO_x at large regional levels. For our case study in California, extracting more temporal basis functions better accounted for temporal variability in concentrations at the state level, and incorporating small-scale spatial effects in the distribution of Thiessen polygons improved the performance for sub-regions. For the purpose of illustrating improvement in the models’ performance, we compared the performance of our new statewide models with the southern California models [29] using the site-based 10-fold cross validation (Supplementary Table S2) even though the 2017 models were developed for southern California and a direct comparison may not be appropriate. Performance was in general higher (with about 5% increase in R² for both NO₂ and NO_x) for our statewide models than for the southern California models (R² 0.82–0.84 vs. 0.77–0.79). In site-based cross validation for southern California, our statewide models showed notable improvements of about 16% for NO₂ and 10% for NO_x compared with the southern California only models (0.82–0.84 vs. 0.66–0.74 in R²). For other regions such as northern California and field locations, our method performed either similarly or better than the southern California models. This comparison demonstrates the importance of combining sufficient regional temporal variability with finer-scale spatial effects to generalize spatiotemporal mixed-effects models for large regions, as well as other spatiotemporal covariates and cluster-based bagging. Subsequently, with the high-accuracy point estimates of NO₂ and NO_x available, the time series simulated by constrained optimization presented strong correlation (mean range: 0.92–0.96) with the observed series in validation and independent test. Constrained optimization has the advantage of capturing the whole temporal profile within a target location even without a complete set of covariates at all the time slices. But due to the use of temporal smoothing regression by temporal basis function [29], constrained optimization may not capture very high or very low concentrations well (Figure 7). Compared with the constrained optimization simulated values, ensemble point estimates had much less under-prediction.

We employed the machine learning technique of grid search to obtain an optimal solution for the interaction of temporal basis functions and the scale of spatial effects. The optimal solution was successful in preserving and improving model performance not only in the total region but also in the sub-regions. Although grid search showed limited improvement in model performance with fine-scale spatial effects and more temporal basis function respectively, their combined impact boosted R² by about 5% (10–16% in site-based 10 fold cross validation of the sub-region, southern California). The interaction of temporal and spatial variability factors helped our statewide models to better capture spatiotemporal variability of NO₂ and NO_x concentration for both the whole region and for sub regions. As a way of hyperparameter optimization, grid search is an exhaustive searching with high time complexity in comparison with local optimization methods such as random search and gradient descent, and global optimization methods such as Bayesian optimization and evolutionary algorithms [45]. Local optimization methods may obtain sub-optimal solutions with lower time complexity and the Bayesian method may need a priori knowledge to feed its probability models. In our case study, given limited search space (80 combinations in Figure 4) and a priori knowledge, grid search is a practical method to find a global optimal solution.

As a semi-parametric approach, temporal basis functions are widely used to describe the leading modes of variability of air pollutants in the space-time process for a region where the samples are obtained at representative sites [17]. In our study, the first temporal basis function seemed quite similar with small difference between urban vs. rural samples, or southern vs. northern California, or for NO₂ vs. NO_x. This is illustrated by the common dominant seasonal trends for different regions or related pollutants. But the second temporal basis function varied between rural vs. urban locations, and between southern vs. northern California or for NO₂ and NO_x. This component indicates regional or pollutant emission differences. The urban vs. rural source difference may be reflected in the second temporal function. The second temporal basis function seemed quite similar for southern and northern California, and for NO₂ and NO_x with a small shift. This might indicate a temporal lag effect in season transitions or other factors from one region to the other region (southern vs. northern California) such as the atmospheric chemistry. The third temporal basis function, somehow similar to the first one but probably driven by different factors, was similar for NO₂ vs. NO_x, and southern vs. northern California. The fourth and higher level temporal basis functions displayed more random fluctuation. Our analysis showed that the first four to six temporal basis functions mostly contributed to the model performance while inclusion of more than six temporal basis functions did not enhance model performance. In other applications, more temporal basis functions may need to be considered if there are sufficient representative measurement samples available and the study region is larger [17].

In terms of implementation, the new approach proposed in this paper involves extra computing mainly for spatiotemporal clustering, cluster-based bagging and grid search. We believe these are significant improvements over our earlier work since they establish a more objective, machine learning based framework to guide the selection of model inputs and parameters (compared to relying on somewhat subjective decisions we often have to make in exposure modeling). Spatiotemporal clustering has the added time complexity of K-Means and Kruskal [33]. Since sampling locations for air pollutant monitoring are generally limited, such complexity is easy to accomplish (less than one hour for the 1511 sampling locations of our case study). Compared with our original approach [29], the clustering-based bagging doubles the time of ensemble learning. The grid search of 80 different combinations for the optimal solution is the most demanding, requiring 80 times longer than the original ensemble learning time. However, with modern techniques of parallel computing [46, 47], the time increase is not an issue. With the computing configuration of Intel (R) Xeon(R) 16 CPUs (E5530, 2.4G) and 64G memory, it took less than two months for us to finish grid search and cluster-based bagging. High performance computing could further reduce the computing time.

This study has the following limitations. First, there is a big difference in the size of the samples based on biweekly averages between routine AQS data and field campaign data. The dominant routine AQS monitoring samples may have a negative influence on the models’ performance on the much less frequent non-AQS field samples. However, incorporation of fine-scale spatial effects in the models limited this influence as shown in our site-based cross validation and the independent test (small difference in R² for the field campaign samples). Second, we are aware that the NO₂/NO_x monitoring network has an urban focus due to its use for the U.S. National Ambient Air Quality Standards compliance assessment and this network underrepresents the large rural areas in the domain. The limited accuracy of model estimates in rural areas could be improved in future work by incorporating satellite data and chemical transport model output like CMAQ that provide concentration estimates across the large rural areas. Third, coordinates were used as the input factors for clustering at geographical scale. Geographical heterogeneity in many factors is closely associated with geographical coordinates that can reflect their difference at geographical scale. In the future, we may consider incorporating other factors including population and meteorology that may also affect heterogeneity of the clustered samples. Fourth, the uneven distribution of sampling locations might make spatial effects work better for locations with a higher density of sample locations. However, our results suggested little influence of uneven spatial effect on total model performance. With more field or routine samples becoming available, spatial effects can be updated at a spatially more even scale and this might further improve the models. Fifth, this case study is confined to California and the calendar years 1992–2013, but our approach can be also generalized to other air pollutants and large regions.

6. Conclusion

In this paper, we developed a machine learning approach for cluster-based bagging of constrained mixed-effects models to accurately estimate NO₂ and NO_x concentrations over a large region at high spatiotemporal resolution. Given the inherent heterogeneity in the data samples from different sources, an optimal clustering method was designed to extract spatiotemporal clusters used to stratify the samples to reduce sampling bias and boost bagging to improve generalization in predictions. In single base mixed-effects models, spatial variability was captured by spatiotemporal covariates and spatial effects of Thiessen polygons, and regional temporal variability was captured by temporal basis functions. For the superparameters of the number of temporal basis functions and the scale (aggregate distance) of spatial effects, grid search was employed to find the optimal interaction for both. In the case study of NO₂ and NO_x spatiotemporal estimation of 22 years in California, our approach achieved state-of-the-art accuracy in cross validation (R²: 0.88; RMSE: 3.62–9.63 ppb) and independent tests of random sampling (R²: 0.87–0.90; RMSE: 3.97–9.69 ppb). The small difference between cross validation and independent tests demonstrates robust generalization of our approach for estimation of NO₂ and NO_x at high spatiotemporal resolutions. Our study has important implication for improvement in accurate exposure estimation of NO₂ and NO_x and consequently evaluation of their health effects, particularly with respect with short-term or acute outcomes.

Highlights.

• Challenge of fusing multi-source and heterogeneous data for NO_x estimation in large regions.

• Cluster-based bagging to reduce bias in training samples and errors in prediction.

• Grid search to find optimal combination of parameters with best model performance.

• High spatiotemporal resolution NO₂ and NO_x estimation with high accuracy.

• Robust model generalization based on independent tests.