Shape-based Three-dimensional Body Composition Extrapolation Using Multimodality Registration

Abstract

The ubiquity of commodity-level optical scan devices and reconstruction technologies has enabled the general public to monitor their body shape related health status anywhere, anytime, without assistance from professionals. Commercial optical body scan systems extract anthropometries from the virtual body shapes, from which body compositions are estimated. However, in most cases, these estimations are limited to the quantity of fat in the whole body instead of a fine-granularity voxel-level fat distribution estimation. To bridge the gap between the 3D body shape and fine-granularity voxel-level fat distribution, we present an innovative shape-based voxel-level body composition extrapolation method using multimodality registration. First, we optimize shape compliance between a generic body composition template and the 3D body shape. Then, we optimize data compliance between the shape-optimized body composition template and a body composition reference from the DXA pixel-level body composition assessment. We evaluate the performance of our method with different subjects. On average, the Root Mean Square Error (RMSE) of our body composition extrapolation is 1.19%, and the R-squared value between our estimation and the ground truth is 0.985. The experimental result shows that our algorithm can robustly estimate voxel-level body composition for 3D body shapes with a high degree of accuracy.

1. INTRODUCTION

The ubiquity of optical body scan systems has enabled large-scale automatic digitalized anthropometry data collection for research institutes as well as daily fitness tracking for the general public. High-end 3D body scanners, such as 3dMDbody^®,1 [TC]^2®,2 and TELMAT SYMC-AD^®,3 based on high-end optical sensors and sophisticated calibration^4,5 reconstruct sub-millimeter level highly accurate 3D human body shapes. This type of body scanner has been widely used in digitalized anthropometry surveys with large population cohorts.^6–13 Light-weight consumer-level sensor based optical body scanners such as Fit3D^®,14 Styku^®,15 and ShapeScale^®16 scan and reconstruct 3D body shapes from a static pose based on KinectFusion¹⁷ algorithm. This type of body scanner is typically used by people in the gym or at home to track body shape changes over time. Non-rigid registration based body surface scan and reconstruction systems such as Cui et al.,¹⁸ Li et al.,¹⁹ Dou et al.,²⁰ and Lu et al.²¹ have enhanced the system flexibility by eliminating the need for auxiliary equipment, such as turntable, and arm supporters, which enables users to rotate freely during scan. Full circumference multiple RGB-D sensor systems have also been proposed for 3D body surface reconstruction by Dou et al.²² and Li et al.²³

Large-scale body shape datasets have made it possible to parameterize human body shape space using statistical models. Principal Component Analysis (PCA) has been widely explored for shape parameterization.^8,24–26 Body shape variations associated with phenotypes like Body Mass Index (BMI), weight and age have been modeled in the work of Allen et al.²⁴ and Park et al.^8,27 Digital anthropometries, as summarizations of 3D body shape characteristics, have been explored by Löffler et al. to cluster different body types in a large population cohort.²⁸ Beyond the traditional anthropometries derived directly from 3D body shape geometries, Lu et al.²⁹ proposed utilizing high-order shape descriptors, such as surface curvature, for body type classification.

Studies investigating the linkage between 3D body shapes and the underlying health data, such as body fat percentage or fine-granularity fat distribution, are rare since medical-level body composition assessment equipment, such as the BOD POD, Dual-energy X-ray Absorptiometry (DXA), Magnetic Resonance Imaging (MRI) or Computed Tomography (CT), is not readily available for large-scale data collection. Ng et al.³⁰ studied the relationship between anthropometry features and body fat percentage. Lu et al.²⁹ explored body shape geometry features in multiple levels for body fat percentage prediction. Lu et al.²¹ and Piel³¹ further proposed to infer pixel-level DXA-like body composition based on 3D geometry data.

In this work, we propose a highly innovative shape-based 3D voxel-level body composition extrapolation model (Fig. 1-d) using multimodality registration based on 3D body shape (Fig. 1-c) derived from a commodity-level optical body scan system,²¹ 2D pixel-level body composition reference (Fig. 1-a) derived from DXA body composition assessment, and a generic 3D body composition template with anatomically accurate human skin, muscle and skeleton system (Fig. 1-b). The 3D body shape can be viewed as a boundary constraint for 3D body composition extrapolation, but no information beneath the surface is provided. DXA generates pixel-specific fat distribution and is considered a gold standard for body composition assessment. However, DXA imaging encodes body composition into a 2D orthogonal projection of the subject, and thus, loses information along the depth direction. In other words, we cannot generate a 3D body composition directly based on the fat distribution provided by the DXA and the boundary constraint provided by the 3D body shape due to a lack of shape prior knowledge of the body composition structure in 3D. Therefore, we introduce a generic body composition template as the shape prior.

Figure 1.

Schematic of multimodality registration for 3D body composition extrapolation.

2. METHOD

Our voxel-level body composition extrapolation framework (Fig. 2) consists of two steps. First, we register the 3D generic body composition template to 3D body shapes for shape compliance optimization. We propose a three-fold method to gradually refine the shape registration condition. In gender-specific body composition initialization, we specify the 3D body composition template for different genders. In conditional anthropometries transfer, we conditionally pre-adjust the template surface layer according to the 3D body shape anthropometries. This step is critical for the obese since the amount of subcutaneous fat tends to be much higher than the gender-specific body composition template. Directly optimizing the shape compliance can lead to muscle over-stretching. In 3D-3D body composition template registration, we register the initialized 3D body composition template to the 3D body shape to optimize the shape compliance. Second, we optimize data compliance between the shape-optimized template and the 2D pixel-level body composition reference from DXA imaging. We parameterize the deformation of the muscle layer, and then seek the optimal set of deformation parameters that align local fat distributions in 3D to the local fat distributions assessed by the DXA (3D-2D data compliance optimization).

Figure 2.

3D body composition extrapolation pipeline.

2.1. Shape compliance optimization

2.1.1. Gender-specific body composition initialization

To facilitate shape compliance optimization, we create gender-specific body composition templates for males and females. For each gender, we calculate an average lean body shape. We register the surface layer using non-rigid ICP²¹ to each 3D body shape whose body density is larger than a lean density threshold. We set the threshold to 1.05 kg/L for females, which corresponds to the body fat percentage of 21.4%, and 1.07 kg/L for males, which corresponds to the body fat percentage of 12.6% according to the Siri Equation.³² We consider the body fat percentage of 21.4% for females and 12.6% for males are reasonable thresholds for lean body shapes selection. We calculate an average shape of the registered surface layers as the gender-specific average lean body shape. The next step is to deform body composition template inner layers (fascia, muscle, skeleton) using linear subspace deformation model³³ according to the gender-specific body shape. We generate the tetrahedral mesh³⁴ from the surface layer to define a deformation space. We register inner layers of the body composition template into this space using barycentric coordinates. We deform the tetrahedral mesh towards the average lean body shape using the linear subspace deformation, treating surface layer correspondences as boundary conditions. The inner body compositions are then deformed accordingly. The female gender-specific body composition template is shown in Fig. 3. We define an abstract skeletal structure Fig. 3-(a) based on the gender-specific body composition template for further shape registrations.

Figure 3.

The gender-specific body composition template of females. (a) The skeleton system and abstract skeletal structure. (b) The muscle system. (c) The fascia layer. (d) The skin layer.

2.1.2. Conditional anthropometries transfer

To achieve a better initial condition for shape compliance optimization, we propose to conditionally deform template skin layers according to anthropometries extracted from 3D body shapes. We have defined the template abstract skeletal structure in Fig. 3-(a). Correspondingly, we define the abstract skeletal structure on the 3D body shape with heuristically estimated skeletal joints. We sample level circumferences along each bone direction of the abstract skeletal structure (Fig. 3-(a) cyan). We grow the skin layer regionally using skeletal B-spline skinning if the local level circumference on the template is smaller than the one on the 3D body shape. In the B-spline skinning deformation model, we paint skinning weights of the bones on the surface mesh. We set up multiple key points along each bone to parameterize the surface morph. Each key point is associated with an in-plane scale factor to grow or shrink the surface on its planar direction orthogonal to the bone. In between control points, the in-plane scale factor is interpolated using B-spline interpolation. This step is critical to prevent muscle over-stretching during shape compliance optimization, especially for the obese. Fig. 4 shows examples of the conditional anthropometries transfer of the skin layers, compared with the corresponding 3D body shapes.

Figure 4.

The 3D body shapes (a, c) and corresponding measurements-transferred skin layers (b, d).

2.1.3. 3D-3D body composition template registration

We have a relatively good initial condition for shape compliance optimization after first generating a gender-specific body composition template and then conditionally transferring anthropometries to the gender-specific template skin layer. We recalculate the tetrahedral mesh under the surface layer after the anthropometries transfer and update the braycentric coordinates for the body composition template inner layers accordingly. To optimize the shape compliance, we first register the template surface layer to the 3D body shape uisng non-rigid ICP.²¹ Then, we deform the tetrahedral mesh accordingly using linear subspace deformation,³³ treating the surface layer correspondences as boundary conditions. Body composition template inner layers are then deformed with the new barycentric coordinates calculated inside the new tetrahedral mesh.

2.2. 3D-2D data compliance optimization

So far, we have registered the 3D body composition template into a specific 3D body shape by minimizing the shape compliance error. However, fat distribution reflected by current 3D body composition template does not agree with the ground truth fat distribution assessed by the DXA. To align the 3D body composition to the DXA imaging, we propose a data compliance optimization. We parameterize local fat distributions in 3D using B-spline skinning deformation model and quantify the ground truth local fat distributions from the DXA imaging. Then, we minimize the data compliance error.

2.2.1. 3D local fat distribution parameterization

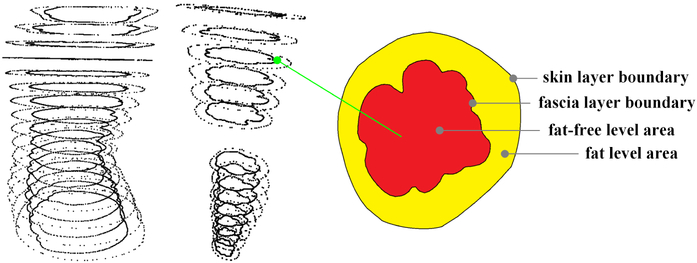
To approximate local fat distributions, we uniformly sample level areas on the fascia layer and 3D body shape (Fig. 5) along the bone direction of the abstract skeletal structure (in Fig. 3-(a) cyan). We approximate each level intersection stack as a right cylinder and the height of each stack is identical because of the uniform sampling. Hence, estimating the stack volume is equivalent to estimating the level area. We denote the fat-free stack volume as $V_{FFM}^l$, which corresponds to the level area of the fascia layer (Fig. 5, area of the red region), and denote the total stack volume as $V^l$, which corresponds to the level area extracted from the 3D body shape (Fig. 5, yellow + red region), where l is the stack sample index. The 3D local fat distribution $Fa{t}_{3D}^l\%$ can be approximated as a function of $V_{FFM}^l$ and V^l, as shown in Eq. (1), where we approximate the fat tissue density as ρFM = 0.9kg / L and the fat-free tissue density as ρFFM = 1.1kg/L.³²

$$Fa{t}_{3D}^l\%=\frac{(V^l-V_{FFM}^l)\times {\rho }_{FM}}{{\rho }_{FM}\times V^l+({\rho }_{FFM}-{\rho }_{FM})\times V_{FFM}^l}$$ (1)

Figure 5.

The mechanism for fat-free volume estimation.

To control 3D local fat distribution $Fa{t}_{3D}^l\%$, we parameterize the deformation of the fascia layer using B-spline skinning. We define multiple control points along each bone with scaling parameter α. Thus, we rewrite the fat-free stack volume as ${\tilde{V}}_{FFM}^l(\alpha )$.

2.2.2. 2D local fat distribution estimation

For each of the 3D local fat distribution parameterized previously, we estimate a corresponding ground truth local fat distribution from the 2D pixel-level body composition assessment of the DXA. First, we register the DXA imaging (Fig. 1-a) to the 2D orthogonal projection of the 3D body shape using free-form deformation²¹ to derive the aligned DXA imaging. Second, we estimate local fat percentage $Fa{t}_{GT}^l\%$ on the aligned DXA imaging corresponding to the local fat distribution in 3D. Third, we convert each local ground truth fat percentage $Fa{t}_{GT}^l\%$ to the target fat-free stack volume ${\widehat{V}}_{FFM}^l$ through Eq. (2).

$${\widehat{V}}_{FFM}^l=\frac{{\rho }_{FM}\times (1-Fa{t}_{GT}^l\%)\times V^l}{Fa{t}_{GT}^l\%\times ({\rho }_{FFM}-{\rho }_{FM})+{\rho }_{FM}}$$ (2)

2.2.3. Data compliance optimization

We formulate the objective function as Eq. (3) to minimize data compliance error. We search for deformation parameter α such that the fat-free stack volume ${\tilde{V}}_{FFM}^l(\alpha )$ derived from the morphed fascia layer aligns with the target stack volume ${\widehat{V}}_{FFM}^l$ estimated by the ground truth local fat distribution derived from the DXA imaging.

$$\underset{\alpha }{\text{arg min}}\sum _l\Vert {\widehat{V}}_{FFM}^l-{\tilde{V}}_{FFM}^l(\alpha )\Vert$$ (3)

3. RESULTS

To evaluate the performance of our method, we test the method on six different data sets, corresponding to six different subjects. The Body Mass Index (BMI) and Body Fat Percentage (BFP) distributions of the subjects are illustrated in Tab. 1. Each data set contains a 3D body shape derived from the commodity-level optical body scan system by Lu et al.,²¹ and the corresponding pixel-level body composition reference derived from the DXA. The gender-specific body composition template has been generated by registering the 3D body composition template into the average lean body shape. We register the reference image to the 2D orthogonal projection of the 3D body shape to derive the aligned reference image. For implementation detail, we refer to the work of Lu et al.²¹ We define an abstract skeleton system on the 3D body shape, where we drop the value in z-dimension to unify the skeleton systems of the 2D aligned reference image and the 3D body shape. We extract local fat percentages $Fa{t}_{GT}^l\%$ from the aligned pixel-level body composition reference image. We extract the corresponding level total stack volumes V^l from the 3D body shape. We take 9 key points per bone (Fig. 3-(a) cyan) for local fat estimation and B-spline skinning. We calculate the target fat-free level stack volumes ${\widehat{V}}_{FFM}^l$ through Eq. (2). We search for the deformation parameter α such that level stack volumes of the morphed fascia layer ${\tilde{V}}_{FFM}^l(\alpha )$ minimize the data compliance error in Eq. (3). Finally, we deform the muscle system according to the deformation of the fascia layer. The body composition extrapolation results for the six test subjects are illustrated in Fig. 6.

Table 1.

The Body Mass Index (BMI) and Body Fat Percentage (BFP) distributions of the subjects.

	Subject A	Subject B	Subject C	Subject D	Subject E	Subject F
BMI	21.5	28.2	21.9	31.0	29.0	29.9
BFP	24.8%	41.2%	15.1%	42.7%	33.0%	38.1%

Figure 6.

Visualization of 3D body composition extrapolation results.

To evaluate the accuracy of our method, we densely sample the local fat distribution of the extrapolated 3D body composition for each subject with 99 samples on each body part (i.e., the trunk, left leg, right leg). Correspondingly, we calculate the local fat distribution from the aligned pixel-level body composition reference as the ground truth. In Fig. 7, we demonstrate the estimated local fat distribution versus the ground truth fat distribution for each validation sample point. As shown in Tab. 2, the average R-squared value for the different body parts is 0.985, which indicates there is a good agreement between the extrapolated local fat distribution and the ground truth local fat distribution. The average Root Mean Square Error (RMSE) is 1.19% and the average Mean Absolute Error (MAE) is 0.81%, from which we conclude that our 3D body composition extrapolation method has a high degree of accuracy.

Figure 7.

Estimated local fat distribution versus the ground truth fat distribution for the trunk, left leg and right leg.

Table 2.

3D body composition extrapolation accuracy evaluation.

	Trunk	Left Leg	Right Leg	Mean
R-squared	0.981	0.988	0.986	0.985
Root Mean Square Error	1.307%	1.086%	1.189%	1.19%
Mean Absolute Error	0.853%	0.799%	0.792%	0.81%

4. CONCLUSIONS

We present an innovative method to extrapolate 3D voxel-level body composition with a high degree of accuracy based on the 3D body shape and 2D pixel-level body composition reference. Our work provides a practical solution to assess the voxel-level body composition, which would typically be generated with CT or MRI, using easy-to-access, cost-effective equipment such as the Kinect. The work of Lu et al.²¹ has shown the feasibility of predicting the DXA-like 2D pixel-level body composition image based on the 3D body shape. Therefore, our method can be totally DXA independent by adopting the inferred 2D pixel-level body composition. There are several limitations of our work that provide opportunities for further research. First, the 3D body composition template is generated by the artist modeling rather than by the real data derived from the CT or MRI scans. Second, there are small artifacts during registration such as the mesh penetration among different body compositions. Third, we do not model the visceral fat distribution in our 3D body composition extrapolation method. Quantifying and locating the visceral adipose tissue are extremely important since this type of fat has been considered a significant factor for the etiology of various metabolic and cardiovascular diseases.