3D Shape-based Body Composition Prediction Model Using Machine Learning

Abstract

A booming development of 3D body scan and modeling technologies has facilitated large-scale anthropometric data collections for biomedical research and applications. However, usages of the digitalized human body shape data are relatively limited due to a lack of corresponding medical data to establish correlations between body shapes and underlying health information, such as the Body Fat Percentage (BFP). We present a novel prediction model to estimate the BFP by analyzing 3D body shapes. We introduce the concept of “visual cue” by analyzing the second-order shape descriptors. We first establish our baseline regression model for feature selection of the zeroth-order shape descriptors. Then, we use the visual cue as a shape-prior to improve the baseline prediction. In our study, we take the Dual-energy X-ray Absorptiometry (DXA) BFP measure as the ground truth for model training and evaluation. DXA is considered the “gold standard” in body composition assessment. We compare our results with the clinical BFP estimation instrument—the BOD POD. The result shows that our prediction model, on the average, outperforms the BOD POD by 20.28% in prediction accuracy.

I. Introduction

The prevalence of 3D scan technologies has brought endless opportunities for biomedical researchers to conduct experiments that were previously impossible and to develop novel applications that are more accurate, cost-effective, and suitable for everyday use. In recent years, many large-scale anthropometric data collections have been conducted worldwide using state-of-the-art body scanners. For instance, the Civilian American and European Surface Anthropometry Resource Project (CAESAR^®)[1] used Cyberware^®, a laser-based 3D body scan system to create a database with 4800 subjects from the United States and Europe aged between 18-65. Allen et al. proposed to analyze the variation of 3D body shapes in large-scale shape database using Principal Component Analysis (PCA)[2]. Löffler-Wirth et al. proposed using the Self-Organizing Maps (SOM) to classify body types in 3D body shape database of residents living in Leipzig, Germany[3]. However, the analyses based purely on 3D body shapes are limited, especially for biomedical studies, since there is no link between the characteristics of shapes to the corresponding underlying body parameters of clinical interest. In our study, we explore correlations between 3D body shapes and the Body Fat Percentage (BFP), and develop our prediction model based on such correlations.

Early on, body composition researchers found that BFP has a strong correlation to body density. The Siri equation[4], derived from anatomical experiments, has been widely used to map body density to BFP. Along with this line of research, various methods have been proposed to estimate the human body volume. The most commonly used approach early on was hydrostatic weighing, which computes the body volume underwater based on Archimedes’ Principle[5]. However, this method is difficult to apply in clinical practice. The hydrostatic weighing method has been replaced by whole-body air displacement plethysmography (the BOD POD) since the end of the last century, which exploits the relationship between air pressure and volume to derive the body volume[5]. The current gold standard body composition assessment is Dual-energy X-ray Absorptiometry (DXA) scanning[6] which uses low dose X-ray to discriminate among bone, muscle, and fat content of the body. However, both BOD POD and DXA suffer from the drawbacks of the prohibitive cost, immobility of the equipment, and requiring professional operators. A number of studies in clinical nutrition have investigated the correlation between 3D body shapes and body compositions[7][8], but their scope is limited by using 3D body scans merely as a tool to automatically extract anatomical measurements, such as waist and hip circumferences. In contrast, we propose to explore the shape features using the full 3D geometry comprehensively without any presuppositions. Our goal is to elegantly integrate the most effective shape descriptors into one prediction model. To the best of our knowledge, this is the first attempt to model the BFP prediction using 3D body shapes problem in a machine learning framework. We emphasize the utilization of shape descriptors at multiple levels, derived from 3D geometry, to reach a high-level understanding of the body shapes. Our prediction model shows robustness in analyzing 3D body shapes reconstructed by commodity-level body scan system[9], which makes our system more compelling for widespread general use.

II. Methods

A. Feature Extraction

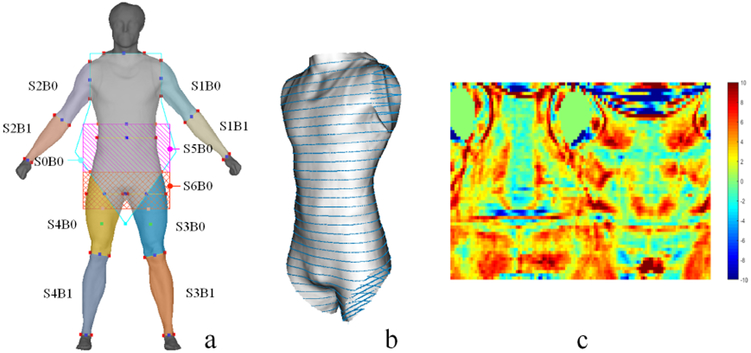
We define shape descriptors in three levels based on the order of derivations. The zeroth-order shape descriptors derive from the 3D geometry directly, including the circumference (Fig. 1-b), surface area, volume, and volume-to-surface-area ratio. The first-order shape descriptors derive from the first-order derivate of the geometry, namely surface normal. The second-order descriptors derive from the second-order derivate of the geometry, namely curvature (Fig. 1-c). To reduce feature redundancy, we drop the first-order descriptors since the information provided overlaps with the second-order one. In practice, we first automatically segment the 3D body shape into 11 segments as illustrated in Fig. 1-a based on a few anatomical landmarks, and then conduct the feature extraction respectively for each segment.

Fig. 1.

Feature extraction. (a) The 3D body shape and 11 segments. (b) Circumferences extraction on the trunk. (c) The second-order shape descriptors mapped in 2D.

B. Shape-prior Classification

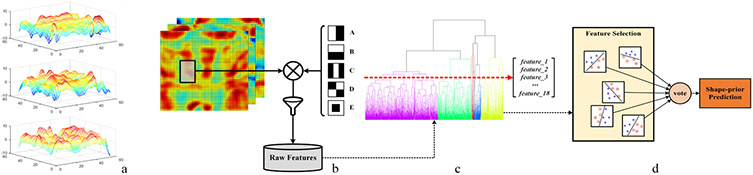
Humans can easily perceive differences between different types of body shapes, such as lean and obese, solely based on a few visual cues, like surface curvature, body proportion, and lateral contour. Here we aim to investigate this phenomenon by modeling different body shapes as a function of the geometry curvature. To be specific, we illustrate our idea in Fig. 2-a, where we compare the surface curvature distribution of three types of body shapes (obese, average, and lean) in the abdomen area. Our goal is to model an accurate classifier that automatically identifies different body shapes based on the distribution of the second-order geometry features. Such prediction will be used as a shape-prior to guide the BFP estimation.

Fig. 2.

Shape-prior classification. (a) A comparison of curvature distribution between three types of body shapes: obese (top), average (middle), and lean (bottom). (b) Raw feature extraction with Haar-like basis functions. (c) Using agglomerative hierarchical clustering to reduce the feature redundancy. (d) Feature selection and model training.

To make the second-order geometry features comparable across samples, we register the 3D body shape into a cylinder system, map the curvature data to the cylinder surface, and then flatten the cylinder into a 2D intensity image, where each pixel intensity corresponds to the assigned curvature value. To make the model concise, we crop the 2D curvature image to keep only the region of interest—the frontal trunk from chest to hip.

We propose a novel approach to discriminate the lean and non-lean curvature mappings using Haar-like basis functions. Our work is inspired by Viola and Jones, who proposed to use Haar-like feature detectors to detect human face by matching the facial patterns to specific Haar-like patterns[10]. We adopt this idea to match lean curvature patterns with Haar-like patterns on the 2D image to classify the body shapes. As illustrated in Fig. 2-b, five different Haar-like basis functions are applied. The integral image[10] is calculated beforehand to facilitate feature extraction. We impose the five types of Haar-like basis functions (Fig. 2-b) on every possible sub-image window to derive the feature values, which results in a highly redundant feature space. We filter out irrelevant features by calculating the approximated training error for each feature with (1) using a randomly selected subset of training samples. L denotes the true labels (lean is 1, non-lean is 0) and γ denotes the feature threshold. Operator ⊕ denotes the bitwise XOR of two vectors and sum denotes the summation of all elements in a vector. ∣a∣ denotes the number of elements in a.

$$\tilde{\epsilon }=\underset{\gamma }{\text{min}}\Phi (1_{>\gamma }(feature),L)$$ (1)

$$\Phi (\mathbf{a},\mathbf{b})=\text{min}\left\{\frac{sum(\mathbf{a}\oplus \mathbf{b})}{\mid \mathbf{a}\mid },1-\frac{sum(\mathbf{a}\oplus \mathbf{b})}{\mid \mathbf{a}\mid }\right\}$$ (2)

After preliminary filtering, we have roughly 1000 raw features left in the feature pool, all of which are relatively strong predictors (i.e., $\tilde{\epsilon }$ < 0.1). However, these features are highly redundant in position and size. Hence, we propose to reduce the locality redundancy using agglomerative hierarchical clustering. We define the feature similarity by the Euclidean distance of two features’ attribute vectors, each of which consists of its position, size, approximated training error and basis function type. We scale the approximated training error by 100 and basis type by 1000 to mitigate the merging of features derived from different basis functions. As illustrated in Fig. 2-c, the branch structures of features derived from five different basis functions, color-coded in five different colors, are preserved during the agglomeration. We set the cutoff threshold to 18 clusters, from which, we select 18 features that are closest to the cluster center as candidates for feature selection.

We conduct feature selection during model training. We consider all possible four-feature-combinations of the 18 candidates and evaluate each combination using the quadratic support vector machine (SVM) classifier (Fig. 2-d). We believe that SVMs are appropriate in our case because the features are strong predictors (i.e., $\tilde{\epsilon }$ < 0.1). The combination of strong predictors tends to result in low training error during feature selection. In most cases, we have multiple feature combinations that yield zero training error. We compare the number of zero training error combinations out of total combinations between three different classifiers: the SVM (88/3060), the k-nearest neighbors (k-NN, 1/3060), and the decision tree (0/3060). We adopt a majority vote mechanism to make the final shape-prior prediction, taking all the predictions from the top-ranking feature combinations into account (Fig. 2-d). While there is a risk of feature subset selection bias with such a large collection of candidate features, we perform rigorous Leave-One-Out-Cross-Validation (LOOCV) to evaluate the generalization error of this approach (see the Results Section for more details).

C. Baseline Regression

Despite the shape-prior classification offering a high-level description of the body shape, it does not explicitly map the shape features to the quantity of fat. We propose to utilize the zeroth-order shape descriptors to train a baseline regression model, which yields a baseline result of the BFP prediction. We extract 47 zeroth-order features from the 3D geometry, including the circumference, surface area, and volume of the trunk; the volume-to-surface-area ratio for each of the 11 segments; and the whole-body volume, surface area, and the ratio. We also extract hip, waist, and abdomen circumferences from the 3D geometry according to their anatomical definitions. In addition to the geometry features, we also introduce three basal features (weight, height, and Body Mass Index (BMI)) into the model. Now we have 50 features in total for the baseline training, and we desire to choose a small subset of the features for the baseline prediction. It is infeasible to enumerate all possible combinations of feature candidates even if we limit the maximum number of features to five. We adopt a forward search algorithm for feature selection during baseline model training, which greedily searches for the one optimal candidate in each iteration, who, combined with the selected features, generates the lowest training error. We adopt Gaussian Process Regression (GPR)[11] with the quadratic kernel as a regressor of our baseline model.

D. Prediction Model: Baseline Regression + Shape-prior

So far, we have two stand-alone prediction models. We use the second-order shape descriptors to classify the body shape into lean and non-lean, which provides an abstract classification of the body shapes. However, the classification is not constructive in quantifying the BFP. We use the zeroth-order shape descriptors (along with the basal features) to generate a baseline BFP. However, the baseline model suffers from overestimating the BFP of the lean subjects since it is difficult to distinguish the body shape types using anthropometric measurements.

$$\underset{\alpha }{\text{min}}{\Sigma }_{{\tilde{Y}}_i⩽\tau }\Vert {\tilde{Y}}_i-Y_i+\alpha \delta ({\widehat{L}}_i){\Vert }_p$$ (3)

$${\widehat{Y}}_{new}={\tilde{Y}}_{new}+\lambda \alpha \delta ({\widehat{L}}_{new})$$ (4)

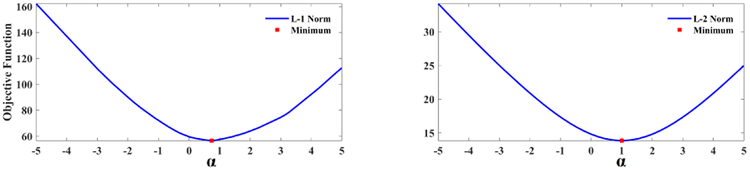
We propose to integrate the shape-prior into the baseline model by parameterizing the discrepancy due to the lack of shape-prior knowledge with a compensation factor a that minimizes the objective function (3). ${\tilde{Y}}_i$ denotes the training prediction, Y_i denotes the ground truth, ${\widehat{L}}_i$ denotes the predicted shape-prior, and δ denotes the function δ(x) = (−1)^x. We set up a threshold τ to rule out irrelevant samples whose predicted BFP is outside of the range of lean bodies. We optimize the objective function with parameter α during model training, where we compare two types of norms: the l₁ norm and the l₂ norm (Fig. 3). Then, we correct the test predictions ${\tilde{Y}}_{new}$ with (4), where λ denotes the learning rate.

Fig. 3.

Plots of minimization with l₁ norm (left) and l₂ norm (right).

III. Results

In this section, we describe the details of our model training and testing experiments and analyze the results. We have conducted rigorous data collection with a sample size of 50 adult males. Such sample size is comparably large in the clinical body composition studies[7][8]. The data collection and study presented in this paper involving human subjects were approved by the Institutional Review Board (IRB). Since our primary goal is to compare the prediction model accuracy with the Siri equation (as used in BOD POD), all samples derive from the counterpart ethnicity groups of the Siri equation[4]. However, the proposed methodology is not limited to adult males.

A. Shape-prior Classification

To train the shape classification model, we first manually labeled the lean and non-lean bodies purely based on the curvature distribution, yielding 24 lean and 26 non-lean samples. Then we train and test the proposed model rigorously under the LOOCV framework. For each round, we leave one sample out for testing and use the rest for training. We run the training and testing for 50 rounds in total and evaluate the model by its generalization error. Our result shows that we have four misclassifications out of the 50 tests—three false positives (wrongly classified as lean). Therefore, we claim our classification accuracy to be 92%. The implementations of the SVM, k-NN and decision tree classifiers and the agglomerative hierarchical clustering are based on the MATLAB^® [12]. Classification results from the test will be used to guide the baseline regression.

B. Baseline Regression

Analogous to the shape-prior classification, we perform LOOCV for the model training and testing. For each iteration, we leave one sample out for the test and perform forward feature selection with the rest. We set the maximum number of features thresholds to 5-10 to prevent overfitting. Once the features are defined, we train the model and then test it on the unseen sample. The generalization error in Root-Mean-Square (RMS) is calculated with all the test results after the LOOCV. The implementation of GPR is based on the MATLAB^® [12].

For comparison, we conduct two more tests. In the first test, we use BMI as the only predictor in the regression model to predict the BFP. In the second test, we use the non-shape features (weight, height, BMI, waist, hip, and abdomen) to predict the BFP. We perform the same LOOCV to evaluate the generalization error of these two comparison models. For the second test, we perform the same feature selection procedure as the baseline training.

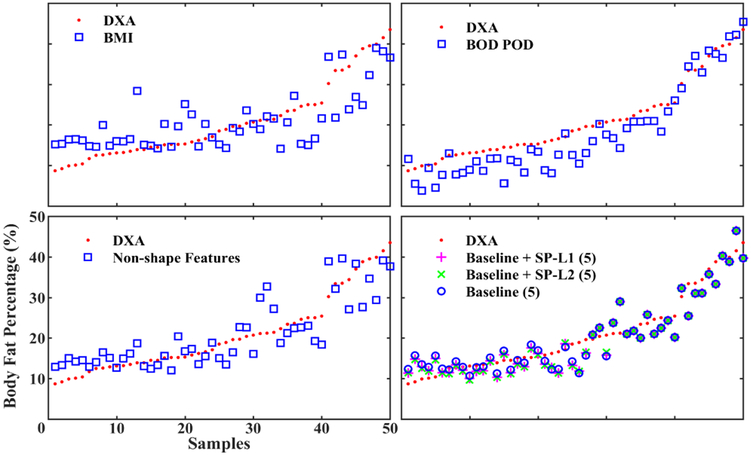
In Table I, we list the generalization error of our baseline regression model with six different maximum number of features thresholds, from 5 to 10. We compare our results with the generalization error of the BMI regression model, the generalization error of the non-shape features regression model and the BOD POD BFP estimation error. The result shows that our baseline method, on the average, outperforms the BOD POD by 18.6%, the non-shape model by 28.76%, and the BMI model by 44.31%. The BFP predictions are plotted in Fig. 4.

Table I.

Results comparison (generalization error)

Methods	Prediction Accuracy (RMSE)
BMI	6.05
Non-shape Features	4.73
BOD POD	4.14
Number of Features	5	6	7	8	9	10
Baseline	3.45	3.44	3.49	3.28	3.25	3.30
Baseline+SP-L1	3.41	3.39	3.44	3.22	3.17	3.21
Baseline+SP-L2	3.38	3.37	3.42	3.21	3.17	3.21

Fig. 4.

Results comparison. We compare the generalization error of our proposed prediction model (bottom right, Maximum Number of Features = 5) with other three models. The comparison models including the BOD POD (top right), the BMI baseline regression (top left), and the without-shape-descriptors baseline regression (bottom left).

C. Prediction Model: Baseline Regression + Shape-prior

In our work, we propose to use the shape-prior to improve upon the baseline prediction accuracy. We assume that the baseline model tends to overestimate the BFP of the lean body and underestimate the BFP of the non-lean body. Hence, the parameter α which minimizes the energy function (3), either with l₁ or l₂ norm, should be greater than zero, as illustrated in Fig. 3. In each round of the LOOCV, we solve (3) for α during model training and then use the parameter in new predictions to evaluate the generalization error.

We compare the use of l₁ norm and l₂ norm optimization for α in our prediction model (see in Table I). We set the threshold τ = 20, as a reasonable lean BFP cutoff threshold. We set the learning rate λ to 1. We plot out how the proposed prediction models help to correct the prediction discrepancy of the baseline model in Fig. 4 (bottom right). The result shows that the proposed prediction model with l₁ norm outperforms the BOD POD by 20.16%, the non-shape model by 30.12%, and the BMI model by 45.36% on the average. The proposed prediction model with l₂ norm outperforms the BOD POD by 20.39%, the non-shape model by 30.32%, and the BMI model by 45.52% on the average.

IV. Conclusions

We present a novel method to predict the BFP based on 3D body shapes. Our prediction model elegantly integrates perceptual level geometry features, i.e., the visual cue, into the general regression model to compensate for the deficiency of the zeroth-order geometry features, and hence, to increase the prediction accuracy. The generalization error of our prediction model outperforms the medical-level body composition assessment instrument—the BOD POD. Our prediction model has shown its robustness in BFP prediction with 3D body shapes reconstructed by the commodity-level body scanner[9]. This has the potential to make our body composition assessment application readily available to be used by medical professionals as well as the general public.