A Molecular Subtype-Specific Stochastic Simulation Model of US Breast Cancer Incidence, Survival and Mortality Trends from 1975 to 2010

Abstract

We present a Monte Carlo simulation model that reproduces U.S. invasive breast cancer incidence and mortality trends from 1975–2010 as a function of screening and adjuvant treatment. This model was developed for multiple purposes, including to quantify the impact of screening and adjuvant therapy on past and current trends, predicting future trends, and evaluate potential outcomes under hypothetical screening and treatment interventions. The model first generates the life histories of individual breast cancer patients by determining the patient’s age, tumor size, estrogen receptor (ER) status, human epidermal growth factor 2 (HER2) status, SEER (Surveillance Epidemiology and End Results) historic stage, detection mode at time of detection, preclinical tumor course, as well as death age and cause of death (breast cancer versus other causes). The model incorporates common inputs used by the Cancer Intervention and Surveillance Modeling Network (CISNET) including the dissemination patterns for screening mammography, breast cancer survival in the absence of adjuvant therapy, dissemination and efficacy of treatment by ER and HER2-status and death from causes other than breast cancer. In this manuscript, predicted mortality outcomes are compared assuming a proportional versus non-proportional hazards effects of treatment on breast cancer survival. We found that the proportional hazards treatment effects are sufficient for ER-negative disease. However, for ER-positive disease, the treatment effects appear to be higher during the early years following diagnosis and then diminish over time. Using non-proportional hazards effects for ER-positive cases, the predicted breast cancer mortality rates closely match the SEER mortality trends from 1975–2010, particularly after 1995. Our work indicates that population level simulation modeling may have a broader role in assessing the time-dependence of treatment effects.

INTRODUCTION

The impact of specific cancer control interventions, such as screening and adjuvant treatment, on cancer incidence and mortality are increasingly being quantified with the use of simulation-based models. We have developed and applied such a simulation-based model in order to estimate the separate and combined effects of screening and adjuvant therapy on the breast cancer incidence and mortality trends in the general population. In prior work, our model, often referred to as Model S or BCOS (Breast Cancer Outcomes Simulator), was one of seven Cancer Intervention and Surveillance Network (CISNET) models used to estimate the relative contributions of screening mammography and adjuvant therapy to the reduction in breast cancer mortality for the overall U.S. population from 1975 to 2000.¹ Since its initial development, BCOS has been continually refined to incorporate the latest data on breast cancer control and surveillance in order to capture changes in incidence and mortality patterns due to usage of menopausal hormonal therapy (MHT) and the increased use of adjuvant treatments that are dependent on molecular subtype. In this manuscript, we will focus on one of the model changes that had the biggest impact on reproducing breast cancer mortality trends, namely changes in modeling treatment effectiveness.

When incorporating breast cancer treatment effectiveness into our model, we originally adopted the hazard ratios obtained from the literature.^2–9 The treatment effects were summarized as a single value, for each age and ER-status group, computed as the hazard ratio using the Cox proportional hazards regression.¹⁰ Incorporating these effects directly into our simulation model implied that the hazard reduction of breast cancer death attributable to any treatment remained constant over the course of the individual’s lifetime following treatment. However, emerging evidences have suggested that the benefits of commonly used adjuvant treatment may change over time. For example, a methodology work on data from a trial in the National Surgical Adjuvant Breast and Bowel Project (NSABP) showed time-dependent treatment effects among ER-positive patients treated with adjuvant tamoxifen versus placebo;¹¹ data from the Cancer and Leukemia Group B and US Breast Cancer Intergroup demonstrated that the reduction in risk of breast cancer recurrence and death with high-dose adjuvant cyclophosphamide, doxorubicin, and fluorouracil (CAF), compared with low-dose CAF, was 55% in the first year and 30% in the second year, with little benefit after three years, for ER-negative patients;¹² an analysis based on five NSABP trials suggested that a large early chemotherapy benefit was followed by a consistently low recurrence hazard over an extended time period for ER-negative patients whereas the benefit appeared to concentrate primarily in earlier follow-up for ER-positive patients.¹³ More recently, a study systemically assessed the proportional hazards assumption for all 19 trials in NSABP and concluded that breast cancer adjuvant therapy could have statistically significant time-dependent effects.¹⁴ Therefore, we considered the impact of time-dependent treatment effects on our model.

MODEL OVERVIEW

Our current model’s basic formalism has not significantly changed compared to the original version.¹⁵ The main model modifications include: (1) updated the secular trend in breast cancer incidence to reflect the incidence rates in the absence of screening and MHT use; (2) modified the preclinical tumor growth curves to account for MHT use; (3) ER- and HER2-status assignment based on age, size, stage at clinical detection and tumor volume doubling time (TVDT); (4) incorporation of ER and HER2-specific baseline survival curves in absence of screening, treatment or MHT; (5) updated mammography detection thresholds according to MHT use and by ER-status; (6) updated dissemination and effectiveness of adjuvant therapies to be ER and HER2-specific, specifically, accommodated time-dependent treatment effects.

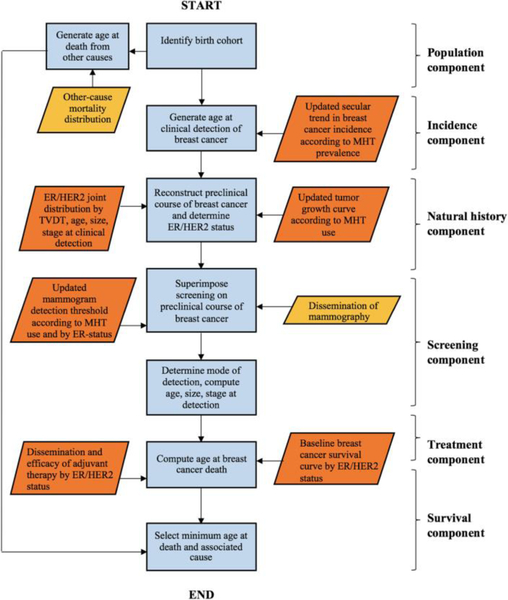
These changes are briefly described in the following sections. A flowchart of our updated simulation model is presented in Figure 1 and the corresponding pseudocode of the simulation algorithm is provided in Table 1 (the model was implemented using C++).

Figure 1.

Flowchart of the updated Monte Carlo algorithm per simulated individual. Orange parallelograms indicate inputs that have been modified. ER, estrogen receptor; HER2, human epidermal growth factor 2; MHT, menopausal hormonal therapy; TVDT, tumor volume doubling time.

Table 1.

Pseudocode of the Monte Carlo Simulation Algorithm

For birth cohorts 1890 to 1990

For individuals 1 to 2,000,000 in each birth cohort

Step 1: Generate date of birth (Population Component)

Step 2: Generate age at other-cause death given birth cohort (Population Component)

Step 3: Generate age at clinical detection (Incidence Component)

Step 4: Generate tumor size at clinical detection given age at clinical detection (Natural History Component)

Step 5: Generate tumor growth rate given age and tumor size at clinical detection (Natural History Component)

Step 6: Generate tumor size at the onset of regional and distant stage given age at clinical detection and tumor growth rate, assuming MHT is not used (Natural History Component)

Step 7: Compute stage of the tumor at clinical detection

Step 8: Determine ER/HER2 status given age, tumor growth rate, tumor size, and stage at clinical detection

Step 9: Determine MHT usage given ER status (ER-negative breast cancers are not affected by MHT usage)

Step 10: If MHT is used, determine the start and end year of MHT usage and modify the tumor growth curve (Natural History Component)

Step 11: Based on the modified tumor growth curve, update age and stage at clinical detection (Natural History Component)

Step 12: Generate ages undergoing screening given birth cohort (Screening Component)

Step 13: Generate the tumor size detection threshold of mammography by age at the time of screening, ER status, and MHT usage (Screening Component)

Step 14: Compute the tumor size at the time of screening and determine age, year, tumor size, and stage at screen detection by comparing to the detection threshold (Screening Component)

Step 15: Comparing the year at clinical and screen detection, determine the mode of detection and year, age, size, and stage at detection

Step 16: Given year, age, size, and stage at detection, as well as ER/HER2 status, assign adjuvant therapy and obtain the corresponding treatment efficacy (Treatment Component)

Step 17: Generate age at breast cancer death given detection mode, treatment efficacy, age, size, stage at detection, and ER/ HER2 status (Survival Component)

Step 18: Assign age of death to the smaller of age of breast cancer death and age of other-cause death

Repeat for next individual

Repeat for next birth cohort

ER, estrogen receptor; HER2, human epidermal growth factor 2; MHT, menopausal hormonal therapy.

OVERVIEW OF MODEL COMPONENTS

The underlying components of our simulation model with the corresponding input(s) are shown in Figure 1 and in the following, we provide a more detailed explanation about each component.

Population Component

The population component specifies the U.S. birth cohort’s underlying survival. The model generates a sample of U.S. women born between 1890 to 1990 to reproduce the breast cancer associated outcomes among women aged 20–84 for each calendar year from 1975 to 2010. To reduce the sampling variability of the Monte Carlo method, two million women are generated in each birth cohort. Each simulated woman is assigned a birth date as well as an age at death from causes other than breast cancer using the CISNET common input parameter.^{16, 17}

Breast Cancer Incidence Component

The breast cancer incidence component determines whether an individual from a particular birth cohort would be clinically detected with invasive breast cancer in the absence of screening and MHT use. In this component, each simulated woman is assigned an age when her first primary invasive tumor clinically surfaces, meaning that it becomes symptomatically detected in the absence of screening. This component relies on an input referred to as the “secular trend in breast cancer incidence”. This input was originally derived from an age-period-cohort (APC) model¹⁸ formulated as described by Holford and others^19. In the current model, we re-estimated the age, period and cohort effects by applying an iterative approach that simultaneously estimates underlying parameters of the natural history model (described below), the impact of MHT on breast cancer progression and mammography sensitivity fit to breast cancer incidence in the presence of screening and MHT use. We found this approach better addresses the non-identifiability issues with the APC model. Moreover, it provides estimates of the breast cancer trends in the absence of screening and MHT.²⁰

Natural History Component

In the natural history component, the size and stage (SEER historic stage) of each breast cancer patient’s first primary invasive breast tumor are reconstructed from the time the tumor is a small (2mm), localized, invasive mass to the time it clinically surfaces. We model the natural history of an individual tumor as a progressive disease that stochastically advances in stage as the tumor increases in size. We assume that the tumor grows exponentially in the screen detectable window, and the growth rate is a random variable drawn from a probability distribution dependent on the patient’s age and tumor size at clinical detection. A difference from our original model with regards to this component is that the growth rate (or equivalently, TVDT) and ER/HER2-status are jointly determined for each patient and MHT usage is assigned subsequently based on the ER status. The use of MHT also affects the tumor growth curve so that the age and stage at clinical detection need to be re-specified based on dynamic changes in MHT use and disuse. As mentioned above, these parameters are estimated jointly with the APC model.²⁰ Note that we do not model the progression of ductal carcinoma in situ (DCIS) to invasive cancer due to issues related to non-identifiability with our existing data and estimation methods.

Screening Component

Once the natural history of a patient’s disease is constructed, we then superimpose onto it a screening schedule to determine if and when screening mammography affects tumor detection. For the mammography dissemination, we use the CISNET common input parameter based on national survey self-reported data to estimate the distribution of the time to first mammography and Breast Cancer Surveillance Consortium (BCSC) data to model repeat screening behavior.¹⁶ Additionally, each woman is assigned a screen detection threshold, conditioned on her ER status and age at the time of screening. If the woman is on MHT at the time of screening, then her detection threshold is inflated by a factor associated with MHT use. A tumor in the pre-clinical phase and with a size above the detection threshold at the time of screening could be screen-detected if screening occurs in this period.

Treatment Component

The use of adjuvant treatment and the corresponding survival benefit associated with adjuvant treatment are identified in the treatment component. As many new breast cancer treatments have been approved and disseminated, the original BCOS model, which assigned only poly-chemotherapy and tamoxifen to patients, has been updated to include more adjuvant treatment options (e.g. anthracyclines, taxanes, aromatase inhibitors, and trastuzumab). In the current BCOS model, treatments are assigned based on the patient’s age, tumor size, stage, year of diagnosis, as well as ER, HER2-status, and the corresponding treatment effectiveness is dependent on tumor stage and ER, HER2-status using the CISNET common input parameter.¹⁶

Survival Component

The purpose of the survival component is to specify a patient’s breast cancer survival time from the moment her first primary invasive tumor is detected. Each patient is assigned a breast cancer survival randomly sampled from a distribution dependent on her age, tumor size, and stage at detection, as well as the use of adjuvant treatment and ER, HER2-status. The distribution is obtained by applying the adjuvant treatment effectiveness to the baseline survival curves (i.e. survival curves in the absence of screening and treatment), assuming a non-proportional hazards reduction in breast cancer mortality to incorporate time-dependent treatment effects (described below). The baseline survival curves in our original model are conditioned on age, tumor size, and stage at detection, which are now updated to be conditioned on ER, HER2-status as well. The ER and HER2-specific baseline survival curves are obtained through a back-calculation procedure.²¹ Mode of detection affects breast cancer survival through stage-shifting due to early detection from screening. Ultimately, each woman’s age and cause of death (breast cancer vs. other causes) are obtained by comparing her ages at breast cancer death and other-cause death.

MODEL CALIBRATION FOR TIME-DEPENENT TREATMENT EFFICACY

In prior work¹⁵, we modeled the efficacy of adjuvant treatment on underlying breast cancer survival assuming proportional hazards. As stated in the Introduction section, evidences suggest that the effects of adjuvant treatment may be time-dependent, and the time-dependence may vary by molecular-subtypes.^11–14 To explore the possibility of subtype-specific, time-dependent treatment efficacy, we leveraged our ER-specific natural history model to infer the annual effect of treatment by first comparing SEER breast cancer survival curve estimates with those predicted from the model in the presence of screening only.

We define $H_{ei}^s$ as the annual breast cancer death hazard for a tumor with ER-status e in year i after detection in the presence of screening alone (superscript s). $H_{ei}^s$ is computed as an output of our BCOS model when run under the screening and no adjuvant treatment scenario. We then compute the annual hazard reduction in breast cancer death attributable to treatment, $H_{ei}^t$, for a tumor with ER-status e in year i after detection, as the ratio of the breast cancer death hazards observed in SEER, which are observed in the presence of both screening and treatment, versus those from the BCOS model only in the presence of screening. In other words,

$$H_{ei}^t=S_{ei}/H_{ei}^S$$

where S_ei is the annual hazard of breast cancer-specific death in the presence of screening and treatment as computed from SEER. Note that $H_{ei}^t$ is calculated as the percent reduction in deaths observed in each individual year i for each ER-status e.

To allow for the possibility of time-dependent treatment effects, we assumed that there exists a time-dependent and ER-specific hazard multiplier, M_ei, that characterizes the time trend in hazard reduction observed with respect to an average effect μ_e, such that:

$$M_{ei}=H_{ei}^t/{\mu }_e$$

for any year i and ER-status e. We computed μ_e as the average hazard reduction observed after n years:

$${\mu }_e=\frac{\sum _{i=1}^n{H}_{ei}^t}{n}$$

Note that it was not our intent to quantify separate hazard reductions for each individual treatment, but rather to identify the time-dependent effects that are attributable to composite treatments for patients with particular molecular subtype. In our analysis, M_ei was estimated with survival data from breast cancer patients who were detected between calendar year 1990–2010 and molecular subtype e. During this time period, multiagent chemotherapy and tamoxifen were the most common adjuvant therapies administered to the breast cancer patients on the basis of their ER-status. Note that the treatment efficacy was calibrated after accounting for the screening effect, therefore it relies on the estimation of the screening effect.

When implementing this effect into our model, we assumed that all the treatment effectiveness estimates obtained from clinical trial literature²⁻⁹ are averaged annual hazard reductions of the form of μ_e, that can be adjusted by M_ei to obtain time-dependent annual hazard reductions. In other words, the time-dependent reduction in the hazard of breast cancer death attributable to any molecular-subtype-specific treatment combination T was computed as:

$$H_{ei}^T=M_{ei}*{\mu }_e^T$$

for i years after detection and ER-status e. The multiplier was only applied for breast cancer cases after 1995 because the ER-status was underreported in SEER prior to 1995.

MODEL RESULTS AND VALIDATION

Hazard Ratio for Proportional vs. Non-proportional Assumptions

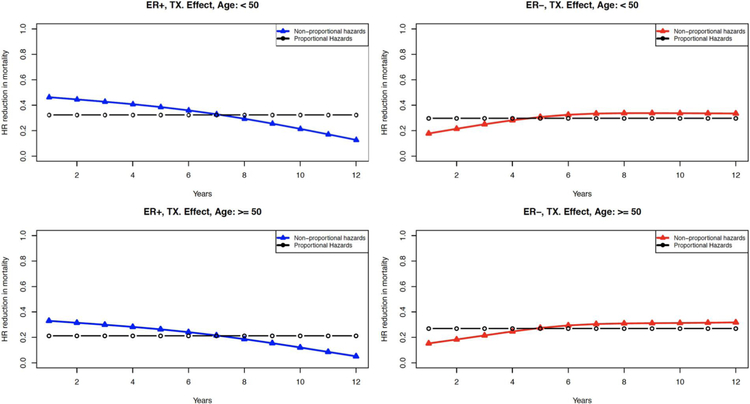
Figure 2 shows the annual hazard ratio (HR) in breast cancer death attributable to treatment by ER-status and age at diagnosis (<50 and >−50), under both the proportional and non-proportional assumptions. By calibrating to ER-specific breast cancer survival, we find that the effects of treatment show a time-dependency that varies by ER-status. Compared to the proportional hazards assumption, the treatment effects under the non-proportional hazards assumption for ER-positive disease appear stronger in the first 7 years and diminish gradually. However, for ER-negative cases, the treatment effects under the two assumptions are consistent except for a small initial difference. With these findings and considering the evidence from literature^11–14, we adopted the non-proportional hazards assumption (i.e. time-dependent treatment effects) for ER-positive disease only and retain the proportional hazards assumption for ER-negative disease.

Figure 2.

Annual contribution of treatment to reducing the hazard of death from breast cancer for cases detected between 1990 and 2010 by estrogen receptor (ER) status and age (<50, >50). The black curves are the estimates assuming proportional hazards, and the colored curves are the hazard estimates using our nonproportional hazard assumption (blue for ER-positive cases and red for ER-negative cases). HR, hazard ratio; TX, treatment.

Breast Cancer Survival Curves and Annual Hazards

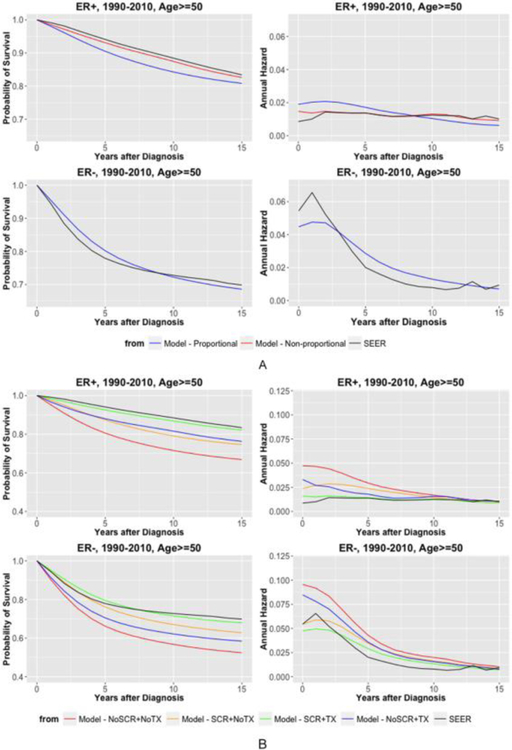
Figure 3(A) shows the comparison between proportional and non-proportional treatment effects for ER-positive disease on predicted survival curves and annual hazards of breast cancer death. We also compare these curves to SEER data for the same calendar years. For ER-positive disease, we reproduce SEER curves under the non-proportional hazards assumption, while the proportional hazards assumption cannot capture either the low initial hazards nor the persistent later hazards. On the other hand, ER-negative disease shows a high hazard peak followed by a rapid and consistent decrease, which is adequately captured by the proportional hazards assumption. Because the registry data is in the presence of both screening and treatment, the predicted curves are under the scenario with screening and treatment, which also serves as a form of validation.

Figure 3.

Comparison of estimated and Surveillance, Epidemiology, and End Results (SEER) survival curves (first column) and annual hazards (second column) by estrogen receptor (ER) status for cases detected at age 50 years or older between 1990 and 2010: (A) breast cancer survival under proportional v. nonproportional treatment effects and (B) breast cancer survival for alternative treatment and screening scenarios assuming nonproportional hazards for ER-positive disease and proportional hazards for ER-negative disease.

Based on the non-proportional hazards assumption for ER-positive disease, Figure 3(B) shows our model-derived estimates for ER-specific survival curves and annual hazards for women detected at age 50 or above between 1990–2010 under four different screening and treatment scenarios: (i) no screening and no treatment (NoSCR+NoTX), (ii) screening and no treatment (SCR+NoTX), (iii) no screening and treatment (NoSCR+TX), and (iv) screening and treatment (SCR+TX). The survival curves indicate that treatment have slightly greater benefit than screening for ER-positive disease, whereas treatment has less benefit than screening for ER-negative disease (blue vs. orange curves). The annual hazards further show that the screening effect (orange vs. red curves) diminishes over time for both ER-subtypes and the treatment effects (green vs. orange curves) decrease over time for ER-positive disease but remain stable for ER-negative disease.

Overall and ER-specific Breast Cancer Incidence and Mortality Trends

Our simulation model was evaluated by comparing the predicted incidence and mortality rates from the model with the observed rates from SEER, overall and by ER status. Since ER status started to be collected in SEER in 1990, ER-specific SEER incidence and mortality rates were calculated with imputations for unknown cases, assuming the same proportions of ER-positive records as those among the known cases by calendar year. To avoid a large fraction of unknown cases, the ER-specific rates were compared from year 1995 onward. Figure 4(A) and (B) show that the general shape of the observed breast cancer incidence and mortality curves were captured by the corresponding predicted curves, both for the overall population and ER-specific subpopulations. Note that Figure 4(B) was based on non-proportional treatment effects for ER-positive disease, which is the default assumption. If we had applied proportional treatment effects instead, the resulting mortality curves are shown in Figure 4(C). The predicted mortality curve for the overall population in Figure 4(C) deviates from the observed curve from 1995 onward, demonstrating that the simple proportional hazards assumption for ER-positive cases is not sufficient in our simulation model.

Figure 4.

Age-adjusted (to the 2000 US standard population) rates (per 100,000) for women aged 30 to 79 years at diagnosis (incidence) or at death (mortality) from 1975 to 2010 (overall) or from 1995 to 2010 (ER specific), SEER (solid curves) v. simulation model (dashed curves): (A) breast cancer incidence, (B) breast cancer mortality under nonproportional hazards assumption (for ER-positive cases), and (C) breast cancer mortality under proportional hazards assumption. ER, estrogen receptor; NoSCR + NoTX, no screening and no treatment; NoSCR + TX, no screening and treatment; SCR + NoTX, screening and no treatment; SCR + TX, screening and treatment; SEER, Surveillance, Epidemiology, and End Results.

CONCLUSION

Our simulation model reproduces U.S. breast cancer incidence and mortality rates from 1975 to 2010 and ER-specific trends from 1995 onward. The model also specifically models natural history based on a biological model of tumor doubling times, making it well suited to address questions about survival by molecular subtypes that vary in terms of tumor progression. However, BCOS does not include DCIS due to issues of model parameter non-identifiability. Hence BCOS is limited in its inferences about the impact of screening on over-diagnosis and over-treatment, particularly related to DCIS. However, the natural history model of invasive cancer underlying BCOS can be adapted to new research directions including incorporating deeper molecular profiling of invasive disease for assessing risk stratified screening guidelines and evaluating the effect of new treatments of primary invasive disease and distant recurrence.

The modularity of the BCOS model enables us to isolate effects of differing modeling assumptions. Here we demonstrated the impact of assuming proportional versus non-proportional treatment-related hazards on breast cancer survival and mortality. We found non-proportional treatment effects for ER-positive disease, but not for ER-negative disease. For ER-positive disease, we found that the treatment effects are stronger in the early years after diagnosis, then diminish over time. By assuming time-dependent treatment effects to better reproduce ER-positive breast cancer survival curves, BCOS more closely reproduced breast cancer mortality rates over time.

The time-dependent treatment effects for breast cancer patients with ER-positive disease may be related to the amount of time women are prescribed tamoxifen. In the 1990s, some women were prescribed tamoxifen for 2 years, then the recommended treatment duration was increased to 5 years. More recently, the American Society of Clinical Oncology recommended tamoxifen for 10 years, suggesting greater benefits of extending beyond 5 years.²² Others have also suggested a time-dependent effect of tamoxifen, as indicated in the Introduction section.¹¹ The results of our analysis are consistent with these studies. That said, our results have some limitations. They are dependent on treatment dissemination patterns and the estimated effect of screening. Moreover, we did not quantify separate time-dependent hazard reduction for each individual treatment. Nevertheless, with the fact that our findings of time-dependent treatment effects for ER-positive patients are consistent with other studies and we are able to better reproduce mortality, our work suggests that population level simulation modeling may have a broader role in assessing the time-dependence of treatment effects.