Suppressive Traveling Waves Shape Representations of Illusory Motion in Primary Visual Cortex of Awake Primate

Abstract

How does the brain link visual stimuli across space and time? Visual illusions provide an experimental paradigm to study these processes. When two stationary dots are flashed in close spatial and temporal succession, human observers experience a percept of apparent motion. Large spatiotemporal separation challenges the visual system to keep track of object identity along the apparent motion path, the so-called “correspondence problem.” Here, we use voltage-sensitive dye imaging in primary visual cortex (V1) of awake monkeys to show that intracortical connections within V1 can solve this issue by shaping cortical dynamics to represent the illusory motion. We find that the appearance of the second stimulus in V1 creates a systematic suppressive wave traveling toward the retinotopic representation of the first. Using a computational model, we show that the suppressive wave is the emergent property of a recurrent gain control fed by the intracortical network. This suppressive wave acts to explain away ambiguous correspondence problems and contributes to precisely encode the expected motion velocity at the surface of V1. Together, these results demonstrate that the nonlinear dynamics within retinotopic maps can shape cortical representations of illusory motion. Understanding these dynamics will shed light on how the brain links sensory stimuli across space and time, by preformatting population responses for a straightforward read-out by downstream areas.

SIGNIFICANCE STATEMENT Traveling waves have recently been observed in different animal species, brain areas, and behavioral states. However, it is still unclear what are their functional roles. In the case of cortical visual processing, waves propagate across retinotopic maps and can hereby generate interactions between spatially and temporally separated instances of feedforward driven activity. Such interactions could participate in processing long-range apparent motion stimuli, an illusion for which no clear neuronal mechanisms have yet been proposed. Using this paradigm in awake monkeys, we show that suppressive traveling waves produce a spatiotemporal normalization of apparent motion stimuli. Our study suggests that cortical waves shape the representation of illusory moving stimulus within retinotopic maps for a straightforward read-out by downstream areas.

Introduction

When two stationary stimuli are successively flashed in spatially separated positions, it generates the so-called “apparent motion” illusion (Wertheimer, 1912; Burr and Thompson, 2011). The illusion depends on the spatiotemporal (ST) characteristics of the stimulus, being called “short-range” versus “long-range” apparent motion (lrAM) depending on spatial and temporal separations (Braddick, 1980), possibly underlined by different processes (Cavanagh and Mather, 1989). In physiology, we have a clear idea on the neuronal processing involved in short-range apparent motion (Mikami et al., 1986a), but not for lrAM. In the latter case, it has been proposed that a “reviewing process” (Kahneman et al., 1992) is necessary to link the transient apparitions of stimuli in different spatial and temporal positions. This process will allow for a coherent motion percept of a single object, hereby solving the “correspondence problem” (Ternus, 1926; Ullman, 1978). Downstream areas with large receptive fields are the expected integration unit for such extended ST input. Indeed, it has been recently shown in human that the feedback from MT to V1 plays an important role in the processing of lrAM (Muckli et al., 2002; Wibral et al., 2009; Vetter et al., 2015), as well as evidence of downstream activation along the ventral stream (Zhuo et al., 2003). However, it is still unclear whether and how the “reviewing process,” needed to keep track of the object identity along the motion trajectory, can be achieved within these large receptive fields.

It has been suggested that the population activity within V1 could participate upstream in the processing of lrAM (Muckli et al., 2005). The extended precise retinotopic map in V1 makes it indeed an ideal platform for representing the trajectory of the apparent motion to be read-out by downstream areas (Mumford, 1991; Lee et al., 1998). In particular, V1 has the highest resolution to achieve the interactions in space and time needed to link the individual strokes of the apparent motion (Adelson and Bergen, 1985; Lee et al., 1998). In such context, intracortical and intercortical connectivity are the natural substrate to underlie the needed ST interactions (Deco and Roland, 2010; Muller et al., 2018). Importantly, these two networks have intrinsically different ST properties, the intercortical network operates over very large extent but with poor resolution (Angelucci et al., 2002; Stetter, 2002), and the intracortical network has a more limited extent but with high resolution (Bringuier et al., 1999; Bullier, 2001; Muller et al., 2014). They also constitute the vast majority of synaptic contacts in the cortex (Markov et al., 2011). Such connectivity is therefore a good candidate to link transient ST events (Jancke et al., 2004; Gerard-Mercier et al., 2016; Muller et al., 2018). However, it is still unclear whether and how the corticocortical interactions could participate to shape the representation of lrAM within V1 retinotopic map in the awake monkey.

To answer this question, we used optical imaging of voltage-sensitive dyes (VSDI) in the awake fixating monkey, to measure how V1 neuronal population integrates a two-stroke lrAM. In response to a single stroke, activity in V1 propagates in space and time (Grinvald et al., 1994; Bringuier et al., 1999; Slovin et al., 2002; Sato et al., 2012; Muller et al., 2014), with spatial and temporal constants that cover ∼3 mm and 80 ms. In response to lrAM of various ST separations that were chosen to encompass several V1 receptive fields, we observed the emergence of a direction-selective representation of the lrAM in V1. This is the result of a systematic wave of suppression triggered by the second stimulus, propagating in the opposite direction of the lrAM. Using a mean-field computational model, we show that the observed suppressive waves can result from a gain control fed by intracortical interactions. We further demonstrate that the suppression waves explain away ambiguous representation of stimulus position along the apparent motion trajectory. As a result, the observed ST pattern encodes the actual stimulus velocity for a straightforward read-out by downstream areas.

Materials and Methods

The experiments were conducted on 2 male rhesus macaque monkeys (Macaca mulatta, aged 14 and 11 years old, respectively, for Monkey WA and Monkey BR) over a period of 3 years. The experimental protocols had been previously approved by the local Ethical Committee for Animal Research (approval A10/01/13, official national registration 71-French Ministry of Research), and all procedures complied with the French and European regulations for Animal Research as well as the Guidelines from the Society for Neuroscience.

Surgical preparation and VSDI protocol.

The monkeys were chronically implanted with a head-holder and a recording chamber located above the V1 and V2 cortical areas of the right hemisphere. After full recovery, the monkeys were trained to perform foveal fixation of a small red target presented over different static and moving backgrounds for up to 2–3 s, with their head fixed. Once a good fixation behavior was achieved, a third surgery was performed. The dura was removed surgically over the recording aperture (18-mm-diameter) and a silicon-made artificial dura was inserted under aseptic conditions to allow for a good optical access to the cortex over the whole period of weekly recordings. Before each recording session conducted in awake animal, the cortical surface was stained with the voltage-sensitive dye (VSD) RH-1691 (Optical Imaging) with the following procedure: The optical chamber was open, artificial dura mater was removed, and the cortical surface was cleaned under strict sterile conditions. The dye solution was prepared in aCSF at a concentration of 0.2 mg/ml, and filtered through a 0.2 μm filter. The recording chamber was filled with this solution and closed for 3 h, corresponding to the time lapse needed for a correct cortical staining. The chamber was then rinsed thoroughly with filtered aCSF to remove any supernatant dye. Before imaging, the artificial dura was placed back in position and the chamber was closed with transparent agar and cover glass. Experimental control, data collection, and eye position and fixational behavior monitoring (sampling rate: 1 kHz, ISCAN ETL-200 Eye tracking system) were performed by the ReX software (National Eye Institute, National Institutes of Health) running under the QNX operating system (Hays et al., 1982). During each trial, the cortex was illuminated at 630 nm using epi-illumination, and we recorded optical signals high-pass filtered at 665 nm with a Dalstar camera (512 × 512 pixels resolution, frame rate of 110 Hz) driven by the Imager 3001 system (Optical Imaging). The beginning of both online behavioral control and image acquisition was heartbeat-triggered. The surgical preparation and VSD imaging protocol have been described previously (Reynaud et al., 2012; Muller et al., 2014).

Behavioral task and visual stimulation.

Monkeys were trained for a simple fixation task. For each experimental trial, the monkeys were required to fixate a central red dot within a precision window of 1° × 1°. When correct fixation was achieved, the next heartbeat, detected with a pulse oximeter (Nonin 8600V), triggered the beginning of the acquisition window. A visual stimulus appeared 100 ms after this trigger, after which a blank screen was presented, ending the trial. Each trial ran for 699–999 ms. If the monkey had maintained fixation up to the end of the acquisition period, a reward (fruit compote drop) was given. Otherwise, the trial was canceled, an alert sound was delivered, and the procedure was reinitiated. The visual stimuli were computed online using VSG2/5 libraries and were displayed on a 22 inch CRT monitor at a resolution of 1024 × 768 pixels. Refresh rate was set to 100 Hz. Viewing distance was of 57 cm. Luminance values were linearized by mean of a look-up table. We used Gaussian blobs with SD (controlling the spatial width) of 0.5°. They were presented at different positions, located at 0.5° or 2° on the left of the vertical meridian, respectively, for Monkey WA and Monkey BR (retinotopic map variability across monkeys), and between 1.5° and 4.5° below the horizontal meridian. We used different stimulus durations, 10 ms (1 frame), 50 ms or 100 ms and different interstimulus intervals (ISIs) for the two-stroke apparent motion stimuli (from 20 to 100 ms, except where stated otherwise). During a single session (i.e., 1 d of recordings), stimuli conditions (single blobs of different durations, lrAM sequences, and two blank conditions, i.e., where no visual stimulus is presented) were randomly interleaved with an intertrial interval of 8 s for dye bleaching prevention. We usually recorded and averaged 50 trials per condition.

Data analysis.

Stacks of images were stored on hard-drives for offline analysis. The analysis was carried on with MATLAB R2014a (The MathWorks) using the Optimization, Statistics and Signal Processing Toolboxes. VSD-evoked responses to each stimulus were computed in three successive basic steps. First, the recorded value at each pixel was divided by the average value before stimulus onset (“frame 0 division”) to remove slow stimulus-independent fluctuations in illumination and background fluorescence levels. Second, this value was subsequently subtracted by the value obtained for the blank condition (“blank subtraction”) to eliminate most of the noise due to heartbeat and respiration. Third, a linear detrending of the time series was applied to remove residual slow drifts induced by dye bleaching.

ST representation (ST data).

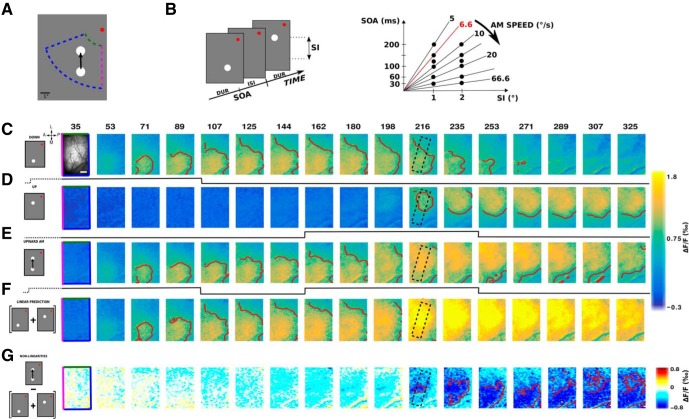
For each time frame, activity was averaged across the x dimension within the apparent-motion trajectory (see, e.g., Fig. 1C–G, dotted rectangle at frame 216 ms) to provide a unique spatial cortical dimension as a function of time.

Figure 1.

Experimental protocol and time sequence of the cortical response to the lrAM. A, Two-step lrAM stimuli were presented to 2 awake fixating monkeys in their bottom left visual field, while recording in their right visual cortex using VSDI. B, ST characteristics of lrAM stimuli, that is, duration (DUR), Inter Stimulus Interval (ISI), and Spatial Interval (SI), were varied to cover a range of speed (5°/s–66.6°/s), computed using stimulus onset asynchrony (SOA = DUR + ISI). C–E, Cortical representation of evoked VSDI activity as a function of time, in response to, respectively, a 100 ms local stimulus in the down position (C), another one in the up position (D), and the sequence (E) of these two stimuli (ISI = 50 ms and SI = 1°) for 1 monkey. Top left in C, The cortical area imaged. The edge of the image color codes the retinotopic borders as represented in A, such as the vertical meridian (magenta) and eccentricities (green and blue). Scale bar, 2 mm. A, Anterior; P, posterior; M, medial; L, lateral. Top, Time in milliseconds after stimulus onset. Bottom, Black lines indicate stimulation time. F, Activity pattern predicted by the linear combination in space and time of the response to stimulus 1 (row C) and the response to stimulus 2 (row D). G, Suppression pattern obtained by subtracting the observed apparent motion response (row E) and the linear prediction (row F). Red contours delimit amplitude activity above a certain threshold: C–F, 1‰; G, −0.5‰.

Latency estimation.

Response latency was defined as the point in time at which the signal derivative crossed a threshold set to 2.57 times (99% confidence) the SD of its baseline computed during a 100-ms-long window right before stimulus onset.

Speed estimation.

Within the ST representation, the speed of activity propagation was estimated by computing the slope of the linear regression between each latency estimate as a function of the cortical distance in the ST representation

Data fitting.

For extracting the space and time constants of the VSD responses, we fitted the ST data in space (for each time frame) to a Gaussian function of the following form:

where σ, κ, and μ, respectively, denote the width (as the SD), amplitude, and spatial position of the Gaussian. We use the slope of the linear regression of μ(t) for quantifying the displacement of the response peak (see Fig. 4E).

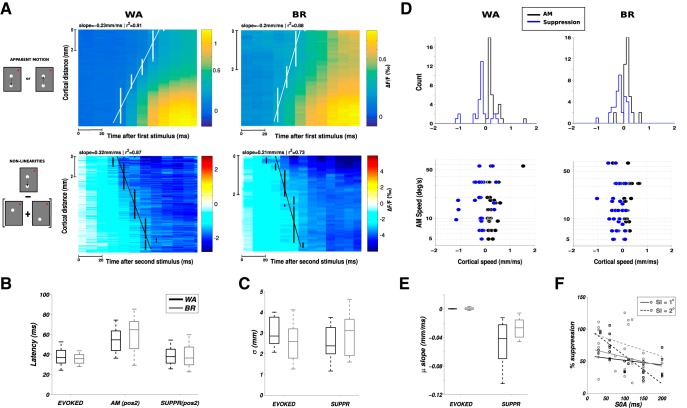
Figure 4.

The suppressive wave has the same properties as the evoked intracortical propagation. A, ST VSDI activity (top row) and nonlinearities (bottom row) averaged across all lrAM speed conditions (n = 30 for Monkey WA and n = 34 for Monkey BR) and centered on stimulus 1 (S1, top row) or stimulus 2 (S2, bottom row) onset, for both monkeys (columns). B, Boxplot of latency estimates comparing the onset of activity evoked by S2 alone (“evoked” condition), the response onset evoked by S2 when embedded in the lrAM sequence (“AM” condition), and the onset of the suppression at S2 position (“suppr” condition). Boxplots represent median, 25% and 75% quartiles, and minimum and maximum of the distributions across all lrAM speed conditions, for the 2 monkeys (black represents Monkey WA; gray represents Monkey BR). C, Boxplot of space constants (parameter σ of a Gaussian spatial fit) comparing the evoked response and the suppression, for the 2 monkeys. D, For each condition in both monkeys (columns), we estimated the speed of propagation of the VSDI (black) and the nonlinearity (blue). Top row represents frequency histograms, values are positive when the direction of the propagation is the same as the direction of the apparent motion, negative otherwise. Bottom row represents these speeds as a function of the speed of the lrAM stimulus. E, Boxplot of the response peak propagation speed (slope of the linear regression on the parameter μ of a Gaussian spatial fit) comparing the evoked response and the suppression, for both monkeys. F, Suppression strength (normalized to the maximal response activity) as a function of stimulus onset asynchrony and SI (open circle represents SI = 1°; open square represents SI = 2°), for both monkeys: black represents Monkey WA; gray represents Monkey BR. Linear regressions are also plotted: solid lines indicate SI = 1°; dashed lines indicate SI = 2°.

In time (for each spatial point), the data was fitted to the combination of two halve Gaussian functions as follows:

where τ_on and τ_off denote the time constants of each half Gaussian, whereas k₁, k₂, and t_c are, respectively, their peak to peak amplitudes and the time of their common center.

Statistical procedure.

We used a two-sample t test procedure to test whether or not the distributions of the VSD response properties (i.e., space constant, time constants, latencies, and cortical speed) were independent of stimulus duration or lrAM speed. p < 0.01 is considered significant.

Mean-field computational model.

We consider a spatially extended ring model where every node of the ring represents the network activity of a large population of excitatory regular spiking (RS) and inhibitory fast spiking (FS) cells (see Fig. 5A). We consider Adaptive Exponential integrate and fire (AdExp) neurons evolving according to the following differential equations:

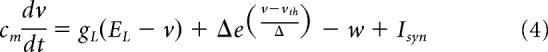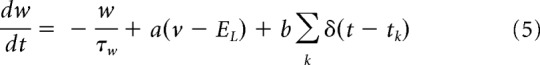where c_m = 100 pF is the membrane capacity, v is the voltage of the neuron and, whenever v > v_th = −50 mV at times t_k, v is reset to its resting value v_rest = −50 mV. The leak term has a conductance g_L = 10 nS and a reversal potential E_L = −65 mV. The exponential term has a different strength for RS and FS cells, that is, Δ = 2 mV (resp.Δ = 0.5 mV) for excitatory (resp. inhibitory) cells. Inhibitory neurons do not have adaptation (a = b = 0) whereas excitatory neurons have an adaptive dynamics with a = 4 nS, b = 40 nS, and τ_w = 500 ms. The synaptic current can be expressed as follows:

where $S_{\frac{E}{I}}={\displaystyle {\sum }_{pre}\theta \left(t-t_{pre,\frac{E}{I}}\right)e^{\frac{t-t_{pre,\frac{E}{I}}}{{\tau }_{E,I}}}}$ is the postsynaptic current due to all presynaptic excitatory/inhibitory neurons spiking at time $t_{pre,\frac{E}{I}}$ and θ is the Heaviside function. The reversal potentials are E_E = 0 mV and E_I = −80 mV, the synaptic decays are equal for excitatory and inhibitory cells,

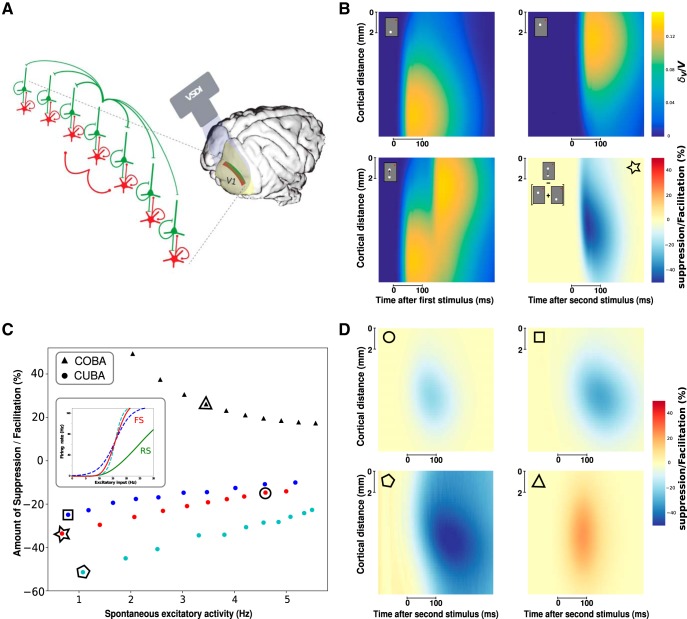
Figure 5.

A computational model to investigate the possible origin of the suppressive wave. A, Mean-field model of excitatory and inhibitory neurons distributed on the cortical trajectory of the stimulus with horizontal connectivity (longer for excitatory than inhibitory neurons). B, Model ST response to the first stimulus (top left), the second (top right), the apparent motion sequence (bottom left), and the nonlinearities normalized to the maximal response over space and time of the response to single stimuli (bottom right). The input has an amplitude ν₀ = 20 Hz. C, Amount of suppression/facilitation as a function of the spontaneous excitatory firing rate. Colored dot represents different interneuron gain (see inset). Black triangles represent the CUBA model, which shows little suppression but facilitation. The input has an amplitude ν₀ = 10 Hz. D, Representative ST suppressive/facilitative patterns as marked in C by different geometric shapes (circle, square, pentagon, triangle). C, Star represents the model parameters used for obtaining the suppressive pattern shown in B.

τ_E,I = 5 ms. The quantal conductances are Q_E = 1 nS and Q_I = 5 nS. We then consider a random network with p = 5% of connectivity and 80% of excitatory neurons.

The activity of the network is simulated using a mean-field model of recurrent dynamics (for review, see Renart et al., 2003). The mean-field approach reduces the complex recurrent dynamics resulting from the single-cell integration and synaptic interactions within the network (Eqs. 4–6) to the temporal evolution of the firing rates of the populations. Briefly, to perform such a reduction, we hypothesize that spike trains follow the statistics of Poisson point processes (and can therefore be statistically described by their underlying rate of events) and that all neurons receive an average synaptic input derived from the connectivity property of the network and the mean firing rate (the “mean-field” hypothesis) of their input populations. From those hypotheses, it results that the firing rate of a population follows the behavior of a prototypical neuron whose dynamics are captured by a single function (the transfer function) that translates the set of input rates to an output firing rate. For the model presented here, such a derivation has been shown capable of quantitatively predicting the stationary activity of the network and its response to external stimuli (Zerlaut et al., 2018; di Volo et al., 2019). Together, the dynamical system describing the temporal evolution of the excitatory and inhibitory populations of the spatially extended ring model read as follows:

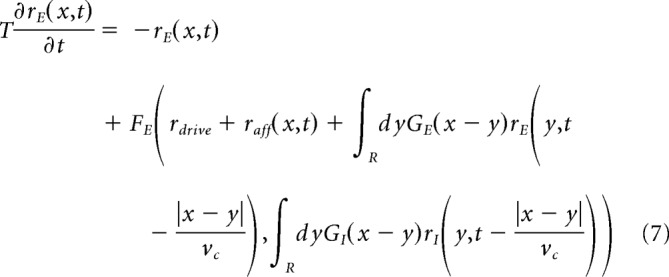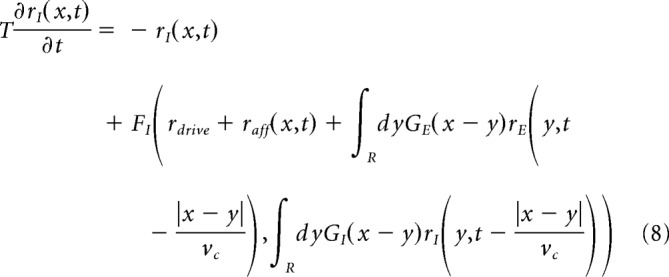where r_E/I(x,t) is the population rate of excitatory/inhibitory cells at the space-time position (x,t), r_aff(x,t) is the excitatory afferent input targeting both excitatory and inhibitory populations, and G_E/I is the spatial connectivity in between subpopulations that we chose as Gaussian of width l_exc = 5 mm (excitation) and l_inh = 2.5 mm (inhibition). We consider a higher lateral extent of the excitatory connectivity with respect to the inhibitory one, in accordance to anatomical data (Buzás st al., 2006). Moreover, v_c = 300 mm/s is the axonal conduction speed, r_drive is the time/space constant average rate of Poissonian excitatory spikes that every neuron receives, and T = 5 ms is the decay time of population rate. The functions F_E,I are the transfer functions of excitatory/inhibitory neurons and are calculated according to a semianalytical tool as in Zerlaut et al. (2018) through an expansion in function of the three statistics of neurons voltage, that is, its average μ_v, its SD σ_v, and its autocorrelation time τ_v as follows:

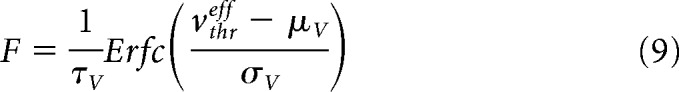where Erfc is the error function and the effective threshold v_thr^eff is expressed as a first-order expansion with some fitting coefficients in function of (μ_v, σ_v, τ_v). More details on this procedure can be found in Zerlaut et al. (2018) and di Volo et al. (2019). The values (μ_v, σ_v, τ_v) are calculated from shot-noise theory (Daley and Vere-Jones, 2007). Introducing the following quantities:

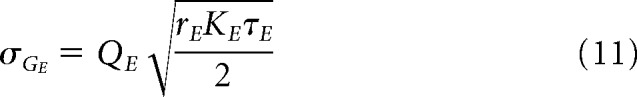where K_E/I is the amount synapses related to presynaptic excitatory/inhibitory neurons (we consider a network of N = 10,000 neurons inside each node of the ring), we obtain the following equations for the voltage moments:

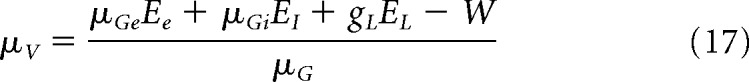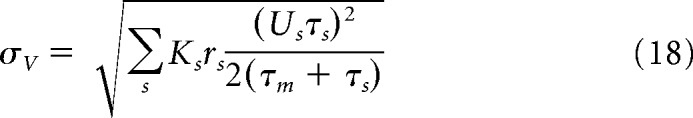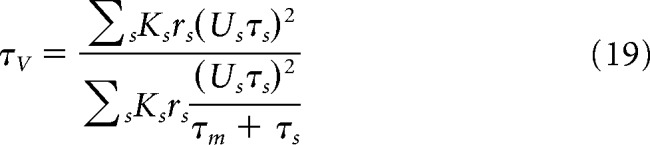In a static version of this mean-field model (Zerlaut et al., 2018), the adaptation W is considered as a function of the excitatory firing rate (i.e., W = τ_w × b × r_E). Now if we take into account the time evolution of adaptation (see Eq. 5), W obeys the following dynamical equation (di Volo et al., 2019):

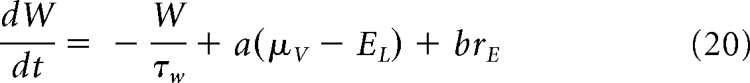In this article, we use mainly the static version of the mean-field model, but we compare with its dynamical version to investigate the role of adaptation (see Fig. 6).

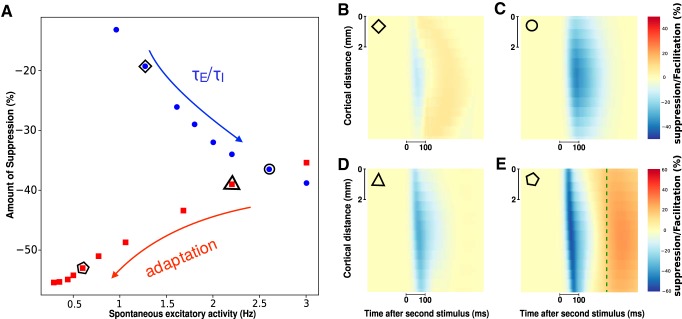
Figure 6.

The effect of spike-frequency adaptation on the suppressive wave. A, Maximum of wave suppression (across space and time) for different values of adaptation strength b (dynamic adaptation model, red squares) and ratio between excitatory and inhibitory synaptic time scales (static adaptation model, blue dots). The values of b range from 0 to 100 pA, and the values of τ_E range from 3 to 9 ms (while τ_I = 5 ms); both arrows point to an increase in the values of b and τ_E. On the x axes, we report the corresponding value of spontaneous excitatory firing rate. B–E, Suppressive wave for four parameter values (see associated symbols in A). E, Dashed green line indicates the beginning of the hyperpolarization period of the model response due to adaptation. The excitatory external drive is r_drive = 3.5 Hz for blue dots (b = 80 pA) and r_drive = 1.2 Hz for red squares (τ_E = τ_I = 5 ms), and the amplitude of the input is A = 10 Hz for both blue dots and red squares.

The afferent input has the following form:

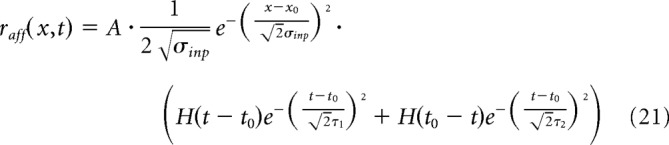where A is the input amplitude, (x₀, t₀) the stimulus location, and H is the Heaviside function. The spatial extension of the stimuli is σ_inp = 3.5 mm, the time rise τ₁ = 15 ms, and the decay time τ₂ = 90 ms.

The time delay in between stimulus 1 and stimulus 2 is Δ_t = 100 ms (if not stated differently) and the spatial distance Δ_x = 7 mm. The VSDI signal is calculated as follows:

where μ_V⁰ is the average voltage prestimuli.

Current-based (CUBA) model.

The CUBA is obtained by considering the following synaptic coupling:

where Q_E^CU = 0.03 pA and Q_I^CU = − 0.15 pA are the coupling with excitatory and inhibitory neurons. The rest of the parameters are the same. The voltage of the neurons is calculated as follows:

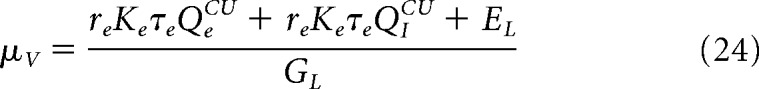Also in this case, we use the same methodology to estimate the neurons transfer function as done for the conductance-based (COBA) model.

Different FS gain.

To modify the gain of FS cells, we manually change the transfer function F_I(r_E, r_I). In practice, for any r_I, we calculate the value r*_E for which F_I changes convexity. This gives us the slope ${\sigma }_r=\frac{dF\left(r_E,r_I\right)}{d{r}_E}·\left(r_E^{*},r_I\right)$ and the maximal value F_max that we estimate calculating F for very high rates (typically r_E = 200 Hz). We then use the following function:

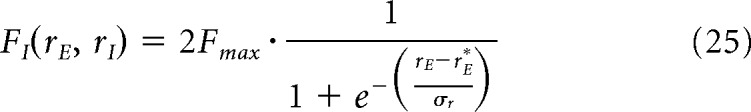where we recall that r*_E and ν_r change in function of r_I. This permits us to have a sigmoidal form of the transfer function F. To change its slope, we use a factor γ that scales the slope, which becomes then γσ_r. In Figure 4, we use γ equal to 1.2 or 0.8.

Decoding model.

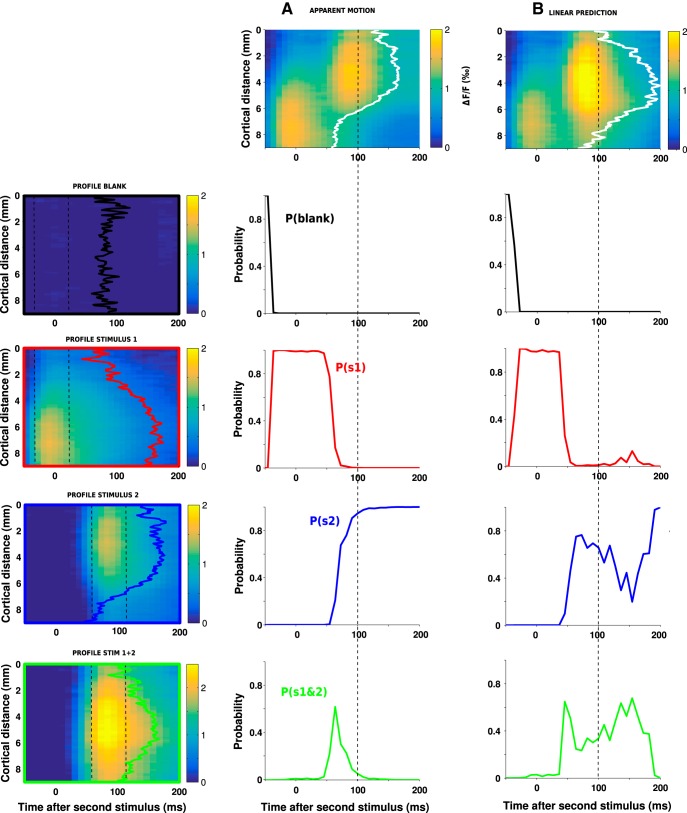
The algorithm for the decoding model used in Figures 7 and 8 is detailed here. First, the ST data (i.e., space-time matrix) were whitened by applying a ZCA transformation, such that, on average, the dimensions are statistically decorrelated and the variance along each dimension is equal to 1. This transformation is necessary to satisfy the hypothesis underlying the decoding model, which computes joint probabilities in multiple dimensions. The whitening matrix was computed from the eigen-decomposition of the covariance matrix of the blank data. Next, the four spatial profiles (blank, stimulus 1, stimulus 2, and joint stimulus 1 and 2) were computed by averaging the corresponding ST response in a 50 ms window around the time of maximum response and then normalized. The decoding of any ST data (e.g., the observed activity evoked by a 6.6 °/s two stroke apparent motion stimulus “obs” or its linearly predicted pattern “pred”) thus consisted of evaluating the likelihood that the spatial profile observed at one point in time of the data A(x,t) was best correlated with one of the four spatial profiles S_j with j ∈ {1:4}. This comes down to calculating the four probability P_j(t) of the following form:

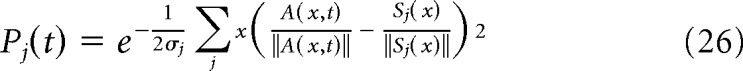where σ_j is the averaged SD of the residual activity between A(x, t) and S_j(x).

Figure 7.

A dynamic decoding of stimulus position: principle. The decoding of stimulus position on ST maps, here taking the example of the activity evoked by a 6.6°/s lrAM stimulus shown in A or the activity pattern predicted by the linear combination in space and time of the responses to both individual stimuli in B. The decoding consists of evaluating the probabilities that the spatial profile observed at each point in time (A,B, white contours) is similar to one of the four spatial profiles shown on the left column: Blank (first row, black profile), S1 (second row, red profile), S2 (third row, blue profile), and the joint S1 and S2 (last row, green profile). Each profile was computed by averaging the corresponding ST response in a 50 ms window around the time of maximum response and normalized. The four color-coded probabilities are, respectively, plotted as a function of time: time 0 corresponds to the onset of S2 for the lrAM response (column A) and for the linear prediction (column B). Compared with the linear prediction, the actual signal is more rapidly decoded, revealing a likely function of the suppressive wave: shaping stimulus position representation.

Figure 8.

A dynamic decoding of stimulus position: Application to all lrAM speeds and sessions. A, Color-coded probabilities (same as Fig. 7) for the observed lrAM response (first row) and its corresponding linear prediction (second row) for Monkey WA, averaged across three ISI categories: ISI ≤ 25 ms (left column, n = 2), ISI = 50 (central column, n = 6), and ISI ≥ 100 ms (right column, n = 4). Shaded areas represent SEs across sessions. B, Application of the decoding algorithm to all the data of Monkey BR (n = 4, n = 4, and n = 5 sessions for the three ISIs, respectively). C, Explaining away index (see Materials and Methods) computed as the probability of detecting joint S1 and S2 in the observed response minus the probability of detecting joint S1 and S2 in the linear prediction, from Monkey WA data shown in A. D, Explaining away index from Monkey BR data shown in B.

Then, we defined the explaining away index as the probability of detecting joint S1 and S2 in the observed P₄^obs or P_s1&s2^obs minus the probability of detecting joint S1 and S2 in the linear prediction P₄^pred or P_s1&s2^pred as follows:

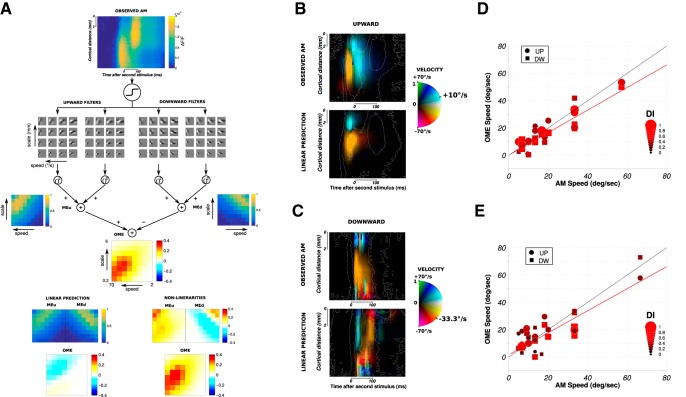
Opponent motion energy (OME) model.

To extract motion information from the population responses, we used the OME model developed by Adelson and Bergen (1985). Briefly, this model consists of combining quadrature pairs of spatial and temporal filters to obtain oriented ST filters (i.e., Gabors) tuned in spatial frequency. The ranges of spatial and temporal frequencies were chosen so that the speed (i.e., FT/FS) of the resulting ST filters varies from 2 to 70°/s and the scale (i.e., 1/FS) from 0.2 to 6 mm. It resulted in 64 (FS, FT) couples representing 8 different speeds and scales. For each couple, we obtained two filters tuned for upward motion and two filters tuned for downward motion. The outputs of quadrature pairs of such filters are then squared and summed to give a phase-independent measure of local motion energy for both directions (i.e., MEu and MEd values). Last, the opponent motion stage computes the difference between the oriented opposite energies (i.e., OME values). Before applying the OME model, the ST data were first normalized and passed through a nonlinearity to account for the VSD to spike rate transformation as proposed by Chen et al. (2012) as follows:

where R_SU and R_VSDI are, respectively, the average firing rate and the average normalized VSDI response, k is a constant and N is an exponent. Here, we took k = 10 and N = 3.8.

Finally, for each ST position on the map, we could extract the velocity of the filter that generated the strongest OME and provide a ST velocity map representation (see Fig. 9B,C) with velocity and amplitude as color hue and color intensity, respectively. We then averaged the encoded velocity within a ST ROI, spatially between S1 and S2 center positions and in time from 10 to 200 ms after stimulus 2 onset, to report a single value of filter speed for each apparent motion speed condition (Fig. 9D,E). The direction-selectivity index is given by the following:

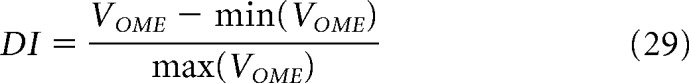where V_OME is the amplitude of the OME.

Figure 9.

Encoding of direction-selective motion signal. A, Application of the OME model (Adelson and Bergen, 1985) to the ST representation of cortical response to an upward 10°/s AM sequence shown at the top (Monkey WA). The first step consists of convolving the ST data with a set of oriented ST filters. Phase independency is obtained by squaring and summing the outputs of quadrature pair of filters, whereas motion opponency is obtained by subtracting the two oriented motion energies (OME = Meu − MEd). The maximal energy values for each ST filter are plotted as a function of speed (in °/s) and scale (in mm). The energy values resulting from the same computation applied on the linear prediction and the nonlinearities for this AM sequence are shown at the bottom left and right, respectively. B, ST representation of the opponent motion energies computed in A. For each ST position, the filter velocity for which the energy was maximal is represented as color hue. The actual speed of the stimulus (here 10°/s) is marked on the color code as a landmark. The amplitude of the energy is coded as color intensity. For comparison, the result for the corresponding linear prediction is shown below. Nonlinearities correspond to observed AM minus the linear prediction. C, Same as in B for Monkey BR, for another AM sequence condition (33.3°/s downward motion). D, For each AM condition (n = 30), the filter speed that generated the strongest OME within an ST ROI (see Materials and Methods) is plotted as a function of the actual lrAM speed for Monkey WA. The color and size of the dots (upward motion conditions) and squares (downward motion conditions) code for the value of the direction-selectivity index (DI). Red line indicates the linear regression fit between OME speed and stimulus speed. Black line indicates the exact linear relationship. E, Same as in D for Monkey BR (n = 32).

Results

Characterizing the mesoscopic ST impulse response function

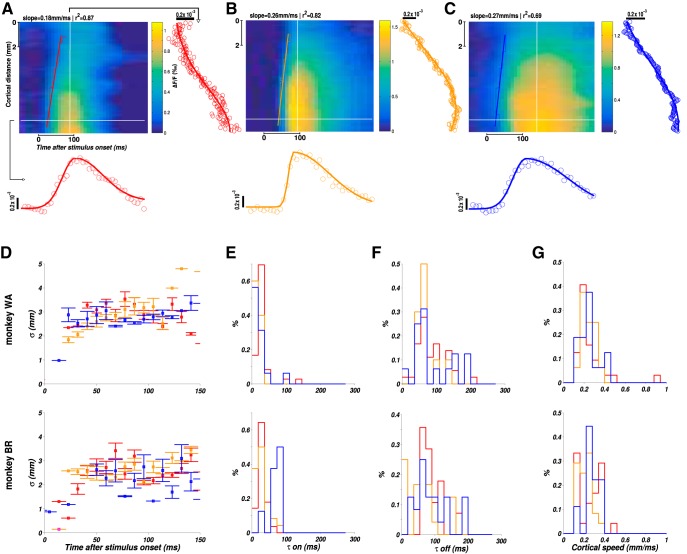
Two-step apparent motion sequences of various ST characteristics (Fig. 1A,B) were presented to 2 behaving monkeys involved in a fixation task. The primary visual cortical response was measured at the level of the population using VSDI (Grinvald and Hildesheim, 2004; Chemla and Chavane, 2010a). In response to a local stimulus (0.25° in diameter) presented for 100 ms in two different visual positions (separated vertically by 1°), activity arises at the retinotopic representation of these two positions and then spreads laterally over millimeters of cortical surface (Fig. 1C, lower position; Fig. 1D, upper position) as already reported in the literature (Grinvald et al., 1994; Reynaud et al., 2012; Muller et al., 2014). V1 activity is hereby reaching positions in space and time well beyond 1° and 50 ms. As a consequence, the evoked spread covers a large cortical extent that can reach the representation of the other stimulus in space and beyond the interstimulus interval in time. The space and time constants of our responses were systematically quantified on the 2 monkeys and for the three stimulus durations we used (10, 50 and 100 ms) on a 2D ST (ST) map (Fig. 2A). To produce these ST maps, cortical activity was averaged within the apparent-motion trajectory (Fig. 1C–G, dotted rectangle at frame 216 ms) to provide a unique spatial cortical dimension (Fig. 2A, ordinate). First, we extracted the space constant of a Gaussian spatial fit for all time points (Fig. 2A, right side of the maps). In both monkeys and across 19 sessions overall (11 for Monkey WA and 8 for Monkey BR), the space constant increased from 1.6 ± 0.5 mm at response onset to reach a maximum of 3.3 ± 0.2 mm, independent of the stimulus duration and monkeys (Fig. 2B; no significant difference observed between all stimuli durations, n = 62 conditions, t test with p > 0.01). The time constants of the response time course at the central representation of the stimulus were measured using two halve Gaussian functions fits (Fig. 2A, below the maps). In both monkeys, the time constant at response onset was on average 23.6 ± 17.2 ms for all stimuli durations, except for Monkey BR with a mean value of 44.5 ± 14.5 ms for 100 ms stimuli (n = 12 conditions; Fig. 2E, blue histogram), and 80 ± 43.6 ms for response offset (Fig. 2F; no significant difference observed between all stimuli durations, t test with p > 0.01). Last, we also extracted the speed at which the response spreads across the cortical surface (Fig. 2A, slanting lines) and obtained a distribution with peak values of ∼0.26 ± 0.14 m/s, similar across monkeys and stimulus durations (t test with p > 0.01), and similar to what has been observed in different species and states (Bringuier et al., 1999; Slovin et al., 2002; Reynaud et al., 2012; Sato et al., 2012; Muller et al., 2014). This analysis showed that the ST integrative properties of the primary visual cortex are mostly independent of stimulus duration and are able to cover a large spatial (3 mm) and temporal (100 ms) extent, bridging the cortical representation between our individual stimuli in space and time.

Figure 2.

ST characteristics of cortical responses to local stimuli. A–C, ST representations of the evoked cortical response to, 10 ms (A, red), 50 ms (B, purple), and 100 ms (C, blue) local stimuli. To produce the ST representation, we averaged spatial data along the stimulus trajectory (Fig. 1C–G, rectangle in frame 216 ms). For each spatial point, the temporal data were fitted to a combination of two half Gaussians, as illustrated for one specific point in space (horizontal white line on the ST diagram) below the ST maps. Similarly, for each time frame, the spatial data were fitted to a Gaussian function as shown on the right side of each ST map for one specific point in time (vertical white line). D, Space constant of the Gaussian spatial fit (σ parameter) plotted as a function of time for the three considered durations (10 ms in red, 50 ms in magenta, and 100 ms in blue) and for the 2 monkeys (top: Monkey WA; bottom: Monkey BR). Error bars indicate SEs across sessions (n = 8 for each of the three duration conditions). E, Histograms of time constant at response onset (τ_on) estimated from the temporal fit of the response for the three considered durations and the 2 monkeys. F, Histograms of time constant at response offset (τ_off) estimated from the temporal fit of the response for the three considered durations and the 2 monkeys. G, Histograms of cortical speed of propagation estimated by linear regression on response latency (stairs-step contours, slanting lines, and slope of the linear regression in Fig. 2A–C) for the three considered durations and the 2 monkeys.

The evoked response to the lrAM is shaped by a suppressive wave

We next asked whether such lateral interactions contribute to shape the evoked population response to the temporal succession of these two stimuli. For that purpose, we measured the cortical population response to a two-stroke upward apparent motion sequence (Fig. 1E). Such temporal sequence generates a propagation of activity starting at the cortical representation of the first stimulus (S1) and moving to the cortical representation of the second stimulus (S2), a cortical correlate of the illusory motion (Jancke et al., 2004). The observed pattern of activity departs from the pattern predicted by a simple linear summation of the lower and upper stimuli (Fig. 1F). If we subtract the observed (Fig. 1E) and the linear predicted responses (Fig. 1F), two deviations from linearities are observed. First, a suppression emerges at response onset and at the cortical representation of S2 (compare 1D and 1G at frame 216 ms). The suppression then gradually propagates over the cortical surface toward the representation of S1 (Fig. 1G). We can hypothesize that the evoked activities by the two stimuli composing the lrAM sequence interact together to generate this dynamic pattern of suppression. Because the suppression is observed at the onset time of the response to S2, it has to be due to the activity dynamics generated by S1 interacting with the integration of S2. However, the propagation of suppression from the representation of S2 toward the representation of S1 is probably due to the activity dynamics evoked by S2 interacting with the residual activity evoked by S1. Therefore, the suppression wave could likely be the result of multiple interactions (e.g., bidirectional) between the activities evoked by the stimulus sequence.

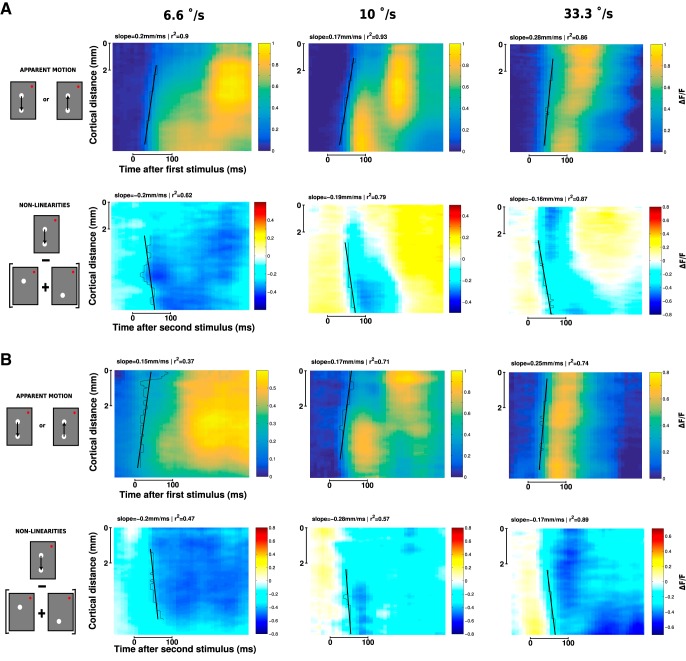
The suppressive wave is systematically observed

To better investigate how spreads of evoked activity and suppression shape the representation of lrAM, we first show ST representations of examples taken for both monkeys and three stimuli speeds. The example of Figure 1 is shown in Figure 3A (6.6°/s). In these ST representations, we can observe a clear propagation of activity in response to a local stimulus (Fig. 3A,B, slanting lines) that is qualitatively remarkably similar across both monkeys (Fig. 3A,B, first rows) and speeds (three columns, respectively, for 6.6, 10, and 33.3°/s), as shown in Figure 2G. The ST representation of nonlinearities (lower rows), recentered on S2 onset, shows that suppression first appears at the cortical representation of S2 and at S2 response onset, and then propagates toward the representation of S1, at a similar speed than the one observed for the evoked activity to the first stimulus (Fig. 3A,B, second rows, slanting lines). In both monkeys and the three examples shown, this suppression propagates in a direction opposite to the apparent motion sequence, from S2 to S1 representations. Functionally, we propose that it results in dampening the residual activity generated by S1.

Figure 3.

The apparent motion stimulus induces a systematic suppression wave. ST representation of VSDI responses to two-stroke apparent motion stimuli for three different speeds (6.6, 10, and 33.3°/s separated in 3 columns) and 2 animals: A, Monkey WA; B, Monkey BR. A, B, Top rows represent the observed response. Bottom rows represent the nonlinearities of the response (observed − linear prediction). Estimates of speed propagation are reported on each ST diagram. Black stairs step represents contours at threshold level. Slanting lines indicate the slopes of the linear regressions. Similar speeds are observed for both the observed activity and the nonlinearities.

The suppressive wave propagates at the same speed and with the same extent as the evoked spread

This suppressive wave was systematically observed for all two-stroke lrAM conditions tested (Fig. 1B). This can be seen in the ST-evoked response (centered on the onset of S1) and nonlinearities (centered on the onset of S2) averaged across all conditions and sessions for both monkeys (Fig. 4A, left: n = 30 conditions for Monkey WA, right: n = 32 conditions for Monkey BR). To better understand the origin of the suppression dynamics and its dependence on stimulus conditions, we characterized its ST properties. First, we measured the onset of the appearance of the suppression at S2 position. The latency of the observed suppression was the same as the latency of the activity evoked by S2 alone (Fig. 4B; the values of mean ± SE across conditions are, respectively, 39.5 ± 2.0 ms vs 38.6 ± 1.6 ms for Monkey WA and 36.6 ± 1.8 ms vs 36.9 ± 2.1 ms for Monkey BR, nonsignificantly different, t test with p = 0.77 and p = 0.35, respectively, for Monkeys WA and BR). However, the suppression resulted in significantly delaying the response onset evoked by S2 when presented within the apparent motion sequence (54.2 ± 2.0 ms and 68.3 ± 5.3 ms for Monkeys WA and BR, respectively; Fig. 4B). Then, we quantified the spatial extent of the suppression (σ of a Gaussian fit; Fig. 4C). In all conditions, the spatial extent of the suppression was of ∼2.8 mm (2.49 ± 0.14 mm for Monkey WA and 3.08 ± 0.18 mm for Monkey BR), similar and nonsignificantly different from the spatial extent of the evoked response (2.99 ± 0.11 mm and 2.41 ± 0.17 mm for Monkeys WA and BR, respectively). Thus, the suppressive wave starts at similar latency and covers similar spatial extent as the evoked activity. We next characterized the speed of propagation of activity (Fig. 4D, black) and suppression (Fig. 4D, blue), plotted as a function of stimulus speed. Remarkably, on both monkeys, the observed cortical speeds were identical for both the propagation of activity and the suppression and completely independent of the lrAM speed (0.28 ± 0.26 and 0.27 ± 0.4 m/s, respectively, for Monkey WA and 0.21 ± 0.15 and 0.27 ± 0.2 m/s, respectively, for Monkey BR). However, from the individual ST plots in Figure 3, we noticed that the suppression does not seem to spread but rather propagates as a wave (Muller et al., 2014, 2018). To probe for this hypothesis, we thus compared the dynamics of the response peak position (μ of a Gaussian fit). In a spread, typically, the response peak will not move in space, as observed for the evoked response (Fig. 4E; the peak spatial position is not changing with time, slope of −1.3 × 10⁻⁵ ± 1.1 × 10⁻⁴ m/s and 1.6 × 10⁻⁴ ± 3.4 × 10⁻⁴ m/s for Monkeys WA and BR, respectively), whereas in a wave it will follow the onset spatial displacement, which is what we found for the suppression (Fig. 4E; the peak moves from position 2 to position 1, negative slope of −0.05 ± 0.007 m/s and −0.034 ± 0.005 m/s for Monkeys WA and BR, respectively). However, in contrast to what we previously showed (i.e., the evoked activities are waves hidden by spatial averaging) (Muller et al., 2014), the suppression is still seen as a wave in the averaged data. This is likely to be due to the anisotropy of the suppressive wave traveling from stimulus 2 to stimulus 1, which makes it more resistant to averaging than the evoked propagation of activity, which is isotropic. Together, our results show that the suppression is initiated right at response onset and has similar spatial extent and propagation speed as the activity evoked response. This strongly suggests that the dynamics of the evoked activity and the suppression are mediated by the same general network subtending the observed propagation of evoked activity: the intracortical horizontal network (Muller et al., 2014). If the suppression is generated along the propagation of activity, one prediction is that it should decrease in strength with spatial and temporal separation between the two stimuli composing the lrAM. This is indeed what is observed: the suppression strength decreases as a function of stimulus onset asynchrony and spatial separation (Fig. 4F; t statistics on the slope of the linear regression gives t = −0.92 with p = 0.18 and t = −6.3 with p = 3.6 × 10⁻⁶, respectively, for a spatial interval (SI) of 1° and 2° (Monkey WA); t = −1.2 with p = 0.12 and t = −1.6 with p = 0.05 (Monkey BR)). This suggests that, beyond some spatial and temporal offsets (2° and 200 ms), the suppressive wave will disappear.

The suppressive wave can be the result of a dynamic gain control

What can be the origin of such suppressive wave? Because inhibitory intracortical axons have more limited spatial extent (Buzás et al., 2001), and that feedback from higher areas are excitatory (Salin and Bullier, 1995), we can hypothesize that it does not result from a simple net inhibition, but rather as a byproduct of the excitatory/inhibitory balance (Tsodyks et al., 1997; Ozeki et al., 2009). Indeed, as demonstrated using center-surround stimulations, the suppressive wave can be the result of a simple dynamic input normalization fed by propagation along the horizontal network (Reynaud et al., 2012). To determine the possible mechanisms generating the observed suppression, we used a mean-field model designed to reproduce accurately VSDI (Zerlaut et al., 2018). In this model, it was assumed that each pixel of the VSDI represents the average V_m of two populations of interacting neurons: excitatory RS neurons and inhibitory FS neurons (Chemla and Chavane, 2010b). Arranging this model into a spatially extended interconnected population of RS-FS cells (Fig. 5A; see Materials and Methods) allows to simulate the propagating waves observed in awake monkey under VSDI. The great advantage of such model is to explicitly take into account COBA interactions as well as a different gain between excitation and inhibition. These ingredients are often neglected as they introduce difficulties in mathematical tractability of mean-field models (Vogels et al., 2005; Landau et al., 2016). Nevertheless, these features are biologically relevant and, as we show here, are actually the main elements determining wave suppression. Examples of two independent waves are shown in Figure 5B (top row). When the two stimuli are presented in succession (Fig. 5B, bottom left), the observed response shows a suppression (Fig. 5B, bottom right), whose values are quantitatively similar to those of experimental data (suppression of ∼50% of the response max). Such suppressive effect was robustly observed across a wide range of parameter space. The first parameter that was found to strongly affect the suppression is the ongoing spontaneous activity of the system before stimulus. As we report in Figure 5C (COBA model, red dots), the suppression decreases when the spontaneous activity of the system increases (Fig. 5D, example marked by circle). Moreover, two further mechanisms were necessary to explain this suppressive effect. First, inhibitory cells need to have a higher gain than excitatory cells. When the gain of FS cells was reduced (Fig. 5C, inset) to have a gain closer to the one of RS cells, the suppression effect was strongly affected (Fig. 5C, blue dots; Fig. 5D, example marked by square). Accordingly, increasing FS cell gain (Fig. 5C, cyan dots; Fig. 5D, example marked by pentagon) increases the suppression strength. Second, the interaction between excitatory and inhibitory inputs needed to occur through conductance-based mechanisms. Indeed, when using a CUBA model (see Materials and Methods), we mostly observed facilitation (Fig. 5C, black triangles) that do not appear to propagate (Fig. 5D, example marked by triangle). While we do not exclude that such suppression may be observed with current-based synapses, it is clear from these data that the nonlinearity of conductance-based synapses induces a strong suppression in the VSDI signal. The suppression can thus be explained by the mesoscopic combination of the nonlinearity of conductance interactions and the differential gain of excitatory and inhibitory cells. Even if the fundamental mechanisms yielding the suppressive wave are linked to voltage-dependent synapses and a higher gain for inhibition than excitation, the intensity of the suppression wave can be affected by additional nonlinearities. By comparing with a recently developed mean-field model (di Volo et al., 2019) where spike-frequency adaptation evolves dynamically, we observed that the intensity of the suppressive wave is affected by adaptation (Fig. 6, red squares). Moreover, by increasing adaptation strength, we report an increase in the intensity of suppression (Fig. 6D,E) together with a decrease in the spontaneous firing activity of the network (Fig. 6A, red arrow). Nevertheless, the suppression wave appears before the hyperpolarization due to adaptation (Fig. 6E, dotted green line), thus indicating that the observed phenomenon is mainly due to conductance changes and not related to cell repolarization after the appearance of the first stimulus. The presence of an asynchronous irregular spontaneous dynamic is necessary for observing such phenomena, as in our model a pathological synchronous regular state does not show any responsiveness to external stimuli (Zerlaut and Destexhe, 2017). Furthermore, such dynamical regimen of spontaneous activity is present for a large portion of parameters (external drive, synaptic time scale, and quantal coupling) and is an emergent property of the network and not a consequence of an ad hoc parameter choice (Tsodyks and Sejnowski, 1995; van Vreeswijk and Sompolinsky, 1996). By increasing the ratio between excitatory and inhibitory synaptic time scale (spanning over a range of τ_E/τ_I between 0.8 and 1.6), we observe an increased suppression in the propagating wave (Fig. 6A, blue dots). Accordingly, even if its intensity may vary, the suppressive nature of wave interaction is robustly observed over the whole range of parameters corresponding to an asynchronous irregular spontaneous regimen (Fig. 6B,C). Moreover, the connectivity profile (excitatory vs inhibitory connectivity length) can affect the overall dynamics, even though we verified that the stability of the asynchronous irregular state is robust with respect to relatively small variations of these parameters. In addition, excitatory and inhibitory connectivity distances have been inferred by a minimization procedure to match model results with VSDI data and are in agreement with anatomical information (Zerlaut et al., 2018).

The function of the suppressive wave is to explain away ambiguous representations

What can be the function of the suppressive wave? Here we propose that it will shape an unambiguous representation of motion along the apparent-motion trajectory. Indeed, dampening the cortical representation of the initial stimulus when the second stimulus is being processed will have as a consequence to represent only one stimulus at a time, hereby improving motion representation by explaining away ambiguous position representation (problem of “phenomenal identity”) (Ternus, 1926). To test such a hypothesis, we developed a simple algorithm to decode, at every instant, what is the most probable stimulus position that evoked the observed cortical spatial profile out of four categories: no stimulus, S1, S2, or joint S1 and S2. We used the ST representations of the evoked activity to the apparent motion sequence (Fig. 7A) and used the linear prediction (Fig. 7B) as a control. The decoding was computed using the joint probability that the spatial profile observed at one point in time (white profile) is drawn from the spatial profile observed during blank (first row, black), S1 (second row, red), S2 (third row, blue), or the joint S1 and S2 (last row, green). In the example shown in Figure 7, we apply this decoding method to the activity evoked by a 6.6°/s two stroke apparent motion stimulus (Fig. 7A). When S1 is presented (red), the probability that the spatial profile of the evoked response will be similar to the blank distribution is quickly dropping from 1 to 0 and the probability that the evoked response will be decoded as being evoked by S1 alone is jumping from 0 to 1 very rapidly (in 10 ms). When S2 is presented (at time 50 ms), there is a sharp and rapid transition from the evoked activity being decoded as S1 to S2 (blue) in ∼50 ms. In contrast, the probability that the evoked activity is evoked by S1 and S2 at the same time (green) increases moderately (peaking at 0.5) and transiently. In contrast, when we apply the same approach to the linear prediction (Fig. 7B), while the beginning of the decoding is the same (two first rows), as expected, when S2 appears, the evoked activity is ambiguously decoded as being attributed to S2 or S1 and S2 conjointly with similar probability (∼0.5) and sustained over the response duration.

We applied this approach to all speeds and sessions in both monkeys (Fig. 8A,B), for SI of 1°, differentiated across the different ISIs. We separated these conditions because, when S2 appears, the residual activity in response to S1 will be less important for long ISI (the offset time constant being of the order of 80 ms). In both monkeys and for ISI ≤ 50 ms, the averaged results confirm the individual example shown in Figure 7: the evoked activity results in a sharp and clear transition from the representation of S1 to the representation of S2, with only transient and moderate increase of the representation of S1 and S2 conjointly. In comparison, the linear prediction always leads to an ambiguous representation that cannot tease apart the probability that the evoked activity is coming from S2 alone or S1 and S2 together (blue and green curves merging together). For an ISI ≥ 100 ms, in contrast, the evoked activity resembles more the linear prediction, as expected given the reduction of the suppression strength (Fig. 4F).

To quantify the effect of explaining away ambiguous positional representations during lrAM stimulations, we calculated an index by subtracting the probability of detecting joint S1 and S2 in the observed and the linear prediction for both monkeys, I_E.A. = P_s1&s2^obs − P_s1&s2^pred (Fig. 8C,D), and both stimuli SIs of 1° and 2° (first and second rows, respectively). In all conditions but the long SI and long ISI, a systematic decrease of the index was observed. This reveals a dynamic effect of explaining away the ambiguous representation of S1 and S2. Importantly, in both monkeys and practically all conditions (ISIs and stimulus separations), we observed two peaks in the index decrease. They correspond to the bidirectional interactions occurring for each of the two evoked waves. The first peak corresponds to the effect of delaying response onset to S2 (by propagating activity from S1 to S2), and the second peak corresponds to a shortening of the representation of S1 (by propagating activity from S2 to S1). Importantly, this calculation revealed two further phenomena that are expected because of the propagation delay and spatial extent. First, the timing of the second peak is delayed when going from 1° to 2° spatial separation. Second, the general amplitude of the decrease diminishes from short to longer ISI and from short to larger spatial separation, as expected from the observed reduction in the suppression strength with spatial and temporal offsets (Fig. 4F).

Unambiguous representation for encoding the stimulus velocity in V1

Shaping the cortical population representation of the lrAM could promote an accurate encoding of direction-selective motion signals for a straightforward read-out by downstream area. Indeed, keeping the representation of only one stimulus at a time on the cortex will automatically detect motion signal. Actually, the residual transient ambiguous representation often observed between stimulus 1 and stimulus 2 could also participate in shaping the motion energy signal by providing an intermediary activity in space and time. To test whether the measured cortical response encodes an accurate direction-selective signal, we applied OME filters directly to V1 population responses (Adelson and Bergen, 1985). Indeed, direction selectivity in MT is well described and captured by motion energy models (Adelson and Bergen, 1985; Rust et al., 2006). Such an approach is generally developed to model MT receptive field from an ST input image. The rationale here is to apply the same processing directly to V1 population responses that feed downstream areas, such as MT or V4. This is justified by the fact that the cortical extent imaged here (∼9 mm, corresponding to 3°) (Dow et al., 1981; Van Essen et al., 1984) actually corresponds to the V1 cortical extent converging to a MT or V4 neuron at our recorded eccentricity (3°) (Albright and Desimone, 1987; Gattass et al., 1988). Because we record VSD responses that represent both subthreshold and suprathreshold activities (Chemla and Chavane, 2010b), we first processed our ST maps through a nonlinearity to account, as a first approximation, for the VSD to spike rate transformation (Chen et al., 2012) (Fig. 9A; see Materials and Methods). The resulting ST maps were convolved with a set of ST filters covering a wide range of speeds and scales. For a given value of filter speed and scale, we squared and summed the convolution from filters in quadrature, and subtracted the resulting phase-independent measure of local motion energy for opposite directions (i.e., MEu − MEd) to obtain the OME response (Fig. 9A). We thereby obtained the OME for all speeds, scales, and directions. For each position on the ST map, we could hence extract the filter velocity for which the OME is maximal, that we represented for both monkeys, and different velocities (10°/s upward in Monkey WA, Fig. 9B; and −33°/s downward in Monkey BR, Fig. 9C). In this representation, the color hue represents the velocity of the filter yielding a maximal OME, and the color intensity its amplitude (as a fraction of the maximum evoked fluorescence response). The contour of the evoked response is overlaid in white to ease comparison. The same analysis on the corresponding linear predictions serves as a control (Fig. 9B,C, bottom). For all the conditions we explored, we then extracted the values of the encoded velocity averaged within a ST ROI (between S1 and S2 centers and from 10 to 200 ms after stimulus 2 onset) and represented them as a function of the AM speed for both monkeys (Fig. 9D,E). Our results show that the ST response, shaped through the suppressive wave, is indeed generating a direction selective motion energy for a speed that is well correlated with the stimulus speed (R² of the regression lines, in red, shown in Fig. 9D,E; R² = 0.80 and R² = 0.65 for Monkeys WA and BR, respectively). In other words, intracortical nonlinear interactions in V1 promote an unambiguous encoding of velocity-selective motion signal along the apparent motion path.

Discussion

We have shown that intracortical interactions play a key role in shaping the sensory representation of the lrAM within the retinotopic map of V1 in awake monkeys. Our results demonstrate that intracortical propagation encompasses large spatial and temporal distances allowing to link information separated by 1°–2° and ∼100 ms. Importantly, above these values, the apparent motion illusion gradually fades out (Kolers, 1972; Cavanagh and Mather, 1989). In response to the lrAM sequence, we observe a clear displacement of activity on the cortical surface that deviates from the linear prediction in two aspects. First, the initial stimulus suppresses and delays the response to the second stimulus. Second, a suppressive wave is evoked by the second stimulus that attenuates the residual activity evoked by the first stimulus. The ST characteristics of the suppression show similar spatial constant and propagation speed as for the evoked activity, independent of the speed of the stimulus. We propose that the suppression arises from a simple gain-control mechanism pooling feedforward and horizontal inputs (Reynaud et al., 2012). To demonstrate this, we used a conductance-based mean-field model developed to account for VSD dynamics (Zerlaut et al., 2018). This model shows that the observed suppression can be explained by nonlinear conductance interactions, combined with the different gain of excitatory and inhibitory cells. We further demonstrate that the suppressive wave acts as explaining away the ambiguous representation allowing to represent only one stimulus at a time in the cortex. Likewise, such unambiguous representation allows V1 to encode accurately the velocity signal of the lrAM.

Suppression and normalization as generic operations in the visual system

The dynamics of the suppression is seen here as a central and key mechanism by which the input is shaped and normalized by V1 population. When more than one stimulus is present in a visual scene, suppressive interactions between the feedforward-driven activities is what is traditionally reported, such as the surround suppression (Blakemore and Tobin, 1972; Angelucci et al., 2002; Cavanaugh et al., 2002). This suppression is generally attributed to be an emergent property of the divisive normalization computation (Carandini and Heeger, 2011), that is dynamic and propagates from the stimulus surround toward the center (Reynaud et al., 2012). Adding a new lateral input, which presumably contains excitatory and inhibitory synapses, therefore results in a net suppression, the so-called paradoxical inhibitory effect (Tsodyks et al., 1997; Ozeki et al., 2009). It is noteworthy that similar suppression was also seen in response to line-motion stimuli (Jancke et al., 2004), temporal sequence of dark and bright stimuli eliciting motion percepts (Rekauzke et al., 2016) and apparent motion presentation with >2 strokes (data not shown). We believe that dynamic nonlinear interactions subtended by intracortical network acts as a canonical gain control shaping the representation of visual stimulus in space and in time.

Modeling the suppressive waves

Possible mechanisms underlying the observed suppressive effects were investigated using a mean-field computational model (Markounikau et al., 2010), that has been spatially extended. Earlier studies also suggested the importance of inhibition to shape the time course of the evoked response (Ozeki et al., 2009; Jancke and Erlangen, 2010). We found that the model can reproduce the observed suppression, provided two mechanisms are present: excitatory and inhibitory cells have a different gain and excitatory and inhibitory synaptic inputs must combine through conductance-based interactions. Although these two mechanisms are well known, they are usually neglected in mean-field models because they represent a mathematical difficulty. The classic mean-field models with linear (current-based) interactions and uniform gain in all cells fail to reproduce the suppressive effect of propagating waves, and thus the present model can be considered as a step toward biologically more realistic mean-field models. Hereby, we could demonstrate that this suppressive wave is an expected byproduct of the known anatomy and does not need to be expressed solely by pure inhibition.

Backward suppression to keep track of object identity along the apparent motion path

This suppression can help to represent unambiguously one object at a time on the cortical surface, as our decoding model suggests. This means that the lateral interactions can link the transient ST events while keeping track of the object moving along the trajectory. This could be one mechanism involved in solving the correspondence problem (Ullman, 1978). This problem, first introduced by Ternus (1926; see also Ullman, 1978), shows that we need to keep track of the identity of an object in movement to resolve the problem of correspondence. Moreover, ST coherence seems to be more important than shape or color consistency through a backward “reviewing” mechanism (Kahneman et al., 1992). We believe that the mechanism of suppression we unveil here, also moving backwards, is an elementary and preliminary form of this reviewing process, explaining away undesired motion signal in the representation of the object trajectory. This could explain the ability of our visual system to detect objects based solely on the coherence of their ST trajectory (Watamaniuk et al., 1995). Furthermore, computational studies suggested that this ability to detect coherent trajectories necessitates propagation of information in retinotopic reference frames (Perrinet and Masson, 2012), in full accordance with our results.

Local versus global motion processing

The processing that we describe here clearly departs from classical motion integration documented in short-range apparent motion (Mikami et al., 1986a,b) In these stimuli, motion occurs and is evenly distributed within a stationary aperture typically covering a receptive field, and motion is extracted locally through motion energy detectors (Pack et al., 2006; Majaj et al., 2007). Simple L-NL hierarchical models account very well for the selective properties of neurons in V1 and MT in response to such kind of drifting or RDK stimuli (Carandini et al., 2005; Rust et al., 2006). However, there should be intrinsic differences in the processes involved in integrating local drifting motion versus global trajectory motion of a single object. Indeed, Hedges et al. (2011) have shown that MT receptive fields are only sensitive to local motion presented within stationary aperture, totally independent of the direction of long-range trajectory simulation in which these local motion stimuli are embedded. What are the neuronal processing involved to extract motion information along a trajectory? The experiments of Watamaniuk et al. (1995) show that this processing cannot be simply integrated from large receptive field of downstream areas. Our experiment here strongly reinforces the idea that the visual system encodes motion trajectory at mesoscopic level within retinotopic map (Jancke et al., 1999, 2004; Chavane et al., 2000; Roland et al., 2006; Zhang et al., 2012; Muller et al., 2014, 2018; Rekauzke et al., 2016).

Encoding the motion trajectory in the retinotopic map for read-out by downstream areas

The suppressive wave we documented decreases the residual activity evoked by the first stimulus, hereby shaping the dynamic response within the retinotopic map of V1 that could be read out as motion information by a downstream area. V4 or MT neurons have receptive fields whose retinotopic size encompasses the cortical region we imaged in this study. As shown by our read-out analysis (Fig. 9), those neurons will be able to simply detect this population-encoded direction selective motion information through motion energy detectors (Adelson and Bergen, 1985). This signifies that V1 intracortical interactions would preformat the population representation of lrAM for read-out by downstream areas (Adelson and Bergen, 1985; Mumford, 1991, 1992). These results are in accordance with human fMRI experiments that showed that V1 is actively involved in the network that processes the perceived illusory lrAM (Muckli et al., 2005).

lrAM along ventral and dorsal streams, feedback versus horizontal propagation

In the visual cortex of the ferret, it was shown, using VSDI, that lrAM induces feedback propagation of differential activity from area 21 (Ahmed et al., 2008). Similarly, using stimuli that could span a much larger visual scale (16.5° spatial separation) and systematically larger cortical separations, it was suggested that human MT complex feedbacks on early visual cortices to process lrAM (Wibral et al., 2009; Vetter et al., 2015). However, Hedges et al. (2011) suggested that MT may not be the most appropriate area for extracting motion along an lrAM trajectory. Areas on the ventral stream seems to be also implicated in processing such stimuli (Zhuo et al., 2003). Ventral stream areas may actually be well suited because they will process the information about object through strong feedback interactions with V1 (Poort et al., 2012) and are as well strongly involved in motion processing (Ferrera et al., 1994; Roe et al., 2012).

In conclusion, as recently proposed by Muller et al. (2018), traveling waves within and between cortical areas can provide an advantageous framework for dynamic computations that will influence neuronal processing. However, in this review, it was also noted that clear functional roles of these waves have yet to be discovered. Here we show that two discrete stimuli composing the lrAM illusion induce multiple wave interactions, resulting in propagation of suppression in a direction opposite to that of the AM stimulation. This suppression shapes the stimulus response and allows to keep track of the stimulus position along the motion trajectory. We believe that our work has revealed a first elementary step in how the brain links visual stimuli in space and time. Further work will be needed to understand which areas, if any, are reading out the population representation of motion trajectory on V1 retinotopic map and the relative role of intra and intercortical interactions.