Cortical Electrocorticogram (ECoG) Is a Local Signal

Abstract

Electrocorticogram (ECoG), obtained by low-pass filtering the brain signal recorded from a macroelectrode placed on the cortex, is extensively used to find the seizure focus in drug-resistant epilepsy and is of growing importance in cognitive and brain–machine-interfacing studies. To accurately estimate the epileptogenic cortex or to make inferences about cognitive processes, it is important to determine the “spatial spread” of ECoG (i.e., the extent of cortical tissue that contributes to its activity). However, the ECoG spread is currently unknown; even the spread of local field potential (LFP) obtained from microelectrodes is debated, with estimates ranging from a few hundred micrometers to several millimeters. Spatial spread can be estimated by measuring the receptive field (RF) and multiplying by the cortical magnification factor, but this method overestimates the spread because RF size gets inflated due to several factors. This issue can be partially addressed using a model that compares the RFs of two measures, such as LFP and multi-unit activity (MUA). To use this approach for ECoG, we designed a customized array containing both microelectrodes and ECoG electrodes to simultaneously map MUA, LFP, and ECoG RFs from the primary visual cortex of awake monkeys (three female Macaca radiata). The spatial spread of ECoG was surprisingly local (diameter ∼3 mm), only 3 times that of the LFP. Similar results were obtained using a model to simulate ECoG as a sum of LFPs of varying electrode sizes. Our results further validate the use of ECoG in clinical and basic cognitive research.

SIGNIFICANCE STATEMENT Brains signals capture different attributes of the neural network depending on the size and location of the recording electrode. Electrocorticogram (ECoG), obtained by placing macroelectrodes (typically 2–3 mm diameter) on the exposed surface of the cortex, is widely used by neurosurgeons to identify the source of seizures in drug-resistant epileptic patients. The brain area responsible for seizures is subsequently surgically removed. Accurate estimation of the epileptogenic cortex and its removal requires the estimation of spatial spread of ECoG. Here, we estimated the spatial spread of ECoG in five behaving monkeys using two different approaches. Our results suggest that ECoG is a local signal (diameter of ∼3 mm), which can provide a useful tool for clinical, cognitive neuroscience, and brain–machine-interfacing applications.

Introduction

Electrocorticogram (ECoG) refers to the signal obtained from macroelectrodes (typically 2–3 mm in diameter) placed directly on the pial surface of cortex of epileptic patients for localization of the seizure focus (Lesser et al., 2010; Buzsáki et al., 2012; Morshed and Khan, 2014; Yang et al., 2014; Im and Seo, 2016), which is also being increasingly used to study cognition in humans (Engel et al., 2005; Mukamel and Fried, 2012; Parvizi and Kastner, 2018).

To accurately estimate the epileptogenic cortex from ECoG activity or to make inferences about cortical areas involved in cognition, it is essential to determine the spatial spread of ECoG (the cortical tissue around the ECoG electrode that contributes to its activity), but this is currently unknown.

Spatial spread is best studied for multiunit activity (MUA) and local field potential (LFP) recorded using microelectrodes implanted in sensory areas, especially in visual (Xing et al., 2009; Dubey and Ray, 2016) or auditory (Kajikawa and Schroeder, 2011) cortices that contain topographic maps, by presenting small visual stimuli or tone pulses. For example, small visual stimuli activate a small part of the cortex, which can be shifted relative to the electrode by shifting the stimulus in the visual field. This allows an estimation of the “visual spread” or receptive field (RF), which is the visual area (typically measured by fitting a 2D Gaussian and reporting the SD in degrees) that elicits a response. This, when multiplied with the linear cortical magnification factor (MF, defined as the length of cortex that processes a unit degree of visual space), yields the cortical spread. Using this approach, the cortical spread of LFP in the primary visual cortex (V1) has been reported to be local (SD of <∼0.5 mm (Xing et al., 2009; Dubey and Ray, 2016), which has been confirmed by other methods as well (Katzner et al., 2009). However, using analogous methods in auditory cortex, the LFP spread has been shown to be much larger than MUA, extending up to several millimeters (Kajikawa and Schroeder, 2011).

This approach has been used to estimate the RFs of ECoG in humans in a clinical setting as well (Yoshor et al., 2007). Unfortunately, this method overestimates the cortical spread because the RF gets inflated for a variety of reasons such as retinotopic scatter (Albus, 1975) and eye movements. To overcome this issue, Xing et al. (2009) observed that some of these factors inflate the RFs of different types of brain signals, such as MUA and LFP, by the same amount. Therefore, a model that estimates the cortical spread based on the difference of the RFs of MUA and LFP can partially cancel out common factors. In their model, “spatial spread” represented a spatial weighting function that primarily depends on the properties of the recording electrode such as its size, impedance, and location and potential filtering properties of the tissue, but not on the spatial extent of cortical activation (which were captured by other terms that eventually cancelled out). In their data, this approach reduced estimates of the cortical spread of LFP by ∼40%. This model can be applied for estimation of LFP spread because microelectrodes simultaneously provide MUA and LFP signals, but it cannot be applied using only ECoG electrodes, which provide only one signal. Further, a direct comparison of the spreads of LFP in monkeys and ECoG in humans is difficult because of differences in referencing schemes, eye movements, and other experimental details.

To address these issues, we designed a hybrid electrode array that allowed us to simultaneously record MUA, LFP, and ECoG and used the model developed by Xing et al. (2009) to estimate the spatial spread of LFP and ECoG. We also estimated the spread by simulating the ECoG as the sum of LFPs over a progressively larger area and comparing the slope of the power spectral density (PSD) of the simulated and actual ECoG.

Materials and Methods

Animal preparation and recording.

Data used in this study were collected in two separate sets of experiments. The first set was conducted on two male monkeys (Macaca mulatta; weight 11 and 14 kg) at Harvard Medical School and animal protocols were approved by the Harvard Medical School Institutional Animal Care and Use Committee. For this set of experiments, microelectrode and ECoG recordings were performed separately. The behavioral task and recording set up for microelectrode recordings are described in detail in our previous study (Dubey and Ray, 2016). We describe them only briefly here. After monkeys learned the behavioral task, a 10 × 10 microelectrode array grid (96 active channels; Blackrock Microsystems) was implanted in the right V1 (∼15 mm anterior to the occipital ridge and ∼15 mm lateral to the midline). The microelectrodes were 1 mm long and 400 μm apart, with an active electrode region made of platinum and a tip diameter of 3–5 μm. After the microelectrode recordings were completed, we performed a second surgery to insert a custom-made 8 × 8 array of μECoG electrodes (diameter of 40 μm spaced 800 μm apart) and 2 single contact ECoG electrodes (one on each side of the μECoG array) over V1 of the left cerebral hemisphere of the same monkeys. These electrodes were made of platinum (Ad-Tech Medical Instrument) and were attached to the connector made by Blackrock Microsystems (used for microelectrode array recordings) such that the same data acquisition system could be used to record from all types of electrodes. ECoG electrodes were slid under the dura so that they were far away from the μECoG grid. The presence of the large μECoG grid prevented us from putting more ECoG electrodes in V1. However, data from the μECoG array were very noisy and the RFs could not be accurately measured, so these data were not used for further analysis. The ECoG electrodes were discs with an exposed diameter of 2.3 mm, a standard design used in human subdural recordings for monitoring epilepsy. One ECoG electrode in Monkey 2 did not show any stimulus evoked response and was therefore excluded from analysis, yielding three ECoG electrodes from these two monkeys.

In the second set of experiments, we simultaneously recorded spikes, LFP, and ECoG signals from three awake adult female monkeys (Macaca radiata; weight 3.3, 4, and 4.3 kg) at the Indian Institute of Science, Bangalore. The Institutional Animal Ethics Committee of the Indian Institute of Science and the Committee for the Purpose of Control and Supervision of Experiments on Animals approved the guidelines. After monkeys learned the fixation task, a custom-made hybrid electrode array (Fig. 1) was implanted in the left (Monkeys 3 and 4) or right (Monkey 5) hemisphere. This hybrid array had 9 (3 × 3) ECoG electrodes (Ad-Tech Medical Instrument) and 81 (9 × 9) microelectrodes (Blackrock Microsystems), both attached to same connector made by Blackrock Microsystems. As in the previous case, the ECoG contacts were platinum discs of 2.3 mm diameter with a center-to-center inter electrode distance of 10 mm and the microelectrodes were 1 mm long, separated by 400 μ with a tip diameter of 3–5 μm. The silastic between four ECoG electrodes was removed so that the microelectrode array could be inserted in the gap (Fig. 1). Under general anesthesia, a large craniotomy (∼2.8 × 2.2 mm) and a smaller duratomy were performed. Next, the ECoG sheet was inserted through the durotomy and slid on the cortex such that the gap in the silastic was aligned with the duratomy. Finally, the microelectrode array was inserted (Fig. 1). Microelectrode array was placed 10–15 mm from the occipital ridge and 10–15 mm lateral from the midline with the entire length inserted into cortex. Six ECoG electrodes in Monkeys 3 and 5 were posterior to the lunate sulcus (electrodes 1, 2, 4, 5, 7, and 8 in Fig. 1) and were considered for analysis. For Monkey 4, the ECoG grid did not slide easily on the cortex, so one column (electrodes 1–3) had to be removed. Therefore, only four electrodes were in V1 for this monkey. Two reference wires, common for both microelectrode and ECoG grid, were either inserted near the edge of the craniotomy or secured to the metal strap that was used to secure the bone on the craniotomy.

Figure 1.

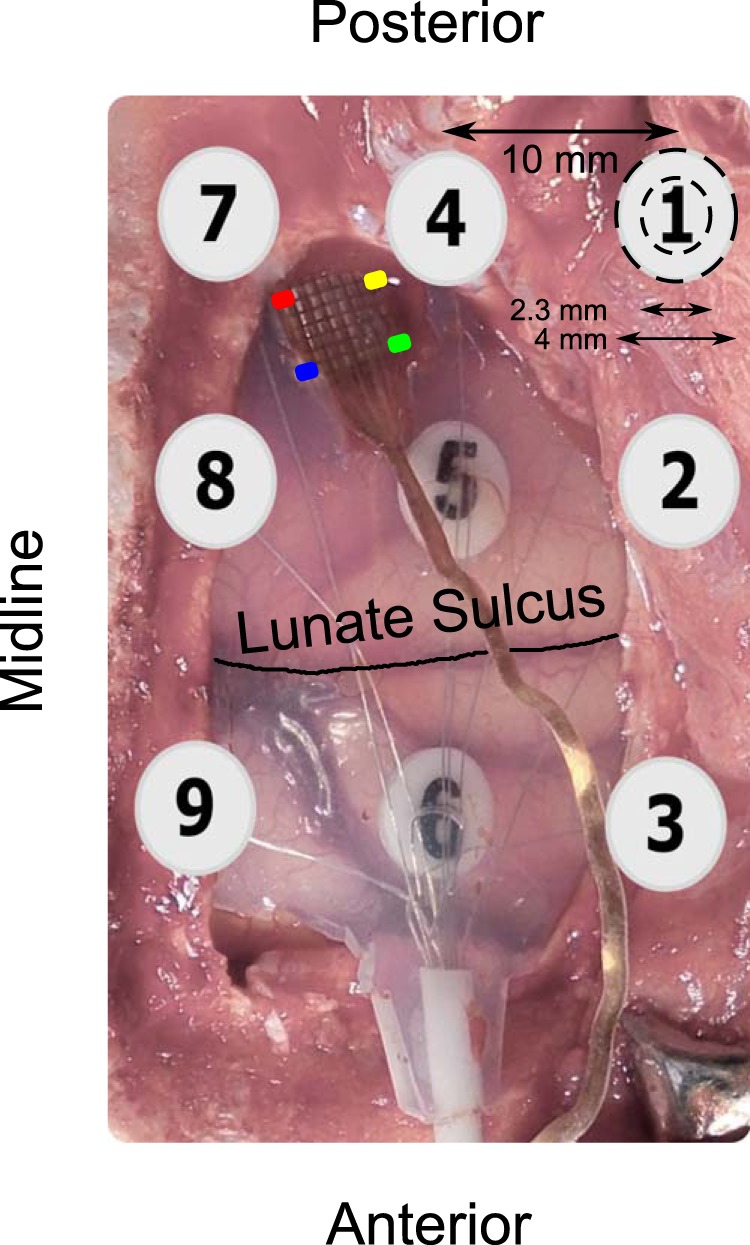
Image of the hybrid grid during surgery. Four corners of the microelectrode array are color coded to provide a reference to the RF centers plotted in Figure 3B. ECoG electrodes posterior to the lunate sulcus are in V1. Only ECoG electrodes 5 and 6 are visible; the remaining electrodes are under the skull and their approximate positions are indicated. ECoG electrodes were 4 mm in diameter with an exposed recording area of 2.3 mm.

The mean impedance of microelectrodes was ∼0.9 MΩ (range: 0.2–1.8 MΩ) at 1 kHz for Monkeys 1 and 2 and ∼0.6 MΩ (range: 0.1–1.8) for Monkeys 3–5. ECoG electrodes had an impedance of ∼50 kΩ for Monkeys 1 and 2 and between 8 and 12 kΩ for Monkeys 3–5. It is unclear why the impedances varied so much, but despite the difference in impedance, the results were very similar across the two sets of recordings.

All signals were recorded using the Blackrock Microsystems data acquisition system (Cerebus neural signal processor). LFP and MUA were recorded from the microelectrode array. LFP and ECoG were obtained by band-pass filtering the raw data between 0.3 Hz (Butterworth filter, first order, analog) and 500 Hz (Butterworth filter, fourth order, digital), sampled at 2 kHz, and digitized at 16-bit resolution. MUA was derived by filtering the raw signal between 250 Hz (Butterworth filter, fourth order, digital) and 7500 Hz (Butterworth filter, third order, analog), followed by an amplitude threshold (set at ∼6.25 (Monkey 1), ∼4.25 (Monkey 2) and ∼5 (Monkey 3, 4 and 5) SDs of the signal).

Behavioral task and RF mapping.

Monkeys 1 and 2 were trained to do an orientation change detection task, in which they held their gaze within 1° of a small central dot (0.05°-0.10° diameter) at the center of a CRT video display (100 Hz refresh rate, 1280 × 768 pixels, gamma corrected) while two achromatic odd symmetric Gabor stimuli were flashed for 200 ms with an interstimulus period of 300 ms. The monkeys were cued to attend to a low-contrast (∼2.6% for Monkey 1 and ∼5.4% for Monkey 2) Gabor stimulus outside of the RF and to respond to a change in the orientation of the Gabor stimulus by 90° in one of the presentations by making a saccade within 500 ms of orientation change. The second stimulus was a small static Gabor [SD of 0.05° and 0.1° for the two monkeys; spatial frequency of 5 cycles per degree (CPD), 100% contrast, 4 orientations: 0°, 45°, 90° and 135°, chosen psuedorandomly] that was flashed over a large rectangular grid covering the RFs of the microelectrodes (interstimulus distance of 0.25° and 0.3° for the two monkeys). In separate experiments, the RFs of each of the three ECoG electrodes were mapped by flashing the stimulus in a pseudorandom order at locations surrounding the center of the RFs (SD of 0.1° for both monkeys, other parameters were the same as microelectrode recordings). At each location, stimuli were presented on average 16.9 times (range 11–21) for Monkey 1 and 13.3 times (range 8–17) for Monkey 2 (pooled across orientations) for the microelectrode recordings. For ECoG experiments, stimuli were presented 17.8 times (range 14–21) and 19.7 times (15–27) for the two electrodes in Monkey 1 and 21.5 (range 15–26) times for Monkey 2.

Monkeys 3, 4, and 5 performed a fixation task while they were in a monkey chair with their head fixed by the head post. The monkeys were required to hold their gaze within 2° of a small central dot (0.10° diameter) located at the center of a monitor (BenQ XL2411, LCD, 1280 × 720 pixels, 100 Hz refresh rate, gamma corrected) and were rewarded with juice at the end of the trial upon successful fixation. The stimulus was a grating with radius of 0.3°, spatial frequency of 4 CPD (Monkeys 3 and 4) or 1 or 2 CPD (Monkey 5; for this monkey lower spatial frequencies produced a stronger response), full contrast, and one of four different orientations (0°, 45°, 90°, and 135°). The stimulus was flashed for 200 ms (interstimulus period was set to 0) at various locations in the visual space spanning the RF centers of microelectrode array and ECoG electrodes. For Monkey 3, the RF estimates of ECoG 7 and 8 (Fig. 1) were mapped in separate experiments because these electrodes had large eccentricities (see Fig. 3B). On average, at each location, stimuli were presented 19 times (range 11–26) for Monkey 3, 17.7 times (range 12–22) for Monkey 4, and 15 times (range 9–19) for Monkey 5 (pooled across orientations). For the two separate ECoG experiments, the average number of stimuli at each stimulus location were 20 (range 12–28) and 19.3 (range 11–26). All data were analyzed using custom codes written in MATLAB (The MathWorks, RRID:SCR_001622).

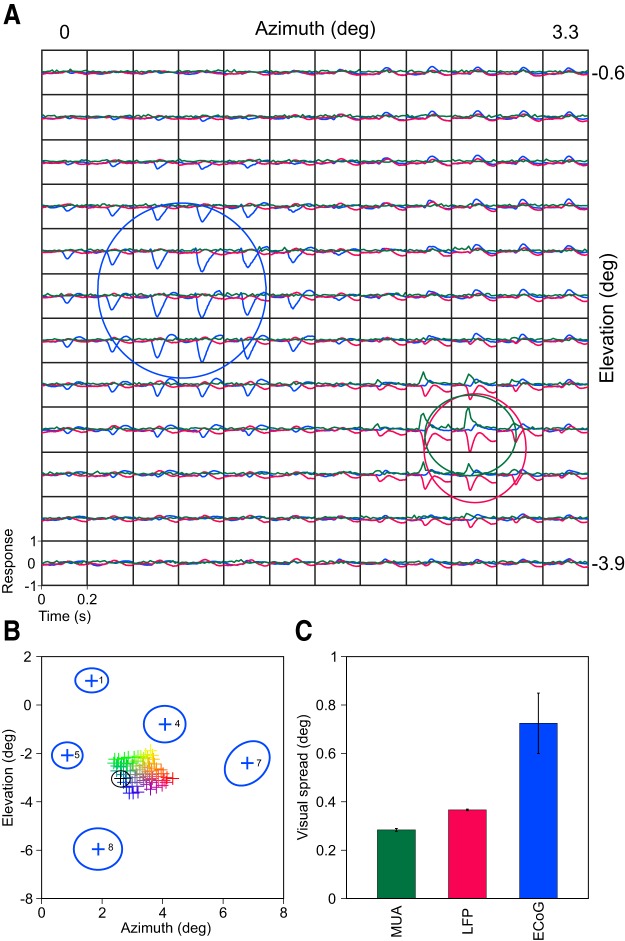
Figure 3.

Comparison of ECoG, LFP, and MUA visual spreads recorded from Monkey 3. A, Mean evoked ECoG of one electrode (blue) along with LFP (red) and MUA (green) responses from one microelectrode averaged across trials and recording sessions at each of the 144 positions (12 × 12 square grid, a subset of the 19 × 25 rectangular grid that was used for mapping). Estimated RF sizes (σ of the best fitted 2D Gaussian) are plotted in solid traces. B, Estimated RF centers of the LFP electrodes color coded based on their position on the microarray grid (Fig. 1). The RF size and center of the example LFP electrode plotted in A is shown in black. Estimated RF centers and sizes of ECoG electrodes are plotted in blue. C, Median RF size of MUA (n = 44), LFP (n = 77), and ECoG (n = 5) for Monkey 3. Error bars indicate SEM computed using bootstrapping.

RF estimation.

To estimate the RF sizes, we first averaged the MUA, LFP, and ECoG responses across stimulus repeats (for details, see Materials and Methods and Fig. 2 in Dubey and Ray, 2016). Next, the minimum (Min) values of the mean LFP signal were calculated for stimulus (40 to 100 ms) and baseline (0 to 40 ms) epochs. We found that the trough for ECoG electrodes was at longer latencies and therefore used the stimulus epoch between 40 and 150 ms. The baseline epoch was taken after stimulus onset to avoid any stimulus offset transients in Monkeys 3–5 because the interstimulus period was zero. We used Min values (as used in Xing et al., 2009) as opposed to root-mean-square (RMS) values because we observed nonspecific, small positive fluctuations at many stimulus positions. For example, small positive fluctuations at ∼100 ms after the stimulus onset in the evoked response can be seen in Figure 2A, the top right corner of Figure 3A, and in Figure 3A in Dubey and Ray (2016), which shows data from Monkeys 1 and 2. The reasons for these fluctuations are unclear, but we suspect that these are due to volume conduction because they were not observed in the corresponding current source density plots (Fig. 3B in Dubey and Ray, 2016). Because these positive peaks at positions far from the RFs were not accompanied by pronounced negative peaks, taking the Min essentially removed the positive peaks and yielded RFs with centers that were well aligned with the MUA.

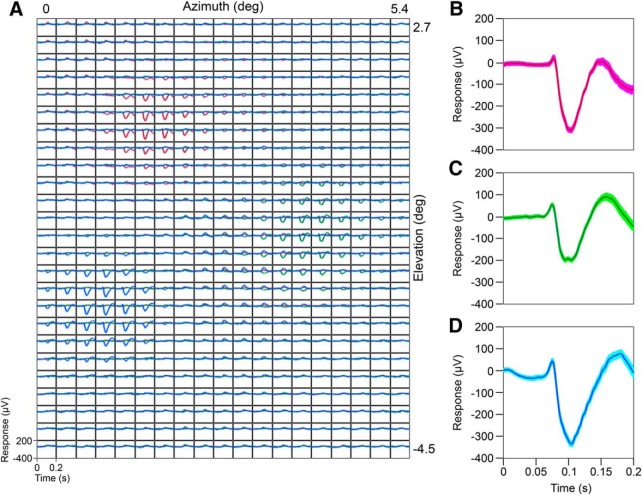
Figure 2.

Mean evoked ECoG responses. A, Simultaneously recorded mean evoked responses for three ECoG electrodes: 1 (red), 4 (green), and 5 (blue) from Monkey 3 (electrode positions shown in Fig. 1) averaged across trials and six recording sessions at each of the 475 (19 × 25 rectangular grid) stimulus positions. B–D, Mean evoked responses of the three ECoGs shown in A for the stimulus position that generated the maximum response. SEs (after bootstrapping) computed after pooling trials across all the recording sessions are shown in lighter shades.

We subtracted the Min values obtained during the baseline period from the stimulus period and fitted the following 2D Gaussian function:

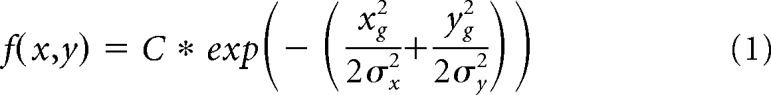Where C is the scaling factor, σ_x and σ_y denote the SD of the Gaussian along major and minor axis. The terms x_g and y_g are defined as follows:

Where θ is the angle of rotation with respect to the coordinate system and x₀ and y₀ denote the center of the 2D Gaussian. We defined the RF center as (x₀, y₀) and size as follows:

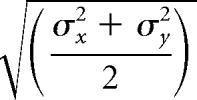For MUA responses, instead of Min values, we used the difference between the mean firing rates between stimulus and baseline epochs.

Electrode selection.

We have explained the selection process for LFP and MUA electrodes in detail for Monkeys 1 and 2 in a previous report (Dubey and Ray, 2016); here, we briefly describe it for Monkeys 3, 4, and 5. First, we selected electrodes with an absolute Min value (across all stimulus positions) that exceeded a particular threshold (130, 60, and 65 μV for Monkeys 3, 4, and 5, respectively). Next, for each electrode, we rejected recording sessions for which the estimated RF size was too small (<0.1°), too large (> 0.5°), or had an RF center that was beyond the area of stimulus presentation. We only used electrodes for which at least 50% of the sessions were selected. Overall, we rejected ∼2.8%, 5.6%, and 37% recording sessions, which yielded 77, 18, and 26 LFP electrodes for Monkeys 3, 4, and 5, respectively. The RF centers of the remaining sessions were very stable across sessions (SD of <0.1° for Monkeys 4 and 5 and 0.13° for Monkey 5). Finally, for each electrode, we averaged the waveforms across selected sessions at each position and calculated the RF for this pooled data to get a single estimate of RF size and center per electrode. MUA data were less stable across days, so for a particular electrode, we only used sessions for which at least 10 spikes/s were recorded when the probe was at the center of the RF. This yielded 44, 13, and 9 electrodes for the three monkeys.

In all cases, the RF centers of the MUA and LFP matched closely and followed the known retinotopy in V1. For example, Figure 3B shows the RF centers for 77 LFP color coded based on their position on the grid. The left edge of the microelectrode grid (blue to red) was most medial (almost parallel to midline), whereas the bottom edge (blue to green) was most anterior (Fig. 1). This corresponds to the retinotopic organization of V1 (see Fig. 3B): moving along yellow to green or red to blue (i.e., lateral direction) yielded more foveal receptive fields. Similarly, moving from green to blue or yellow to red decreased the elevation. Similar results can be observed in Figure 1D in Dubey and Ray (2016) for Monkeys 1 and 2.

Not all of the ECoG electrodes in a 3 × 3 grid were in V1; we visually examined the electrode positions during the surgery and from the pictures taken and selected electrodes that were posterior to the lunate sulcus (see Fig. 1). The subset of ECoG electrodes with an absolute Min value that was >100 μV were used for further analysis, yielding 5, 4, and 4 ECoG electrodes for Monkeys 3, 4, and 5, respectively. For all three measures, the final RF centers and sizes computed from the pooled data were very similar to the average of the RF centers and sizes computed for individual sessions.

Conversion from visual to cortical spread.

The cortical spread of LFP and ECoG was computed using two approaches. First, simply as the product of the experimentally estimated RF size (σ_v) and MF (calculated as shown in Fig. 4A for LFPs and estimated from previous reports for ECoGs as shown in Fig. 4B) as follows:

Second, we estimated the cortical spread of LFP and ECoG using a model proposed by Xing et al. (2009) that accounts for several factors that inflate the visual spread. In their model, the visual spread of LFP is obtained by convolving the spatial weighting function of the LFP (multiplied by the MF) with the visual spread of single-unit activity (SUA). However, because of the scatter present in retinotopic map on the cortex, the visual spread of SUA also gets convolved by a scattering function. All of the spreads are assumed to be Gaussian, such that the convolution yields another Gaussian with a spread that is the sum of the spreads of the individual Gaussians. Therefore, for LFP recorded at eccentricity “x”, the visual spread is denoted as follows (equation 5 from Xing et al., 2009):

Here, σ_vLFP is the visual spread of LFP that we can measure experimentally, σ_cLFP is the cortical spread of LFP that we are interested in, σ_vSUA is the visual spread of SUA, and σ_vv represents the visual variation or RF scatter (unknown). Compared with the “no model” condition (for which MF_x²σ_vLFPx² = σ_cLFPx²), the visual spread therefore gets inflated because of the last two terms, which are difficult to compute experimentally. Note that the last two terms (MF² · σ_vv² + MF² · σ_vSUA²) have been described as the cortical point image (CPI) in previous studies (Albus, 1975; Dow et al., 1981), which is the cortical representation of a geometric point on the sensory epithelium (Palmer et al., 2012).

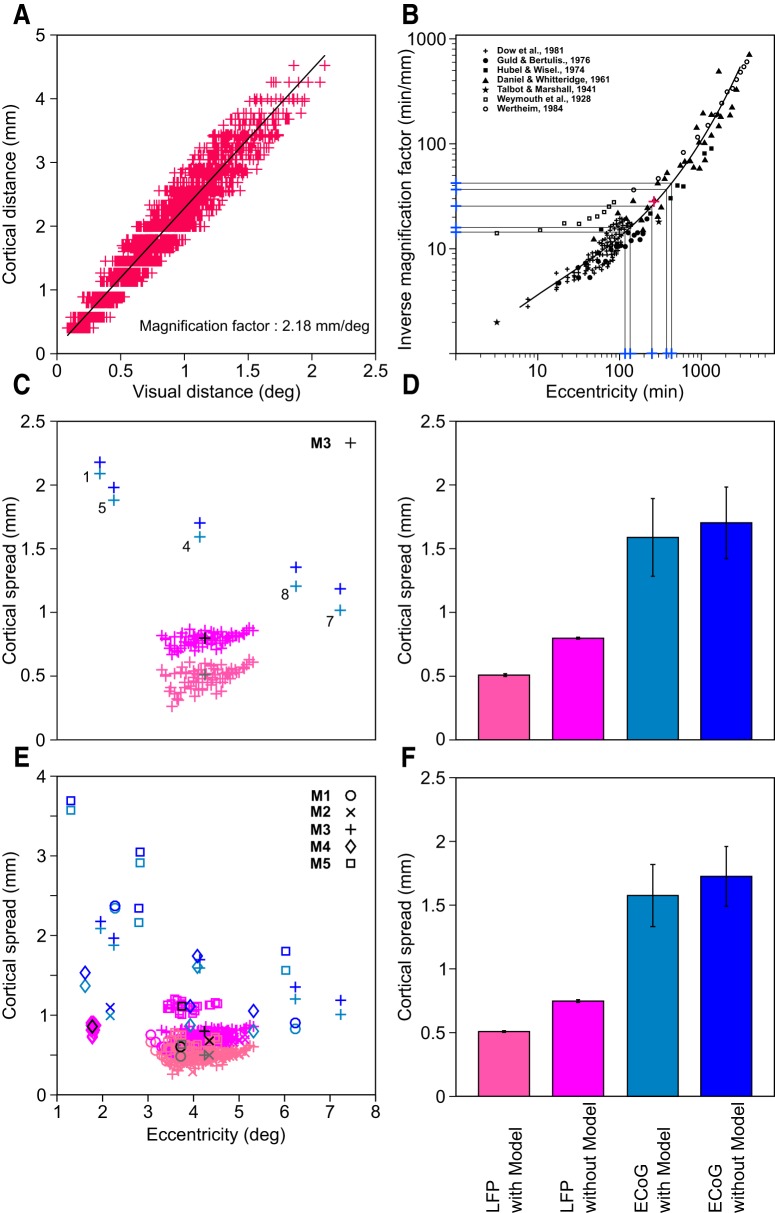
Figure 4.

Conversion of visual (in degrees) to cortical (in millimeters) spread. A, Estimation of MF for LFP for Monkey 3. Visual distance between the RF centers for each electrode pair is plotted on the x-axis and the corresponding cortical distance is plotted on the y-axis. B, MF of ECoG obtained from previous studies. The area shown in black is adapted from Figure 6 of Dow et al. (1981). The magenta plus indicates the experimentally calculated MF of Monkey 3 (y-axis) at the average eccentricity of the RF centers in this monkey (x-axis), which falls on the black curve. Blue plus markers on the x-axis are the experimentally determined RF eccentricities of the five ECoG electrodes and the corresponding markers on the y-axis are the estimated MFs for these ECoG electrodes. C, Cortical spread estimated with (light shades) and without (dark shades) model for Monkey 3 (blue: ECoG; pink: LFP). The median values for the LFP are plotted in gray (with model) and black (without model). D, Median and SE (after bootstrapping) estimates of the cortical spread for Monkey 3. E, F, Same as C and D for the full dataset. For Monkey 4, the model could not be applied for the estimation of the LFP spread and therefore is not shown in E (see Materials and Methods for details).

To determine the cortical spread, Xing et al. (2009) argued that the visual spread of MUA σ_vMUA at the distance “x” from the fovea would be inflated in a similar fashion as follows:

Because MUA and LFP are recorded from the same electrode and their RFs have the same eccentricity (“x”; see Fig. 4A in Dubey and Ray, 2016), the difference in σ_vLFP² and σ_vMUA² (Eqs. 3 and 4) cancels the unknown terms and yields the cortical/spatial spread of LFP in terms of MF, visual spreads of LFP and MUA, and the cortical spread of MUA as follows:

Because we recorded from awake animals whereas Xing et al. (2009) used anesthetized monkeys, our visual spreads are further inflated due to eye jitter. Similarly, whereas Xing et al. (2009) used sparse noise, we used small Gabor/grating, so the size of the stimulus could also inflate the visual spread. Accommodating the variables for eye jitter and stimulus size, the visual spread of LFP (σ_vLFP) estimated experimentally at a distance “x” from the fovea can be defined as follows:

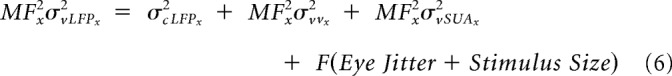Where F is a function that depends on the eye jitter and stimulus size. However, because these additional terms are independent of the type of measure, they get canceled out in a similar fashion as before.

In our analysis, the cortical spread of MUA (σ_cMUA) was set at 60 μm, which was the value used by Xing et al. (2009) based on previous studies (Gray et al., 1995; Buzsáki, 2004). We used the MF for LFP in Equation 5 to compute the cortical spread; results were similar if MFs obtained from MUA were used instead (data not shown).

Model extension.

We now extend this model to ECoG. Assuming that the visual spread of ECoG can be obtained by applying a different weighting function on the visual spread of SUA, this model can be modified to define the spread of ECoG at a distance “x” from fovea as follows:

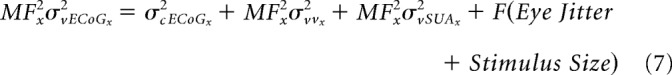Note that, unlike the previous case with LFP and MUA, the spatial spread of LFP is not available at “x” but a different location (say “y”). We first rearrange the terms to have the visual and cortical spreads on one side and the inflation terms on the other as follows:

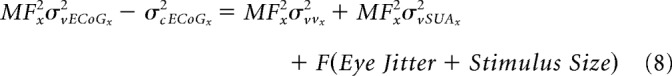For the LFP obtained at eccentricity “y,” we get:

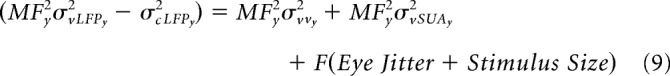To proceed further, we make an assumption that CPIs (MF² · σ_vv² + MF² · σ_vSUA²) are comparable for eccentricities “x” and “y.” The magnitude of error because of this assumption is unlikely to be large because the MF tends to decrease, whereas σ_vv and σ_vSUA tend to increase with eccentricity (Albus, 1975; Dow et al., 1981) such that the CPI is almost constant. For example, Albus (1975) showed that the RF scatter increased from ∼1° to 3–4° as the eccentricity increased from 1° to ∼10° (see Fig. 9B in Albus, 1975). However, the magnification factor over this range of eccentricities decreased from ∼2.5 to ∼0.5 mm/° (see Fig. 9A in Albus, 1975). Therefore, the product was about the same. Similarly, using voltage-sensitive dyes, Palmer et al. (2012) have shown that CPI does not vary appreciably with eccentricity in V1.

Under these assumptions, the right side of the two equations are equal and therefore can be subtracted and rearranged to yield the following:

In Monkey 4, only a few MUAs were available and their RFs were comparable to the LFPs such that the model could not be used for this monkey. To compute the ECoG spread for this monkey, we used average estimate of σ_cLFP from the other four monkeys. Note that whereas this model reduced the LFP spread by ∼32%, for ECoG, the reduction was only ∼9%. Therefore, none of the results shown here critically depended on the model.

Factors affecting the spatial spread.

Although the Xing et al. (2009) model accounts for differences in the CPIs (which may depend on lateral/feedforward connectivity profile), there are other properties that critically determine the cortical spread. This is easiest to understand by comparing the spreads of LFP and MUA because the difference is mainly based on the frequency content of the signal recorded from the same microelectrode. In this case, conductance or filtering properties of the tissue become crucial (Bédard et al., 2004, 2006, 2010; Logothetis et al., 2007; Lindén et al., 2011). For example, if the tissue is capacitive (for arguments and debates on this topic, see Bédard et al., 2004, 2006, 2010; Lindén et al., 2011), then lower frequencies can travel farther than higher frequencies, such that the spatial spread of MUA is lower than LFP and this should be captured in the weighting functions (i.e., σ_cLFP should be larger than σ_cMUA). Note that the proposed model places MUA and LFP on an “equal footing” because it does not imply that the spatial spread of LFP is necessarily larger than MUA (e.g., if the cortical medium were then the inductive, σ_cMUA would be larger than σ_cLFP and we would subtract Eq. 3 from Eq. 4 instead of the other way around). The tissue does not even necessarily have to capacitive: even in a purely resistive medium, the shrinkage in the dipole length with increasing frequencies causes an effective “low-pass filtering” of the signal (Pettersen and Einevoll, 2008), which would reduce the spatial spread of MUA compared with LFP. Consistent with this, we have previously shown that the spatial spreads of different frequencies of the LFP are different, with a higher spread in the high-gamma band (see (Dubey and Ray, 2016)), and the spread of higher LFP frequencies (>250 Hz) approaches the spread of the MUA. Therefore, factors that could govern conductance and filtering characteristics of the cortical tissue, which could include the morphology of the cortical neurons, their density, cell type, level of myelination, the presence of glial cells, etc. (Bédard et al., 2004, 2006), could change the spatial spread of the LFP.

Another important property that could play a role in determining the spatial spread is noise. To observe a measurable signal on the electrode upon the activation of a small part of the cortex, this signal must be above the noise floor. However, the noise recorded from an electrode may be frequency dependent and therefore different for MUA and LFP. For example, several studies have suggested that the slope of the PSD could be ∼2 because of shot noise, the origin of which might be due to an exponential relaxation process of synaptic currents that are driven by random spiking or due to up-down states that have properties of a telegraphic process (Miller et al., 2009; Milstein et al., 2009; Baranauskas et al., 2012). Systematic differences in noise characteristics between MUA and LFP will also not cancel out in this model and therefore will contribute to the spatial spread of LFP (larger noise will reduce the spatial spread).

While extending this model to ECoG by comparing its RF size with LFP, an important factor that is not accounted in the model is that LFP and ECoG may be reflecting fundamentally different aspects of the neuronal activity. Specifically, it has been suggested that, as the size of the neural population increases, the contribution of synchronous activity increases. Specifically, power in the signal due to asynchronous activity scales as N, but scales as N² for synchronous activity, where N is the size of the recorded population (Nunez and Srinivasan, 2006; Ray et al., 2008). When a small stimulus is presented, the spatial profiles of asynchronous and synchronous activity may be different. For example, it is possible that the initial stimulus-locked response is restricted to a local population of neurons and therefore has a narrow spatial spread. However, this activated cortical area may activate nearby neurons over a broader time scale, leading to an increase in asynchronous firing that is more spread out in the cortex. Therefore, LFP and ECoG could be differentially sensitive to the synchronous sources/sinks and this could also be reflected in their spatial spreads.

PSD slope analysis.

For slope analysis, segments of 500 ms length during stimulus-free (spontaneous) period were used, as reported elsewhere for Monkeys 1 and 2 (Shirhatti et al., 2016). Monkeys 3 and 4 performed the fixation task while a full screen grating was presented for 800 ms with an interstimulus period of 700 ms. The grating was static with one of the five spatial frequencies, 0.5, 1, 2, 4, and 8 cpd, and eight orientations evenly spaced between 0° and 157.5° chosen randomly (a period between 500 and 0 ms before the stimulus onset was used). We observed high-frequency noise in case of Monkey 5 and therefore did not use this dataset for PSD analysis. PSDs were computed using the multitaper method with three tapers, implemented in Chronux 2.0 (Bokil et al., 2010). We calculated the slopes for frequency ranges 20–100 Hz and 200–400 Hz by fitting the function log₁₀(P) = m * log₁₀(f) + c where P is the PSD, f is the frequency, c is the constant or noise floor, and m is the slope (Miller et al., 2009; Shirhatti et al., 2016). The frequency range of 20–100 Hz was chosen to avoid the alpha band (see Fig. 5A). The PSDs were normalized to have the value of 0 at 20 Hz (this normalization only affects the vertical offset (c), not the slope (m).

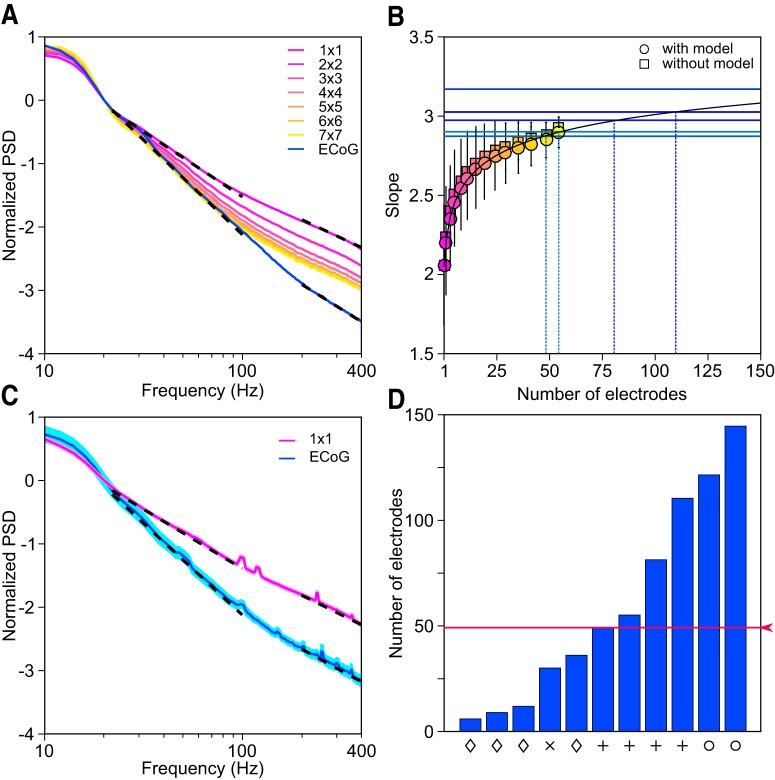
Figure 5.

PSD and slope analysis. A, Mean PSD across 77 LFP (pink; indicated as 1 × 1) and 5 ECoG (blue) electrodes and mean PSDs of signals obtained by first averaging the LFPs over progressively larger subgrids (pink to yellow). Slopes calculated for the 20–100 Hz and 200–400 Hz frequency ranges are plotted in dotted black (see Materials and Methods for details). The PSDs are normalized to have a value of 0 at 20 Hz for comparison of slopes. B, Average slopes and SDs (for 20–100 Hz frequency range) of the electrode grid combinations estimated with model (as described in Materials and Methods; circles) and without model (squares) are plotted on the y-axis (pink to yellow) for Monkey 3. The number of electrodes in each grid combination is plotted on the x-axis. Apart from squares as shown in A, we also considered rectangles of microelectrode populations (such as 2 × 3, 3 × 4, 4 × 6, etc.). The curve fitted on these slopes is shown in black. Blue horizontal lines are the experimentally determined slopes of the five ECoG electrodes for this monkey. The intersection of the fitted curve and ECoG slope yielded the number of LFP electrodes that needed to be averaged to produce the same slope as ECoG. C, Mean PSD of the LFP (pink) and ECoG (blue) averaged across four monkeys (Monkeys 1–4; data from Monkey 5 were not used because of the presence of noise at high frequencies). The SE is shown in lighter shade. Slopes are plotted in dotted black as before. D, Number of LFP electrodes that need to be averaged to match the slope of each of the 11 ECoG electrodes from four monkeys between 20 and 100 Hz (for Monkey 3, slope of one ECoG electrode was too steep and did not intersect the fitted black curve; see B). The symbols on the x-axis indicate the monkey (same as used in Fig. 4E). Red trace shows the median.

The slope of the PSDs have been interpreted to reflect important characteristics of the brain such as state, filtering properties, noise, etc. (Bédard and Destexhe, 2009; Miller et al., 2009; Milstein et al., 2009). However, the error-free estimation of PSD slope requires correction of the low-pass filter as well as the noise floor of the amplifier (Miller et al., 2009). We have previously used a similar procedure and shown that the transfer function of the amplifier is almost close to 1 (and consequently the correction factor is negligible) up to ∼400 Hz and therefore not critical for PSD slopes up to 400 Hz (Shirhatti et al., 2016; the transfer function is shown in supplementary Figure 1 in that paper). In that dataset, the noise floor was also negligible (i.e., the PSD did not flatten up to 500 Hz). To make sure that our results shown in Figure 5 were not affected by noise, we experimentally determined the noise floor by recording signals (using the same amplifier and same filter settings) from six passive disc electrodes (Grass Technologies) that were kept in a saline solution and contacted each other. Because the inputs were shorted, the output signal mainly reflected amplifier noise. A comparison of PSDs of this noise signal and PSDs of the LFP and ECoG signals revealed that instrument noise was at least an order of magnitude smaller (and >30 times in the frequency ranges of interest), so none of our results in Figure 5 could be affected by the noise or filtering characteristics of the amplifier.

ECoG data modeling.

ECoG and LFP signals capture the activity of the underlying neuronal population depending on their size and location. The microelectrodes sample the activity from the layer 2/3, whereas ECoG electrode is placed on the surface of the cortex. We estimated the slope of ECoG signal from the LFP activity in a simple model-based approach proposed by Ray et al. (2008). We briefly explain the model here for simulating ECoG from LFPs (see the Materials and Methods section of Ray et al., 2008 for details). This model is based on the observation that, once an electrode is sufficiently far away from a neuron, the waveform recorded at that location and another location farther away are usually scaled versions of each other (the scaling factor depends on the distance) because both can be expressed in terms of the transmembrane currents flowing through the neuron (Gold et al., 2006). Specifically, suppose a microelectrode records LFP ψ(t) near a neuron and the ECoG electrode records the potential φ(t) due to the activity of the k^th neuron (as shown in supplementary Fig. 1 in Ray et al., 2008). The two potentials can be related using the following equation:

where R is the distance between the ECoG electrode and the neuron. The constant C incorporates several factors such as the distance between the soma and the microelectrode, the conductivity of the medium, the size of the soma, and the orientation of the current sources, and the exponent n accounts for the distribution of transmembrane currents across the membrane. Because in our case the LFPs were all recorded from the same layer (layer 2/3 or 4) that was far away from the surface of the cortex, the relative difference in R is likely to be negligible across neurons and therefore the denominator can be dropped. Under the assumption of linear superposition, the neuronal activity recorded by an ECoG electrode due to a population of N neurons is therefore given by the following:

Where ψ(t) is the mean LFP signal recorded from a microelectrode (in our setup, a 500 ms period of spontaneous activity before stimulus onset).

In our model, we averaged the LFP activity of nearby electrodes that constituted either a square grid (1 × 1, 2 × 2, 3 × 3, and so on) or rectangular grids in which one side was greater than the other by one (i.e., 2 × 3, 3 × 4, 4 × 5). For smaller grid sizes, we considered all combinations for which the grid had no missing electrodes. For higher grid sizes (3 × 3 onwards), the number of combinations was lower, so to increase the number of different combinations, we also allowed up to 1 missing electrode (for example, if a 3 × 3 grid had one missing electrode, it was still averaged, and the resultant slope was put against 8 instead of 9). For Monkey 3, for which all but 4 microelectrodes could be used for analysis (77 out of 81), the grid combinations (number of electrodes) were 1 × 1 (1), 1 × 2 (2), 2 × 2 (4), 2 × 3 (6), 3 × 3 (9), 3 × 4 (12), 4 × 4 (16), 4 × 5 (20), 5 × 5 (25), 5 × 6 (30), 6 × 6 (36), 6 × 7 (42), 7 × 7 (49), and 7 × 8 (56). Only a few electrodes were selected for RF analysis for Monkeys 1 and 4 (27 and 18, respectively), so this analysis could be performed only for grid combinations up to 3 × 4 for both the monkeys. For Monkey 2, the highest grid size was 6 × 6.

The coefficient C in Equation 12 was varied randomly between 0 and 1 (uniformly distributed) to incorporate the diversity in cell size/type/conductivity/orientation, etc. We estimated the ECoG potential φ(t) 1000 times for each grid combination to get the standard deviation. For the “without model” condition, C was set to 1 (see Fig. 5B). Other ranges were also tried (e.g., C uniformly distributed between 0.4 and 0.6) and yielded similar results. Further, results without the model (for which the random factor was set to 1) produced similar results (compare circles vs squares in Fig. 5B).

Cortical spread in spectral domain.

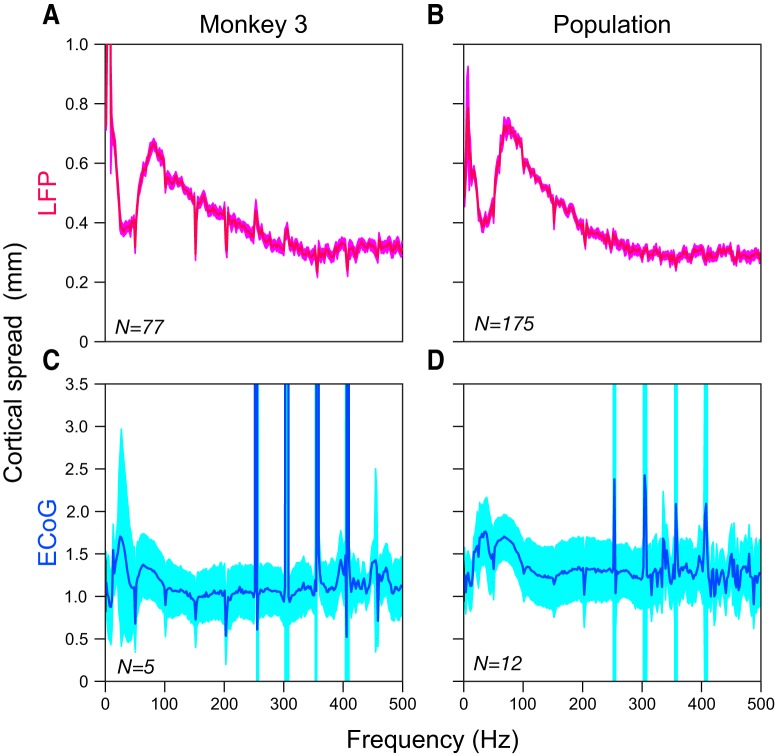
The cortical spreads as a function of frequency were estimated by first decomposing the signal in time–frequency domain by using the matching pursuit (MP) (Mallat and Zhang, 1993) algorithm and then fitting a 2D Gaussian to the difference in the root of the average energy values for stimulus (40–150 ms) and baseline (0–40 ms) time epochs for each frequency. This time range was used for both LFP and ECoG for better comparison. The MP algorithm is explained in detail in our previous study (Dubey and Ray, 2016). Briefly, MP is an iterative algorithm that decomposes the signal into a linear combination of waveforms selected from an overcomplete dictionary. As in our previous study (Dubey and Ray, 2016), we used a dictionary of Gaussian-modulated sinusoidal functions (Gabor functions). MP was performed on signals of length 2048 points (−549.5 to 474 ms at 0.5 ms resolution, where 0 denotes the time of stimulus onset), yielding a 2048 × 2048 array of time–frequency energy values (with a time resolution of 0.5 ms and frequency resolution of 2000/2048 = ∼1 Hz). This was downsampled by a factor of 8 in the time domain and a factor of 2 in the frequency domain, yielding a time resolution of 4 ms and a frequency resolution of ∼2 Hz. The cortical spreads were estimated for each frequency by applying the model proposed by Xing et al. (2009) as explained in the “Conversion from visual to cortical spread” section. As described in that section, the model could not be applied to Monkey 4 because the MUA RFs were comparable to the LFPs. Further, this analysis could not be performed on Monkey 5 because of high-frequency noise (this monkey was excluded from the PSD slope analysis for the same reason). Therefore, the LFP spreads as a function of frequency (see Fig. 6B) were estimated only for Monkeys 1–3 (total 175 electrodes). Importantly, the model could be used for Monkey 4 for estimation of the ECoG spread (by using the average LFP spread, same as Fig. 4E), yielding 12 ECoG electrodes from four monkeys (see Fig. 6D).

Figure 6.

Cortical spread as a function of frequency. A, Median LFP cortical spread for Monkey 3. The RF sizes (in degrees) were first estimated at each frequency and then the model was applied to obtain the cortical spread (in millimeters). B, Median LFP cortical spread across three monkeys (Monkeys 1–3; for Monkey 4,the model could not be applied; data from Monkey 5 were excluded because of the presence of noise at high frequencies). C, D, Median ECoG cortical spread for Monkey 3 and population data across four monkeys (Monkeys 1–4). The SEs (after bootstrapping) are shown in lighter shades.

Statistical analysis.

The LFP and ECoG slopes in the 20–100 Hz and 200–400 Hz frequency ranges were compared using a two-sample t test. The null hypothesis assumed mean from the same distribution and unequal variances.

The SEs of mean or medians were computed using bootstrapping. Given a sample of n elements, a new sample was first created (termed “resample” or bootstrap sample) by randomly taking n elements with replacement from the original dataset. The mean or median was computed for this bootstrap sample. This process was iterated 1000 times, yielding 1000 means or medians. The SD of this population of means or medians was reported as SE.

Results

Data were collected in two separate set of experiments. The first dataset involved ECoG recordings from three electrodes in two monkeys (Monkeys 1 and 2) in which microelectrode data had been collected previously (Dubey and Ray, 2016). For the second set, we performed simultaneous recordings of MUA, LFP, and ECoG in three trained, behaving monkeys using a custom-made hybrid electrode array (Monkeys 3–5; Fig. 1). This hybrid grid consisted of 9 (3 × 3) ECoG electrodes and 81 (9 × 9) microelectrodes, both attached to the same connector and referenced to the same wire. The ECoG electrodes were circular platinum recording surfaces 2.3 mm in diameter, the standard size used in clinical applications, with a center-to-center distance of 10 mm. During surgery, the ECoG grid was first placed on the pia and then the microelectrode array was inserted in a previously made gap between four ECoG electrodes (Fig. 1). Only ECoG electrodes that were posterior to lunate sulcus lying over V1 were used for further analysis. In total, we recorded from 16 ECoG and 219 LFP electrodes in five monkeys.

Visual evoked responses of ECoG

We estimated the RFs by presenting a small Gabor/grating stimulus in random order at locations spanning the RFs of microelectrode and ECoG electrodes (see Materials and Methods for details). Figure 2A shows the evoked responses of three neighboring ECoG electrodes: 1 (red), 4 (green), and 5 (blue) from Monkey 3 (electrode positions are shown in Fig. 1), averaged across trials and recording sessions for 475 (19 × 25) stimulus positions. Interestingly, the RFs of ECoGs were highly localized in the visual field: stimulus positions that elicited strong evoked responses in one ECoG electrode produced almost no response in a neighboring electrode that was separated by only 10 mm. The responses were very robust across trials and sessions (Fig. 2B–D, SEs computed after bootstrapping are shown in light shades). Therefore, we averaged the data across recording sessions for which robust activity was observed and estimated the RF parameters by fitting a 2D Gaussian to the pooled data (see Materials and Methods for details).

Comparison of ECoG, LFP, and MUA visual spreads

Next, we compared the evoked responses of one ECoG electrode (Fig. 3A, blue trace, ECoG 5 shown in Fig. 1 and Fig. 2) and one microelectrode (LFP in red and MUA in green) in Monkey 3. The ellipses are the estimated RFs, which were taken as 1 SD of the fitted Gaussians (see Materials and Methods). Surprisingly, although the ECoG electrode had an exposed diameter of 2.3 mm whereas the microelectrode had a tip diameter of only a few micrometers, the RF size of ECoG was only ∼1.7 times the LFP (SD of the fitted Gaussians were 0.52°, 0.32°, and 0.26° for ECoG, LFP, and MUA, respectively). Similar results were obtained for full dataset of 5 ECoG, 77 LFP, and 44 MUA electrodes for Monkey 3, although the RF sizes of ECoGs varied depending on the eccentricity (Fig. 3B; see Materials and Methods for electrode selection procedure). The medians ±1 SE (computed by bootstrapping) of the RF sizes of ECoG, LFP, and MUA were 0.72° ± 0.120°, 0.37° ± 0.003°, and 0.28° ± 0.006°, respectively, for this monkey (Fig. 3C) and 0.66° ± 0.07°, 0.28° ± 0.02°, and 0.24° ± 0.02° for the full dataset of 16 ECoG, 219 LFP, and 151 MUA electrodes in five monkeys, respectively. These monkey ECoG RF sizes were comparable to those in humans (Yoshor et al., 2007).

Conversion of visual (in degrees) to cortical (in millimeters) spread

To obtain the cortical spread, we first estimated the MF (in millimeters/degree) for the LFP electrodes by plotting the cortical distance between electrode pairs against the distance between their RF centers (Fig. 4A). These experimentally determined MF_LFP values were in good agreement with previous studies (Daniel and Whitteridge, 1961; Guld and Bertulis, 1976; Dow et al., 1981; Xing et al., 2009), which had estimated the MFs over a broad range of eccentricities (Fig. 4B, which is adapted from Fig. 6 in Dow et al., 1981). Although, in our experimental setup, we could not measure the MF at the eccentricity of the ECoG, we extrapolated the MF_ECoG based on previous measurements (Fig. 4B). Figure 4C shows the cortical spread of LFP (pink) and ECoG (blue) for Monkey 3 estimated using the model (for details, see Materials and Methods and Xing et al., 2009; light shades) and without the model (simply the product of MF and RF size; dark shades). The median ± 1 SE estimates of the cortical spread with and without the model were 0.51 ± 0.011 and 0.79 ± 0.007 mm for LFP and 1.59 ± 0.311 and 1.70 ± 0.287 mm for ECoG (Fig. 4D). For the full dataset (Fig. 4E), these values were 0.51 ± 0.006 and 0.75 ± 0.011 mm for LFP and 1.57 ± 0.244 and 1.73 ± 0.229 mm for ECoG (Fig. 4F). Although we observed some variability across monkeys, the ratio between LFP and ECoG spreads typically remained similar across monkeys. Further, although the RF sizes were variable, the LFP spreads were comparable across monkeys (gray symbols in Fig. 4E). Note that we have used the SD of the fitted Gaussian as a measure of spatial spread to be consistent with the study of Xing et al. (2009). The diameter of the spread could be approximated as 2 SDs or ∼3 mm for the ECoG. Therefore, an ECoG electrode measures the activity of a brain area only slightly larger than its own diameter.

PSD and slope analysis

Next, we estimated the spatial spread using a different approach based on the observation that the slope of the PSDs, which could reflect important characteristics of the network such as noise (Freeman et al., 2000; Bédard and Destexhe, 2009; Miller et al., 2009; Milstein et al., 2009) and filtering characteristics (Bédard et al., 2006; Lindén et al., 2010; Łęski et al., 2013; Dubey and Ray, 2016), was much steeper for ECoG than LFP between 20 and 100 Hz (Fig. 5A). This can be explained based on the LFP–LFP coherence profile, which is typically high at low frequencies and decreases to very low values beyond ∼200 Hz (Srinath and Ray, 2014; Shirhatti et al., 2016). Further, the phase difference across microelectrode pairs is on average zero (Shirhatti et al., 2016). This means that the low-frequency components of the LFP are more phase aligned than high-frequency components. Therefore, if LFPs from nearby electrodes are averaged, then there is greater reduction in amplitude at high frequencies (because the phases are random and cancel each other out) than low frequencies, which increases the overall slope. Indeed, in a simple model based on linear superposition (see Materials and Methods) in which we simulated the ECoG signal by averaging LFP signals over a progressively larger set of microelectrodes, we found that the slopes of the simulated ECoG increased (1 × 1 to 7 × 7; Fig. 5A; see Materials and Methods for details). For this monkey, averaging ∼50 to ∼110 microelectrodes yielded slopes comparable to the actual ECoG slopes (Fig. 5B). Similar results were observed over the population (Fig. 5C): the mean slopes and SEs of ECoG and LFP were significantly different between 20 and 100 Hz (ECoG: 2.89 ± 0.06, n = 12; LFP: 1.87 ± 0.033, n = 193; p = 4.22 × 10⁻¹¹, two-sample t test) and averaging 49 ± 14.5 microelectrodes yielded a slope comparable to the ECoG (Fig. 5D). Although this approach makes a series of simple assumptions (discussed in Materials and Methods) and the simulated and real ECoG PSDs do not match over the entire frequency range (Fig. 5A), the final estimate of the ECoG spread obtained only from spontaneous data is similar to the first method (∼50 microelectrodes correspond to a 7 × 7 grid that corresponds to summation >7 × 400 μm = 2.8 mm; this measure of spread should be approximately twice the previous measure that was based on the SD of a fitted Gaussian). Also note that this model predicts that the ECoG and LFP slopes should not be different at high frequencies (200–400 Hz) because the phases are completely random over this range and therefore the reduction in amplitude should be the same throughout. Indeed, the slopes between 200 and 400 Hz were comparable (ECoG: 1.69 ± 0.08, n = 12; LFP: 1.54 ± 0.02, n = 193; p = 0.098, two-sample t test).

Cortical spread as a function of frequency

We further studied the cortical spread of LFP and ECoG as a function of frequency (as done previously for LFPs; Dubey and Ray, 2016) for Monkeys 1–4 (as for the PSD slope analysis, Monkey 5 was excluded because of high-frequency noise). Figure 6A shows the median cortical spread of LFP across 77 electrodes for Monkey 3. Similar to our previous findings (Dubey and Ray, 2016), LFP spread showed a band-pass effect in this monkey also, with high-gamma (60–150 Hz) range spreading more than lower- and higher-frequency ranges. Also note that the spatial spread increased at very low frequencies, as was observed in our previous study as well (Dubey and Ray, 2016). This was due to nonspecific, small positive fluctuations observed for many microelectrodes and ECoG electrodes ∼100 ms after the stimulus onset in the evoked response (see top right corner of Fig. 3A and in Fig. 3A in Dubey and Ray, 2016), which, in the frequency domain, had energy at low frequencies (for the RF analysis shown before, this issue was largely addressed by using the absolute Min value for RF estimation instead of RMS values; see Materials and Methods for details).

Figure 6B shows the population cortical spread across 175 electrodes from three monkeys (data from Monkey 4 was excluded because the model to convert visual to cortical spread could not be applied; see Materials and Methods for details). For Monkey 4 also, the visual spread was larger in the high-gamma range than higher frequencies (>250 Hz), although the spread remained large at lower frequencies (gamma range and below), likely because the nonspecific fluctuations described above were sharper in this monkey. Unlike LFP, ECoG showed no frequency-specific increase in cortical spread in the high-gamma range (Fig. 6C, median cortical spread across 5 ECoG electrodes in Monkey 3), but instead at frequencies up to ∼100 Hz before flattening out. Similar results were seen for a population dataset of 12 ECoG electrodes across four monkeys (Fig. 6D). Interestingly, for higher frequencies (>100 Hz), the median cortical spread was ∼1.2 mm, comparable to the radius of the exposed surface of the ECoG electrode. This suggests that, at high frequencies, the ECoG electrode measures the activity of brain area that is about the size of its diameter.

Discussion

Here, we compared the spatial spreads of two distinct brain signals: LFP (typically recorded using microelectrodes inserted in the brain) and ECoG (or intracranial field potentials, typically recorded using large macroelectrodes placed on the surface of brain). Using a unique hybrid electrode array containing both microelectrode and macroelectrode arrays to simultaneously record MUA, LFP, and ECoG RFs at several cortical sites from awake, behaving monkeys, we here show that the spatial spread of ECoG is surprisingly local (SD of ∼1.5 mm or 2 SDs of ∼3 mm), not much larger than the diameter of the ECoG electrode (2.3 mm) and only ∼3 times the spread of the LFP, even though the size of the ECoG electrode is several hundred times larger than the microelectrode. Furthermore, we confirmed this result using an independent approach in which we compared the change in the slope of the PSD of ECoG and a simulated ECoG signal obtained by averaging LFPs over progressively larger square or rectangular grids. Similar to the first approach, the estimated ECoG spread corresponded to summation over a square of side ∼2.8 mm, suggesting local origins of ECoG. Although the use of multiple recording modalities allowed us to use a model that accounted for some factors that inflate the estimates of spatial spread, the results were similar even without the model.

Comparison with previous studies

Our estimates of LFP spread using the model proposed by Xing et al. (2009) were similar to previous studies reporting the LFP spread in V1 to be a few hundred micrometers (Katzner et al., 2009; Xing et al., 2009). However, recording from auditory cortex, Kajikawa and Schroeder (2011) reported the LFP spread to be several millimeters. The differences in their results and other studies could potentially be due to differences in recording areas (for further discussion on LFP spread estimates, see Dubey and Ray, 2016).

Unlike LFP, there are only a few reports on the spatial spread of ECoG (Yoshor et al., 2007; Winawer et al., 2013; Winawer and Parvizi, 2016). For example, Yoshor et al. (2007) performed their experiments in humans using the same type of ECoG electrodes (diameter of ∼2.3 mm) and estimated the RFs of ECoG placed in different visual areas. However, their RF estimates (in degrees) were not converted to the spatial spread (in millimeters). In two previous studies, Winawer and colleagues correlated ECoG responses with blood oxygen level-dependent (BOLD) responses (Winawer et al., 2013) and electrical stimulation (Winawer and Parvizi, 2016). They measured the stimulus-locked and broadband components of the ECoG responses (obtained after computing the Fourier transform of the recorded response) to a moving flickering bar and estimated the visual spreads of ECoG using a pRF model (Kay et al., 2013). To estimate the spatial spread, they multiplied the visual spreads with the magnification factor, similar to our “no model” approach. The ECoG spread estimated for broadband responses was comparable to our ECoG spread estimates. However, spatial spread estimated this way essentially yields the CPI and depends on the properties of the stimulus and other factors, as discussed below.

Spatial spread and its interpretation

The term “spatial spread” has been interpreted differently in different experimental and modeling studies. We interpret it based on the model proposed by Xing et al. (2009) where the “spatial spread” of a particular measure (such as LFP or MUA) is a spatial weighting function that primarily depends on the properties of the electrode (impedance, size, layout, etc.). If an arbitrarily small part of the cortex can be activated, then this spatial spread function determines the cortical area over which this activation can be observed using the electrode. Specifically, if a point on the visual field stimulated a single neuron in cortex, such that both σ_vSUA and σ_vv are 0, then the cortical spread would be equal to the product of visual spread and MF (Eqs. 3 and 4, Materials and Methods). However, in general, it is not possible to activate an arbitrarily small part of the cortex because neighboring cortical regions may be receiving correlated inputs and therefore may also get activated or because the activated part of the cortex may be densely connected to its neighboring regions and may activate those parts (these are captured in the CPI). In the definition used here, the spatial spread function (σ_cLFP) (Eq. 5, Materials and Methods) is independent of the CPI and in fact could be arbitrarily small (in fact, σ_cMUA is taken to be only 60 μm in this model). The model captures variations in CPI using σ_vSUA and σ_vv (which is the variance in the RF centers estimated at a particular location and therefore could be different for different parts of the cortex (Albus, 1975; Dow et al., 1981). However, these two terms get canceled out when comparing across measures (MUA and LFP). Note that this is different from the definition of cortical spread used by Lindén et al. (2011), who measured the LFP spread based only on the LFP activity recorded from the microelectrode, so the spread depended on the level of correlations in the inputs.

Our estimates of ECoG spread decreased with eccentricity (Fig. 4C,E). It is unclear why this is the case, especially because this dependence persisted even after the model was applied (dark vs light shades of blue). As described earlier, it could be because of differences in filtering characteristics of the foveal versus parafoveal tissue due to differences in cell density, morphology, etc., which can produce different filtering characteristics (Bédard et al., 2004, 2006). Our inability to actually measure the MF at the eccentricities at each of the ECoG positions could also have potentially biased the results, especially for the most foveal electrodes, where the MF increased quickly. In particular, the MF may be anisotropic (i.e., MF may depend on the actual azimuth and elevations and could be different for upper and lower quadrants even for the same eccentricity), as reported in previous studies (Van Essen et al., 1984; Palmer et al., 2012), but not considered in the study of Dow et al. (1981) from which we extrapolated the MFs for ECoG positions. Another source of error could be due to residual eye movements, which could also be eccentricity dependent. Specifically, to map RFs of foveal electrodes, the visual stimuli need to be close to the fixation point and may induce large eye jitters than eccentric electrodes. Unlike the spatial spread estimation of LFP, applying the model does not completely eliminate this error. This is because, to estimate the spatial spread of ECoG, we subtract the estimated RF parameters from two signals (ECoG and LFP) obtained from two different electrodes compared with LFP spread, for which both the LFP and MUA were obtained from the same electrode at the same eccentricity (Eqs. 3 and 4, Materials and Methods). Therefore, if the residual eye movement error is more for the RF estimates of foveal ECoG electrodes, then subtracting it from the RF estimates of an eccentric LFP electrode will not completely eliminate the eye-movement-related error. A more elaborate recording setup using multiple small microelectrodes or micro-ECoG arrays that can be placed near each ECoG electrode (such that the MF can be experimentally determined at each ECoG position) will be needed to better study the relationship between ECoG spatial spread and eccentricity.

Although, while using the model, there was a ∼32% reduction in LFP spread, the final effect of the model was modest in case of the ECoG (∼9%). This is because the difference in visual spreads of ECoG and LFP was huge compared with factors that cause the inflation and thus got overshadowed (especially because taking the square further reduced the contribution of the smaller term (Eq. 10, Materials and Methods)). Therefore, although further refinements in the model can improve the estimate of the spatial spread, computing the spread without using the model also gave reasonably accurate results. Therefore, none of our results critically depended on the validity of the model.

Interestingly, we observed that the final ECoG spread was approximately equal to the spread of the LFP (∼0.5 mm) and the radius of the ECoG electrode (∼1.15 mm), suggesting that the ECoG spread should increase linearly with increasing electrode size, with an offset equal to the spread of an infinitesimally small conductor. This is also consistent with RF estimation as a function of frequency (Fig. 6C,D) for which, at higher frequencies, the total spread was approximately equal to the radius of the electrode and spread of the MUA (assumed to be only ∼60 μm in the model). More experiments with ECoG electrodes of varying sizes are needed to verify this experimentally.

ECoG spread as a function of frequency

In our previous study (Dubey and Ray, 2016), we have shown that, in V1, high-gamma (∼60–150 Hz) frequencies of LFP spread significantly greater than the lower frequencies. Further, we found that this was accompanied by an increase in phase coherency across neighboring sites in the same frequency range and could possibly give rise to the band-pass LFP spread (see “Factors affecting the spatial spread” section in Materials and Methods for details). However, unlike LFP, ECoG spread did not show any frequency-specific preferential increase in the spatial spread in the high-gamma range, but instead showed a shallow peak at lower frequencies (beta and gamma ranges). This is a deviation from the earlier observation that ECoG spread could be approximated as the LFP spread plus the size of the ECoG electrode. One reason could be that the increase in phase coherency observed for LFP was very localized (mainly observed between electrode pairs separated by 1.2 mm or less; see Fig. 7 in Dubey and Ray, 2016) and thus was not relevant in case of ECoG signals that involved spatial summation over ∼3 mm. Unfortunately, we did not have enough ECoG electrodes (nor were they as closely spaced as the microelectrodes) to perform an analogous coherence analysis for ECoG (as done for LFPs in Dubey and Ray, 2016), which could have shed some light on the increase in RF size at beta/gamma frequencies for the ECoG.

Recent studies have shown that different brain signals (e.g., LFP, ECoG, EEG, and fMRI) are modulated by different types of underlying processes (Whittingstall and Logothetis, 2009; Musall et al., 2014; Hermes et al., 2017 and references therein). For example, Hermes et al. (2017) showed that neuronal synchrony strongly influences gamma oscillations, but not the BOLD signal. It should be noted that we did not observe stimulus-induced gamma oscillations in either LFP or ECoG signals because the stimulus size was very small. Gamma power has been shown to be critically dependent on the stimulus size (Gieselmann and Thiele, 2008; Ray and Maunsell, 2011; Jia et al., 2013).

To conclude, we found that the ECoG spreads were local and not much larger than the size of the macroelectrode. Although we recorded only from V1, it is possible that these results will extend to other brain areas because the model used here accounted for differences in cortical activation. Our results present the first steps toward carefully describing the spatial spread of ECoG and further validate the use of ECoG for clinical purposes in cognitive neuroscience and BMI applications.