Mathematical Model for Computer-Assisted Modification of Medication Dosing Rules

Abstract

Objective:

Medication dosing in pediatrics is complex and prone to errors that may lead to patient harm. To improve computer-assisted dosing, a mathematical model and algorithm were developed to optimize clinical decision support dosing rules and reduce spurious alerts. The objective was to evaluate the feasibility of using this algorithm to adjust dosing rules.

Materials and methods:

Incorporating historical ordering data, a mathematical model and algorithm were developed to automatically determine optimal dosing rule parameters. The algorithm optimizes the dosing rules by balancing the number of alerts generated for a medication with a minimal length dose interval. In all, 5 candidate medications were tested. An analysis was performed to compare the number of alerts generated by the new model with the current dosing rules.

Results:

For the 5 medications, the algorithm generated multiple clinically relevant rule possibilities and the rules returned performed as well as current dosing rule or matched historical prescriber behavior. The rules were comparable to or better than the existing system rules in reducing the total alert burden.

Discussion:

The mathematical model and algorithm are an accurate and scalable solution to adjusting medication dosing rules. They can be implemented to change suboptimal rules more quickly than current manual methods and can be used to help identify and correct poor quality rules.

Conclusions:

Mathematical modeling using historic prescribing data can generate clinically appropriate electronic dosing rule parameters. This approach represents an automatable and scalable solution that could help reduce alert fatigue and decrease medication dosing errors.

Introduction and Background

Computerized Provider Order Entry (CPOE) is a core functionality of electronic health records (EHRs) and is a system where health care providers enter medication orders for use in patient care. Clinical decision support (CDS), which provides assistance in clinical decision-making, is often implemented within CPOE. Electronic medication rules (eRules) help the prescriber determine whether a medication order is within reasonable and safe parameters based on factors such as the weight and age of a patient.¹ If an order does not satisfy the conditions of the eRule, it will produce an alert or some other form of notification to the prescriber.

Prescribers override CDS alerts for a variety of reasons. As clinicians are familiar with traditional dosing patterns (often through textbooks and other sources of truth), they will often ignore electronic alerts because they feel the system is overwhelming or that the alerts are inaccurate, clinically inappropriate, or simply not helpful.² All these factors contribute to alert fatigue, which increases overrides of medication order-related CDS alerts.³ This raises safety concerns because clinicians are then more likely to ignore a correct alert (true positive) that may be lost among a sea of false-positive alerts.

In pediatrics, it is important that dosing eRules are accurate because medication dosing is extremely complex due to weight-based factors and is prone to error.^4-8 Weight-based prescribing errors are often due to single-dose overdoses that lead to adverse drug events (ADEs). Unfortunately, most of the eRules in modern CDS systems are not tailored for pediatrics and orders entered into CPOE produce high amounts of alerts. Improving the eRules to make the CDS more accurate for pediatrics will theoretically reduce alert burden (thereby improving alert and CDS salience) and dosing errors, improving medication safety. Efforts have been made to change some of these rules and changes have been shown to reduce alerts on a small scale.⁹ However, medication-related CDS on the whole is still immature in many health care organizations; specificity of the alerts themselves is frequently cited as a main cause.¹⁰ This phenomenon of poor attention to alerts is seen in both inpatient¹¹ and outpatient environments.¹² Very little evidence exists regarding the effectiveness of medication-related CDS interruptive ordering alerts (especially in pediatrics), and what does exist shows mixed results of effectiveness.¹³ Attempts to change the specificity and performance of alerts on a large scale is challenging as common vendor eRule databases contain hundreds of thousands of records. The modification of medication rules is labor-intensive and minor changes in dosing parameters of one medication formulation may require the modification of dozens of eRules due to the granularity of the databases. Proper configurations of CPOE and CDS systems have the potential to mitigate this issue.^14,15 Currently, there is no automatable, scalable, and efficient solution to this problem. The application of computational and mathematical modeling to historic prescribing data presents an opportunity to overcome these issues.

Objective

The objectives of this study were to (1) develop a mathematical model that can optimize eRule dosing parameters based on historical order data, (2) use the model to develop an algorithm that determines optimal medication dosing rule parameters, and (3) perform an offline simulation test and evaluate the process, comparing the output against our institution’s existing operationally active eRules. Our hypothesis is that the model and algorithm will be able to empirically adjust the dosing rule parameters and will perform favorably when compared with the performance of current eRules.

Materials and Methods

Setting

Cincinnati Children’s Hospital Medical Center is a level-1 trauma center with 628 licensed beds. It has 1.2 million patient encounters annually, including 30 000 admissions, 33 000 surgeries, 900 000 ambulatory encounters, and 125 000 emergency department visits. There are approximately 200 000 medication orders a month, which generate 75 000 dosing alerts. The institution implemented an enterprise EHR (EpicCare^®, Verona, WI, USA) in 2007. The EHR is configured to use a combination of the Medi-Span (Wolters Kluwer Health, Philadelphia, PA, USA) drug dosing decision support rules and supplemented with custom dosing rules created and maintained by the pharmacy.

Dosing rules description

There are 2 sets of dosing rules used in this study: actual dosing rules and the model-generated dosing rules. The actual dosing rules are the electronic rules (eRules) that are used in the study site’s production CPOE system rules engine and clinical care. The actual dosing rules were purchased from a third-party vendor. All the dosing parameters for the candidate medications selected in this study were already customized and overrode the vendor’s default rule parameters. The model-generated dosing rules are the dosing rules output by the mathematical model created to optimize the rule parameters. The 2 sets of dosing rules represent different CPOE configurations for weight-based dosing CDS. The theoretical performances of these sets of dosing rules were compared with demonstrate the viability and feasibility of the model-generated dosing rules (refer sections “Assessing the performance of the Model-generated Dosing Rules” and “Results”).

Clinical dataset for dosing rules model development

Historical medication order data from 2011 to 2015 were retrieved from a previously described decision support analytic data warehouse.^9,16 A total of 5 medications were selected to use in developing the model: Acetaminophen, Ibuprofen, Diphenhydramine, Amoxicillin, and Ursodiol. The order counts and the Actual eRules in the CPOE of these medications are listed in Table 1. These medications were selected based on criteria that included frequency of ordering and frequency of alerting. Ursodiol was selected because it was previously known to have a poor match between the formal dosing eRules and how it is ordered in practice. A pediatrician (ESK) aggregated different formulations for the selected medications based on ordering behavior (Table 2). For example, in our dataset, Ibuprofen has formulations of suspension, tablets, chewable tablets, solution, and capsule. These were grouped together for analysis as those formulations are typically prescribed with the same dosing guidelines. The data were filtered for orders placed using weight-based dosing, eg, in milligram/kilogram. Orders placed using absolute dosing, eg, in milligrams, were excluded as the model calculated weight-based dosing parameters only. The data include all medication dosing orders that were attempted as well as orders canceled and removed by prescribers after they attempted to sign the orders and received an alert.

Table 1.

Dosing rule parameters (actual eRule) and medication data counts.

Medication	Actual eRule	Order count
Acetaminophen	5-15 mg/kg	376 794
Diphenhydramine	0.1-1.5 mg/kg	163 225
Ibuprofen	4-11 mg/kg	42 884
Amoxicillin	8-45 mg/kg	61 323
Ursodiol 0-12a	10-15 mg/kg	1191
Ursodiol 12-99a	2-5 mg/kg*	39
Total		645 456

^aUrsodiol has a different eRule for different age groups: the split was based on the construct of the current eRules.

Table 2.

Medication formulation groupings.

Medication	Cap	Tab	Chew Tab	Solution	Liquid	Elixir	Suspension	Recon suspension	Gel	Syrup	Tablet dispersible
Acetaminophen	X	X	X	X	X	X	X		X	X	X
Diphenhydramine	X	X	X	X	X	X
Ibuprofen	X	X	X	X			X
Amoxicillin	X	X	X					X
Ursodiol 0-12	X						X
Ursodiol 12-99	X						X

Generation of the artificial dataset

The mathematical model and optimization algorithms require dosing data to generate meaningful dosing rules. Using the assumption that future dosing behavior can be approximated using historical dosing data, we could generate dosing rules directly using historical data. A disadvantage of the direct use of historical data is that it neglects the potential for the appearance of unseen doses in the future. For example, typographical mistakes where the user hits the wrong/multiple keys or unit errors where the user inputs the incorrect units could be reasonably expected to occur eventually. For frequently ordered medications, the probability of an unseen dose appearing in the future would be small, but for infrequently ordered medications, using only historical data may not be sufficient. To incorporate the knowledge that doses unseen in historical datasets could appear in the future, we develop a model of future historical dosing behavior that is statistically consistent with historical dosing data and incorporates unseen doses.

The clinical dataset described in section “Clinical dataset for dosing rules model development” was used to generate an artificial dataset. Our artificial data model is based on 2 assumptions: that future ordering behavior will match historical ordering behavior and that there exists doses that were unseen in the historical data but could appear in the future. Here, we use a frequentist statistical model based on these assumptions. Other approaches to generate meaningful artificial data such as Bayesian models can be used in lieu of this approach as the mathematical model and optimization algorithm are indifferent to the origin of the data.

For large historical dosing datasets from commonly prescribed medications such as Acetaminophen or Ibuprofen, the probability of a specific dose can be estimated using the maximum likelihood estimate (MLE), where the probability is the frequency of the specific dose divided by the total number of orders. A limitation in this approach is that doses that do not appear in the historical dataset have a zero probability of occurring in the artificial dataset. Various data entry errors that might have not occurred historically but have a small but non-zero probability of occurring in the future would be neglected from our study. It is important that the probability of these orders is not zero.

To address this limitation, we use an alternative statistical model to the MLE that assigns certain unseen dose orders a non-zero probability. Our statistical model uses Good-Turing frequency estimation (GTE)^17-19 to generate the probability of set of seen and unseen dose orders.

From the historical dataset, we have the set, ${\mathit{D}}_{\mathrm{observed}}$, that contains all the observed dose orders and we can compute the frequency each dose is prescribed. We define the frequency of dose frequency, $N_r$, as the number of doses in ${\mathit{D}}_{\mathrm{observed}}$ ordered with the frequency $r$. For example, $N_1$ is the number of doses that were ordered only once in the dataset. The total number of orders can be computed from the frequency of frequency data by the relation

$$N=\sum _{r=1}^{\mathrm{\infty }}r{N}_r.$$

The MLE estimate of the probability a specific dose is ordered $r$ times is $p_r=r/N$ and the probability of a dose not in ${\mathit{D}}_{\mathrm{observed}}$ is $p_0=0$. The GTE of the total probability of all unseen doses is estimated by

$$p_0=\frac{N_1}{N}.$$

Note that this is the probability that any unseen dose will appear in the future, not the probability of a single, specific unseen dose. The probability of individual doses in ${\mathit{D}}_{\mathrm{observed}}$ that appear with frequency $r$ is estimated by

$$p_r=\frac{\left(r+1\right)S\left(N_{r+1}\right)}{NS\left(N_r\right)},$$

where $S(N_r)$ denotes a smoothed frequency estimate generated by linear regression.^17,20

The GTE estimates the total probability of all unseen dose orders but we need to generate specific dose values that are unseen. As the set of possible unseen orders is uncountably infinite, we will restrict it to a finite set of more probable unseen doses, ${\mathit{D}}_{\mathrm{unseen}}$ containing $N_0$ elements. For each dose in ${\mathit{D}}_{\mathrm{unseen}}$, we assign an equal probability

$${\tilde{p}}_0=\frac{p_0}{N_0}=\frac{N_1}{N_{0}N}.$$

The set of all possible doses from the artificial data generator will be the union of the 2 sets $\mathit{D}={\mathit{D}}_{\mathrm{observed}}{\cup }^{}{\mathit{D}}_{\mathrm{unseen}}$. To generate artificial data from the GTE of the probabilities, we begin by computing the discrete cumulative distribution function (CDF) for the dose set $\mathit{D}$: for dose $d\in \mathit{D}$

$$CDF\left(d\right)=\sum _{d_j<d}p\left(d_j\right),$$

where $d_0<d_1<\cdots <d_j<d_M$ are the sorted doses in $\mathit{D}$, $M$ is the total number of possible dose orders, and $p(d_j)$ is the GTE of the probability of dose. As the CDF is a monotonically increasing function and $0″CDF(d)″1$, we can use the CDF to map a uniform random variable, $0″X″1$, to a specific dose through the relation

$$d=\underset{d_j\in D}{\max }CDF\left(d_j\right)\le X.$$

This relation is used to generate the artificial data by mapping a set of values from a uniform random distribution to a set of dose orders. Python (version 3.5.1, 2015; Python Software Foundation, Delaware, Beaverton, USA) was used to generate the historical frequency of frequency data, implement the GTE, and the artificial dose data and the respective histograms and to implement the following model and optimization algorithm. A total of 100 000 order instances were generated for each medication.

Development of the dosing rule model

Based on our goal of decreasing alert burden to improve alert salience, we created a model to optimize CDS dosing eRules with the express intent of reducing alerts. The model evaluates a discrete number of possible rule range intervals, based on the number of alerts each range would produce when the artificial dataset is applied, ie, it assesses the number of theoretical alerts that would be generated with the model dosing limits. The multiple discrete combinations of dosing rule intervals considered are based on the values of where most of the medication dose orders occur, eg, as most dosing orders for Acetaminophen occur between 0 and 20 mg/kg, multiple combinations of rule intervals between 0 and 20 are considered. To find the optimal rule, we must assign a score to each one being considered. We developed a measure of the quality of any given rule. As it is mathematically easier to study the inverse of the quality of the dosing rules, we propose this measure as the inferiority score of a dosing rule. Our inferiority measure assigns a score to each rule based on the number of theoretical alerts produced. We assume that our quality measure of a given dosing rule depends on 2 factors:

1. The number of alerts produced by a set of simulated dosing data: our goal is to empirically create dosing rules that are both clinically accurate (increase true positive alerts and true negatives) and decrease alert burden (through reduction of false-positive alerts). A dosing rule that generates a large number of alerts will, in general, have a poor quality measure.

2. Length of the rule interval: This term penalizes the quality measure if the dosing interval size is larger than the length of the actual eRule, which is included to prevent the degenerative case where an arbitrary large interval that produces no alerts is acceptable.

The function will return an inferiority score for each dosing rule. A high inferiority score for a dosing rule range means that this rule is producing high amounts of alerts or that the rule interval is too large. A low inferiority score means that a dosing rule has few alerts and an acceptable interval size. Given a rule interval $R=(x,y)$, where $x$ is the lower dosing limit and $y$ is the upper dosing limit and a series of dose orders, $E$, the measure of the inferiority, $I$, of a rule is defined as

$$I\left(R,E\right)=w_1\frac{A}{N}+w_2\frac{\left|y-x\right|}{L_0},$$

where $A$ is the number of alerts generated from the set of orders, $E$; $N$ is the total number of orders in the dataset; $L_0$ is the length of the actual dosing rule interval; and $w_1$ and $w_2$ are arbitrary weights. Each term is scaled so that the alert term is less than 1 and the other term has a value close to unity. The weights are arbitrary and affect the relative importance between the 2 terms. For example, having $w_1>w_2$ implies that reducing the number of alerts is more important than reducing the interval length when improving the quality of the rule. Note that these 2 terms are proxies for false positives (total number of alerts) and false negatives (interval length) and the weights can be viewed as their relative importance. While these proxies are crude, they could be an improvement compared with the status quo until more accurate proxies are developed.

As multiple discrete combinations of dosing rules are considered, multiple inferiority scores are returned. The goal is to find the lowest inferiority score, which will be associated with a dosing rule interval.

Implementation of the dosing interval optimization algorithm

An algorithm was implemented to find the lowest inferiority score. The algorithm computed the inferiority scores for each dosing interval and stored the values in a grid where the position in the grid corresponds to the lower and upper dosing rule limit. For optimization, the algorithm found the lowest score in the grid and returned the associated lower and upper rule limits of the dosing interval. Surface plots of the resulting grids were visualized using MATLAB (Release 2012b; The MathWorks, Inc., Natick, MA, USA).

Applying a weights simulation algorithm

In lieu of choosing the weights a priori, we developed an algorithm that assesses the impact of various weights on the model output. We prioritize reducing the number of alerts, so we chose to restrict the weights where $w_1>w_2$. As it is the relative sizes of the weights to each other, we set $w_2=1$ and scan the results for various values of $w_1$. We use a modified form of the bisection method to search through the range of weight values, $w_1$, looking for the critical weight values where changes in the model’s dosing rule output occur. Once each critical weight value was found, the associated dosing rules returned were recorded and considered as part of the model’s output. This provides a complete set of optimal dosing rules based on the relative importance of reducing the number of alerts to the interval length.

Assessing the performance of the model-generated dosing rules

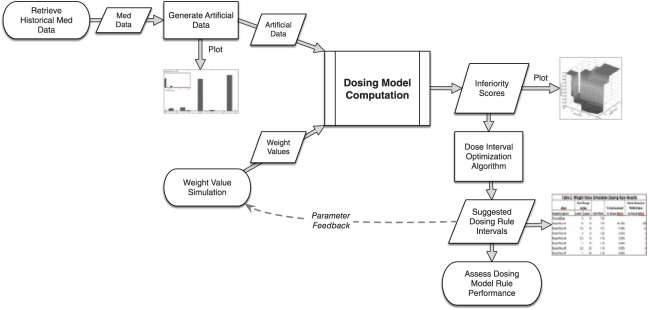
Finally, we evaluated the theoretical performance of the model-generated dosing rules compared with the actual dosing rules currently applied in the EHR. We computed the alert rates using our artificial dataset on each of the model dosing rules returned and the actual eRule. The alert rate is the percent of dosing orders that generate an alert for a given rule. We then used the alert rates to calculate the percent improvement of the returned dosing rules from the alert rate of the actual eRule as well as the number of alerts saved per 100 000 dosing orders. The integration and flow of all of these processes are shown in Figure 1.

Figure 1.

Flowchart for generating and assessing empirically-derived dosing rules. Process diagram for the study, showing the methods of the study integrated to produce data-driven dosing thresholds.

Results

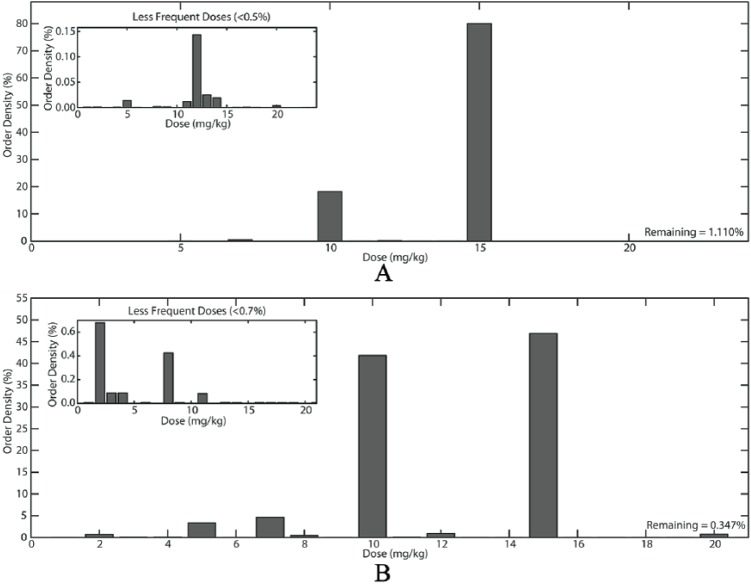
Artificial datasets were visualized using histograms (Figure 2). The insets allow the user to better understand the distribution of the lesser frequent doses.

Figure 2.

Artificial dataset for (A) Acetaminophen and (B) Ursodiol 0-12 years. The large histograms show 2 examples of the distribution of the artificial dataset doses. The histograms in the insets show the less frequent doses; visualization of these less-frequent doses is difficult otherwise.

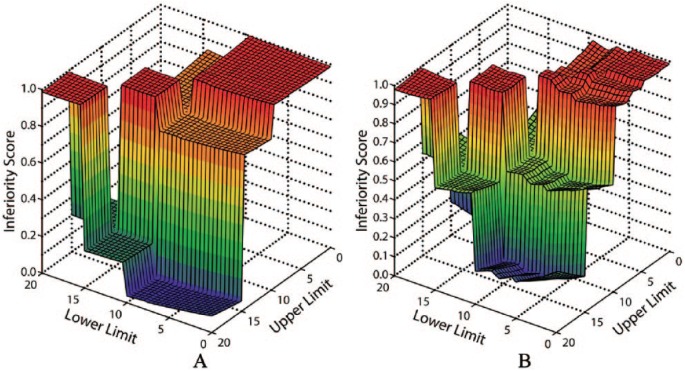
After the model computation used the artificial data and a set of weight values to generate inferiority scores, the optimization algorithm found the minimum value for this score and the output was visualized as shown in the example medications (Figure 3). This visualization permits the capability to understand how prospective changes in the dosing rule parameters would affect the score. In the case of acetaminophen, the optimal dosing range is 10-15 mg/kg. Decreasing the upper limit (eg to 13 mg/kg) would drastically impact the inferiority score, while increasing the lower limit to 13 mg/kg would not have such a profound affect.

Figure 3.

Surface plots of dosing rule interval limits; grid output from the optimization algorithm. Each dosing rule limits considered between 0 and 20 mg/kg was assigned an inferiority score. The lowest inferiority score denotes the optimal dosing range as defined by a priori criteria. In both A and B, the lowest inferiority score returned was 10-15 mg/kg in this instance of weight values, thus the optimal dosing interval for both (A) Acetaminophen and (B) Ursodiol (0-12 years) is 10-15 mg/kg.

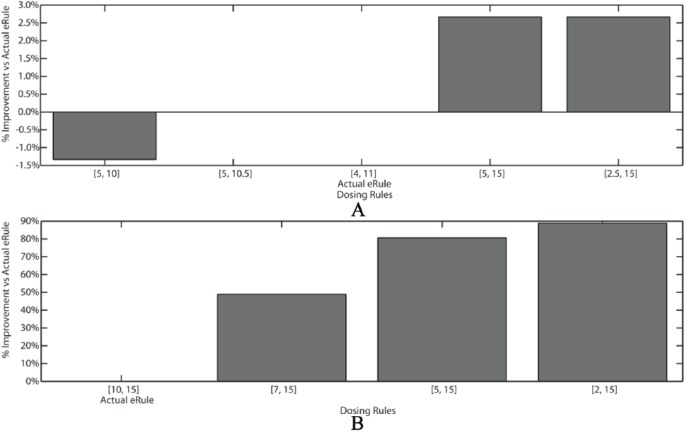
Table 3 represents the results of the model output and weight simulation experiments; the different rules are the result of the model computation with the weights selected by the weight simulation algorithm. Varying the weights on the model terms output differing optimal rule ranges, with varying affects on alert rates and alerts saved. These tables allow users to quickly scan the model output and select most clinically appropriate rule thresholds that have the largest reductions in alert burden. Figure 4 demonstrates these gains graphically. Gains to commonly and uniformly prescribed medications such as ibuprofen are modest as the threshold limits are widened (Figure 4A; alert reduction gains of 2%-3%), while modest changes to threshold limits impart bigger gains in more heterogeneously prescribed medications such as Ursodiol (Figure 4B; 50%-100% alert reduction).

Table 3.

Weight value simulation dosing rule results.

Weight ratio (r = w1/w2)	eRule	Rule range (mg/kg)		Alert rate	Percent improvement vs actual eRule	Alerts saved per 100 000 orders vs actual eRule
		Lower	Upper
Acetaminophen
	Actual eRule	5	15	1.20
(2, 54)	Model Rule 1	10	15	1.73	–44.19%	–529
(55, 2734)	Model Rule 2	7.5	15	1.21	–1.00%	–12
(2735, 16 124)	Model Rule 3	5	15	1.20	0.00%	0
(16 125, 24 000)	Model Rule 4	3.5	15	1.14	0.05%	6
Ibuprofen
	Actual eRule	4	11	0.75
(16, 3571)	Model Rule 1	5	10	0.76	–0.80%	–6
(3572, 7117)	Model Rule 2	5	15	0.75	–0.27%	–2
(7118, 20 918)	Model Rule 3	5	15	0.73	2.40%	18
(20 919, 21 938)	Model Rule 4	2.5	15	0.73	2.66%	20
Diphenhydramine
	Actual eRule	0.1	1.5	1.25
(1, 38)	Model Rule 1	0.5	1	3.28	–166.64%	–2133
(39, 1453)	Model Rule 2	0.5	1.5	1.34	–6.25%	–80
(1454, 56 578)	Model Rule 3	0	1.5	1.25	–0.16%	–2
>56 579	Model Rule 4	0	5	1.26	1.64%	21
Amoxicillin
	Actual eRule	8	45	2.06
(1, 4)	Model Rule 1	40	45	13.27	–544.03%	–11 207
(5, 9)	Model Rule 2	25	45	7.03	–241.41%	–4973
(10, 11)	Model Rule 3	20	45	5.26	–155.53%	–3204
(11, 37)	Model Rule 4	12.5	45	2.33	–13.25%	–273
(37, 61)	Model Rule 5	12.5	50	1.70	17.52%	361
(61, 1887)	Model Rule 6	10	50	1.43	30.58%	630
(1888, 3250)	Model Rule 7	7.5	50	1.42	31.07%	640
(3251, 3360)	Model Rule 8	4.5	50	1.41	31.36%	646
Ursodiol 0-12
	Actual eRule	10	15	10.25
(3, 7)	Model Rule 1	10	15	10.25	0.00%	0
(8, 43)	Model Rule 2	7	15	5.18	49.43%	5068
(44, 320)	Model Rule 3	5	15	1.98	80.68%	8271
(321, 802)	Model Rule 4	2	15	1.16	88.73%	9097
Ursodiol 12-99
	Actual eRule	2	5	50.62
(8, 24)	Model Rule 1	5	10	16.08	68.24%	34 538
(25, 119)	Model Rule 2	4	10	11.05	78.17%	39 564
(120, 237)	Model Rule 3	4	14.5	4.08	91.94%	46 535
(238, 498)	Model Rule 4	4	15	3.56	92.96%	47 052

Figure 4.

Visual representation of rule % improvement vs actual eRule. “Actual eRule” label is directly beneath the bar representing the parameters or the actual dosing rule in clinical use. Other bars represent the comparison to different algorithmically derived dosing rule parameter choices. (A) Ibuprofen shows about 3% improvement in alert savings if the dosing rule is 5-15 mg/kg vs the actual eRule of 4-11 mg/kg. (B) Ursodiol shows significant improvement in alert reduction if the rule range is increased.

Discussion

Current methods for adjusting medication dosing rules have many challenges and are largely predicated on time-consuming procedures that are dependent on expert opinion and knowledge. The approach outlined in this study represents an alternative set of procedures for setting and adjusting electronic rule (eRule) dosing parameters, one that is empiric, scalable, and scientific. It uses data generated by the EHR through previous activities by prescribers (empiric), is automatable (thus scalable and addressing the current state of entirely manual adjustment), and can serve as a basis for a CDS learning system.²¹ This secondary use of data means that resources used to input data into the model are minimal—there is no requirement for gathering primary data as substrate. The mathematical model and algorithm are a feasible alternative solution to adjusting medication dosing rules.

The candidate medications for this study were carefully selected. Their commonality allows for plentiful data to serve as the foundation for our test data. They represent one end of the prescribing spectrum. Unfortunately, these medications are also commonly used for a multitude of clinical indications, and the eRules for these drugs have been heavily customized with great scrutiny. The results (Table 2) reflect as such. The dosing intervals are generally very liberal, which limits our ability to demonstrate a large alert savings. Heavy customization of the eRules has also led to a pre-study adjustment that limits the alert savings results, especially with Acetaminophen, Ibuprofen, and Diphenhydramine, all of which are dosed heterogeneously in our clinical environment.

The real value of the model and algorithm will be demonstrated in less mainstream circumstances; in situations where dosing is more heterogeneous, rule customization has not been performed or customization thresholds have been configured that do not match clinical practice. The comparison of the model-generated dosing rules to the customized eRules for Amoxicillin and Ursodiol demonstrates a greater alert savings. The next step for this work should seek to validate the approach and demonstrate realized alert savings in a wider range and number of medication formulations.

Automating the process of dosing rule adjustment through this method does not alleviate the need for clinical judgment. Because the system generates several optimized possibilities for dosing rule thresholds, clinicians with pharmacy expertise need to provide the context to (1) select reasonable parameters presented to them by the system and (2) ensure clinical validity before integrating into practice. The rule that decreases alert burden the most may not be clinically appropriate. Until the model has matured and can receive input regarding the validity of the rules, a human validator will continue to play a key role in the process and this role must understand the balance between alert burden from false positives and safety risks from false negatives. The goal of this work is to reduce that burden in creating better dosing rules, not eliminate the clinical expert entirely or fall prey to automation bias.^22,23 This tool has the capability to rapidly assess all drug rules in a corpus in an automated fashion, identify and prioritize candidate rules for editing based on the potential decrease in alert burden or other factors, and present these rules to a human expert for validation and implementation. Like almost all informatics tools, the goal is to leverage the strengths and capabilities of both humans and machines. The system can become more intelligent and efficient with additional feedback, helping to identify and correct poor-quality rules. The efficient identification and correction of poor quality rules will lead to many attractive gains including decreases in alert burden through fewer false-positive alerts, improved EHR efficiency through a decrease in alert fatigue, and most importantly, potential decreases in medication errors as providers are able to pay more attention to the remaining alerts.⁹

This study has several limitations. First, we assumed that historical ordering patterns are representative of future ordering patterns. The inclusion of data across a long time span mitigates this concern somewhat, but methods to determine clinically accurate changing prescribing patterns (new indications and/or dosing for a medication outside of the normal dosing range) should be considered to overcome this limitation. Another limitation is that the system is based on the assumption that historic prescribing patterns represent appropriate and safe dosing. It is possible that aspects of EHR configurations (such as order sets) could introduce frequent unsafe orders, which could feed into the model and affect its output. At our institution, we have only witnessed this phenomenon on a small scale, but this limitation speaks to the importance of the role of the clinical validator in optimal dosing rule selection process and in evaluating for “false negative” instances, which could lead to a dosing error because no alert was activated.

The generated rules are not patient-specific and the algorithm represents a population-based approach. While this could potentially lessen the clinical impact, with this method we could aggregate data across different populations or disease indication to come up with more specific rules for those patients. Unfortunately, most dosing rules in production systems are not currently patient-specific, including at our institution. As this becomes more common, our method will need to be expanded to account for this. Finally, as demonstrated with the results of this study, the largest gains in decreasing alert burden are minimized by previously implemented, well-constructed operational dosing rules. However, given the hundreds of thousands of dosing rules in vendor products, further study of this automated empiric approach will demonstrate which types of dosing rules (frequently used, most alerted, etc) will return the most value.

Future work includes augmenting the model with additional parameters to increase its accuracy. Incorporating factors such as the type of alerts produced and the override rate of alerts from clinicians’ behavior will be undertaken. Large-scale studies across more types of medications and prescribing environments, as well as for different indications for the same medications, should be performed to further add validity to this approach. The algorithm will be implemented in user-facing software as a tool for pharmacists to use in improving CDS systems. It could then be applied to both pediatric and adult populations.

Conclusions

Mathematical modeling using historic prescribing data can generate more clinically appropriate electronic dosing rule parameters. This approach represents an automatable and scalable solution that could help address alert fatigue and decrease medication dosing errors.