Interpretation of a new biomarker for the right ventricle introduced to evaluate the severity of pulmonary arterial hypertension

Assessment of right ventricular (RV) performance can be a challenge for clinicians and researchers, especially in the diseased heart. In their study on pulmonary arterial hypertension (PAH) in pediatric patients, Yang et al. sought to identify a quantitative measure to predict disease progression and to assist treatment planning.¹ The authors defined a potential biomarker (based on MRI and right heart catheterization data) that appears to correlate with clinical worsening, and outperforms several other metrics studied. During follow-up for a period from 1 to 10 years since diagnosis, an upward trend of the new biomarker was found for patients with clinical worsening (N = 8) compared with a well-defined stable subgroup (N = 9).

Like other investigators, the authors choose stroke work (SW) as a starting point but noted that, in two situations, SW may numerically be equal but clinically not the same, even after indexation (i) for body surface area (BSA). In good approximation, SW is obtained by multiplying the pertinent pressure difference (ΔP, Fig. 1(a)) with the corresponding volume difference, stroke volume (SV).² This method is an accepted alternative for the more rigorous integration of the area within the pressure-volume (PV)-loop as applied by the authors.

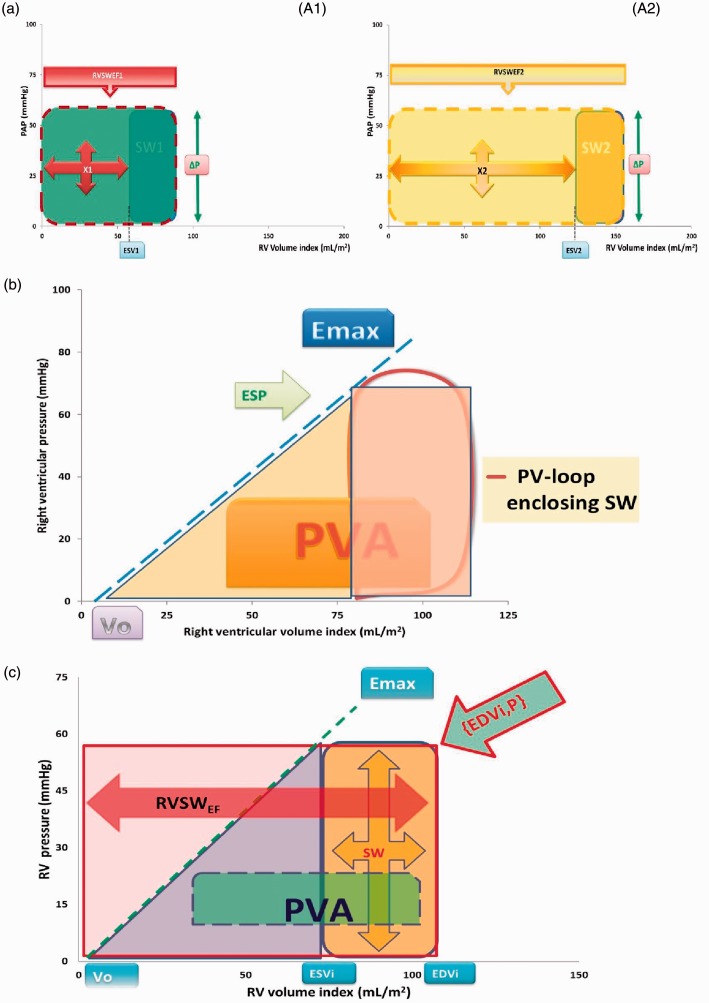
Fig. 1.

(a) Schematic representation of pressure-volume (PV) loops for the right ventricle (RV) for two theoretical situations (marked as A1 and A2, left and right panel), here with equal values for stroke work (SW) and the same systolic-diastolic pressure difference (ΔP). Ejection fraction (EF) decreases as the PV loop shifts to larger volume ranges, as from SW1 to SW2. The suggested metric RVSW_EF as introduced by Yang et al.¹ corresponds with the rectangular areas enclosed by the red and yellow contours (with broken lines). These areas consist of two components: SW and what is indicated as X, where X1 = (SW1/EF1)–SW1 and X2 = (SW2/EF2)–SW2. Unfortunately, RVSW_EF is not a unique index, as further explained in the text. (b) PV loop for the right ventricle (similar as in Figures 1 and 2 of Yang et al.¹), illustrating the end-systolic elastance concept with slope Emax and intercept Vo. This method has been employed to estimate myocardial oxygen consumption (MVO₂) on the basis of SW and the triangular area under the Emax line from Vo to ESP. Pressure volume area (PVA) is the sum of this triangle and SW, and has been shown to relate to MVO₂. (c) Schematic representation of the contributions of pulmonary arterial pressure (PAP) and end-diastolic volume index (EDVi) to RV SW penalized by EF (RVSW_EF). The latter equals the colored rectangular area with red borders. The position of the right upper corner fully determines RVSW_EF as defined by Yang et al.¹ Obviously, RVSW_EF is not unique, because many combinations of EDVi and ΔP yield the same area. Subdivision in two portions, namely reflecting SW (orange) and the remaining area bounded by end-systolic volume index (ESVi), respectively, opens a route to connect to interpretation in terms of physiology by considering the broken line, which refers to end-systolic elastance (Emax). Emax is defined as ESP/(ESVi–Vo), where ESP is end-systolic pressure, and Vo is an extrapolated intercept. The triangular area under the Emax line added to SW is the PVA. This sum reflects a basic component of myocardial oxygen consumption. Note that the triangular area contributing to PVA is half of the area defined by RVSW_EF after subtraction of the contribution by SW.

Obviously, there are many combinations of ΔP and SV that yield the same SW. To accurately capture differences in physiology, the authors introduced what they call penalized SW by dividing SW by ejection fraction (EF). However, EF has shortcomings similar to those of SW in the sense that any given value is not unique.² Also, two patients can differ in terms of pathophysiology, but still have the same EF and SW, because matched alterations of ΔP can compensate for RV volume changes. Statisticians warn against problems involved with ratios.³ In fact, upon dividing SW by the ratio EF, the SV cancels out, implying that the newly defined biomarker is not purely reflecting SW. Interestingly, the proposed penalized metric (Fig. 1(a) depends only on the end-diastolic volume index (EDVi) and on ΔP, however precisely defined:

$$\begin{array}{c}{\text{RVSW}}_{\text{EF}}=\text{SWi}/\text{EF}\\ =(\text{SVi}*\Delta \text{P})/(\text{SVi}/\text{EDVi})=\Delta \text{P}*\text{EDVi}\end{array}$$

where ΔP can be regarded as RV end-systolic pressure (ESP) or any appropriate approximation such as RV mean systolic pressure minus mean RV diastolic pressure.² The proposed metric consists of the traditional SWi (=ΔP * SVi) plus an extra component X equal to (ΔP * ESVi), where end-systolic volume index ESVi = EDVi-SVi. Based on figure 2 in Yang et al.,¹ the true SW ranges from approximately 800 to 5000 mmHg·mL, implying that X is substantial in many cases, and certainly in the clinically most relevant target group of PAH patients.

Basically the new biomarker is composed of a rectangular PV-area that includes SW (Fig. 1(a)), where the precise contours of the PV-loop become irrelevant by virtue of its definition. Moreover, deterioration of RV function caused by increasing ΔP and/or EDVi implies that the relative contribution of SW to RVSW_EF becomes less important as time progresses. Indeed, larger values for ΔP and EDVi contribute to the value found for X, which equals RVSW_EF minus SWi. Therefore, it is of paramount interest to analyze, and possibly interpret, the area X, which often dominates the impact of the newly introduced biomarker RVSW_EF.

Decades ago, physiologists introduced the concept of end-systolic elastance (Emax) as an insightful description (Fig. 1(b)) with which to analyze ventricular function, which idea was also incorporated by the authors in their appendix.¹ Earlier investigations on Emax concerned animal studies,⁴ and also clinical applications involving the RV.⁵ The elastance concept offers an attractive tool to interpret the reported findings by establishing a relationship with myocardial oxygen consumption (MVO₂). To utilize this type of analysis based on energetics, we consider half of the area of RVSW_EF NOT occupied by actual SW, and given by the triangular area in Fig. 1(b). This triangular area (being 0.5 X) added to SW yields the pressure-volume area (PVA), and has been related to MVO₂ (Fig. 1(b)).^4,5 Although the precise extent of the volume intercept (Vo) of the end-systolic elastance concept requires further clarification, this route may lend physiologic interpretation to the approach proposed by Yang et al.¹ In their lumped parameter model, the authors apply the Runge-Kutta method to obtain SW, while, for simplicity, we employ a more rectangular contour permitting direct multiplication of SV and ΔP. Indeed, the integral of ΔP * dV over the range of SV divided by SV is the average ΔP of the PV-loop. Thus, their formula decomposes to ΔP * EDVi, and, therefore, the shape of the PV-loop becomes irrelevant. The authors found a 7% difference between two methods to derive SW acceptable, and our approximation may well be within this limit when judging their figure 2.¹ Besides, the extra area X introduced by the authors is determined by ESVi and the choice of ΔP (Fig. 1(b)) and independent of the approach preferred to obtain SW. As the authors emphasize in the legend of their figure 2,¹ the PV-loops for patients who clinically worsened tended to be generally larger and rightward. This means that both an increase of ΔP (or PAP for that matter) and elevation of EDVi point to a more severe disease state. Interestingly, multiplication of these two components yields the rectangular area that we emphasize for two examples in Fig. 1(a)). Given a particular ΔP level, PVA is essentially determined by SVi and 0.5 * ESVi, assuming that Vo can be neglected (Fig. 1(b)). ESVi is, in turn, inversely and nonlinearly related to EF, as demonstrated for the RV.^6,7

We conclude that, rather than the isolated value of SW, even when obtained by a lumped parameter model, the ESVi is a dominant component of the proposed RVSW_EF, especially in worsening PAH states. Total RVSW_EF is determined by the area subtended by ΔP and RV EDVi (Fig. 1(a)). Selection of ΔP is not critical, as proportional relationships between systolic, diastolic, and mean PAP have been documented in health and RV disease.⁸ Thus, the practical impact of the biomarker may be based on the fortunate product of two variables (namely ΔP and EDVi), which each independently already reflect disease severity in PAH (as specified in their legend to figure 2).¹ Importantly, the temporal trajectory followed by {EDVi,ΔP} as the disease process develops may be clinically relevant. Finally, RVSW_EF suffers from the same shortcoming as initially noted for SW. Indeed, many combinations of ΔP and EDVi may yield the same value for the freshly introduced metric. We favor a representation in the PV domain (Fig. 1(c)), rather than the combination of ΔP and EDVi into a single number (namely RVSW_EF) as created by multiplication.

Conflict of interest

The author(s) declare that there is no conflict of interest.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.