The effect of different image reconstruction techniques on pre-clinical quantitative imaging and dual-energy CT

Abstract

Objective:

To analyse the effect of different image reconstruction techniques on image quality and dual energy CT (DECT) imaging metrics.

Methods:

A software platform for pre-clinical cone beam CT X-ray image reconstruction was built using the open-source reconstruction toolkit. Pre-processed projections were reconstructed with filtered back-projection and iterative algorithms, namely Feldkamp, Davis, and Kress (FDK), Iterative FDK, simultaneous algebraic reconstruction technique (SART), simultaneous iterative reconstruction technique and conjugate gradient. Imaging metrics were quantitatively assessed, using a quality assurance phantom, and DECT analysis was performed to determine the influence of each reconstruction technique on the relative electron density (ρ_e) and effective atomic number (Z_eff) values.

Results:

Iterative reconstruction had favourable results for the DECT analysis: a significantly smaller spread for each material in the ρ_e-Z_eff space and lower Z_eff and ρ_e residuals (on average 24 and 25% lower, respectively). In terms of image quality assurance, the techniques FDK, Iterative FDK and SART provided acceptable results. The three reconstruction methods showed similar geometric accuracy, uniformity and CT number results. The technique SART had a contrast-to-noise ratio up to 76% higher for solid water and twice as high for Teflon, but resolution was up to 28% lower when compared to the other two techniques.

Conclusions:

Advanced image reconstruction can be beneficial, but the benefit is small, and calculation times may be unacceptable with current technology. The use of targeted and downscaled reconstruction grids, larger, yet practicable, pixel sizes and GPU are recommended.

Advances in knowledge:

An iterative CBCT reconstruction platform was build using RTK.

Introduction

Pre-clinical cone beam CT (CBCT) X-ray image reconstruction is typically described by the Feldkamp, Davis, and Kress¹ (FDK) algorithm to solve the inverse Radon transform through filtered back-projection (FBP). While the FDK algorithm produces usually acceptable images, it copes poorly with noise. Iterative reconstruction (IR) algorithms use multiple repetitions in which a current solution converges towards a better solution. Subsequent to projection acquisition, a forward projection creates artificial data, which is compared with measured projections to compute a correction term. In case of discrepancy, the first image estimate is updated based on the characteristics of the underlying algorithm. Image and projection data correction are repeated until a condition predefined by the algorithm is satisfied and the final image is generated.²

IR algorithms may allow considerable dose reduction due to a more precise modelling of the acquisition process, which can reduce image noise. They avoid introducing new artefacts due to approximations and are suited for dealing with missing data or irregular sampling. The main drawback of IR is the increased computational cost of the iteration cycle.

It has been suggested^3–5 that IR algorithms could provide superior material segmentation when performing dual energy CT (DECT). Radiotherapy applications in which tissue segmentation accuracy plays an important role have benefitted by DECT⁶ and a number of pre-clinical studies has also shown advantages of DECT.^4,7,8 Furthermore, DECT can improve Monte Carlo dose calculations accuracy for accuracy for low-energy photons and protons.^3,6,9,10

This work presents a software platform for pre-clinical CBCT image reconstruction, built using the open-source reconstruction toolkit (RTK),¹¹ which comprises FBP and four IR algorithms. Imaging parameters were quantitatively assessed and a DECT analysis was performed to determine the influence of each reconstruction technique on the image quality.

Methods and materials

(Pre) Image acquisition

Image projections for this study were acquired using the CBCT electronic portal imaging device integrated in the small animal irradiator X-RAD 225Cx (Precision X-ray, North Branford, CT), illustrated in Figure 1f. The irradiator consists of a dual-focus X-ray tube with a maximum tube potential of 225 kV (225 Cx, Comet, Switzerland) and a 20° angled tungsten stationary target. Using the small focal spot (1.0 mm), the X-ray tube acts as photon source for CT imaging. Photons are filtered through a 0.8 mm beryllium exit window and an additional 2.0 mm aluminium filter. The source to isocentre distance was fixed at 303.6 mm. The electronic portal imaging device (XRD-0820-AN3-ES, Perkin Elmer^®, Waltham, MA) has 1024 × 1024 active pixels in an area of 20 x 20 cm.

Figure 1.

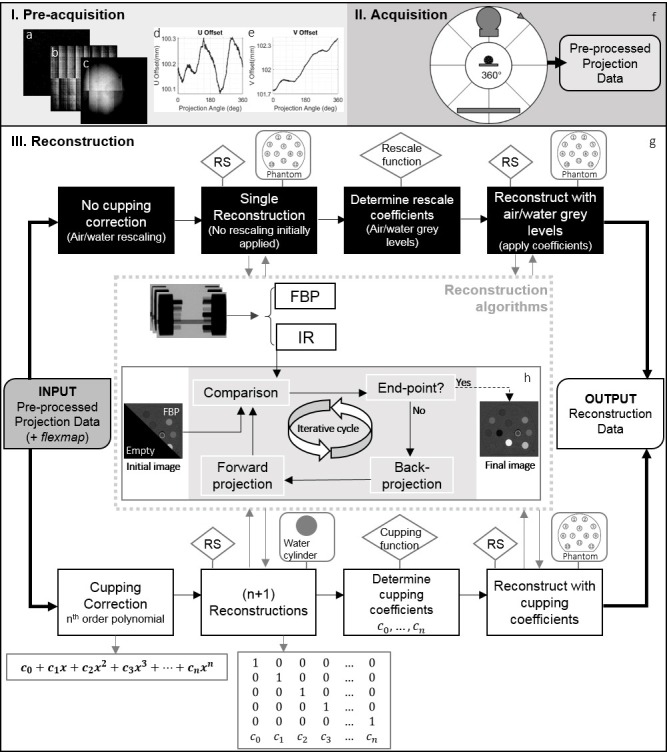
Image acquisition and reconstruction workflow. Pre-acquisition corrections: (a) defective pixels, (b) dark field, (c) flood field, (d) lateral and (e) longitudinal offset for each gantry angle (flexmap). (f) Cone beam CT acquisition, X-ray tube and the flat panel rotate 360° around the object and generate the pre-processed projection data. (g) Reconstruction cycle, with or without cupping correction. The boxes with RS, rescale and cupping function indicate where the RS and where MATLAB routines were used, respectively. The boxes with phantom or water cylinder illustrate the reconstructed object at that step. The inner image at the centre indicates the reconstruction algorithms. They could be either FBP or IR. IR methods follow the cycle of panel (h). FBP, filtered back-projection; IR, iterativere construction; RS, reconstruction software.

The pre-processing of the raw data is described in (Supplementary Material 1A) and Figure 1a–e. Table 1 shows scan pre-sets for this study. The exposures were chosen to yield an average dose of 30 cGy for each energy in a DECT scenario. The absorbed dose to water at a solid water phantom surface was verified using a TN30012 Farmer ionization chamber (PTW, Freiburg, Germany) according to the AAPM TG-61 protocol for 40–300 kV X-ray beam dosimetry (in-air calibration method).¹²

Table 1.

Cone beam CT scan pre-sets for energies in the range of 40 to 120 kVp

Image acquisition pre-sets
Subject position			Feet first prone (FFP)
Voxel pitch			0.1034 × 0.1034 × 0.1034 [mm3]
Mean protocol dose			30 [cGy]
Energy	Current	Frame rate	Rotational speed	Gain	Exposure
[kVp]	[mA]	[fps]	[rpm]		[mAs]
40	9.26	7.5	0.50	Mid	1111.2
50	5.59	10.0	0.50	Mid	670.8
60	3.18	10.0	0.40	Mid	477.0
70	1.54	7.5	0.25	Mid	369.6
80	2.50	5.0	0.50	Low	300.0
90	2.08	5.0	0.50	Low	249.6
100	1.78	5.0	0.50	Low	213.6
110	1.54	5.0	0.50	Low	184.8
120	1.36	5.0	0.50	Low	163.2

FFP, feet first prone;

For dual-energy CT protocols, the mean dose is 30 cGy for each energy.

Image reconstruction software

To compare and characterize both methods, FBP and IR, software was developed using the open-source RTK toolkit^11,13 in the language C++. The software currently comprises five of RTK’s reconstruction algorithms, namely, FDK, and four IR methods: iterative FDK,^14,15 simultaneous algebraic reconstruction technique (SART),^16,17 simultaneous iterative reconstruction technique (SIRT)¹⁸ and conjugate gradient (CG).¹⁹ (Supplementary Material 1B) has a brief description of the IR techniques. Table 2 shows the possible reconstruction scenarios and filters included in the software.

Table 2.

Possible reconstruction scenarios using the software developed with the RTK toolkit

Reconstruction algorithm	FDK, Iterative FDK, SART, SIRT, CG
Characteristics	Number of iterations, convergence factor, enforce positivity, offset factor
Reconstruction size	Any, used: 1024 pixels × 1024 pixels × 1024 pixels
Reconstruction spacing	Any, used: 0.1034 × 0.1034 mm × 0.1034 mm
Output format	DICOM, MHA, MHD
Cupping correction	yes or no
Specimen position	FFP, FFS, FFDR, FFDL
	HFP, HFS, HFDR, HFDL
Back-projection filter	None, (Cuda) Voxel-based back-projection, Joseph, normalized Joseph, Cuda ray cast
Forward projection Filter	None, Joseph, Ray Cast Interpolator, Cuda Ray Cast
Window type	None, Hann, Cosine, Hamming, RamLak or SheppLogan (cut-off frequency)

CG, conjugate gradient; FDK, Feldkamp, Davis, and Kress; FFDL, feet first decubitus left; FFDR, feet first decubitus right; FFP, feet first prone; FFS, feet first supine; HFDL, head first decubitus left;HFDR, head first decubitus right; HFP, head first prone; HFS, head first supine;SART, simultaneous algebraic reconstruction technique; SIRT, simultaneous iterative reconstruction technique.

A cupping correction²⁰ was included in the software. As cupping artefacts are induced by nonlinearities in the projection data, a polynomial pre-correction was applied to the attenuation data for linearization. In the image domain, for each energy and reconstruction algorithm, polynomial coefficients were determined once using a homogeneous water cylinder (with a diameter of ${\displaystyle \varnothing }$=4 cm) as a calibration scan. A series of basis images were fitted to a template image, obtained from the pre-processed calibration scan, to generate the coefficients. Raw data were passed through the polynomial and pre-corrected.

Figure 1 shows the image acquisition/reconstruction workflow. After initial corrections (Figure 1a–e) the object was scanned (Figure 1f). If no cupping correction was applied, the cycle would follow the upper part of the diagram (Figure 1g). A single reconstruction of the object was generated with the RS, followed by a MATLAB^® v. R2017b (The MathWorks Inc., Natick, MA) routine to determine air and water grey levels (rescale function), and a second reconstruction with corrected levels to yield Hounsfield Units (HUs). In case of cupping correction, to determine the coefficient ${\displaystyle c_n}$ of the term ${\displaystyle x^n}$, of the polynomials,²⁰ ${\displaystyle \left(n+1\right)}$ reconstructions of the water phantom were performed. The coefficients were determined through a MATLAB^® script (cupping function), followed by a final reconstruction with the identified polynomial values. No further correction was necessary; this method results in attenuation images which are subsequently converted to HU^[i]. For the two cycles, apart from the correction coefficients, all other parameters were maintained for both reconstruction rounds.

Image quality assurance

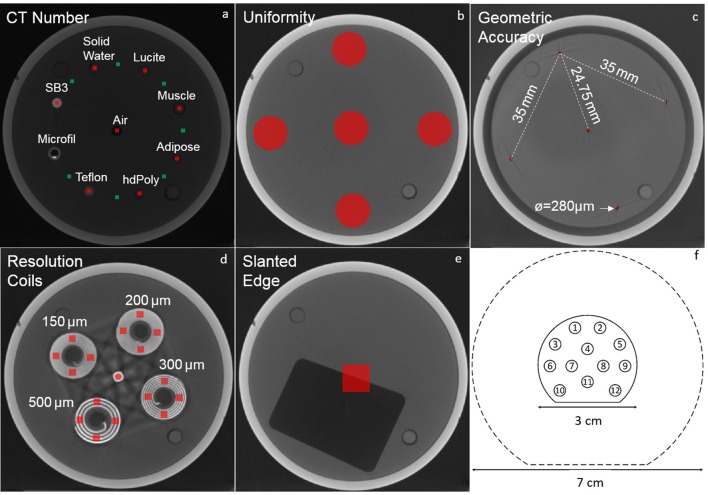
A quantitative image analysis was performed to verify the impact of the different reconstruction techniques using the mCTP-610 phantom (Shelley Medical Imaging Technologies, Toronto, Canada),²¹ Figure 2a–e. It is a single device with modular plates, each designed to assess one aspect of image quality, such as CT number, image uniformity, geometric accuracy, spatial resolution and noise. The plates used in this study are enclosed in a polycarbonate cylindrical housing of 8.4 cm length, 7.0 cm diameter and 4.8 mm thickness. The analysis following previously published methods^21–23 is briefly described.

Figure 2.

Phantoms used in this study. (a–e) Different plates of the mCTP-610 quality assurance phantom: (a) CT Number, (b) uniformity, (c) geometric accuracy, (d) resolution coils and (e) slanted edge. The regions of interest used for the image analysis are shaded in red and green. (f) Schematic drawing of the calibration and validation phantoms used for the dual-energy CT analysis. The dashed line represents the 7 cm diameter phantom, which is composed by an outer ring encompassing the 3 cm phantom, represented by the solid line. Both rings are made of the same bulk material (solid water).

Figure 2a shows the CT evaluation plate with volumes of interest (VOIs) of 10 × 10 × 4 pixels. The VOIs shaded in red were used to calculate the mean CT numbers of seven tissue-equivalent embedded materials: SB3, solid water, Lucite, muscle, adipose, high-density polyethylene and Teflon. The material Microfil, a silicone-based vascular contrast agent, was not analysed due to its non-uniformity. The green shaded VOIs were used to calculate the contrast-to-noise ratio (CNR), according to equation (1), where ${\displaystyle {\stackrel{-}{I}}_{tissue}}$ is the mean CT number of a tissue (red VOI), ${\displaystyle {\stackrel{-}{I}}_{Background}}$ is mean CT number of the background (adjacent green VOI) and ${\sigma }_{\mathrm{ti}\mathrm{ss}\mathrm{ue}}$ and ${\sigma }_{\mathrm{ba}\mathrm{ck}\mathrm{gr}\mathrm{ou}\mathrm{nd}}$ are the standard deviations of ${\stackrel{-}{I}}_{\mathrm{ti}\mathrm{ss}\mathrm{ue}}$ and ${\stackrel{-}{I}}_{\mathrm{Ba}\mathrm{ck}\mathrm{gr}\mathrm{ou}\mathrm{nd}}$.

$${\displaystyle CNR=\frac{{\overline{I}}_{tissue}-{\overline{I}}_{Background}}{\sqrt{Q_{tissue}^2+Q_{background}^2}}}$$

Image uniformity was evaluated by average signal difference (centre to peripheral) of five circular regions of interest (ROIs) with diameters (${\displaystyle \varnothing }$) of 100 voxels at a uniform polycarbonate plate positioned near the centre of the phantom (Figure 2b). From the geometric accuracy plate (Figure 2c), the voxel size was determined by dividing the known physical distance between five neighbouring tungsten-carbide beads by the measured distance between the centroid of the respective beads in voxels.

The modulation transfer function (MTF) was obtained using the resolution coil plate (Figure 2d), according to equation (2)²⁴

$${\displaystyle MTF\left(f\right)=\frac{\pi \sqrt{2}}{4}\cdot \frac{M\left(f\right)}{M_0}}$$

where $M\left(f\right)$ is the standard deviation of pixel values from VOIs of 20 × 20 × 20 voxels within each coil, corrected for noise and $M_0$ is half of the absolute difference between the aluminium and Mylar in HU. The coils are made of alternating aluminium and Mylar sheets with 500, 300, 200, and 150 µm thicknesses, corresponding to spatial resolution of 1, 1.67, 2.5, and 3.3 line pairs per mm (lp∙mm⁻¹). MTF was also determined using the slanted edge plate.²⁵ A profile through the slanted edge (Figure 2e) defines the edge-spread function, when differentiated yields the line spread function and the Fourier transform of the line spread function determines the MTF.²⁴

Dual-energy CT

Two pairs of geometrically identical cylindrical phantoms (SmART Scientific Solutions BV, Maastricht, etherlands), Figure 2f, were used for DECT analysis. The phantoms were 3.0 or 7.0 cm diameter, which corresponds to the cross-section of small rodents, mice to large rats. All phantoms were 1 cm in length. They were composed of a solid water bulk and 12 cylindrical inserts of 0.35 cm diameter and 1.60 cm length. Table 3 lists the composition of the inserts, which mimic human tissue attenuation properties.

Table 3.

Reference values of mass density (ρ), relative electron density (ρ_e), effective atomic number (Z_eff) and elemental composition of the tissue-substitute materials present in the calibration and validation phantoms

n°	Material	ρ [g/cm3]	ρe	Zeff	Elemental composition (%)				Z > 8
					H	C	N	O
Calibration phantom
1	AP6 (Adipose)	0.947	0.928	6.210	9.06	72.30	2.25	16.27	F(0.13)
2	Solid water	1.022	0.992	7.735	8.00	67.30	2.39	19.87	Cl(0.14), Ca(2.31)
3	IB3 (Inner bone)	1.134	1.086	10.418	6.67	55.64	1.96	23.52	P(3.23), Cl(0.11), Ca(8.86)
4	SR2 (Brain)	1.051	1.047	6.090	10.83	72.54	1.69	14.86	Cl(0.08)
5	CB2-30% CaCO3	1.331	1.276	10.898	6.68	53.48	2.12	25.61	Cl(0.11), Ca(12.01)
6	BR12 (Breast)	0.980	0.956	6.931	8.59	70.11	2.33	17.90	Cl(0.13), Ca(0.95)
7	Air	0.001	0.001	7.714			75.47	23.20	Ar(1.28)
8	Water	1.000	1.000	7.477	11.20			88.80
9	B200 (Bone mineral)	1.152	1.103	10.423	6.65	55.52	1.98	23.64	P(3.24), Cl(0.11), Ca(8.87)
10	LV1 (Liver)	1.096	1.064	7.736	8.06	67.01	2.47	20.01	Cl(0.14), Ca(2.31)
11	SB3 (Cortical bone)	1.822	1.695	13.638	3.41	31.41	1.84	36.50	Cl(0.04), Ca(26.81)
12	CB2-50% CaCO3	1.559	1.469	12.538	4.77	41.63	1.52	32.00	Cl(0.08), Ca(20.02)
Validation phantom
1	BR12 (Breast)	0.980	0.956	6.931	8.59	70.11	2.33	17.90	Cl(0.13), Ca(0.95)
2	Teflon	2.153	1.860	8.461		24.00			F(76.00)
3	Lucite	1.180	1.146	6.529	8.05	59.98		31.96
4	Air	0.001	0.001	7.714			75.47	23.20	Ar(1.28)
5	Poly(methyl methacrylate) - PMMA	1.190	1.156	6.529	8.05	59.98		31.96
6	Paraffin wax	0.930	0.959	5.483	14.90	85.10
7	Water	1.000	1.000	7.477	11.20			88.80
8	Muscle	1.062	1.041	7.588	9.10	69.70	2.10	16.80	Cl(0.10), Ca(2.20)
9	Air	0.001	0.001	7.714			75.47	23.20	Ar(1.28)
10	Air	0.001	0.001	7.714			75.47	23.20	Ar(1.28)
11	Adipose	0.967	0.956	6.439	10.00	71.30	1.80	16.40	Cl(0.20), Ca(0.30)
12	Bone	1.600	1.507	11.895	4.83	37.03	0.97	35.66	Mg(6.19), Cl(0.05), Ca(15.24)

HU, Hounsfield unit;

The calibration phantom is used to obtain the relation between the CT numbers (in HU) and the ρ_e and Z_eff for known tissue mimicking inserts. The validation phantom, composed of a different set of tissue inserts, is used to test the performance of the calibration mode.

CT numbers were extracted from ROIs of the inserts in the four central slices of a high energy (HU_H) and a low energy (HU_L) scan of the DECT phantoms. The procedure described by Schyns et al²⁶ to determine the relative electron density ρ_e, according to equation (3)

$${\displaystyle {\rho }_e=\frac{\left(\frac{N_A\rho Z}{A}\right)}{\left(\frac{N_A{\rho }_w{Z}_w}{A_w}\right)}}$$

where N_A is the Avogadro constant, ρ, Z and A are the mass density, atomic number, and atomic mass of a material, while the subscript w indicates water, using Saito’s²⁷ approach, and to extract the effective atomic number Z_eff, according to equation (4)

$${\displaystyle Z_{eff}={\left({\sum }_i{w}_i{Z}_i^{\beta }\right)}^{\frac{1}{\beta }}}$$

where w_i is the weight fraction of ith element with atomic number Z and β = 3.31⁷, following the method proposed by Landry et al²⁸ was adopted. The reference values of Z_eff and ρ_e, calculated from the compositions and mass densities provided by the manufacturer, and the calculated values from the DECT images were used to assign a tissue composition to each voxel.

Results

Reconstruction time

To generate optimal and reproducible results for image analysis, reconstruction matrices of 1024 × 1024 × 1024 pixels³ were used. This matrix size was chosen to avoid reconstruction artefacts and inaccuracies smaller grids could cause, and to fully reconstruct the mCTP-610 phantom and the pair of 7 cm DECT phantoms, which were positioned parallel to each other with a gap in between. The small pixel size of (0.1034 mm)³ was used as it is typically the minimum size at MAASTRO/UM laboratory and as the resolution of the scanner was being tested. Figure 3a shows that this choice yielded long reconstruction times. The techniques SIRT and CG require a higher number of iterations to converge (Figure 3b,c,h): after 40 iterations and 45 computational hours CG presented acceptable results and after 80 h and 100 iterations, using a smaller grid, SIRT had not yet converged. They proved to be impractical for further analysis. In the following sections, the techniques SART (Figure 3d,e), Iterative FDK (Figure 3f,g), both with three iterations, and FDK (Figure 3i) are compared. Figure 3j shows the reconstruction time of objects with 250 × 250 × 200 pixels³ and pixel sizes of (0.20 mm)³ to illustrate a practical pre-clinical scenario, where a smaller volume of interest within a mouse is chosen, with largely reduced reconstruction times.

Figure 3.

(a) Reconstruction time for each technique vs number of iterations for the 90kVp images with 602 projections, required by an AMD Opteron^™ Processor 6272, 32 physical cores and 128 GB of RAM. CG image after (b) three and (c) 40 iterations (45 h). Iterative FDK image after (d) one and (e) three iterations. SART image after (f) one and (g) three iterations. (h) SIRT image after 100 iterations for a grid of (512 pixels)³ with pixel size of (0.2 mm),³ which took 80 h—if the 1024 grid used for the other methods was repeated here the reconstruction times would be even longer. (i) FDK reconstruction. The numbers in the top right corner indicate the number of iterations used in each image. Figures b-i were extracted from a central region of the 7 cm phantom. (b) and (h) present a background different colour because they have not yet converged. (j) Reconstruction times using a smaller grid of 250 pixels × 250 pixels × 200 pixels and voxel size of (0.2 mm)³ to illustrate a scenario closer to a pre-clinical practice workflow, where only a region of interest in the object is selected. Vertical scale is in minutes here, while in panel a it is in hours. CG, conjugate gradient; FDK, Feldkamp, Davis, and Kress; SART, simultaneous algebraic reconstruction technique.

Cupping correction

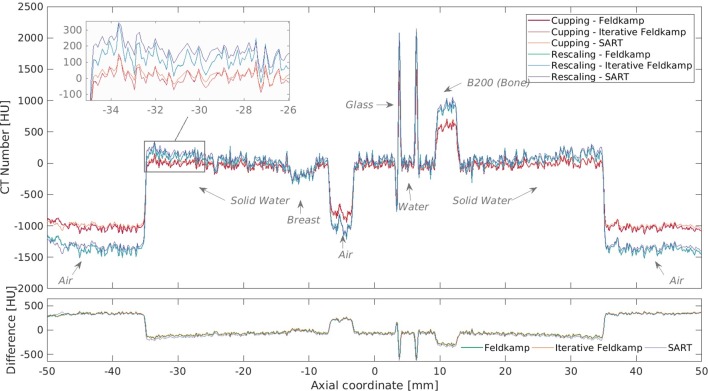
Different polynomials were tested, ranging from first to fifth order. Figure 4 shows phantom HU profiles where a second-order polynomial was applied in contrast to the rescaling method. For the corrected cases, the solid water region, or the bulk of the phantom, presents a flatter profile with less pronounced edges. Additionally, the CT values are consistent for bulk, inserts and the outside air. For the rescaling method, air and water grey levels were extracted from inserts within the phantom, which yielded the expected values of −1000 and 0 HU in the phantom but values lower than −1000 HU outside. The second- and third-order polynomials yielded the best results in terms of flatter profiles and images with increased visual quality. The method also worked better for energies below 100 kVp.

Figure 4.

Comparison of phantom HU profiles for different reconstruction methods with and without cupping correction for the 40 kVp scan, where cupping is most evident, of the 7 cm phantom using a second order polynomial (C2). HU, Hounsfield unit.

Quantitative image analysis

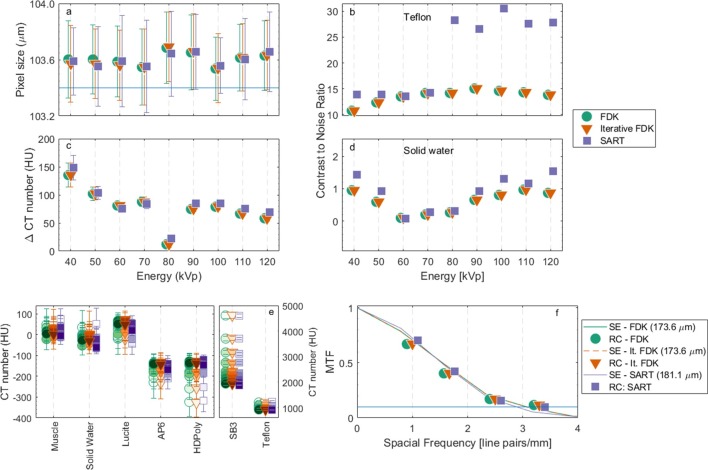
Figure 5a shows the pixel size values derived from the geometric accuracy plate. The values found for the different reconstruction methods and energies were within 0.2 to 0.3% in agreement with the value of 103.4 µm, used in this study. Figure 5b,d show the CNR for Teflon and solid water. While similar values are obtained for FDK and Iterative FDK, within −0.05 to 0.3%, SART yields a higher ratio, up to 76% higher for solid water and 2.09 times higher for Teflon, which can be explained by the lower levels of noise associated with this technique. Additionally, the panel gain is set to low for energies higher than 70 kVp, to avoid saturation. The uniformity in terms of centre to peripheral average signal difference (Figure 5c) also yielded similar results for the three methods, with a variation of 12 to 148 HU among the nine investigated energies. CT numbers of seven tissue equivalent materials for energies between 40 and 120 kVp (Figure 5e) showed little variation, with a maximum standard deviation of 45 HU amongst techniques. The values for soft and osseous (or high atomic number) tissues are also within the expected literature values. The 80 kVp acquisition pre-sets changes, in terms of gain and frame rate, are possibly the underlying reason for its decreased uniformity.

Figure 5.

Quantitative image analysis tests with the mCTP-610 phantom. (a) Geometric accuracy, the blue horizontal line represents the utilized pixel size. (b) CNR for Teflon. (c) Uniformity. (d) CNR for solid water. (e) CT number for tissue equivalent materials for 40 to 120 kVp, the markers colour shade darkens as the energy increases. (f) MTF using both SE and RC techniques for the 50kVp image. The line indicates the MTF at 10%. CNR, contrast-to-noise ratio; MTF, modulation transfer function; RC, resolution coil; SE, slanted edge.

Figure 5f shows that the MTF for both the slanted edge and the resolution coil methods were similar. The highest resolution in terms of equivalent lp∙mm⁻¹ at the 10% MTF (2.5 lp∙mm⁻¹ is comparable to 200 µm²¹), was found for 50 kVp, with values of 173.6 µm (2.73 lp∙mm⁻¹) for both FDK and Iterative FDK and 181.1 µm (2.72 lp∙mm⁻¹) for SART, and the lowest for 120 kVp with 201.4 µm (2.39 lp∙mm⁻¹), 201.3 µm (2.38 lp∙mm⁻¹) and 234.4 µm (2.07 lp∙mm⁻¹) for FDK, Iterative FDK and SART, respectively. Resolution results for SART were consistently lower when compared to the other two techniques, from 2% lower, for 60 kVp, to 28%, for 100 kVp.

Dual-energy CT analysis

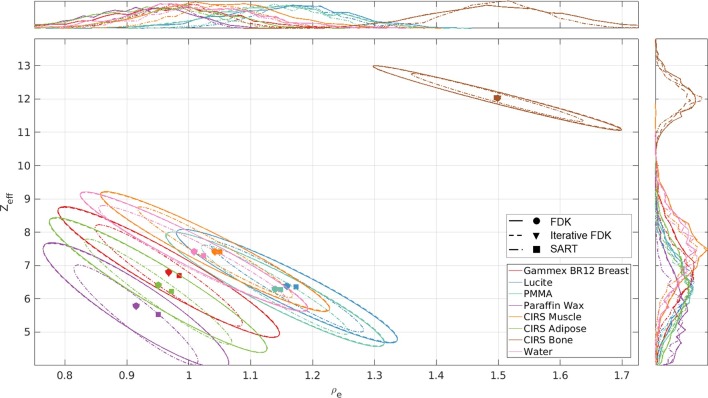
Figure 6 shows the relationship between Z_eff and ρ_e for the materials of the validation phantom. All voxels to which no Z_eff value could be assigned, predominantly located at sharp transitions between air and the solid water bulk, were excluded from the analysis (<0.01% in the ROIs). Ellipses were drawn considering the direction of the eigenvectors of the covariance matrix. Thus, each distribution confidence ellipse defines the region that contains 95% of all samples that can be drawn from the underlying gaussian distribution, with the mean value indicated by the circle, triangle or square. Although the data distribution is similar for FDK and Iterative FDK, the smaller spread of the SART ellipses indicate a reduced image noise effect, expected for an iterative method.

Figure 6.

ρ_e–Z_eff plot for the 7 cm validation DECT phantom and the energy combination 50 and 90 kVp. The colours and the lines indicate the tissue-equivalent inserts and reconstruction methods. Histograms of ρ_e and Z_eff values are illustrated on top and on the right, respectively. The circles, triangles and squares indicate the mean value of each distribution for FDK, Iterative FDK and SART, respectively. DECT, dual-energy CT; FDK, Feldkamp, Davis, and Kress; SART, simultaneous algebraic reconstruction technique.

Figure 7a,b show the mean residuals (absolute difference between the calculated and reference value) of Z_eff and ρ_e using the three reconstruction techniques, for a number of energy combinations, where the difference between low and high energy was at least 20 kV apart to avoid large spectral overlap, maximizing the amount of information provided by each energy. For all shown combinations, Z_eff and ρ_e residuals were on average 24 and 25% lower, respectively, using SART in comparison with Iterative FDK and FDK— which were within 0.2 and 0.05% in agreement with each other in terms of Z_eff and ρ_e residuals, respectively. Additionally, the mean standard deviations were on average 20 and 30% lower with SART in comparison to the other two reconstruction techniques, which once more showed little variation among themselves (average differences of 0.4 and 0.02% for Z_eff and ρ_e residuals).

Figure 7.

Mean (a) Z_eff and (b) ρ_e residuals, and mean (c) Z_eff and (d) ρ_e standard deviations for a number of DECT energy combinations. DECT, dual-energy CT; FDK, Feldkamp, Davis, and Kress; SART, simultaneous algebraic reconstruction technique.

Discussion

Iterative reconstructions used in this study were computationally costly and would be impractical for studies with live animals under anaesthesia. The decision to favour the reproducibility, repeating a same grid of 1024 × 1024 × 1024 pixels³ for different objects, and using the smallest voxel size of the CBCT scanner of our institution, for a thorough image analysis, affected the speed of the IR. Smaller grids and larger voxel sizes are more typical in pre-clinical practice. In such cases, IR methods were found to be feasible, with reconstruction times under 20 min for three iterations (Figure 3j). Additionally, increased computational power, by means of, e.g. graphics processing units, would highly increase the IR speed.

The correction for cupping artefacts included in the software provided accurate CT numbers. The second- and third-order polynomials yielded the best results, a higher number of coefficients caused further instability and overfitting. The method was more effective for energies below 100kVp, as the cupping effect is more pronounced for lower energies. For IR techniques, reconstructing an object a number of times to derive a polynomial, which will correct a final reconstruction, is a lengthy process. Applications that require increased image quality and larger objects, more prone to beam hardening, could benefit from this approach. For the rescaling method, the coefficients to correct for air and water grey levels are derived from values within the object to account for the beam hardening and other artefacts the object is subjected, as it would be the case of an air pocket within a mouse, for example.

IR provided favourable results for the DECT analysis. SART resulted in a significantly smaller spread for each material in the ρ_e–Z_eff space (Figure 6) and the residuals on Z_eff and ρ_e were on average 24 and 25% lower, in comparison to FDK—with an increasing number of iterations, the residuals decreased further. In terms of image quality, the techniques FDK, Iterative FDK and SART provided acceptable results. Regarding geometric accuracy, the pixel size agreement was within 0.2 to 0.3% with the used value of 103.4 µm. The three techniques showed similar uniformity and CT number results, with the latter presenting a maximum standard deviation of 45 HU amongst techniques and soft and osseous tissues within the expected literature values. Although the CNR presented by SART was compelling, a ratio up to 76% higher for solid water and over twice higher for Teflon, the resolution results were up to 28% lower when compared to the other two techniques. Because of the iterative cycle, IR techniques may produce smoother images, less affected by noise.

Accuracy on the image metrics listed above is crucial for dose calculations, which are based on the CBCT image of small animals. Accuracy of contours of anatomical structures can suffer from reduced resolution, abundance of noise or non-uniformity. Different reconstruction techniques could be used for alternative purposes.²⁹ In a possible irradiation workflow, following the CBCT scan of a mouse, the projections could be quickly reconstructed using the iterative FDK method. Availing from the increased resolution and diminished presence of artefacts, the images could be contoured while the projections are reconstructed using the SART technique. The user could see the result of each iteration, choose the most adequate image, and stop the iterative cycle. The iteratively reconstructed image could be used for dose calculations, which could benefit from the lower levels of noise.

The influence of the scanning parameters and the reconstruction filters could be further investigated. The imaging pre-sets were adopted from previous studies,²⁶ where they were deemed optimal. IR could provide satisfactory results with decreased tube current or scanning time and consequently decreased imaging dose, which although worth to investigate was outside the scope of the present study. Lastly, one should be aware of the biological consequences of high CT imaging doses which may even alter the experimental outcome.²²

Conclusion

An image reconstruction platform has been built, for modern small animal image-guided irradiation platforms using RTK. The software includes back-projection, different iterative algorithms, filters and cupping correction. Pre-processed projections reconstructed with the software showed acceptable results regarding image quality assurance and DECT Z_eff and ρ_e residuals. The iterative technique SART showed improved results regarding noise, which may be important for tissue assignment for dose calculations. In a nutshell, advanced image reconstruction can be beneficial, but the benefit is rather small, and calculation times may be unacceptable with current technology.mic number (Zeff) and elemental composition of the tissue-substitute materials present in the calibration and validation phantoms.