The potential impact of ultrathin filter design on dosimetry and relative biological effectiveness in modern image-guided small animal irradiators

Abstract

Objective:

Modern image-guided small animal irradiators like the Xstrahl Small Animal Radiation Research Platform (SARRP) are designed with ultrathin 0.15 mm Cu filters, which compared with more heavily filtrated traditional cabinet-style biological irradiators, produce X-ray spectra weighted toward lower energies, impacting the dosimetric properties and the relative biological effectiveness (RBE). This study quantifies the effect of ultrathin filter design on relative depth dose profiles, absolute dose output, and RBE using Monte Carlo techniques.

Methods:

The percent depth-dose and absolute dose output are calculated using kVDoseCalc and EGSnrc, respectively, while a tally based on the induction of double-strand breaks as a function of electron spectra invoked in PENELOPE is used to estimate the RBE.

Results:

The RBE increases by >2.4% in the ultrathin filter design compared to a traditional irradiator. Furthermore, minute variations in filter thickness have notable effects on the dosimetric properties of the X-ray beam, increasing the percent depth dose (at 2 cm in water) by + 0.4%/0.01 mm Cu and decreasing absolute dose (at 2 cm depth in water) by –1.8%/0.01 mm Cu for the SARRP.

Conclusions:

These results show that modern image-guided irradiators are quite sensitive to small manufacturing variations in filter thickness, and show a small change in RBE compared to traditional X-ray irradiators.

Advances in knowledge:

We quantify the consequences of ultrathin filter design in modern image-guided biological irradiators on relative and absolute dose, and RBE. Our results show these to be small, but not insignificant, suggesting laboratories transitioning between irradiators should carefully design their radiobiological experiments.

Introduction

Recent advances have led to development and rapid rise in utilization of small-animal irradiators in preclinical and basic radiation biology studies¹ Modern small-animal irradiators feature a number of technological advances over traditional cabinet style irradiators including image guidance through radiographic, cone-beam CT (CBCT) X-ray imaging, and bioluminescence, a robotic stage to position animals with submillimeter accuracy,² 3-dimensional radiation treatment planning, and isocentric delivery of radiation fields from any angle, collimated as small as 1 mm. Two image-guided small animal irradiators models are commercially available: the SARRP from Xstrahl (Xstrahl Inc., London, UK)^3–5 and the X-RAD Small Animal RadioTherapy (SmART) from Precision X-ray (PXi; North Branford, CT).^6–9 Cabinet-style X-ray irradiators, such as the PXi X-RAD 320 (Precision X-ray) typically include a stationary X-ray beam and are limited to larger field sizes.¹⁰

Modern irradiators use a smaller X-ray tube capable of maximum potential of only 225 kVp, coupled with an ultrathin copper filter (0.15 and 0.30 mm Cu for the SARRP and SmART, respectively) to maintain dose rate in the 2–3 Gy min^–1 range (depending on field size). In contrast, the X-RAD 320 operates at 320 kVp and uses a much thicker filtration: a thoraeus filter comprising 2 mm Al, 0.25 mm Cu, and 0.75 mm Sn.¹⁰ This difference in X-ray tube design between traditional and modern radiobiological irradiators has consequences for X-ray beam quality, which in turn has the potential to affect the relative biological effectiveness (RBE) of the radiation,¹¹ as well as absolute and relative dosimetry. It is important to systematically quantify these consequences, because they can affect the observed biological outcomes attributed to the delivered radiation, which can, in turn, complicate interstudy comparisons.

Two concerns arise from the use of ultrathin filter designs. First, the additional filtration impacts the beam quality of the X-ray beam, which in turn increases its penetration while decreasing the absolute dose output. As higher-Z materials disproportionately attenuate lower-energy X-rays through the photoelectric effect, thick filters depopulate the lower-energy component of the energy spectrum. In contrast, in ultrathin filters, the proportion of low-energy X-rays attenuated will be highly dependent on the filter thickness, thus small variations due to manufacturing error or damage could have a disproportionate impact on the dosimetric properties of the beam. Second, the spectral differences may affect the RBE of the radiation, i.e. the relative doses required to induce a given biological end point may vary between the different spectra. Since the RBE is disproportionately impacted by low-energy X-rays, particularly in the 5–30-keV range,¹¹ the RBE may be significantly different in new designs compared to traditional biological irradiators.

To study these effects, we investigate the quantitative impact of ultrathin filter tube designs on beam quality, RBE, percent-depth dose, and absolute dose output. Each of these is simulated using previously validated Monte Carlo (MC) models: Penelope (RBE), EGSnrc (absolute dose) and kVDoseCalc (relative depth dose). In the case of relative and absolute dose simulations, we vary the thickness of the external filtration and assess the effect on the absolute dose output or the relative depth dose profile. RBE is also calculated for both a cabinet irradiator and the SARRP.

methods and Materials

Irradiators

We modeled two preclinical X-ray sources: a traditional PXi X-RAD 320 cabinet-style X-ray irradiator system, and an Xstrahl SARRP image-guided small animal irradiator. The physical parameters affecting beam quality, i.e. the tube potential / energy (kVp), the half-value layer (HVL), the effective and mean energies, and the typical source-to-axis distance (SAD), are described in Table 1. Although not explicitly modeled, spectra roughly equivalent to that of the SmART were also modeled for the absolute and relative dosimetry.

Table 1. ^abc.

Dosimetric parameters of three biological irradiators

Variable	PXi X-RAD 320	Xstrahl SARRP	PXi XRAD- SmART
Energya	320 kVpb	220 kVp	225 kVp
Filtera	2 mm Al + 0.25 mm Cu +0.75 mm Sna	0.15 mm Cu	0.30 mm Cu
HVLa	4 mm Cub	0.65 mm Cu	0.9 mm Cu
Eeff (Cu)c	158 keV+	65.2 keV	77.1 keV
Emeanc	156 keV	77.2 keV	85.0 keV
Typical SAD	50 cm	35 cm	35 cm

Values reported are nominal and can vary from unit to unit

Variable. Most penetrating combination reported.

Obtained from SpekCalc simulations (see Section Spectra generation).

Spectra generation

Many independent studies show that dose distributions can be accurately calculated by MC algorithms using a spectrum matching two beam quality indicators: the first half-value layer (HVL₁) and the accelerating potential (kVp),¹² or the first and second (HVL₂) half-value layers.¹³ Of these two approaches, it has been shown that matching HVL₁ and kVp is more accurate.^14,15

We generated the spectra for the RBE and relative depth dose simulations using SpekCalc.¹⁶ The absolute dose output simulations instead calculate the spectrum from first principles (see Section Absolute dose). SpekCalc is a software capable of generating kV spectra from thick tungsten anodes (used inbiological irradiators) using previously validated deterministic equations coupled with user-specified parameters including the accelerating potential (kVp), the anode angle, distance from the source, and window/filter composition.

We used nominal values for inherent filtration, external filtration, tube anode angle, and kVp, which were fine-tuned by varying the aluminum filtration until the generated spectra’s HVL₁ matched the nominal value (Figure 1). This approach has been validated in many kV dosimetry applications, including radiographic,^12,17 CT,¹⁸ and CBCT^13,19 imaging, as well as superficial²⁰ and orthovoltage²¹ therapy X-rays. SpekCalc-500, a not-yet commercial version of the software capable of simulating ≤500 kVp beams donated by the author, was used to generate the relevant spectra. The effective energy, which represents the energy of a mono-energetic beam with an equivalent HVL₁, as well as the average energy, are calculated by SpekCalc are listed in Table 1.

Figure 1.

Spectra comparison between the three irradiators of interest in this study, as generated by Spekcalc-500 and normalized to the same modal energy excluding characteristic X-rays. Compared to the X-RAD 320, which features a modal energy of 125 keV, the SARRP and SmaRT spectra are weighted toward much lower energies, featuring modal energies of 48 and 56 keV, respectively.

The impact of the ultrathin filter design is perhaps shown best by the fraction of the spectrum under a specific energy, as seen in Figure 2. Although <10% of the X-RAD 320 spectrum is made up of photons <100 keV, these comprise 76 and 72% of the spectrum for the SARRP and SmART, respectively. This has a significant impact on radiation dose distributions, as mass attenuation coefficients in soft tissue can vary drastically in the 10–100-keV range due to the increased photoelectric effect cross-section at these energies.²²

Figure 2.

Cumulative contribution to spectrum, obtained by integrating the spectrum from Figure 1 between 0 and energy E, as a function of energy.

Relative dose distributions

The relative depth dose curves were calculated using kVDoseCalc, a hybrid deterministic and stochastic kV dose calculation algorithm.²³ Briefly, the algorithm calculates the absorbed dose to a series of points of interest (POIs) from photon interactions in three components: primary (or unscattered), first-order scatter, and n^th-order scatter. Secondary electrons are assumed to be locally absorbed and are not transported. The primary component is calculated using a deterministic approach, and both scatter components are calculated using stochastic approaches. This method was shown to be equivalent to long-established MC algorithms such as EGSnrc and MCNP.²³ Furthermore, kVDoseCalc has been extensively experimentally validated in a variety of kV X-ray dosimetry applications.^12,17–21

As opposed to other MC algorithms, kVDoseCalc features a highly simplified source model, where the user inputs the spatial fluence at the plane of isocenter, as well as a spatially varying spectrum along the cross-plane. Since it does not model the source from first principles, the term specifying the absolute fluence from the source must be obtained either through an independent MC simulation or experimental characterization. This must be repeated for each normalized energy fluence distribution, making absolute dose output calculations very challenging due to the reliance on secondary characterization of the absolute fluence. Furthermore, since it does not transport electrons, it also cannot be used to estimate RBE. However, due to its streamlined hybrid calculation approach featuring a number of variance reduction techniques, percent depth dose curves with negligible statistical uncertainty (<0.2%) can be obtained by simulating as few as 100,000 particle histories per POI.¹⁸ Therefore, it was used in this study to generate the relative dose distributions arising from variations in beam filtration.

Spectra were generated for external filtrations using the method outlined in Section Spectra generation for filters ranging from 0.05 to 0.30 mm Cu. Dose was calculated at 0.5 cm intervals from 0 to 7 cm in water.

Absolute dose

Absolute dose calculations for the Xstrahl SARRP were performed using an MC model of the Xstrahl SARRP created in BEAMnrc²⁴ using the EGSnrc MC code package²⁵ and developed from a previous work.²⁶ For dose computations, 10⁹ histories, directional Bremsstrahlung splitting, and source number 10 was used to generate phase-space files for each respective filter thickness. A solid water phantom was modeled at a 33 cm SSD, with dose calculations scored at a 2-cm depth within the solid water phantom for an uncollimated beam. The National Institute of Standards and Technology cross-section database (NIST, Gaithersburg, MD) is utilized in EGSnrc and takes into consideration all photon interactions relevant to low kV interactions (i.e. Rayleigh scattering, photoelectric effect, and Compton scattering).

The 220-kVp therapy energy of the Xstrahl SARRP was modeled and previously validated with depth dose and profile measurements in homogeneous and heterogeneous phantoms using Gafchromic EBT3 films.²⁶ Additional validation was performed using a 0.6 cc PTW 30013 Farmer-type ionization chamber (PTW, Freiburg, Germany), cross-calibrated with the same model ionization chamber calibrated to national standards at the National Research Council (NRC, Ottawa, Canada), following the American Association of Physicists in Medicine Task Group 61 (TG-61) absolute dosimetry protocol.²⁷ Phase-space files derived from MC simulations were input into BEAMdp²⁸ to obtain spectra for varying filter thicknesses (Figure 3).

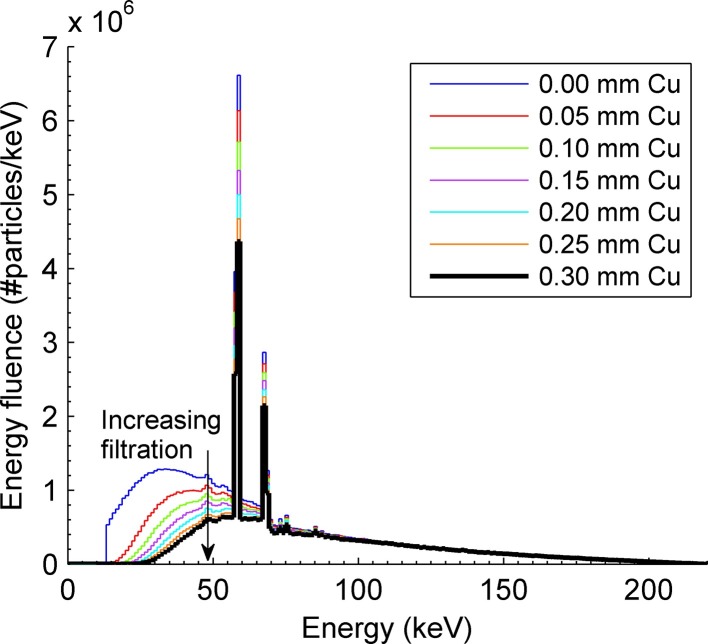
Figure 3.

Xstrahl SARRP spectra for the 220-kVp beam used in absolute dose computation using the EGSnrc MC code package. Depicted are spectra ranging from no added filtration (top curve) to a 0.3 mm Cu filter (bottom curve) in 0.05 mm Cu increments. The spectrum with no added filtration cuts off at a minimum energy of 10 keV due to cut-off energy limitations and is shown for illustrative purposes only.

In contrast to kVDoseCalc, EGSnrc is a more fundamental and more complex algorithm capable of modeling the X-ray source from first principles, which allows for calculation of absolute dose.²⁹ MC output was directly converted into dose in Gy from first principles,

$${\displaystyle D\left(Gy\right)=\frac{MC\cdot I\cdot t}{q}}$$

where MC is the MC output in Gy/particle, I is the tube current in Amperes, t is the exposure time in seconds, and q is the charge of an electron in Coulombs (q = 1.60 × 10⁻¹⁹ C).²⁶

We investigated the effect of variations in filter thickness on absolute dose rate. For each filter thickness, the absolute dose was calculated in water at a depth of 2 cm for an uncollimated field (about18 cm diameter at isocenter) at 33 cm SSD. The choice of these particular parameters was guided by the AAPM TG-61 protocol using the in-water calibration method,²⁷ with dose computed at the 35 cm source-to-axis distance at isocenter.

Relative biological effectiveness

Genetic damage was estimated using a previously validated MC method^30–32 that uses a modified version of the Penetration and Energy Loss (PENELOPE) MC package (version 2011).³³ The transported radiation is coupled to the results of MC damage simulations (MCDS) for monoenergetic electrons that provide an expected value of the damage within the nucleus of a generic mammalian cell in units of double-strand breaks (DSBs) per Gy per gigabasepair (DSB Gy⁻¹ Gbp⁻¹).

Briefly, the MCDS simulates damage induced in a small segment of a DNA molecule in response to a uniform fluence of monoenergetic charged particles,^31,34–36 which is then proportionally scaled up to the full amount of DNA in the cell. In the simulation, the expected number of lesions per Gy per Gbp is distributed randomly over a DNA segment and the lesions are subsequently grouped to generate single-strand breaks, DSBs, or clusters of base damage. Default adjustable parameters were used as in previous work [cite 30–32]. These parameters reliably reproduce observed damage quantities.³⁷ Full oxygenation conditions are assumed. The MCDS results were tabulated as a function of monoenergetic electron kinetic energy and used as a lookup table as reported in Kirkby et al.³⁰

To generate estimates of DNA damage under the specific conditions of interest in this work, the tabulated MCDS results were integrated over weighted electron fluence tallies scored under each set of conditions. This integration is not trivial. The fluence must be weighted by the specific energy deposited in the sensitive volume by each electron either incident on the volume or generated within it. To this end a tally was developed in the PENELOPE MC package to track electrons moving through a sensitive volume.

As described in other work,^30,32 when an electron enters or is created within a sensitive volume, its initial kinetic energy, T_i, is recorded. The code tallies the specific energy (energy per unit mass) deposited in the sensitive volume resulting from that electron, ε_i(T_i). When simulation of all progeny is completed, an estimate of the genetic damage is looked up in the MCDS tables, interpolating based on T_i and the oxygen concentration, O, resulting in a value, Δ_i(T_i,O). The tally then updates its estimate of the genetic damage as:

$${\displaystyle \mathrm{△}(O)=\frac{\sum _{i=1}^{n-1}{\epsilon }_i(T_i).{\mathrm{\Delta }}_i(T_i,o)+{\epsilon }_n(T_n).{\mathrm{\Delta }}_n(T_n,o)}{\sum _{i=1}^{n-1}{\epsilon }_i(T_i)+{\epsilon }_n(T_n)}}$$

The simulation occurs in two phases, as indicated in Figure 4. In the first phase the photon source is incident on a macroscopic phantom and photon fluence in a volume at a depth d was scored in 1-keV bins from 0 to the maximum energy.

Figure 4.

Macroscopic (left) and microscopic (right) geometry of the RBE calculation. The modeled photon source is set incident on a water phantom with a given SSD, and the photon fluence is scored at depth d, including phantom scatter contributions. In the second phase (right), the photon fluence scored in the macroscopic simulations is set incident on a 3.3 × 3.3 × 3.3 µm³ water cube. Electron transport is modified such that charged particles crossing boundaries instantaneously translate to the opposing side of the phantom, such that the track can continue as if an equal track had originated outside the volume in question.

The second phase simulation volume consists of a microscopic box that is transparent to photons, but immediately translates escaping electrons to incident electrons on the opposing side(informally an electronic “Pac Male” universe). As Figure 4 (right) shows, when the electron passes the volume boundary, its coordinate (equal to the boundary value) is multiplied by –1 (the cube is centered at the origin). This technique effectively simulates electronic equilibrium over a large number of tracks. Genetic damage is estimated by tallying the number of DSBs in the volume of this microscopic box..

The RBE is defined as:

$${\displaystyle RBE=\frac{D_0}{D_i}=\frac{DS{B}_i}{DS{B}_0}}$$

D₀, the dose from a reference photon spectrum (⁶⁰Co) and D_i, that from the photon spectra in question, are the doses required to induce the same biological end point, in this case the same number of DSBs. The ratio of these doses simplifies to the inverse ratio of the number of DSBs Gy⁻¹ Gbp⁻¹ generated in the simulations for each of the sources.

Macroscopically, we first considered a “bare source” condition, which used the source spectra as if they were directly incident on a phantom surface with backscatter ignored. Since the motorized variable collimator for the SARRP can reach a field size of 40 × 80 mm²(roughly equivalent to a 53 × 53 mm² square), for the macroscopic simulation we assumed a 50 × 50 mm² field, a depth of 4.5 cm, and an SSD of 50 cm. This approximate the maximal scatter conditions encountered in a rat model. The photon spectra in the sensitive volume were extracted and then used as the incident spectra for the microscopic simulations.

results

Relative dosimetry

Variations in the external filter thickness (shown in Figure 5) have a modest effect on the percent depth dose The percent depth dose at 2 cm increases from 61 to 63.8% when the filter thickness is increased from 0.05 to 0.10 mm Cu, but increasing the filter thickness from 0.25 to 0.30 mm Cu only increases the relative dose from 66.9 to 67.4%.

Figure 5.

Effect of variation in Cu filter thickness from 0.05 to 0.30 mm Cu on relative percent depth dose curves (left) and the relative dose at 2 cm depth (right) for an Xstrahl SARRP irradiator. The red cross shows a 0.5% agreement between kVDoseCalc and EGSnrc, which use different spektra.

In general, these results also show that the Xstrahl SARRP (0.15 mm Cu) is more susceptible to variations in filter thickness than the PXi SmART (0.30 mm Cu). Around 0.15 mm Cu, the slope of the relationship between the relative dose at 2 cm depth and filter thickness is about 0.4% per 0.01 mm Cu of added filtration, compared to 0.2% per 0.01 mm Cu near 0.30 mm Cu, similar to the PXi SmART (Table 1).

As a means of comparison, the value for the percent depth dose was calculated with the EGSnrc beam model used in the absolute dosimetry (see Sections Relative dose distributions and Relative biological effectiveness).

Absolute dosimetry

Variation in filter thickness has a relatively high impact on absolute dose rate, as seen in Figure 6. Relative to the nominal (0.15 mm Cu) filtration, a variation of ± 0.05 mm in filter thickness changes the dose rate by 10.4%/7.3%, respectively. If assumed to be quasilinear locally, this represents a–1.8%/0.01 mm Cu relationship between very slight variations in filter thickness and absolute dose rate. These MC dose outputs have a 0.4% statistical uncertainty, and have been experimentally validated within 2.2% for 0 and 0.15 mm Cu filtration.²⁶

Figure 6.

Absolute dose rate delivered by the SARRP under calibration conditions (at isocenter, at a depth of 2 cm in water, with open field size) as a function of the Cu filter thickness. The result for the unfiltrated beam is shown for comparative purposes even though it excludes photons of < 10 keV energies, as it has been experimentally validated.²⁶

Relative biological effectiveness

In Table 2: RBE results for bare source and photon fluence transported to a 4.5 cm depth our simulations show a small change in RBE relative to a ⁶⁰Co reference: 6.9% for the SARRP and 4.5% for the X-RAD 320, which corresponds to a 2.4% difference between the two systems. There is effectively no difference ($\lesssim 0.2\%)$ between bare source conditions (no scatter or attenuation; see Section Relative biological effectiveness) and full scatter conditions.

Table 2.

RBE results for bare source and photon fluence transported to a 4.5 cm depth

Radiation Source	Conditions	DSB [Gy−1 Gbp−1]	δDSB [Gy−1 Gbp−1]	RBE (±0.001)
Co-60	Bare source	8.409	0.005
SARRP	Bare source	8.992	0.009	1.069
X-RAD 320	Bare source	8.785	0.006	1.045
SARRP	D: 4.5 cm FS: 5 × 5 cm2	8.995	0.006	1.069
X-RAD 320	d: 4.5 cm FS: 5 × 5 cm2	8.804	0.003	1.046

discussion

Absolute and relative dosimetry

Our results show a modest effect from slight variations of filter thickness on relative and absolute dose in the ultrathin filter design of modern irradiators. Since the SARRP is only half as filtrated as the SmART (0.15 vs 0.30 mm Cu), its dosimetry is more sensitive to small machining errors in its filter thickness. For the SARRP, changes of 0.01 mm Cu, which would be almost impossible to measure directly, are associated with changes of +0.4% and –1.8% in relative and absolute dose, respectively, at a depth of 2 cm.

It is unclear to which level of precision these copper filters are machined. Extrapolating from uncertainties in attenuating plate thickness used in HVL, measurement (up to 8–10% for particularly thin plates),^17,38,39 machining accuracy could be approximatively ±0.03 mm Cu. This alone would introduce systematic dosimetric errors of about 1% relative dose and –5% in absolute dose. It is therefore crucial to independently characterize the output of each individual unit, as both commercial manufacturers, Xstrahl and PXi, currently recommend.

Radiation biology effectiveness

Our results show a very modest effect of the ultrathin filter design on RBE, with only a 2.4% difference between the highly filtered X-RAD 320 and the ultrathin filter design of the SARRP. The low energy component of the SARRP spectrum (<30 keV), where the DSBs ramp up as a function of energy, accounts for a larger fraction of the overall spectrum compared to the X-RAD 320 case, which increases the DSBs. These results are roughly in line with previous findings specific to CBCT imaging³⁰ and electronic brachytherapy devices⁴⁰ which show that spectra more heavily weighted towards lower energies exhibit a higher RBE.

The high scatter scenario only increased these results by about 0.2% (roughly the numerical uncertainty of the simulations). This is an important finding, because it (i) limits the physical basis for a change in RBE as the experimental conditions in a kV biological irradiator are varied, and (ii) suggest that the difference in RBE between the two irradiator models is generally small enough so as not to be a compounding factor when reviewing experimental results produced between two different systems.

The estimated ratio of DSBs does not account for the complexity of the induced DSBs or the kinetics of damage repair. That said, damage complexity is generally a more significant factor when dealing with larger particles such as protons or heavy ions.⁴¹ Any RBE differences due to damage complexity differences or differences in repair kinetics are likely of higher order than differences resulting from the damage initially induced.

Other groups have successfully modelled the translation of DSB-based RBE into cell survival-based RBE using a repair-misrepair-fixation model (Carleson 2008, Streitmatter 2017). For kilovoltage photon sources, it has been shown (Streitmatter 2017) that the linear-quadratic α and β terms relate to those derived from a reference radiation (α_ref and β_ref) by

$${\displaystyle \alpha ={\alpha }_{\text{ref}}{\text{RBE}}_{\text{DSB}},\beta ={\beta }_{\text{ref}}\text{ }{\text{RBE}}_{\text{DSB}}^2}$$

where RBE_DSB is the DSB-based RBE used in this work. This link from an RBE_DSB to cell survival as a function of absorbed dose is important since animal experiments often stray from more clinical fractionation schemes.

conclusion

We investigated the influence of ultrathin filter design on absolute dose, relative percent depth dose, and RBE in modern small animal irradiators. Compared to the majority of radiation biological studies historically conducted using high-energy, heavily filtrated cabinet irradiators, the ultra-thin filters ofsmall animal irradiators potentially introduces small (~2%) changes in the RBE, which may serve as source of error when translating experimental results between irradiators. Beam quality and absolute dose are highly dependent on precise machining of the filter, where a change of just 0.01 mm can make a measurable change to the dosimetric properties of the beam. Notably, these results are specific to the SARRP system’s maximum operating potential (220 kVp). If operated at lower voltages, changes in dosimetric properties and RBE could be even more dramatic. These results imply the potential of larger differences in dose and dose rates between different units than in conventional cabinet-style irradiators and emphasize the need for careful unit-specific commissioning by end users of small animal irradiators.