Abstract
Social surveys prospectively linked with death records provide invaluable opportunities for the study of the relationship between social and economic circumstances and mortality. Although survey-linked mortality files play a prominent role in U.S. health disparities research, it is unclear how well mortality estimates from these datasets align with one another and whether they are comparable with U.S. vital statistics data. We conduct the first study that systematically compares mortality estimates from several widely-used survey-linked mortality files and U.S. vital statistics data. Our results show that mortality rates and life expectancies from the National Health Interview Survey Linked Mortality Files, Health and Retirement Study, Americans’ Changing Lives study, and U.S. vital statistics data are similar. Mortality rates are slightly lower and life expectancies are slightly higher in these linked datasets relative to vital statistics data. Compared with vital statistics and other survey-linked datasets, General Social Survey-National Death Index life expectancy estimates are much lower at younger adult ages and much higher at older adult ages. Cox proportional hazard models regressing all-cause mortality risk on age, gender, race, educational attainment, and marital status conceal the issues with the General Social Survey-National Death Index that are observed in our comparison of absolute measures of mortality risk. We provide recommendations for researchers who use survey-linked mortality files.
Keywords: Mortality, Vital statistics, Record linkage, Survey-linked mortality files, National Death Index
Introduction
Several nationally-representative surveys in the United States are linked to death records in the National Death Index (NDI). Survey-linked mortality files (SLMFs) contain detailed, often self-reported, information about survey respondents’ demographic attributes, socioeconomic status, health behaviors, and medical history collected several years, even decades, prior to death or censoring (Muennig et al. 2011; Preston and Taubman 1994; Rogers et al. 2000). These and other individual-level risk factors are measured less comprehensively in other mortality data sources in the United States such as vital statistics or medical claims data. Consequently, SLMFs play a prominent role in U.S. health disparities research because they contain information about key individual-level mortality risk factors that are not available elsewhere.
Population health researchers use SLMF data extensively to monitor adult mortality disparities in the United States. However, basic information about the comparability of SLMF mortality estimates in the United States is limited. A few methodological reports compare mortality data from the National Health Interview Survey Linked Mortality Files (NHIS-LMF; Ingram et al. 2008) and, more recently, the Health and Retirement Study (HRS; Weir 2016) with U.S. vital statistics data. These studies generally show that mortality estimates based on the NHIS-LMF and HRS are comparable to those based on vital statistics data. Several additional studies that use SLMF data to address substantive research questions largely corroborate these results (Brown et al. 2012; Hayward and Gorman 2004; Lariscy et al. 2015; Warner and Hayward 2006). These studies include ancillary results comparing life expectancies and/or age-specific mortality rates based on vital statistics data with those based on NHIS-LMF (Brown et al. 2012; Hummer et al. 1999; Lariscy et al. 2015), HRS (Brown et al. 2012), and National Longitudinal Survey of Older Men data (Black et al. 2017; Hayward and Gorman 2004; Warner and Hayward 2006) and imply that mortality estimates in these SLMFs and vital statistics are comparable.
Although the studies described above are informative, additional research is needed to obtain a more holistic understanding of SLMF data comparability. No single study comprehensively compares mortality estimates from several SLMFs with official mortality estimates reported in U.S. vital statistics data. Prior research that systematically cross-validates results from multivariate models across SLMFs is also sparse. As a result, it is unclear how well SLMF-based mortality estimates align with one another and whether they are comparable with U.S. vital statistics data. These issues warrant further examination because SLMFs are the major data source used in research examining social and economic determinants of U.S. adult mortality risk. Public health initiatives that aim to reduce adult mortality disparities often draw upon research based on SLMF data, and policymakers need accurate information to design efficacious policies.
How comparable are mortality estimates from leading survey-linked mortality files in the United States? To answer this question, we compare mortality estimates from four major survey-linked mortality files: the National Health Interview Survey Linked Mortality Files (NHIS-LMF), Health and Retirement Study (HRS), Americans’ Changing Lives (ACL), and General Social Survey National Death Index (GSS-NDI). We assess SLMF mortality estimate comparability in two ways. First, we compare mortality rates and life expectancies derived from several commonly-used nationally-representative surveys in the United States that have prospective mortality follow-up with mortality estimates from vital statistics data. Second, we compare results from multivariate hazard models that regress all-cause mortality risk on key sociodemographic characteristics across SLMFs to determine whether the various methods used to establish vital status across data sources influence the comparability of their estimates of mortality disparities. The first approach focuses on differences in absolute mortality risk, and the second approach focuses on differences in relative mortality risk. Finally, we outline general recommendations for future research with survey-linked mortality files based on our findings. Our results will help improve understanding of the overall quality of adult mortality research in the United States.
Background
Survey-Linked Mortality Files
Mortality estimates may vary between survey-linked mortality files for several reasons.1 Differences in the performance of the NDI record linkage algorithm is one potential source of variability between surveys. The algorithm probabilistically links decedent survey records and NDI death records using personally identifiable information (PII) recorded in both data sources. The identifiers used in the record linkage process include Social Security Number (SSN), first name, middle initial, last name, father’s surname, birth date, sex, race, state of birth, state of residence, and marital status (National Center for Health Statistics [NCHS] 2018). Both data sources must contain accurate PII to match respondents who died during the follow-up period to their death records. The algorithm can still perform as intended when only a subset of these identifiers are present and accurate, and more unique identifiers (e.g., SSN) are given more weight in the matching process than others (e.g., marital status). However, matching errors can occur when PII in either data source is missing and/or inaccurate (Curb et al. 1985; Harron et al. 2015; Lariscy 2011, 2017; Rogers et al. 1997). False negatives occur when the NDI matching algorithm fails to match survey records and death records among deceased respondents causing them to appear “statistically immortal” (Pablos-Méndez 1994:1237). False positives occur when the NDI matching algorithm incorrectly identifies respondents who survive the follow-up period as deceased when a surviving respondent and decedent have similar PII. These technical problems have substantive implications because matching errors can distort results. Mortality risk will be overestimated when false positives are abundant and underestimated when false negatives are abundant.
Matching error is a potential source of systematic bias because it results from variations in the propensity to report key identifiers between subpopulation groups, data collection periods, and/or surveys. For instance, prior research with the NHIS-LMF has shown that racial/ethnic subgroup differences in record linkage can affect estimates of mortality disparities since members of some groups are more likely to be linked to the death certificates than members of other groups (Black et al. 2017; Lariscy 2011, 2017; Palloni and Arias 2004; Rogers et al. 1997). Matching errors can also arise when survey respondents either refuse or are not asked to provide certain identifiers. Assuming it is recorded and reported accurately, SSN is the most important identifier in the matching process because, unlike other linkage items such as name or date of birth, it uniquely identifies individuals. The matching algorithm is much more likely to link survey records and death records correctly when both files contain accurate SSNs. However, respondents increasingly refuse to report SSNs to interviewers, and some surveys with NDI linkages, such as the GSS, have not always collected SSNs (Kim et al. 2015; NCHS Office of Analysis and Epidemiology 2009). Consequently, linkage errors may have increased over time in some SLMFs because respondents are reluctant to provide SSN due to identity theft concerns (Dahlhamer and Cox 2007). For instance, among male NHIS respondents, SSN was missing for only 17% in 1986 but 72% of respondents by 2004 (NCHS Office of Analysis and Epidemiology 2009).
The extent to which a survey relies on vital status ascertained via the matching algorithm may also influence SLMF comparability. Surveys linked to the NDI use different strategies to prospectively ascertain respondents’ vital status. Some surveys rely exclusively on passive follow-up (i.e., linking records based on PII) while others incorporate active follow-up (i.e., re-contacting surviving respondents or collecting decedent information from knowledgeable proxies). SLMFs that contain cross-sectional survey data are most susceptible to problems associated with passive follow-up because respondents are not re-interviewed. SLMFs that contain longitudinal survey data have an inherent advantage over those that contain cross-sectional survey data because they can incorporate active and passive follow-up techniques. Consequently, SLMFs with longitudinal survey data may have lower false positive/negative error rates than ones with cross-sectional survey data because interviewers have repeated opportunities to collect and/or update missing or inaccurate personal identifiers. Having an opportunity to re-interview respondents may have particularly important implications for obtaining sensitive identifiers, such as SSNs, which respondents are often reluctant to provide.
Some SLMFs may be more susceptible to the issues discussed above than others due to variations in PII reporting between surveys. A comparative analysis is especially important for the GSS-NDI. The GSS-NDI has only been publicly available since 2011, but it has quickly become a popular resource for establishing social disparities in U.S. adult mortality risk. The GSS is a veritable goldmine for population health researchers because it contains variables not available in any other dataset. The GSS-NDI has been used in studies linking social characteristics such as exposure to individual- and institutional-level discrimination, sexual minority status, happiness, political ideology, emotion suppression, observed skin tone, and other statuses, attitudes, and behaviors with adult mortality risk (Chapman et al. 2013; Lawrence et al. 2015; Lee et al. 2015; Morey et al. 2018; Muennig et al. 2013; Pabayo et al. 2015; Stewart et al. 2018). Researchers could not have established these associations with any other nationally-representative datasets.
Problems in the GSS-NDI may arise if the NDI matching algorithm performs sub-optimally. Recall that the NDI record linkage algorithm is probabilistic, and PII must be recorded accurately in both data sources to match decedent survey records with NDI death records. Although the algorithm uses several personal identifiers in the matching process, record linkage success rates are much higher when both data sources contain SSNs because, when accurate, SSNs uniquely identify an individual respondent. However, GSS respondents were not asked to provide SSNs prior to the 1993 survey.
The central role that SSN plays in the matching process is evident when one considers the classification scheme NCHS uses to gauge match quality. NDI record linkage uses a five-class system to describe match quality, where classes 1 and 2 are considered the most reliably-matched decedents whereas the match quality for decedents placed into classes 3 and 4 is less certain (NCHS 2018). Class 5 matches are assumed to have survived the follow-up period. Muennig et al. (2011:3) state that “for the GSS-linked records there were no class 1 matches and a limited number of class 2 matches due to the lack of Social Security information.” In contrast to the small proportion of GSS-NDI decedents in classes 1 and 2, among NHIS-LMF respondents who are identified as having died during follow-up, 61% of matches are in class 1 and 15% are in class 2 (Lariscy 2011). The absence of GSS-NDI deaths from classes 1 and 2 signals lower quality in mortality ascertainment relative to other survey-linked mortality files. This could have major consequences for GSS-NDI mortality data quality because it implies that matching error rates are high.
Comparability of Survey-Linked Mortality Files and Vital Statistics Data
Mortality data in vital statistics may differ from survey-linked data since they include the entire U.S. population whereas most survey samples only include non-institutionalized respondents. Mortality rates are higher among institutionalized populations, particularly nursing home residents, than non-institutionalized populations. Thus, SLMFs should produce lower mortality rates and higher life expectancies when compared with vital statistics data. Discrepancies between SLMF and vital statistics mortality estimates should also increase with age as people increasingly enter nursing homes and other institutional settings that are excluded from most household-based survey sampling frames.
Although mortality rates based on vital statistics data provide a more complete representation of mortality patterns within the population than SLMF mortality rates because they include institutionalized and non-institutionalized persons, they may also have errors that undermine their precision. The most well-known problem is numerator-denominator bias, which arises because vital statistics mortality rates combine data from two sources: death certificate data (numerator) and mid-year population estimates provided by the U.S. Census Bureau (denominator). Content or coverage errors in either data source can bias the resulting mortality rates. Other studies have identified issues in vital statistics data that could bias mortality rates among racial/ethnic minority populations, such as age misreporting, misclassification of race/ethnicity on death certificates, and census undercounts (Arias et al. 2010; Hogan et al. 2013; Preston et al. 1996). These attributes presumably are recorded more accurately in SLMFs than vital statistics because survey respondents typically self-report this information.
The Current Study
This study addresses the following unresolved question: How comparable are mortality estimates from leading survey-linked mortality files in the United States? To answer this question, we compare mortality estimates from four major survey-linked mortality files in the United States. The analyses have two key components. The first component focuses on differences in absolute mortality risk between SLMFs and U.S. vital statistics data. The second component focuses on differences in relative mortality risk between SLMFs. We explain each component in greater detail below. We expect to document four key patterns related to survey-linked mortality file comparability. First, we anticipate that most SLMF mortality estimates will correspond closely with ones based on vital statistics data. However, mortality rates should be lower and life expectancies should be higher in SLMFs relative to those based on vital statistics data because the survey samples exclude institutionalized respondents at baseline while vital statistics data include the entire population. Second, we expect that differences between SLMF and vital statistics mortality rates and life expectancies will increase with age. This pattern is evident in prior research and presumably exists because most institutionalized adults in the United States, especially at older ages, are nursing home residents, a group with higher mortality risk than the overall population. Third, we expect results between SLMFs to vary more in analyses of absolute mortality risk (mortality rates and life expectancies) than in analyses of relative mortality risk (multivariate Cox models). The control variables in the multivariate models should constrain variability between SLMFs because these variables are correlated both with mortality risk and the propensity to report personal identifiers used in the record linkage process. Finally, we anticipate that the GSS-NDI will diverge the most from vital statistics data because it contains fewer high-quality NDI matches than the other SLMFs.
Methods
Data
We compare mortality estimates from the following survey-linked mortality files: National Health Interview Survey Linked Mortality Files (NHIS-LMF), Health and Retirement Study (HRS), Americans’ Changing Lives (ACL), and General Social Survey National Death Index (GSS-NDI). Although other surveys also contain prospective mortality follow-up, we limit our analyses to these datasets for several reasons. First, these SLMFs are used extensively in U.S. population health research. Second, they all contain nationally-representative data, surveys with high response rates, several decades of mortality follow-up, and many decedents. Third, multivariate results can be easily compared between these surveys because key sociodemographic and socioeconomic variables are measured similarly between surveys. Each dataset is described below (also see Table 1).
Table 1.
Characteristics of the NHIS-LMF, HRS, ACL, and GSS-NDI survey and analysis samples
| NHIS-LMF | HRSb,c | ACLb | GSS-NDI | |
|---|---|---|---|---|
| Study Design | ||||
| Respondents | ||||
| Age at interview | 18+ | 51+ | 25+ | 18+ |
| Survey data | ||||
| Interview perioda | 1986–2009 | 1992–2010 | 1986–2011 | 1978–2010 |
| Interview years | 24 | 21 | 5 | 25 |
| Sample design | Cross-sectional | Longitudinal | Longitudinal | Cross-sectional |
| Population sampled | Civilian, non-institutionalized | Civilian, non-institutionalized | Civilian, non-institutionalized | Civilian, non-institutionalized |
| Data collection method | In-person | In-person at baseline, by phone for later waves | In-person at baseline, by phone for later waves | Phone |
| Mortality data | ||||
| Follow-up years | 1986–2011 | 1992–2011 | 1986–2011 | 1979–2014 |
| Follow-up source | NDI, other linkaged | NDI linkage, Tracker file | NDI linkage, survey follow-up | NDI linkage |
| Sample Restrictions in the Current Study | ||||
| Respondents | ||||
| Age at interview | 25–84e | 51–100+ | 25–96 | 25–88 |
| Age at death/censoring | 25–100+ | 51–100+ | 25–100+ | 25–100+ |
| Survey data | ||||
| Interview period | 1986–2009 | 1992–2010 | 1986–2011 | 1986–2010 |
| Sample design | Cross-sectional | Longitudinal | Longitudinal | Cross-sectional |
| Population sampled | Civilian, non-institutionalized | Civilian, non-institutionalized | Civilian, non-institutionalized | Civilian, non-institutionalized |
| Mortality data | ||||
| Follow-up years | 1986–2011 | 1992–2011 | 1986–2011 | 1986–2011 |
| Follow-up source | NDI linkage | NDI linkage | NDI linkage | NDI linkage |
Notes: ACL = Americans’ Changing Lives study; GSS-NDI = General Social Survey National Death Index; HRS = Health and Retirement Study; NHIS-LMF = National Health Interview Survey Linked Mortality Files; NDI = National Death Index.
Only includes survey cross-sections/waves with mortality follow-up.
All respondents are community-dwelling initially (baseline interview). Respondents who subsequently transition into an institution are re-interviewed (respondent or proxy interviews).
The HRS records respondents’ vital status at each interview wave (active follow-up) in addition to NDI linkages (statistical or passive follow-up). The NDI successfully identifies the vast majority of decedents. To increase comparability across surveys, we only include NDI deaths in the HRS.
The NDI is the primary source for vital status in the NHIS-LMF. However, NHIS survey records are also linked with Social Security Administration, Centers for Medicare and Medicaid Services, and death certificate data to ascertain respondents’ vital status. The 1986–2011 NHIS-LMF contains very few deaths identified from data sources other than the NDI (< .5% of all deaths).
Age top-codes in the public-use NHIS vary over time: age 99+ (1986–1995), 90+ (1996), and 85+ (1997–2009).
The NHIS is a nationally-representative cross-sectional survey of the non-institutionalized U.S. adult population ages 18+. NCHS conducts the survey annually. The public-use version of the NHIS-LMF prospectively links the 1986–2009 NHIS to the NDI through 2011 (NCHS 2013). The 1986–2011 NHIS-LMF contains survey records for 1,605,246 respondents deemed eligible for NDI follow-up (N = 265,751 decedents). Respondents with missing values on race (n = 7,686, 0.5%), marital status (N = 7,016, 0.4%), or educational attainment (N = 21,057, 1.3%) are listwise deleted. We also exclude respondents younger than age 25 (N = 205,573) at baseline or whose ages are top-coded (N = 12,914) to increase comparability among datasets. Our NHIS-LMF analytic sample contains 1,112,685 individual respondents and 250,230 decedents. We downloaded public-use NHIS-LMF data from the National Health Interview Series on the Integrated Public Use Microdata Series (IPUMS) Health Surveys website at the University of Minnesota (Blewett et al. 2018). Additional information about the NHIS-LMF is available elsewhere (NCHS 2013).
The HRS is a nationally-representative longitudinal survey of U.S. adults ages 51+ and their spouses regardless of age-eligibility. HRS respondents were first interviewed in 1992 and follow-up interviews have generally occurred bi-annually through the present. The HRS sample transitioned to a steady-state design in 1998. The redesigned HRS includes respondents from the Assets and Health Dynamics of the Oldest Old study (AHEAD) and incorporates refresher cohorts. AHEAD respondents were ages 70+ in 1993 when they were first interviewed (Soldo et al. 1997). Refresher cohorts are added every six years to replenish the sample and ensure the survey remains representative of the 51+ population (Sonnega et al. 2014). The HRS contains approximately 15,000–20,000 respondents in any given interview wave and over 12,000 deaths as of 2011. Respondents with missing values on race (N = 78, 0.2%), age (N = 1, 0%), marital status (N = 17, 0.05%), or educational attainment (N = 121, 0.4%) are listwise deleted.
Our analyses are based on a harmonized version of the 1992–2014 HRS created by the RAND Corporation (RAND HRS, Version P; Bugliari et al. 2016). The public-use HRS contains all-cause mortality data. The HRS Tracker file records respondent vital status across interview waves. Mortality is also ascertained in the HRS via the NDI (HRS: 1992–2011, NDI: 1992–2011). To increase comparability with the other datasets, our HRS analyses only include NDI deaths. Ancillary analyses (available from first author) show that death counts based on the Tracker file and the NDI are very similar. This is encouraging because it implies that the NDI matching algorithm performs well in the HRS. Additional information about the HRS (Sonnega et al. 2014) and HRS RAND File (Bugliari et al. 2016) is available elsewhere.
The ACL is a nationally-representative survey of U.S. adults ages 25+ (see House 2014 for details). Respondents were first interviewed in 1986 (N = 3,617) and follow-up interviews were conducted in 1989 (N = 2,867), 1994 (N = 2,562), 2001/2 (N = 1,787), and 2011 (N = 1,427). The sample is a closed cohort, and all respondents have complete information on all covariates included in the models. Our analyses are based on the restricted-use ACL which contains links to NDI death records through 2011 (N = 1,832 deaths). The analyses also exclude three respondents in the 1986 ACL who were under age 25 at interview. A public-use version of the ACL that does not include respondents’ vital status is available from the Inter-University Consortium for Political and Social Research at the University of Michigan.
The GSS is a nationally representative cross-sectional survey of the non-institutionalized U.S. adult population ages 18+ conducted by the National Opinion Research Center (NORC) at the University of Chicago. The 1972–1993 GSS was conducted annually (except 1979 and 1981) and it has been conducted biannually since 1994. The GSS-NDI links the 1978–2010 GSS (N = 44,174) with NDI death records in 1979–2014 (N = 12,558) (Muennig et al. 2016). To increase comparability with the other SLMFs, the analyses are restricted to the 1986–2010 GSS with NDI follow-up through 2011 (35,371 respondents and 7,056 decedents). We also exclude members of the 1987 black oversample (N = 316, 0.7%) and listwise delete observations missing age (N = 50, 0.1%), educational attainment (N = 89, 0.2%), or current marital status (N = 8, 0.02%). We also restrict the GSS-NDI analyses to respondents ages 25–88 at interview to increase comparability with the other surveys. Our final individual-level GSS-NDI sample (GSS: 1986–2010, NDI: 1986–2011) contains 31,480 respondents and 6,560 decedents. GSS-NDI data are available publicly from NORC (2016). Additional information about the GSS-NDI is available elsewhere (Muennig et al. 2011, 2016).
We compare mortality rates and life expectancies from the NHIS-LMF, HRS, ACL, and GSS-NDI with U.S. vital statistics data for women, men, and both genders combined. We downloaded period life tables constructed using U.S. vital statistics data from the Human Mortality Database (HMD 2018). Mortality rates and life expectancies based on vital statistics data are averaged over the 1986–2011 period to approximately match the follow-up years most SLMFs in our analyses covered. Predicted mortality rates estimated from each respective SLMF represent the average age-specific mortality rate over the follow-up period. Thus, the SLMF life expectancies are averages because we construct life tables from predicted mortality rates that incorporate multiple follow-up years.
Measures
All-cause mortality risk (0 = alive, 1 = dead) is the dependent variable in all SLMF analyses. Vital status of survey respondents at the end of the follow-up period is determined through probabilistic linkage with the NDI. Exposure to the risk of death is measured in calendar years. Survivors receive a partial year of exposure the first year they are interviewed (calculated based on interview month/quarter) and one year of exposure thereafter until the end of the follow-up period. Decedents receive a partial year of exposure the first year they are interviewed (calculated based on interview month/quarter), a full year of exposure each year they survive, and a partial year of exposure the year they die (calculated based on month/quarter of death).
Age and exposure have slightly different specifications in the models used to construct life tables. In these analyses, we reformat each SLMF into a person-year file containing time-varying measures of age, mortality status, and exposure. Each row in the person-year file represents one calendar year of exposure and the number of rows each respondent contributed equals the total number of years (partial or complete) survived. Exact age on January 1st in each year is calculated based on self-reported birth dates2 (month and year) and interview dates (month and year for the GSS, HRS, and ACL and quarter and year for the NHIS-LMF) and calculated using interview quarter and year. We use this information to calculate age x on January 1st in year t, where age x ranges from exact age x – 0.05 to exact age x + 0.49. Other studies take a similar approach (Brown et al. 2012). In the models used to create life tables for each SLMF, this approach predicts mortality rates that closely approximate traditional occurrence-exposure rates (i.e., life table mx). Results are similar in ancillary analyses (not shown) with more precise age and exposure specifications.
Covariates in the Cox proportional hazard models include self-reported age (in years), gender (male and female), race (white, black, and other race), legal marital status (currently married, previously married, and never married), and educational attainment (less than high school, high school graduate, some college, and bachelor’s degree or more). Covariates are all measured at baseline and coded uniformly across datasets to increase comparability. Race, for example, is measured in three categories because this is how it is measured in the 1986–2010 public-use GSS, and Hispanic ethnicity was not assessed in the GSS until 2000. Educational attainment is categorized as follows from variables that measure completed years of schooling: less than high school (0–11 years), high school diploma (12 years), some college (13–15 years), and college degree or more (16+ years). Marital status is recoded from questions asking respondents to report their current legal marital status. Marital status and educational attainment are measured at baseline even though these attributes may vary over time to facilitate comparisons between SLMFs that contain longitudinal (ACL and HRS) and cross-sectional (NHIS-LMF and GSS-NDI) survey data.
Analyses
Our analyses proceed in two stages. The first stage focuses on differences in absolute mortality risk between SLMFs and U.S. vital statistics data. Specifically, we compare age-specific mortality rates and life expectancies from the NHIS-LMF, HRS, ACL, GSS-NDI, and U.S. vital statistics data. We estimate parametric hazard models to predict age-specific mortality rates and construct life tables with the SLMF data. Exploratory analyses (available by request) were performed to determine the optimal specification of the baseline hazard and showed that exponential models generally fit best. Structural constraints on the relationships examined are minimized by predicting adult mortality risk as a function of age in years (i.e., the models only control for a linear age term that varies over time).
We use coefficients from these models to obtain age-specific mortality rates (mx) and construct life tables using a multivariate life table approach (Teachman and Hayward 1993). This approach allows us to estimate age-specific mortality rates in each SLMF which we then use to construct life tables and ultimately calculate life expectancy. We estimate confidence intervals for mortality rates and life expectancy based on 1,000 Monte Carlo simulations (Andreev and Shkolnikov 2010). We perform analyses on person-year files and estimate separate models for women, men, and both genders combined. Mortality rates and life expectancies based on SLMF data and vital statistics data are compared using graphs, tables, and rate ratios. Mortality rates and life expectancies based on vital statistics data should be thought of as the benchmark or reference data that we use to compare and contrast results between data sources. We do not imply that vital statistics data represent a gold standard.
The second stage of the analysis focuses on relative mortality risk between the NHISLMF, ACL, HRS, and GSS-NDI. We estimate two nested semi-parametric hazard models (i.e., Cox proportional hazard models) for each SLMF. Model 1 regresses all-cause mortality risk on age in years, gender (reference group [ref.] = men), and race (ref. = whites). Model 2 regresses all-cause mortality risk on age in years, gender (ref. = men), race (ref. = whites), marital status (ref. = currently married), and educational attainment (ref. = college education). The analyses are performed on individual-level files and all covariates are measured at baseline. The models are parsimonious to increase comparability between our analyses and other studies that use SLMF data. Sample weights are applied and complex variances are computed in all SLMF analyses (StataCorp 2013). Online supplements include complete life tables for each SLMF, ancillary results, and the Stata code necessary to replicate our results.
Results
Mortality Rates and Life Expectancies
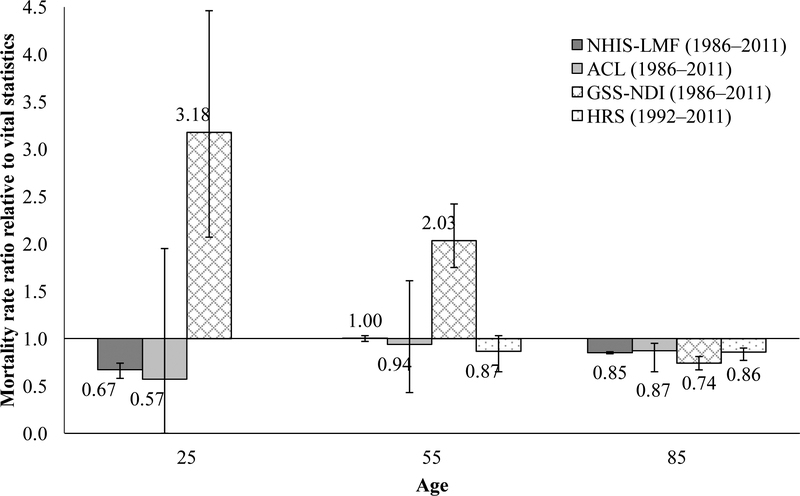
Figures 1 (women) and 2 (men) display mortality rate ratios at ages 25, 55, and 85 for each SLMF relative to vital statistics.3 These three ages were chosen to depict mortality disparities in early adulthood (age 25), middle adulthood (age 55), and older adulthood (age 85). Rate ratios in the HRS are not calculated in early adulthood because the survey is designed to represent persons ages 51+. The figures display rate ratios for age- and gender-specific survey-based mortality rates relative to vital statistics-based mortality rates. For example, the rate ratio for HRS men at age 55 is calculated by dividing the predicted mortality rate for men at age 55 in the HRS by the average mortality rate for men at age 55 in vital statistics between 1992 and 2011. Rate ratios below 1.0 indicate that SLMF rates are lower than vital statistics rates, and rate ratios above 1.0 indicate that SLMF rates are higher than vital statistics rates. SMLF and vital statistic mortality rates are identical when rate ratios equal 1.0.
Fig. 1.
Mortality rate ratios for NHIS-LMF (1986–2011), ACL (1986–2011), GSS-NDI (1986–2011), and HRS (1992–2011) compared with U.S. vital statisitcs (1986–2011), women
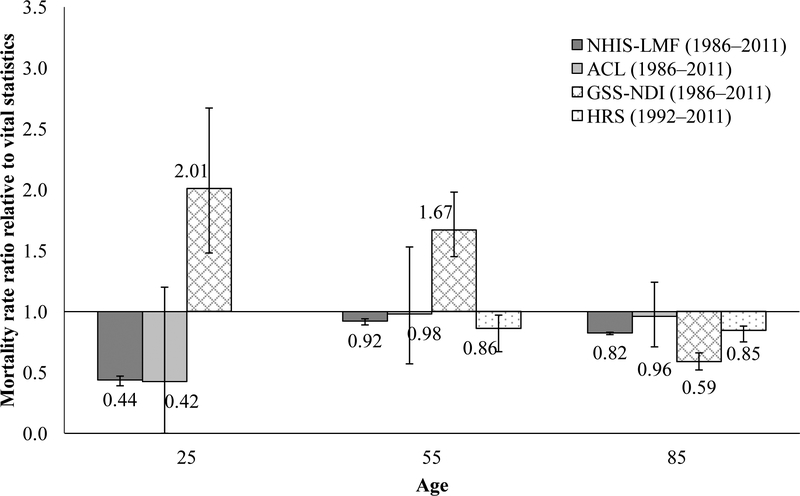
Fig. 2.
Mortality rate ratios for NHIS-LMF (1986–2011), ACL (1986–2011), GSS-NDI (1986–2011), and HRS (1992–2011) compared with U.S. vital statisitcs (1986–2011), men
Figures 1 and 2 show that mortality rates in the NHIS-LMF, ACL, and HRS are lower than or equivalent to mortality rates in vital statistics. Mortality rates in the NHIS-LMF and ACL are much lower in comparison to vital statistics in early adulthood, but the discrepancy with vital statistics narrows in middle and older adulthood. At ages 55 and 85, HRS mortality rates are somewhat lower than vital statistics rates, mirroring the pattern observed for the NHIS-LMF and ACL. Unlike the other SLMFs, GSS-NDI rate ratios exceed 1.0 at ages 25 and 55 years. That is, the GSS-NDI has higher mortality rates in early and middle adulthood relative to the vital statistics rates. For instance, among women, GSS-NDI rates are more than three times as high as vital statistics rates at age 25 (risk ratio [RR] = 3.18) and more than twice as high at age 55 (RR = 2.03). Among men, GSS-NDI rates exceed vital statistics rates by 101% ([2.01 – 1.0] × 100) at age 25 and by 67% at age 55. Like the other SLMFs, mortality rates in the GSS-NDI are lower at age 85 than vital statistics rates, but they diverge more sharply from vital statistics when compared to the other SLMFs. Differences between mortality rates based on SLMFs and vital statistics data are thought to exist primarily because the survey samples in the SLMFs exclude institutionalized persons—most notably, nursing home residents—who, on average, have a higher risk of death than their non-institutionalized counterparts, whereas vital statistics data include mortality information for the entire population.
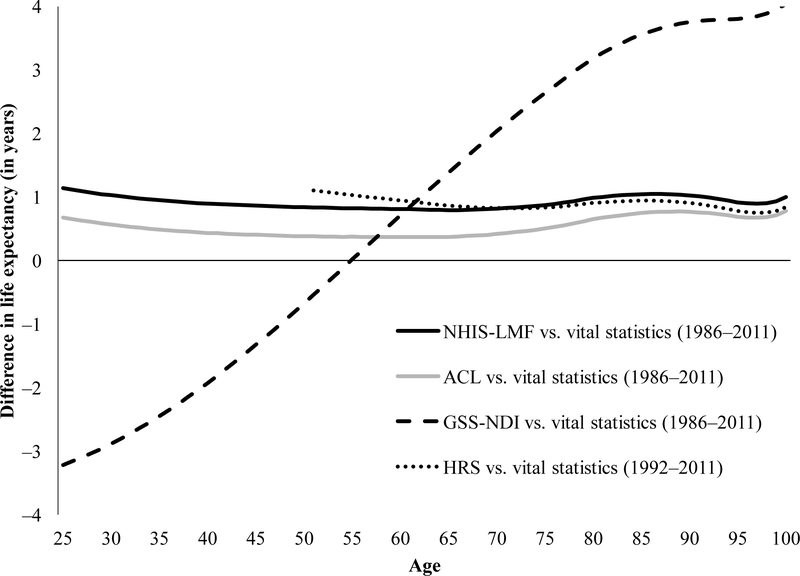
Figure 3 displays the difference in life expectancies (in single years of age) between each SLMF and vital statistics (i.e., SLMF ex – vital statistics ex) for the total population. We show results for women and men combined because the overall and gender-specific patterns are similar. Each line in the graph represents the difference between SLMF life expectancies and vital statistics life expectancies at the same age. Appendix Table B displays the life expectancies from U.S. vital statistics, NHIS-LMF, ACL, HRS, and GSS-NDI data for both genders combined (top panel), women (middle panel), and men (bottom panel).
Fig. 3.
Difference in life expectancy (in years) for NHIS-LMF, ACL, HRS, and GSS-NDI vs. U.S. vital statistics data, men and women
Similar to our findings regarding mortality rate ratios, life expectancy estimates in the NHIS-LMF, HRS, and ACL reflect more favorable mortality risk when compared with life expectancy in U.S. vital statistics (Figure 3). Life expectancies calculated from NHIS-LMF and ACL data are consistently about one year higher than those from U.S. vital statistics. Life expectancy in the HRS is also generally comparable to vital statistics data, but differences between the HRS and vital statistics are larger before age 65 and smaller at the oldest ages when compared with the other surveys. These comparative results resemble those from previous studies; life expectancies based on SLMF data tend to be slightly higher than those based on vital statistics data (Hummer et al. 1999; Lariscy et al. 2015). Previous studies have shown similar patterns in the NHIS-LMF and HRS (Brown et al. 2012), but no published studies document this general pattern in the ACL.
Figure 3 further shows that the age patterns of GSS-NDI life expectancy are very different from the other SLMFs and vital statistics. When compared with life expectancies based on U.S. vital statistics data, GSS-NDI life expectancy estimates are much lower at younger adult ages, similar in midlife where a crossover occurs, and much higher at older adult ages. For example, life expectancy in the GSS-NDI is approximately three years lower at the youngest ages and four years higher at the oldest ages. The gender-specific results shown in the middle and bottom panels of Appendix Table B are very similar to those shown for both genders combined (top panel). These patterns have not been documented previously in the GSS-NDI.
In sum, comparisons of absolute mortality risk reveal two key patterns. Mortality rates and life expectancies based on the NHIS-LMF, HRS, and ACL closely correspond with vital statistics data, but reflect somewhat more favorable survival than vital statistics data. On the other hand, mortality rates and life expectancies based on the GSS-NDI do not correspond with those based on other SLMFs or U.S. vital statistics data, and these discrepancies are most evident among younger and older adults.
Cox Proportional Hazard Models
Tables 2 (ages 25+, excludes HRS) and 3 (NHIS-LMF, ACL, and GSS-NDI: ages 50+, HRS: ages 51+) show descriptive statistics for all variables included in the Cox proportional hazard models. Covariates are distributed similarly across each dataset, with only a few differences that are statistically significant yet small. This finding is important because it implies that the problems in the GSS-NDI uncovered in Figures 1–3 (and Appendix Tables A and B) likely arise from the NDI linkage process rather than from the sampling and collection of the GSS itself. Another exception to the similarity across datasets is the higher proportion of deaths during the follow-up period in the ACL. As Tables 2 and 3 show, a higher proportion of ACL respondents died during follow-up (35.0% at ages 25+ and 71.8% at ages 50+) than in the other SLMF datasets. In contrast, only 16.2% of respondents ages 25+ and 32.3% of respondents ages 50+ died over the same period (1986–2011) in the NHIS-LMF. At first glance, the ACL seems to have an excess of deaths, but differences between the ACL sample design and the other surveys are the most likely reason for these differences in proportion of deaths. The ACL has a closed cohort design while the surveys in the other SLMFs are either pooled cross sections (NHIS-LMF and GSS-NDI) or longitudinal surveys that include refresher cohorts (HRS). Consequently, the proportion of deaths rises sharply over time as the ACL cohort ages. The ACL also oversamples two groups that experience a higher risk of death than the general population: blacks and persons ages 60+. Thus, differences in death distributions between the ACL and the other SLMFs are reasonable and expected.
Table 2.
Descriptive statistics for respondents ages 25+ in the NHIS-LMF, HRS, ACL, and GSS-NDI samples
| NHIS-LMFa | ACLb | GSS-NDIc | |
|---|---|---|---|
| N = 1,334,010 | N = 3,614 | N = 31,480 | |
| Age (mean) | 48.3 (48.2, 48.4) | 41.1 (46.0, 48.2) | 47.6 (47.4, 47.8) |
| Female (%) | 52.2 (52.2, 52.3) | 52.9 (51.0, 54.8) | 54.8 (54.1, 55.4) |
| Race (%) | |||
| White | 83.4 (83.0, 83.8) | 83.5 (79.9, 86.6) | 80.9 (80.0, 81.8) |
| Black | 11.0 (10.7, 11.3) | 10.9 (8.6, 13.8) | 12.3 (11.6, 13.1) |
| Other | 5.6 (5.4, 5.8) | 5.6 (3.8, 8.1) | 6.8 (6.2, 7.3) |
| Marital status (%) | |||
| Currently married | 67.3 (67.0, 67.5) | 69.4 (66.7, 72.0) | 63.6 (62.9, 64.3) |
| Previously married | 19.9 (19.8, 20.1) | 20.4 (18.7, 22.2) | 21.9 (21.4, 22.4) |
| Never married | 12.8 (12.7, 13.0) | 10.2 (8.5, 12.2) | 14.5 (14.0, 15.0) |
| Educational attainment (%) | |||
| Less than high school | 17.1 (16.8, 17.3) | 25.6 (22.7, 28.7) | 17.9 (17.4, 18.5) |
| High school | 34.3 (34.1, 34.5) | 31.4 (29.0, 33.8) | 29.6 (29.0, 30.3) |
| Some college | 23.8 (23.7, 24.0) | 23.3 (20.8, 26.1) | 25.8 (25.2, 26.4) |
| College | 24.8 (24.5, 25.1) | 19.7 (17.3, 22.4) | 26.7 (25.9, 27.4) |
| Deaths (%) | 16.2 (16.0, 16.4) | 35.0 (32.5, 37.6) | 19.5 (19.0, 20.0) |
National Health Interview Survey Linked Mortality File (NHIS-LMF, NHIS: 1986–2009, NDI: 1986–2011).
Americans’ Changing Lives study (ACL, 1986–2011).
General Social Survey-National Death Index (GSS-NDI, GSS: 1986–2010, NDI: 1986–2011).
Notes: The percentages (means) shown in the table are weighted. The analyses are based on individuallevel data.
Table 3.
Descriptive statistics for respondents ages 50+ in the NHIS-LMF, HRS, ACL, and GSS-NDI samples
| NHIS-LMFa | HRSb | ACLc | GSS-NDId | |
|---|---|---|---|---|
| N = 555,795 | N= 31,625 | N = 2,070 | N= 13,255 | |
| Age (mean) | 63.9 (63.8, 64.0) | 60.6 (60.4, 60.7) | 65.0 (64.3, 65.6) | 63.2 (63.0, 63.4) |
| Female (percent) | 54.1 (54.0, 54.3) | 50.9 (50.2, 51.5) | 55.8 (52.6, 58.9) | 55.3 (54.4, 56.3) |
| Race (percent) | ||||
| White | 86.6 (86.2, 87.0) | 82.9 (82.4, 83.4) | 86.9 (83.4, 89.8) | 85.0 (84.0, 86.0) |
| Black | 9.4 (9.1, 9.7) | 11.3 (10.9, 11.6) | 10.4 (7.9, 13.6) | 11.0 (10.1, 11.9) |
| Other | 4.0 (3.8, 4.3) | 5.8 (5.5, 6.2) | 2.7 (1.6, 4.7) | 4.1 (3.6, 4.7) |
| Marital status (percent) | ||||
| Currently married | 66.5 (66.3, 66.8) | 70.8 (70.2, 71.4) | 66.6 (63.5, 69.6) | 65.3 (64.4, 66.3) |
| Previously married | 28.7 (28.4, 28.9) | 23.7 (23.1, 24.3) | 29.5 (26.7, 32.3) | 29.7 (28.8, 30.6) |
| Never married | 4.8 (4.7, 4.9) | 5.5 (5.2, 5.9) | 3.9 (3.0, 5.2) | 5.0 (4.6, 5.4) |
| Education attainment (percent) | ||||
| Less than high school | 24.0 (23.7, 24.3) | 23.7 (23.2, 24.3) | 42.2 (37.7, 46.8) | 25.0 (24.1, 25.9) |
| High school | 35.3 (35.1, 35.6) | 31.0 (30.3, 31.6) | 30.4 (27.3, 33.6) | 31.3 (30.4, 32.2) |
| Some college | 20.1 (19.9, 20.3) | 21.9 (21.3, 22.5) | 16.0 (13.4, 18.5) | 21.1 (20.3, 21.9) |
| College | 20.6 (20.3, 21.0) | 23.4 (22.8, 24.0) | 11.3 (9.0, 13.7) | 22.6 (21.7, 23.6) |
| Deaths (percent) | 32.3 (31.9, 32.8) | 28.9 (28.4, 29.5) | 71.8 (68.9, 74.5) | 33.2 (32.3, 34.1) |
National Health Interview Survey Linked Mortality File (NHIS-LMF, NHIS: 1986–2009, NDI: 1986–2011).
Health and Retirement Study (HRS, 1992–2010).
Americans’ Changing Lives study (ACL, ACL: 1986–2011, NDI: 1986–2011).
General Social Survey-National Death Index (GSS-NDI, GSS: 1986–2010, NDI: 1986–2011).
Notes: The percentages (means) shown in the table are weighted. The analyses are based on individual level data.
Tables 4 (ages 25+) and 5 (ages 50+, HRS: ages 51+) show results from two nested Cox proportional hazard models regressing all-cause mortality risk on several sociodemographic factors. Overall, results from each dataset are similar and all associations are in the expected directions based on previous research. For example, mortality risk is higher among men than women, black adults than white adults, the previously and never married than the currently married, and those with lower educational attainment than those with higher education. Cox proportional hazard models conceal the problems with the GSS-NDI that are observed in our comparison of age-specific absolute measures of mortality risk. That is, mortality rates and life expectancies drawn from our GSS-NDI life table differ substantially from the vital statistics data and the other SLMFs, yet the GSS-NDI hazard ratios are similar to the other SLMFs. We observe differences in hazard ratios for some variables across the SLMFs, but no SLMF consistently performs differently than the others, as was the case with the GSS-NDI in our mortality rate and life expectancy analyses. Interestingly, despite having relatively few decedents, the ACL performs very well when compared with the other datasets. As Tables 4 and 5 show, hazard ratios in the ACL are generally between those found in the GSS-NDI and the NHIS-LMF.
Table 4.
Cox proportional hazard models predicting mortality risk as a function of covariates in the NHIS-LMF, ACL, and GSS-NDI, adults ages 25 and older
| Model 1 | Model 2 | |||||
|---|---|---|---|---|---|---|
| NHIS-LMFa | ACLb | GSS-NDIc | NHIS-LMFa | ACLb | GSS-NDIc | |
| Age (years) | 1.09*** | 1.10*** | 1.06*** | 1.09*** | 1.09*** | 1.06*** |
| (1.09, 1.09) | (1.09, 1.10) | (1.06, 1.06) | (1.09, 1.09) | (1.08, 1.10) | (1.05, 1.06) | |
| Female | 0.67*** | 0.59*** | 0.75*** | 0.62*** | 0.56*** | 0.72*** |
| (0.67, 0.68) | (0.53, 0.66) | (0.71, 0.79) | (0.61, 0.62) | (0.50, 0.63) | (0.68, 0.76) | |
| Race | ||||||
| Black | 1.29*** | 1.44*** | 1.51*** | 1.13*** | 1.26** | 1.36*** |
| (1.28, 1.31) | (1.26, 1.63) | (1.39, 1.64) | (1.11, 1.15) | (1.09, 1.44) | (1.25, 1.48) | |
| Other | 0.78*** | 1.28 | 1.08 | 0 75*** | 1.17 | 1.04 |
| (0.76, 0.80) | (0.70, 2.35) | (0.92, 1.26) | (0.73, 0.77) | (0.62, 2.20) | (0.89, 1.21) | |
| Marital status | ||||||
| Previously married | 1.26*** | 1 24** | 1.18*** | |||
| (1.25, 1.28) | (1.08, 1.42) | (1.11, 1.25) | ||||
| Never married | 1.45*** | 1.19 | 1.24*** | |||
| (1.42, 1.47) | (0.87, 1.65) | (1.13, 1.37) | ||||
| Educational attainment | ||||||
| Less than high school | 1.83*** | 1.78*** | 1.59*** | |||
| (1.80, 1.86) | (1.44, 2.21) | (1.46, 1.73) | ||||
| High school | 1.51*** | 1.35** | 1.33*** | |||
| (1.49, 1.54) | (1.05, 1.74) | (1.22, 1.44) | ||||
| Some college | 1.35*** | 1.32** | 1 22*** | |||
| (1.33, 1.38) | (1.06, 1.66) | (1.11, 1.33) | ||||
Notes:
p < .10,
p < .05,
p < .001.
The table displays hazard ratios and 95% confidence intervals are in parentheses. The results are weighted. Estimates are based on individual-level analyses. The reference categories are as follows: men, white race, currently married, and college education.
National Health Interview Survey Linked Mortality File (NHIS-LMF, NHIS: 1986–2009, NDI: 1986–2011).
Americans’ Changing Lives study (ACL, ACL: 1986–2011, NDI: 1986–2011).
General Social Survey-National Death Index (GSS-NDI, GSS: 1986–2010, NDI: 1986–2011).
Table 5.
Results from Cox proportional hazard models predicting mortality risk as a function of covariates in the NHIS-LMF, HRS, ACL, and GSS-NDI, adults ages 50 years and older
| Model 1 | Model 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| NHIS-LMFa | HRSb | ACLc | GSS-NDId | NHIS-LMFa | HRSb | ACLc | GSS-NDId | |
| Age (years) | 1.09*** | 1.10*** | 1.10*** | 1.06*** | 1.08*** | 1.09*** | 1.09*** | 1.06*** |
| (1.09, 1.09) | (1.10, 1.10) | (1.09, 1.11) | (1.06, 1.07) | (1.08, 1.08) | (1.09, 1.10) | (1.08, 1.10) | (1.05, 1.06) | |
| Female | 0.68*** | 0.70*** | 0.56*** | 0.77*** | 0.63*** | 0.64*** | 0.53*** | 0.72*** |
| (0.67, 0.69) | (0.67, 0.73) | (0.50, 0.63) | (0.72, 0.82) | (0.62, 0.63) | (0.61, 0.67) | (0.47, 0.59) | (0.68, 0.78) | |
| Race | ||||||||
| Black | 1.29*** | 1.28*** | 1.30*** | 1.34*** | 1.06*** | 1.14*** | 1.15* | 1.21*** |
| (1.17, 1.21) | (1.20, 1.36) | (1.14, 1.48) | (1.21, 1.48) | (1.04, 1.08) | (1.07, 1.22) | (0.99, 1.32) | (1.09, 1.34) | |
| Other | 0.72*** | 0.95 | 1.68** | 0.96 | 0.69*** | 0.89 | 1.56* | 0.92 |
| (0.70, 0.74) | (0.83, 1.09) | (1.02, 2.75) | (0.75, 1.21) | (0.67, 0.72) | (0.77, 1.03) | (0.96, 2.54) | (0.73, 1.17) | |
| Marital status | ||||||||
| Previously married | 1.24*** | 1.27*** | 1.23** | 1.18*** | ||||
| (1.22, 1.25) | (1.20, 1.34) | (1.08, 1.41) | (1.10, 1.26) | |||||
| Never married | 1.31*** | 1.48*** | 1.36* | 1.12 | ||||
| (1.28, 1.35) | (1.31, 1.66) | (0.96, 1.91) | (0.97, 1.30) | |||||
| Educational attainment | ||||||||
| Less than high school | 1.66*** | 1.56*** | 1.58*** | 1.50*** | ||||
| (1.63, 1.68) | (1.45, 1.66) | (1.27, 1.96) | (1.35, 1.67) | |||||
| High school | 1.38*** | 1.38*** | 1.28* | 1.32*** | ||||
| (1.36, 1.41) | (1.29, 1.47) | (0.98, 1.66) | (1.19, 1.46) | |||||
| Some college | 1.28*** | 1 24*** | 1.24* | 1.18** | ||||
| (1.25, 1.30) | (1.15, 1.34) | (0.96, 1.61) | (1.05, 1.33) | |||||
Notes:
p < .10,
p < .05,
p < .001.
The table displays hazard ratios and 95% confidence intervals are in parentheses. The results are weighted. Estimates are based on individual-level analyses. The reference categories are as follows: men, white race, currently married, and college education.
National Health Interview Survey Linked Mortality File (NHIS-LMF, NHIS: 1986–2009, NDI: 1986–2011).
Health and Retirement Study (HRS, 1992–2010).
Americans’ Changing Lives study (ACL, ACL: 1986–2011, NDI: 1986–2011).
General Social Survey-National Death Index (GSS-NDI, GSS: 1986–2010, NDI: 1986–2011).
Sensitivity Analyses
We performed sensitivity tests to examine several alternative analytic approaches. First, we conducted extensive tests within each SLMF to determine the optimal specification of the baseline hazard for the mortality rates used in the life tables (results available by request). We compared observed (unsmoothed) age-specific mortality with estimated (smoothed) age-specific mortality rates. The analyses were conducted for the overall samples and did not incorporate sample weights. Overall, these analyses showed that an exponential model adheres most closely to the observed age-specific mortality rates within each dataset.
Second, we considered whether our results change if data are limited to years 1993 forward. Recall that the GSS did not request SSN (i.e., the most important PII for NDI linkage) from respondents before 1993. At the same time, SSN provision declined in the 1990s across all SLMFs due to growing concerns of identity theft. To test the robustness of our results, we examine life expectancy differences between the GSS-NDI and vital statistics and compare with the difference between NHIS-LMF and vital statistics. For this sensitivity test, we find similar patterns before 1993 versus 1993 forward. That is, GSS-NDI life expectancy estimates remain too low (by as much as three years) in early adulthood and too high (by as much as four years) in later adulthood, relative to vital statistics and other SLMFs when data are limited to years 1993 forward.
Third, we compared weighted and unweighted results to gauge the sensitivity of our results to the way in which sample weights are calculated within each SLMF. We applied sample weights in the life table and multivariate analyses so that our results from the SLMFs are generalizable to the U.S. non-institutionalized adult population. Some SLMFs, such as the NHISLMF, reweight the sample after excluding respondents without sufficient PII to undergo the NDI linkage process. In the NHIS-LMF, these respondents are deemed “ineligible” for NDI mortality follow-up and they are assigned a sample weight of zero. We examined life expectancy differences between GSS-NDI and vital statistics and compared with the difference between NHIS-LMF and vital statistics with and without weights. Substantive results from weighted and unweighted models are the same, which suggests that differences in sample weight calculations do not explain discrepancies between mortality estimates based on vital statistics data and SLMF data.
Discussion
Survey-linked mortality files increasingly are an essential source of information on the influence of various social and economic factors on adult mortality risk. This is the first study to systematically assess whether mortality estimates based on these data sources are comparable across surveys and with national mortality estimates in vital statistics data. Our study has four key findings. First, mortality rates and life expectancy estimates are similar in the NHIS-LMF, ACL, and HRS. These similarities are even more remarkable when one considers that these surveys have different sample designs (e.g., NHIS is cross-sectional, HRS is longitudinal with refreshed panels, and ACL is longitudinal with a fixed panel). Compared with the other survey-linked datasets, GSS-NDI mortality rates are much higher at younger adult ages and much lower at older adult ages. This finding is surprising because the GSS data are high-quality, nationally-representative survey data with a large sample. Since the underlying survey data are high quality, we suspect that differences in NDI match quality between the GSS-NDI and the other SLMFs examined are responsible for these discrepancies. Second, life expectancy estimates in survey-linked data are somewhat higher than in vital statistics data by about one year, likely due in part to the survey-linked datasets excluding the institutionalized population (Hummer et al. 1999). GSS-NDI is again an exception; life expectancy in the GSS-NDI is approximately three years lower at the youngest ages and four years higher at the oldest ages. Third, despite the issues with the GSS-NDI observed in our age-specific absolute mortality estimates, multivariate analyses reveal that relative estimates of mortality risk (hazard ratios) are similar across SLMFs. These results indicate that researchers should exercise caution when using the GSS-NDI and underscore the need for researchers to benchmark results from the GSS-NDI with those from other SLMFs whenever possible. Finally, our approach illustrates the importance of examining differences in absolute mortality risk (i.e., mortality rates and life expectancy) in addition to differences in relative mortality risk (e.g., hazard ratios from multivariate models) in adult mortality risk. The life tables provide critically important information about the comparability of mortality estimates across datasets that is not readily apparent in multivariate analyses.
Our findings are notable because they strongly imply that the NDI record linkage algorithm performs sub-optimally in the General Social Survey. Probabilistic record linkage depends on PII reported in both data sources, especially SSN, to correctly match respondents who died during the follow-up period to their death records (Harron et al. 2015; Rogers et al. 1997). In contrast to the ACL, NHIS, and HRS, relatively few GSS-NDI decedents have valid SSNs because the GSS did not collect SSNs before 1993 (Muennig et al. 2011). We expected to find consistently lower estimated mortality rates in the GSS-NDI than in the other datasets at all ages since few GSS-NDI respondents are matched on SSN, which would lead to many decedents not being identified (i.e., false negatives). However, we find that GSS-NDI mortality rates tend to be higher than the other data sources at younger ages and lower at older ages. We speculate that this finding is a result of relaxed matching criteria for linkage in the GSS-NDI. That is, the matching criteria are made more lenient for the GSS-NDI linkage process in order to allow more matches to be made with less PII matching between sources (Muennig et al. 2011).4 In the GSS-NDI, relaxing linkage criteria for all ages may have shifted the vital status of too many cases from survivors to deaths at younger ages but not enough cases to deaths at older ages. Future research with the restricted-use GSS-NDI should explore this possibility and, if warranted, take corrective action.
Limitations
Our analyses have several limitations. First, we cannot be entirely certain that poorer linkage quality in the GSS-NDI than in the other survey-linked datasets is the source of the unanticipated GSS-NDI mortality estimates since indicators of linkage quality (e.g., NDI match class and NDI match score) are not available in the public-use GSS-NDI. Second, we limit our analyses to variables available for all years in each of the four social surveys we compared. Thus, we are unable to statistically adjust for Hispanic ethnicity or nativity status. Additionally, educational attainment is measured in years rather than degrees, which may miscode some respondents who took more or less time to complete degrees (Rogers et al. 2010). Period differences may also exist. This is true especially in the GSS-NDI, which contains mortality records that span more than three decades (1979–2014). Future studies should examine these issues more closely. Third, we limit our analysis to four of the most commonly-used and publicly-available SLMFs. However, our analysis could be extended to include other established SLMFs, including the National Health and Nutrition Examination Survey, the National Longitudinal Mortality Study, and Panel Study of Income Dynamics, or other datasets that have recently been or will be linked to NDI, such as the National Longitudinal Study of Adolescent to Adult Health and the High School and Beyond study. Finally, we only examine all-cause mortality risk and do not conduct detailed analyses for key subpopulation groups. Results for cause-specific mortality risk or certain population subgroups may diverge more across datasets. These analyses will have less statistical power than those presented herein because they contain fewer decedents for some causes of death and/or subpopulation groups, but future research should explore these possibilities.
Recommendations
Based on our findings, we offer several recommendations for researchers using survey-linked mortality files. First, new SLMFs should be compared with existing mortality datasets before proceeding to complex statistical models. Researchers should attempt to benchmark results against multiple data sources because no single dataset is a true “gold-standard” for comparison purposes. Researchers using newly created, or even recently updated, SLMFs should compare mortality estimates from these datasets with those from other SLMFs that are more established. Ideally, researchers should also compare their results with vital statistics data, which offer several advantages over sample-based mortality data. Second, public-use survey-linked mortality files should include variables that allow researchers to assess the quality of the linkage between surveys and NDI records (e.g., match class and match score). Although the PII used to link surveys to death records contains sensitive information (SSN, names, exact birthdates, geographic identifiers, etc.), providing additional information about NDI match quality would not raise confidentiality concerns. Currently, HRS is the only widely-used SLMF that publically releases information about NDI linkage quality. Third, GSS modules, which allow researchers to append supplementary items to the core survey, could be used to explore ways to improve record linkage within the GSS and potentially inform similar efforts within other surveys. Experimental modules, for example, could be used to explore strategies to reduce item non-response on key identifiers conventionally used in the record linkage process. Adding supplementary questions to the GSS would not have immediate consequences for GSS-NDI data quality, but GSS modules could improve NDI record linkage in the future. Fourth, SLMFs linked to the NDI should include recalibrated sample weights that adjust for whether respondents are eligible for NDI follow-up. Eligibility-adjusted sample weights are available in many SLMFs including the NHIS-LMF, and other SLMFs should consider including eligibility-adjusted weights. Fifth, on a more general note, our results imply that researchers should proceed with caution in analyses that focus on relatively small subgroups within SLMFs. This is true generally, but our results imply that this is an important consideration particularly when using the GSS-NDI. Our multivariate results suggest that the GSS-NDI performs adequately relative to the other SLMFs examined in models that control for key sociodemographic and socioeconomic attributes. This may or may not be the case, however, in analyses that focus on relatively small subpopulations because it is difficult to predict how well the GSS-NDI performs. Finally, a working group of mortality researchers should be convened to discuss SLMF data quality issues and make recommendations to ensure the quality of linkages across datasets. Members should have a mix of substantive and methodological expertise and experience with SLMF data. Members should also represent multiple disciplines (demography, epidemiology, biostatistics, survey statistics, computer science, etc.).
Conclusion
Survey linked-mortality files are an increasingly important source of information on population health disparities, but few studies have examined how comparable these types of data are to each other and to vital statistics data. Prior research comparing mortality estimates between multiple SLMFs is also sparse. Our analyses address these important gaps in extant research. Overall, our results suggest that not all survey-linked mortality files are created equally. Mortality estimates based on the NHIS-LMF, HRS, and ACL are comparable to U.S. vital statistics data, but absolute mortality estimates from the GSS-NDI and vital statistics are not comparable. Differences in results between SLMFs are less apparent in multivariate hazard models that include age and other key demographic and socioeconomic controls measured at baseline. The contrast between our life table results and multivariate results is instructive because it demonstrates how multivariate analyses can obscure fundamental structural flaws in SLMF mortality estimation. Analyses examining data quality issues in SLMF mortality data must compare absolute and relative risk measures (King et al. 2012). Although we cannot be certain without detailed information on linkage quality, we suspect that the observed differences between the GSS-NDI and the other surveys arise because the NDI record linkage algorithm performs sub-optimally in the GSS-NDI due to missing personal identifiers. This means that the GSS-NDI differs from other commonly-used mortality data sources in ascertaining respondents’ vital status. We advise researchers to exercise caution when using the GSS-NDI to examine absolute U.S. adult mortality patterns. Estimates of relative mortality risk in the GSS-NDI and other major survey-linked mortality files generally are comparable in multivariate analyses when age and key sociodemographic attributes are controlled, but researchers should exercise caution in analyses that focus on relatively small sub-populations or specific age-groups.
Acknowledgements
An earlier draft of this paper was presented at the 2016 meeting of the Population Association of America meeting, Washington, DC. This research received support from NICHD Center (R24 HD041028) and NIA Training (T32 AG000221) grants to the Population Studies Center at the University of Michigan and an NIA Training (T32 AG000139) grant to the Duke Population Research Institute at Duke University. We thank the Americans’ Changing Lives working group at the University of Michigan, Audrey Dorelien, Benjamin Walker, and three anonymous PRPR reviewers for helpful comments. We also thank the Human Mortality Database, Minnesota Population Center and State Health Access Data Assistance Center, National Center for Health Statistics, and National Opinion Research Center for providing the datasets used in this analysis.
Appendix Table A. Age-specific mortality rates per 100,000 in U.S. vital statistics, NHIS-LMF, HRS, ACL, and GSS-NDI
| Vital statisticsa | NHIS-LMFb | HRSc | ACLd | GSS-NDIe | |
|---|---|---|---|---|---|
| Total | |||||
| Age 25 | 101.0 | 51.0 (47.1, 54.8) |
— | 51.0 (0.0, 138.4) |
233.7 (178.0, 289.5) |
| Age 35 | 150.7 | 119.6 (113.9, 125.4) |
— | 120.7 (27.9, 251.3) |
410.3 (337.9, 482.6) |
| Age 45 | 302.3 | 280.5 (272.0, 290.0) |
— | 285.8 (113.7, 457.6) |
720.3 (623.9, 822.2) |
| Age 55 | 693.0 | 658.2 (643.2, 673.9) |
568.7 (484.2, 659.4) |
676.8 (416.1, 953.7) |
1,264.8 (1,129.9, 1,406.7) |
| Age 65 | 1,620.2 | 1,544.2 (1,521.5, 1,566.8) |
1,395.8 (1,266.5, 1,527.3) |
1,602.5 (1,190.5, 2,092.8) |
2,220.7 (2,012.3, 2,401.3) |
| Age 75 | 3,760.0 | 3,623.0 (3,585.3, 3,663.6) |
3,425.8 (3,193.3, 3,681.5) |
3,794.0 (3,022.6, 4,590.4) |
3,898.8 (3,624.0, 4,234.0) |
| Age 85 | 10,026.8 | 8,500.2 (8,422.6, 8,581.4) |
8,408.0 (7,956.9, 8,910.0) |
8,978.5 (7,432.3, 10,777.6) |
6,843.8 (6,334.8, 7,368.2) |
| Women | |||||
| Age 25 | 53.4 | 35.3 (31.2, 39.6) |
— | 30.6 (0.0, 104.6) |
174.8 (110.4, 238.4) |
| Age 35 | 96.0 | 86.0 (79.4, 93.0) |
— | 76.6 (0.0, 210.3) |
319.0 (237.6, 405.4) |
| Age 45 | 216.4 | 209.7 (198.0, 221.1) |
— | 192.1 (0.0, 372.6) |
582.1 (466.2, 697.0) |
| Age 55 | 511.7 | 511.0 (494.7, 528.4) |
424.0 (331.7, 528.6) |
481.2 (219.0, 823.6) |
1,062.3 (895.2, 1,240.6) |
| Age 65 | 1,239.5 | 1,245.7 (1,218.9, 1,273.8) |
1,094.6 (940.1, 1,252.1) |
1,202.7 (707.6, 1,718.7) |
1,938.5 (1,712.0, 2,169.0) |
| Age 75 | 3,002.0 | 3,036.6 (2,986.5, 3,082.6) |
2,825.7 (2,558.2, 3,113.4) |
2,989.8 (2,200.9, 3,880.4) |
3,537.3 (3,166.0, 3,942.1) |
| Age 85 | 8,734.5 | 7,401.9 (7,308.8, 7,497.9) |
7,294.4 (6738.7, 7,859.3) |
7,331.6 (5,701.0, 9,047.0) |
6,453.6 (5,826.8, 7,090.6) |
| Men | |||||
| Age 25 | 147.4 | 63.6 (57.3, 70.0) |
— | 63.5 (0.0, 176.4) |
305.0 (217.6, 393.5) |
| Age 35 | 205.5 | 148.7 (139.3, 158.0) |
— | 152.4 (0.0, 356.6) |
519.8 (401.9, 651.8) |
| Age 45 | 390.3 | 347.9 (332.8, 362.1) |
— | 365.7 (121.5, 670.2) |
886.1 (727.8, 1,035.2) |
| Age 55 | 886.4 | 813.7 (791.9, 837.5) |
724.1 (597.0, 862.5) |
877.8 (450.6, 1,357.8) |
1,510.6 (1,284.1, 1,754.3) |
| Age 65 | 2,061.2 | 1,903.4 (1,867.5, 1,940.7) |
1,754.4 (1,545.6, 1,973.7) |
2,107.1 (1,405.5, 2,982.1) |
2,574.9 (2,253.0, 2,918.1) |
| Age 75 | 4,807.2 | 4,452.5 (4,387.0, 4,518.7) |
4,251.1 (3,861.7, 4,655.9) |
5,057.1 (3.718.6, 6,491.5) |
4,388.9 (3,902.8, 4,921.8) |
| Age 85 | 12,658.7 | 10,415.2 (10,274.8, 10,554.2) |
10,300.6 (9,482.3, 11,182.0) |
12,127.0 (8,942.8, 15,649.9) |
7,479.3 (6,603.8, 8,370.6) |
Vital statistics for years 1986–2010.
National Health Interview Survey Linked Mortality File (NHIS-LMF, NHIS: 1986–2009, NDI: 1986–2011).
Health and Retirement Study (HRS, 1992–2010).
Americans’ Changing Lives study (ACL, 1986–2011).
General Social Survey-National Death Index (GSS-NDI, GSS: 1986–2010, NDI: 1986–2011).
Notes: Mortality rates are based on weighted analyses. Exponential hazard models are estimated to obtain mortality rates. To construct the life tables (not shown), age-specific mortality rates are estimated for exact ages 25 to 100+ (HRS: 50−100+). The predicted mortality rates used to create the life tables are equivalent to exponentially smoothed central death rates (i.e., the mx column of a life table). Additional information about this approach is available elsewhere (Teachman and Hayward 1993). Other functional forms were considered, but exploratory analyses indicate that the exponential models fit best. The Appendix contains a table that displays the coefficients from the exponential models used to construct the life tables.
Appendix Table B. Life expectancies at selected ages in U.S. vital statistics, NHIS-LMF, HRS, ACL, and GSS-NDI
| Vital Statisticsa | NHIS-LMFb | HRSc | ACLd | GSS-NDIe | |
|---|---|---|---|---|---|
| Total | |||||
| Age 25 | 52.9 | 54.2 (54.1, 54.2) |
— | 53.7 (53.3, 54.2) |
49.5 (49.3, 49.7) |
| Age 35 | 43.5 | 44.5 (44.5, 44.6) |
— | 44.1 (43.7, 44.5) |
40.9 (40.7, 41.1) |
| Age 45 | 34.3 | 35.2 (35.2, 35.3) |
— | 34.8 (34.4, 35.2) |
32.8 (32.7, 33.0) |
| Age 55 | 25.6 | 26.5 (26.5, 26.6) |
27.1 (26.9, 27.1) |
26.1 (25.7, 26.5) |
25.5 (25.4, 25.7) |
| Age 65 | 17.9 | 18.7 (18.7, 18.7) |
19.0 (18.9, 19.1) |
18.3 (18.0, 18.6) |
19.2 (19.0, 19.3) |
| Age 75 | 11.3 | 12.2 (12.2, 12.2) |
12.3 (12.1, 12.3) |
11.8 (11.5, 12.2) |
13.9 (13.7, 14.0) |
| Age 85 | 6.2 | 7.3 (7.2, 7.3) |
7.2 (6.9, 7.2) |
7.0 (6.7, 7.2) |
9.7 (9.6, 9.9) |
| Women | |||||
| Age 25 | 55.6 | 56.4 (56.4, 56.4) |
— | 56.5 (56.1, 57.2) |
51.7 (51.5, 52.0) |
| Age 35 | 45.9 | 46.7 (46.6, 46.7) |
— | 46.8 (46.3, 47.4) |
42.8 (42.6, 43.1) |
| Age 45 | 36.5 | 37.2 (37.2, 37.2) |
— | 37.3 (36.8, 37.9) |
34.5 (34.2, 34.7) |
| Age 55 | 27.5 | 28.3 (28.2, 28.3) |
28.9 (28.7, 29.0) |
28.2 (27.9, 28.8) |
26.8 (26.6, 27.0) |
| Age 65 | 19.3 | 20.1 (20.1, 20.1) |
20.5 (20.3, 20.6) |
20.1 (19.7, 20.6) |
20.0 (19.8, 20.2) |
| Age 75 | 12.2 | 13.2 (13.2, 13.2) |
13.3 (13.2, 13.4) |
13.1 (12.7, 13.5) |
14.4 (14.2, 14.6) |
| Age 85 | 6.6 | 7.9 (7.8, 7.9) |
7.8 (7.7, 7.9) |
7.7 (7.4, 8.0) |
9.9 (9.8, 10.1) |
| Men | |||||
| Age 25 | 50.2 | 51.8 (51.7, 51.8) |
— | 50.6 (49.9, 51.3) |
47.0 (46.7, 47.7) |
| Age 35 | 40.9 | 42.2 (42.2, 42.3) |
— | 41.0 (40.4, 41.7) |
38.6 (38.3, 38.9) |
| Age 45 | 31.9 | 33.1 (33.0, 33.1) |
— | 31.9 (31.3, 32.5) |
30.9 (30.7, 31.2) |
| Age 55 | 23.5 | 24.5 (24.5, 24.6) |
25.0 (24.9, 25.2) |
23.4 (22.9, 24.0) |
24.0 (23.8, 24.3) |
| Age 65 | 16.1 | 17.0 (17.0, 17.0) |
17.3 (17.2, 17.4) |
15.9 (15.5, 16.4) |
18.0 (17.8, 18.3) |
| Age 75 | 9.9 | 10.8 (10.8, 10.9) |
11.0 (10.8, 11.1) |
9.9 (9.6, 10.4) |
13.1 (12.9, 13.3) |
| Age 85 | 5.4 | 6.3 (6.3, 6.3) |
6.3 (6.2, 6.4) |
5.6 (5.3, 6.0) |
9.2 (9.0, 9.4) |
Vital statistics for years 1986–2011.
National Health Interview Survey Linked Mortality File (NHIS-LMF, NHIS: 1986–2009, NDI: 1986–2011).
Health and Retirement Study (HRS, 1992–2010).
Americans’ Changing Lives study (ACL, 1986–2011).
General Social Survey-National Death Index (GSS-NDI, GSS: 1986–2010, NDI: 1986–2011).
Notes: Life expectancies are based on weighted analyses. To construct the life tables (not shown), age-specific mortality rates are estimated for exact ages 25 to 100+ (HRS: 50−100+). The predicted mortality rates used to create the life tables are equivalent to exponentially smoothed central death rates (i.e., the mx column of a life table). Additional information about this approach is available elsewhere (Teachman and Hayward 1993). Other functional forms were considered, but exploratory analyses indicate that the exponential models fit best. The Appendix contains a table that displays the coefficients from the exponential models used to construct the life tables.
Footnotes
We focus on potential sources of systematic bias. Sampling error will cause mortality estimates to vary between SLMFs when survey samples are different (Crimmins et al. 2004). However, sampling error should have modest effects on mortality estimate comparability because it is randomly distributed in surveys that contain large probability samples which are designed to be nationally-representative of the non-institutionalized U.S. adult population. The survey samples contained in most SLMFs, including the ones analyzed herein, meet these criteria.
Respondents’ birth month is not available publicly in the 2000–2010 GSS, but the survey contains respondents’ zodiac sign. This information is used to randomly impute missing birth months in the 2000–2010 GSS. Zodiac sign is missing when birth month is missing in the 1986–1998 GSS. Births are assumed to occur mid-year when both birth month and zodiac sign are missing.
Appendix Table A lists the mortality rates (per 100,000) at additional ages from U.S. vital statistics, NHIS-LMF, ACL, HRS, and GSS-NDI data for the women, men, and both genders combined.
Strategies that analysts can use to alter linkage criteria are described elsewhere (NCHS 2018:18).
References
- Andreev EM, and Shkolnikov VM (2010). Spreadsheet for calculation of confidence limits for any life table or healthy-life table quantity. Max Planck Institute for Demographic Research Technical Report [Google Scholar]
- Arias E, Eschbach K, Schauman WS, Backlund EL, and Sorlie PD (2010). The Hispanic mortality advantage and ethnic misclassification on U.S. death certificates. American Journal of Public Health 100(Supplement 1): S171–S177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black DA, Hsu YC, Sanders SG, Schofield LS, and Taylor LJ (2017). The Methuselah effect: The pernicious impact of unreported deaths on old-age mortality estimates. Demography 54(6): 2001–2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blewett LA, Rivera Drew JA, Griffin R, King ML, and Williams KCW (2018). IPUMS Health Surveys: National Health Interview Survey, version 6.3. Retrieved from 10.18128/D070.V6.3 [DOI]
- Brown DC, Hayward MD, Montez JK, Hummer RA, Chiu CT, and Hidajat MM (2012). The significance of education for mortality compression in the United States. Demography 49(3): 819–840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bugliari D, Campbell N, Chan C, Hayden O, Hurd M, Main R, Mallett J, McCullough C, Meijer E, Moldoff M, Pantoja P, Rohwedder S, and St. Clair P (2016). RAND HRS data documentation, version P. Santa Monica, CA: RAND Center for the Study of Aging. [Google Scholar]
- Chapman BP, Fiscella K, Kawachi I, Duberstein P, and Muennig P (2013). Emotion suppression and mortality risk over a 12-year follow-up. Journal of Psychosomatic Research 75(4): 381–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crimmins EM, Hayward MD, and Seeman TE (2004). Race/ethnicity, socioeconomic status, and health In Anderson NB, Bulatao RA, & Cohen B (Eds.), Critical perspectives on racial and ethnic differences in health in late life (pp. 310–352). Washington, DC: National Academies Press. [PubMed] [Google Scholar]
- Curb JD, Ford CE, Pressel S, Palmer M, Babcock C, and Hawkins CM (1985). Ascertainment of vital status through the National Death Index and the Social Security Administration. American Journal of Epidemiology 121(5): 754–766. [DOI] [PubMed] [Google Scholar]
- Dahlhamer JM, and Cox CS (2007). Respondent consent to link survey data with administrative records: Results from a split-ballot field test with the 2007 National Health Interview Survey Proceedings of the Federal Committee on Statistical Methodology Research Conference. Washington, DC. [Google Scholar]
- Harron K, Goldstein H, and Dibben C (Eds.). (2015). Methodological developments in data linkage. West Sussex, UK: Wiley. [Google Scholar]
- Hayward MD, and Gorman BK (2004). The long arm of childhood: The influence of earlylife social conditions on men’s mortality. Demography 41(1): 87–107. [DOI] [PubMed] [Google Scholar]
- Hogan H, Cantwell PJ, Devine J, Mule VT, and Velkoff V (2013). Quality and the 2010 Census. Population Research and Policy Review 32(5): 637–662. [Google Scholar]
- House JS (2014). Americans’ Changing Lives: Waves I, II, III, IV, and V, 1986, 1989, 1994, 2002, and 2011 [Computer file] ICPSR04690-v7. Ann Arbor, MI: Inter-university Consortium for Political and Social Research. [Google Scholar]
- Human Mortality Database. (2018). University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). www.mortality.org.
- Hummer RA, Rogers RG, Nam CB, and Ellison CG (1999). Religious involvement and U.S. adult mortality. Demography 36(2): 273–285. [PubMed] [Google Scholar]
- Ingram DD, Lochner KA, and Cox CS (2008). Mortality experience of the 1986–2000 National Health Interview Survey Linked Mortality Files participants. Hyattsville, MD: National Center for Health Statistics. [PubMed] [Google Scholar]
- Kim J, Shin HC, Rosen Z, Kang JH, Dykema J, and Muennig P (2015). Trends and correlates of consenting to provide Social Security numbers: Longitudinal findings from the General Social Survey (1993–2010). Field Methods 27(4): 348–362. [Google Scholar]
- King NB, Harper S, and Young ME (2012). Use of relative and absolute effect measures in reporting health inequalities: Structured review. BMJ 345(e5774): 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lariscy JT (2011). Differential record linkage by Hispanic ethnicity and age in linked mortality studies: Implications for the epidemiologic paradox. Journal of Aging and Health 23(8): 1263–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lariscy JT (2017). Black-white disparities in adult mortality: Implications of differential record linkage for understanding the mortality crossover. Population Research and Policy Review 36(1): 137–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lariscy JT, Hummer RA, and Hayward MD (2015). Hispanic older adult mortality in the United States: New estimates and an assessment of factors shaping the Hispanic paradox. Demography 52(1): 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence EM, Rogers RG, and Wadsworth T (2015). Happiness and longevity in the United States. Social Science and Medicine 145: 115–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Y, Muennig P, Kawachi I, and Hatzenbuehler ML (2015). Effects of racial prejudice on the health of communities: A multilevel survival analysis. American Journal of Public Health 105(11): 2349–2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morey BN, Gee GC, Muennig P, and Hatzenbuehler ML (2018). Community-level prejudice and mortality among immigrant groups. Social Science and Medicine 199: 56–66. [DOI] [PubMed] [Google Scholar]
- Muennig P, Johnson G, Kim J, Smith TW, and Rosen Z (2011). The General Social Survey-National Death Index: An innovative new dataset for the social sciences. BMC Research Notes 4(385): 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muennig P, Rosen Z, and Johnson G (2013). Do the psychosocial risks associated with television viewing increase mortality? Evidence from the 2008 General Social SurveyNational Death Index dataset. Annals of Epidemiology 23(6): 355–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muennig P, Rosen Z, Johnson G, and Smith TW (2016). Codebook for the 1978–2010 General Social Survey linked to mortality data through 12/31/2014 via the National Death Index. Retrieved from www.gssndi.com
- National Center for Health Statistics. (2018). The linkage of National Center for Health Statistics survey data to the National Death Index – 2015 Linked Mortality File (LMF): Methodology overview and analytic considerations. Hyattsville, MD: Retrieved from https://www.cdc.gov/nchs/data/datalinkage/LMF2015_Methodology_Analytic_Considerations.pdf [Google Scholar]
- National Center for Health Statistics, Office of Analysis and Epidemiology. (2009). National Health Interview Survey (1986–2004) Linked Mortality Files, mortality follow-up through 2006: Matching methodology. Hyattsville, MD: Retrieved from http://www.cdc.gov/nchs/data/datalinkage/matching_methodology_nhis_final.pdf [Google Scholar]
- National Center for Health Statistics, Office of Analysis and Epidemiology. (2013). NCHS 2011 Linked Mortality Files matching methodology. Hyattsville, MD. [Google Scholar]
- National Opionion Research Center. (2016). General Social Survey-National Death Index 1978–2010. Retrieved from http://gss.norc.org/get-the-data
- Pabayo R, Kawachi I, and Muennig P (2015). Political party affiliation, political ideology, and mortality. Journal of Epidemiology and Community Health 69(5): 423–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pablos-Méndez A (1994). Mortality among Hispanics. Journal of the American Medical Association 271(16): 1237. [PubMed] [Google Scholar]
- Palloni A, and Arias E (2004). Paradox lost: Explaining the Hispanic adult mortality advantage. Demography 41(3): 385–415. [DOI] [PubMed] [Google Scholar]
- Preston SH, Elo IT, Rosenwaike I, and Hill M (1996). African-American mortality at older ages: Results of a matching study. Demography 33(2): 193–209. [PubMed] [Google Scholar]
- Preston SH, and Taubman P (1994). Socioeconomic differences in adult mortality and health status In Martin LG & Preston SH (Eds.), Demography of aging. Washington, DC: National Academies Press. [PubMed] [Google Scholar]
- Rogers RG, Carrigan JA, and Kovar MG (1997). Comparing mortality estimates based on different administrative records. Population Research and Policy Review 16(13): 213–224. [Google Scholar]
- Rogers RG, Everett BG, Zajacova A, and Hummer RA (2010). Educational degrees and adult mortality risk in the United States. Biodemography and Social Biology 56(1): 80–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers RG, Hummer RA, and Nam CB (2000). Living and dying in the USA: Behavioral, health, and social differentials of adult mortality. San Diego, CA: Academic Press. [Google Scholar]
- Soldo BJ, Hurd MD, Rodgers WL, and Wallace RB (1997). Assets and health dynamics among the oldest old: An overview of the AHEAD study. The Journals of Gerontology Series B: Psychological Sciences and Social Sciences 52B(Special Issue): 1–20. [DOI] [PubMed] [Google Scholar]
- Sonnega A, Faul JD, Ofstedal MB, Langa KM, Phillips JWR, and Weir DR (2014). Cohort profile: The Health and Retirement Study (HRS). International Journal of Epidemiology 43(2): 576–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- StataCorp. (2013). Stata statistical software: Release 13. College Station, TX: StataCorp LP. [Google Scholar]
- Stewart QT, Cobb RJ, and Keith VM (2018). The color of death: Race, observed skin tone, and all-cause mortality in the United States. Ethnicity & Disease [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teachman JD, and Hayward MD (1993). Interpreting hazard rate models. Sociological Methods & Research 21(3): 340–371. [Google Scholar]
- Warner DF, and Hayward MD (2006). Early-life origins of the race gap in men’s mortality. Journal of Health and Social Behavior 47(3): 209–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir DR (2016). Validating mortality ascertainment in the Health and Retirement Study. Retrieved from https://hrs.isr.umich.edu/sites/default/files/biblio/Weir_mortality_ascertainment.pdf