The Roles of Transfer of Learning and Forgetting in the Persistence and Fadeout of Early Childhood Mathematics Interventions

Abstract

Although many interventions have generated immediate positive effects on mathematics achievement, these effects often diminish over time, leading to the important question of what causes fadeout and persistence of intervention effects. This study investigates how children’s forgetting contributes to fadeout and how transfer contributes to the persistence of effects of early childhood mathematics interventions. We also test whether having a sustaining classroom environment following an intervention helps mitigate forgetting and promotes new learning. Students who received the intervention we studied forgot more in the following year than students who did not, but forgetting accounted for only about one-quarter of the fadeout effect. An offsetting but small and statistically non-significant transfer effect accounted for some of the persistence of the intervention effect – approximately one-tenth of the end-of-program treatment effect and a quarter of the treatment effect one year later. These findings suggest that most of the fadeout was attributable to control-group students catching up to the treatment-group students in the year following the intervention. Finding ways to facilitate more transfer of learning in subsequent schooling could improve the persistence of early intervention effects.

Introduction

Mathematics achievement gaps between high- and low-income students are evident even before children start school and persist across the school years (Bodovski & Farkas, 2007; Clements & Sarama, 2011; Fryer & Levitt, 2006; Lee & Burkham, 2002; Reardon, 2011). This has stimulated the development of many research-based mathematics interventions targeting children who are at highest risk for persistently low mathematics achievement (e.g., Clements & Sarama, 2011; Bryant, Bryant, Gersten, Scammacca, & Chavez, 2008; Dyson, Jordan, & Glutting, 2013; Fuchs et al., 2013; Smith, Cobb, Farran, Cordray, & Munter, 2013; Starkey, Klein, & Wakeley, 2004).

Unfortunately, it is common for the promising impacts of early academic interventions to diminish or even disappear completely within a few years after the end of the intervention (e.g. Barnett, 2011; Puma et al., 2010; Smith et al., 2013). A study of the effectiveness of Building Blocks, a pre-K mathematics curriculum, showed a substantial effect on children’s mathematics achievement (g = .72) at the end of the pre-K year, but a much smaller effect two years later (g = .28 for the treatment group without follow-through intervention; g = .51 for those who received a follow-through intervention; Clements, Sarama, Spitler, Lange, & Wolfe, 2011; Clements, Sarama, Wolfe, & Spitler, 2013). These results raise important questions about the causes of fadeout and reasons for persistence. This study is the first to analyze item-level data to estimate whether treatment-control differences in forgetting play a role in the fadeout of intervention effects and how much transfer of learning in the post-treatment period may contribute to the persistence of intervention effects.

Theories of Fadeout

A commonly observed pattern in the fadeout of the effects of early childhood interventions is that students receiving an intervention lose their academic advantage because classmates who did not receive the intervention “catch up” to their skill levels in the years following the intervention (Clements et al., 2013; Smith et al., 2013). Although the children who received the intervention continue to learn after the intervention, they learn at a slower pace than the children in the control group.

One intuitively appealing reason for fadeout is that students cannot “learn” material they already know. Thus, effective interventions may be followed by instruction that is repetitive for children who received the intervention but effective for children who did not, resulting in a pattern of catch-up by the control group. However, this hypothesis has received mixed support: In a non-experimental, nationally representative dataset, the estimated effect of early childhood education on achievement has been found to be more persistent for children who attend higher quality elementary schools (Ansari & Pianta, 2018), but not in another analysis of the same dataset (Bassok, Gibbs, & Latham, 2018). In a study of the effects of a randomly assigned early math intervention, higher achieving children who received a boost from an effective early mathematics intervention did not show faster convergence to higher achieving children in the control group than lower achieving children in the treatment group did to lower-achieving control-group children (Bailey et al., 2016).

Further, a recent analysis of persistence for two effective early childhood interventions did not find differing levels of persistence for children who entered kindergarten or first-grade classrooms with more advanced levels of instruction (Jenkins et al., 2018). The somewhat inconsistent findings may reflect the different moderators of persistence tested in different studies (classroom quality, school quality, student achievement), along with other factors: the non-experimental findings likely have more variation in quality of early childhood and later schooling educational experiences, whereas the experimental studies have stronger causal identification strategies.

Catch-up implies that prior knowledge may be necessary, but not sufficient, for later learning. However, given the fundamentality of basic mathematics knowledge for later mathematics learning, this raises a difficult question: Why might students revert to their previous learning trajectories following the conclusion of a successful intervention?

Differences in Forgetting as an Explanation for Fadeout of Intervention Effects

Another possible cause of fadeout is forgetting: Although both intervention and comparison groups learn more than they forget, some or all of the fadeout effect may be caused by group differences in forgetting, with children who received the intervention forgetting more than children who did not receive the intervention. We use the term forgetting throughout this paper to refer to a heterogeneous set of faulty retrieval-based explanations, among which we cannot differentiate using these data. Two broad sets of retrieval-related explanations of greater forgetting by children who just received an effective early math intervention are: 1) the relative intensity and high rate of learning during an effective early math intervention, which provides less opportunity for full consolidation and more opportunity for interference, and 2) the mismatch between children’s contexts during and after the effective early intervention may result in newly learned information interfering with information children learned during the intervention. Children who just received an effective early math intervention may be most likely to forget what they learned in the period directly after learning, as these memories may be altered by new, related memories¹. All of these explanations involve conditions more likely to lead to forgetting: According to Wixted (2004), “What the exact variables are that govern the degree to which prior memories are degraded is not known, but one obvious possibility is that the greater and more variable the new learning is, the greater the interfering effect will be.” (p. 264).

Why might children in the treatment group forget more information than children in the control group? First, interventions generally occur during a limited period of time. Recently-formed memories are less consolidated, less stable, and more vulnerable than older memories to interfering forces of mental activity and memory formation (Wixted, 2004). Memories become more stable over time and memory retrieval consists of a dynamic process in which new information is added to and modifies the existing representation of that memory (Miller & Matzel, 2000). Therefore, children who receive an information-rich intensive intervention may subsequently be more likely to forget the material they learn during that intervention.

Additionally, if the content of the intervention differs greatly from what students are taught in a school setting, children may be most likely to forget the information they learned during this intervention. Given the rudimentary level of the mathematics content knowledge children encounter in most kindergarten classrooms (Claessens, Engel, & Curran, 2013; Engel, Claessens, & Finch, 2014), and a lack of coordination between high-quality early mathematics interventions and subsequent curricula, perhaps children will not have opportunities to link the knowledge they gained during an intervention to what is taught to them in subsequent years.

The cognitive processes of learning and forgetting are not mutually exclusive. Contrary to Thorndike’s (1914) theory that forgetting is the result of memories fading away or decaying over time, McGeoch (1932) argued that information stored in long-term memory remains there, but may become inaccessible due to one or both of two different factors: (1) reproductive inhibition, in which one loses access to previously learned skills stored in one’s memory due to interference from competing information in memory; and (2) altered stimulating conditions, in which the retrieval cues that are available to us change as our lives progress.

Refining McGeoch’s theory, Bjork’s (2011) theory of disuse argues that disuse contributes to forgetting as access to those memories become inhibited due to retrieval of competing memories. Therefore, learning actually contributes to forgetting because newly learned information and skills create potential for competition with preexisting information stored in memory (Bjork, 2011), which implies that learning and forgetting may even occur simultaneously. This leads us to hypothesize that although the students who receive an effective intervention may learn more than they would otherwise, they may also subsequently forget more.

Prior research on fadeout has not been able to measure forgetting directly. In the current study, we use data at the item level, defining forgetting as answering an item correctly at one time and answering the same item incorrectly at a later time. Although children who receive a successful early math intervention experience a net score gain in the year following the end of treatment, we hypothesize for the reasons above that both groups are also forgetting information, with more forgetting in the treatment group than in the control group.

Transfer of Learning, Fadeout, and Persistence of Intervention Effects

Although group differences in forgetting may contribute to fadeout of interventions, group differences favoring the intervention group may be counteracted by greater transfer of learning, which may increase the persistence of some intervention effects. Whereas most studies of transfer often refer to cross-domain learning (e.g. language to math), we focus in this paper on vertical transfer from more basic to more complex content within the same learning domain. Vertical transfer of learning, whereby individuals’ prior knowledge of simpler concepts and procedures are essential to acquiring new knowledge of more difficult concepts and procedures, is a key component of skill building. Vertical transfer is important in children’s mathematical development, as concepts and procedures tend to build upon previous mathematics knowledge (Baroody, 1987; Jordan, Kaplan, Locuniak, Ramineni, 2007; Lemaire & Siegler, 1995). For example, students need to understand basic addition before learning to multiply. Transfer of learning is likely in this context because most children learn multiplication problems by first solving them via repeated addition (Lemaire & Siegler, 1995). Therefore, it follows that the skills that children gain from interventions may help them develop later math skills.

Other types of transfer, such as horizontal transfer, where children see an analogy between some previously learned topic and later material and the former improves learning of the latter, may also occur in mathematics learning; the current study cannot differentiate between types of transfer. Regardless, rich conceptual interventions that help to promote transfer of learning may have positive learning outcomes for students that are not immediately recognized following the intervention. Transfer of learning could explain the persistence of some intervention effects in the years following the intervention.

Although early math skills are known to be important for later learning, it may not necessarily follow that an experimentally-induced enhancement in early math skills from the intervention will lead to substantial transfer of learning. Transfer between contexts and problems that seem very different from one another (far transfer) is less likely to occur than transfer between very similar contexts and problems (near transfer) (Perkins & Salomon, 1992). Successful transfer may require key environmental supports during the years following the intervention, including a close alignment of the intervention with subsequent curricula. But recent research has produced evidence of misalignment in the early grades (Claessens, Engel, & Curran, 2013). Estimates of the effects of early mathematics achievement on much later mathematics achievement suggest that effects are greater than zero, but quickly diminishing as the distance between earlier and later achievement increases (Bailey, Watts, Littlefield, & Geary, 2014; Bailey et al., 2018). Without such support, much of the persistent effect of a successful early mathematics intervention may be a function only of knowledge gained during the intervention, in which case catch-up is a likely consequence.

A final reason to question the possibility of ubiquitous transfer of learning following the conclusion of the intervention is that preschool children exposed to an intervention may struggle with integrating their new knowledge. To illustrate, in experimental studies that have asked children of various ages to integrate two related facts (e.g., dolphins live in groups called pods; dolphins talk by clicking and squeaking) into a single integrated fact (pods talk by clicking and squeaking), pre-K aged children struggle at this task much more than older children. For example, in two such studies, 4-year-olds self-generated integrated facts in 13% of trials, compared with 50% and 67% of trials in samples of 6-year-olds (Bauer & Larkina, 2016; Bauer & San Souci, 2010). Because transfer requires children to both understand individual concepts and integrate facts, the fact that older children are better able to integrate facts suggests that transfer may be more likely to occur for older children. If pre-K aged children struggle to integrate facts, pre-K aged children who received an effective mathematics intervention may struggle to extend this knowledge following its conclusion without clear instruction linking previous knowledge to new concepts.

Prior research on persistence has not separated post-intervention treatment effects into previously unknown material and material learned during the intervention. In the current study, we estimate transfer effects using item level data to estimate the effect of the intervention on difficult items – items that few or no children answered correctly at the end of the treatment – in the year following the end of the intervention.

Current Study

Although most research on forgetting and transfer of learning has been conducted within lab-based settings, we extend the basic research on these cognitive processes into a field setting. This study takes an innovative approach using item-level analyses to investigate the roles of the cognitive processes of forgetting and transfer of learning in the fadeout and persistence of the effects of an early childhood mathematics intervention. The TRIAD intervention included professional development to help teachers learn how to teach early childhood mathematics using Building Blocks, an early childhood mathematics curriculum. To evaluate the effectiveness of the intervention, schools with one or more preschool classrooms were randomly assigned to either a treatment group with Building Blocks or a control group in which children received regular pre-K and school instruction. The treatment group was further divided, again at random, according to whether students received a follow-through intervention after completing preschool. The follow-through group students went into kindergarten classes with teachers who received professional development to help align their mathematics instruction with the material children learned in pre-K. Thus, we will are also able to test whether having a sustaining environment following the intervention mitigated forgetting and promoted learning.

Given the relatively intensive nature of the pre-K intervention we study and its lack of alignment with regular curriculum following the intervention, we expected that some of the intervention fadeout would be explained by group differences in forgetting. However, due to the design of a pre-K mathematics intervention addressing children’s learning trajectories and the conceptually-rich curriculum, we predicted that transfer of learning would account for some of the group differences in achievement in subsequent grades.

Additionally, we assessed the mitigating effects of the follow-through treatment of the intervention, in which the follow-through group received both the pre-K treatment and subsequent instruction in kindergarten by teachers who received some instruction on how to teach in a manner more aligned with the pre-K intervention curriculum. We anticipated a mitigating effect of subsequent instruction with the pre-K mathematics intervention on group differences in forgetting for the follow-through group compared with just the treatment group. This sustaining learning environment may allow students to better retain math knowledge that will help them learn future math skills, increasing the persistence of the intervention effect. We considered the role of item difficulty in treatment effects, forgetting, and transfer of learning. We predicted that students would learn easier items more quickly than difficult ones and that students would be more likely to forget more difficult items and have less transfer on the hardest items, as children would receive less practice on these items and would have learned them more recently.

Methods

Data

Data were obtained from the Technology-enhanced, Research-based, Instruction, Assessment, and professional Development (TRIAD) evaluation study (Clements et al., 2011; Clements et al., 2013; Sarama, Clements, Wolfe, & Spitler, 2012), which evaluated the impact of the scale-up of the Building Blocks pre-K curriculum intervention. The Building Blocks pre-K curriculum was designed to take about 15 to 30 minutes of each school day, and focused on helping students develop numeric/quantitative as well as geometric/spatial skills that were thought to develop a foundation for their later mathematics achievement. For a full description of the curriculum and study procedures, see Clements & Sarama (2007a) and Clements et al. (2011).

The TRIAD evaluation utilized a randomized control trial designed to assess the effectiveness of the early mathematics curriculum, Building Blocks, in 42 low-income schools in two northeastern U.S. cities: Buffalo, New York and Boston, Massachusetts. The sample is predominantly a low-income ethnic minority sample, with 53% African-American, 22% Hispanic, 19% White, and 6% other ethnicity and 84% of the sample qualified for free and reduced price lunch, a measure of low socioeconomic status. The study involved 106 public pre-K classrooms, which were randomly assigned at the school level to one of three conditions: (1) control (standard pre-K curriculum as usual), (2) treatment (Building Blocks pre-K intervention curriculum only), and (3) follow-through (Building Blocks pre-K intervention curriculum + kindergarten curriculum aligned with the pre-K intervention curriculum and intended to provide a sustaining environment for the intervention). In the second group, the pre-K teachers received professional development in curriculum training, but the teachers in the kindergarten classrooms, fed by these Building Blocks pre-K classrooms, did not. In the third group, the pre-K teachers received training equivalent to the training in the second group, and the teachers in kindergarten classrooms fed by Building Blocks pre-K classrooms also received training on ways to build upon the knowledge gained from the intervention using learning trajectories. Teachers in the follow-through group learned about the mathematical content and common developmental progressions for several major mathematical topics, practiced connecting evidence of children’s thinking to these learning trajectories, and were encouraged to use formative assessment based on the learning trajectories. Teachers were given access to an online Building Blocks Learning Trajectories Web application and Building Blocks software activities for students. The professional development for teachers in the follow-through grades did not replace the curriculum and was much less intensive than the pre-K intervention: Teachers in the follow-through grades were provided with 32 hours of out-of-class professional development sessions, compared with 75 hours plus additional hours of in-class mentoring for pre-K teachers in the treatment groups (Clements et al., 2011, 2013). The workshops for all pre-K teachers in the Building Blocks experimental conditions (Building Blocks-NFT and Building Blocks-FT) occurred during the 2006-2007 school year.

Implementation of the intervention curriculum was assessed using the Building Blocks Fidelity of Implementation (Fidelity) and Classroom Observation of Early Mathematics-Environment and Teaching (COEMET) instruments. COEMET scores indicated a high level of fidelity. The instruments were created based on research on the characteristics and teaching strategies of effective teachers of early childhood mathematics (e.g., Clarke & Clarke, 2004; Clements & Sarama, 2007b; Fraivillig, Murphy, & Fuson, 1999; Gálvan Carlan, 2000; Horizon Research, Inc., 2001; Teaching Strategies, Inc., 2001) and were designed to assess the “deep change” that “goes beyond surface structures or procedures (such as changes in materials, classroom organization, or the addition of specific activities) to alter teachers’ beliefs, norms of social interaction, and pedagogical principles as enacted in the curriculum” (Coburn, 2003, p. 4). Prior analyses of the TRIAD data describe the fidelity instruments in greater detail and reported consistently high interrater reliability on these measures and adequate fidelity (Clements & Sarama, 2008; Clements et al., 2011).

Data from the TRIAD evaluation are well-suited for addressing issues of forgetting and trasnfer because they include responses at the item level from the same test administered at the end of treatment and after a follow-up period. Further, the treatment effect is already known to have declined across the early grades (Clements et al., 2013), making it a useful resource for studying fadeout and persistence. Because the study design was a randomized control trial, we can obtain unbiased estimates of the effect of the intervention on students’ math achievement as well as group differences in forgetting and transfer of learning in the year following the intervention. Table 1 presents descriptive statistics for the control (n=396), treatment (n=484), and follow-through (n=495) treatment condition students for the current study. Baseline equivalence was achieved as the random assignment provides groups that are similar in all observable academic and demographic characteristics, including years of mother’s education and dichotomous indicators of whether the child was male or female, had limited English proficiency, was enrolled in special education, qualified for free and reduced price lunch and race/ethnicity, with White children serving as the reference group.

Table 1.

Individual-Level Descriptive Statistics

	Treatment (N=484)		Follow-Through (N=495)		Control (N=396)
	Mean	SD	Mean	SD	Mean	SD	F-test (p-value)
Average Proportion of Assessment Questions Answered Correctly
Beginning of preK (pretest)	.0884	.0654	.0896	.0768	.0947	.0665	0.3570
End of preK (posttest)	.2449	.1066	.2479	.1053	.2107	.1056	0.0000
End of K (follow-up)	.4108	.1255	.4152	.1311	.3967	.1266	0.1114
Demographic Variables
Limited English Proficiency	0.12	0.33	0.14	0.34	0.22	0.41	0.5128
Free/Reduced Lunch (School Level)	0.82	0.38	0.82	0.38	0.88	0.32	0.3731
Special Education	0.17	0.38	0.17	0.38	0.16	0.37	0.8743
Age in Pre-K (Fall)	4.33	0.35	4.31	0.35	4.39	0.35	0.3820
Ethnicity
Black	0.52		0.59		0.48		0.7671
Hispanic	0.20		0.19		0.27		0.7618
White	0.25		0.14		0.17		0.6213
Other	0.04		0.08		0.08		0.3069
Male	0.50		0.48		0.50		0.6607
Mother’s Education
No High School	0.13		0.12		0.14		0.8445
High School	0.29		0.3		0.29		0.9945
Some College	0.36		0.34		0.31		0.5782
College/Higher	0.14		0.18		0.19		0.5842

Note. We had to drop some observations due to some students missing information on their math assessment scores, but this represented only a small proportion of our sample.

Measures

Math Achievement

Students’ math achievement was measured using a well-validated measure, which produced an overall reliability of 0.94—the Research-based Early Math Assessment (REMA: Clements, Sarama, & Liu, 2008; Clements et al., 2011). Students were assessed using the REMA at the beginning and end of preschool, as well as in the spring of kindergarten and first grade. The REMA was designed to measure young children’s (aged 3-8) math achievement, and assessed children’s number sense (counting and arithmetic) and geometry knowledge (shapes, measurement, and patterns). Trained administrators administered the test to students in one-on-one interviews that were taped and then later coded for strategies that the students used to solve math problems and for correctness of their answers. Numerous items involved the use of manipulatives in solving the item, and the test was ordered by difficulty, with each item more difficult than the last.

Due to the large number of items available in the assessment measure used and the fact that it was designed to cover material ranging over multiple grade levels, we found 27 items that no students answered correctly at either the end of pre-K or kindergarten. These items were eliminated from our analysis because they were not answered correctly by the children immediately following the intervention, not on the basis of their content. The assessments stopping rule called for the test to end after a student answered four consecutive questions incorrectly. Our analysis assumes that questions occurring after the stop rule for a given session would have been answered incorrectly. Because our study utilized item-level analysis where each question was the unit of analysis, we created a dichotomous variable that indicated whether the student answered a particular item correctly or incorrectly at each of the two time points, at the end of pre-K and at the end of kindergarten. We wanted to examine fadeout and persistence so these conditions and time points were selected because the treatment effect was previously known to have diminished during that time period (Clements et al., 2013), and because we hypothesized that post-intervention group differences in forgetting and transfer are most likely to occur in the period immediately following the intervention.

Treatment Group Assignment

With three distinct treatment assignment groups (control, treatment and no follow-through, and treatment + follow-through), we created two dichotomous indicators for membership in the second and third groups. Students in the control group thus serve as the reference group in our regression analyses.

Item Difficulty

After excluding the items that no student answered correctly at either the end of pre-K or at the end of kindergarten, we ranked the remaining items by difficulty from 1 to 132, based on the average of the proportion of control group students that answered the item correctly in pre-K and the proportion of control group students that answered the item correctly in kindergarten. We then rescaled this variable to have a range from 0 to 1 by subtracting 1 from the item’s rank and then dividing by 131. We then centered it around a mean of 0 by subtracting the average difficulty of 0.5 to represent difficulty as item difficulty compared to the average difficulty of the items. Our resulting measure of difficulty ranges from −0.5 to 0.5 and is centered on a mean of 0.

Analysis

Fadeout

We measure fadeout in the intervention as the difference between end of treatment (i.e., end of pre-K) and follow-up (i.e., end of kindergarten) impacts. For example, in logistic regressions of whether a item was answered correctly on the treatment indicator at the end of pre-K and end of kindergarten, the absence of fadeout would be indicated by identical coefficients on the treatment indicators. In contrast, if the treatment effect at the follow-up assessment at the end of kindergarten was less than that at the end of treatment in the end of pre-K, then the fadeout effect would equal the difference in the treatment effects across the two different time points. To facilitate the interpretation of treatment impacts, we converted the logit coefficients into their implied probability changes by estimating the marginal effects at the means of the independent variables using STATA’s margins command. To calculate the fadeout effect of the intervention, we subtracted the treatment effect at the follow-up from the treatment effect at the pre-K post-test to determine how much of the treatment effect disappeared within a year of the intervention.

Forgetting

We operationalized forgetting as a child answering an item correctly at the end of the pre-K post-test and then answering it incorrectly at the end of kindergarten follow-up assessment. Because item responses were mostly open-ended and not multiple choice, naÏve guessing is unlikely to yield a high rate of correct responses. We also examined moderation effects of item difficulty since the intervention may expose students to and help them learn more difficult items, but these items may be more prone to forgetting as they may not be as intuitive for, or familiar to, young children as some of the easier items.

Using logistic regression analysis with coefficients converted into marginal probability effects, we regressed whether the item was forgotten on treatment condition and other covariates to calculate the treatment-control group difference in forgetting. We then divided this difference by the fadeout effect to calculate the proportion of the total fadeout effect due to group differences in forgetting.

To address concerns about group differences in the number of items answered correctly, we further examined the role of forgetting in fadeout by checking whether the difference in forgetting across the two groups was due to the treatment group answering more questions correctly at the end of pre-K and thus having more knowledge to forget than the control group. To do this, we controlled for the number of questions that the student answered correctly at the end of pre-K post-test as a robustness check. Additionally, because students cannot forget items that they did not previously know, we restricted the analysis sample to only those cases (child-item combinations) that the child answered correctly at the end of the pre-K post-test, and reran the regression. By restricting the sample to only child-item combinations where children in all groups answered 100% of these items correctly, we can test whether children in the treatment group were more likely to forget items because they know more at the end of the treatment.

To investigate differences in the types of items that were being forgotten, we tested whether this difference was moderated by item difficulty. Perhaps students may be more prone to forgetting difficult items that may not be as intuitive as easier items for young children. Also, we wanted to explore whether the group differences in forgetting may be affected by the learning environment in the year following the intervention, particularly the effects of having a sustaining environment intended to build on the learning produced by the intervention. To determine whether a sustaining environment might reinforce children’s prior learning and mitigate the group differences in forgetting due to the treatment group’s greater amount of recently acquired knowledge, we examined whether there was a difference in the proportion of the fadeout effect due to forgetting between the Building Blocks-NFT treatment vs. control groups and the Building Blocks-FT (Building Blocks plus sustaining environment treatment) vs. control groups.

Transfer of Learning

This study also investigated whether persistence of the treatment effect could be explained by transfer of learning. As noted above, transfer refers to effects that are not immediately realized after the period of the intervention through helping students learn more difficult items after the intervention has ended. We could not simply test which group learned more in the period following the intervention; the existence of fadeout implies that the control group acquired the most knowledge during this time, hence the “catch-up” explanation usually given for the occurrence of fadeout. The treatment groups had less of an opportunity to learn easier items between the end of the intervention and the follow-up assessment, because they were more likely to know the answers to these items at the end of the intervention.

To test whether persistence of the treatment effect could be explained by transfer, we tested for group differences in learning new items. We operationalized transfer as a student’s ability to correctly answer a test item that no child in any group or few children in any group answered correctly at the pre-test or post-test. This required us to restrict our analysis to the more difficult items that few or no students answered correctly to make sure that we were not including items that were already previously learned so as not to bias our estimates, because children cannot learn something they already know. Thus, we used a range of subsets of questions in which anywhere between 0% of students in any group answered correctly at the end of pre-K and less than 50% of students in any group answered correctly at the end of pre-K, controlling for whether the child previously answered the question correctly. This range was chosen because while increasing this range would allow us to capture a larger subsample of items, the inclusion of easier items would negatively bias estimates of transfer, due to the “catching-up” of the control group. We used a range of different cutoffs with the goal of checking the robustness of our estimate of group differences in transfer to the inclusion of different types of difficult items.

For each of these subsets of items, we estimated the difference in transfer of learning between the treatment and control groups by running logistic regressions of whether an item was answered correctly at the end of kindergarten and the treatment condition and utilizing marginal effects centered at the means of the covariates to estimate the effect of the treatment on the likelihood of answering an item at the end of kindergarten follow-up assessment for these different subsets of items. To look at whether there were differences in the types of items where transfer of learning was observed, we tested whether this difference was moderated by item difficulty. Given we are already using only a subset of the more difficult items where transfer of learning may be occurring, perhaps students may show less transfer of learning on the most difficult items, as harder items are less likely to be answered correctly.

Modeling Specifications

All models were estimated in STATA 13, using logistic regression analysis. Because we used student responses to test items as the unit of analysis, and each child responded to many items, item responses were clustered within individual students. This non-independence of items his may bias standard error estimates, so all of the standard errors in our models were estimated using adjustments to account for child-level clustering using robust clustered standard errors.

Results

Treatment Effects

Estimates of basic intervention impacts at the end of the pre-K year are shown in the first column of Table 2. When compared with the control group, the average differences in the probabilities of answering a given math achievement item at the end of pre-K were .042 (p < .001) for students who would subsequently be assigned to Follow-Through condition teachers and .039 (p < .001) for student who would be assigned to regular kindergarten and first-grade classrooms. In other words, on average, an item on the REMA was about 4 percentage points more likely to be answered correctly by a student who had just finished a year in a treatment classroom than by a student just finishing a year in a control group classroom. Yet another way to interpret this effect is that students in the treatment group scored an average of 3.9 percentage points higher on math achievement than students in the control group. Although this effect may seem small, it is important to consider that none of the three groups had an average proportion of questions answered correctly at the end of pre-K above 0.25 (Table 1) and that dividing by the standard deviation of math achievement for the control group at the end of pre-K (.11), the effect size is equivalent to .37 standard deviations of math achievement for the control group at the end of pre-K (Figure 1). Although the more familiar estimated effect of Building Blocks on REMA scores is about .72 standard deviations (Clements et al., 2013), our item-level analysis differs from prior analyses of REMA’s Rasch scores. The second and third columns of Table 2 show that while correct answers were much less likely for difficult than easier items, treatment impacts did not differ significantly by question difficulty.

Table 2.

The Effect of Building Blocks Intervention Treatment on Students’ Math Achievement by Item Difficulty (end of preK)

	(1)	(2)	(3)
Building Blocks-NFT Group	.0390*** (.0068)	.0212*** (.0038)	.0210*** (.0066)
Building Blocks-FT Group	0419*** (.0066)	.0227*** (.0037)	.0252*** (.0066)
Question Difficulty		−.5175*** (.0196)	−.5201*** (.0212)
Building Blocks-NFT * Difficulty			−.0012 (.0176)
Building Blocks-FT * Difficulty			.0102 (.0176)
N	170698	170698	170698
Pseudo R2	.002	.520	.520

Note. Analyses were done on item-level data, so each observation is a child-item combination, hence why the N is much larger than the number of students in the dataset. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for the nonindependence of observations for any given child.

^*p<0.05

^**p<0.01

^***p<0.001

Figure 1. Summary of Treatment, Forgetting, and Transfer of Learning Effects by Treatment Group (as compared with the Control Group).

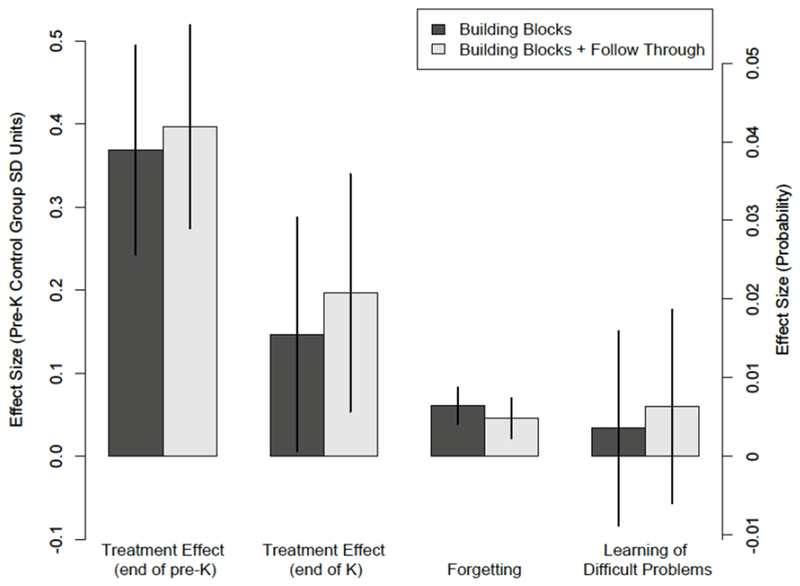
Note. The bars are differences in the outcomes between the respective treatment group and the control group, with 95% confidence intervals shown. The left vertical axis shows the units in terms of the pre-K control group standard deviation units, while the right vertical axis shows the units in terms of probability differences. The last group uses only a subset of the data (only items that fewer than 10% of students from the end of pre-K had answered correctly from any treatment assignment group) and shows transfer of learning for the Building Blocks treatment group (Building Block-NFT) and differences in the learning of difficult problems between the Building Blocks + Follow Through group (Building Blocks-FT) and the control group.

By the end of kindergarten, and in the absence of assignment to the Follow-Through condition, the treatment effect decreased to .016 ($\widehat{\beta }$ = .016, p = .042), which was 40% of the initial intervention effect (first column of Table 3 and Figure 1). This means that a year following the intervention, a student who was initially in the treatment group in pre-K was only 1.6 percentage points more likely to answer an item on the REMA correctly than a student in the control group. This translates to an effect size of .15 standard deviations of math achievement for children in the control group at the end of pre-K.

Table 3.

The Remaining Effect of Building Blocks Intervention at the end of Kindergarten on Students’ Math Achievement by Item Difficulty

	(1)	(2)	(3)
Building Blocks-NFT Group	.0155* (.0076)	.0301* (.0149)	.0302 (.0179)
Building Blocks-FT Group	.0208** (.0077)	.0406** (.0151)	.0436* (.0181)
Question Difficulty		−1.9091*** (.0313)	−1.9191*** (.0451)
Building Blocks-NFT * Difficulty			−.0008 (.0580)
Building Blocks-FT * Difficulty			.0296 (.0573)
N	160933	160933	160933
Pseudo R2	.000	.551	.551

Note. Analyses were done on item-level data, so each observation is a child-item combination, hence why the N is much larger than the number of students in the dataset. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for the nonindependence of observations for any given child.

^*p<0.05

^**p<0.01

^***p<0.001

Impact estimates also declined for the Building Blocks-FT children, who received both the pre-K intervention and a sustaining environment in Kindergarten, but to a smaller degree than for children in the NFT group (first column of Table 3 and Figure 1) – from 4.2 percentage points to 2.1 percentage points. These are equivalent to a decline from .40 to .20 standard deviations of math achievement. These patterns are consistent with those found in the Clements et al. (2013) analysis of aggregated math scores. As shown in the second and third columns of Table 3, impact estimates did not vary systematically with question difficulty.

Fadeout/Persistence of Effects

We calculated the size of the fadeout effect from pre-K to kindergarten for the Building Blocks-NFT group by subtracting the remaining treatment effect at the end of kindergarten in Table 3 ($\widehat{\beta }$ = .016) from the initial treatment effect from the end of pre-K in Table 2 ($\widehat{\beta }$ = .039), yielding an estimated fadeout effect size of .024. Dividing the size of the fadeout effect (.024) by the initial treatment effect at the end of pre-K ($\widehat{\beta }$ = .039) indicates that about 60% of the treatment effect dissipated a year after the intervention for the Building Blocks-NFT.

The fadeout effect for the Building Blocks-FT group was slightly smaller than that of the Building Blocks-NFT group. Subtracting the remaining treatment effect at the end of kindergarten from Table 3 ($\widehat{\beta }$ = .021) from the initial treatment effect from the end of pre-K from Table 2 ($\widehat{\beta }$ = .042) produced an estimated fadeout effect size of .021. Dividing the size of the fadeout effect (.021) by the initial treatment effect at the end of pre-K ($\widehat{\beta }$ = .042) indicated that about 50% of the treatment effect dissipated a year after the intervention for Building Blocks-FT group.

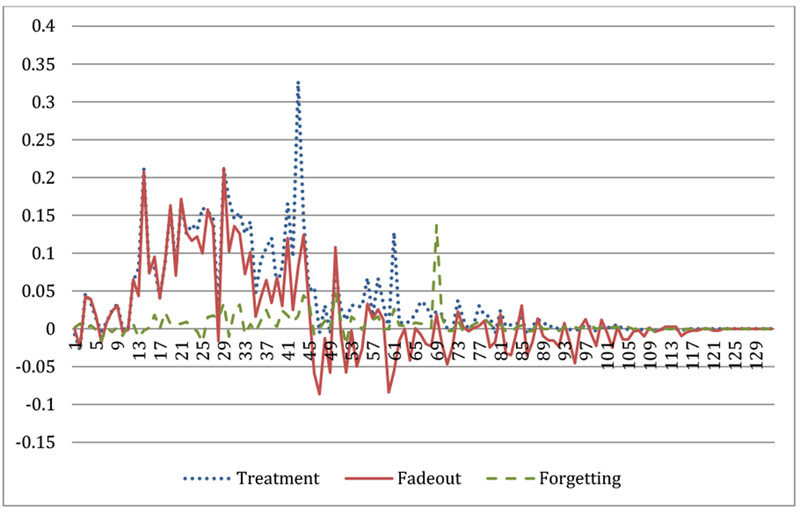
A visual representation of the different effect sizes by item difficulty seems to support the hypothesis that most of the fadeout is due to catch-up of the control group on easier items (Figures 2 and 3). These plots are generated using lowess, a locally weighted scatterplot smoothing function, in STATA. The largest fadeout effects occurred for the easier items, where the control group may partially or fully catch-up to the treatment group. This is indicated by the almost overlapping treatment and fadeout effect curves for the items with lower difficulty levels. The smaller proportion of fadeout compared with the initial treatment effect for the Building Blocks-FT group is indicated by the slightly larger gap between the initial treatment effect and the fadeout effect in Figure 3 compared with the gap between the initial treatment effect and the fadeout effect in Figure 2. More detailed plots of the comparison of these effects sizes by item difficulty are provided in the appendix (Appendix, Figures S1–S2).

Figure 2. Differences in Effect Sizes Between Control and Building Blocks-NFT Group by Item Difficulty.

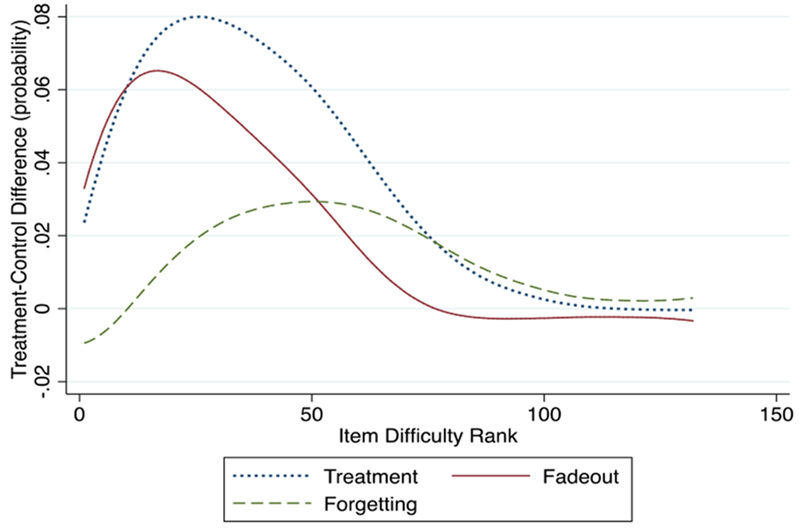
Note. Figure was created using a lowess smoothing function.

Figure 3. Differences in Effect Sizes Between Control and Building Blocks-FT Group by Item Difficulty.

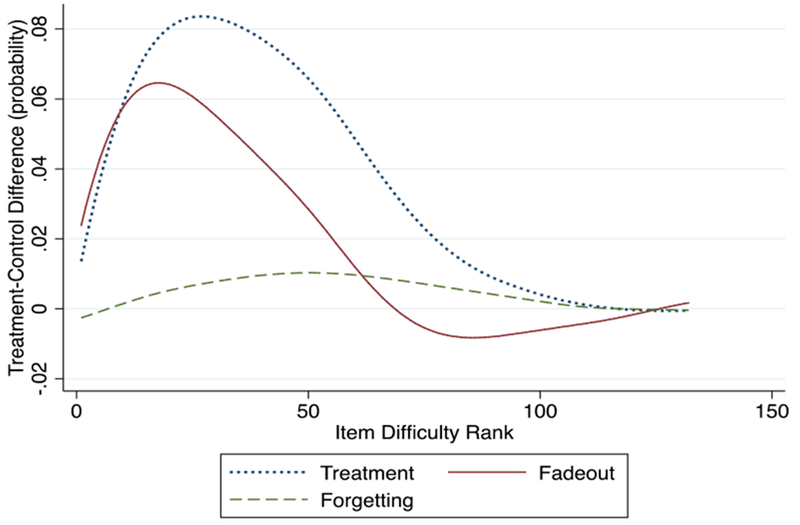
Note. Figure was created using a lowess smoothing function.

Forgetting

As described above, we operationalized forgetting as a child answering an item correctly at the end of the pre-K post-test but incorrectly at the end of kindergarten follow-up assessment. Table 4 shows a .0064 treatment-control group difference in forgetting ($\widehat{\beta }$ = .006, p < .001). This indicates that, on average, the treatment group was .64 percentage points more likely to forget an item than the control group. Dividing the group differences in forgetting between the treatment and control groups (.006) by the fadeout effect (.024) shows that the group difference in forgetting was 27% of the size of the fadeout effect of Building Blocks from the end of pre-K to kindergarten. Students were more likely to forget more difficult items than easier items (Figure 2). In particular, students who received the treatment forgot fewer of the easiest items than students who did not receive the intervention, but forgot relatively more of the more difficult items but not the most difficult items as shown by the curvilinear relationships between forgetting and item difficulty.

Table 4.

The Effect of Building Blocks Intervention Treatment on Forgetting Math Knowledge by Item Difficulty

	Overall Items	Items Correct in preK (Models 2-4)
	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0064*** (.0012)	.0130** (.0047)	.0029 (.0044)	.0030 (.0111)
Building Blocks-FT Group	.0049*** (.0013)	.0058 (.0049)	−.0046 (.0047)	−.0152 (.0111)
Question Difficulty			.3893*** (.0146)	.4073*** (.0297)
Building Blocks-NFT * Difficulty				.0015** (.0363)
Building Blocks-FT * Difficulty				−.0477 (.0367)
N	160585	38283	38283	38283
R2	.002	.001	.180	.181

Note. Analyses were done on item-level data, so each observation is a child-item combination, hence why the N is much larger than the number of students in the dataset. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for the nonindependence of observations for any given child. The regression in Model 1 utilized the overall dataset, while the regressions in Models 2-4 utilized only the subset of data in which the item was answered correctly in preK.

^*p<0.05

^**p<0.01

^***p<0.001

In the case of the Building Blocks-FT group (Table 4), there was a .0049 Building Blocks-FT-control group difference in forgetting ($\widehat{\beta }$ = .005, p < .001). This indicates that, on average, the treatment group was .49 percentage points more likely to forget an item than the control group. We then divided the group differences in forgetting between the follow-through and control groups (.005) by the fadeout effect (.021), finding that the group differences in forgetting account for 23% of the size of the fadeout effect. Figure 3 provides a summary of the trend in the differences in forgetting between the follow-through and the control groups. While most of the fadeout of the treatment effect occurred over the easier items, students seemed to be forgetting more difficult items, but not the most difficult items.

Comparing the forgetting effects for the Building Blocks-FT group to those of the Building Blocks-NFT treatment group to determine whether there was a mitigating effect of having a sustaining environment on forgetting, the Building Blocks-FT group appears to have forgotten fewer items a year after the pre-K intervention than the Building Blocks-NFT treatment group (Table 4). However, while both effects were statistically significant (Table 4), they were not statistically significantly different from each other (χ²(1) = 1.83, p = 0.18). Still, the magnitude of the size of the group differences in forgetting between the Building Blocks-FT and the control groups were about half the size of that between the Building Blocks-NFT and control groups. A visual comparison of the forgetting curve in Figure 2 to that in Figure 3 also suggested a mitigating effect of the sustaining environment as Figure 3 has a flatter forgetting curve. This indicates that for the items in which many of the Building Blocks treatment group forgot, these items were forgotten less by students in the follow-through group. These analyses provided limited evidence for a mitigating effect of having a sustaining environment after an intervention on forgetting, although the study was not well-powered to detect such a difference.

Transfer of Learning

We estimated end of kindergarten treatment effects on subsets of difficult items, ranging from those that no student in any group answered correctly at the end of pre-K to those that less than 50% of students from each group answered correctly at the end of pre-K. We present a representative set of results, based on the subset of questions in which less than 10% of students from any treatment group answered correctly at the end of pre-K in Table 5, and present the results for all other subsets of items we considered in the appendix (Appendix B, Tables T1–T5).

Table 5.

The Effect of Building Blocks Intervention Treatment on Transfer of Math Knowledge by Item Difficulty (subset 10% preK correct)

	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0096 (.0074)	.0036 (.0063)	.00625 (.0029)	.0021 (.0027)
Building Blocks-FT Group	.0131 (.0075)	.0063 (.0063)	.0039 (.0029)	.0030 (.0027)
Item Answered Correctly in preK		2419*** (.0091)	.0646*** (.0063)	.0644*** (.0063)
Question Difficulty			−.2909*** (.0150)	−.3002*** (.0197)
Building Blocks-NFT * Difficulty				.0090 (.0189)
Building Blocks-FT * Difficulty				.0187 (.0163)
N	90132	88999	88999	88999
Pseudo R2	.001	.051	.281	.281

Note. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for different variances across different individuals.

^*p<0.05

^**p<0.01

^***p<0.001

After controlling for whether the item was answered correctly by the student, the treatment effect on the probability of answering one of these items at the end of kindergarten was estimated to be .004 (p = .57; Table 5).

Although this difference in transfer of learning does not appear to be very large, dividing by the remaining treatment effect at the end of kindergarten from Table 3 ($\widehat{\beta }$ = .016) indicates that transfer of learning accounts for approximately 23% of the remaining treatment effect a year after the intervention. However, comparing the effect on transfer to the initial treatment of the Building Blocks intervention in Table 2 ($\widehat{\beta }$ = .039), the ratio of transfer to the initial intervention impact is small (approximately 9%), as shown in Figure 1.

In the follow-through group, there is a difference of .006 (p = .3 17) between the Building Blocks-FT and control groups of answering a mathematics question at the end of kindergarten that less than 10% of students from each group answered correctly at the end of pre-K (Table 5). Dividing this effect by the remaining treatment effect at the end of kindergarten from Table 3 ($\widehat{\beta }$ = .021, p = .007) indicates that learning new difficult items accounts for approximately 30% of the remaining treatment effect a year after the intervention. However, comparing the effect on new learning to the initial treatment of the Building Blocks intervention in Table 2 ($\widehat{\beta }$ = .042, p < .001), the ratio of learning new items to the initial intervention impacts is only about 15% (Figure 1). For the Building Blocks-FT group, we cannot attribute an impact on learning more difficult items to transfer alone, as the new learning effect is a combination of learning new items due to the follow-through treatment and transfer of learning.

New item learning in the Building Blocks-NFT treatment group and the Building Blocks-FT group did not differ significantly different from new item learning in the control group (Table 5), nor were the treatment groups significantly different from each other (χ²(1) = 0.21, p = 0.64).

Robustness checks using different subsets of items, ranging from those that no student in any group answered correctly at the end of pre-K to those that less than 50% of students from each group answered correctly at the end of pre-K, shown in the appendix (Appendix B, Tables T1–T5) show similar results. Transfer effects for the Building Blocks-NFT intervention group range from 0.004 to 0.005 and transfer and learning of new material effects for the follow-through group range from 0.004 to 0.011. None of these effects was statistically significant.

Discussion

Using item-level analyses, we estimated the contributions of forgetting and transfer of learning to the fadeout and persistence of the effects of an early childhood mathematics intervention. Although students from all experimental conditions showed overall growth in their math achievement from the end of pre-K to the end of kindergarten, students from the treatment groups were more likely to forget previously learned math knowledge during this period. This is consistent with the idea that the mathematics knowledge of students who received the intervention may be more fragile due to learning a lot of material quickly in a relatively short period of time.

Students who received the intervention received much more information concentrated within that preschool year than students who did not receive the intervention. Perhaps as a result, students who received the Building Blocks intervention forgot more math items in the year following the intervention than students who did not receive the intervention, even after controlling for the number of questions they had previously answered correctly. The group difference in forgetting accounted for a small but significant proportion of the fadeout effect, only about 23% of the overall fadeout of the intervention effects, while the rest of the fadeout was mostly attributable to catch-up by the control group.

The skills gained from Building Blocks may have supported transfer of learning and learning of more new difficult items in the year following the intervention. Differences in transfer of learning between students who received the Building Blocks intervention and students who did not receive the intervention were not statistically significant. The magnitude of the effect size was about a quarter of the size of the remaining treatment effect a year following the intervention, but was almost exactly offset by the treatment-control differences in forgetting. This suggests that the intervention may have helped students learn more material in the years following the intervention, but this effect is small, which is consistent with the idea that younger children may have more difficulty integrating facts (especially given the routine mathematics curricula and teaching that constitute most U.S. kindergarten classes) and transferring learning to new types of problems in the period following the treatment.

Limitations and Future Directions

Comparisons between the Building Blocks-NFT and Building Blocks-FT groups found differences in forgetting and promoting new learning favoring the Building Blocks-FT group, but neither was statistically significant, and the patterns of effects relative to the control group were similar for both groups. These findings are consistent with previous studies of the effects of the TRIAD intervention’s follow-through condition (Sarama & Clements, 2015). Unfortunately, the current study could not estimate group differences due to transfer of learning on easier items, as performance on easier items was likely affected both by catch-up in the control group and transfer of learning in both groups. This limited our study to only looking at the effects of differences in the transfer of learning on more difficult items that only a small percentage of students answered correctly at the end of pre-K. However, robustness checks indicate that these effects were generally consistent across the different subsets of difficult items used in analyzing the effect of transfer (Appendix B, Tables T1–T5).

A more precise estimate of the contribution of transfer of learning to impact persistence might have been possible for an intervention with a larger follow-up treatment effect. But since treatment effects in the TRIAD intervention were quite large compared with typical post-test and one-year follow-up treatment effects in early childhood studies (Li et al., 2017), this may be difficult to obtain. Still, while the difference in the transfer of learning between students who received the intervention and those who did not was not statistically significant, we did get some sense of its magnitude relative to other important effects. The difference was large enough to explain about a quarter of the remaining treatment effect in the year following the intervention, yet it was approximately the same size as the treatment-control difference in forgetting. Thus, for interventionists, our findings pertaining to transfer are both pessimistic and optimistic. These mixed interpretations, along with the imprecision of our estimates, indicate a need for more research into not only the effects of transfer of learning from interventions but also the types of knowledge that contribute to the remaining intervention effects.

A limitation of this study is that we only studied the effects of a pre-K intervention. These results may not generalize to different grade levels, as students in higher grade levels may be better able to transfer knowledge because they are better able to integrate facts (Bauer & Larkina, 2016; Bauer & San Souci, 2010).

A potential moderator is the type of intervention examined. Because most studies do not utilize item-level analyses, we can only speculate about the generalizability of these results to other kinds of interventions. There are some reasons to hypothesize that these findings would hold for other kinds of interventions targeting children around the same age. First, in meta-analyses of the impacts of early childhood interventions, declining treatment impacts are found for different types of outcome measures (e.g., tests of achievement in different domains, tests of fluid intelligence; Li et al., 2017; Protzko, 2015), so fadeout is not a phenomenon unique to only early mathematics interventions. Additionally, factors that might lead one to predict that forgetting would be a significant problem, such as teaching children information in a very short time or in a way devoid of meaning do not appear to be at high levels in this study. The Building Blocks curriculum, that lasted an entire school year, was theoretically informed by children’s learning trajectories, and the instruction was designed to build on what children already know (Clements & Sarama, 2011; Clements et al., 2011; Clements et al., 2013). However, whether these effects would generalize over to other interventions, contexts, topic/content areas, and children is still an empirical question that warrants further investigation.

In addition, the math achievement test used in the study (REMA) was somewhat aligned with the Building Blocks curriculum. An advantage of this is that growth in the treatment groups during the treatment interval are likely attributable in great part to the curriculum. However, the extent to which forgetting and transfer findings might generalize to different tests is not clear: The magnitude of the transfer effect in the post-treatment period may be smaller on other tests (if the testing material is even more distal to the curriculum), but it may be a higher percentage of the initial treatment effect (which may be smaller on a test less aligned with the curriculum). Forgetting could be less likely on other tests if the distal material is not directly taught in the treatment curriculum, but it is not clear whether or how the magnitude of the forgetting effect as a fraction of the initial treatment effect would differ. These hypotheses are speculative and are important to address in future research, which should also include assessments that are less closely aligned with the curriculum.

Another limitation was the lack of power to detect statistically significant effects. While the initial treatment effects are highly statistically significant, the remaining treatment effects in the year following the intervention are smaller; given that forgetting effects are likely to be smaller than the total fadeout effect and that transfer effects are likely to be smaller than the treatment effect at the follow-up interval, our estimates are likely to be noisy. The transfer analyses are based on fewer items (only the difficult ones), so estimates are less precise and are not significantly different from zero. Although the data allow for examining whether there were differential intervention impacts by math domain, we were unable to do so as the study was underpowered to detect the overall transfer and forgetting effects. Further research may determine whether intervention impacts and differences in forgetting and transfer of learning may differ by math domain.

Here we speculate about the implications of our emerging understanding of fadeout and persistence for educational practice. In the short-term, a deeper understanding of these phenomena and their boundary conditions would be valuable. In the intermediate term, possible outcomes that may lead to greater treatment effect persistence include larger initial intervention effects, mitigating forgetting of learned material and improving the potential for transfer in the years following the intervention by increasing the alignment between pre-k and kindergarten mathematics curricula and teaching (Bailey, Duncan, Odgers, & Yu, 2017; Bobis, 2011; Stipek, Franke, Clements, Farran, & Coburn, 2017). Additionally, designers of early interventions might make more use of insights from cognitive science on how to mitigate forgetting, such as ideally spaced retrieval practice (Cepeda, Vul, Rohrer, Wixted, & Pashler, 2008) and interleaving problems of different types to give children practice in selecting the correct strategy for solving varied problems (Braithwaite, Pyke, & Siegler, 2017; Patel, Liu, & Koedinger, Rohrer & Taylor, 2007). On the other hand, perhaps some amount of forgetting is adaptive, to the extent it facilitates strengthening core, generalizable knowledge (Robertson, 2018). Tests of these possibilities in real-world educational settings with long-term follow-up assessments may yield important practical and theoretical insights. Finally, to the extent that transfer of learning is unlikely to be affected by interventions in the very long term, identifying and targeting skills that children are not likely to learn in the absence of intervention may be a useful approach.

The present study suggests that delving into the causes of fadeout and persistence of the effects of early childhood interventions might provide useful information. Further studies using item-level analyses may help identify other contributing factors or even give a better idea of the processes that are occurring to help explain fadeout and promote persistence of effects.

Educational Impact and Implications Statement.

Positive effects of early childhood interventions on students’ achievement often fade out during the years following the intervention. This study investigates whether fadeout can be attributed to differences between children in the treatment and control group in forgetting previously learned content and whether transfer of learning contributes to the persistence of these intervention effects. We find that differences in forgetting account for some of the fadeout effect, but much of fadeout is still due to catch-up of the control group. Differences in transfer of learning account for only a small and statistically non-significant amount of the persistent effect of the intervention one year later. Our study implies that incorporating strategies for retention in order to mitigate forgetting may prove beneficial in prolonging intervention effects.

Figure S1.

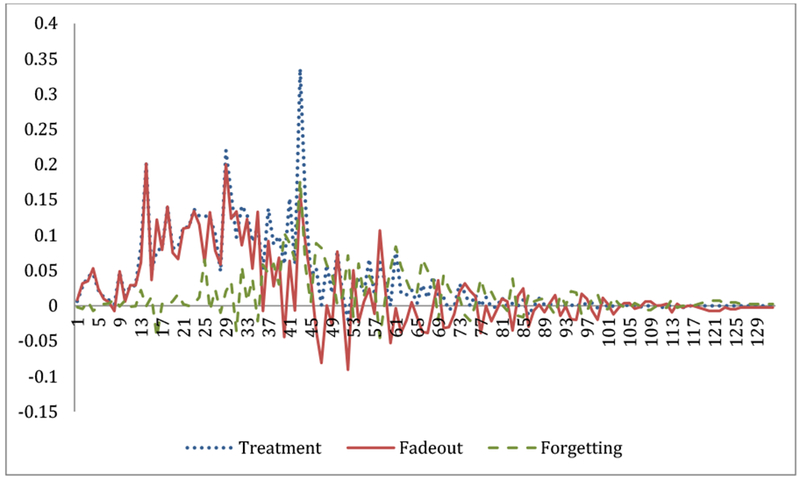
Comparison of Effect Sizes Across Control and Building Blocks-NFT Groups by Item Difficulty

Figure S2.

Comparison of Effect Sizes Across Control and Building Blocks-FT Groups by Item Difficulty

Table F1.

The Effect of Building Blocks Intervention Treatment on Forgetting Math Knowledge by Item Difficulty Controlling for Total Number of Items Correct at End of pre-K

	Overall Items	Items Correct in preK (Models 2-4)
	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0045*** (.0011)	.0149** (.0047)	.0089** (.0028)	.0077 (.0057)
Building Blocks-FT Group	.0029* (.0012)	.0078 (.0050)	.0029 (.0030)	−.0065 (.0058)
# Questions Correct at End of preK assessment	.0005*** (.0000)	−.0007*** (.0002)	−.0034*** (.0002)	−.0034*** (.0002)
Question Difficulty			.4169*** (.0128)	.4345*** (.0204)
Building Blocks-NFT * Difficulty				−.0044 (.0214)
Building Blocks-FT * Difficulty				−.0417 (.0224)
N	160585	38283	38283	38283
R2	.010	.002	.238	.238

Note. Analyses were done on item-level data, so each observation is a child-item combination, hence why the N is much larger than the number of students in the dataset. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for the non-independence of observations for any given child. The regression in Model 1 utilized the overall dataset, while the regressions in Models 2-4 utilized only the subset of data in which the item was answered correctly in preK.

^*p<0.05

^**p<0.01

^***p<0.001

Table T1.

The Effect of Building Blocks Intervention Treatment on Transferring Math Knowledge by Item Difficulty (subset 0% preK correct)

	(1)	(2)	(3)
Building Blocks-NFT Group	.0046 (.0025)	.0007 (.0006)	.0006 (.0003)
Building Blocks-FT Group	.0044* (.0019)	.0007 (.0004)	.0007* (.0003)
Question Difficulty		−.0292*** (.0086)	−.0280*** (.0069)
Building Blocks-NFT * Difficulty			.0048 (.0036)
Building Blocks-FT * Difficulty			.0006 (.0023)
N	28014	28014	28014
Pseudo R2	.001	.600	.602

Note. To estimate transfer of learning, we used a small subset of data (child-item combinations) that only contained difficult questions that none of the students in any treatment assignment group answered correctly at the end of preK. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for different variances across different individuals.

^*p<0.05

^**p<0.01

^***p<0.001

Table T2.

The Effect of Building Blocks Intervention Treatment on Transferring Math Knowledge by Item Difficulty (subset 20% preK correct)

	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0116 (.0084)	.0039 (.0071)	.0033 (.0037)	.0032 (.0037)
Building Blocks-FT Group	.0170* (.0085)	.0089 (.0071)	.0061 (.0038)	.0059 (.0037)
Item Answered Correctly in preK		.3126*** (.0086)	.0759*** (.0068)	.0758*** (.0068)
Question Difficulty			−.4047*** (.0174)	−.4133*** (.0225)
Building Blocks-NFT * Difficulty				.0100 (.0214)
Building Blocks-FT * Difficulty				.0155 (.0196)
N	100033	98830	98830	98830
Pseudo R2	.001	.067	.318	.318

Note. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for different variances across different individuals.

^*p<0.05

^**p<0.01

^***p<0.001

Table T3.

The Effect of Building Blocks Intervention Treatment on Transferring Math Knowledge by Item Difficulty (subset 30% preK correct)

	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0136 (.0086)	.0051 (.0073)	.0047 (.0043)	.0048 (.0044)
Building Blocks-FT Group	.0201* (.0087)	.0112 (.0073)	.0085 (.0044)	.0085 (.0044)
Item Answered Correctly in preK		.3206*** (.0076)	.0754*** (.0064)	.0753*** (.0063)
Question Difficulty			−.4775*** (.0178)	−.4841*** (.0231)
Building Blocks-NFT * Difficulty				.0066 (.0232)
Building Blocks-FT * Difficulty				.0129 (.0214)
N	106123	104920	104920	104920
Pseudo R2	.001	.074	.317	.317

Note. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for different variances across different individuals.

^*p<0.05

^**p<0.01

^***p<0.001

Table T4.

The Effect of Building Blocks Intervention Treatment on Transferring Math Knowledge by Item Difficulty (subset 40% preK correct)

	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0169 (.0089)	.0048 (.0075)	.0073 (.0054)	.0072 (.0058)
Building Blocks-FT Group	.0220* (.0091)	.0090 (.0076)	.0107 (.0055)	.0112 (.0058)
Item Answered Correctly in preK		.4067*** (.0073)	.0943*** (.0069)	.0942*** (.0069)
Question Difficulty			−.6156*** (.0197)	−.6197*** (.0254)
Building Blocks-NFT * Difficulty				−.0045 (.0260)
Building Blocks-FT * Difficulty				.0168 (.0241)
N	114649	113446	113446	113446
Pseudo R2	.001	.101	.366	.366

Note. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for different variances across different individuals.

^*p<0.05

^**p<0.01

^***p<0.001

Table T5.

The Effect of Building Blocks Intervention Treatment on Transferring Math Knowledge by Item Difficulty (subset 50% preK correct)

	(1)	(2)	(3)	(4)
Building Blocks-NFT Group	.0173 (.0090)	.0022 (.0075)	.0078 (.0061)	.0080 (.0067)
Building Blocks-FT Group	.0222* (.0092)	.0057 (.0076)	.0114 (.0062)	.0125 (.0067)
Item Answered Correctly in preK		.4534*** (.0072)	.1069*** (.0073)	.1068*** (.0073)
Question Difficulty			−.7002*** (.0207)	−.7097*** (.0269)
Building Blocks-NFT * Difficulty				.0028 (.0283)
Building Blocks-FT * Difficulty				.0253 (.0266)
N	119521	118318	118318	118318
Pseudo R2	.000	.118	.387	.387

Note. Coefficients are probabilities predicted from logistic regression marginal effects, with the margins estimated at the means of the covariates. Standard errors (in parentheses) were clustered by child to account for different variances across different individuals.

^*p<0.05

^**p<0.01

^***p<0.001