Cell membranes resist flow

SUMMARY

The fluid-mosaic model posits a liquid-like plasma membrane, which can flow in response to tension gradients. It is widely assumed that membrane flow transmits local changes in membrane tension across the cell in milliseconds, mediating long-range signaling. Here we show that propagation of membrane tension occurs quickly in cell-attached blebs, but is largely suppressed in intact cells. The failure of tension to propagate in cells is explained by a fluid dynamical model that incorporates the flow resistance from cytoskeleton-bound transmembrane proteins. Perturbations to tension propagate diffusively, with a diffusion coefficient D_σ ~ 0.024 μm²/s in HeLa cells. In primary endothelial cells, local increases in membrane tension lead only to local activation of mechanosensitive ion channels and to local vesicle fusion. Thus membrane tension is not a mediator of long-range intra-cellular signaling, but local variations in tension mediate distinct processes in sub-cellular domains.

INTRODUCTION

Membrane tension affects cell migration (Gauthier et al., 2011; Houk et al., 2012; Keren et al., 2008; Mueller et al., 2017), vesicle fusion and recycling (Boulant et al., 2011; Gauthier et al., 2011; Maritzen and Haucke, 2017; Masters et al., 2013; Shillcock and Lipowsky, 2005; Shin et al., 2018; Thottacherry et al., 2017; Wen et al., 2016), the cell cycle (Stewart et al., 2011), cell signaling (Basu et al., 2016; Groves and Kuriyan, 2010; Houk et al., 2012; Huse, 2017; Romer et al., 2007), and mechanosensation (He et al., 2018; Phillips et al., 2009; Ranade et al., 2015). However, there has been controversy over the speed and degree to which localized changes in membrane tension propagate in cells (Diz-Muñoz et al., 2013). In artificial lipid bilayers, changes in membrane tension propagate across a cell-sized region in milliseconds (Fig. S1) (Shi and Baumgart, 2015). Fluorescently tagged transmembrane proteins typically diffuse freely in both artificial bilayers and in intact cells, albeit with a 10-100 fold lower diffusion coefficient in cells (Kusumi et al., 2005). Together these results, each consistent with the fluid mosaic model (Singer and Nicolson, 1972), led to the widespread belief that two-dimensional (2D) flow of lipids in cells mediates rapid intracellular equilibration of membrane tension (Basu et al., 2016; Diz-Muñoz et al., 2013; Fogelson and Mogilner, 2014; Gauthier et al., 2012; Gauthier et al., 2011; Houk et al., 2012; Huse, 2017; Keren et al., 2008; Keren, 2011; Kozlov and Mogilner, 2007; Lieber et al., 2015; Morris and Homann, 2001; Mueller et al., 2017; Mueller et al., 2017; Ofer et al., 2011; Pontes et al., 2017; Saha et al., 2018; Schweitzer et al., 2014; Sens and Plastino, 2015; Watanabe et al., 2013; Winkler et al., 2016), providing a long-range signaling mechanism analogous to the rapid propagation of electrical signals in neurons (Keren, 2011). Some studies have contemplated the possibility of tension gradients in rapidly migrating cells (Basu et al., 2016; Fogelson and Mogilner, 2014; Lieber et al., 2015; Schweitzer et al., 2014), but in these studies the role of membrane-cytoskeleton friction was assumed to be a modest perturbation on the essentially fluid nature of the membrane.

Intact cell membranes contain many features not found in artificial lipid bilayers. In eukaryotic cells, approximately half of the transmembrane proteins, corresponding to ~10 - 20% of total membrane area (Bussell et al., 1995; Zakharova et al., 1995), are bound to the underlying cortex and therefore are effectively immobile on timescales of minutes to hours (Bussell et al., 1995; Groves and Kuriyan, 2010; Sadegh et al., 2017). Are these obstacles a minor perturbation to lipid flow, or do they qualitatively change the dynamics? Aqueous solutions with ~10% immobile protein, such as collagen gels, behave as bulk solids, not liquids, yet still permit lateral diffusion of small molecules and proteins. Thus it is plausible that cell membranes, too, could exist in a state that behaves as a 2D fluid on the nanoscale but that is closer to a semi-solid gel on the cellular scale. The 2D-gel hypothesis is incompatible with the many conjectures in the literature that rapid propagation of membrane tension can mediate long-range intracellular signaling (Basu et al., 2016; Diz-Muñoz et al., 2013; Fogelson and Mogilner, 2014; Gauthier et al., 2012; Gauthier et al., 2011; Houk et al., 2012; Huse, 2017; Keren et al., 2008; Keren, 2011; Kozlov and Mogilner, 2007; Lieber et al., 2015; Morris and Homann, 2001; Mueller et al., 2017; Mueller et al., 2017; Ofer et al., 2011; Pontes et al., 2017; Saha et al., 2018; Schweitzer et al., 2014; Sens and Plastino, 2015; Watanabe et al., 2013; Winkler et al., 2016).

RESULTS

Membrane tension propagates in membrane blebs but not in cell membranes

Working with HeLa cells at 37 °C, we pulled short membrane tethers as a means of simultaneously perturbing and measuring local membrane tension (Fig. 1A, 1D). Tether diameter and local membrane tension are inversely related, coupled via the membrane’s finite bending stiffness (Supplementary Discussion) (Derényi et al., 2002; Pontes et al., 2017). Tether diameters were too small to resolve optically, so we used fluorescence of a membrane-bound tag (GPI-eGFP) to estimate tether diameter. Under wide-field fluorescence excitation, flare from the cell body prevented accurate quantification of the fluorescence from the far dimmer tether. We used a custom micromirror-based patterned illumination system to restrict fluorescence excitation to the tethers, leading to high-contrast images of individual tethers. By calibrating tether fluorescence against the fluorescence of a patch of cell membrane with known area, we determined the tether diameter. We used simultaneous fluorescence and optical trap force measurements to calibrate the relationship between tether diameter and tension (Fig. S2A – S2D). Global perturbations to membrane tension via osmotic shocks induced the expected changes in both tether pulling force and tether fluorescence (Fig. S2E – S2G).

Fig. 1. Propagation of membrane tension in cells.

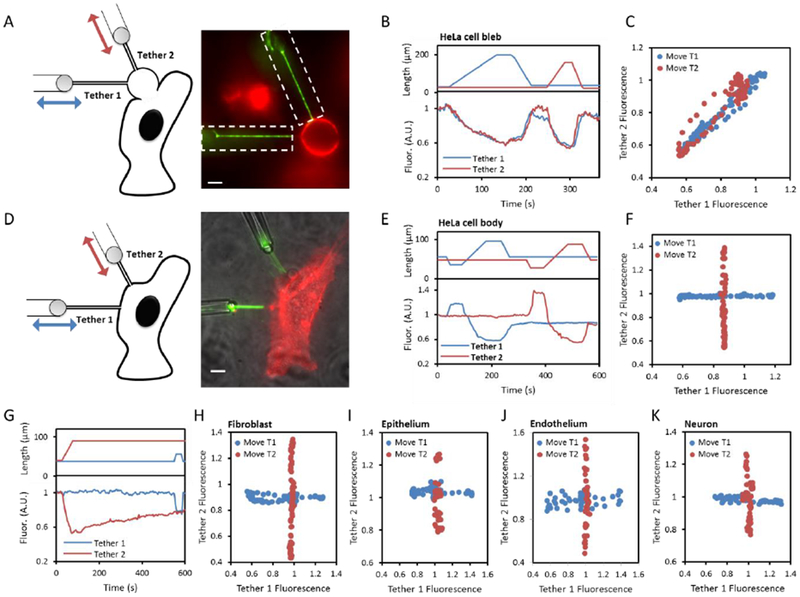
A,D) Schematic (left) and fluorescence image (right) showing a pair of tethers pulled from (A) a cell-attached bleb or (D) the cell body of a HeLa cell expressing GPI-eGFP. Green: fluorescence under patterned illumination (restricted to dashed boxes). Red: fluorescence under wide-field illumination. In (D) a transmitted light image (grey) is combined with the fluorescence images. Scale bars 5 μm. B,E) The two tethers were stretched sequentially (top) and the fluorescence of each tether was monitored (bottom). C,F) Relation between the intensities of the two tethers when either the first or second tether was stretched. G) Test for slow coupling between tethers in a HeLa cell. A change in length of tether 2 did not affect fluorescence of tether 1 within a 500 s measurement window. H-K) Repetition of the experiment in (D-F) in H) NIH 3T3 fibroblasts, I) MDCK epithelial cells, J) mouse brain endothelial cells, and K) rat hippocampal neurons. T1: Tether 1, T2: Tether 2.

Two membrane tethers were then simultaneously pulled from nearby locations on a single cell (typically 5-15 μm apart) and fluorescence from each was excited with micromirror-patterned illumination (Fig. 1A, 1D, Fig. S3). Each tether was successively stretched and relaxed, while the fluorescence of both tethers was monitored to measure local tension. In cell-attached membrane blebs, we observed tight coupling of the tension in the two tethers (Fig. 1A – C). Stretching of either tether led to a decrease in the fluorescence of both tethers, with the response of the unstretched tether lagging by < 1 s. Measurements on 10 pairs of tethers pulled from different blebs all showed strongly coupled fluorescence changes. Thus tension rapidly equilibrated across blebs, consistent with observations in artificial lipid vesicles (e.g. Fig. S1). In intact cells, in contrast, we failed to observe any coupling between the tethers (Fig. 1D – F). Measurements lasted up to 500 s, and attachment points were as close as 5 μm (Fig. 1G). We tested HeLa cells (Fig. 1E, 1F, n = 30 cells), NIH 3T3 fibroblasts (Fig. 1H, n = 10 cells), MDCK epithelial cells (Fig. 1I, n = 5 cells), mouse brain endothelial cells (Fig. 1J, n = 5 cells), and proximal dendrites of rat hippocampal neurons (Fig. 1K, n = 5 neurons) and did not observe tension propagation in any of these cell types.

The failure to observe propagation of membrane tension in cells might be explained by rapid assembly of cytoskeletal barriers that isolated the tether from the rest of the cell. To test for such barriers, we first checked for the presence of actin in pulled tethers. In cells co-expressing a membrane label (mOrange2-KRAS) and an actin label (Lifeact-CFP), no actin signal was observed in the tether in experiments lasting up to 15 min (Fig. S4A). We then performed fluorescence recovery after photobleaching (FRAP) experiments to test for diffusive interchange between the tether and the cell membrane. In cells expressing a transmembrane tracer, DRD2-eGFP, we photobleached all fluorescence in the tether and then monitored the recovery (Lippincott-Schwartz et al., 2003). The fluorescence recovery profile quantitatively matched simulations of free diffusion between the cell and tether, ruling out local cytoskeletal isolation of the tether (Fig. S4B, S4C). Adhesive interactions between a tether and the cytoskeleton have been proposed to introduce an offset between the tether tension and the membrane tension (Dai and Sheetz, 1999), but such an offset would not affect the interpretation of our results.

Hydrodynamic model of membrane flow

In two-dimensional flows, an immobile obstacle creates a logarithmically diverging long-range perturbation to the flow field, a phenomenon sometimes called the Stokes paradox. We hypothesized that cytoskeleton-bound transmembrane proteins might significantly impede the membrane flow required to propagate tension changes in cells (Fig. 2A). Over length scales large compared to the inter-obstacle spacing, the poroelastic equations governing lipid flow lead to a diffusion-like equation for propagation of membrane tension, with tension diffusion coefficient D_σ = E_mk/η, where E_m is the effective area expansion modulus of the membrane, η is the two-dimensional membrane viscosity, and k is the Darcy permeability of the array of obstacles (Supplementary Discussion; See Table S1 for definitions and values for all physical parameters). The diffusion coefficient for the spread of membrane tension represents the balance of viscous and elastic forces in the membrane (Fig. 2B), and is physically distinct from the diffusion coefficients that govern motion of tracer molecules within the lipid bilayer.

Fig. 2. Hydrodynamic model of membrane flow past immobile obstacles.

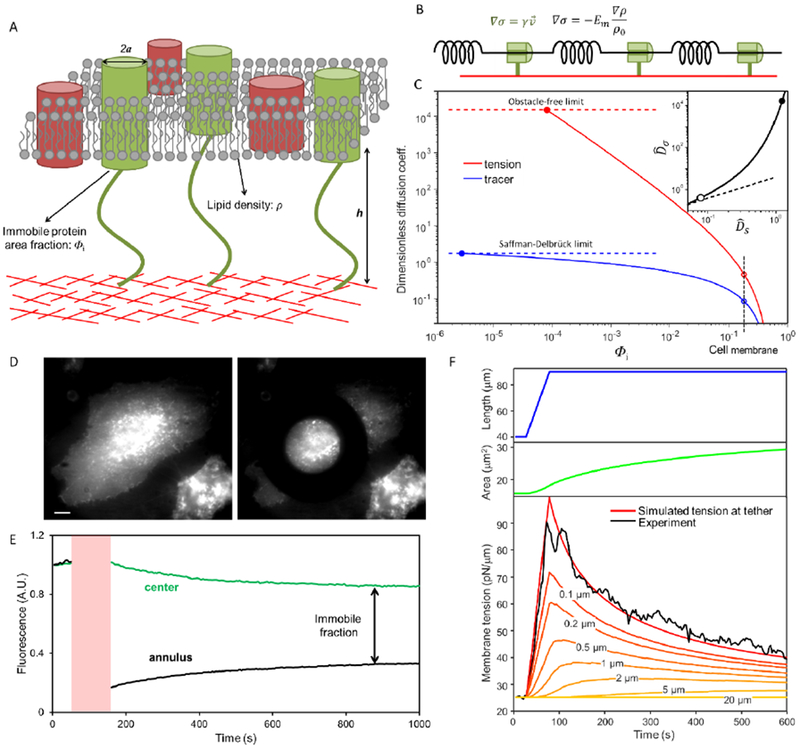
A) Illustration of the cell plasma membrane with some transmembrane proteins bound to the underlying cortex. B) Simple viscoelastic model of the cell membrane. Springs represent the elastic response of the membrane to stretch, and dampers represent the viscous drag from immobile transmembrane proteins. C) Dependence of diffusion coefficients for membrane tension (red) and molecular tracers (blue) on the area fraction Φ_i of immobile proteins. This plot shows the model’s predictions for the dimensionless diffusion coefficients, ${\widehat{D}}_{\sigma }=\frac{\eta D_{\sigma }}{E_m{a}^2}$ for tension and ${\widehat{D}}_s=\frac{\pi \eta D_s}{k_{B}T}$ for tracers. The upper limit on tension diffusion is set by the hydrodynamic drag between plasma membrane and cytoskeleton cortex in the absence of obstacles. The upper limit on tracer diffusion is set by the Saffman–Delbrück model (Supplementary Discussion). Open circles: diffusion coefficients in intact cell membranes. Inset: Relation between dimensionless diffusion coefficients of membrane tension and molecular tracers (solid line). The dashed line shows a linear relation. Closed circles: obstacle-free membrane. Open circles: Φ_i = 0.18. D) Fluorescence image showing a HeLa cell in which transmembrane proteins have been labeled non-specifically with Alexa488-NHS before (left) and after (right) bleaching with a donut shape laser spot. Scale bar, 10 μm. E) Fluorescence intensity profile of the bleached ring (black) and non-bleached central (green) regions. The photobleaching epoch is shaded red. F) Comparison of simulation and experiment for time-dependent membrane tension in a stretched membrane tether and surrounding cell membrane (E_m = 40 pN/μm; D_σ = 0.024 μm²/s). Top: tether stretch protocol with initial tension σ₀ = 25 pN/μm, ramp increase in tether length from 40 μm to 90 μm at a pulling speed v_pull = 1 μm/s. Middle: simulated surface area of the tether. Bottom: membrane tension in the tether inferred from measurements of tether radius (black) and simulated membrane tension in the tether and in the cell at distances of 0.1 μm to 20 μm from the tether. See Materials and Methods for details of the simulation.

The Darcy permeability, k, scales with obstacle radius, a and area fraction of the obstacles, Φ_i, as k = a²f(Φ_i), where f(Φ_i) is a dimensionless function which varies steeply at small Φ_i (Fig. S5) (Bussell et al., 1995; Howells, 1974). Bussell et al. (Bussell et al., 1995) showed that one can estimate Φ_i from the diffusion of transmembrane tracer molecules. We compared the diffusion coefficients, D_S, of tracer molecules on an intact cell versus on cytoskeleton-free membrane tethers (Fig. 2C and Fig. S6). For a transmembrane dopamine receptor fused to eGFP (DRD2-eGFP), FRAP measurements yielded diffusion coefficients on the cell 21 ± 4 fold lower than on the tether (D_S^cell = 0.037 ± 0.005 μm²/s, D_S^tether = 0.76 ± 0.08 μm²/s, mean ± s.e.m., n = 10 pairs of tethers and cells). We explored a variety of other tracers to control for possible molecularly specific interactions with cytoskeletal components and obtained similar results (Table S2), consistent with literature (Kusumi et al., 2005). We used the Saffman–Delbrück model (Saffman and Delbrück, 1975) to fit the diffusion on the cytoskeleton-free tethers, and the Bussel model (Bussell et al., 1995) to fit the diffusion on the cell body. The pair of fits yielded a membrane viscosity η = (3.0 ± 0.4) × 10⁻³ pN∙s/μm and an area fraction of immobile obstacles Φ_i = 0.18 ± 0.03 (Fig. 2C), consistent with literature results (Bussell et al., 1995; Kusumi et al., 2005).

We performed additional FRAP experiments to make an independent estimate of Φ_i in HeLa cells. Transmembrane proteins were labeled nonspecifically with a broadly reactive cell-impermeant dye, and then photobleached in a sub-cellular region (Fig. 2D). Mobile proteins thereafter diffused back into the bleached region, while immobile proteins did not. The degree of partial fluorescence recovery at long time (15 min) showed that 54 ± 5% (mean ± s.e.m., n = 5 cells) of all labeled transmembrane proteins were immobile (Fig. 2E, Fig. S7). When combined with literature estimates that ~25% of membrane area is occupied by transmembrane proteins (Dupuy and Engelman, 2008; Zakharova et al., 1995), these results are broadly consistent with our estimate of Φ_i = 0.1 – 0.2 based on molecular diffusion measurements.

Combining the estimates of membrane viscosity, η = (3.0 ± 0.4) × 10⁻³ pN∙s/μm, and obstacle area fraction (Φ_i = 0.18 ± 0.03) with reasonable values of the obstacle radius (a ~ 2 nm) (Bussell et al., 1995) and effective membrane area expansion modulus (E_m = 40 pN/μm) (Hochmuth, 2000; Needham and Hochmuth, 1992) yields a tension diffusion coefficient: D_σ = 0.024 ± 0.005 μm²/s. Tension therefore requires tens of minutes to equilibrate over cellular length scales (~10 μm). These experiments additionally yielded an estimate of an effective drag coefficient for membrane flow relative to the cytoskeleton, γ = η/k. We found γ = 1700 ± 300 pN∙s/μm³. Microrheometry measurement of cell plasma membrane with magnetic particles yielded a similar drag coefficient, γ ≈ 2000 pN∙s/μm³ (Bausch et al., 1998).

The hydrodynamic model establishes that the tension diffusion coefficient D_σ is far more sensitive to obstacles than is the tracer diffusion coefficient, D_S. An obstacle density that decreases tracer diffusion 10-fold from the free-membrane limit, decreases diffusion of tension 10⁴-fold (Fig. 2C and Supplementary Discussion). Obstacles at densities that modestly suppress tracer diffusion will almost completely block lipid flow, causing the membrane to appear rheologically like a gel.

The hydrodynamic model predicts the distribution of membrane tension in space and time after a localized perturbation to the membrane. Using the experimentally determined tension diffusion coefficient (D_σ = 0.024 μm²/s), we simulated the propagation of tension around a tether attachment point after a ramp increase in tether length. We accounted for the gradual changes in tether tension and radius as lipid flowed into the tether. These simulations, which had no adjustable parameters, quantitatively matched the measurements of the time-dependent tether tension (inferred from the tether radius, Fig. 2F). The simulations predicted that the perturbation to membrane tension decayed to 50% of the maximum at a distance of 0.2 μm from the tether, and to 3% of the maximum at a distance of 5 μm from the tether. Fig. 2F shows that local perturbations to membrane tension remained predominantly localized within a sub-micron domain. For other perturbation geometries, the spatio-temporal distribution of membrane tension will depend on the geometry and time-course of the perturbation, and can be calculated by solving the diffusion equation.

Localized activation of mechanosensitive ion channels (MSCs) and vesicle fusion

To test whether membrane tension is a local or global regulator of membrane signaling, we examined the effect of local perturbations to tension on the activation of mechanosensitive ion channels. We pulled tethers in endogenously mechanosensitive MDCK cells (Gudipaty et al., 2017), and performed simultaneous dual-color imaging of tether fluorescence (via GPI-eGFP) and intracellular Ca²⁺ (via R-CaMP2, Fig. 3A–C, Fig. S8A). These experiments revealed that MSCs in MDCK cells activated at a membrane tension ~10-fold higher than the resting tension (Fig. S9). We then switched to using GCaMP6f to improve Ca²⁺ sensitivity. In 18 out of 27 trials (15 out of 21 cells) tether pulling triggered Ca²⁺ influx (Fig. 3D). In all tether pulling experiments the Ca²⁺ influx, if detected, initiated at the tether attachment to within our ability to resolve these two sites (Fig. 3F). We never observed initiation of tether-induced Ca²⁺ influx in any regions of the cell distal from the tether attachment, even at the slowest pulling speeds tested (1 μm/s), establishing that membrane tension acted locally, not globally, to gate endogenous MSCs. Ca²⁺ diffused from the point of entry to gradually fill the cell, consistent with the well-established role of Ca²⁺ as a mediator of long-range intracellular signaling.

Fig. 3. Membrane tension mediates local activation of mechanosensitive ion channels and local vesicle fusion in MDCK cells.

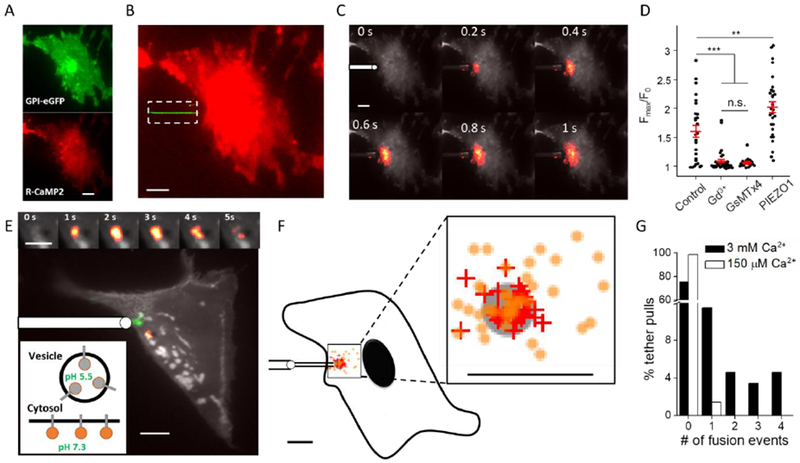
A) MDCK cell co-expressing GPI-eGFP (green) and R-CaMP2 (red). B) Composite fluorescence image of tether (green) and R-CaMP2 (red). Fluorescence excitation of eGFP was confined to the tether (dashed box). C) Localized Ca²⁺ influx triggered by tether stretch. Images are composites of mean fluorescence (grey) and changes in fluorescence (heat map). Tether pulling pipette shown schematically at 0 s. D) Blockers of MSCs, GdCl₃ (500 μM) or GsMTx4 (8 μM), suppressed Ca²⁺ influx during tether pulling. Over-expression of PIEZO1-mCherry increased Ca²⁺ influx during tether pulling (n = 27 cells in control extracellular buffer, n = 36 with GdCl₃, n = 18 with GsMTx4, n = 31 with PIEZO1 over-expression, ** p<0.01, *** p < 10⁻³, n.s.: p > 0.5, Student’s t-test). Data points represent maximal fractional increase in fluorescence of Ca²⁺ reporter. Red lines: mean. Error bars: s.e.m. E) Composite fluorescence image of mean fluorescence (grey), changes in fluorescence after tether pull (heat map) and tether location (green). Tether pulling pipette shown schematically. Upper inset: close-up view of the vesicle fusion events triggered by tether stretch. Lower inset: membrane-tethered mOrange2-TM reported vesicle fusion via pH-mediated changes in fluorescence. F) Distribution of Ca²⁺ influx initiation points (+) and vesicle fusion (o) sites relative to the tether attachment point (grey circle). Each mark represents one event (33 Ca²⁺ influx events from 25 cells; 43 vesicle fusion events from 21 cells). Average distance between Ca²⁺ initiation and tether attachment was 1.7 ± 0.2 μm (mean ± s.e.m), smaller than the localization uncertainty (3 μm). Average distance between vesicle fusion site and tether attachment was 3.5 ± 0.4 μm (mean ± s.e.m), much smaller than the the null hypothesis of uniform fusion throughout the cell (27 ± 2 μm). The outline of the cell is a schematic to illustrate size. G) In control extracellular medium (3 mM Ca²⁺) tether pulling triggered fusion of one or more vesicles in 21 out of 87 trials (black). In low [Ca²⁺] buffer (150 μM Ca²⁺ buffered by EGTA) tether pulling triggered fusion of only one vesicle in 71 trials (white), establishing that elevated intracellular Ca²⁺ mediated vesicle fusion. Scale bars in all panels 10 μm, except 5 μm for the upper inset in (E).

The Ca²⁺ influx was largely blocked by Gd³⁺ (2 Ca²⁺ influx events in 36 tether pulls, Fig. 3D) confirming that the influx was through stretch-activated mechanosensitive ion channels (Hua et al., 2010). The peptide toxin GsMTx4 also blocked the tether-induced Ca²⁺ influx (1 Ca²⁺ influx event in 18 tether pulls, Fig. 3D). This toxin blocks PIEZO1 but not other MSCs such as TREK-1 (Bae et al., 2011), suggesting that PIEZO1 likely mediates localized tension sensing in MDCK cells. Overexpression of PIEZO1-mCherry in MDCK cells led to increased but still localized Ca²⁺ influx during tether pulling (Fig. 3D, Fig. S10), confirming that PIEZO1 responds to local, not global, membrane tension (Saotome et al., 2017). Sequential tether pulling from different locations of the same cell led to local Ca²⁺ influx at each pulling location but not at the previously pulled site, further demonstrating sub-cellular compartmentalization of mechanosensation (Fig. S10C).

Increases in membrane tension have been reported to facilitate vesicle release (Gauthier et al., 2011; Shillcock and Lipowsky, 2005; Shin et al., 2018). We next tested whether this effect was local or global. We expressed in MDCK cells membrane-tethered mOrange2 (mOrange2-TM), targeted to the inside of vesicles and to the extracellular face of the plasma membrane (Materials and Methods). This pH-sensitive reporter (pK_a 6.5 (Shaner et al., 2008)) was dark in the acidic lumen of vesicles and became fluorescent upon vesicle fusion to the plasma membrane (Fig. 3E). Addition of the Ca²⁺ ionophore ionomycin (5 μM) led to Ca²⁺ influx and vesicle fusion as reported by the dye FM 4-64, confirming that ionomycin triggered vesicle release (Fig. S11). In MDCK cells expressing mOrange2-TM, ionomycin led to a cell-wide appearance of bright fluorescent puncta, confirming the ability of mOrange2-TM to report vesicle fusion (Fig. S11). We then pulled tethers (from fresh cells expressing mOrange2-TM) and mapped the distribution of ensuing vesicle fusion events (Fig. 3E,F). We compared to the distribution anticipated from the null hypothesis of uniform fusion throughout the cell (Materials and Methods). The tension-induced events were significantly clustered around the tethers (Fig. 3F, mean distance 3.5 ± 0.4 μm, vs. 27 ± 2 μm for null hypothesis, mean ± s.e.m, n = 43 fusion events from 21 cells).

The vesicle fusion events were more broadly distributed around the tether attachment points than were the Ca²⁺ influx initiation sites (p = 0.001), leading us to hypothesize that the vesicle fusion might be predominantly mediated by Ca²⁺ influx at the tether attachment and then Ca²⁺ diffusion over a larger, but still sub-cellular, region. Indeed, buffering extracellular Ca²⁺ concentration to 150 μM with EGTA largely eliminated tension-induced vesicle fusion (Fig. 3G, only 1/71 pulls induced fusion), establishing that the local vesicle fusion was mediated by local influx of Ca²⁺ through MSCs followed by intracellular Ca²⁺ diffusion. Diffusion of Ca²⁺, not propagation of membrane tension, caused the distribution of vesicle fusion events to extend beyond the tether attachment point.

Endothelial cells respond to changes in shear flow in vivo (Geiger et al., 1992; Li et al., 2014; Schwarz et al., 1992) via activation of PIEZO1 (Guo and MacKinnon, 2017). We thus asked whether tension-induced activation of mechanosensitive ion channels in primary mouse brain endothelial cells (mBECs) was local or global. As in the MDCK cells, tether pulling led to local influx of Ca²⁺ and local vesicle fusion (Fig. 4A–C, Fig. S8B). The vesicle fusion events were more broadly spread compared to in MDCK cells. We hypothesized that this effect was due to longer-range propagation of localized Ca²⁺ influx in mBEC cells due to Ca²⁺ induced ER Ca²⁺ release (Mumtaz et al., 2011). Pre-incubation of mBECs with 2-APB to deplete ER Ca²⁺ stores(Mumtaz et al., 2011) significantly reduced the spatial spread of tether pulling induced fusion events (Fig. 4D). This result confirmed that in mBECs as in MDCK cells, intracellular spread of Ca²⁺, not propagation of membrane tension, caused the distribution of vesicle fusion events to extend beyond the tether attachment point.

Fig. 4. Tension mediates local activation of mechanosensitive ion channels and local vesicle fusion in primary mouse brain endothelial cells.

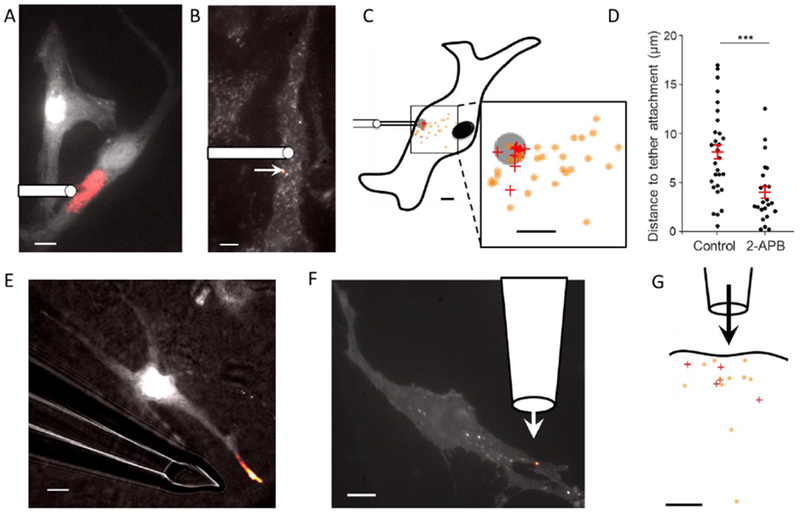
A) Tether stretch triggered localized Ca²⁺ influx and B) vesicle fusion events. Images are composites of mean fluorescence (grey) and changes in fluorescence (heat map). Tether pulling pipette shown schematically. C) Distribution of Ca²⁺ influx (+) and vesicle fusion (o) sites relative to the tether attachment point (grey circle). Each mark represents one event (9 Ca²⁺ influx events from 7 cells; 29 vesicle fusion events from 6 cells). Average distance between Ca²⁺ initiation and tether attachment was 2.2 ± 0.5 μm (mean ± s.e.m), within the localization uncertainty (3 μm). Average distance between vesicle fusion and tether attachment was 8.0 ± 0.8 μm (mean ± s.e.m, vs. 28 ± 3 μm for null hypothesis). D) 2-APB (100 μM) significantly reduced the spread of vesicle fusion events relative to the tether attachment (3.9 ± 0.6 μm, n = 23 with 2-APB, *** p < 0.001. E-F) Local flow of extracellular buffer at 12 cm/s led to localized Ca²⁺ influx (E) and localized vesicle fusion (F). Images are composites of mean fluorescence (grey) and changes in fluorescence (heat map). In E, transmitted light shows the location of the pipette for flow delivery. G) Distribution of Ca²⁺ influx (+) and vesicle fusion (o) sites relative to the local flow. Each mark represents one flow-induced event (5 cells for Ca²⁺ influx; 11 fusion events from 4 cells for vesicle fusion). Scale bars in all panels 10 μm.

Tethers are a non-physiological perturbation, so we then tested the effect of localized shear flow on Ca²⁺ influx in mBECs. We used a small glass capillary (exit diameter 12 μm) to apply a sub-cellular flow to mBECs, with a maximal surface shear of 2×10⁴ s⁻¹, corresponding to a surface stress of 20 pN/μm², approximately twice the mean value in vivo (Koller and Kaley, 1991). Bead tracers showed a nearly pencil-like laminar flow emerging from the pipette (Fig. S12). This flow clearly induced localized Ca²⁺ influx (Fig. 4E, n = 5 cells, Fig. S8C) and localized vesicle fusion (Fig. 4F, n = 4 cells) in the high-shear zones, without activating either mechanosensitive channels or vesicle fusion in other parts of the cell. This experiment establishes that localized changes in membrane tension drive sub-cellular signaling in a physiologically relevant context.

DISCUSSION

Despite the well-established importance of membrane tension for many physiological processes (Basu et al., 2016; Boulant et al., 2011; Gauthier et al., 2011; Groves and Kuriyan, 2010; Houk et al., 2012; Huse, 2017; Keren et al., 2008; Maritzen and Haucke, 2017; Masters et al., 2013; Phillips et al., 2009; Ranade et al., 2015; Romer et al., 2007; Stewart et al., 2011), the path to equilibrium for local tension perturbations has not been measured quantitatively (Raucher and Sheetz, 1999). Most studies have assumed that membrane tension is homogeneous across a cell (Basu et al., 2016; Diz-Muñoz et al., 2013; Fogelson and Mogilner, 2014; Gauthier et al., 2012; Gauthier et al., 2011; Houk et al., 2012; Huse, 2017; Keren et al., 2008; Keren, 2011; Kozlov and Mogilner, 2007; Lieber et al., 2015; Morris and Homann, 2001; Mueller et al., 2017; Mueller et al., 2017; Ofer et al., 2011; Pontes et al., 2017; Saha et al., 2018; Schweitzer et al., 2014; Sens and Plastino, 2015; Watanabe et al., 2013; Winkler et al., 2016). This assumption was justified either by analogy to isolated lipid bilayers (Keren et al., 2008; Watanabe et al., 2013), or by reference to experiments where membrane tension was globally perturbed via osmotic shocks or drug addition (Gauthier et al., 2011; Houk et al., 2012; Mueller et al., 2017; Raucher and Sheetz, 2000). Several studies considered imbalances in membrane tension as a transient effect relevant to rapidly migrating cells (Basu et al., 2016; Fogelson and Mogilner, 2014; Lieber et al., 2015; Schweitzer et al., 2014).

Our data and model provide direct evidence that there is no long-range propagation of membrane tension in cells over ~10 minute timescales. The diffusion coefficient for membrane tension, D_σ ~ 0.024 μm²/s, is so low that on experimentally relevant timescales imbalances in tension are essentially static. Local perturbations to tension can locally activate Ca²⁺ influx. Ca²⁺ ions diffuse in cytoplasm with a diffusion coefficient D_Ca ~ 500 μm²/s,(Donahue and Abercrombie, 1987) more than 20,000-fold higher than D_σ. Ca²⁺-induced Ca²⁺ release can further enhance the propagation of local Ca²⁺ influx. Thus Ca²⁺ provides a far more effective means of mediating long-range signaling than does membrane tension, and indeed we observed Ca²⁺-mediated vesicle release in regions distal to local mechanical perturbations (Fig. 4C). Other small-molecule second-messengers will also diffuse much faster than membrane tension.

The literature on activation of mechanosensitive ion channels in mammalian cells contains a number of inconsistencies. These inconsistencies are reconciled if one treats membrane tension as a local rather than a global parameter. For instance, activation of PIEZO1 mechanosensitive ion channels in cells via pipette aspiration produced a current proportional to the area of the pipette aperture, not the whole cell area (Cox et al., 2016; Gottlieb et al., 2012; Lewis and Grandl, 2015). This observation was reported as a surprise, but is easily explained by the fact that the increased tension was localized near the pipette, not distributed over the cell.

In another example, direct measurements of resting cell membrane tension across various mammalian cells range from 3 to 40 pN/μm (Morris and Homann, 2001; Raucher and Sheetz, 1999), whereas the activation of mechanosensitive ion channels such as PIEZO and TREK channels has been reported to require a >100-fold higher membrane tension: 1000~5000 pN/μm (Cox et al., 2016; Gauthier et al., 2012; Morris and Homann, 2001). It was unclear how these channels were ever activated under physiological conditions. Our study shows that large local deviations in membrane tension can readily arise in cells, suggesting that measurements of mean cell-wide membrane tension may not be relevant to mechanosensation. For instance, when a cell has localized attachments to its matrix via focal adhesions, body forces applied to the cell can propagate through the cytoskeleton to localize the membrane stress at the attachment points. Consistent with this model, Ellefsen et al. recently reported that traction forces at focal adhesion sites induce local Ca²⁺ influx through PIEZO1 (Ellefsen et al., 2018), a phenomenon that would be hard to explain if membrane tension were homogeneous over the cell. The typical spacing between focal adhesions (~ 5 μm)(Kim and Wirtz, 2013) is larger than the distance over which local perturbations to membrane tension propagate (Fig. 2F), so gating of mechanosensitive ion channels occurs independently at distinct focal adhesions.

A third consequence of our model is the extreme sensitivity of the tension diffusion coefficient D_σ to the area fraction of cytoskeleton-bound obstacles, Φ_i, at low Φ_i. The dramatic effect of ~10% immobile obstacles on membrane rheology might seem counterintuitive. However, a similar effect is familiar in everyday life. An aqueous 10% collagen gel behaves as a solid and can be eaten with a fork. The Stokes paradox applies in both cases because in the 3D gel, the proteins assemble into long 1D fibers, leading to an effectively 2D flow profile transverse to the fibers (Ramanujan et al., 2002). While the density of transmembrane obstacles has not been systematically studied, we anticipate that this important biophysical parameter will vary between cell types, between sub-cellular regions, and throughout the cell cycle. There may be physiologically or pathophysiologically important situations (such as during mitosis or when cells are forming blebs) where tension can diffuse rapidly.

Changes in intracellular pressure could mediate long-range changes in membrane tension via the Laplace relation between pressure, membrane tension, and membrane curvature. A poroelastic model, analogous to our model for membrane tension, showed that intracellular hydrostatic pressure propagates diffusively, with a diffusion coefficient of D_P ~ 10 μm²/s (Charras et al., 2005). The more than 100-fold difference between D_P and D_σ reflects the correspondingly lower viscosity of cytosol versus membrane (Kusumi et al., 2005).

Cytoskeletal reorganization could also mediate long-range mechanical signaling (Bussonnier et al., 2014; Wu et al., 2013). One should think of the membrane and cytoskeleton as a composite material, in which deformation of the two components is tightly coupled. The far greater stiffness of the cytoskeleton compared to the membrane implies that the cytoskeleton dominates the rheology. In this composite picture, perturbations to the cytoskeleton could propagate quickly and cause long-range changes in membrane tension.

Several papers have proposed rapid transmission of membrane tension as a mechanism for long-range coordination of actin polymerization (Gauthier et al., 2011; Houk et al., 2012; Keren et al., 2008; Mueller et al., 2017). However, the membrane tension itself was not directly measured. Alternate mechanisms for long-range mechanical signalling include via hydrostatic pressure in the cytoplasm, or via the actin cortex. We suggest these possibilities as alternate hypotheses to explain the literature data.

Many revisions to the fluid mosaic model have been proposed (Nicolson, 2014). Specialized structures, such as cytoskeletal corrals and lipid rafts, have been invoked to explain sub-cellular confinement in membranes (Kusumi et al., 2005). Indeed such structures are necessary to account for diffusional confinement and for local variations in membrane composition. Our results establish that a random array of transmembrane obstacles is sufficient to qualitatively change the membrane rheology from fluid to gel-like dynamics, without invoking any specialized structures. This mechanism of membrane gelation is unrelated to the lipid gel phases that arise at lower temperatures through phase transitions of the lipids themselves (Koynova and Caffrey, 1998). Within our model, the lipids remain liquid-like on the nanoscale, permitting free diffusion of molecular cargoes. Our model is entirely consistent with the thermodynamic data used to support the fluid-mosaic model (Nicolson, 2014; Singer and Nicolson, 1972), while adding a picture of the slow and heterogeneous approach to equilibrium.