Activation-dependent changes in soleus length-tension behavior augment ankle joint quasi-stiffness

Abstract

The triceps surae muscle-tendon units are important in governing walking performance, acting to regulate mechanical behavior of the ankle through interaction between active muscle and passive elastic structures. Ankle joint quasi-stiffness (the slope of the relation between ankle moment and ankle rotation, k_A), is a useful aggregate measure of this mechanical behavior. However, the role of muscle activation and length-tension behavior in augmenting k_A remains unclear. Here, 10 subjects completed eccentric isokinetic contractions at rest and at two soleus activation levels (25% and 75% isometric voluntary contraction - IVC) prescribed using electromyographic biofeedback. Ultrasound imaging quantified activation-dependent modulation of soleus muscle length-tension behavior and its role in augmenting k_A. We found that soleus muscle stiffness (k_M) and k_A exhibit non-linear relations with muscle activation and were both more sensitive to the onset of activation than to subsequent increases in activation. Our findings also suggest that k_A can be modulated via activation through changes in soleus muscle length-tension behavior. However, this modulation is more complex than previously appreciated – reflecting interaction between active muscle and passive elastic tissues. Our findings may have implications for understanding normal and pathological ankle joint function and the design of impedance-based prostheses.

Introduction

The triceps surae muscle-tendon units are important in governing walking performance, acting to regulate mechanical behavior of the ankle joint through the interaction between active muscle and passive elastic structures^1-3. Ankle joint quasi-stiffness (k_A), the slope of the relation between ankle moment and ankle rotation, is a useful aggregate measure of this presumably complex mechanical behavior⁴. For example, quasi-passive lower limb prostheses with impedance controls have garnered attention and their designs are benchmarked against the quasi-stiffness of the biological ankle⁵. Some evidence suggests that muscle stiffness is activation dependent⁶; however, it remains unclear precisely how the neuromechanical behavior of the triceps surae muscles and series elastic tendon interact to modulate k_A, with implications for functional activities such as walking.

In walking, k_A increases with walking speed and positively correlates with positive work performed about the ankle during push-off^{5, 7}. In addition, the profile of k_A across the stance phase mirrors that of net ankle moment and triceps surae muscle activation. Together, these findings allude to activation-dependent modulation of k_A^{4, 8}. However, other evidence^{9, 10} suggests that the relation between ankle moment and rotation is linear, and thereby can be estimated by a linear torsional spring, potentially reflecting contributions from passive elastic structures. Throughout the gait cycle, and notably during the transition between single and double support during terminal stance (30-60%), complex changes in the relation between ankle moment and ankle rotation, reflecting the aggregate contribution from active and passive structures, impacts the mechanical behavior of the ankle^{5, 11-13}. However, it can be challenging to decompose active (i.e., triceps surae muscle) from passive (i.e., Achilles tendon) contributions underlying ankle joint mechanical function. For example, Farris and Raiteri (2017) suggest that soleus muscle-tendon interaction during the transition between single and double support of accelerated walking modulated the quasi-stiffness of the ankle differently than during that of constant speed walking¹⁴. As a consequence, devices that model ankle mechanics purely as a passive spring may not fully capture mechanical power generated by the triceps surae¹⁵. On the other hand, Lee and colleagues state that even neuromuscular model-based controllers currently fall short in mimicking human ankle behavior^16-18. Atri et al. (2018) add that powered devices often require advanced optimization that fail to replicate ankle dynamics due to a complex relation between ankle joint quasi-stiffness and muscle activation¹⁹. Accordingly, a better understanding of the relation between muscle activation and ankle joint quasi-stiffness could lead to improvements in sophisticated powered devices.

While it is entirely intuitive that the control of triceps surae muscle behavior can functionally augment k_A via changes in activation, we lack direct empirical evidence for this interaction. For example, recent studies examining the relation between triceps surae muscle stiffness and k_A have done so in the absence of muscle activity. The resistance to passive ankle joint rotation is garnered through some combination of muscle stiffness, tendon stiffness, and the intrinsic stiffness of other periarticular structures spanning the ankle²⁰. Surprisingly, Chino and Takahashi (2018) revealed no significant correlation between passive medial gastrocnemius muscle stiffness and k_A at four different ankle angles²¹. Similarly, Chino and Takahashi (2016) found no significant correlation between medial gastrocnemius stiffness and k_A in plantarflexed and neutral ankle angles²². They interpret their findings to suggest that muscle stiffness may augment k_A only when sufficiently lengthened, and support their conclusion by noting a significant correlation in dorsiflexed conditions²². However, very rarely does the ankle joint undergo passive rotation during functional activities. Thus, it is a logical and important next step to determine the sensitivity of both muscle stiffness and k_A to varying levels of activation, thereby better informing the functional relation between tissue- and joint-level behavior at the ankle joint. Moreover, successful determination of the relation between activation and stiffness in healthy groups may establish a useful methodological approach that allows for a follow up comparison with people with gait pathology (e.g., stroke survivors). Indeed, those individuals may experience deleterious changes in the magnitude and timing of muscle activation patterns during functional activities^23,24.

The purpose of this study was to couple ultrasound imaging with electromyographic biofeedback to quantify activation-dependent modulation of soleus muscle length-tension behavior and its role in augmenting k_A. We hypothesized that soleus muscle stiffness (k_M) and k_A would increase with increasing muscle activation. However, we anticipated that the sensitivity of k_M and k_A to altered activation would change with activation level. Specifically, based on earlier findings of no relation between k_M and k_A during passive ankle rotation, we hypothesized that both would be more sensitive to the onset of activation (0% to 25% maximum activation) than to a subsequent increase in activation (25% to 75% maximum activation). Finally, we tested the null hypothesis that activation-dependent changes in soleus k_M would be proportional to and correlate with those in k_A.

Methods

Subjects and protocol:

Ten subjects participated (age: 24.5 ± 5.4 years, mass: 74.7 ± 12.7 kg, height: 1.8 ± 0.1 m). Subjects provided written informed consent as per The University of North Carolina at Chapel Hill Biomedical Sciences Institutional Review Board (16-0379). We excluded subjects using the following criteria: leg injury or fracture within the past 6 months, neurological disorder affecting the legs, taking medications that cause dizziness, or having a leg prosthesis. Subjects first walked for 6 minutes at 1.25 m/s on a treadmill to pre-condition their muscles and Achilles tendon (AT) ²⁵. Subjects then completed 3 maximum voluntary isometric plantarflexor contractions (IVCs) at a neutral ankle angle (i.e., 0°) in a dynamometer (Biodex Medical Systems, Inc.), from which we immediately extracted a reference maximum activation from a single differential wireless electrode (Trigno, Delsys, Inc., Natick, MA) with 10 mm inter-electrode distance placed over the soleus muscle of the right leg. Specifically, we placed the electrode approximately 2/3^rd distal to the lateral femoral condyles along a line projecting to the lateral malleolus, in line with the muscle fascicles following published recommendations²⁶. We prepped the skin by shaving, abrading, and using an alcohol wipe to clean the placement site. A MATLAB script (Mathworks, Inc., Natick, MA) stored the peak value from a 250 ms moving average of demeaned, full-wave rectified and bandpass filtered (20-450 Hz) electromyographic (EMG) data. To combat ankle joint rotation, we instructed subjects to keep their foot firmly fixed to on the dynamometer pedal, and secured the foot and leg using Velcro straps. During isometric trials, we measured that undesired heel-lift resulted in an ankle rotation of less than 5 degrees – an outcome fully consistent with that from other groups²⁷.

Subjects then watched a screen on which we projected their conditioned soleus activation in real-time as a dot with a target line corresponding to a percent of their reference maximum (Figure 1). Here, subjects completed 3 eccentric isokinetic plantarflexor contractions between 20° plantarflexion and 15° dorsiflexion at 30°/sec both at rest and at each of two prescribed activation levels (25% and 75% of their 0° IVC activation), all presented in a randomized order, and separated by at least 1 min. The subjects’ ankle angular velocity and right knee posture (~20° flexion) replicated the midstance phase of walking, during which the ankle is dorsiflexing against resistance from the active plantarflexor muscles and shared series elastic tendon²⁸. While keeping their foot firmly fixed to the dynamometer, we instructed subjects to “push like a gas pedal” (i.e., isolating their plantarflexor muscles) while matching their instantaneous EMG signal to the prescribed target line across the range of motion. Before the start of each isokinetic movement, subjects preloaded their plantarflexor muscles by matching their EMG signal to the prescribed target. Before collection, subjects briefly practiced the isokinetic movement and reported being comfortable in matching their EMG signal with prescribed target activations.

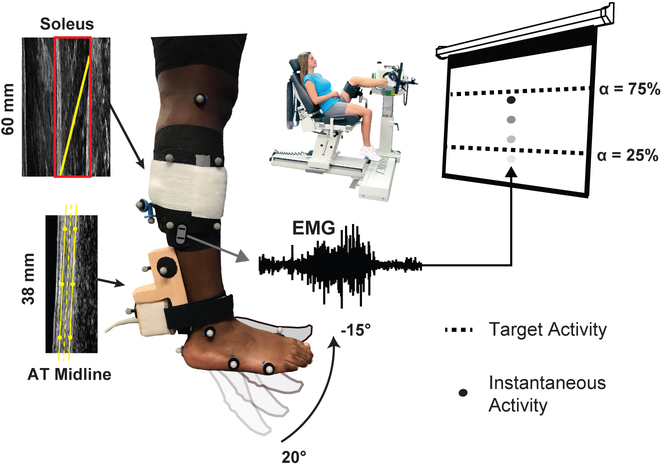
Figure 1.

Our approach utilized a custom visual biofeedback interface that prescribed soleus muscle activation (α = 25% and 75% maximum voluntary isometric activation), in addition to passive ankle rotation, during eccentric isokinetic plantarflexor contractions. Simultaneously, ultrasound imaging captured soleus muscle fascicle length changes (proximal probe) and the Achilles tendon moment arm (distal probe).

Measurements:

A 60 mm Telemed Echo Blaster 128 ultrasound transducer (LV7.5/60/128Z-2, UAB Telemed, Lithuania) placed along the line of action of the soleus through the mid-belly of subjects’ right medial gastrocnemius recorded cine B-mode images from a longitudinal cross-section at 61 frames/s through a depth of 65 mm. Post collection, the same investigator completed all muscle tracking analysis, following the recommended best practices outlined by Farris and Lichtwark (2016). Briefly, we defined a static polygon region of interest surrounding the soleus and its corresponding aponeuroses. Within the region of interest, we then defined one soleus muscle fascicle in the mid-region of the imaged plane, considered representative of the muscle belly, from superficial to deep aponeurosis. An available MATLAB routine (UltraTrack²⁹) performed an affine extension to an optic flow model to estimate time series of soleus fascicle length and pennation angle (relative to the horizontal axis of the image). Finally, we defined soleus muscle length as the product of soleus fascicle length and the cosine of the pennation angle.

To determine subject specific moment arms, a second 38-mm transducer (L14-5W/38, Ultrasonix Corporation, Richmond, BC) operating at 70 frames/s recorded 128 lines of ultrasound radiofrequency data from the subjects’ right Achilles free tendon, distal to the soleus muscle-tendon junction. For each subject, we quantified the soleus muscle-tendon moment arm using a previously published technique³⁰. Briefly, we first defined an AT line of action as the best fit line centered between superficial and deep tendon edges. We then co-registered the AT line of action with the instantaneous location of the transmalleolar midpoint, estimated from the lateral and medial malleoli marker trajectories. Finally, we applied a coordinate transformation between AT ultrasound images and three rigid markers on the custom orthotic and estimated the perpendicular distance from the AT midline to the transmalleolar axis, which we defined as the AT moment arm.

Eight cameras from a 14-camera motion capture system (Motion Analysis, Cor., Santa Rose, CA, 100 Hz) recorded trajectories of 14 retroreflective markers located on the subjects right lower leg and each ultrasound transducer. We estimated the ankle joint angle during each contraction using an inverse kinematics routine previously described³¹. Finally, we recorded the net ankle moment at 1000 Hz using an analog-to-digital converter (NI USB-6225 Pinout, National Instruments, Austin, TX) in synchrony with motion capture and ultrasound measurements. We corrected for gravity using a built-in zeroing procedure which adjusted the dynamometer torque measurements at a neutral ankle angle prior to the isolated contractions.

Stiffness Calculations:

“Muscle stiffness” is often described in terms of short-range stiffness - the intrinsic stiffness of myofilaments, without input from neural control³². In contrast, we define muscle stiffness in terms of the muscle’s length-tension relation, which some authors suggest is more relevant to locomotor function^{33, 34} Here, we first resolved net triceps surae muscle force by dividing subjects’ net ankle moment by their moment arm. We then estimated soleus muscle force by scaling triceps surae force by the relative physiological cross-sectional area attributed to the soleus (i.e., 63%)³⁵. Finally, for each subject, we defined: (i) muscle stiffness (k_M) as the change in soleus muscle force divided by the change in soleus muscle length, and (ii) ankle joint quasi-stiffness (k_A) as the change in ankle moment divided by the change in ankle angle.

Statistical Analysis:

A repeated measures ANOVA tested for significant main effects of muscle activation on k_M and k_A using an alpha level of 0.05. We report Cohen’s d effect sizes for all comparisons³⁶. We calculated sensitivities (i.e., slope) of k_M and k_A to altered activation over two differences in soleus activation (i.e., from passive to 25% IVC and from 25% IVC to 75% IVC), defined as the change in stiffness divided by the change in activation. Two series of paired sample t-test compared differences in sensitivity between: (i) k_M and k_A and (ii) between regions of activation. To assess the relation between k_M and k_A, we performed linear regressions and report Pearson’s correlation coefficients between these outcome measures at each of our three muscle activation target levels. Finally, we also calculated Pearson’s correlation coefficients between the sensitivities of k_M and k_A for both changes in activation.

Results

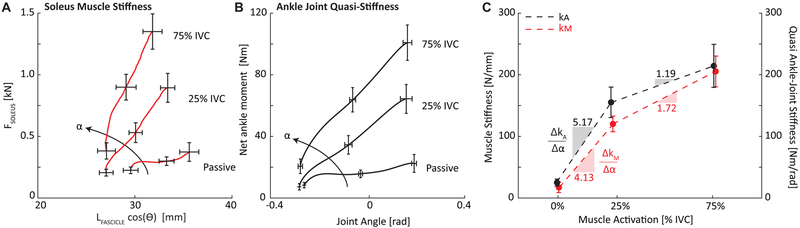
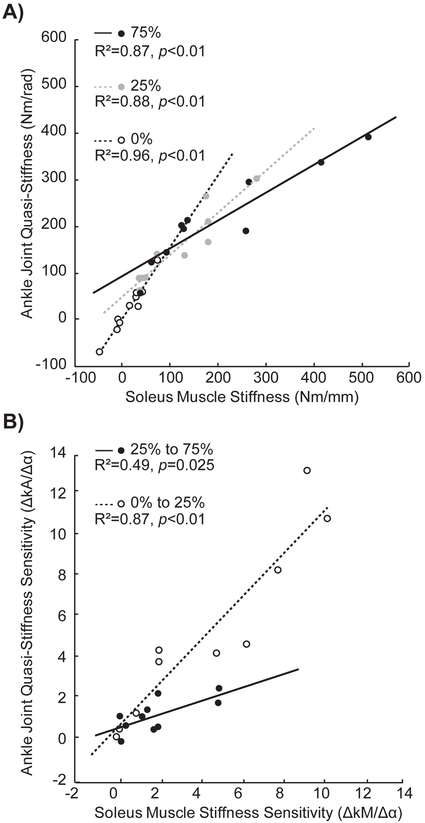
Using the Shapiro-Wilk test for normality, k_M and k_A were both normally distributed at each activation condition (passive, 25%, and 75% soleus activation). In the absence of muscle activity, we found relatively negligible values of k_M and k_A across the range of ankle rotation observed during walking. In contrast, both values increased significantly with increased muscle activation (p-values<0.001). On average, k_M was 15 N/mm during passive rotation, 118 N/mm at 25% IVC rotation, and 204 N/mm at 75% IVC rotation (Figure 2A). On average, k_A was 24 Nm/rad during passive rotation, 154 Nm/rad at 25% IVC rotation, and 213 Nm/rad at 75% IVC rotation (Figure 2B). The sensitivity of k_A to altered activation tended to average 25% greater than that of k_M from 0% to 25% IVC (p=0.069, d=2.25, Figure 2C). Compared to changes at 25% IVC, k_A was significantly less sensitive to further increasing activation to 75% IVC (p=0.016, d=1.25) – a change indistinguishable from that of k_M (p=0.230) (Figure 2C). Likewise, k_M was also less sensitive to further increasing activation to 75% IVC (p=0.025, d=0.81). Independent of activation level, k_A positively correlated with k_M (0% IVC: R²=0.96, 25% IVC: R²=0.88, 75% IVC: R²=0.87; p-values<0.001, Figure 3A). Similarly, the sensitivities of k_A to changes in muscle activation positively correlated with those of k_M (0% IVC to 25% IVC: R²=0.87, p<0.001; 25% IVC to 75% IVC: R²=0.49, p=0.025; Figure 3B).

Figure 2.

(A) Group mean data for soleus muscle stiffness, k_M, as given by the relation between soleus muscle force (F_SOLEUS) and soleus muscle length (L_SOLEUS). L_SOLEUS gives length change along the line of action of the soleus muscle, equal to the length of the fascicle (L_FASCICLE) multiplied by the cosine of pennation angle (θ). (B) Group mean data for ankle joint quasi-stiffness, k_A, at each soleus activation level (α), given by the relation between net ankle moment and ankle joint angle (dorsiflexion positive). (C) Group mean k_M and k_Aas a function of soleus activation. Sensitivity to altered activation was calculated as the slope of each region of stiffness versus activation (group mean values shown). Bars on all panels represent standard error of the mean.

Figure 3.

(A) During passive rotation, and at each target activation level, ankle joint quasi-stiffness positively correlated with soleus muscle stiffness. (B) Similarly, the sensitivity (change in stiffness, Δk, divided by the change in activation, Δα) of k_A for each change in activation positively correlated with that of k_M.

Discussion

Ankle joint quasi-stiffness has been commonly used as an aggregate measure of the complex mechanical behavior of the human ankle joint, but the extent to which that measure reflects the neuromechanical behavior of the triceps surae muscle-tendon units spanning the ankle remains unclear⁵. Here, we investigated the role of muscle activation and thus soleus muscle length-tension behavior in augmenting ankle joint quasi-stiffness during controlled contractions. Our findings fully support our first hypothesis; soleus k_M and k_A increased with increasing muscle activation. We also found convincing evidence that not only were soleus k_M and k_A significantly and positively correlated, but so too were their sensitivities to changes in soleus activation. However, in support of our second hypothesis, activation-dependent changes in k_A and k_M were more complex than perhaps previously appreciated; the sensitivity of k_A and k_M to the onset of soleus activation (i.e., from 0% to 25% maximum activation) was much greater than that to subsequent increases in activation (i.e., from 25% to 75% maximum activation). Furthermore, the sensitivity of k_A to soleus activation tended to be larger than that of k_M for low, but not high activation levels. As we elaborate in more detail below, we suspect this difference may reflect the interaction between activation-independent elastic components (i.e., tendon stiffness) and activation-dependent active components (i.e., muscle stiffness) comprising the triceps surae muscle-tendon unit. Taken together, our findings provide additional insight into how the control of triceps surae muscle behavior serves to functionally augment ankle joint quasi-stiffness via changes in activation.

In the absence of muscle activity, we found near negligible stiffness values for k_M and k_A - findings consistent with those of Chino and Takahashi (2018) and Lamontagne et al. (2000) for k_A^{21, 37}. For the range of motion tested, a range resembling that in walking, the Achilles tendon may not have been sufficiently engaged during passive rotation³⁸. Accordingly, for this condition, we posit that k_M and k_A were influenced only by the passive mechanical properties of other periarticular structures spanning the ankle. This may explain the exceptionally strong relation between k_M and k_A during passive rotation, wherein muscle stiffness explained 96% of the measured variance in ankle joint quasi-stiffness. This strong relation may at first appear at odds with the recent findings of Chino and Takahashi (2018), who found no significant correlation between passive medial gastrocnemius muscle stiffness and k_A at four different ankle angles²¹. However, earlier work from those authors reported significant correlations between k_M and k_A at more dorsiflexed postures, suggesting that in the absence of muscle activation, k_M may augment k_A only when those muscle-tendon units are sufficiently lengthened²². Furthermore, the medial gastrocnemius, unlike the soleus, is a biarticular muscle that is necessarily affected by knee rotation³⁹.

Compared to values measured during passive ankle rotation, k_M and k_A both increased significantly and in relative proportion to one another with increased soleus activation. However, as anticipated, k_M and k_A were much more sensitive to the onset of activation to than to a subsequent increase in activation. There are several potential mechanisms for those non-linear relations with soleus activation. As one conceptual explanation, from 0% to 25% IVC, increased muscle activity could augment k_a directly by increasing k_M and indirectly by engaging the series elastic tendon. Consistent with this premise, we found that the sensitivity of k_A to altered activation averaged 25% greater than that of k_M from 0% to 25% IVC (i.e., Δk_A>Δk_M). Thereafter, the contribution of tendon stiffness to k_A is presumably independent of activation⁶; further increases in muscle activity should augment k_A only by increasing k_M (i.e., from 25% to 75% IVC), a notion fully consistent with our experimental findings (i.e., Δk_A≈Δk_M).

However, those factors alone would not necessarily explain the non-linear relation between k_M and soleus activation. Intuitively, one might presume a positive linear relation between k_M and muscle activation. Indeed, Kubo (2014) found something approximating such a relation for the medial gastrocnemius⁶. We do not suspect that the soleus is altogether different from the gastrocnemius. Rather, the approach used by Kubo (2014) incorporated a short-range stretch experiment with non-uniform angular velocity, and the viscoelastic behavior of the medial gastrocnemius could have influenced their outcomes⁴⁰. Ultimately, we suspect that the non-linear relation between k_M and soleus activation likely arises from some combination of the effects of muscle activation on soleus fascicle operating length, biaxial aponeuroses strain, the contribution from other plantarflexor muscles, and/or muscle gearing. Compared to those during passive ankle rotation, soleus fascicles became notably shorter at the same initial ankle joint position with the onset of muscle activation, but not with further increases in activation. This disproportionate shift toward shorter muscle fascicles could itself explain the non-linear relation between k_M and activation, as could the accompanying shift in soleus contractile behavior to a steeper region of their active length-tension relation. In addition, Azizi and Roberts (2009) revealed that in the presence of muscle activation, biaxial aponeurosis strain along the lateral gastrocnemius may modulate effective stiffness in the longitudinal direction^41,42. Moreover, there is growing evidence that biaxial shape change of perimuscular structures can directly alter muscle force-length relations⁴³. It thus seems plausible that these effects could augment the sensitivity of k_M to changes in soleus activation. Finally, muscle gearing, the relation between fascicle shortening and rotation, may also play a role in regulating k_M in response to muscle activation. Soleus muscle fascicle rotation is inversely proportional to muscle activation and is altered by shortening velocity^44-46. During low-load contractions (i.e., 25% activation), dynamic muscle-shape changes promote an increase in fiber rotation⁴⁷ to facilitate faster muscle-tendon unit shortening. In contrast, muscle-shape changes during high-load contractions (i.e., 75% activation) resist fiber rotation in order to meet mechanical demand and favor force output over velocity output⁴⁷. Together, these findings allude to a complex interaction between muscle activation and the length and force profiles used here to estimate stiffness at the muscle level. In addition, we only explored two changes in soleus activation level, which may limit our ability to make higher resolution inferences. Future studies should consider investigating intermediate activations to study the extent to which these relations are truly non-linear.

Limitations:

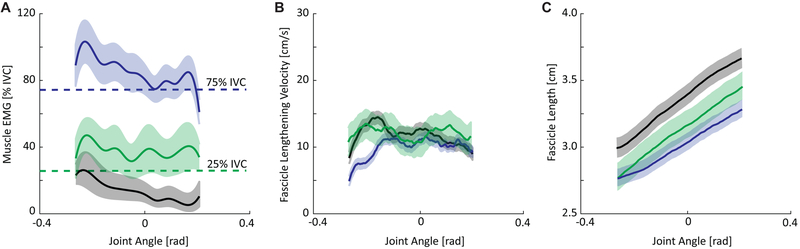
First, we used default settings in this tracking routine, which defined pennation angle relative to the horizontal axis of the image, and thus is not representative of true pennation angle. To minimize aponeuroses misalignment, the same investigator placed the ultrasound probe for all subjects and took care to ensure that the superficial aponeuroses of the soleus muscle was parallel with the imaging plane during data collection. Second, the soleus muscle is but one contributing to ankle plantarflexion and is itself comprised of different components that differ in architecture⁴⁸. We only imaged the posteromedial soleus, which may not represent other regions (i.e., anterior medial, anterior lateral, and posterolateral). Two-dimensional ultrasound imaging may not fully capture the three-dimensional behavior of the soleus muscle. Moreover, the behavior of the soleus maybe not fully represent other muscles of the triceps surae. Conversely, the soleus has by far the largest force generating capacity of the three muscles⁴⁹, experiences greater fascicle shortening and rotation⁵⁰, and has the greatest influence on Achilles tendon tissue displacements⁵¹. Third, subjects generally adhered well to activation targeting in our biofeedback paradigm, though visual inspection revealed that activation did vary across the range of motion. However, biofeedback was successful in prescribing distinct ranges of soleus activation necessary to test our hypotheses (Figure 4A). Fourth, although likely negligible compared to reported values for maximum isometric tasks, undesired ankle rotation via heel-lift may have influenced the isokinetic nature of our isolated contractions and resulting muscle fascicle kinematics. Fifth, we did not collect EMG from the hamstring or quadriceps muscles, and therefore cannot fully exclude their contribution to the measure net ankle moment. However, we believe that proper alignment between the axis of rotation of the dynamometer and that of the ankle joint mitigated those effects. Finally, we focus on soleus length-tension behavior but acknowledge that muscle stiffness can exhibit velocity dependence – a parameter for which we did not control ⁵². In a post-hoc analysis, we found only relatively small effects of condition on lengthening velocity beyond the initial onset of rotation (Figure 4B).

Figure 4.

(A) Group mean data for electromyographic activity of the soleus muscle during passive ankle rotation (black) and during the 25% IVC (green) and 75% IVC (blue) prescribed activations across the range of motion tested (dorsiflexion positive). Horizontal dashed lines represent target EMG activations based on maximum activation extracted from the 0° isometric voluntary contraction (IVC). (B) Group mean data for soleus fascicle lengthening velocity during passive ankle rotation (black) and during the 25% IVC (red) and 75% IVC (blue) prescribed activations across the range of motion tested. Here, shaded regions represent standard error of the mean. A post-hoc repeated measures ANOVA (condition × 20% ankle rotation bins) revealed that the 75% IVC condition exihibited slower fascicle lengthening compared to the other conditions (p-values<0.050), but only during the first 40% of ankle rotation (i.e., 14°). (C). Group mean soleus fascicle length behavior during passive ankle rotation (black) and during the 25% IVC (red) and 75% IVC (blue) prescribed activations across the range of motion tested.

We first conclude that soleus k_M and k_A exhibit non-linear relations with muscle activation and were more sensitive to the onset of activation than to subsequent increases in activation. Our findings also suggest that, over a relatively large activation range, k_A emerges as a combination of activation independent elastic components (i.e., tendon stiffness) and activation dependent active components (i.e., muscle stiffness). These findings could be important to improve our understanding of normal and pathological ankle joint function. Our data also has the potential to inform the design and efficacy of wearable assistive devices that replace or augment mechanical behavior of the biological ankle joint. Finally, we posit that a similar approach could inform the personalized prescription of such devices; tendon stiffness decreases in aging⁵³ and following stroke⁵⁴, with effects that could alter the mapping between muscle activation and ankle joint quasi-stiffness.