Effect of hot carcass weight on the rate of temperature decline of pork hams and loins in a blast-chilled commercial abattoir

Abstract

Adequate carcass chilling is required to optimize pork quality and food safety. The rate at which carcasses chill is dependent on their mass. Hot carcass weight has increased steadily over the years, certainly affecting the chilling rate of the average carcass in contemporary abattoirs. Therefore, the objective was to model the effect of HCW on temperature decline of a contemporary population of pork carcasses slaughtered at a commercial abattoir that used a blast-chilling method. In addition, carcasses were sorted into HCW classes, and the effect of HCW group was tested on the rate of temperature decline of the longissimus dorsi and semimembranosus. Hot carcass weight, internal temperature of the loin muscle (at the 10th rib) and ham, as well as ambient temperature, were recorded from 40 to 1,320 min postmortem (45 time points) on 754 pork carcasses. An exponential decay model based on Newton’s law of cooling, $T(t)=T_a+(T_0-T_a)e^{-kt}$, was fit to temperature decline of the ham and loin of the whole population using PROC MODEL of SAS. The initial models for the decline of both ham and loin temperature displayed significant autocorrelation of errors based on evaluation of the autocorrelation function plots and Durbin–Watson test (P < 0.0001). Therefore, second- and third-order autocorrelation parameters were tested. Based on Durbin–Watson test, the use of second-order autocorrelation model with lags of 1 and 2 was deemed adequate and was therefore included in all subsequent models. This base model and its respective parameter estimates were all significant (P < 0.01) for the whole population. Carcasses approximating 85, 90, 95, 100, and 105 kg (± 1 kg) were selected and binned into their respective weight classes. Dummy variables were used to compare the effect of HCW class on parameter estimate of ham and loin models. The developed model significantly fit all weight classes (P < 0.01) for both ham and loin temperature decline. For both loin and ham models, estimates of the rate constant (k) generally decreased as HCW increased. For loin temperature, k estimate for 105-kg carcasses was 0.00124 less (P = 0.02) than 85-kg carcasses, with the intermediate HCW classes not differing from the 85-kg class. For ham temperature, estimates of k for 90, 95, 100, and 105 kg HCW were all significantly and successively less than the k estimate for 85 kg class. For perspective, loins of 95-kg carcasses were estimated to reach 2 °C in 17 h, whereas loins from 105-kg carcasses would not reach 2 °C until 27 h. For hams, 95-kg carcasses were projected to reach 2 °C in 21 h, whereas those from 105-kg carcasses would take 28 h. Overall, HCW significantly affects the rate of temperature decline of pork hams, but not loins from pork carcasses weighing between 85 and 100 kg.

INTRODUCTION

The rate of temperature decline of pork carcasses has manifold effects on the safety and quality of the meat. As an example, when meat quality traits of pork carcasses chilled in blast-chilled systems (rapid chilled) were compared with conventional spray chilled systems, loins from spray chilled carcasses were >10°C warmer after 6 h postmortem (Shackelford et al., 2012). This difference in chill rate resulted in 0.16 percentage unit reduction in purge loss of rapidly chilled carcasses, but a 13-fold increase in the frequency of excessively tough (slice shear values > 25 kg) loin chops (Shackelford et al., 2012). This influence on instrumental tenderness plays a major role in determining the eating quality of meat. In both beef and pork, a phenomenon known as “cold-shortening” can occur when pre-rigor muscle is cooled to below 10 °C in 3 h or less (Dransfield and Lockyer, 1985). The result is a shortening of the muscle fibers and the meat yielded being tougher and having lesser water-holding capacity than carcasses that have undergone a more moderate temperature decline (Ertbjerg and Puolanne, 2017). On the other extreme, temperature decline that occurs too slowly causes other problems. The conversion of muscle to meat is, in large part, defined by the decline in pH from physiological homeostasis (~7.2) to an ultimate pH of 5.5 to 5.8, typically achieved by approximately 24-h postmortem. There are certain conditions, such as acute ante-mortem stress, which can cause this temperature decline to be expedited or for the ultimate pH of the meat to decline to below 5.5. When such a rapid pH decline is coupled with an inadequate decline in temperature, myofibrillar, and sarcoplasmic proteins are denatured. The product of this rapid pH decline coupled with elevated temperature is meat that is pale in color, soft in texture, and has a drastically reduced ability to hold and retain moisture (Wismer-Pederson and Briskey, 1961). In pork, this condition is known as Pale, Soft, and Exudative, and severely reduces the eating quality of the meat and poses significant challenges when further processed into sausage or ham (Barbut et al., 2008).

In a study using conventional chilling, Brown and James (1992) reported that chilling time required to reach an optimal temperature of 7 °C can be reduced by either lowering the ambient air temperature or increasing the air velocity. Brown and James also calculated the heaviest carcass that could be cooled to optimal temperature within 16 h at various ambient air temperatures and velocities. The heaviest carcass to reach optimal temperature was 110 kg, chilled at 0 °C with a velocity of 3.0 m/s. All other chilling combinations of temperature and air flow resulted in only lighter carcasses reaching temperature, with 95-kg carcasses being the heaviest cooled at 4 °C and 60-kg carcasses being the heaviest cooled at 6 °C (Brown and James, 1992). However, due to the few number of carcasses used, ambient temperature was able to be maintained throughout the chilling period following a minimal increase during loading, and air velocity was constant over the entire surface of the carcass. These conditions would rarely, if ever, be attainable in a modern commercial packing facility. Furthermore, the implementation of blast chilling prior to storage in a cooler may change these parameters.

Prior to 2016, the most recent large (>1,000 pigs/d) U.S. pork abattoir to begin production was in 2006. At that time, the average U.S. pork carcasses weighed 90 kg (USDA, 2018). Today, the average U.S. pork carcass weighs 95 kg (USDA, 2018). In fact, over the last 30 years, the average HCW in the U.S. pork industry has increased by approximately 0.5 kg per year (Harsh et al., 2017). Though this has its advantages, with more saleable product yielded per unit (Wu et al., 2017), it does pose potential challenges for the industry. There are more than 40 pork abattoirs in the United States (National Pork Board, 2017). Many were built when pork carcasses were much lighter than today. This means it is possible that the cooling systems were designed to chill a lighter carcass. This juxtaposition of facility design and the carcass weight of pigs currently being marketed presents many challenges to the industry, of which a primary concern is carcass chilling. Heavier carcasses have a smaller surface area to volume ratio and almost certainly do not reach desired internal temperatures at the same rate as smaller carcasses. However, differences in chilling rate have not been routinely reported, and no such model has been developed for a large-scale blast-chilled pork abattoir.

Therefore, the objective of this study was to model the temperature decline of the loin and ham of a population of pork carcasses from a commercial abattoir that used a “blast”-chilling method. In addition, carcasses were sorted into subpopulations based on HCW, and the effect of HCW group was tested on the estimated parameters of the model.

MATERIALS AND METHODS

Carcass Description

All carcass measurements followed humane slaughter and removal of organs. No live animal interactions occurred during this study; therefore, Institutional Animal Care and Use Committee approval was not obtained. Pork carcasses (753 total) used in the present study represented 10% of the population used in the study by Arkfeld et al. (2016). Greater details about the pig’s background, marketing program, and production strategy of the pigs were outlined by Arkfeld et al. (2016). Pigs were slaughtered under the supervision of the USDA Food Safety Inspection Service at a federally inspected abattoir using carbon dioxide gas followed by exsanguination. Data presented from this study represent 16 individual slaughter days. Investigators were not made aware of management information regarding diet, genotype, barn type, or floor space.

Temperature Measurement

At 31 min postmortem, 3 temperature data loggers were inserted into the carcasses (Thermochron-iButton-40Cthru-85C, Embedded Data Systems, Lawrenceburg, KY). The loin temperature data logger was placed in an incision made between the tenth and eleventh ribs; semimembranosus temperature was measured posterior to the symphysis pubis bone; ambient temperature was recorded by attaching the data logger to a shroud pin in the spinous process of the thoracic vertebrae at approximately the fifth rib. Data loggers recorded the time and temperature at 1-min intervals. The data loggers were removed from the carcasses as the carcasses entered the cutting floor (approximately 22 h postmortem). Temperature recordings from 40 min to 22 h postmortem were used for analyses. Carcasses were also evaluated for HCW, back fat depth, and loin depth using a Fat-O-Meater probe (SFK Technology A/S, Herlev, Denmark).

Model Development

Newton’s law of cooling states that the rate of change in temperature of an object is proportional to the difference in temperature of the object and the ambient temperature of its environment, defined by the following differential equation:

$${\displaystyle \begin{array}{l}{\displaystyle \frac{dT}{dt}=-k(T-T_a)}\end{array}}$$ (1)

where k is the fractional rate constant, T is the temperature of the object, and T_a is the ambient temperature. This function can be manipulated to solve for the temperature of the object:

$${\displaystyle \begin{array}{l}{\displaystyle T(t)=T_a+(T_0-T_a)e^{-kt}}\end{array}}$$ (2)

where T_a is the ambient temperature, T₀ is the initial temperature (in this case, the maximum temperature), and k is the fractional rate constant (°C/min).

Statistical Analyses

Data were analyzed using nonlinear, autocorrelation regression, fitting the data to a modified exponential decay model using the MODEL procedure of SAS (v. 9.4, SAS Inst. Inc., Cary, NC). The Durbin–Watson (DW) test was used to test for autocorrelation of the model and models were considered significantly autocorrelated when the DW statistic was <0.80 or >3.20. Parameter estimates for each modeling parameter were considered significant at P ≤ 0.10. Comparisons of estimated parameters between HCW classes were conducted by using “dummy” variables. Parameter estimates were considered different at P ≤ 0.10. Means of muscle temperatures among carcasses of increasing weight were considered different at P < 0.05.

RESULTS AND DISCUSSION

Modeling the Population

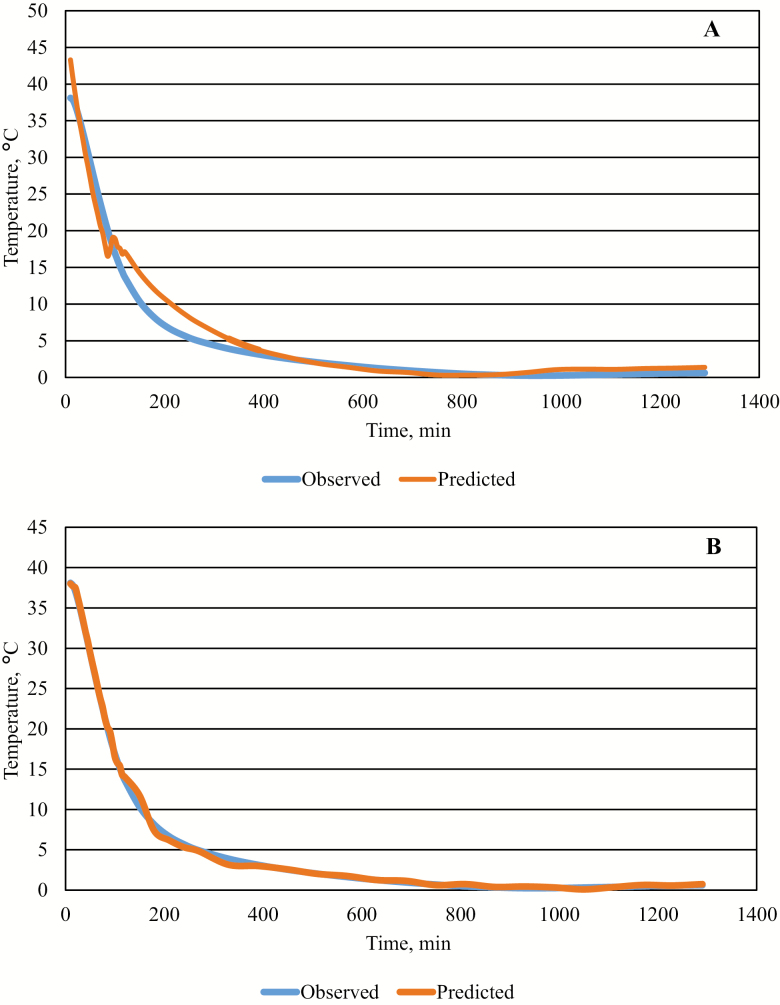
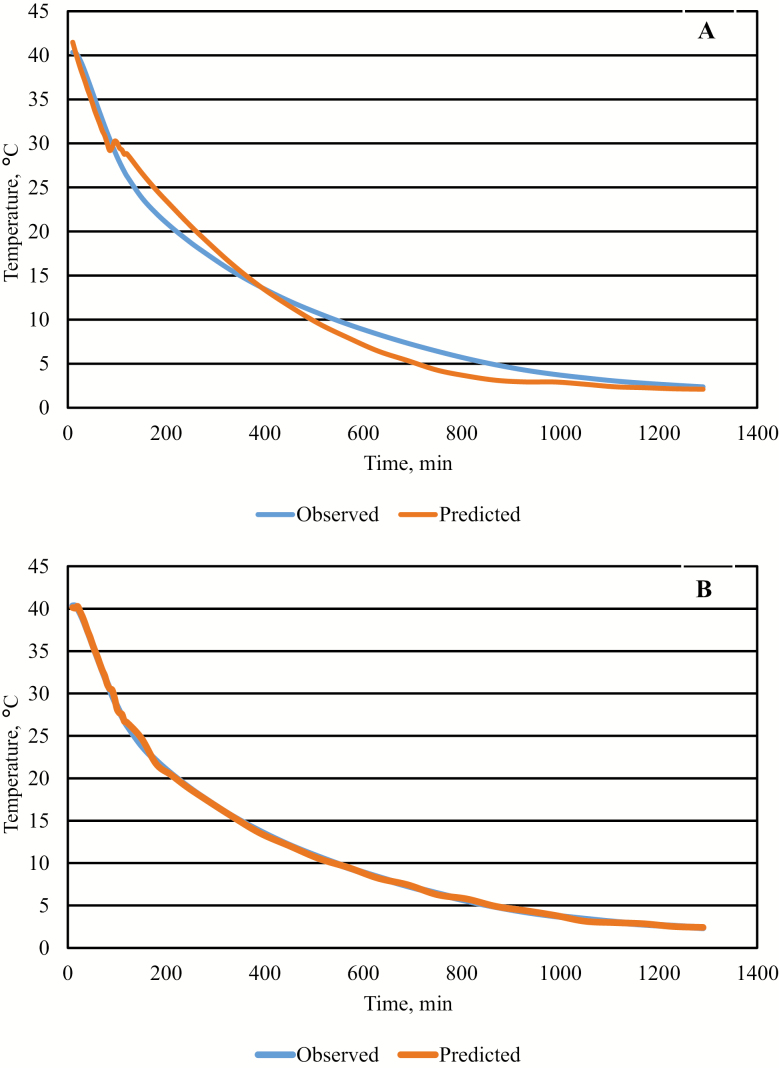
Hot carcass weight of split carcasses sourced for the present study averaged 94.5 kg (Arkfeld et al., 2017) and was representative of the average HCW of pigs currently slaughtered in the United States (USDA, 2018). The average HCW of the subpopulation (94.0 kg) of carcasses used for this analysis was representative of the parent population (Table 1). The model shown in Eq. 2 was first fit to the data points representing the mean loin and mean ham temperature over the course of the chilling period. Although the models were approximate fits for both the loin and ham temperature decline (Figs. 1A and 2A), both exhibited significant autocorrelation (“Durbin–Watson”; Tables 2 and 3) and estimates of initial temperature (T₀) were approximately 5 °C greater than what was actually observed. Furthermore, the prediction equation became unstable around the 90 min postmortem time point, when the carcasses transitioned from the subzero ambient temperature of the blast chill into the considerably warmer equilibration coolers. This large change in ambient temperature presents the primary challenge in predicting chilling curves for blast-chilling systems: there are essentially 2 chilling systems, which results in what could be considered 2 distinct chilling curves. Previous researchers have attempted to address this through splining 2 or more polynomial functions (van de Ven et al., 2014). Although such an approach may be adequate for modeling temperature decline on a case-by-case basis, it lacks the ability to be broadly applied to all-such systems, which may have different blast-chilling durations, or even step-up chilling protocols. Furthermore, a spline approach does not address the root cause of the instability in the models: the correlation between temperatures at adjacent time points, regardless of differences in the ambient temperature. Such correlation, or more specifically, autocorrelation is common in time series data. It is this same property that necessitates the use of repeated measures approaches to calculating errors when estimating treatment effects in studies where the same experimental unit is measured repeatedly over time (e.g., shelf life studies). To address the autocorrelation issue, lags were accounted for in the model by using a second-order autoregressive adjustment using the AR(2) macro in the MODEL procedure of SAS 9.4. First and third autoregressive structures were also tested. The first-order model did not sufficiently mitigate the autocorrelation, and the third-order model did not return a significant benefit of reducing the autocorrelation compared with the second-order model (as determined by comparison of Akaike’s information criterion between models). All parameter estimates of this lag-corrected model were significant (P < 0.01), and issues of autocorrelation were resolved for both the temperature decline of the loin (Table 2) and ham (Table 3). The resulting prediction curves displayed reduced instability around the 90-min time point, more closely resembling the observed data than the prediction curve from the base model, further substantiating the efficacy of the autocorrelation regression approach. Models have been previously developed to monitor temperature decline for beef (Bruce, 2004; Kuffi et al., 2016) and pork (Coulter et al., 1995). However, many of these studies, especially those focusing on pork, were conducted to understand the specific mechanisms affecting heat transfer and thermodynamics. As such, these studies were conducted under highly controlled conditions, with constant temperatures. Although such experimental conditions provide an ideal setting for understanding fundamental mechanisms, temperatures in modern U.S. pork packing facilities routinely fluctuate throughout the course of a production day. The progression through the slaughter and chilling process is often accompanied with changes in ambient temperature, especially in the cases where blast chilling at temperatures below −20°C are followed by an equilibration period at around 0 to 2 °C. Even so, it was not surprising that heavier carcasses from this study chilled slower than lighter carcasses. Daudin and Kuitche (1996) demonstrated differences in chilling kinetics due to a host of parameters associated with increasing carcass weights. Because of that a dynamic model, such as the one used in this study, is necessary to account for the varying nature of ambient temperature in a U.S. abattoir. However, accounting for this alone was not sufficient, and in fact, probably contributed to the severe autoregressive nature of the errors. Previous attempts to model temperature decline of carcasses or carcass components have proven challenging. This difficulty can be attributed to the irregular shape of carcasses (Wang and Sun, 2003) and the autocorrelation of errors often inherent with time series data. With the models including the fluctuating ambient temperature, the correlation among time points was probably reinforced.

Table 1.

Summary statistics of pork carcass traits¹

Trait	Min	Q1	Median	Q3	Max	Mean	SD
HCW, kg	56.7	88.9	94.8	99.8	118.8	94.0	9.0
BF depth,2 mm	6.0	12.0	15.0	18.0	29.0	15.3	3.9
Loin depth, mm	41.0	62.0	67.0	73.0	90.0	67.7	8.4

¹Q1 = first quartile; Q3, third quartile.

²BF = back fat.

Figure 1.

Predicted and observed temperature decline of the loin of pork carcasses from a commercial blast-chilled abattoir. (A) Not accounting for lag. (B) Using a second-order autoregressive [AR (2)] model. Temperatures reported in °C. Time reported in minutes.

Figure 2.

Predicted and observed temperature decline of the ham of pork carcasses from a commercial blast-chilled abattoir. (A) Not accounting for lag. (B) Using a second-order autoregressive [AR (2)] model. Temperatures reported in degrees °C. Time reported in minutes.

Table 2.

Parameter estimates for temperature decline of the loin in a commercial pork abattoir that uses blast chilling¹

Parameter	Estimate	SE	P-value2	DW3	R 2 (adj.)
No lag
T0	47.34	1.33	<0.0001	0.13	0.97
k	0.008	0.0004	<0.0001
Autoregressive (2)
T0	38.77	0.30	<0.0001	1.77	0.99
k	0.002	0.0004	<0.01
ρ1	1.92	0.06	<0.0001
ρ2	−0.93	0.06	<0.0001

¹T₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

² P is the probability that the parameter estimate is equal to zero.

³The Durbin–Watson (DW) statistic tests for the presence of autocorrelation among errors and possible values range from 0 to 4. DW = 2, no autocorrelation; DW < 2, positive autocorrelation; DW > 2, negative autocorrelation. Autocorrelation was considered significant when 1.5 > DW > 2.5.

Table 3.

Parameter estimates for temperature decline of the ham in a commercial pork abattoir that uses blast chilling¹

Parameter	Estimate	SE	P-value2	DW3	R 2 (adj.)
No lag
T0	42.99	0.55	<0.0001	0.09	0.99
k	0.003	0.0001	<0.0001
Autoregressive (2)
T0	40.80	0.19	<0.0001	1.84	0.99
k	0.0014	0.0002	<0.0001
ρ1	1.88	0.080	<0.0001
ρ2	−0.88	0.082	<0.0001

¹ T ₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

² P value is the probability that the parameter estimate is equal to zero.

³The Durbin–Watson statistic tests for the presence of autocorrelation among errors and possible values range from 0 to 4. DW = 2, no autocorrelation; DW < 2, positive autocorrelation; DW > 2, negative autocorrelation. Autocorrelation was considered significant when 1.5 > DW > 2.5.

Modeling by HCW

Hot carcass weight has been following an upward trajectory over the past 30 or more years in the United States (USDA, 2018), with HCW increasing at a rate of approximately 0.5 kg per year (Harsh et al., 2017). There is little indication that this trend will change in the foreseeable future. As carcasses increase in size and weight, all sectors of the industry are beginning to ponder and address the challenges that heavier carcasses may pose. The chilling rate of the carcasses stands at the forefront of these concerns, at least from the packer’s point of view. As carcasses increase in size, they are likely to have a reduced surface area to volume ratio. As heat generated by the carcass can only escape from the surface, it is likely that the rate of heat dissipation from larger carcasses will be reduced.

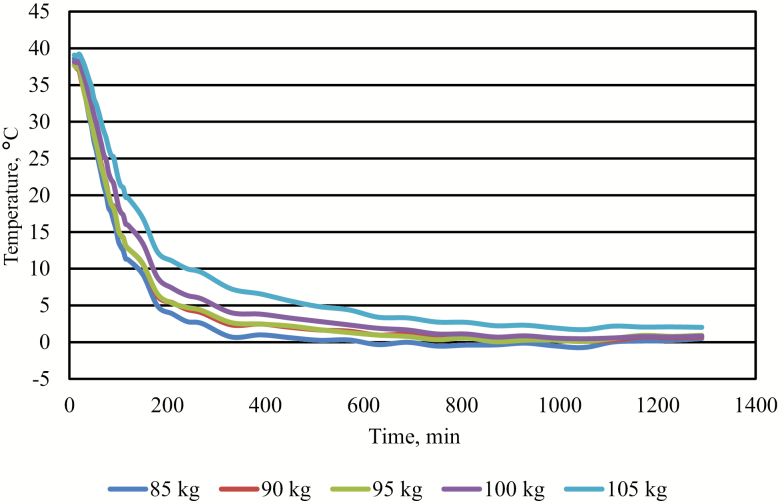
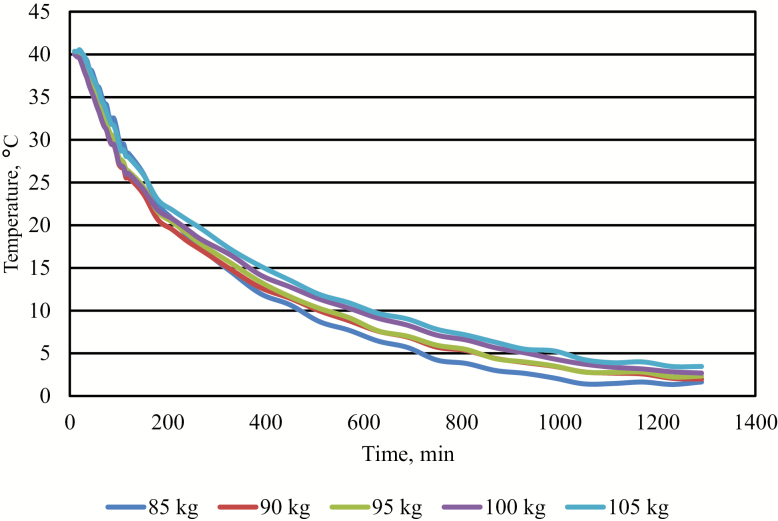
The model employed for the mean temperature decline of the loin and ham was used on groups selected from the larger population of carcasses into 5 HCW groups, in 5-kg increments (85, 90, 95, 100, and 105 kg; Table 4). The plot of the predicted loin temperature decline of these HCW groups is reported in Fig. 3 and Table 5, whereas predicted ham temperature decline is shown in Fig. 4 and Table 6. Comparing parameter estimates among the HCW groups revealed that there were in fact differences in initial temperature (T₀). However, there were no differences for the estimate of fractional rate constant (k) among the groups for either the loin (Table 7) or ham models (Table 8). In both the ham and loin, initial temperature (T₀) generally increased with carcass weight. However, this result appeared to be likely due to an error in the application of the analyses. The lack of difference in k parameter estimates appeared contradictory to the relationships displayed in the observed temperature decline, with there being no discernible difference among the HCW groups at the earliest time points and the predicted and observed lines deviating from one another at approximately 90 min into the chilling period. This fact was supported statistically when analysis of the raw data was conducted comparing the mean loin temperatures of the weight classes at the first three time points. There was no difference in loin temperature among the weight classes at the first (P = 0.81) or second time point (P = 0.25), but at the third time point measured (90 min), there were differences (P < 0.01) among the weight classes. The lack of difference in loin temperature among the weight classes at the earliest time points indicated that the significant differences in the estimates of initial temperature (T₀) were not valid. Furthermore, despite there being no statistical difference in the mean initial temperatures among HCW classes, temperatures separated at 90 min indicating that the differences in the shape of the temperature decline curves among the weight classes were in fact not due to differences T₀, but instead the rate of decline (k).

Table 4.

Observed temperatures of loins and hams from carcasses chilled using a blast-chill system during the first 22 h postmortem

HCW class, kg
Time	85	90	95	100	105	SEM	P-value
Postmortem, h:min	Observed loin temperatures, °C
1:00	34.1	34.0	33.9	35.3	35.9	1.4	0.53
5:00	2.5a	4.1ab	4.4b	6.0c	6.4c	0.8	<0.001
10:00	0.0a	1.3b	1.3b	2.1c	2.4c	0.4	<0.0001
15:00	−0.4a	0.3bc	0.1ab	0.5c	0.6c	0.2	0.01
20:00	0.1	0.5	0.7	0.5	0.7	0.2	0.23
22:00	0.3	0.6	0.8	0.6	0.7	0.2	0.52
Observed ham temperatures, °C
1:00	39.6	38.8	39.1	37.9	38.5	1.1	0.63
5:00	17.2	17.0	17.8	18.5	19.4	1.0	0.22
10:00	7.7a	8.8a	9.0a	10.3b	10.6b	0.6	<0.001
15:00	3.0a	4.4b	4.4b	5.6c	5.8c	0.5	<0.0001
20:00	1.5a	2.4b	2.6bc	3.1c	3.3c	0.4	<0.01
22:00	1.5a	2.1ab	2.3abc	2.8bc	2.9c	0.4	0.02

Least squares means within a row lacking a common superscript are different (P ≤ 0.05).

Figure 3.

Predicted temperature decline of the loin of pork carcasses sorted by HCW (kg) from a commercial blast-chilled abattoir. Temperatures reported in degrees °C. Time reported in minutes.

Table 5.

Parameter estimates for temperature decline of the loin of pork carcasses of various weights sourced from a commercial pork abattoir that uses blast chilling¹

	HCW, kg
	85	90	95	100	105
n	8	16	18	21	10
T 0	39.26	38.46	38.46	38.91	39.98
k	0.0015	0.0017	0.0017	0.0017	0.0020
ρ1	1.93	1.92	1.93	1.91	1.87
ρ2	−0.94	−0.93	−0.94	−0.92	−0.88
Durbin–Watson2	2.06	1.98	1.71	1.77	1.89
R 2 (adj.)	0.99	0.99	0.99	0.99	0.99

¹ T ₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

²The Durbin–Watson statistic tests for the presence of autocorrelation among errors and possible values range from 0 to 4. DW = 2, no autocorrelation; DW < 2, positive autocorrelation; DW > 2, negative autocorrelation. Autocorrelation was considered significant when 1.5 > DW > 2.5.

*The parameter estimate is different from zero (P ≤ 0.05).

Figure 4.

Predicted temperature decline of the ham of pork carcasses sorted by HCW (kg) from a commercial blast-chilled abattoir. Temperatures reported in degrees °C. Time reported in minutes.

Table 6.

Parameter estimates for temperature decline of the ham of pork carcasses of various weights sourced from a commercial pork abattoir that uses blast chilling¹

	HCW, kg
	85	90	95	100	105
n	8	16	18	21	10
T 0	40.81*	40.95*	41.05*	40.56*	41.09*
k	0.0018*	0.0014*	0.0015*	0.0012*	0.0015*
ρ1	1.80*	1.86*	1.86*	1.90*	1.84
ρ2	−0.81*	−0.87*	−0.86*	−0.90*	−0.84*
Durbin–Watson2	2.04	2.05	2.00	2.0731	1.90
R 2 (adj.)	0.99	0.99	0.99	0.99	0.99

¹ T ₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

²The Durbin–Watson statistic tests for the presence of autocorrelation among errors and possible values range from 0 to 4. DW = 2, no autocorrelation; DW < 2, positive autocorrelation; DW > 2, negative autocorrelation. Autocorrelation was considered significant when 1.5 > DW > 2.5.

*The parameter estimate is different from zero (P ≤ 0.05).

Table 7.

Testing effects of HCW class on estimates of T0 and k for temperature decline of the loin¹

	Estimate2	SE	P-value3
T 0
85 kg	39.27	0.30	<0.0001
(+/− compared with estimate of 85 kg)
90 kg	+5.26	2.48	0.04
95 kg	+5.20	2.46	0.04
100 kg	+5.66	2.54	0.03
105 kg	+6.36	2.70	0.02
k
85 kg	0.0015	0.0004	<0.0001
(+/− compared with estimate of 85 kg)
90 kg	+0.00006	0.00046	0.89
95 kg	+0.00002	0.00048	0.96
100 kg	−0.00004	0.00048	0.93
105 kg	+0.00026	0.00052	0.59
ρ1	1.92	0.026	<0.0001
ρ2	−0.93	0.026	<0.0001

¹ T ₀ is the initial temperature measured in °C, k is the rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

²Parameter estimates corresponding to the 85-kg class were considered the control. Values presented in the estimate column corresponding to 90- to 105-kg classes are adjustments compared with the parameter estimated for 85-kg class.

³All P values represent to probability that the estimate is equal to zero. For adjusted estimates, significant P values indicate that the parameter estimate for that weight class is different from the 85-kg class.

*The parameter estimate is different from zero (P ≤ 0.05). Lags (ρ1, ρ2) were not adjusted for HCW.

Table 8.

Testing effects of HCW class on estimates of T0 and k for temperature decline of the ham¹

	Estimate2	SE	P-value3
T 0
85 kg	40.73	0.20	<0.0001
(+/− compared with estimate of 85 kg)
90 kg	+5.64	1.74	<0.01
95 kg	+8.21	2.27	<0.01
100 kg	+7.60	2.31	<0.01
105 kg	+10.06	2.78	<0.01
k
85 kg	0.00149	0.00023	<0.0001
(+/− compared with estimate of 85 kg)
90 kg	−0.00023	0.00028	0.40
95 kg	−0.00020	0.00029	0.50
100 kg	−0.00039	0.00029	0.17
105 kg	−0.00017	0.00030	0.58
ρ1	1.88	0.03	<0.0001
ρ2	−0.88	0.03	<0.0001

¹ T ₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

²Parameter estimates corresponding to the 85-kg class were considered the control. Values presented in the estimate column corresponding to 90 to 105 kg classes are adjustments compared to the parameter estimated for 85-kg class.

³All P values represent to probability that the estimate is equal to zero. For adjusted estimates, significant P values indicate that the parameter estimate for that weight class is different from the 85 kg class.

*The parameter estimate is different from zero (P ≤ 0.05). Lags (ρ1, ρ2) were not adjusted for HCW.

Therefore, a second analysis was conducted to compare only the differences in k among the weight classes, with the initial temperature (T₀) fixed, for both the loin (Table 9) and ham (Table 10). Testing the effect of HCW class on just k, it is apparent that the results are more indicative of the shape of the observed temperatures, and the decreasing value of k as HCW increases is indicative of a decrease in the rate of temperature decline as carcasses increased in weight. Based on this model, there were no differences in the estimate of the fractional rate constant (k) of the loin for carcasses from 85 to 100 kg, and therefore, there was no difference in the rate of temperature decline among these classes. However, the estimate of the fractional rate constant (k) for loins of 105-kg carcasses was significantly less (P = 0.02) than that of 85-kg carcasses. Thus, it can be concluded that the rate of temperature decline for 105-kg carcasses was slower than that of 85-kg carcasses. A similar result was observed when the effect of HCW class was tested on the estimate of k alone for temperature decline of the ham, as the estimate of k for each of the HCW classes from 90 to 105 kg was significantly less than (P < 0.01) that of 85-kg carcasses. Previously, Maribo et al. (1998a,b) reported that neither carcass weight nor lean meat content influenced the course of temperature decline. However, the carcasses evaluated in that study averaged 75.7 kg, and almost certainly did not represent the range of HCW, or the range in lean meat percentage or carcass adiposity evaluated in the present study. It should also be noted that Maribo et al. (1998a,b) used a fifth-order polynomial model to fit their temperature decline data, which almost certainly would not have reflected to latent physical mechanisms driving temperature change.

Table 9.

Testing effects of HCW class on estimates of the fractional rate constant (k) for temperature decline of the loin, with initial temperature (T0) assumed to be unaffected by HCW¹

	Estimate2	SE	P-value3
T 0	40.47	0.20	<0.0001
k
85 kg	0.0031	0.0003	<0.0001
(+/− compared with estimate for 85 kg)
90 kg	−0.00033	0.00031	0.30
95 kg	−0.00025	0.00034	0.46
100 kg	−0.00039	0.00034	0.24
105 kg	−0.00124	0.00052	0.02
ρ1	1.89	0.03	<0.0001
ρ2	−0.89	0.03	<0.0001

¹ T ₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

²Parameter estimates corresponding to the 85-kg class were considered the control. Values presented in the estimate column corresponding to 90- to 105-kg classes are adjustments compared to the parameter estimated for 85-kg class.

³All P values represent to probability that the estimate is equal to zero. For adjusted estimates, significant P values indicate that the parameter estimate for that weight class is different from the 85-kg class.

*The parameter estimate is different from zero (P ≤ 0.05). Lags (ρ1, ρ2) and initial temperature (T₀) were not adjusted for HCW.

Table 10.

Testing effects of HCW class on estimates of the fractional rate constant (k) for temperature decline of the ham, with initial temperature (T0) assumed to be unaffected by HCW¹

	Estimate2	SE	P-value3
T 0	41.89	0.17	<0.0001
k
85 kg	0.0029	0.00019	0.04
(+/− compared with estimate for 85 kg)
90 kg	−0.00039	0.00019	<0.01
95 kg	−0.00062	0.00019	<0.01
100 kg	−0.00068	0.00019	<0.01
105 kg	−0.00117	0.00032	<0.01
ρ1	1.74	0.05	<0.0001
ρ2	−0.75	0.05	<0.0001

¹ T ₀ is the initial temperature measured in °C, k is the fractional rate constant, ρ1 is the first-order lag, and ρ2 is the second-order lag.

²Parameter estimates corresponding to the 85-kg class were considered the control. Values presented in the estimate column corresponding to 90- to 105-kg classes are adjustments compared with the parameter estimated for 85-kg class.

³All P values represent to probability that the estimate is equal to zero. For adjusted estimates, significant P values indicate that the parameter estimate for that weight class is different from the 85-kg class.

*The parameter estimate is different from zero (P ≤ 0.05). Lags (ρ1, ρ2) and initial temperature (T₀) were not adjusted for HCW.

CONCLUSIONS

A nonlinear model was developed and validated that can be used in commercial abattoirs for modeling the temperature decline in both the loin and the ham in blast-chilled facilities. There appears to be meaningful differences in the rate of temperature decline between heavy and lighter carcasses, especially in the loin, even though this relationship was not statistically different. Moreover, loins, regardless of HCW, achieved a deep muscle temperature approximately equal to ambient temperature, prior to the end of the chilling period. On the other hand, hams from carcasses 100 kg or heavier, were warmer than hams from lighter carcasses at the end of the chilling period. Finally, each 5-kg increase in HCW reduced the fractional rate constant (k) of the semimembranosus muscle by 2%. Thus, hams from heavier carcasses would probably be warmer than those from lighter carcasses at the end of the chilling period or will need additional time to chill before reaching temperatures required for fabrication.