Linear classification scores in beef cattle as predictors of genetic merit for individual carcass primal cut yields

Abstract

Having access to early predictions of both the genetic merit and expected phenotypic performance of an individual or its progeny can contribute to more informed decision-making. The objective here was to evaluate the usefulness of routinely available subjectively scored linear conformation information on live animals to predict genetic merit for primal carcass cut yields of their relatives. Data on 6 muscular and 6 skeletal traits on 43,078 live animals were used; the weights of up to 14 primal cuts plus 3 groups of primal cuts of 31,827 cattle were also used. Genetic correlations between the linear scores and the primal cut weights were estimated using sire linear mixed models; correlations were estimated with or without phenotypic adjustment of the primal cut weights to a constant carcass weight. The genetic correlations between each of the muscular and skeletal linear type traits with each of the primal cut weights (not adjusted for carcass weight) were all positive with the exception of the correlations between both chest width and pelvic length with cuberoll. On average, the muscular type traits were more strongly correlated (on average 0.42) with the primal cut weights than the skeletal traits (on average 0.35). Moreover, the average of the genetic correlations between each of the 6 muscular traits with all 8 hindquarter traits was, on average, 10% to 18% stronger than the average of the genetic correlations between the same muscular traits with all 5 forequarter primal cuts. When adjusted for differences in carcass weight, the correlations between all linear scores and the carcass traits regressed to zero or became negative. The skeletal traits were, in general, weakly genetically correlated with the primal cuts adjusted to a common carcass weight. The average of the genetic correlation between the muscular type traits and the primal cuts adjusted for differences in carcass weight was only 0.09 with only 13 of the 84 pairwise correlations being stronger than 0.30; the genetic correlation between silverside with the muscular traits was all stronger than 0.30, whereas the majority of the muscular traits had a correlation stronger than 0.30 with the topside primal cut. In fact, the average of the genetic correlations between the topside and silverside cuts with all the muscular traits was 0.50 and 0.42, respectively, with none of the correlations being negative.

Introduction

Measurement of phenotypic characteristics often requires some element of destruction; carcass merit phenotypes are one such phenotype, in that the animal must be sacrificed to obtain accurate phenotypes. Carcass merit represents the main revenue source of many beef cattle enterprises and thus contributes a large proportion of the relative emphasis within cattle breeding objectives (Phocas et al., 1998; Amer et al., 2001). Although the evaluation of carcass merit is not sex-limited, the time to measurement on an animal (and thus on the progeny of a sire) can be several years. Waiting for phenotypic information on the progeny of candidate parents of the next generation can therefore slow down the rate of annual genetic gain. Although the use of genomic information in beef cattle evaluations can help achieve genetic evaluations for carcass merit with some level of accuracy, even when the candidate parent is still young, augmenting this accuracy without lengthening the generation interval would obviously be beneficial. This implies measuring phenotypes on young animals, ideally before reaching sexual maturity, or, in seasonal calving herds at least, measuring the candidate parents sufficiently early, so the animal produces progeny in the calving season immediately following sexual maturity. For male and female cattle, this implies phenotypic measurement prior to 10 to 15 mo of age. Notwithstanding the use of such an approach for increasing genetic gain, being able to more accurately predict the primal cut yields of (genotyped) commercial animals, ideally prior to the procurement of the animal for slaughter, has obvious additional benefits.

Linear classification of animals has been traditionally used in both dairy (Veerkamp and Brotherstone, 1997) and beef (Gutiérrez et al., 2002; Bouquet et al., 2010) cattle as a visual appraisal of the conformation of an animal, generally on a linear scale from one extreme to another. While linear classification can be undertaken at any age, in beef cattle, the majority of linear classification tends to be undertaken in the period of 6 to 16 mo of age (Doyle et al., 2018). Because linear classification systems evaluate the skeletal and muscular characteristics of an animal, these characteristics should relate to eventual carcass conformation and primal cut yield. Moreover, because linear classification of animals tends to be undertaken before or around when an animal reaches sexual maturity, should the classification traits strongly relate to primal cut yield (and be heritable), they could be potentially very useful early predictors of genetic merit for carcass merit without the necessity to sacrifice the potential candidate parent. Linear type traits are indeed heritable in beef cattle (Bouquet et al., 2010; Bonfatti et al., 2013; Doyle et al., 2018) and studies have documented moderate genetic correlations between visually scored linear traits and carcass conformation (Bouquet et al., 2010; Bonfatti et al., 2013); these studies however have mainly been limited to carcass conformation as described by the European carcass grading system which itself is merely a predictor of saleable carcass yield (Conroy et al., 2010) and genetic correlations between the European carcass classification scores with primal cut weights are less than unity (Judge et al., 2019). The objective of the present study, therefore, was to estimate the genetic correlations between routinely captured linear type classification records on purebred live animals with a range of primal cut weights in their slaughtered commercial crossbred relatives. The outcome will be useful to conclude on the merits in accuracy of selection of using such linear classification data in multitrait genetic/genomic evaluations and, in doing so, accelerate the rate of genetic gain for overall carcass merit. Moreover, the potential improvements in predicting the genetic merit of individual commercial animals destined for slaughter will also be evaluated.

MATERIALS AND METHODS

The data used in the present study were obtained from a preexisting database managed by the Irish Cattle Breeding Federation (ICBF). Therefore, it was not necessary to obtain animal care and use committee approval in advance of conducting this study.

Carcass Data

Primal cut yields were available on 127,635 steers and 64,606 heifers slaughtered in a single abattoir between the years 2013 and 2017, inclusive. For inclusion in the present study, animals could not have resided in >3 herds during their lifetime and had to be resident for at least 70 d in the herd from which they were slaughtered from. The sire and dam of all animals had to be known and all animals had to be slaughtered between 16 and 36 mo of age. Only animals with a carcass weight record between 200 and 550 kg for steers and between 180 and 550 kg for heifers were retained.

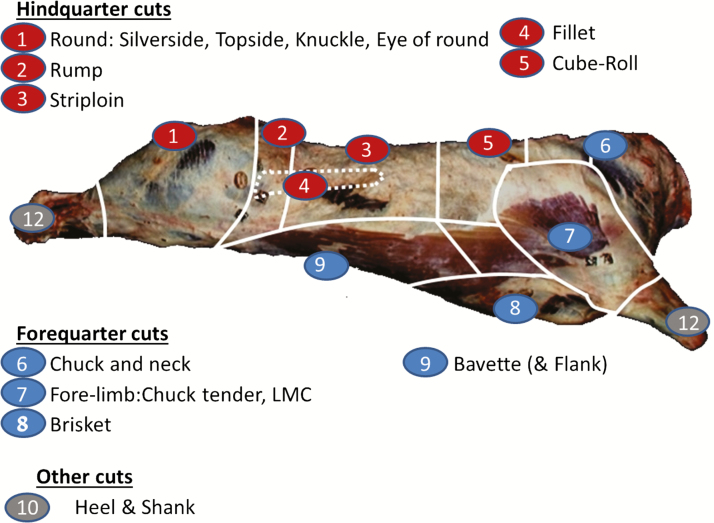
Although the weights of all primal cuts were available for each side of each carcass, the actual cuts, and the specifications of those cuts, differed across time and even within the same day depending on the prevailing retail market. For consideration in the present study, only primal cuts with the same cut specification from a large number of carcasses in the data set were considered. Fourteen primal cuts remained where a weight was available for both sides of the carcass for the cut in question and the intra-animal coefficient of variation of the weight of the cut on both sides of the carcass was <10%; following this edit, the mean coefficient of variation per cut varied from 0.02 (knuckle) to 0.04 (bavette). Primal cut weights that were greater than ±4 standard deviations from the mean cut weight of the respective animal gender (i.e., steer or heifer) were discarded. The 8 primal cuts with available weights in the hind quarter were the topside, silverside flat, eye of round, knuckle, rump, striploin, fillet, and cuberoll. The 5 cuts with available weights in the fore quarter were the bavette, brisket, chuck tender, leg of mutton and miscellaneous forequarter cuts (LMC), and chuck and neck. The weight of the heel and shank combined was also available. The location of each cut on the carcass is in Figure 1 and the latin name of each cut is in Supplementary Material.

Figure 1.

Location of primal cuts.

The combined weight of the striploin, fillet, and rump was used to generate a group of “frying cuts” which was only generated if weight records existed for each of the 3 contributing primal cuts in the edited data set; the cuberoll was not included in the frying cuts group due to fewer number of records for this cut. Similarly, where weight information on all relevant primal cuts were available, the topside, knuckle, silverside flat, and eye of round were summed to generate a group of cuts, here termed “roasting cuts,” for use in the subsequent analyses. Finally, a group of cuts termed “mince cuts” was generated as the sum of the bavette, chuck and neck, heel and shank, chuck tender, and leg of mutton and forequarter miscellaneous. Only animals with a primal cut weight observation, after all edits, for at least 5 of the 14 primal cuts were retained.

Linear Type Trait Data

Individual animal records on 6 muscular and 6 skeletal linear traits were available on 190,921 animals classified between 6 and 16 mo of age during the years 2000 and 2017, inclusive. The muscular traits, recorded on a scale of 1 to 15, were development of hind quarter, loin development, thigh width, development of thigh, width at withers, and width behind withers. The skeletal traits, recorded on a scale of 1 to 10, were chest depth, chest width, height at withers, pelvic length, length of back, and width at hips. All animals had to have a sire and dam recorded. Only data from classifiers that scored ≥500 animals were retained and each trait was separately standardized to a common variance within classifier-by-year as described in detail by Brotherstone (1994). Only cattle deemed to be ≥87.5% Angus, Charolais, Hereford, Limousin, or Simmental based on the available pedigree information were retained; 143,217 records remained. Finally, only data from herd-dates with at least 10 animals classified were retained. Following all edits, data were available on 43,078 animals in 633 herds (Table 1); no carcass data were available on any of these animals as classified animals are generally purebred candidate bulls either for artificial insemination or natural mating. Live-weight data recorded at the same time of linear classification were available on 73% of these animals (i.e., 31,217 live-weight records).

Table 1.

Number of records (N), mean (µ), genetic standard deviation (σ_g), and heritability (h²; standard error in parentheses) for the different muscular and skeletal traits

	Trait	N	µ	σg	h2 (SE)
Muscular, scale 1–15	Development of hind quarter	43089	10.35	0.547	0.27 (0.01)
	Loin development	43093	10.14	0.490	0.19 (0.01)
	Thigh width	43089	9.93	0.532	0.22 (0.01)
	Development of thigh	36284	10.24	0.597	0.28 (0.02)
	Width at withers	35636	9.51	0.410	0.18 (0.01)
	With behind withers	43082	9.08	0.484	0.20 (0.01)
Skeletal, scale 1–10	Chest Depth	36282	7.39	0.291	0.16 (0.01)
	Chest width	36286	6.71	0.272	0.12 (0.01)
	Height at withers	43087	6.82	0.510	0.31 (0.01)
	Pelvic length	42424	7.94	0.383	0.19 (0.01)
	Length of back	43078	7.91	0.418	0.22 (0.01)
	Width at hips	43078	6.97	0.299	0.13 (0.01)

Additional Data Edits

A general heterosis coefficient for each animal was categorized into 0%, >0% and ≤10%, >10% and ≤20%, …. >90% and <100%, and 100%. The general recombination loss coefficient for each animal was categorized as 0%, >0% and ≤10%, >10% and ≤20%, >20% and ≤30%, >30% and ≤40%, >40% and ≤50%, and >50%. Contemporary groups of herd-year-season-gender of slaughter were generated using an algorithm used in Irish national genetic evaluations (Mc Hugh et al., 2011; Berry and Evans, 2014). Within a herd, the algorithm clusters together animals of the same gender that are slaughtered in close proximity (≤10 d) of each other; where <10 animals are initially clustered together, the group is amalgamated with an adjacent contemporary group to form a single larger group. This process is repeated until the contemporary group contains ≥10 animals, provided the number of days between the initial and final slaughter date does not exceed 30. Only animals within contemporary groups of at least 4 animals were retained. The final data set consisted for 31,827 animals (9,414 heifers and 22,413 steers) from 3,566 contemporary groups originating from 1,446 herds. The number of records per primal cut is summarized in Table 2. Of the edited data set, the overwhelming majority of the animals were crossbred with the major breed component of almost two thirds of the animals being either Limousin (27% of the entire population), Charolais (17% of the entire population), or Hereford (15% of the entire population).

Table 2.

Number of records (N), mean (µ; kg), genetic standard deviation (σ_g; kg), and heritability (h²; standard error in parentheses) for the different cut traits analyzed as raw data (i.e., no adjustment), or where phenotypically adjusted for carcass weight

Cut	N	µ	No adjustment		Adjustment for carcass weight
			σg	h2 (SE)	σg	h2 (SE)
Topside	29,822	23.56	2.01	0.75 (0.03)	1.10	0.58 (0.03)
Silverside	23,281	16.64	1.35	0.58 (0.03)	0.58	0.27 (0.03)
Eye of round	22,107	6.67	0.67	0.68 (0.04)	0.45	0.56 (0.04)
Knuckle	26,632	14.46	1.12	0.68 (0.03)	0.58	0.45 (0.03)
Rump	28,602	19.28	1.31	0.45 (0.03)	0.69	0.26 (0.03)
Striploin	15,707	16.35	0.97	0.30 (0.04)	0.59	0.17 (0.03)
Fillet	19,943	7.23	0.46	0.37 (0.04)	0.29	0.22 (0.03)
Cuberoll	10,955	12.52	0.66	0.23 (0.05)	0.53	0.19 (0.04)
Bavette	16,192	13.76	0.66	0.14 (0.03)	0.54	0.12 (0.03)
Brisket	20,251	16.56	1.22	0.39 (0.03)	0.72	0.28 (0.03)
Chuck Tender	17,751	13.48	0.88	0.48 (0.04)	0.45	0.32 (0.03)
LMC1	27,800	26.98	1.81	0.54 (0.03)	0.66	0.22 (0.02)
Chuck and Neck	29,172	37.44	2.79	0.51 (0.03)	1.40	0.34 (0.03)
Heel and shank	28,379	12.16	0.92	0.68 (0.03)	0.50	0.49 (0.03)
Frying	11,350	43.28	2.36	0.42 (0.05)	1.10	0.25 (0.05)
Roasting	18,560	60.94	4.91	0.73 (0.04)	2.22	0.51 (0.04)
Mince	7,333	104.10	5.56	0.46 (0.07)	1.98	0.35 (0.07)

¹LMC is the leg and mutton cuts plus miscellaneous.

(Co)variance Component Estimation

Residual and genetic variance components for all linear type traits, live-weight, and carcass-related traits were estimated using a series of univariate animal linear mixed models in ASReml (Gilmour et al., 2009). The fitted model for all traits were

$${\displaystyle \begin{array}{ll}{\displaystyle {\mathrm{y}}_{\mathrm{i}\mathrm{j}\mathrm{k}\mathrm{l}\mathrm{m}\mathrm{n}\mathrm{p}}=}& \mu +\mathrm{C}{\mathrm{G}}_{\mathrm{j}}+\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}{\mathrm{r}}_{\mathrm{k}}\mathrm{x}\mathrm{a}\mathrm{g}{\mathrm{e}}_{\mathrm{l}}+\mathrm{h}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{i}{\mathrm{s}}_{\mathrm{m}}\\ & +\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}{\mathrm{n}}_{\mathrm{n}}+\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{a}{\mathrm{l}}_{\mathrm{i}}+{\mathrm{e}}_{\mathrm{i}\mathrm{j}\mathrm{k}\mathrm{l}\mathrm{m}\mathrm{n}\mathrm{p}},\end{array}}$$

where y_ijklmnp is either the linear score or carcass traits of animal i, µ is the population mean, CG_j is the contemporary group j of either herd-date of scoring (linear scores and live-weight) or herd-year-season-gender of slaughter (carcass traits), gender_k is the kth gender of animal i (male or female), age_l is the age l at either linear classification (linear scores and live-weight) or slaughter in months fitted as a class effect, heterosis_m is the heterosis coefficient value m (0%, >0% and ≤10%, >10% and ≤20%, …. >90% and <100%, and 100%) of animal i fitted as a class effect, recombination_n is the recombination coefficient value n (0%, >0% and ≤10%, >10% and ≤20%, >20% and ≤30%, >30% and ≤40%, >40% and ≤50%, and >50%) of animal i fitted as a class effect, animal_i is the random direct additive genetic component of animal i N(0,A${\sigma }_a^2$), and e_ijklmnp is the random residual term N(0,I${\sigma }_e^2$), where ${\sigma }_a^2$ is the additive genetic variance, ${\sigma }_e^2$ is the residual variance, A is the numerator relationship matrix, and I is an identity matrix. The pedigree of all animals was traced back to the founder population which was allocated to genetic groups based on breed.

The genetic correlations within and between the carcass and live-animal traits were estimated using a series of bivariate sire linear mixed models; fixed effects in the model were those described for the univariate analyses. Because no animal had data on both linear scores and carcass traits or live-weight and carcass traits, the residual covariance between these sets of traits was set to zero. In a separate series of both univariate and bivariate analyses, the primal cuts were adjusted to a common carcass weight by including a covariate for carcass weight in the statistical model. Furthermore, the estimated genetic (co)variances were used to estimate the partial genetic correlation between the linear scores and the primal carcass cut traits adjusted genetically for difference in live-weight.

RESULTS

Summary statistics for the linear type traits are shown in Table 1, whereas the summary statistics for the primal cut traits are shown in Table 2. Population parameters including variance components for the linear types traits, from which the data used in the present study were a subset, have been discussed elsewhere (Doyle et al., 2018); similarly the population parameters including the variance components for the carcass-related traits of the exact dataset used in the present study have been discussed at length elsewhere (Judge et al., 2019).

Individual Primal Cuts Without Adjustment For Carcass Weight

The genetic correlations between each of the muscular and skeletal linear type traits with each of the carcass-related traits, not adjusted to a common carcass weight, are shown in Table 3; all correlations with the primal cut weights were positive with the exception of the correlations between both chest width and pelvic length with cuberoll. On average, the muscular type traits were more strongly correlated (on average 0.42) with the primal cut weights than the skeletal traits (on average 0.35). Moreover, the average of the genetic correlations between each of the 6 muscular traits with all 8 hindquarter primal cuts was, on average 10% to 18% stronger than the average of the genetic correlations between the same muscular traits with all 5 forequarter primal cuts. The opposite was true for the skeletal traits; with the exception of width at hips, the average of the correlations between the 6 skeletal type traits and the 6 forequarter primal cuts was up to 30% stronger than the average of the correlations with the hindquarter primal cuts. Of all the 6 muscular linear traits, width at withers was the most strongly correlated with all primal cut traits (average correlation of 0.51 with a range of 0.24 to 0.67). Of all the 6 skeletal linear traits, length of back was the most strongly correlated with all primal cut traits (average correlation of 0.44 with a range of 0.29 to 0.60). Of the muscular linear traits, loin development was the most weakly correlated with all primal cut traits (average correlation of 0.34 with a range of 0.25 to 0.50). Of all the 6 skeletal linear traits, chest width was, on average, the most weakly correlated with the primal cuts (average correlation of 0.27 with a range of 0.08 to 0.57).

Table 3.

Genetic correlations (standard errors in parentheses) between the linear type traits¹ (and live-weight) with the carcass traits without adjustment for differences in carcass weight

	Muscular						Skeletal						Live-weight
	DHQ	LD	TW	DT	WaW	WbW	CD	CW	HW	PL	LB	WH
Live-weight	0.80 (0.02)	0.65 (0.04)	0.55 (0.08)	0.86 (0.02)	0.92 (0.01)	0.91 (0.01)	0.98 (0.00)	0.98 (0.01)	0.90 (0.01)	0.91 (0.01)	0.92 (0.01)	0.95 (0.01)
Carcass weight	0.45 (0.09)	0.41 (0.10)	0.54 (0.09)	0.52 (0.09)	0.60 (0.09)	0.54 (0.09)	0.58 (0.09)	0.41 (0.11)	0.51 (0.08)	0.48 (0.09)	0.59 (0.09)	0.47 (0.1)	0.66 (0.08)
Carcass conformation	0.50 (0.08)	0.44 (0.09)	0.61 (0.08)	0.63 (0.07)	0.66 (0.08)	0.58 (0.08)	0.24 (0.11)	0.46 (0.11)	0.22 (0.09)	0.25 (0.10)	0.23 (0.10)	0.47 (0.09)	0.45 (0.09)
Carcass fat	−0.26 (0.10)	−0.19 (0.11)	−0.24 (0.10)	−0.26 (0.10)	−0.41 (0.11)	−0.21 (0.11)	−0.04 (0.12)	0.00 (0.08)	−0.11 (0.11)	−0.13 (0.11)	−0.21 (0.11)	−0.08 (0.12)	−0.21 (0.11)
Topside	0.50 (0.08)	0.37 (0.10)	0.55 (0.08)	0.49 (0.09)	0.63 (0.09)	0.55 (0.08)	0.40 (0.10)	0.23 (0.12)	0.42 (0.09)	0.46 (0.09)	0.50 (0.09)	0.42 (0.10)	0.54 (0.09)
Silverside	0.60 (0.09)	0.50 (0.10)	0.66 (0.09)	0.67 (0.09)	0.67 (0.10)	0.62 (0.09)	0.45 (0.12)	0.34 (0.13)	0.41 (0.10)	0.54 (0.10)	0.60 (0.09)	0.59 (0.10)	0.66 (0.09)
Knuckle	0.47 (0.09)	0.36 (0.10)	0.53 (0.09)	0.47 (0.09)	0.57 (0.10)	0.49 (0.09)	0.36 (0.11)	0.29 (0.13)	0.32 (0.10)	0.41 (0.10)	0.41 (0.10)	0.36 (0.11)	0.53 (0.09)
Rump	0.28 (0.11)	0.31 (0.11)	0.43 (0.10)	0.36 (0.11)	0.44 (0.12)	0.44 (0.10)	0.37 (0.12)	0.20 (0.14)	0.32 (0.11)	0.38 (0.11)	0.39 (0.11)	0.44 (0.11)	0.50 (0.10)
Eye of the Round	0.56 (0.09)	0.36 (0.11)	0.59 (0.09)	0.57 (0.09)	0.57 (0.10)	0.56 (0.09)	0.36 (0.12)	0.26 (0.13)	0.29 (0.10)	0.40 (0.10)	0.38 (0.10)	0.46 (0.11)	0.49 (0.10)
Striploin	0.25 (0.14)	0.32 (0.14)	0.19 (0.15)	0.27 (0.15)	0.40 (0.16)	0.39 (0.14)	0.38 (0.16)	0.08 (0.18)	0.30 (0.14)	0.08 (0.16)	0.35 (0.15)	0.10 (0.16)	0.50 (0.14)
Fillet	0.18 (0.13)	0.28 (0.13)	0.24 (0.13)	0.21 (0.13)	0.41 (0.14)	0.29 (0.13)	0.29 (0.14)	0.13 (0.16)	0.39 (0.12)	0.29 (0.14)	0.50 (0.12)	0.28 (0.14)	0.42 (0.13)
Cuberoll	0.23 (0.20)	0.36 (0.11)	0.25 (0.20)	0.35 (0.20)	0.58 (0.22)	0.44 (0.20)	−0.19 (0.25)	0.15 (0.25)	0.18 (0.22)	−0.17 (0.23)	0.29 (0.22)	0.16 (0.24)	0.36 (0.22)
Bavette	0.22 (0.18)	0.26 (0.19)	0.35 (0.19)	0.31 (0.19)	0.59 (0.19)	0.37 (0.19)	0.63 (0.20)	0.57 (0.22)	0.29 (0.20)	0.23 (0.21)	0.48 (0.19)	0.48 (0.20)	0.75 (0.18)
Brisket	0.32 (0.12)	0.31 (0.13)	0.33 (0.12)	0.42 (0.12)	0.40 (0.14)	0.35 (0.12)	0.49 (0.13)	0.18 (0.15)	0.46 (0.11)	0.45 (0.12)	0.50 (0.12)	0.38 (0.13)	0.50 (0.11)
Chuck tender	0.27 (0.12)	0.34 (0.12)	0.32 (0.12)	0.31 (0.12)	0.52 (0.13)	0.47 (0.11)	0.42 (0.13)	0.32 (0.15)	0.27 (0.12)	0.28 (0.13)	0.32 (0.13)	0.22 (0.14)	0.42 (0.12)
LMC	0.53 (0.09)	0.40 (0.10)	0.54 (0.09)	0.57 (0.09)	0.54 (0.11)	0.52 (0.10)	0.41 (0.11)	0.34 (0.13)	0.39 (0.10)	0.36 (0.11)	0.48 (0.10)	0.26 (0.12)	0.50 (0.10)
Check and neck	0.29 (0.10)	0.25 (0.11)	0.35 (0.10)	0.32 (0.10)	0.24 (0.12)	0.37 (0.10)	0.43 (0.11)	0.22 (0.13)	0.38 (0.10)	0.32 (0.11)	0.48 (0.10)	0.32 (0.11)	0.49 (0.10)
Heel and shank	0.44 (0.09)	0.35 (0.10)	0.56 (0.09)	0.48 (0.09)	0.64 (0.09)	0.51 (0.09)	0.48 (0.10)	0.50 (0.12)	0.39 (0.09)	0.38 (0.10)	0.47 (0.09)	0.33 (0.11)	0.50 (0.09)
Frying	0.43 (0.14)	0.43 (0.14)	0.52 (0.14)	0.46 (0.14)	0.69 (0.13)	0.55 (0.13)	0.53 (0.14)	0.15 (0.18)	0.45 (0.14)	0.28 (0.16)	0.69 (0.12)	0.55 (0.14)	0.69 (0.12)
Roast	0.62 (0.09)	0.44 (0.11)	0.68 (0.09)	0.68 (0.09)	0.69 (0.10)	0.66 (0.09)	0.46 (0.11)	0.40 (0.13)	0.37 (0.10)	0.49 (0.10)	0.53 (0.10)	0.53 (0.11)	0.58 (0.10)
Mincing	0.37 (0.16)	0.45 (0.17)	0.47 (0.16)	0.47 (0.17)	0.47 (0.19)	0.48 (0.17)	0.24 (0.20)	0.07 (0.15)	0.15 (0.18)	0.32 (0.18)	0.49 (0.17)	0.30 (0.19)	0.50 (0.17)

¹DHQ = development of hind quarter; LD =loin development; TW = thigh width; DT = development of inner thigh, WaW = width at withers; WbW = width behind withers; CD = chest depth; CW = chest width; HW = height at withers; PL = pelvic length; LB = length of back; WH = withers height.

Silverside was the hindquarter cut most strongly correlated with the muscular traits (average correlation of 0.62 with a minimum and maximum of 0.50 and 0.70, respectively); the fillet was the hindquarter cut most weakly correlated with the muscular traits with an average (minimum, maximum) of 0.27 (0.18, 0.40). LMC was the forequarter cut most strongly correlated with the muscular traits (average correlation of 0.52 with a minimum and maximum of 0.40 and 0.60, respectively); chuck and neck was the forequarter cut most weakly correlated with the muscular traits with an average (minimum, maximum) of 0.30 (0.24, 0.44). Silverside and cuberoll were the strongest and weakest correlated hindquarter cuts, respectively, with the skeletal traits; bavette and chuck-tender were the strongest and weakest correlated forequarter cuts, respectively, with the skeletal traits.

Individual Primal Cuts With Adjustment For Carcass Weight

The genetic correlations between the 12 linear type traits with each of the carcass-related traits when adjusted to a common carcass weight are shown in Table 4. When adjusted for differences in carcass weight, the genetic correlation between the linear traits and the primal cuts either weakened towards zero or became negative. The average of the genetic correlation between the muscular type traits and the primal cuts was only 0.09, with only 13 of the 84 pairwise correlations being stronger than 0.30; the genetic correlation between silverside with the muscular traits was all stronger than 0.30, whereas the majority of the muscular traits had a correlation stronger than 0.30 with the topside primal cut. In fact, the average of the genetic correlations between the topside and silverside cuts with all the muscular traits was 0.50 and 0.42, respectively, with none of the correlations being negative. The average of the genetic correlation within each linear type trait individually and the 8 hindquarter traits varied from 0.14 to 0.18.

Table 4.

Genetic correlations (standard errors in parentheses) between the linear type traits¹ (and live-weight) with the carcass traits where all carcass traits are phenotypically adjusted to a common carcass weight

	Muscular						Skeletal						Live-weight
	DHQ	LD	TW	DT	WaW	WbW	CD	CW	HW	PL	LB	WH
Carcass conformation	0.39 (0.09)	0.33 (0.10)	0.47 (0.09)	0.51 (0.09)	0.53 (0.10)	0.45 (0.09)	−0.07 (0.12)	−0.19 (0.12)	−0.01 (0.10)	0.04 (0.11)	−0.02 (0.10)	0.34 (0.10)	0.16 (0.11)
Carcass fat	−0.32 (0.09)	−0.25 (0.10)	−0.32 (0.10)	−0.34 (0.10)	−0.47 (0.10)	−0.29 (0.10)	−0.15 (0.12)	−0.19 (0.12)	−0.19 (0.01)	−0.21 (0.11)	−0.30 (0.10)	−0.16 (0.11)	−0.32 (0.10)
Topside	0.42 (0.10)	0.27 (0.11)	0.42 (0.10)	0.56 (0.09)	0.48 (0.11)	0.39 (0.10)	0.12 (0.12)	0.05 (0.13)	0.23 (0.10)	0.26 (0.11)	0.23 (0.11)	0.24 (0.12)	0.22 (0.11)
Silverside	0.57 (0.12)	0.43 (0.13)	0.54 (0.13)	0.61 (0.12)	0.45 (0.14)	0.41 (0.13)	−0.04 (0.15)	0.11 (0.16)	0.11 (0.14)	0.29 (0.14)	0.28 (0.14)	0.40 (0.14)	0.43 (0.14)
Knuckle	0.28 (0.11)	0.14 (0.12)	0.28 (0.11)	0.19 (0.11)	0.25 (0.13)	0.17 (0.12)	−0.11 (0.13)	0.01 (0.14)	0.00 (0.11)	0.12 (0.12)	0.02 (0.12)	−0.02 (0.13)	0.14 (0.12)
Rump	−0.10 (0.12)	−0.06 (0.13)	−0.04 (0.13)	−0.10 (0.13)	−0.16 (0.15)	−0.07 (0.13)	−0.23 (0.15)	−0.19 (0.16)	−0.22 (0.13)	−0.13 (0.14)	−0.29 (0.13)	−0.02 (0.15)	−0.21 (0.14)
Eye of the Round	0.37 (0.10)	0.20 (0.12)	0.43 (0.11)	0.41 (0.11)	0.37 (0.13)	0.33 (0.11)	0.08 (0.13)	0.37 (0.10)	0.07 (0.12)	0.37 (0.10)	0.09 (0.12)	0.25 (0.13)	0.22 (0.12)
Striploin	−0.05 (0.17)	0.13 (0.18)	−0.12 (0.18)	−0.07 (0.18)	−0.03 (0.21)	0.04 (0.18)	−0.07 (0.21)	−0.13 (0.21)	−0.05 (0.19)	−0.26 (0.19)	−0.19 (0.19)	−0.14 (0.20)	0.04 (0.20)
Fillet	−0.12 (0.14)	0.00 (0.16)	−0.16 (0.15)	−0.25 (0.15)	0.03 (0.18)	−0.14 (0.15)	−0.10 (0.17)	−0.26 (0.18)	0.00 (0.15)	−0.05 (0.16)	0.02 (0.16)	−0.17 (0.17)	−0.14 (0.15)
Cuberoll	−0.29 (0.21)	0.05 (0.23)	−0.24 (0.22)	−0.10 (0.23)	0.03 (0.26)	−0.05 (0.23)	−0.61 (0.25)	−0.13 (0.27)	0.02 (0.24)	−0.26 (0.25)	−0.23 (0.25)	−0.10 (0.26)	−0.19 (0.25)
Bavette	−0.10 (0.19)	0.00 (0.21)	−0.01 (0.20)	−0.04 (0.20)	0.19 (0.23)	0.03 (0.21)	0.16 (0.23)	0.24 (0.24)	−0.14 (0.20)	−0.14 (0.21)	−0.03 (0.21)	0.12 (0.23)	0.21 (0.22)
Brisket	−0.02 (0.13)	0.00 (0.14)	−0.02 (0.14)	0.05 (0.14)	−0.04 (0.16)	−0.08 (0.14)	−0.01 (0.16)	−0.07 (0.17)	0.09 (0.14)	0.14 (0.15)	−0.04 (0.15)	0.24 (0.15)	0.12 (0.15)
Chuck tender	−0.18 (0.13)	−0.14 (0.14)	−0.24 (0.14)	−0.22 (0.14)	−0.04 (0.16)	−0.03 (0.14)	0.09 (0.16)	−0.06 (0.17)	−0.28 (0.13)	−0.26 (0.14)	−0.29 (0.14)	−0.34 (0.15)	−0.31 (0.15)
LMC	0.26 (0.12)	0.11 (0.14)	0.22 (0.13)	0.21 (0.13)	−0.03 (0.15)	0.13 (0.14)	−0.10 (0.15)	0.03 (0.16)	−0.17 (0.13)	−0.21 (0.14)	−0.10 (0.14)	−0.32 (0.14)	−0.23 (0.14)
Check and neck	−0.15 (0.11)	−0.16 (0.12)	−0.13 (0.12)	−0.22 (0.12)	−0.44 (0.12)	−0.14 (0.12)	−0.08 (0.14)	−0.18 (0.14)	−0.15 (0.12)	−0.19 (0.13)	−0.02 (0.12)	−0.08 (0.13)	−0.11 (0.13)
Heel and shank	0.23 (0.10)	0.14 (0.12)	0.33 (0.11)	0.24 (0.11)	0.43 (0.12)	0.26 (0.11)	0.16 (0.13)	0.05 (0.14)	0.10 (0.11)	0.13 (0.12)	0.14 (0.12)	0.04 (0.13)	0.09 (0.12)
Frying	−0.01 (0.18)	0.10 (0.19)	−0.02 (0.19)	−0.33 (0.18)	0.17 (0.22)	−0.02 (0.19)	−0.26 (0.21)	−0.31 (0.21)	−0.10 (0.20)	−0.23 (0.20)	−0.20 (0.20)	−0.19 (0.21)	0.05 (0.21)
Roast	0.54 (0.11)	0.29 (0.13)	0.54 (0.11)	0.68 (0.09)	0.51 (0.13)	0.38 (0.12)	−0.01 (0.14)	0.14 (0.15)	0.08 (0.13)	0.20 (0.13)	0.17 (0.13)	0.10 (0.14)	0.25 (0.13)
Mincing	0.04 (0.19)	−0.02 (0.20)	0.07 (0.19)	0.09 (0.20)	0.02 (0.23)	0.20 (0.20)	−0.16 (0.13)	0.09 (0.32)	−0.38 (0.19)	−0.17 (0.21)	−0.11 (0.20)	−0.39 (0.21)	0.16 (0.21)

¹DHQ = development of hind quarter; LD = loin development; TW = thigh width; DT = development of inner thigh; WaW = width at withers; WbW = width behind withers; CD = chest depth; CW = chest width; HW = height at withers; PL = pelvic length; LB = length of back; WH = withers height.

The average of the genetic correlations between the skeletal traits and all the primal cuts was −0.02 with the mean linear trait genetic correlation with each primal cut, on average, also being negative for all traits except width at hips which was 0.01. None of the 84 pairwise genetic correlations between the skeletal traits and each of the primal cuts was stronger than 0.4 with only 3 being stronger than 0.30 and 12 being stronger than 0.20; 57% of the pairwise correlations were actually negative.

Groups of Primal Cuts

Without adjustment to a common carcass weight, of the 3 group cuts, the roasting groups of cuts were almost consistently the most strongly correlated with the muscular traits (Table 3); in fact, the correlations between the muscular traits with the roasting group of cuts were always stronger than the correlations between the muscular traits within the individual primal cuts. There was no consistent trend in which group of cuts was most strongly correlated with the skeletal traits.

Even when adjusted to a common carcass weight, the correlations between the linear type traits and the roasting group of cuts remained moderately positive (0.30; Table 4); the correlations between the 6 muscular traits and the roasting group of cuts were, on average, 0.49 with the correlation of the development of thigh, development of hind quarter, thigh width, and width at withers each having a correlation stronger than 0.50. Genetic correlations between the individual linear traits and either the frying or mince group cuts were generally all close to zero with two thirds of the genetic correlations actually being negative.

Carcass Weight, Conformation, and Fat Score

The genetic correlations between the individual linear type traits with carcass weight, conformation and fat score, without and with adjustment for differences in carcass weight, are shown in Tables 3 and 4, respectively. The genetic correlations between the different linear type traits and carcass weight were, on average, 0.51 varying from 0.41 to 0.60 with no real difference in the correlations between muscular and skeletal traits. The average of the correlations between the muscular traits and carcass conformation (0.57 when not adjusted to a common carcass weight and 0.45 when adjusted to a common carcass weight) was considerably stronger than the average of the correlations between the skeletal traits with carcass conformation (0.31 when not adjusted to a common carcass weight and 0.02 when adjusted to a common carcass weight). Irrespective of whether adjusted for differences in carcass weight, all linear scores were negatively correlated with carcass fat score with the correlations with the muscular traits being, on average, stronger than the correlations with the skeletal traits.

Genetic Correlations With Live-Weight

The heritability of live-weight was 0.32 (0.02) with a genetic standard deviation of 26.9 kg. The genetic correlations between the 6 muscular traits and live-weight were, on average, 0.78 varying from 0.55 (thigh width) to 0.98 (chest depth). The genetic correlations between the 6 skeletal traits and live-weight were, on average, 0.94 varying from 0.90 to 0.98. The genetic correlations between live-weight and the different primal cuts (Table 3), when not adjusted to a common carcass weight, were, on average, 0.51 varying from 0.36 (with cuberoll) to 0.75 (bavette). When the primal cut traits were adjusted to a common carcass weight, the correlations with live-weight were, on average, −0.31, with 6 of the traits (rump, fillet, cuberoll, chuck tender, LMC, and chuck and neck) being negatively correlated with live-weight; irrespective, most of the correlations were not different from zero (Table 4). Even after adjusting for differences in genetic merit for live-weight, the partial genetic correlations between the muscular linear traits and the primal cuts adjusted to a common live-weight were, on average, 0.55 varying from 0.17 (thigh width) to 0.94 (development of thigh). Hence, the muscular linear type traits in particular, although correlated with live-weight, still provide very useful information on the genetic merit of especially the roasting group of cuts, even when adjusted to a common carcass weight.

Discussion

Although the possibility of paying for data for use in genetic evaluations (Gonzalez-Recio et al., 2014) cannot being ruled out, genetic evaluations for most traits in cattle have traditionally been based on the exploitation of often already collected data for management or regulatory purposes. Where data on the goal standard is either not freely available, or is available (too) late in life, predictor traits, or what are often nowadays termed biomarkers, can be useful. The usefulness of such predictor traits in enhancing the accuracy of genetic evaluations, and thus accelerating genetic gain, is dependent on the genetic correlation between the predictor traits and the goal traits, as well as being a function of the combination of the heritability of the trait and the quantity of data available; the extent of genetic similarly between the predictor and predicted populations is also important. An obvious predictor trait for primal cut yields would be animal live-weight and this was clearly demonstrated in the present study. However, heavier cattle, on average, eat more (Arthur et al., 2001) and this has implications for their feed energy requirements. Therefore, of particular interest in the present study was the ability to alter the morphology of carcasses by directing more of the carcass weight towards higher value cuts, thereby negating, as much as possible, any impact of heavier (higher value) primal cuts on the feed requirements of the animal. Although ultrasound information of live animals has previously been demonstrated in several studies of cattle (Devitt and Wilton, 2001; Bergen et al., 2005) to be a very useful predictor of some carcass quality traits, the focus of the present study was on the usefulness of subjective linear scores.

Beef cattle have been linearly classified since the early 20th century as a mean of characterizing the different physical attributes of an animal. As far back as the early 20th century, Lush (1932) documented strong phenotypic correlations between (objectively taken) live animal measurements in steers and subsequent carcass value. Although most modern-day linear scoring systems also assess animal functionality, especially focusing on leg conformation, only the assessments of the skeletal size and muscularity of the animal were considered in the present study. Of the 12 traits assessed in the present study, 3 focused on the anterior section of the animal (i.e., height at withers, width at withers, and width behind withers), 2 focused on the middle portion of the animal (i.e., chest width and chest depth), and the remaining 7 traits focused on the posterior section of the animal. Because the exterior view of the muscling and size of the animal should bear some relation to the carcass yield, it seems logical that the subjectively scored muscular and skeletal traits should correlate with primal cut yields. Given that both linear type traits (Table 1; Doyle et al., 2018) and primal cut weights (Judge et al., 2019) in beef cattle are known to be heritable, if the expected phenotypic correlations translate to moderate genetic correlations, then these traits could be useful in multitrait genetic evaluations to improve the accuracy of selection for primal carcass cut weights and, by extension, overall carcass value. Of particular interest, however, in the present study was which linear scores would be expected to deliver a faster rate of genetic gain, the result of which is a function of both the heritability of the trait and its genetic correlation with not just primal cut weights, on average, but in particular the most valuable primal cuts namely those in the frying cut groups (i.e., striploin, fillet, and rump). In fact, little variability existed in trait heritability estimates among the 12 different traits assessed in the present study with a standard deviation in heritability estimates of just 0.06. Intertrait differences in the genetic standard deviation within the muscular (scale 1 to 15) and skeletal (scale 1 to 10) traits separately were also minimal. Hence, it is the genetic correlation with the (high value) primal cut weights, especially when adjusted to a common carcass weight, that affects the usefulness of the trait in a selection index; the marginal information the linear trait contributes to the prediction of the primal cut weights over and above that achieved from other traits in the selection index is also important. One such trait included in several selection indexes or breeding goals (Phocas et al., 1998; Amer et al., 2001), or at least usually routinely available, is the live-weight of the animal either at weaning or yearling. Although a linear type trait could correlate strongly with a primal cut weight, if the majority of that covariance is also captured through live-weight (i.e., the linear trait is strongly correlated with live-weight which in itself is also strongly correlated with the primal cut weight), then the marginal contribution of the type trait would be low.

The scientific literature is void of estimates in cattle populations of the genetic correlations between a range of different subjectively scored traits on a linear scale and eventual primal carcass cut yield. Some studies have estimated genetic correlations between a single or few subjective animal morphological measures and carcass-related traits. In a population of up to 3,109 Piemontese intact male cattle, Bonfatti et al. (2013) reported genetic correlations of between 0.14 and 0.35 between the European carcass conformation classification system and the live animal measures of width at withers, shoulder muscularity, loin width, loin thickness, thigh muscularity, and thigh profile; all standard errors, however, were ≥0.16. Tonussi et al. (2015) reported a genetic correlation of 0.45 (se = 0.12) and −0.37 (se = 0.37) between yearling hip height with hot carcass weight and longissimus muscle area, respectively, in a large population of Nellore cattle. Bouquet et al. (2010) documented genetic correlations in Limousin and Blonde d’Aquitaine cattle for age-adjusted carcass weight with visually assessed muscular score at weaning of between 0.18 and 0.32; the genetic correlations between the muscular score and the European carcass classification score were 0.54 to 0.78.

Of particular interest in the present study was which subjective live animal measures would be useful to predict the proportioning of a given carcass weight into the higher value cuts, which in many markets are the steaks cuts, namely, the rump, striploin, and fillet. None of the muscular traits correlated with either of these 3 cuts; the strongest correlation was 0.13 between the striploin-adjusted weight and loin development. Only 2 linear traits (loin development and width at withers) had a positive genetic correlation with the frying group of cuts (adjusted to a common carcass weight). Therefore, the current linear scores assessed in beef cattle (in Ireland) are not good predictors of the distribution of the frying cuts within the carcass. Hence, either new linear scores should be trialed or alternative measures to assess these traits in live cattle should be evaluated.

The next most valuable cuts tend to be the roasting group of cuts and all 6 genetic correlations between the roasting group of cuts and the muscular cuts were stronger than 0.28 with development of hind quarter, thigh width, development of thigh, and width at withers each having a genetic correlation >0.50 with the roasting group of cuts. The correlations were particularly strong with the topside and silverside cuts. These muscular traits therefore do provide useful information on the genetic merit of individuals for these roasting groups of cuts. For example, the coheritability of the development of the thigh with the topside and silverside cuts was 0.23 and 0.17, respectively; the respective heritability of the primal cuts adjusted to a common carcass weight was 0.58 and 0.27. Assuming a record for the development of the thigh was available on the selection candidate itself, then the accuracy of selection achievable for the roasting cuts (adjusted to a common carcass weight) would be 0.35. If, however, linear scores for development of thigh were available on 100 progeny, then an accuracy of 0.63 could be achieved for the roasting cuts (adjusted to a common carcass weight); this would increase to 0.71 if information was also available on 100 progeny for loin development (as well as development of thigh). Therefore, substantial genetic gain could be achieved through indirect selection; in the latter example this could equate to 1.58 kg (i.e., 0.71 times 2.22 kg) for roasting cuts per selection intensity unit per generation.

Irrespective of primal cut, all skeletal traits correlated poorly suggesting minimal information content in these traits for predicting genetic merit for the relative partitioning of the different primal cuts for a given carcass weight. However, the skeletal traits are recorded more for information on body size and possibly feed intake related metrics (Crowley et al., 2011). Indeed all skeletal traits were strongly genetically correlated with live-weight, but, if live-weight records already exist, then the added value of these traits is questionable. Nonetheless, an animal can achieve the same live-weight from different morphological dimensions (e.g., a tall animal that is short in length can have the same live-weight as a long animal that is short in height); therefore, the skeletal traits can provide some additional information on the dimensions of the animal.

Deployment Strategies and Uses

Being able to estimate individual animal genetic merit for primal yields has many benefits, namely, the ability to predict whether the animal is a suitable candidate parent of the next generation but also whether the animal itself, even if measured at a young age, could produce a high-value carcass. The exploitation of genomic predictions (Meuwissen et al., 2001) for either the linear scores or the actual primal yields (supplemented with phenotypic data on linear scores) could contribute to increased accuracy, even at a younger age. The high heritability of the primal cut traits (Table 2) signifies that a large proportion of the inter-animal variability in primal cut weights (even when adjusted to a common carcass weight) is influenced by additive genetic merit; therefore, genetic merit alone is expected to be a relatively good predictor of primal yield, especially for a group of animals (Berry et al., 2017). The linear type traits are also heritable (Table 1) and, given the moderate genetic correlation with some of the primal cut traits (Tables 3 and 4), the coheritability of the primal cut and linear type traits is moderate. Thus, breeding programs could undoubtedly benefit from the inclusion of (some of the) linear type traits (e.g., development of thigh) in a selection index underpinning the goal traits of primal cut yields, especially if useable observations on primal cut yields are limiting. The main benefit of utilizing the linear type traits in breeding programs is that it removes the necessity to slaughter an animal to acquire its actual primal cut yield phenotype. This is particularly important in reducing the generation interval and thus accelerating annual genetic gain (Rendel and Robertson, 1950). For example, candidate bulls and dams of the next generation could be phenotypically assessed for muscularity and skeletal characteristics, and those that excel genetically, assuming they also excel in other traits of interest, could graduate into the breeding program. Even with genomic predictions for primal yields available, the high heritability of the linear trait phenotypes should further improve the accuracy of the predicted genetic merit of individuals for primal yield.

The data used in the present study were generated from the physical observation and assessment of the live animals by humans. Such an approach can be resource intensive, but also somewhat subjective even if the assessors are highly trained and standardized. Veerkamp et al. (2002) in an analysis of linear scores taken by 18 trained classifiers scoring 19 traits on 91,589 first lactation cows reported differences among classifiers in within-trait estimated genetic variances but also genetic correlations between the same trait scored by 1 classifier vs. that of all others differing from unity; the extent of the discrepancies differed by trait. Novel sensing technologies in agriculture, including livestock (for review see Ruttena et al., 2018), are emerging at an accelerating rate. Image capture of live individual cattle shape and size is now a reality (Kawasue et al., 2013) and subsequent downstream analyses provide a potentially lower cost, more objective and repeatable, strategy to linearly assess live animals. Video image analysis is already used in the crude classification of beef carcasses (Craigie et al., 2012) but can also be used to generate more granular data on individual carcasses such as primal cut yields (Pabiou et al., 2011). Moreover, the present study focused on just 12 linear traits and these traits were chosen by breed societies to describe different animal characteristics reflective of not just primal cut yields. Furthermore, the actual linear traits assessed would not have been devised from knowledge on individual animal primal cut yields. The opportunity therefore clearly exists to generate images of individual animals at different stages of life, decompose these images into an array of parameters that describe the animals, and, using advanced prediction algorithms (e.g., machine learning; Nasrabadi, 2007) relate these parameters to the eventual primal cut weights (as well as other carcass characteristics). This should contribute to more accurate predictions of carcass value, but possibly also even at a younger age, thus facilitating (with other information such as genetic merit for age at slaughter) early segregation of animals on-farm for different retail markets and customers.

The ability to alter the morphology of carcasses with breeding has already been demonstrated both through breed substitution (Kause et al., 2015) but also by within-breed selection (Clarke et al., 2009; Judge et al., 2019). Strict criteria are often imposed by retail markets on animal and carcass credentials such as gender, age, but also dimensions of individual primal cuts. Meat from carcasses which do not adhere to these criteria have to be either excessively trimmed, with the trimmings generally being sold for a lower value, or the carcass itself enters another, often lower value, market stream. Although differentiation of carcasses for different markets can be undertaken at the time of carcass classification, this is usually undertaken without cognizance of the animals yet to be slaughtered or the carcasses yet to be catalogued. Therefore, having a prediction of the carcass specifications of animals in lairage can be useful to aid in abattoir-based linear programming algorithms to maximize the value of the day’s kill within the constraints of market quotas and requirements. Of more potential, however, is the usefulness of such information, concurrent with other information like expected slaughter date, to forecast the number of animals of different specifications for slaughter in the subsequent days, weeks, or months. Potential shortfalls in supply for individual markets can be filled by specifically targeting individual farms, or groups of animals within farms. Although individual animal parentage recording tends to be poor in beef herds, knowledge of the team of sires used in a given herd will provide a reasonable estimate of the genetic merit of that herd, or a group of animals, as a whole (Berry et al., 2017). Through the vertical integration of multiple data sources (i.e., herd size, genetic merit of sires most recently used, and calving season), abattoirs can potentially generate accurate models of not only animal supply but also expected animal quality. Additionally, crude approaches of initially identifying herds with likely suitable cattle based on the sires used can firstly be invoked and, on visiting these farms, image-capture technologies can be used to further phenotypically identify animals that are likely to fulfill the immediate market requirements. Furthermore, because the heritability is less than 1, the contribution of management to differences in carcass primal meat yield cannot be ignored and should ideally coevolve with the imposed breeding strategies.

As society, in general, strives for perfection, beef breeders, and farmers are constantly trying to produce the ideal carcass. Because of the evolutionary forces contributing to genetic variation and the mendelian sampling of germplasm between generations, in the absence of whole-scale cloning, it will never be possible to achieve absolute consistency among animals. Therefore, corrective or assortative mating will remain an important component of a breeding program where bulls are matched with cows to address the respective deficiencies without, hopefully, compromising on other traits. Most market has strict rules on the quality, appearance, and/or size of some primal cuts. Therefore, being able to corrective mate parents to best fit within these criteria could be beneficial; exploiting knowledge on the predicted genetic merit of both parents based on live animal measures would be critical to achieving this objective. The live animal measures could be supplemented with feedback from abattoirs on the actual primal cut weights and dimensions of progeny for the different family lines, further proving the benefit of vertical integration of different data repositories to achieve a common goal among different actors along the food chain.

In conclusion, some linear type traits (i.e., muscularity traits) have some predictive ability of genetic merit for especially the roasting primal cuts and thus may be useful in multitrait genetic evaluations for such. This could be particularly important should producers be paid on the more granular individual primal cut weights as opposed to the current EUROP classification system. Notwithstanding this, although moderate genetic correlations existed between some of the linear scores and primal cuts, efforts to improve the predictive ability further, either by supplementing with other informative data which may be collected (e.g., ultrasound information on live-animals) or new potential (image) technologies should continue to be investigated.