Deep Generative Adversarial Neural Networks for Compressive Sensing (GANCS) MRI

Abstract

Undersampled magnetic resonance image (MRI) reconstruction is typically an ill-posed linear inverse task. The time and resource intensive computations require trade offs between accuracy and speed. In addition, state-of-the-art compressed sensing (CS) analytics are not cognizant of the image diagnostic quality. To address these challenges, we propose a novel CS framework that uses generative adversarial networks (GAN) to model the (low-dimensional) manifold of high-quality MR images. Leveraging a mixture of least-squares (LS) GANs and pixel-wise ℓ₁/ℓ₂ cost, a deep residual network with skip connections is trained as the generator that learns to remove the aliasing artifacts by projecting onto the image manifold. The LSGAN learns the texture details, while the ℓ₁/ℓ₂ cost suppresses high-frequency noise. A discriminator network, which is a multilayer convolutional neural network (CNN), plays the role of a perceptual cost that is then jointly trained based on high quality MR images to score the quality of retrieved images. In the operational phase, an initial aliased estimate (e.g., simply obtained by zero-filling) is propagated into the trained generator to output the desired reconstruction. This demands very low computational overhead. Extensive evaluations are performed on a large contrast-enhanced MR dataset of pediatric patients. Images rated by expert radiologists corroborate that GANCS retrieves higher quality images with improved fine texture details compared with conventional Wavelet-based and dictionary-learning based CS schemes as well as with deep-learning based schemes using pixel-wise training. In addition, it offers reconstruction times of under a few milliseconds, which is two orders of magnitude faster than current state-of-the-art CS-MRI schemes.

I. Introduction

Magnetic resonance imaging (MRI) is a major imaging modality in clinical practice, due to its superb soft tissue contrast. Unfortunately, MRI is also a relatively slow imaging modality. This is particularly true for high-resolution, volumetric image, and time series images. One possible solution is to decrease the scan duration through significant undersampling. However, such undersampling leads to an ill-posed linear inverse reconstruction problem, which requires long reconstruction times. This is an issue in clinical MRI, where images are not available for immediate review to guide subsequent scans, and is a critical concern for interventional or real-time MRI, where immediate image feedback is an overiding concern.

To render the MRI reconstruction well-posed, conventional compressed sensing (CS) incorporates prior information about the inherent low dimensionality of images by means of sparsity regularization in a proper transform domain such as Wavelet (WV), or, finite differences (or Total Variation, TV) [9], [16], [17], [20], [23], [28]. This however typically demands running iterative algorithms, for solving non-smooth optimization programs, that are time and resource intensive. These are not practical for applications such as real-time MRI. Moreover, the sparsity assumption is oblivious to the inherent latent structures that are specific to each dataset. In essence, the sparsity prior spans a large manifold of images. Adapting and specifying the image manifold to the historical patient datasets enables further undersampling, and creating higher diagnostic quality images.

A few attempts have been recently carried out to speed up medical image reconstruction by leveraging historical patient data; see e.g., [5], [15], [18], [26], [30], [35], to name a few. The major consensus is that they train a network that learns the relation map between an initial aliased image and the gold-standard image. For MR image recovery, for instance, [18] trains a fully-connected (FC) denoising auto-encoder, while the AutoMap scheme in [35] adopts a FC network followed by a convolutional neural network (CNN) to directly map the k-space data to the image domain for robust reconstruction. The multi-coil superCNN scheme in [15] also trains a CNN from the undersampled multichannel images to the gold-standard images. A deep cascade of CNNs is also used in [26] for Cartesian undersampling of 2D cardiac MR images that outperforms dictionary learning MRI in terms of quality and speed. In computer tomography (CT) reconstruction, [5] applied the U-net [24] based CNNs for residual learning. While the reconstruction speeds up, these approaches suffer from blurring and aliasing artifacts. This is mainly because they adopt a pixel-wise ℓ₁/ℓ₂ cost for training, that is oblivious to structured artifacts and high-frequency texture details. Revealing these details is crucial for accurately making diagnostic decisions. In addition, these schemes lack any mechanism to ensure that the retrieved images are faithful to the measurements.

In another approach, [1], [4], [6], [10], [12], [29] use deep neural networks to learn image priors, or, sparsifying transforms from historical data. These are then used to solve a nonlinear system using iterative optimization algorithms as in the conventional CS methods. [29] unrolls the ADMM optimization for solving the inverse problem for CS-MRI, and improves the modeling by representing projections with neural networks. Similarly, [12] uses a deep U-net to learn priors for converting sparse-view CT images to the full-view images. The work in [10] also uses a variational autoencoder for learning the priors, which is then evaluated on knee images. The work in [4] also performs iterative reconstruction and shows better recovery when the sparsity model uses a pre-trained multi-layer generative model. While improving the reconstruction performance, these methods incur high computational cost for finding the optimal reconstruction with iteration.

Generative adversarial networks (GANs) have been lately proven very successful [8], [22] in modeling distributions (low-dimensional manifolds) and generating natural images (high-dimensional data), that are perceptually appealing [36]. In particular, GANs achieve state-of-the-art perceptual quality for image super-resolution tasks for up to 4× upscaling for natural images e.g., from ImageNet [14], [27]. GANs have also been recently deployed for image inpainting [32], style transfer [13], and visual manipulation [36], with excellent performance relative to the existing alternatives. Despite the success of GANs for local image restoration such as super-resolution and inpainting, to date, they have not been studied for correcting the aliasing artifacts in MRI reconstruction tasks. There is a very recent study on using GANs in [31] for denoising CT images where the generator is a deep CNN and the evaluations are performed mostly with phantom models. Aliasing artifacts in MRI emanate from data undersampling in a different domain (e.g., Fourier) which globally impact the entire image, which is harder to recover and reconstruct.

Contributions.

Inspired by the sharp, high texture-quality images retrieved by GANs, and the high contrast of MR images, we employ GANs for modeling the low-dimensional manifold of high-quality MR images. The images lying on the manifold are not however necessarily consistent with the observed undersampled data. As a result, the reconstruction models the intersection of the image manifold and the subspace of data-consistent images. Such a space is simply an affine subspace for linear measurements. To this end, we proposed GANCS in which we adopt a tandem network of a generator (G), an affine projection operator, and a discriminator (D). The generator aims to create gold-standard images from the complex-valued aliased inputs using a deep residual network (ResNet) with skip connections which are proven to retain high resolution information. The data-consistency projection builds upon the known signal model and performs an affine projection onto the space of data consistent images. The D network is a multilayer convolutional neural network (CNN) that is presented with both the fake images created by G, and the corresponding gold-standard images, and aims to correctly distinguish fake from real. We adopt least-squares GANs (LSGANs) due to their stability properties [19]. To control the high-frequency texture details returned by LSGANs, and to further improve the training stability, we partially use the pixel-wise ℓ₁ and ℓ₂ costs for training the generator.

We perform extensive evaluations on a large dataset of pediatric patients with contrast-enhanced abdominal images. The reconstructed images using the proposed GANCS method and other state-of-the-art CS-MRI schemes are rated by expert radiologists for diagnostic quality. Our observations indicate that the GANCS results have almost similar quality to the gold-standard (fully-sampled) images, and are superior in terms of diagnostic quality relative to the existing alternatives including conventional iterative CS (for both TV and WV) as well as deep learning based methods that solely adopt the pixel-wise ℓ₂-, and ℓ₁-based criteria. Moreover, the reconstruction only takes around 30 msec, which is two orders of magnitude faster than state-of-the-art conventional CS toolboxes. Finally, the scope of our novel GANCS framework goes beyond MR image reconstruction, and applies to other image restoration tasks for aliasing artifacts.

The rest of this paper is organized as follows. Section II introduces the preliminaries and states the problem. Manifold learning using LSGANs is discussed in Sections III and IV. Section V reports the data evaluations, while the conclusions are drawn in Section VI.

II. Preliminaries and Problem Statement

Consider a generic MRI acquisition model that forms an image $\text{x}\in {ℝ}^N$ from k-space projections $\text{y}\in {ℝ}^M$

$$\text{y}=\mathcal{A}(\text{x})+\text{v}$$ (1)

where the (possibly) nonlinear map $\mathcal{A}:{ℂ}^N\to {ℂ}^M$ en-compasses the effects of sampling, coil sensitivities, and the Discrete Fourier Transform (DFT). The error term $\text{v}\in {ℝ}^M$ also captures the noise and unmodeled dynamics. It is natural to assume the unknown complex-valued image x lies in a low-dimensional manifold, say $\mathcal{M}$. No information is known about the manifold besides the training samples $\mathcal{X}:={\left\{{\text{x}}_k\right\}}_{k=1}^K$ drawn from it with the corresponding noisy observations $\mathcal{Y}:={\left\{{\text{y}}_k\right\}}_{k=1}^K$. The data $\{\mathcal{X},\mathcal{Y}\}$ can be obtained for instance from the K past patients in the dataset that have been already scanned for a sufficient time, with their high-quality reconstructions. Given the training data $\{\mathcal{X},\mathcal{Y}\}$, our goal is to quickly recover the image x after collecting the undersampled measurements y.

Instead of relying on a simple sparsity assumption of $\mathcal{X}$, we aim to automate the image recovery by learning the nonlinear inversion map x = f (y) from the historical training data $\{\mathcal{X},\mathcal{Y}\}$. We begin with an initial estimate $\tilde{\mathrm{x}}$ that is a linear transform (approximate zero-filling solution) from undersampled measurement and possibly contains aliasing artifacts. Reconstruction can then be envisioned as artifact suppression, that we propose to model as a mapping on the manifold of high quality images. Learning the corresponding manifold is the subject of next section.

III. Manifold Learning via Generative Adversarial Networks

The inverse imaging problem is to find a solution at the intersection of a subspace defined by the acquisition model, and the image manifold. In order to effectively learn the image manifold from the available limited number of training samples, we first need to address the following important questions:

• How to ensure the trained manifold contains plausible MR images?

• How to ensure the points on the manifold are data consistent, namely $\text{y}\approx \mathcal{A}(\text{x})$, $\forall \text{x}\in \mathcal{M}$?

A. Alternating mapping with GANs for plausible reconstruction

To address the first question to ensure plausibility of the reconstruction, we adopt GANs that have recently proven very successful in estimating the prior distributions for images. GANs provide sharp images that are visually plausible [8]. In contrast, variational auto-encoders [14], an important class of generative models, use a pixel-wise mean-squared-error (MSE) cost that results in high peak signal-to-noise (PSNR) ratios, but often produces overly-smooth images and patterned artifacts [34] that have poor perceptual quality. A standard GAN consists of a tandem network of G and D networks. Consider and plausible that can fool D. Various strategies have been devised to reach the equilibrium. They mostly differ in terms of the cost function adopted for G and D networks; see e.g., [3], [8], [19]. The standard GAN uses a sigmoid cross-entropy loss that leads to vanishing gradients which renders the training unstable, and as a result it suffers from severe degrees of mode collapse. In addition, for the generated images classified as real with high confidence (i.e., with large decision variable), no penalty is incurred. Hence, the standard GAN tends to pull samples away from the decision boundary, which can introduce non-realistic images [19]. Such images can be hallucinated, and are thus not reliable for diagnostic decisions. Motivated by the improved stability of LSGANs we adopt an LS cost for the discriminator decision. In essence, the LS an initial estimate of the image $\tilde{\mathrm{x}}:={\mathcal{A}}^{†}(\text{y})$ as the input cost penalizes the decision variables without any nonlinear to the G network. The estimate $\tilde{\mathrm{x}}$ could be simply obtained via zero-filling the missing k-space components, which is the least squares solution for data-consistency, and then running a single iteration of conjugate gradient optimization. The G network then projects $\tilde{\mathrm{x}}$ onto the low-dimensional manifold $\mathcal{M}$ containing the high-quality images $\mathcal{X}$. Let $\check{\text{x}}$ denote the output of G. It then passes through the discriminator network D, that tries to output one if $\check{\text{x}}\in \mathcal{X}$, and zero otherwise. As will be clear later, eventually the G net learns to project to the low-dimensional manifold and achieves a realistic reconstruction, such that the D net cannot always perfectly assign the right labels to the real fully-sampled and fake recovered images.

B. Affine projection and soft penalty for data-consistency

The output of G, $\check{\text{x}}$, however may not be consistent with the data. To tackle this issue, G is followed by another layer that projects onto the set of data-consistent images, $\mathcal{C}:=\{\text{x}\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\text{y}\approx \mathcal{A}(\text{x})\}$ (see Fig. 1). For a Cartesian grid with the linear acquisition model y = Ax, the projection is easily expressible as $\widehat{\mathrm{x}}={\text{A}}^{†}\text{y}+(\text{I}-{\text{A}}^{†}\text{A})\check{\mathrm{x}}$. Alternatively, one can impose data consistency to the output of G through a soft least-squares (LS) penalty when training the G network, as will be seen below in (P1).

Fig. 1.

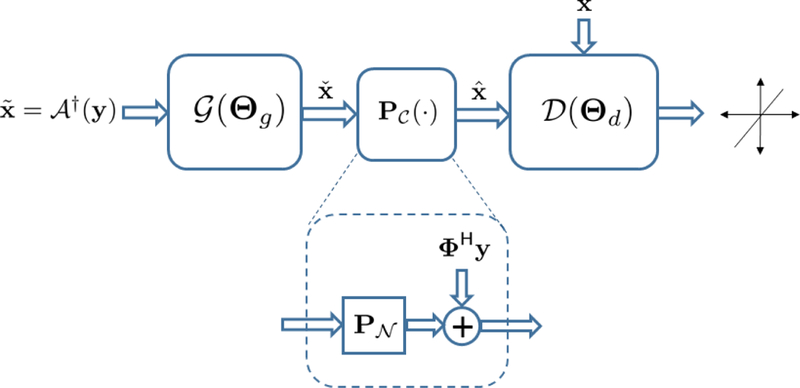
GANCS structure for image reconstruction $(\widehat{\mathbf{x}})$ starts with an initial estimate $\tilde{\mathbf{x}}$. The dashed module specifies affine projection onto the set of data-consistent images.

To further ensure that $\widehat{\mathrm{x}}$ falls in the intersection of the manifold $\mathcal{M}$ and the set of data-consistent images $\mathcal{C}$, we can perform multiple back-and-forth mappings. The network structure in Fig. 1 can then be extended by repeating the G network and ${\mathcal{P}}_{\mathcal{C}}(\cdot )$ serially for a few times. In this paper we only adopt a single back-and-forth mapping for simplicity of exposition. However, our observations for using multiple mappings show significant performance improvement, and is reported in our companion work [21]. The overall network architecture is depicted in Fig. 1, where ${\text{P}}_{\mathcal{N}}:=(\text{I}-{\text{A}}^{†}\text{A})$ resembles projection onto the nullspace of A.

C. Least-squares GANs for stable training

Training the network in Fig. 1 amounts to playing a game with conflicting objectives between the generator G and the discriminator D. The D network aims to score one for the real gold-standard images, and zero for the fake/reconstructed images by G. The G network also aims to map the input aliased image $\tilde{\mathrm{x}}$ to a fake image $\check{\text{x}}$ that looks so realistic and plausible that can fool D. Various strategies have been devised to reach the equilibrium. They mostly differ in terms of the cost function adopted for G and D networks; see e.g., [3], [8], [19]. The standard GAN uses a sigmoid crossentropy loss that leads to vanishing gradients which renders the training unstable, and as a result it suffers from severe degrees of mode collapse. In addition, for the generated images classified as real with high confidence (i.e., with large decision variable), no penalty is incurred. Hence, the standard GAN tends to pull samples away from the decision boundary, which can introduce non-realistic images [19]. Such images can be hallucinated, and are thus not reliable for diagnostic decisions.

Motivated by the improved stability of LSGANs we adopt an LS cost for the discriminator decision. In essence, the LS cost penalizes the decision variables without any nonlinear transformation, and as a result it tends to pull the generated samples toward the decision boundary [19].

D. Mixed costs to avoid high-frequency noise

One issue with GANs is that they may overemphasize the high-frequency texture, and thus ignore the image content. To discard the high-frequency noise and avoid hallucination, we use a supervised ℓ₁/ℓ₂ cost as well for training the G net. Such mixtures with pixel-wise costs have been shown to be promising for natural image restoration tasks since they can properly penalize noise and stabilize the training [34]. In particular, the smooth ℓ₂-cost better preserves the main structure and leads to a stable training at the expense of introducing blurring artifacts. The non-smooth ℓ₁-cost however may not be as stable as ℓ₂ in training, but it can better discard the low-intensity noise and achieve better solutions. All in all, to reveal fine texture details while discarding noise, we are motivated to adopt a mixture of LSGAN and ℓ₁/ℓ₂ cost to train the generator. The overall procedure aims to jointly minimize the expected discriminator cost

$$\begin{gathered} \underset{{\mathbf{\Theta }}_d}{\min \hspace{0.17em}}{\mathbb{E}}_{\mathbf{x}}\left[{\left(1-\mathcal{D}(\text{x};{\mathbf{\Theta }}_d)\right)}^2\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\mathbb{E}}_{\mathbf{y}}\left[{\left(\mathcal{D}\left(\mathcal{G}(\tilde{\mathrm{x}};{\mathbf{\Theta }}_g);{\mathbf{\Theta }}_d\right)\right)}^2\right] \end{gathered}$$ (P1.1)

and the expected generator cost

$$\begin{gathered} \underset{{\mathbf{\Theta }}_g}{\min \hspace{0.17em}}{\mathbb{E}}_{\mathbf{y}}\left[{\Vert \text{y}-\text{A}\mathcal{G}(\tilde{\mathrm{x}};{\mathbf{\Theta }}_g)\Vert }^2\right]+\eta {\mathbb{E}}_{\mathbf{x},\mathbf{y}}\left[{\Vert \text{x}-\mathcal{G}(\tilde{\mathrm{x}};{\mathbf{\Theta }}_g)\Vert }_{1,2}\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\lambda {\mathbb{E}}_{\mathbf{y}}\left[{\left(1-\mathcal{D}\left(\mathcal{G}(\tilde{\mathrm{x}};{\mathbf{\Theta }}_g);{\mathbf{\Theta }}_d\right)\right)}^2\right] \end{gathered}$$ (P1.2)

where $\mathbb{E}[\cdot ]$ refers to the expectation operator, and ${\Vert \hspace{0.17em}\cdot \hspace{0.17em}\Vert }_{1,2}$ denotes a convex combination of the element-wise ℓ₁- and ℓ₂-norm with non-negative weights η₁/(η₁ +η₂) and η₂/(η₁ +η₂) respectively such that η₁ + η₂ = η. The LS data fidelity term in (P1.2) is a soft alternative to the hard affine projection step after the generator, and is kept in (P1.2) only for the sake of generality. Tuning parameters λ and η also control the balance between manifold mapping, noise suppression and data consistency.

Looking carefully at (P1.2) shows there is a similarity with regularized-LS schemes used in conventional CS. Taking the initial estimation $\tilde{\mathrm{x}}$ as input, the generator reconstructs the image $\check{\text{x}}=\mathcal{G}(\tilde{\mathrm{x}};{\mathbf{\Theta }}_g)$ from k-space measurement y using the expected regularized-LS estimator, where the regularization is not based on sparsity but learned from training data via LSGAN and ℓ₁-net. This is different from the conventional CS scheme, which involves an iterative optimization algorithm to solve for the ℓ₁/ℓ₂-regularized LS cost. The optimization only happens in training and the optimized weights in the network can generalize to any future samples. The learned generator can be immediately applied to new test data to retrieve the image “on the fly”. As argued in [19], it can be shown that LSGAN game yields minimizing the Pearson-χ² divergence. For (P1) following the same arguments as for the standard GANS in [8] and [19] it can be readily shown that even in the presence of LS data consistency and ℓ₁/ℓ₂ penalty, the distribution achieved by the G network coincides with the true data distribution. The overall procedure ensures the reconstruction is both data consistent and MRI realistic.

Remark 1. [Controlling image hallucination] One possible concern is that adversarial training may cause image hallucination that could mislead diagnosis. It is important to emphasize that the proposed GANCS scheme controls/avoids hallucination by modifying the conventional GAN in the following ways: First, the data consistency step after mapping onto the image manifold ensures that the resulting reconstructed image conforms to the k-space measurements. Second, the mixture cost used for the generator training, namely (P1.2), includes a pixel-wise cost that assures the image pixels are closely aligned with the ground-truth pixels.

IV. Network Architecture for Gancs

The detailed architecture of G and D nets are described in this section.

A. Residual networks for the generator

The input and output are complex-valued images of the same size, where the real and imaginary components are considered as two separate channels. As mentioned earlier, the input image $\tilde{\mathrm{x}}$ is simply an initial estimate obtained via zero-filling, which produces aliasing artifacts. After convolving the input channels with different kernels, they are added up in the next layer. All network kernels are assumed real-valued. Inspired by super-resolution networks in [13], [14] we adopt a deep residual network (ResNet) for the generator that contains 5 residual blocks. As depicted in Fig. 2, each block consists of two convolutional layers with small 3 × 3 kernels and 128 feature maps that are followed by batch normalization (BN) and rectified linear unit (ReLU) activation. It is then followed by three convolutional layers with map size 1 × 1, where the first two layers undergo ReLU activation, while the last layer uses no activation to return two output channels corresponding the real and imaginary image components. The network architecture is depicted in Fig. 2.

Fig. 2.

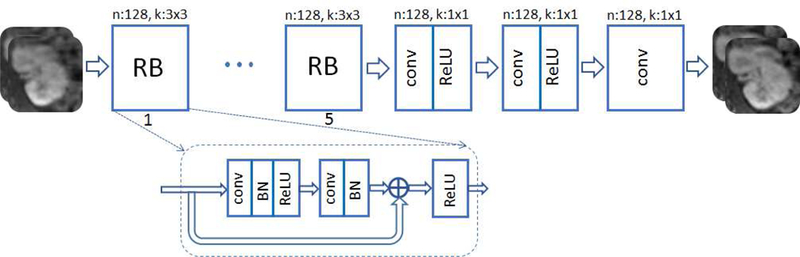
Generator ResNet architecture with residual blocks (RB), n and k refer to number of feature maps and filter size, respectively.

The G network learns the mapping onto the manifold of realistic MR images. The manifold dimension is controlled by the number of residual blocks (RB), feature maps, stride size, and the size of discriminator.

B. Convolutional neural networks for discriminator

The D network takes the magnitude of the complex-valued output of the G net and data consistency projection as an input. It is composed of 8 convolutional layers. In all layers except the last one, convolution operation is followed by batch normalization, and subsequently by ReLU activation. No pooling is used. For the first four layers, the number of feature maps is doubled from 8 to 64, while at the same time convolution with stride 2 is used to reduce the image resolution. Kernel size 3 × 3 is adopted for the first 5 layers, while the two to the last layers use kernel size 1 × 1. For the sixth and seventh layer we use 64 and one feature maps, respectively. The last layer simply averages out the seventh layer features to form the decision variable for binary classification. No soft-max operation is used. The network structure is concisely depicted in Fig. 3.

Fig. 3.

Discriminator multilayer CNN architecture with the input magnitude image, where n, k, and s refer to number of feature maps, filter size, and stride size, respectively.

V. Evaluations

The effectiveness of the GANCS scheme is assessed in this section for a single-coil MR acquisition model with Cartesian sampling. For n-th patient the acquired k-space data is $y_{i,j}^{(n)}={[\mathcal{F}({\text{X}}_n)]}_{i,j}+v_{i,j}^{(n)}$, (i, j) ∈ Ω. We adopt the single coil model for demonstration purposes, but the extension to multi-coil MRI acquisitions is straightforward by simply updating the signal model. Sampling set Ω indexes the sampled Fourier coefficients. As it is conventionally performed with CS MRI, we select Q based on a variable density sampling with radial view ordering [7] that tends to sample more low frequency components from the center of k-space. Different undersampling rates (5 and 10) are chosen throughout the experiment. The input zero-filled (ZF) image $\tilde{\mathrm{x}}$ is simply generated using an inverse 2D FT of the sampled k-space data, which produces images that are severely contaminated by aliasing artifacts. Input images are normalized to have the maximum magnitude of unity per image.

Adam optimizer is used with the momentum parameter β = 0.9, mini-batch size 4, and initial learning rate 10−6 that is halved every 10, 000 iterations. Training is performed with the TensorFlow interface on an NVIDIA Titan X Pascal GPU, 12GB RAM. We allow 20 epochs that takes around 10 hours for training.

Abdominal dataset.

Tl-weighted abdominal image volumes were acquired for 350 pediatric patients with gadolinium-based contrast enhancement. For each scan an RF-spoiled gradient recalled-echo sequence is used with a TR and TE of approximately 3.3 msec and 1.3 msec, respectively. An intermittent fat saturation pulse with an inversion time 9 msec is also used for fat suppression. The field of view for x and y axis is approximately 280 mm and 224 mm, respectively, with the slice thickness of 2.4 mm, and a 15-degree flip angle. Each volumetric Cartesian dataset was acquired using a variable-density sampling with radial view-ordering where the center k-space values in a 20 × 20 region were repeatedly sampled over 50 times. The raw data consisted of 18 temporal frames where each temporal frame was undersampled 6-fold along the axial direction (k_y — k_z undersampling). The total scan was 2 minutes to capture the contrast and motion dynamics. The raw data is then combined over all time frames to create fully-sampled 3D images that are used as the gold-standard. Additionally, respiratory motion was measured intrinsically using a self-navigated approach. This motion information was used to retrospectively soft-gate the data based on the respiratory motion. With the use of light anesthesia, the volunteer subjects had regular period respiratory motion that was simple to address in the image reconstruction to avoid image artifacts. After normalizing the 3D images, we adopt a consistent 256 × 128 resolution for the axial slices that are used as the input for training the G network. Each 3D image consists of 192 axial slices. 336 patients (64,512 2D slices) are used for training, and 10 patients (1,920 2D slices) for test. All in vivo scans were acquired at the Stanfords Lucile Packard Childrens Hospital on a 3T MRI scanner (GE MR750).

Knee dataset.

This dataset includes 19 subjects scanned with a 3T GE MR750 whole body MR scanner at the Stanfords Lucile Packard Childrens Hospital. The full description is available at [25], that is briefly summarized as follows for completeness. Fully sampled sagittal images are acquired with a 3D FSE CUBE sequence with proton density weighting including fat saturation. Other parameters include FOV=160mm, TR=1550 (sagittal) and 2, 000 (axial), TE=25 (sagittal) and 35 (axial), slice thickness 0.6mm (sagittal) and 2.5mm (axial). Each image is a complex valued 3D volume of size 320×320×256. Axial slices of size 320 × 256 are considered as the input for training and test. 16 patients are used for training (5, 120) and 3 patients for test (960).

Under this setting, the ensuing parts address the following intriguing questions:

Q1. Whether the manifold learning via training GAN is stably converged?

Q2. How much speed up and quality improvement can be achieved using GANCS relative to the conventional CS?

Q3. How is the perceptual quality of GANCS images rated by expert radiologists?

Q4. Is GANCS reliable in reconstructing the regions of interest for patients with and without abnormalities?

Q5. How many samples/patients are needed to achieve a reasonable image quality?

Q6. What MR image features drive the network to learn the manifold and remove the aliasing artifacts?

A. Training convergence

To confirm the stable convergence of GANCS, evolution of different components of G and D costs for training are depicted in Fig. 4 over batches (size 4), with η = 0.025 and λ = 0.975 as an example to emphasize the GAN loss in training. According to (P1.2), the G cost mainly pertains to the last term which shows how well the G net can fool the D net. The D cost also includes two components based on (P1.1) associated with the classification performance for both real and fake images. It is apparent that all cost components decrease, and after about 5, 000 batches it reaches the equilibrium cost 0.25. This implies that upon convergence the G-net images become so realistic that the D-net will start flipping coin, i.e., $D(\widehat{\mathrm{x}})=1/2$. Notice also that in this setting with a hard affine projection layer no data-consistency cost is incurred.

Fig. 4.

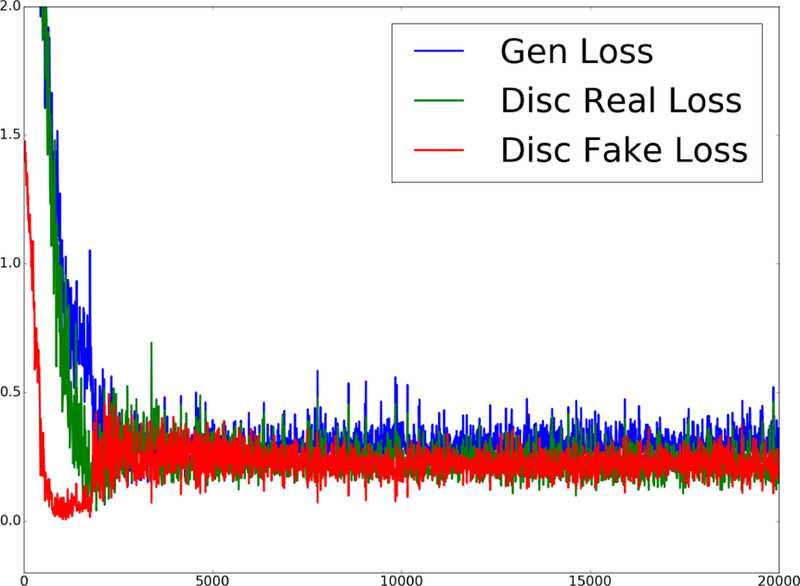
Evolution of different cost components for G and D nets when η = 0.025 and λ = 0.975.

It is also worth mentioning that to improve the convergence stability of GANCS, and to ensure the initial distributions of fake and real images are overlapping, we trained with pure ℓ₁ cost (η = 1, λ = 0) at the beginning and then gradually switch to the mixture loss intended.

B. Image evaluation and comparison: Abdominal data

Retrieved images by various methods are depicted in Fig. 5 with 5-fold undersampling of k-space. For a random test patient, representative coronal slice is shown, where the columns from left to right depict, respectively, the gold-standard image, and the images reconstructed by GANCS with ℓ₁-cost (η = 1,λ = 0), GANCS with ℓ₁-cost (η = 0.975,λ = 0.025), and CS-WV. For 5-fold undersampling, the ZF reconstruction is quite blurred and not shown in Fig. 5. CS reconstruction is performed using the Berkeley Advanced Reconstruction Toolbox (BART) [11], where the tunning parameters are optimized for the best SNR performance.

Fig. 5.

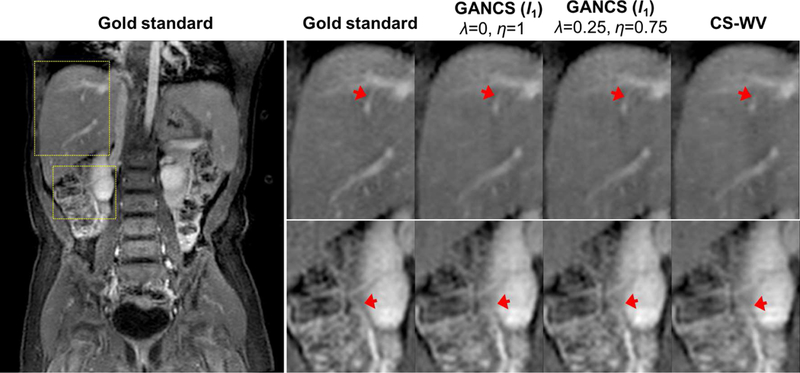
Representative coronal images for a representative test patient with 5-fold undersampling. The first column (1th) shows the full view gold standard image, and the rest of columns from left to right indicate the enlarged areas of liver (top row) and kidney (bottom row) for (2th) the gold-standard, and reconstruction under (3th) GANCS with ℓ₁-cost (η = 1, λ = 0), (4th) GANCS with ℓ₁-cost (η = 0.75, λ = 0.25), and (5th) CS-WV.

As apparent from the magnified regions, GANCS with ℓ₁-cost (η = 0.75,λ = 0.25) returns the sharpest images with highest contrast and texture details that can reveal the small anatomical details. Images retrieved by GANCS with ℓ₁-cost alone results in smooth textures as the ℓ₁-cost encourages finding pixel-wise averages of all plausible solutions. We also tested GANCS with ℓ₂-cost for training, where we observed smoother texture relative to ℓ₁-cost. Thus, we only illustrate the ℓ₁ cost for subjective comparison. Note, in compromise the smooth ℓ₂-cost leads to a more stable training; see e.g., [34] for more details about the trade-offs between ℓ₁ and ℓ₂ costs. The reconstructed images however are not as sharp as the GANCS ones (η = 0.975,λ = 0.025) which leverages both ℓ₁-net and GANs.

Zooming on the liver (top) and the kidney (bottom) areas in Fig. 5, as pinpointed by the arrows, the liver texture is more realistic and the vessels are shaper to delineate. Focus on the thin liver vessel pinpointed by the arrow. It is almost lost in CS-WV, and blurry in GANCS with ℓ₁-cost alone, but it is delineated by GANCS that relies on a 25% GAN cost. The kidney vessels in the bottom images are also seen sharper and more clear with the GANCS using 25% GAN cost. We have observed that using GAN alone, namely η = 0, λ = 1, the retrieved images are quite sharp with a high-frequency noise present over the image that can distort the image structure. It turns out that including the ℓ₁ cost during training behaves as a low-pass filter to discard the high-frequency noises, while still achieving reasonably sharp images. It is also evident that CS-WV introduces blurring artifacts. We also tested CS-TV, but CS-WV is observed to consistently outperform CS-TV, and thus we choose CS-WV as the representative for CS-MRI.

Quantitative metrics including SNR (dB), SSIM, and the reconstruction time (sec) are reported in Table I. These metrics are averaged out over axial slices of all ten test patients (1, 920 slices). The reconstruction time for CS schemes refers to the elapsed time for running 300 iterations of conjugate gradient descent using the optimized BART toolbox. It takes around 10 seconds, that is 300 times longer than the neural-network based schemes as reported in Table I. Reconstructing 30 slices per second makes GANCS a suitable choice for real-time imaging. In terms of SNR and SSIM, GANCS with ℓ₁-cost alone achieves the best performance. GANCS with proper ℓ₁-cost mixing can achieve good performance with a marginally decrease from GANCS with ℓ₁-cost alone. However, GAN based application is not designed and trained to achieve the highest SNR which does not capture the visual perception [14]. GANCS is however trained to achieve a high perceptual quality for diagnostic purposes, which is also shown Fig. 5. This motivates us to ask expert opinions from radiologists regarding the diagnostic value as discussed in the next section.

TABLE I.

Average SNR (dB), SSIM, and reconstruction time (sec) comparison of different schemes under 5-fold (top) and 10-fold (bottom) acceleration.

Scheme	GANCS (ℓ1) η = 0.975, λ = 0.025	GANCS (ℓ1) η = 1, λ = 0	GANCS (ℓ2) η = 1, λ = 0	GANCS (ℓ1) η = 0.75, λ = 0.25	CS-WV	CS-TV	ZF
5-fold acceleration
SNR	20.56	21.40	21.21	18.03	18.22	16.75	13.66
SSIM	0.82	0.84	0.84	0.76	0.80	0.77	0.64
Time	0.03	0.03	0.03	0.03	12.28	1.81	9 × 10−4
10-fold acceleration
SNR	17.06	17.82	17.53	13.7	15.65	15.67	11.92
SSIM	0.67	0.69	0.68	0.57	0.61	0.69	0.45
Time	0.03	0.03	0.03	0.03	11.17	2.59	4 × 10−4

Before moving on, it is worth mentioning that we also managed to compare GANCS reconstruction with the combination of ℓ₁ and SSIM costs, recently proposed in [34], to capture sharpness for natural image restoration tasks. Our observations for MRI reconstruction however indicate no improvement relative to ℓ₁-net. The results are not included due to space limitations. It is also worth noting that the trained discriminator offers a novel score that can be a better metric for perceptual assessment of the images.

Remark 2 [Impact of iteration count]. In essence, the network architecture in Fig. 1 resembles only a single back- and-forth iteration between the image manifold and the affine subspace of data consistent solutions. One can however adopt a recurrent network architecture to model multiple iterations by simply repeating the network architecture in Fig. 1 for a few times. This is extensively studied in our companion work [21], which indicates that using more iterations can significantly improve the reconstruction quality by about 2 − 3 dB in terms of SNR.

C. Image evaluation and comparison: Knee data

For the adopted high-resolution Knee dataset described in Section V-F, the reconstructed images under different schemes are depicted in Fig. 6. In particular, the data-driven CS scheme in [23] based on dictionary learning is adopted as a baseline for comparison. [23] models the images patches as sparsely represented over an overcomplete dictionary, and uses the undersampled data to jointly learn the dictionary and impute the missing k-space entries. We adopt the publicly available code provided by the authors, and choose the patch size 8 × 8 with overlap stride 1, 64 atoms, and 200 ∗ 64 training samples for training the dictionary. We also use 30 iterations with 20 iterations for the operation of KSVD algorithm [2]. The optimization formulation includes a data fidelity term regularized with the ℓ₁ penalty on the dictionary coefficients as well as a penalty term to impose dictionary constraint on the image patches. The regularization parameter is optimized for the best performance. Note, CS-DL is known as one of state-of-the-art data-driven CS scheme that consistently outperforms the conventional CS techniques relying on fixed sparsifying transforms such as Wavelet and TV.

Fig. 6.

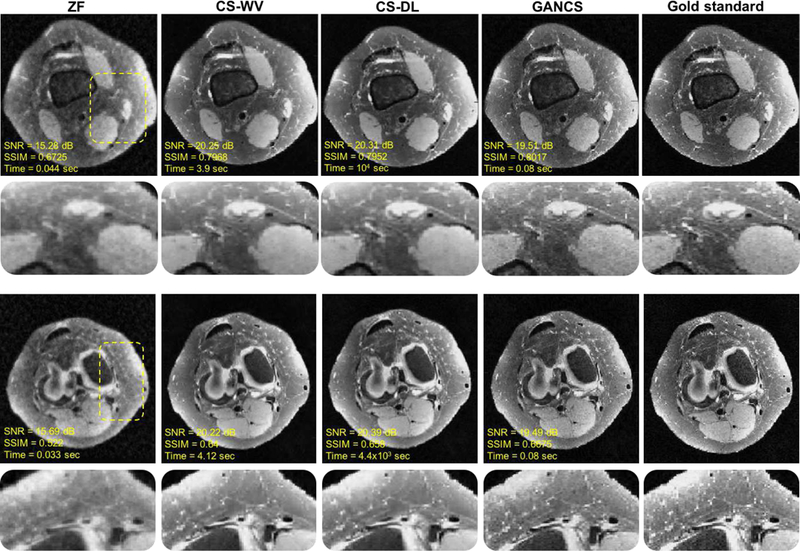
Representative axial knee images for a test patient with k-space data acquired under 5-fold variable density sampling with radial view ordering. For GANCS we choose η = 0.99, λ = 0.01. The quantitative metrics are also listed under the images. SSIM is calculated on a window of size 100 × 50 chosen from the image center. GANCS images look sharpest and look more similar to the gold-standard.

For a test patient, two representative axial slices are depicted in Fig. 6 with their corresponding quantitative metric including the SNR, SSIM, and inference time listed under the images. It is apparent that CS-DL retrieves overly smooth images. It also takes about an hour to reconstruct the image. GANCS (η = 0.99, λ = 0.01) images however seem to better retain the high-frequency details, and reconstructs more realistic texture with sharper edges. Note, for GANCS pixel-wise ℓ₂ loss is used. CS-DL achieves the highest SNR, but as discussed in Remark 2 by using more iterations for the denoiser, GANCS can outperform CS-DL even in terms of SNR.

In order to study the breaking point of GANCS, experiments are run under various undersampling rates, namely 3, 5, 7, 10. k-space data is sampled based on a variable density with radial view ordering mask. The network is trained and tested with the same sampling mask, and the weights are set to λ = 0.1 and η = 0.9 that uses 10% of the GAN loss for all undersampling rates. It is apparent that for 5- and 7-fold undersampling the images miss some high-frequency texture details, but they are still diagnostically valuable. For 10-fold however due to the large space of data consistent images, the texture seems to carry some high-frequency noise, that can hallucinate images. This can be alleviated by lowering the GAN loss weight at the expense of over smoothing the images.

D. Diagnostic quality assessment

To quantitatively assess the image quality of GANCS we performed an experiment based on the expert opinion of two pediatric radiologists at the Stanford Medical Center. Five patients with 3D images are considered where two of those suffer from subtle liver lesion and inflated adrenal gland. The radiologists were blind to the history records and diagnosis results of the patients. They independently rated the overall quality of images as well as the quality of delineation of several anatomical structures including hepatic vein and portal vein. For completeness, the criteria for the radiologists opinion score (ROS) is listed under Table II; see [33] for more details. ROS is ranged from one to five, where 1 refers to a “non-diagnostic” image, while 5 indicates “excellent” diagnostic quality. The readers are first asked to individually assess the reconstruction, and then asked for their preference of side-by-side comparisons.

TABLE II.

Scoring criteria for image diagnostic quality, where we abbreviate hepatic veins as HV, and portal veins as PV.

Score	overall quality	portal veins	hepatic veins
nondiagnostic (1)	no structures assessed	PV blurred	RHV blurred
limited (2)	limited assessment of several structures	lst-order branches of PV blurred	lst-order branches of RHV blurred
diagnostic (3)	all but 1–2 structures assessed	sharp first order branches of PV	sharp first order branches of RHV
good (4)	all structures assessed	sharp 2nd-order branches of PV	sharp 2nd-order branches of RHV
excellent (5)	sharp delineation of all structures	braches seen to within lcm of periphery	braches seen to within lcm of periphery

Rating is provided for the gold-standard as well as the GANCS (η = 0.75, λ = 0.25), and CS-WV schemes. Radiologists are blind to the schemes. The mean scores with their standard deviation are reported in Table III. Similar score is reported for the overall quality and the hepatic and portal vein diagnostic quality. The pairwise difference between different schemes is statistically significant. Radiologists confirm that GANCS provides sharper images with better texture than CS-WV which can better delineate the structures. They also specifically examined the GANCS images for possible hallucinations, but no sign of hallucination was observed. It is also worth noting that the merits of GANCS become more pronounced when dealing with high-resolution images with sharp edges for the structures. Our observations with simulated phantoms with sharp edges indicate the sharp delineation of structures using GNACS relative to CS-WV and pixel-wise costs. Our current research focuses on using a high-resolution dataset with sharper edges to evaluate the diagnostic quality of images.

TABLE III.

Mean and standard deviation of the diagnostic quality scores given by radiologists for the gold standard, GANCS (η = 0.75, λ = 0.25), and CS-WV.

score/scheme	overall quality	portal vein	hepatic vein
gold-standard	4.l ± 0.22	4.l ± 0.22	4.l ± 0.22
GANCS	3.6 ± 0.37	3.6 ± 0.37	3.6 ± 0.37
CS-WV	3.l ± 0.05	3.l ± 0.05	3.l ± 0.05

E. Performance for pathological cases

When operating the trained GANCS on new patients with novel and abnormal cases, one concern is that GANCS may create hallucinated images, which are not reliable for diagnosis. This could be either due to lack of generalization of GANCS, or, unstable training that can lead to local minima. To validate this safety concern we pick a pathological patient that suffers from a hypertrophic adrenal gland as pinpointed by the arrow on top of the kidney in Fig. 8. The adrenal gland has a similar texture as the kidney and thus not very obvious. We make sure the training data does not include patients with hypertrophic adrenal glands. Normal adrenal gland is typically a small structure compared with the kidney size. A representative coronal slice of the full-view gold-standard image and the zoomed area are shown in the first and second columns, respectively. Likewise, GANCS reconstruction with η = 0.75, λ = 0.25 is also shown in the third and fourth column for 5-fold undersampling. It appears from the enlarged regions of interest that GANCS faithfully delineates the inflated adrenal gland, and does not introduce/miss any structures that can lead to misdiagnosis.

Fig. 8.

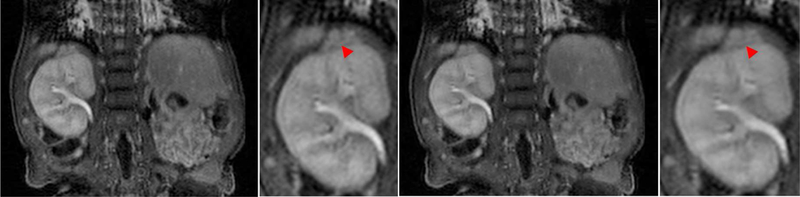
Representative coronal images with inflated adrenal gland. From left to right first column (1st) shows the gold-standard image with the zoomed kidney and adrenal gland area in the 2nd column. Likewise, 3rd and 4th columns are GANCS reconstruction for 5-fold undersampling when η = 0.75, λ = 0.25.

In general, quantifying the hallucination risk is a very challenging task that is yet an open problem in medical imaging. The challenge emanates from lack of a clear definition, and the need for an extensive subjective assessment. It is a subject of our current research that needs an extensive separate study beyond the scope of this work. Nonetheless, it should be emphasized that this is a generic problem with any reconstruction scheme (compressed sensing as well) from undersampled data that deals with a huge space of image ambiguity. In order to shed more light on the hallucination risk of GANCS, we perform a simple test to check the generalization accuracy for novel cases that are not seen during the training phase. In essence, the generative model learns a manifold of structured MR images. To simulate novel cases, we take a test MR image and perturb its entries independently with Gaussian noise $\mathcal{N}(0,{\sigma }^2)$ to fall off the MR image manifold. For a normalized image x with ${\Vert x\Vert }_F=1$, different noise levels ranging from σ = 0.0001 to σ = 1 are simulated and subsampled to feed into the G network (trained with real Knee images) as a test example. The Gaussian white noise impacts all frequency components due to its uniform and unlimited spectrum, and thus considered as an extreme adversary for the image reconstruction task that heavily relies on the structures. The reported SSIM and NMSE indicate that the network is robust against perturbations with intensities even larger than σ = 0.1. As argued in Remark 1 this robustness is fairly attributed to the data consistency and pixel-wise loss in the training of GANs. For very large noise intensities (around σ = 1) the performance can significantly drop as the input image is quite off the manifold, and it thus inherits no structures. Of course, developing robust regularization techniques against such adversarial examples is an important part of our future research.

F. Number of patients for prediction

Prediction (generalization) performance of the deep learning model heavily depends on the amount of training data. This becomes more important when dealing with scarce medical data that are typically not accessible in large scales due to privacy concerns and institutional regulations. To address this question we examined an evaluation scenario to assess the reconstruction performance for a fixed test dataset, described in the beginning of this section, for variable number of patients used for training. Fig. 10 plots the test SNR versus the number of training patients for the GANCS scheme with η = 0.975, λ = 0.025. For all cases we use the same number 12 training epochs. Apparently, when the number of patients increases from 1 to 130, a noticeable SNR gain is observed as more patients used for training. The performance gain then gradually saturates as the number of patients is over 150. It thus seems with 150 or more patients we can take full advantage of both learning from historical data and the complexity of the networks. Recall that a fixed sampling mask is used for training and testing. GANCS however captures the signal model, and therefore it can easily accommodate different sampling trajectories. Also note that, if more datasets are available for training, we can further improve the model performance by increasing model complexity. Further study of the number of patients needed for other random sampling schemes and different network models is an important question that is a focus of our current research.

Fig. 10.

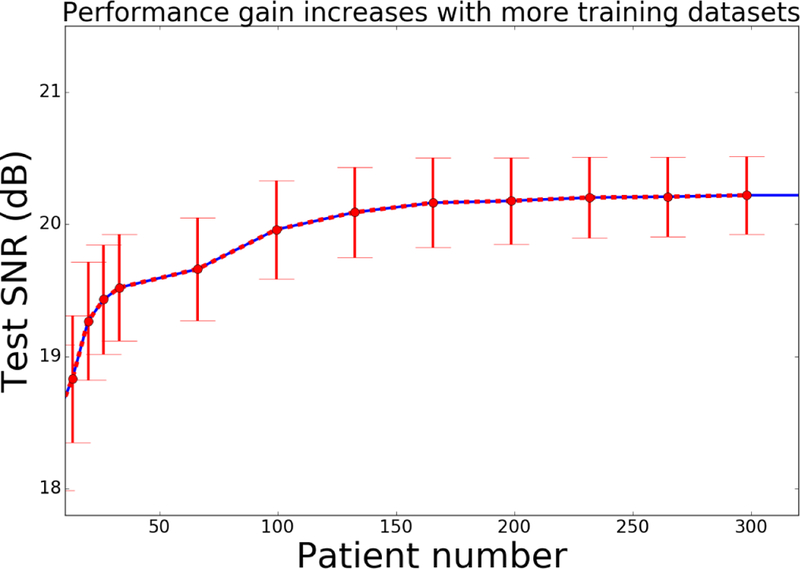
Average SNR for a subset of test dataset under different number of training patients when η = 0.975 and λ = 0.025.

G. Discriminator interpretation

As suggested by the training strategy, the discriminator plays a role like a radiologist thats scores the quality of images created by the generator. During adversarial training D learns to correctly discern the real fully-sampled images from the fake ones, where the fake ones becomes quite realistic over training. It is thus insightful to understand image features that drive the quality score. To this end, we visualize the feature maps of D net at the sixth hidden convolutional layer. Recall that the D net has eight layers. In essence, the sixth layer is the last convolutional layer before the fully-connected layers that form the decision variable for classification. It thus carries the most abstract representation of regional features declaring whether an image is real, or, fake (with artifacts). Fig. 11 depicts the heat-maps of feature maps, and when overlaid on the original images. Three representative image slices are shown from left to right, and different (eight) feature maps are shown from top to bottom. Each layer includes 128 feature maps, and thus for conciseness we depict only the the first 8 dominant principal images (found via principal component analysis) for the sixth layer.

Fig. 11.

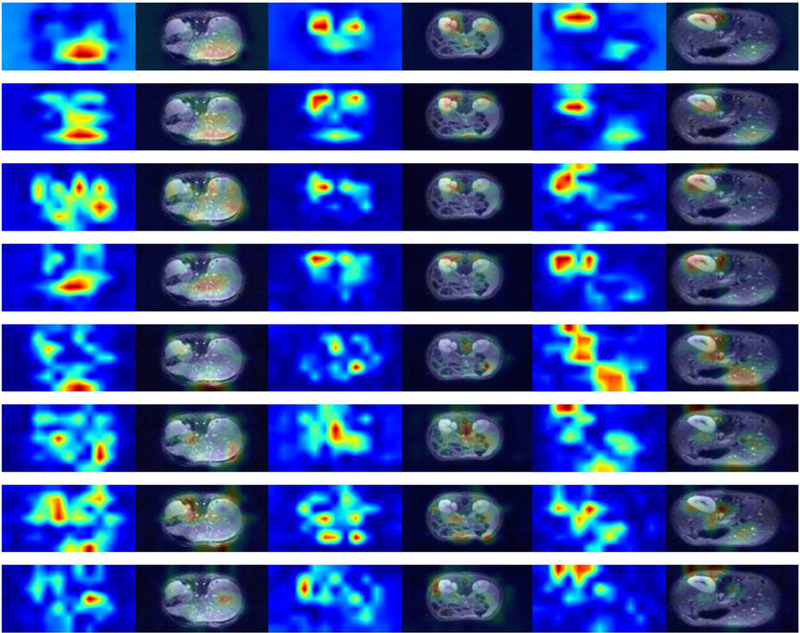
Heat-map of discriminator feature maps at the sixth hidden layers for three MRI images with different anatomies. Each row demonstrates the eight dominant principal components of the feature maps. Each image corresponds to two consecutive columns; the fist column highlights the activation corresponding at the sixth hidden layer, while the second column visualizes the feature maps overlaid on top of corresponding MR image.

Fig. 11 indicates that after learning from tens of thousands of generated MRI images by the G network together with the corresponding gold-standard ones, where different organs are present, the D network learns to focus on certain regions of interest that are more susceptible to artifacts. The score is determined based on feature maps of the last several layers that pick up regions with rich texture details, and particularly focus on the periphery of important organs such as kidneys and liver. Note that there is no labels to instruct the network, but the network learns from the reconstruction how to correctly pick up the important organs as shown on the top rows in Fig. 11.

VI. Conclusions and Future Work

This paper caters a novel CS framework that leverages the historical data for rapid and high diagnostic-quality image reconstruction from highly undersampled MR measurements. A low-dimensional manifold is learned where the reconstructed images have not only superior sharpness and diagnostic quality, but also consistent with both the real MRI data and the acquisition model. To this end, a neural network scheme based on LSGANs and ℓ₁/ℓ₂ costs is trained, where a generator is used to map a readily obtainable undersampled image to a realistic-looking one consistent with the measurements, while a discriminator network is trained jointly to score the quality of the resulting image. The overall training acts a a game between generator and discriminator that makes them more intelligent at reconstruction and quality evaluation.

Extensive experiments based on a large cohort of abdominal MR data, with the evaluations performed by expert radiologists, confirm that the GANCS retrieves images with noticeable diagnostic quality improvement “on the fly” (30 msec, 300× faster than state-of-the-art CS-MRI toolboxes). Last but not least, the scoring model offered by the trained discriminator can highlights the organ of interests automatically and can be used as a metric for perceptual assessment of future patients. There are still intriguing directions that can further improve GANCS, that go beyond the scope of this paper but are important subjects of our future studies. Such directions pertain to improving the robustness of the models against patients with abnormalities, variations in the sampling trajectory, residual motion artifacts in training data, and using 3D spatial correlations for improved quality of volumetric images. In this direction, quantifying possible hallucination risks for GANCS, and devising regularization approaches to robustify the reconstruction is an important step of our current research. Using the perceptual metric learned by the discriminator network as a image quality assurance metric is also another intriguing direction to pursue.

Fig. 7.

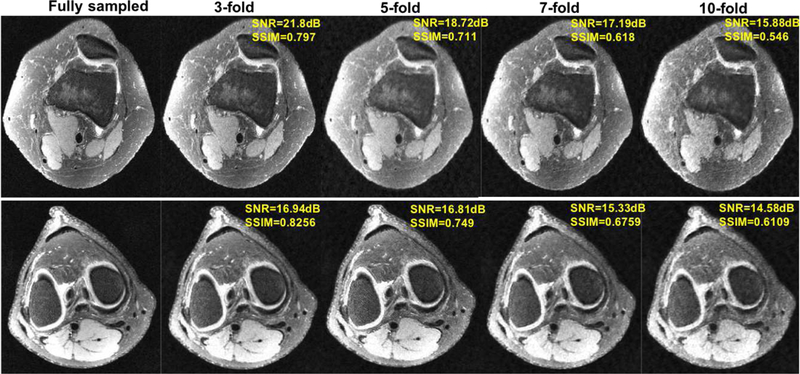
Representative axial knee image slices for GANCS reconstruction with undersampling rates 3, 5, 7, 10 compared with the fully sampled gold standard one. For GANCS we choose η = 0.9, λ = 0.1. SSIM is calculated on a window of size 100 × 50 chosen from the image center.

Fig. 9.

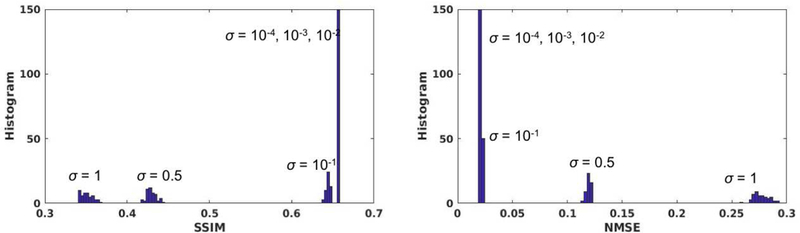
Histogram of SSIM and NMSE for GANCS reconstruction with noise perturbed MR images. Various noise levels with standard deviations σ = 10−4, 10−3, 10−2, 10−1, 0.5, 1 are considered. 50 random examples from each noise level are drawn, and we set λ = 0.1, η = 0.9.