Computational Methods for the Aortic Heart Valve and its Replacements

Abstract

Introduction.

Replacement with a prosthetic device remains a major treatment option for the patients suffering from heart valve disease, with prevalence growing resulting from an ageing population. While the most popular replacement heart valve continues to be the bioprosthetic heart valve (BHV), its durability remains limited. There is thus a continued need to develop a general understanding of the underlying mechanisms limiting BHV durability to facilitate development of a more durable prosthesis. In this regard, computational models can play a pivotal role as they can evaluate our understanding of the underlying mechanisms and be used to optimize designs that may not always be intuitive.

Areas covered.

This review covers recent progress in computational models for the simulation of BHV, with a focus on aortic valve (AV) replacement. Recent contributions in valve geometry, leaflet material models, novel methods for numerical simulation, and applications to BHV optimization are discussed. This information should serve not only to infer reliable and dependable BHV function, but also to establish guidelines and insight for the design of future prosthetic valves by analyzing the influence of design, hemodynamics and tissue mechanics.

Expert commentary.

The paradigm of predictive modeling of heart valve prosthesis are becoming a reality which can simultaneously improve clinical outcomes and reduce costs. It can also lead to patient-specific valve design.

1 -. Introduction

Heart valves are responsible for ensuring directional blood flow through the chambers of the heart. For example, the aortic valve (AV) regulates the flow between the left ventricle of the heart and the ascending aorta. The detailed anatomical features of the AV and its microstructure have been described previously [1]. Diseases affecting the AV result in either obstruction to forward flow (stenosis) or reversal flow across an incompetent valve (regurgitation). In either case, although the AV can sometimes be surgically repaired, using prosthetic heart valves is a major treatment option for a vast majority of patients [2]. According to the recent report from American Heart Association [3], the number of heart valve procedures in 2013 was more than 102,000 with a consistent increasing number of surgeries compare to the previous years. According to the data from the Nationwide Inpatient Sample (NIS), approximately 50,000 aortic heart valves are replaced annually in the United States [4].

The ideal AV replacement should have sufficient durability, high resistance to thrombosis, and excellent hemodynamics [5]. Current prosthetic AV designs are divided into mechanical heart valves (MHV) and bioprosthetic heart valves (BHVs). The former is made of highly durable pyrolytic carbon and metal alloys, while the latter is fabricated from biologically derived exogenously crosslinked soft collagenous tissue to form the leaflet biomaterials. Most BHVs are made of bovine pericardium leaflets sutured to a rigid stent [6]. As an alternative design, stentless valves have a greater effective orifice area compared to stented valves, but are technically more difficult to implant and therefore are not clinically popular. BHVs provide excellent, native-like hemodynamics and usually do not require the long-term use of anticoagulants. On the contrary, MHVs have important disadvantage as they do require permanent anticoagulation therapy.

The choice of a MHV or BHV replacement is an important consideration, influenced by the trade-offs between the eventual need for reintervention due to BHV deterioration and the risk associated with long-term anticoagulation for the MHV. Patient age is also an important factor because the incidence of structural deterioration of a BHV is greater in younger patients but the risk of bleeding from anticoagulation is higher in older patients. The AHA/ACC Task Force recommendation for the selection of prosthetic valve [7] suggests that a BHV is reasonable for patients of any age for whom anticoagulant treatment is not possible or desired. A MHV is reasonable for patients less than 50 years old, however, for those who are unwilling or unable to have anticoagulant treatment the BHV remains an option. The age limit for MHV prosthesis was lowered from 60 to 50 years age in the recent AHA/ACC guideline, which demonstrates that BHVs are becoming the optimal choice for many patients undergoing AV replacement. In fact, BHVs are considered as the most popular replacement valve choice. About 64% of all the AV replacement surgeries in 2001 used BHV, increasing to 82% in 2011 [8]. However, BHV durability remains a major limitation [9]; generally lasting 10–15 years [10]. Therefore, current BHVs do not provide end-point treatment; for young patients, the need for an additional valve replacement later in life is highly likely.

Despite continued developments in BHV design in particular transcatheter aortic valve implantation or TAVI [11], an ideal valve substitute does not yet exist, and robust methods to extend its durability remain largely unexplored. It should be noted that even increasing BHV functional life span for an additional 3–5 years will have a substantial clinical impact [12]. Hence, there is a strong need to develop a greater understanding of the underlying mechanisms involved in BHV durability to improve its present clinical performance. BHV failure is the result of leaflet structural deterioration mediated by fatigue and/or tissue mineralization. Structural valve deterioration has been reported as the most common form of primary failure of BHV [13], mostly appearing as tears in BHV leaflets near the free edges and commissural connections. In-vivo experimental studies examined the influence of multiple valve-related parameters on BHV degeneration such as valve design, leaflet material properties, and anticalcification treatments [14, 15]. Mechanical stress has long been known to play a key role in this deterioration process [16]. Therefore, improving the durability of BHVs is possible through understanding the underlying stress-driven mechanism of fatigue within the leaflets over the cardiac cycle.

Many studies have indicated that computational methods applied to valve design can reduce mortality and morbidity by allowing for customized design of medical devices [17, 18, 19]. Simulation techniques can thus provide information regarding optimal geometries of the replacement valve that would be valuable for clinical diagnosis and treatment [20, 21, 22, 23, 24]. Moreover, performing the preliminary tests is crucial in analyzing the design factors to produce the most favorable design of the prosthesis. By using simulation, the number of in vitro and animal tests required in the design optimization process can thus be reduced. Simulation technologies can also provide information that are extremely difficult to obtain using other testing techniques, such as stress distributions within the leaflets.

However, these simulations cannot be performed using over-simplified or incomplete models. Valve dynamics and corresponding performance attributes are highly dependent on the geometry of the root and leaflets as well as the mechanics of leaflet materials. Valve performance is usually characterized with a combination of hemodynamics and structural-biomechanical aspects, such as sufficient effective orifice area, transvalvular pressure gradient, and good leaflet coaptation without regurgitation. Advanced simulation technologies for simulating BHV can combine state-of-the-art numerical methods with novel constitutive models of BHV biomaterial responses, to simulate long-term cyclic loading. Considering the rapid advancement of numerical algorithms and imaging techniques in recent years, we review studies relevant to the computational simulations for the design of BHV.

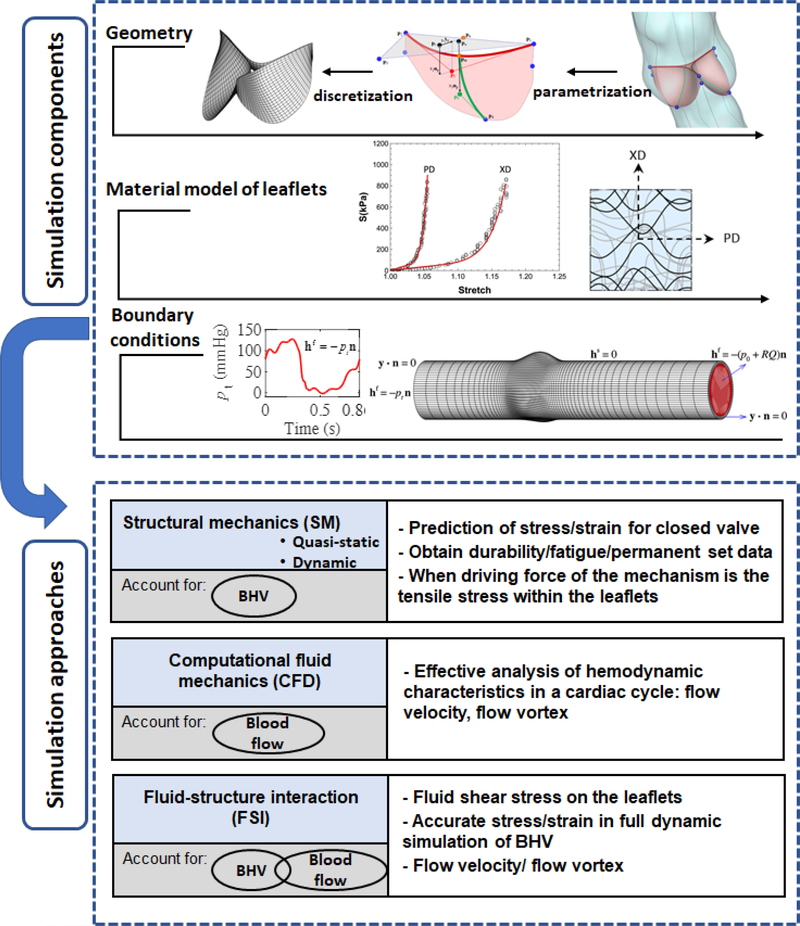
In general, computational approaches for BHV require the following components: (1) the geometry of the valvular apparatus, (2) accurate time-evolving biomaterial models; and (3) accurate boundary conditions (e.g. physiological loads) over the cardiac cycle (Figure 1). Computational models used for BHV simulation solve the equations of continuum mechanics for leaflet deformation and hemodynamics of blood flow, using numerical approaches. These models can be classified in three main categories: structural mechanics (SM), computational fluid dynamics (CFD), and coupled fluid-structure interaction (FSI) models. To examine the role of different aspects of valvular function, the choice of appropriate model needs to be made.

Figure 1.

Components of computational analyses of BHV; creating valve geometry, choosing appropriate material model and specifying realistic boundary conditions; and their interaction with different approaches for BHV simulation. The objective of the study determines which simulation approach needs to be chosen.

SM models which only include the structural domain (i.e. valve leaflets), are divided into two groups: quasi-static-SM and dynamic-SM models. In SM models, the effect of the surrounding blood is considered by applying a transvalvular uniformly distributed pressure load to the leaflets as a boundary condition. SM analyses are typically performed using quasi- static-SM simulations of leaflets deformation with the valves in the fully closed position, when larger pressure loads on the leaflets occur. Since this pressure difference is the principal load that causes leaflet deformation during closure, a uniform pressure distribution on the leaflet surface yields reasonably accurate results. These simulations are more reliable for simulation of static configurations such as prediction of strain and related stress field for closed valve, as well as identification of regions of stress concentrations that can be correlated with leaflet structural damage.

Quasi-static-SM simulations are suitable to obtain BHV durability information by providing an accurate understanding of the mechanical response of the BHV in a cyclic loading and underlying mechanism of structural damage. More precisely, by performing quasi-static-SM simulations, one can acquire the time evolving mechanical response and geometry evolution of BHV leaflets which is the most significant change in response to the long-term cyclic loading. Fatigue mostly occurs when the closed valve is exposed to the fully loaded state and the primary loading mode is tensile. Therefore, quasi-static-SM simulations are useful to study fatigue mechanisms for BHV applications. Although quasi-static-SM simulations are prevalent approach for SM models, few studies also exist on the dynamic-SM simulation of the BHV throughout the cardiac cycle including the opening and closing phases of the valve function. However, this type of model is simplified as it neglects blood flow and therefore doesn’t reliably simulate the dynamics of the valve.

With respect to the flow, CFD models with moving boundaries are acceptable over the cardiac cycle. From a numerical standpoint, these models are less sophisticated than the full FSI approach as the motion of the structural domain needs to be specified based on a priori knowledge (which can be derived from clinical imaging data), and will be imposed as a boundary condition to the fluid domain. This allows, however, for effective analysis of valve hemodynamic features such as flow and vortex dynamics throughout the cardiac cycle. Two moving boundary algorithms used for the modeling of flow in deforming heart valves include the arbitrary Lagrangian-Eulerian (ALE) and the immersed boundary (IB) method.

However, for accurate dynamic analysis that incorporates blood flow during the cardiac cycle coupled to the structural mechanics of the valve, FSI analysis is required as they consider both structural and fluid flow domains. In these simulations, the applied load to the leaflets is the result of coupling between two domains. FSI models are essential in order to accurately simulate full dynamic behavior of the BHV. This dynamic behavior is important in the simulation of valvular repair, such as the reduction of valve orifice area in stenosis, or the effect of repair on regurgitation. For increasing our understanding of the details of the fluid induced shear stresses on the leaflets as well as flow velocity and the effect of flow vortex in the aortic sinuses on the dynamics of AVs, FSI analysis is necessary.

This review thus seeks to provide a comprehensive look at recent developments in computational modeling of AV and its BHV replacement by evaluating the techniques for simulation of valve dynamics, construction of the valve geometry, and realistic material properties specification of the valvular structure. The review is organized as follows. In Section 2, we present the computational methods for the optimal design of the BHV geometry and leaflet’s shape. The computational approaches for choosing material models are summarized in Section 3. In Section 4, we review the most recent developments in simulation techniques. Section 5 summarizes our findings. Finally, in Expert commentary and Five-years view we outline the limitations and future directions.

2 -. Geometrical design of BHV

The geometrical design of a BHV has a key role for its performance characterized by an appropriate valve opening and closure during a cardiac cycle, as well as valve durability. Simulation of the BHV in the physiological setting can provide useful information for the purpose of improving the design. The approaches that are exploited for improving the BHV design, in combination with simulation techniques are the topic of this section. In particular, by performing simulations using the different combinations of the valve geometry and dimensions, one can obtain the hemodynamics features and strain/stress distributions and magnitude throughout the leaflet which are difficult to obtain otherwise. Valve performance can be evaluated in terms of different indices such as coaptation area and stress field; the former gives a direct indication of the efficiency of the valve closure while the latter identifies the weakest points within the valve leaflets. Hence, the design of BHV can be improved by optimizing the distribution of the mechanical stresses in the leaflets, and durability is likely to be improved. The computational tests can also reduce the number of required in-vitro tests in the design and optimization process.

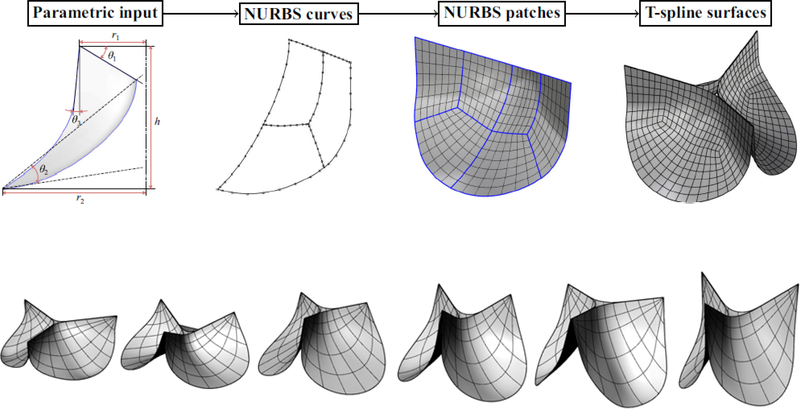
In earlier studies, the valve geometry is constructed based on the typical dimensions of the human AV [25] or using the mathematical models [26, 27]. In [28], Thubrikar introduced a 3D geometry description of the AV where the surfaces of the leaflets were constructed by considering the intersecting surfaces of a cone with inclined planes. He used this description to search for optimal prosthetic dimensions with appropriate coaptation, minimum volume, and efficient use of energy. Labrosse et al. [29] used this design configuration to obtain the range of dimensions for the AV that maintains the normal valve dynamics by preventing blood from flowing back through the valve. The importance of including precise representation of the valve leaflets in the computational model to accurately describe the blood flow characteristics and wall shear stress has been highlighted in [30]. The authors presented a 3D mathematical parametric model for the AV geometry using three independent parametric curves for the representation of the heart valve structure including the cusps, commissures and sinuses. Later in [31], Marom et al. showed how coaptation and mechanical stresses are affected by the aortic annulus diameter. Furthermore, it has been suggested that sinotubular junction diameter can affect the valve function by impacting hemodynamics and structural mechanics features of the valve [31]. The optimal value for aortic annulus and sinotubular junction diameter were determined by defining design criteria as having relatively large coaptation area, low stress within the leaflets during diastole, and low flow shear stress during systole. A Rhino-Grasshopper based interactive geometry design platform [32] was used in [33] to construct the valve according to the aortic root geometry. Geometrical parameters of the leaflet including the surface curvature were considered as design parameters, represented as the input for the Grasshopper program to construct a spline surface representation of the leaflet geometry (Figure 2).

Figure 2.

Top panel: Parametric BHV leaflet geometry modeling flowchart, taken from [36]. Bottom panel: selected examples of the valve designs showing various perturbation of the leaflets geometry obtained using the parametric design framework.

The idea of applying immersogeometric FSI analysis to parametric BHV designs is provided in [34], where authors presented an efficient simulation workflow for valve dynamics. BHV geometry is directly used as a computational model with isogeometric analysis (IGA) and then immersed in an unfitted mesh of the fluid domain. Other studies on presenting a parametric study on mathematical formulation and geometrical construction of an aortic heart valve include Labrosse et al. [23], Auricchio et al. [35], Kouhi and Morsi [36], and Li and Sun [37]. These studies have focused on defining general guidelines for valve design that are expected to improve average-population outcomes. For example, in [37], authors performed a parametric study to investigate the impact of leaflet geometry on the transcatheter AV peak stress. The study resulted in an optimal leaflet design that could reduce the peak stress on the leaflets by about 5% compared with the original leaflet design. The idea of using parametric geometrical framework to obtain the optimal design for valve has been extended to pulmonary valve in [38] by perturbing the initial shape of an elastomeric scaffold that represents the potential leaflet replacement tissue, and simulating its shape under quasi-static diastolic loading. Optimal leaflet design was determined by minimizing the difference between the deformed shape obtained from quasi-static-SM simulation and an ex-vivo microCT scan of the leaflet.

As discussed in Section 1, many BHVs designs have a stent structure which supports the soft-tissue leaflets [10]. The leaflet and stent geometry designs are dependent on each other and both had to complement each other to provide an optimal BHV geometry. The design of the optimal valve by Thubriikar [39] defines that the criteria for optimum performance of the valve are minimum coaptation height to ensure valve closure, and a minimum valve height to reduce dead space. Another study for the analysis of the stent height conducted by Chandran et al. [40] suggested that Increasing stent height decreases the BHV leaflet stress. Also, design features of stented valve may lead to reduction in the stent true internal diameter [41] which is an important factor in order to choose a right size prosthesis for patient.

Stented valves are available in multiple sizes adjusted for different patient size, but this may not provide optimal hemodynamics performance. Clinical studies have demonstrated when the effective orifice area is too small for the body size, “patient-prosthesis mismatch” and therefore structural valve degeneration can occur [42]. Therefore, the intermediate-term or long-term survival rate after valve replacement will be reduced. The other category of BHVs is stentless valves [10], offering larger orifice areas and improved hemodynamics. However, their implantation procedure is more complex, and, as stated in Xiong et al. [43], in stentless valve the leaflet geometry has an important role on valve efficiency as it contributes to better dynamic leaflet behavior, increased effective valve orifice area, and increased leaflet coaptation height and area. This has also been investigated by Auricchio et al. [35] by performing finite element analysis of stentless valve implantation to simulate the prosthesis inside the patient-specific aortic root and evaluating both the coaptation and the stress/strain pattern. The simulation results proved the effect of valve size on replacement procedure outcome and also suggested that geometrically symmetric stentless valves may lead to valve insufficiency since the valve is not able to close completely during diastole. Therefore, the general asymmetry of the sinuses affects the implantation procedure. More recently, a computational comparison was provided by Scrofani et al. [44] on the performance of stentless and stented BHVs, in terms of aortic root displacements and internal stresses, using FSI technique. They performed simulations for these two designs of prosthesis (i.e. stentless and stented) and compared them with the case of no-prosthesis representing the healthy configuration. The results suggested that for the stented case, higher stresses were found, which were not physiological. However, good agreement was found between stentless and native displacements and internal wall stresses.

The scope of using medical images to construct the more realistic geometries for the purpose of using in computational mechanics models may allow for more accurate simulation of native AV [21] and customized design of medical devices such as stentless heart valves. This claim has been addressed recently by academic researchers [35, 45, 46]. More precisely, by using the patient-specific computational models obtained from medical images, one can improve the outcome of the complicated stentless heart valve surgical procedure in advance. In Hsu et al. [45], the authors explored the potential role of computational methods in the design of patient-specific stentless prosthesis where the valve geometry conforms to the aortic root geometry of individual patients obtained from computed tomography (CT) angiography images. Construction of patient-specific geometrical models of heart valve has also been addressed by medical device industries such as the method reported in [47] by Siemens. More precisely, a valvular heart apparatus model is presented, which derives personalized models of the heart valves including AV. This technology uses acquired 4D cardiac CT image data by constructing the surfaces representing the AV leaflets and aortic root, and can also be used to extract geometrical quantities such as annulus diameter and orifice area from medical images of patient’s heart valves.

3 -. Material model for BHV leaflets

BHV leaflet mechanical properties have been demonstrated to be anisotropic [48, 49]. Almost all BHV designs use exogenously crosslinked (EXL) collagenous soft tissues obtained from bovine pericardium to manufacture leaflets [104] and the material is highly nonhomogeneous. Fiber bundles have a preferred direction of alignment and some degree of dispersion. Moreover, these parameters change spatially within the leaflet which results in local anisotropy of the tissue. Spatial distribution can be accurately captured experimentally [50].

One conspicuous shortcoming of some earlier work in this area is the relatively simple material model of the valve leaflets [33, 51]. To enhance the realism of the BHV simulations for the design purpose, choosing an accurate material model is imperative as the material properties affect the mechanical behavior of the valve and may have an impact on the stress distributions and therefore the onset and incidence of leaflet tear and calcification [52]. Considering that collagen fibers are the main load-bearing structure, it is expected that the anisotropy of the BHV leaflets due to the network of collagen fibers embedded in the material at varying levels of tortuosity, plays and important role in the overall valve function. Moreover, leaflet stiffness has a considerable effect on dynamic valve motion [53]. In particular, increasing leaflet stiffness induces high bending which can cause flexural stresses in the leaflet tissue, associated with tissue breakdown and valve failure. These findings are also in agreements with the numerical results presented by Avazini et al. [54], who used a finite element approach to investigate the effect of leaflet anisotropy and stent stiffness, by neglecting the direct effect of blood flow and comparing BHV motion under quasi-static and dynamic loadings. They found regions of high stress concentration at the commissure near the stent tip and at the base of the leaflet cusp. These studies have implications to improve the design of BHVs through developing novel chemical fixation technologies that minimize flexural induced damage by minimizing leaflet stiffness, and therefore extends biomaterial durability. Computational models have been used to examine which materials may be subject to tears and fatigue as well as investigating the change in mechanical properties after the damage. Chew et al. [55] studied the progressive damage of the bioprosthetic porcine valve as propagation of the initial tear, and failure of the tissue to the damage of the collagen fiber bundles.

In a modeling context, the structure of the BHV leaflets can be idealized as a “thin- walled” structure, so that the transmural variations of the in-plane stresses are ignored. BHV leaflets have been modeled as membranes [56, 57, 58] or shells [59, 60]. Material incompressibility are typically enforced by the kinematic condition for the plane stress [61]. The membrane element cannot account for the bending of the leaflet, which is an important subject when there is large deformation of the leaflets in a cardiac cycle. In fact, some previous studies using shell elements did show that due to the large deflections of the leaflets, bending stresses are substantial in BHVs during the cardiac cycle [60, 62].

3.1 -. Modeling BHV material nonlinearity

Variety of material models have been explored for modeling native valve and BHV leaflets. A comprehensive review on phenomenological and structurally-informed constitutive models for the BHV can be found in [63]. In the past, linear elastic model were used to describe valve tissue [25, 56, 57, 64]. However, linear models are only appropriate in the case where the stress-strain relationship is linear and displacement gradient is small. Hyperelastic models have been employed to describe biological tissue under finite deformations for simulation of the BHVs [61, 65]. The most common hyperelastic material model is the exponential model proposed by Fung [66], and has been utilized to date for characterizing the mechanical response of many soft biological tissues, including skin [67], pericardium [68], and epicardium [69]. Following studies incorporated nonlinear material model for the leaflet using shell elements with isotropic [60, 70, 71] and anisotropic [65, 72] models.

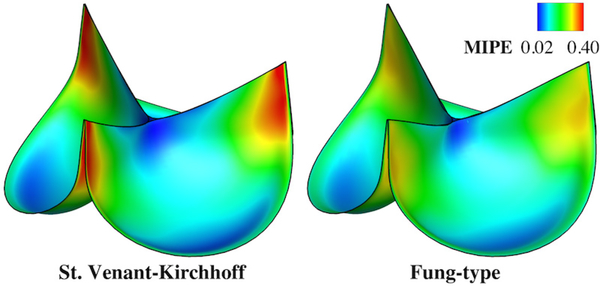
The importance of including nonlinear material models for the BHV was also studied by Patterson et al. [70] by comparing linear and nonlinear isotropic models of leaflets. The authors found that the nonlinear model induced a lower compressive, but higher tensile stresses in leaflets and leaflets deformed into more complex shape during valve opening and closing phases. In a recent paper, Hsu et al [33] illustrated the physical significance of including material nonlinearity in the context of BHV design by comparing the Fung-type material model with the classical St. Venant-Kirchhoff material which assumes a linear stress-strain relationship without capturing the exponential stiffening behavior of the soft tissues. Fully- closed configurations of a valve and maximum in-plane principal Green-Lagrange strain obtained using SM simulation for both models (Figure 3), showing that the peak strain in the St. Venant-Kirchhoff material is much larger, while the Fung-type model has the effect of distributing strains more evenly through the leaflets because of its exponential term.

Figure 3.

Comparison between different isotropic material models. The valve is loaded with a spatially-uniform pressure of 100 mmHg. The maximum values of strain are 0.490 and 0.319 for St.Venant-Kirchhoff and Fung-type cases, respectively. Reprinted from [31] with the permission of authors.

3.2 -. Modeling BHV material anisotropy

The influence of incorporating anisotropic material model for the BHV leaflets has been studied either by assuming an isotropic matrix with fiber-reinforcement [73, 74] or with a Fungtype nonlinear anisotropic model [23, 75, 76]. Integrating anisotropic behavior with finite element model affects the stress distribution in the tissue [77], and the opening and closing times during the cardiac cycle [78]. De Hart et al. preformed FSI analysis on the stentless BHV, and observed that using fiber-reinforced materials for the valve material model alleviated stresses within the leaflet by reducing bending deformation at the closing stage of the cardiac cycle. Therefore, the stress distribution and magnitude within the BHV leaflets depends on the orientation and number of fibers [74, 79]. In [80], the influence of anisotropy of a pericardial heart valve has been studied using orthotropic materials, showing that even a small amount of orthotropy can significantly affect the mechanical behavior of the valve. Li et al. [77] observed significant changes in the stress distribution and the location of the peak stress due to the nonlinear anisotropic behavior of the porcine heart valves modeled as a fiber-reinforced transversely isotropic material. Sun et al. [81] adopted a nonlinear fiber-based structural model to evaluate the impact of leaflet properties on the stress distribution of the BHV and noticed a significant change in stress distribution of the leaflet as a result of anisotropy, concluding the importance of using actual leaflet material properties and the profound impact of the degree of material anisotropy for accurate BHV finite element simulations.

Another significant impact of an anisotropic material model is to facilitate proper coaptation which is needed to ensure the valve closure. This has been investigated in Koch et al. [82] by performing static simulation, where they used nonlinear anisotropic material model through a transverse isotropic model, by including leaflet anisotropy with pronounced stiffness in the circumferential direction. The remarkable effect of anisotropy on leaflet mechanics has also supported by more recent numerical models presented by Sotiropoulos et al. [83] and Korossis et al. [84]. In [83], the May-Newman-Yin anisotropic model was compared to the St.Venant-Kirchhoff for analysis of opening and closing of the valve, concluded that May- Newman-Yin model is more suitable for describing valve behavior, especially to provide the adequate coaptation of the leaflets and ensure tolerating high blood pressure in diastole.

For design purposes, it is also important to consider that BHV has different microstructural properties compared to the native valve. In native valve, most collagen fibers are aligned in the circumferential direction [85]. And therefore, the extension is limited in this direction, and the tissue will mainly extend in radial direction when the valve is loaded. However, it has been shown by Sun et al. [65] that the BHV leaflets have a ±45° preferred orientation and a uniform degree of orientation throughout the leaflet. In the aforementioned study, the authors utilized Fung material model for the predicted leaflet using the material parameters derived from actual leaflet biaxial tests and measured leaflet collagen fiber structure axes obtained from physical pericardial BHV leaflets [61, 86]. Quasi-static-SM simulations were performed under 40, 80, and 120 mmHg transvalvular pressure loading and the strain field obtained from finite element simulations are compared to the experimental data for validation. Overall discrepancy of 2.36% was reported, indicating excellent agreement between computed and measured principal strains.

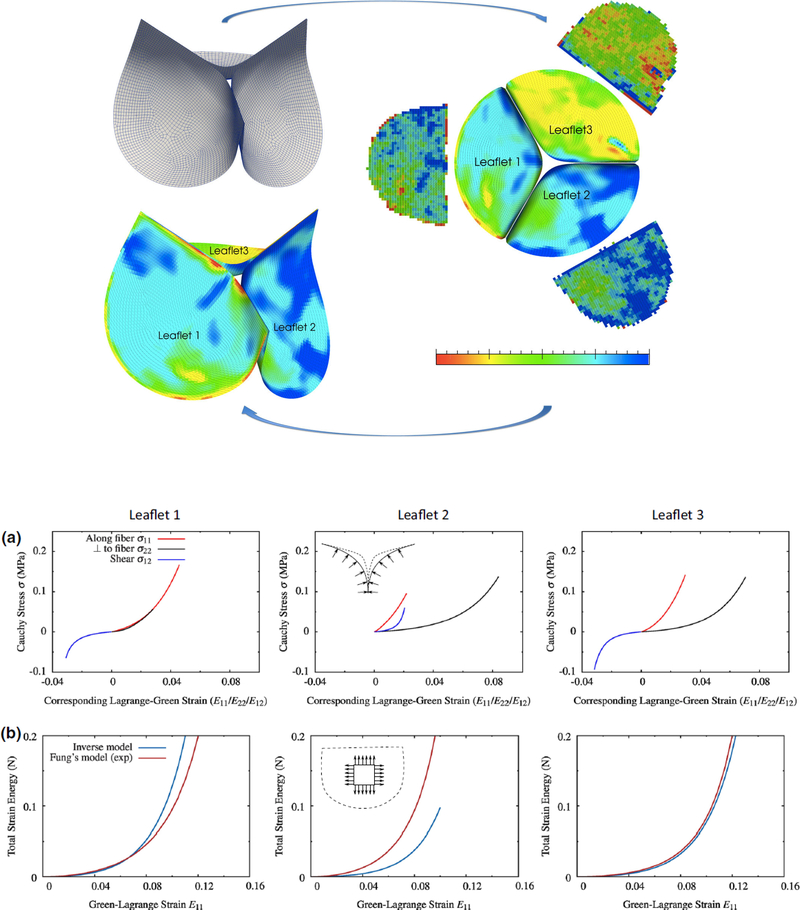
Techniques based on population averages and three-dimensional mapping have also been used for incorporating biological material inhomogeneity into the computational models such as the work by Aggarwal et al. [87] where a spline fitting technique was developed to connect surface deformation with structure (top panel Figure 4). Determining the physical properties of heart valve leaflet tissues in a non-invasive manner remains an important clinical goal. Aggarwal et al. [88, 89] developed a novel leaflet shape-based framework based on invivo valve geometric data obtained from 3D imaging, to estimate the biomechanical behavior of heart valves from surface deformations using an inverse modeling approach. By exploiting the shape of the valve at the loaded state and fiber structural information as the input, the authors determined the stress-strain relationship using converged material parameters resulted from inverse method. The inverse model response has also been validated against experimental data (bottom panel Figure 4) which provides reasonably good match. The obtained discrepancy between inverse model and experimental results has been argued to be mainly due to the preconditioning and inelastic effect of excising the leaflets from an intact valve. In fact, an inverse model provides a more accurate estimate of the leaflet properties as it avoids the artifacts from excision of the native state of the valve and in-vitro experimental results. Convergence improvement for parameter estimation of this inverse model has also been addressed [90].

Figure 4.

Top panel: fiber structure of three leaflets measured experimentally and then mapped onto valve geometry using spline technique. Bottom panel: (a) stress-strain relationship from inverse model [90] by using shape of the valve during valve closure (b) Validation of the inverse model against experimental results. Reprinted from Aggarwal and Sacks [90] with permission.

3.3 -. Modeling BHV material evolution

Truly predictive BHV modeling cannot proceed without accurate fatigue constitutive models [91, 92]. In pericardial BHVs, high tensile stresses are considered to be the major cause of structural failure [93]. Therefore, fatigue mostly happens when the closed valve is exposed to the fully loaded state and the primary loading mode is tensile. Fatigue has been studied for BHV application using quasi-static-SM simulations in [94], where permanent set of the leaflets were incorporated in the material model to describe the fatigue damage of BHVs subjected to cyclic loading. However, it is important to note that fatigue model parameters in the aforementioned study were fit to the experimental data obtained from cycle loading of bovine pericardium patches, and a linear progression of permanent set factors and stress softening is assumed. The pressure driven loading conditions of an intact BHV are much more complex than in the cyclic loading due to the bending in addition to tensile deformations, which results in heterogeneous leaflet deformation. Therefore, a more comprehensive approach is needed to determine the fatigue model parameters and capture the response for intact valve. As the first step to potentially increasing BHV durability, we need a material model which allows us to predict the change in biomaterial response with time, to the long-term cyclic loading.

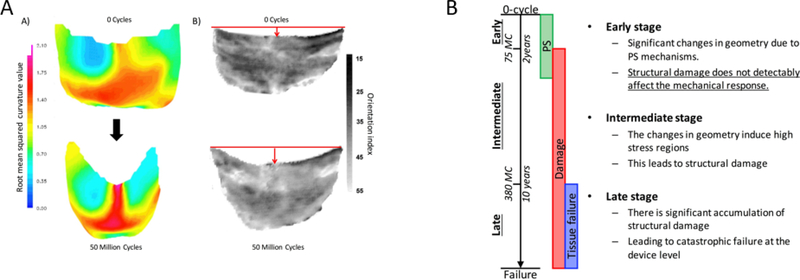
Recently, Sacks and Zhang [95, 96] developed a novel constitutive model for exogenously crosslinked soft tissue to evaluate BHV leaflet behavior. This novel structural model accounts for three contributors to the mechanical response of soft tissue: collagen fibers, exogenously crosslinked (EXL) matrix, and the interactions between the fiber-fiber components. They found that exogenously crosslinking does not increase the collagen fiber modulus, but significantly increases the interactions between collagen fibers, which is responsible for up to 30% of the stress in the fully loaded state. Using this rigorous full structural model [95] Sacks et al. developed the extension of EXL matrix model form to present the first permanent set model [96] and study the time evolving properties of EXL collagenous soft tissue under cyclic loading. Permanent set is defined as the mechanism causes significant changes in BHV geometry in the early stage of cycling (Figure 5). This geometry change leads to stress concentration and therefore can cause structural damage.

Figure 5.

A) Left: 3D unloaded geometry a BHV leaflet before and after cyclic loading, showing the most significant change in geometry is in the belly region. Right: BHV leaflet collagen fiber architecture, showing that the collagen fiber architecture is convected by the dimensional changes. B) graphical representation of the structural damage and permanent set of BHV leaflets progression during cyclic loading. Picture is taken from [93] with permission.

By defining S as the second Piola-Kirchhoff stress tensor, the following final form of the constitutive model was used [96] as following

$$S=S\left(k,F_{\text{PS}},A(\widehat{s}),C\right)=S_{\text{col}}+S_{\text{int}}+S_{\text{m}},$$ (1)

The final model form is a function of the permanent set rate constant k, the permanent set deformation F_PS, the strain history A(s), and the material parameters of the constitutive model in the uncycled state. $\widehat{s}$ is the intermediate time for which the exogenously crosslinked matrix is formed. Also, deformation C = F^T F is the input of the model where F is the deformation gradient. The collagen contribution is

$$S_{\text{col}}\left(k,F_{\text{PS}},A(\widehat{s}),C\right)={\varphi }_{\text{col}}{\eta }_C{\displaystyle \underset{\theta }{\int }{\mathrm{\Gamma }}_1}\left(F_{\text{PS}},\theta \right)\left\{{\displaystyle \underset{1}{\overset{{\lambda }_{\theta }}{\int }}\frac{D_1\left(F_{PS},x\right)}{x}}\left(\frac{1}{x}-\frac{1}{{\lambda }_{\theta }}\right)\text{d}x\right\}{n}_{\theta }\otimes n_{\theta }\text{d}\theta ,$$ (2)

In (2), ϕ_col is the mass fraction of the collagen fibers and D₁ and Γ₁ are the collagen fiber recruitment distribution function and orientation distribution function, and ${\lambda }_{\theta }=\sqrt{n_{\theta }\cdot C{n}_{\theta }}$ is the stretch of the fiber ensemble oriented along θ. ηc is defined as the modules of collagen and terms for fiber ensemble interactions and EXL matrix are presented by (3) and (4) respectively.

$$\begin{gathered} S_{\text{int}}\left(k,F_{\text{PS}},A(\widehat{s}),C\right)={\varphi }_{\text{col}}{\eta }_{\text{int}}{\displaystyle \underset{\alpha }{\int }}{\displaystyle \underset{\beta }{\int }}{\mathrm{\Gamma }}_1\left(F_{\text{PS}},\alpha \right){\mathrm{\Gamma }}_1\left(F_{\text{PS}},\beta \right) \\ \times \left[\right\{{\displaystyle \underset{1}{\overset{{\lambda }_{\alpha }}{\int }}{\displaystyle \underset{1}{\overset{{\lambda }_{\beta }}{\int }}\frac{2{\lambda }_{\beta }{D}_1\left(F_{PS},x_{\alpha }\right)D_1\left(F_{PS},x_{\beta }\right)}{x_{\alpha }{x}_{\beta }}}}\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)\text{d}{x}_{\alpha }\text{d}{x}_{\beta } \\ +{\displaystyle \underset{1}{\overset{{\lambda }_{\beta }}{\int }}{D}_1}\left(F_{\text{PS}},x_{\beta }\right){\left(\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)}^2\text{d}{x}_{\beta }\}\frac{n_{\alpha }\otimes n_{\alpha }}{{\lambda }_{\alpha }} \\ +\{{\displaystyle \underset{1}{\overset{{\lambda }_{\alpha }}{\int }}{\displaystyle \underset{1}{\overset{{\lambda }_{\alpha }}{\int }}\frac{2{\lambda }_{\beta }{D}_1\left(F_{PS},x_{\alpha }\right)D_1\left(F_{PS},x_{\beta }\right)}{x_{\alpha }{x}_{\beta }}}}\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}\frac{{\lambda }_{\beta }}{x_{\beta }}-1\right)\mathrm{d}{x}_{\alpha }\mathrm{d}{x}_{\beta } \\ +{\displaystyle \underset{1}{\overset{{\lambda }_{\alpha }}{\int }}{D}_1}\left(F_{\text{PS}},x_{\alpha }\right){\left(\frac{{\lambda }_{\alpha }}{x_{\alpha }}-1\right)}^2\text{d}{x}_{\alpha }\left\}\frac{n_{\beta }\otimes n_{\beta }}{{\lambda }_{\beta }}\right]d\alpha \text{d}\beta , \end{gathered}$$ (3)

$$\begin{gathered} S_{\text{m}}\left(k,F_{\text{PS}},A(\widehat{s}),C\right) \\ ={\varphi }_m{\eta }_m[\mathrm{Exp}[-k\cdot s]\left({\left({\overline{I}}_1\left(F_{\text{PS}},A(0)\right)-3\right)}^{\alpha -1}+r{\left({\overline{I}}_1\left(F_{\text{PS}},A(0)\right)-3\right)}^{\beta -1}\right) \\ \times \left(\tilde{B}{\left(F_{\text{PS}},A(0)\right)}^{-1}-{\tilde{B}}_{33}^{-1}\left(F_{\text{PS}},A(0)\right)C_{33}{C}^{-1}\right) \\ +{\displaystyle \underset{0}{\overset{s}{\int }}k}\mathrm{Exp}[-k(s-\widehat{s})]\left({\left({\overline{I}}_1\left(F_{\text{PS}},A(\widehat{s})\right)-3\right)}^{\alpha -1}+r{\left({\overline{I}}_1\left(F_{\text{PS}},A(\widehat{s})\right)-3\right)}^{\beta -1}\right) \\ \times \left(\tilde{B}{\left(F_{\text{PS}},A(\widehat{s})\right)}^{-1}-{\tilde{B}}_{33}^{-1}\left(F_{\text{PS}},A(\widehat{s})\right)C_{33}{C}^{-1}\right)\text{d}\widehat{s}]. \end{gathered}$$ (4)

The first invariant ${\overline{I}}_1(\widehat{s})$ for the right Cauchy Green tensor $\overline{C}(\widehat{s})$ defined as ${\overline{I}}_1(\widehat{s})=\mathrm{Trace}(\overline{C}(\widehat{s}))=\mathrm{Trace}\left(A^{-\top }(\widehat{s})\cdot C\cdot A^{-1}(\widehat{s})\right)$ and $\tilde{B}$ is the left Cauchy deformation tensor. ϕ_m is the mass fraction of the matrix and α and β are directions in the tissue that two fiber ensembles are oriented along them, and λ_α and λ_β denote stretches of the collagen fibers in these directions. For details of this model readers is referred to [96].

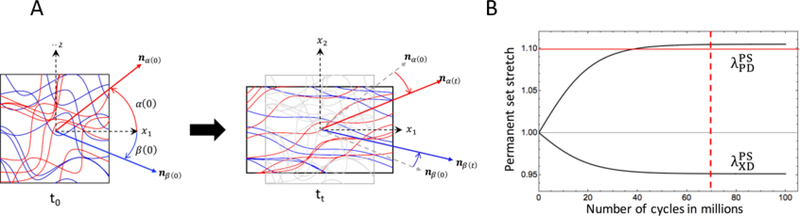
It has been observed that collagen fibers recruitment limits the maximum change in BHV geometry that can occur due to permanent set (Figure 6, B). This novel model can capture the change in geometry of the BHV leaflets; which is the most significant change in response to cyclic loading; and therefore have a significant impact on the prosthesis design as we can optimize the BHV geometry from permanent set model to minimize the leaflet stresses[96]. More precisely, the approach presented in [96] has the potential to reduce changes in BHV geometry during cyclic loading and thus optimize for permanent set and actual damage effects and minimize the effects of these factors on valve performance and durability. This constitutive model has also the power to predict the time evolving BHV geometry and mechanical response for unmeasured experimental regimes of cyclic loading.

Figure 6.

A Illustration of collagen fiber architecture by changes in the dimension of the bulk tissue. B) Permanent set deformation reaches plateau after approximately 70 million cycles, PD and XD denote preferred and cross preferred direction respectively. Picture is taken from [93] with permission.

As a future direction, in-vitro accelerated wear tests (AWT) which has long been used as a required pre-clinical evaluation test of BHV durability in the FDA heart valve guidance [97], can also be used to derive more fundamental information on the fatigue process. The key metric for the calibration of evolving fatigue material parameters will be how well the deformed BHV geometry after AWT matches the predicted geometry obtained from structural analysis simulations by incorporating permanent set material model [96].

4 -. Simulation approaches for BHV

In this section, we present the major progress made in the last years to numerically simulate the BHV under physiological conditions. In SM simulations, stress/strain analysis in the tissue is performed under the assumption that assumed pressure load to the leaflets approximates the interaction between blood flow and the leaflet’s structure. SM simulation of heart valves have been studied in several previous numerical models using standard finite element method [46, 98, 99, 100]. In particular, these studies focused on mechanical behavior of BHVs by using quasi-static-SM [65, 100] and dynamic-SM [101] approach to compute deformation and stress distribution within the leaflets.

The quasi-static-SM approach is more commonly used in BHV simulations. A quasistatic-SM analysis is valid when a hydrostatic transvalvular pressure load is applied to the closed valve which only represents a portion of the full cardiac cycle and cannot capture the transient response of an opening valve. Moreover, such approach ignores the dynamic moving leaflets, especially during the opening/closing phases of the cardiac cycle when leaflet flexure occurs that can contribute to the leaflet structural damage. These considerations motivate the need to consider more sophisticated modeling approach that simulates the dynamic opening and closing of the BHV interacting with hemodynamics, to overcome the limitation of the structure dynamics analysis and enforce more accurate tractions to the leaflets during the entire cardiac cycle.

Quasi-static-SM or dynamic-SM models can be used to study the mechanics of native and prosthetic valve leaflets and fatigue mechanism, while FSI approaches can be applied to study the flow patterns and fluid stresses resulting from leaflet flexure due to opening and closing of the valve. Modeling the fluid-structure interaction between the valve leaflets and blood flow can provide useful additional information by explicitly accounting for the coupling between fluid dynamics and solid mechanics models. However, adopting FSI techniques for the simulation of BHV involves some difficulties. The leaflets contact one another and the mesh topology of the fluid domain changes significantly.

In all simulation approaches, it is important to specify appropriate boundary conditions to obtain meaningful and accurate results from simulations. For quasi-static-SM models the appropriate choice of boundary condition is a uniform pressure field applied to the aortic side of the leaflets. This uniform pressure usually has a maximum value of 120 mmHg for AV closure. A limitation of this approach is that the “water hammer” effect due to the dynamic loading of blood flow is neglected. However, this method is sufficient for structural analysis of the leaflets and to obtain the valve stress distribution. For dynamic-SM models a time dependent pressure difference across the leaflets (transvalvular pressure) can be applied on the ventricular side of the leaflets. A drawback of this approach is that the calculated effective orifice area from simulation results may not be accurate since neglecting the viscosity damping effect of blood on the leaflets causes unrealistic flutters in the leaflet motion. For FSI simulations the loading condition on the leaflets is modeled through the fluid dynamics of the blood flow. More precisely, pressure on the leaflets is a consequence of applying the physiologically-realistic left ventricular pressure waveform at the inflow and resistance boundary conditions [33, 102, 103] such as Windkessel model [104, 105] at the outflow to model the compliance derives from stretching of the aorta and the effect of surrounding tissue on valve motion (See [104] for a complete overview of loading conditions in FSI analysis of AV dynamics).

4.1 -. Methods for coupling blood flow with valve dynamics

In general, there are two strategies for coupling the fluid dynamics equation of blood flow with structure mechanics equation of valve leaflets: the IB method and the moving mesh method (also known as the boundary-fitted approach). The IB method is more flexible regarding the discretization procedure for the problems involving large deformations such as heart valve dynamics. Moving mesh approach is more accurate especially at the interface of the fluid and structure since this class of methods has the advantage of satisfying kinematic constraints naturally. The drawback of moving mesh approach is that the fluid mesh can become highly distorted due to the large structural deformation and contact. Another alternative approach for handling FSI simulations of heart valve is to discretize the fluid using a mesh-free approach, such as smoothed-particle hydrodynamics (SPH) [106]. SPH has been applied to evaluate mechanical, bioprosthetic [107], and native mitral valve function [108].

In the FSI literature, several heart valve studies employed boundary-fitted approach where the deformation of the fluid mesh matches the Lagrangian structure mesh at the shared interface. Boundary-fitted FSI methods have been applied to study rigid motions of hinged MHVs [109, 110], as well as to 3D FSI model of BHV studied by Makhijani et al. [111]. However, as it had been already discussed, maintaining mesh quality is a difficult task in a boundary-fitted simulation of BHV, where flexible leaflets deform and contact each other. The problem for handling extreme deformations can be solved by generating a new mesh for the fluid domain through the re-meshing process [112, 113, 114, 115]. However, this introduces additional computational cost for calculation of the mesh motion and also causes some numerical errors due to artificial diffusivity associated with the projection of fluid solutions from the old to the new mesh. Therefore, standard schemes such as arbitrary Lagrangian-Eulerian (ALE) [116, 117, 118] or deforming-spatial- domain/space-time (DSD/ST) [119, 120], which continuously deform the fluid domain so that its motion matches that of the structure domain through the moving fluid-structure interface, are no longer directly applicable. Takizawa et al. [121] extended the DSD/ST framework to allow for the topology changes without re-meshing, by introducing the space-time with topology change (ST-TC) method to solve the coupling of the heart valve with the fluid flow, with prescribed leaflet motion [122].

The alternative technique to the boundary-fitted approach is the IB concept. It is originally introduced by Peskin in 1972 for the purpose of FSI analysis of the heart valve by representing the valve as a collection of markers connected by elastic fibers [123]. A comprehensive overview of the various IB methods, their properties, and diverse applications is summarized in [124, 125]. IB method allows the independent movement of the structure discretization with respect to the fluid mesh and therefore significantly simplifies the treatment of large structural deformations and contact. However, it has been reported that this method has some disadvantages in capturing boundary layers near the immersed fluid-structure interface [126]. In fact, to capture the information accurately near the IB, an excessive resolution is required. The importance of capturing information at the interface with high resolution is essential to obtain accurate shear stresses in hemodynamic analysis, which is important in biomedical applications [127]. To alleviate this shortcoming, sharp-interface IB methods have been proposed. By coupling the sharp-interface curvilinear immersed boundary (CURVIB) method [128, 129] with a non-linear large deformation finite element solver, Borazjani [130] simulated FSI of a BHV while neglecting the bending stiffness in the structural model. Gilmanov et al. [131, 132] extended the CURVIB method to include fluid-shell structure interaction, but the problem was solved only for the opening phase of the cardiac cycle. Effectiveness of this method needs to be also explored when leaflets contact each other with large pressure gradient. Griffith et al. [133] introduced a modification of the standard IB scheme near the outer boundaries of the fluid domain to mediate the fluid-structure coupling. This modified Peskin’s IB method is applied to the simulation of fluid dynamics of heart valves, including a model of a natural AV and a model of a prosthetic valve [104, 133, 134].

The IB concept used by Baaijens [135], which is another fixed mesh method referred to as fictitious domain, was used by De Hart et al. [74, 79, 136] and van Loon et al. [137, 138, 139] to couple the fluid subproblem of the blood flow with the structural subproblem of valve dynamics. A Lagrange multiplier is used to weakly couple the fluid and structure domains. This partitioned approach suffered from numerical instability for the physiological Reynolds numbers using the realistic transvalvular pressure gradient. Hsu et al. [33] presented an enhanced framework on geometry design and constitutive modeling, building on an immersogeometric FSI methodology for the BHV modeling. Immersogeometric analysis [34, 140] is a type of immersed methods, with focus on faithfully capturing immersed design and geometry in analysis in a non-boundary-fitted background mesh. Also, the fluid problem is solved using finite element method, instead of finite volume or finite difference approach which are what have been mostly used in other IB methods. More precisely, the variational multiscale (VMS) formulation of the Navier-Stokes equations of incompressible flow [141] is employed for the modeling of blood flow. In immersogeometric method, similar to other IB methods, there is no need to keep track of mesh quality throughout the computation. It also can easily handle leaflet-leaflet contact. This method has been used by Hsu et al. [33] to perform BHV-FSI simulations using isogeometric analysis (IGA) [142, 143]. It has been reported in [46] that IGA greatly improves the representation of the leaflet coaptation in structural simulations of AVs with the advantage of computational speed and efficiency, as it requires approximately 200 times less number of nodes compare to the traditional finite element method to capture the coaptation area adequately.

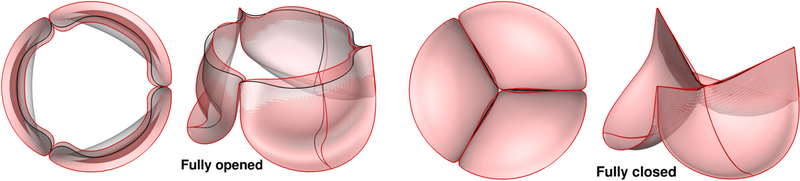
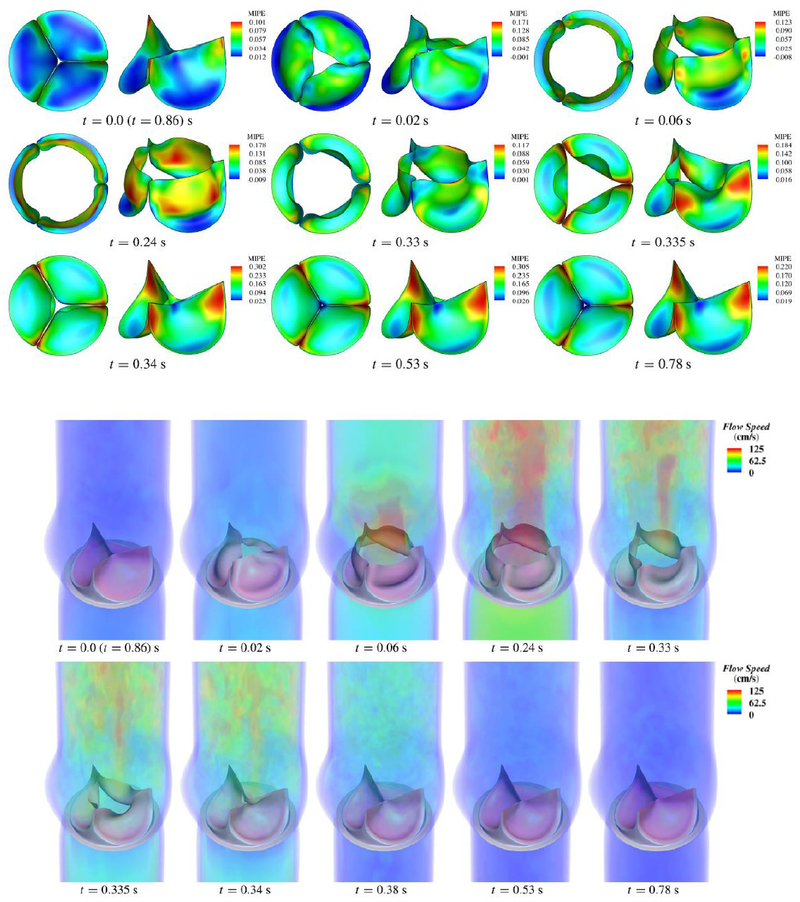
A comparison between two FSI simulations of a BHV, one using ALE formulation and the other using IB technique, was presented in [144]. The study emphasized the significant advantage of the immersed method in terms of computational cost, even though the number of elements required was much higher. A comparison between FSI analysis and dynamics-SM simulation using immersogeometric method [33] has been provided in Figure 7. The results superposed in the configurations corresponding to fully-open and fully-closed phases. Moreover, it has been observed in [33] that FSI computation provides a more realistic leaflet deformation compare to the dynamic-SM simulation. The results of the FSI simulation showing the deformations and strains and the corresponding flow fields in the artery lumen are depicted in Figure 8. Maximum in-plane Green-Lagrange strain contours generally indicate that the peak of the principal strain always occurred near the commissures, with the lower strain occurring near the free edges.

Figure 7.

The comparison between the dynamic-SM simulation result (gray) and the FSI result (red) using immersogeometric solver presented in [31].

Figure 8.

Top panel: Deformations of the valve from the FSI computation, colored by the maximum in-plane Green-Lagrange strain evaluated on the aortic side of the leaflet. Bottom panel: Volume rendering of the velocity field at several points during a cardiac cycle. Reprinted from [31] with permission.

For the FSI in BHV, the solution of equations for problem configuration using physiological parameters needs advanced computational tools and can hardly be handled by commercial software packages. Therefore, most of the IB-FSI approaches have relied on inhouse research codes. Nevertheless, in some previous studies on this subject, commercial software LS-DYNA [145] and Abaqus [144] have been used for FSI simulations of BHV and native AVs [55, 84, 146, 147, 148]. The coupled Eulerian-Lagrangian (CEL) approach in Abaqus solves the FSI simultaneously within the software. On the other hand, LS-DYNA uses the operator splitting approach, which is similar to the fictitious domain method. The limitation of this software is that very small time-steps are required due to the explicit coupling approach implemented in the solver, and therefore the computation time would be high. Since the blood is nearly incompressible, the time-explicit procedures implemented in LS-DYNA result in severe Courant-Friedrichs-Lewy (CFL) conditions that limit the maximum stable time step size in hemodynamic computations, [149, 150].

Another approach for using commercial software for heart valve FSI simulation is to use “black-box” coupling algorithms [151], which are designed to connect independent finite element analysis of the valve dynamic-SM and CFD sub-domain solvers, such that no access to the source code is needed. The black-box coupling typically requires applying methods to ensure the stability of the coupled FSI problem [152, 153] because of the use of loosely coupled approaches to connect fluid and structure solvers. This issue is especially important in heart valve simulation since coupling of the fluid to the thin, light structure of the leaflets causes the fluid to appear as an added mass to the structural operator, and the stability and convergence properties of the coupled problem depends significantly on the ratio of this apparent added mass to the actual structural mass. In [154], a black-box coupling algorithm is applied to an idealized AV. A set of non-convex constraints are imposed to represent contact between different leaflets and the structure solver is not supposed to handle contact by itself.

5 -. Conclusions

Recent advances in computational methods to enhance the physical realism of BHV simulations have been reviewed. These computational techniques utilize the advanced numerical methods for the simulation of heart valve function to assess the impact of selecting different constitutive models in the organ-level simulation of a BHV as well as the effect of valve shape and geometry on its performance, to further improve the design and durability of BHVs. Computational modeling of the BHV can provide insight on the performance by quantifying the features related to both fluid and structure dynamics sub-problems: hemodynamics data represents the valve influence on the flow characteristics and can identify the non-physiological patterns of the flow, while the stress distribution data of the valve structure can be obtained through the structural analysis which elucidates the possibility of the failure. Moreover, comparing different designs of the valve leaflets indicates that which material model or geometric design provides the best setting. In fact, in-situ modeling allows for parametric studies of the valve. The effect of variables can be investigated individually by simulating a variety of situations. It is a big advantage compare to the in-vivo testing techniques.

Recently, using parallel platforms, computational models can be used to perform highfidelity simulations of the valve by utilizing the complex and computationally expensive patientspecific geometries. Future utilization of this methodology for clinical applications will depend on improving the numerical methods for valvular algorithms and progressing its computational implementation by taking advantage of parallel supercomputers as well as the integration of computational tools with the imaging software. This provides highly accurate and individual personalized framework and facilitates a tailored plan for durability.

6 -. Expert commentary

This review focused on the importance of advancing computational methods for simulating the valve performance and capturing the material properties of BHV with high accuracy, which outlines the approaches for designing a durable heart valve. These computational models have potential to be used as a tool for the optimization of a new prosthesis design such as the work presented in [155] where optimal leaflet thickness is defined such that it leads to maximum coaptation area while reducing stress on the leaflet. With the similar approach, the model can be used to investigate the influence of other geometrical parameters (e.g., leaflet height, curvatures, commissure shape, etc.) and of the material properties. Parametric design of the leaflets allows for wide variety of designs for automatic valve reconstruction, such as the design framework presented in the recent paper by Hsu. et al [45]. Evaluation and optimization of a prosthetic valve design can be observed from hemodynamics perspective or structural mechanic perspective. CFD modeling enables the best design that yields the optimal hemodynamics and lowest achievable risk of designrelated thrombosis by interpreting fluid stresses to avoid potential thrombosis [156] while computational SM approaches gives information about the mechanical response of the device. Depending on the purpose of the problem at hand, CFD, FSI or SM modeling can be the most effective approach for BHV simulation.

The development of the computational methods reviewed in this paper are encouraging. There are however some challenges in numerical simulation of BHV and several foreseeable obstacle and possible pitfalls needs to be addressed before these methods can be translated into clinical use. One potential obstacle is the issue of the temporal scale for BHV simulations. The valve function occurs in cycles of approximately 1 second for a full cardiac cycle including opening and closing, but on the other hand, BHV dysfunction occurs after millions of cycles over long periods in the order of years. It is not practical to perform full FSI simulation for such a high number of cycles. Developing multi-timescale techniques combining these two timescales would be an option. Another limitation of all existing computational models is that realistic boundary conditions are difficult to specify. The other potential problem is the lack of experimental validation of in-silico simulations. To ensure that the resulting computational framework is clinically relevant and useful, the advances in computational modeling should be validated with carefully designed in-vitro and in-vivo experiments.

The numerical methods still need to be improved. For example, the accuracy of shear stress is a well-known problem in IB method because of the poor approximation for the pressure field. Another problem is the robustness and convergence of the coupled FSI algorithm due to the stability of the black-box coupling. Efficiency of the contact algorithm is another challenging issue. Material models should also be improved to provide more accurate description of inhomogeneous, nonlinear, and anisotropic leaflet mechanical properties. In this regard, there is also a need to focus on high-fidelity material models for BHV leaflets which account for inelastic changes to the material’s local stress-free configuration in a computationally-efficient way. The leaflet tissues are composed of collagen fibers aligned along preferred directions and this preferred direction as well as distribution of collagen fibers vary spatially within the leaflet. Although initial fiber orientation of the BHV is available experimentally, inverse modeling approaches should be considered to determine the possible evolutions of fiber structure after implantation and obtain mechanical properties [157, 158].

Effect of residual strains, which is usually neglected, is essential to quantify the in-vivo deformation of the valve in computational simulations. In a recent work by Aggarwal et at. [159], a framework for calculating heterogeneous strains in AV leaflet is proposed to obtain residual strains related to excision based on 3D echocardiographic (3DE) images. Accounting for the geometry change and time evolving mechanical response in the BHV material model is another key aspect for accurate biomechanical simulations in cyclic loading and fatigue process.

Proper determination of valve geometry obtained from ultrasound, CT, or magnetic resonance imaging (MRI) data presents another challenge. Leaflets are very thin (in the order a few hundred μm) which can pose certain problems regarding spatial discretization due to its thinness. Moreover, it is difficult to predict the time evolution of the resultant in-vivo geometry of a BHV. With the rapidly increasing power of parallel computational platforms and significant advances in medical imaging in the recent years, some of these challenges can be overcome.

Overall, the application of using computational methods to study the BHV and to supply vital information is very promising and can have a huge impact on the success rates of clinical outcome. Currently, clinicians have only a finite number of valves to choose from for each patient. However, in the direction of personalized medicine and looking forward to emerging technologies such as 3D printing, we anticipate that future replacement valve geometries could be optimized and fabricated on a per-patient basis, and we feel that the robust and efficient simulation methods for valve dynamics coupled with the imaged based geometries and physical parameters as described here would make the future BHV simulation routine for engineering predictions and identifying optimal designs. It will impact millions of patients worldwide with heart valve disease over the next coming years.

7-. Five-years view

Clearly for the next 5–10 years BHVs will continue to be extensively used as the most common replacement valve owing to their natural hemodynamic characteristics, high resistance to thrombosis, and good medium-term durability. However, structural valve deterioration may occur which necessitates replacement particularly in younger patients and the replacement surgery has higher risk of mortality. Therefore, the heterograft tissue needs to be refined and modified to improve the life span of BHV so it remains as the dominant valve replacement option. Otherwise durability in the range of 10–15 years continues to hamper BHVs.

The field has reached a point that computational analysis of BHV durability and high- level interpretation of valve behavior are becoming feasible. The in-silico analysis of native and prosthetic valve mechanics has been performed mainly with the aim of computing the strain/stress distributions within the leaflets and specifying the high stress concentration regions to guide the overall design process with such information. Moreover, with the advent of 3D printing [160] (which has already been studied in the context of AV replacement [161]), it may soon be possible to perform optimization of geometry on a per-patient basis, by taking into account variations in patient aortic root geometry and other patient-specific factors. Using computational models is crucial to investigate how the patient-specific BHV behaves in different loading configurations, as well as in estimating the performance of the valve by varying the geometry of the leaflets. These models can predict hemodynamics and valve performance by solving FSI for in-vivo condition and therefore guide a robust and reliable design of BHV. Since FSI approaches are computability expensive to carry out, the application of reduced order modeling aiming at reducing the computational costs, is a very active field in numerical simulation of cardiovascular application and fluid-valve interaction [20].

Although computational methods have been demonstrated to show a very high potential and some basic models are available, reliability of any analysis conducted with a computational model depends on all modeling assumptions made. Most initial studies have been conducted with some modeling limitations such as simplified geometries and basic material models, and sometimes, with idealized physical settings which resulted in relative success [59, 60, 162, 163, 164, 165, 166, 167]. To obtain a model that can more closely replicate the physiological problem, it is highly beneficial to combine advanced patient-specific geometries image information with state-of-the-art computational approaches and accurate experimental and processing techniques for the assessment of tissue material properties. The advancement of methods for simulation of heart valve function reviewed here offer a rational approach to provide an optimal diagnosis and prognosis clinical tool, by further improving the design and durability of BHVs. It is also expected that utilizing computational models by incorporating time evolving mechanical response and geometry change of valve, can improve our understanding of underlying mechanism happens to BHV in fatigue testing environments such as AWT, where BHV leaflet opens and closes faster compare to the physiological state. In fact, a computational approach to extract fatigue information utilizing the AWT tests would be extremely beneficial and can be used in evaluation of novel designs of prosthesis as well as the development of specialized biomaterials for heart valves.

8-. Key issues.

• The main goal of computational simulation of BHVs is to predict the onset and progression of damage in BHV leaflets in relation to BHV function. BHVs will likely remain as the dominant valve implant design, with increasing number of valve replacements annually. Durability of BHVs is still the major limitation of the current technology. Thus, improvements that lead to even modest improvements in BHV durability (e.g., an increase in average valve durability by 3–5 years) can have a dramatic clinical impact.

• The simulation approaches of the BHVs are divided into three categories: 1) SM analyses in which the fluid pressure is specified as a boundary condition, enforced to the leaflets surface to obtain the deformation and stress distribution; 2) CFD models to study the hemodynamics during the cardiac cycle and 3) FSI analysis in which the fluid dynamics of the blood flow is coupled to the structural mechanics of the leaflets. Depending on the problem at hand, all methods can provide useful information. For example, FSI enables the computation of the hemodynamics features and the shear stress; however, it is almost always more computationally expensive than SM simulation; and in fact, if the objective is investigating the structure features during valve closure phase, it is not necessary to perform FSI simulations.

• Computational models carefully coupled with experimental validation provide a very powerful tool for the predictive description of physical valve function and can shed light into the clarification of possible mechanisms of valve failure to quantify BHV design improvements. In analyzing the geometrical designs, usually the coaptation and mechanical stress in the leaflets is compared during diastole. The coaptation indicates the quality of closure since it provides a safety margin for preventing regurgitation, whereas the maximum principal stress could imply valve durability. Relatively large coaptation area, low stress within the leaflets during diastole, and proper flow shear stress that doesn’t cause damage to the leaflet surface [168] or results in valve thickening [169], are appropriate design criteria. Using simulation techniques, optimized BHV will be developed with more uniform stress distribution and minimized bending moments to reduce the chance of fatigue and calcification. The modeling process helps to avoid costly trial-and-error approaches.

• Computational simulations have shown the impact of different choices of constitutive models to simulate valve function and have observed that the stress and strain distribution in the leaflets was severely impacted by the homogeneous/inhomogeneous and isotropic/anisotropic modeling choice, as well as the effect of permanent set as the responsible mechanism for the geometry change of BHV leaflets in the long-term cyclic loading. These numerical studies also demonstrate that BHV performance is highly dependent on the valve geometry.