Histological Method to Study the Effect of Shear Stress on Cell Proliferation and Tissue Morphology in a Bioreactor

Abstract

Background:

Tissue engineering represents a promising approach for the production of bone substitutes. The use of perfusion bioreactors for the culture of bone-forming cells on a three-dimensional porous scaffold resolves mass transport limitations and provides mechanical stimuli. Despite the recent and important development of bioreactors for tissue engineering, the underlying mechanisms leading to the production of bone substitutes remain poorly understood.

Methods:

In order to study cell proliferation in a perfusion bioreactor, we propose a simplified experimental set-up using an impermeable scaffold model made of 2 mm diameter glass beads on which mechanosensitive cells, NIH-3T3 fibroblasts are cultured for up to 3 weeks under 10 mL/min culture medium flow. A methodology combining histological procedure, image analysis and analytical calculations allows the description and quantification of cell proliferation and tissue production in relation to the mean wall shear stress within the bioreactor.

Results:

Results show a massive expansion of the cell phase after 3 weeks in bioreactor compared to static control. A scenario of cell proliferation within the three-dimensional bioreactor porosity over the 3 weeks of culture is proposed pointing out the essential role of the contact points between adjacent beads. Calculations indicate that the mean wall shear stress experienced by the cells changes with culture time, from about 50 mPa at the beginning of the experiment to about 100 mPa after 3 weeks.

Conclusion:

We anticipate that our results will help the development and calibration of predictive models, which rely on estimates and morphological description of cell proliferation under shear stress.

Introduction

A variety of bioreactor principles for tissue engineering has been proposed to simplify, optimize, and control the production of tissue substitutes. In particular, bioreactor designs relying on hydrodynamic culture environments utilize the flow of culture medium to improve homogeneous supply of nutrient and oxygen within the tissue construct, and provide mechanical stimuli to the cells. Despite numerous proofs of concepts [1–4], the use of bioreactors in biomedical applications is still limited due to a lack of understanding of the mechanisms leading to enhanced substitute production. This underlies the need for systematic and quantitative studies characterizing bioreactor culture environments and their effect on cell and tissue production.

Due to the mechanosensitive nature of bone cells, bioreactors relying on hydrodynamic culture environment are particularly relevant for bone tissue engineering, resulting in enhanced cell differentiation and proliferation [5–11]. Specifically, bone cells are sensitive to flow induced shear stress [10–19], influencing cell fate through mechanotransduction [20–24] effects [25].

A difficulty associated with evaluating the fluid-induced shear stress in bioreactors is due to the use of three-dimensional (3D) scaffolds with often-complicated porous structures. Parameters influencing spatial distribution and intensity of local shear stress include the bioreactor geometry, the scaffold porosity, isotropy, pore size, and interconnectivity, as well as the fluid flow rate and physical properties. Computational fluid dynamics approaches have shown promising results to estimate wall shear stress distribution in idealized geometries and numerically reconstructed scaffold geometry from X-ray tomography [26–33], however the effect on cell proliferation within the packed bed remains to be assessed.

In this work, we aim to quantify the effects of shear stress on cell proliferation in a perfusion bioreactor. We propose a design of a perfusion bioreactor based on a simplified version of the “double-porosity” bioreactor presented in David et al. [4], which was developed to overcome limitations related to bone tissue engineering. In their original study, David et al. used stacks of naturally porous coral cubes (3 × 3 × 3 mm) as the scaffold, therefore providing two porosities (around the cubes, and inside the cubes). They cultured mesenchymal cells (C3H10T1/2) seeded on the scaffold, under culture medium perfusion for up to 3 weeks, and found enhanced cell production and more homogeneous distribution than in static conditions. Additionally, they demonstrated the system’s suitability to produce relatively large volumes of bone substitutes (up to 30 cm³), and showed that the resulting bone constructs were osteogenic when implanted subcutaneously in a sheep.

Although highly encouraging, the advancement of this type of bioreactor design rely on a better, quantitative, understanding of the culture environment on cell proliferation and tissue production. To this aim, we choose to simplify this design in order to facilitate the quantification and interpretation of the observed cell proliferation. We culture mouse fibroblast cells on a scaffold constituted of a stack of 2 mm diameter glass beads, under constant perfusion for various culture times. Cell and tissue production are quantified through a combination of histological analysis and image processing. Finally we interpret the biomass production in relation to the mechanical environment in the bioreactor by proposing an analytical expression for the mean wall shear stress as a function of the flow rate and scaffold properties.

Materials and methods

Cell culture

The cells used in all the experiments are fibroblasts NIH/3T3 (ATCC), cultured in DMEM Glutamax (Gibco, Life Technologies, Waltham, MA, USA) supplemented with 10% Foetal Calf Serum (Pan-Biotech, Aidenbach, BY, Germany), 1% Penicillin-Streptomycin (Pan-Biotech, Aidenbach, BY, Germany) under standard cell culture conditions (37 °C, 5% CO₂, 100% humidity). Cell suspensions for seeding were prepared according to standard protocols, where pre-confluent cells were detached from the culture plate using Trypsin-EDTA (Pan-Biotech, Aidenbach, BY, Germany) solution, suspending them in culture medium, counting them on a Malassez chamber, and adjusting the cell suspensions to 10⁶ cell/mL with culture medium.

Cell seeding

The scaffold is constituted of a stack of 2 mm glass beads. To seed the scaffold, about 4.5 mL of glass beads are placed in a 15 mL tube. Then 2.5 mL of fibronectin solution is added (10 µg/mL) and let 1 h at 37 °C. The solution is aspirated with a pipette and beads are rinsed with PBS. Glass beads are seeded with 2 mL of cell suspension at 10⁶ cell/mL, and are then let to rest overnight in a CO₂ incubator. 24 h post seeding, beads are washed with culture medium.

Perfusion bioreactor

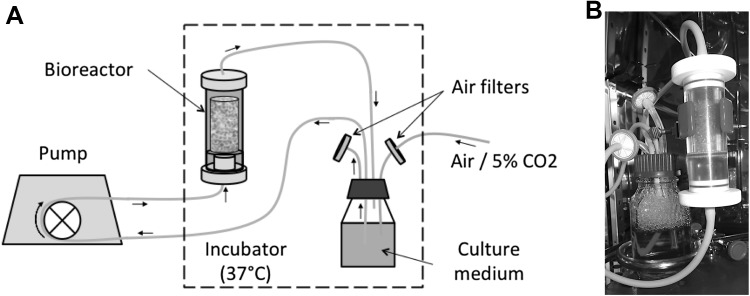
The bioreactor chamber is a cylinder made of Polycarbonate (PC). A circular grid also made of PC divides the bioreactor chamber into the entry chamber and the perfusion chamber. The grid maintains the stack of beads in the perfusion chamber, maintains a laminar fluid flow, and promotes a uniform supply of culture medium at the packed bed inlet. In order to be able to remove the construct from the bioreactor without damaging it, a glass tube (inner diameter 12 mm, 50 mm height) is inserted in the perfusion chamber. The external diameter of the tube fits the internal diameter of the chamber so that all the perfusion takes place in the tube. The culture medium flows in a closed loop (Silicon-tubing, Pharm-Med, Saint-Gobain Tubing, Charny, BFC, France) from a culture medium reservoir to the bioreactor and back to the reservoir (Fig. 1). A constant supply of 5% CO₂ gas is maintained into the reservoir to maintain the culture medium pH.

Fig. 1.

Experimental setup: a schematic of the experimental set up: the bioreactor and culture medium reservoir are placed into an incubator (37 °C). To maintain the pH at 7.4, CO₂ (mixture air/5% CO₂) is directly and constantly supplied through an air filter into the cell culture medium reservoir. The peristaltic pump for the perfusion bioreactor is placed outside the incubator. b Photography of the bioreactor containing a scaffold during culture under perfusion

Cell culture in the bioreactor

Twenty-four hours post seeding, the bioreactor is filled with the seeded glass beads. The flow rate is 10 mL/min. Cultures under perfusion are carried for 1, 2 or 3 weeks, during which the culture medium is replaced with fresh one twice a week.

Static control samples are performed under standard cell culture conditions. A glass tube (inner diameter 12 mm, 50 mm height), closed at the bottom by a grid, filled with seeded glass beads is placed inside a 40 mL container. The culture medium is changed twice a week.

Finally, to assess the initial cell seeding, a T₀ control is performed for each perfusion experiments. A glass tube (inner diameter 12 mm, 50 mm height), closed at the bottom by a grid, filled with seeded glass beads is fixed 24 h post seeding.

After 1, 2 or 3 weeks of cultures, the constructs are removed from the bioreactor or container and processed for histological characterization.

Histological procedure

Quickly after ending the cultures, samples are placed for at least 24 h in a chemical fixative solution (4% formaldehyde (Sigma-Aldrich, St. Louis, MO, USA) in phosphate buffered saline (Pan-Biotech, Aidenbach, BY, Germany), room temperature) that allows preserving the cells and tissue from degradation, and maintaining the structure of the construct. The samples are then dehydrated following a series of ethanol bath of increasing concentration (70, 80, 90, 96 and 100%), 15 min each. The Osteo-Bed Embedding kit (Sigma-Aldrich, St. Louis, MO, USA) is used according to manufacturer instructions for the embedding process. The formulation is based on methyl methacrylate (MMA). Once the polymerization process is over, the construct is a polymerized cylinder of approximately 30 mm length and 12 mm diameter. Three marks are made at 5, 15 and 25 mm (bottom, middle, upper) from the bottom of the construct in order to relate proliferation to the position from its entrance. Three transverse slices are cut (IsoMet Low Speed Saw, Buehler, Lake Bluff, IL, USA) at each mark, leading to a total of nine slices per construct. After polishing, a staining procedure is required in order to specifically colour the cells. We choose a reliable, rapid and simple method, which can stain the cells embedded in MMA polymer. Stevenel Blue has been shown to answer these prerequisites [34]. The construct slices are immersed in the dye solution at 60 °C for 10 min and then rinsed with distilled water. In order to reconstruct an entire slice, twenty pictures are taken for each slice using bright field microscopy with a 4× objective (Optika, B350, Ponteranica, BG, Italy). Pictures are numerically merged (Adobe Photoshop). At this point, cells appear in blue, while the glass beads are recognizable by their shape and texture.

In order to determine the extent of biomass growth in the bioreactor, we estimate the surface area occupied by the cells and the tissue for each histological slice. Image treatment and segmentation are carried with ImageJ software [35] following the protocol reported in Chabanon [36]. Briefly, we define the total area occupied by the cells (Σ_cells) as the total area of blue pixels in each slice. The estimation of the surface occupied by the tissue requires a manual segmentation of the regions with high cellular density. We choose to define the tissue area (Σ_tissue) for each slice as the total area with homogeneous cell distribution where the distance between cells is inferior to 10 cell diameters. The cell and tissue surface fractions within a bioreactor slice are then defined as f_cells = Σ_cells/Σ and f_tissue = Σ_tissue/Σ respectively, where Σ is the glass tube internal cross-section area. For each culture condition, and each location within the bioreactor, the surface fractions reported are average values of a total of nine slices from three independent experiments. We further determine the surface area occupied by the glass beads (Σ_beads) by manual segmentation, leading to the bead surface fraction f_beads = Σ_beads/Σ.

Assuming the slices to be representative of the bioreactor region from which they are cut from, we deduce from stereology principles that the bead, cell and tissue volume fractions of a bioreactor region (bottom, middle or top) coincide with the bead, cell and tissue surface fractions of its slices, respectively. Consequently, in the rest of the text, the notation f will indistinctly refer to the surface fraction within a slice or the volume fraction within the bioreactor. This allows us to estimate the bioreactor porosity as ε = 1 − f_beads − f_tissue.

Although the present histological procedure does not strictly quantify the number of cells, it allows comparing the evolution of f_cells and f_tissue with time and space for the different cultures performed in the perfusion bioreactors.

Estimation of the mean wall shear stress

We aim to estimate the mean modulus of the so-called wall shear stress exerted by the fluid in the bioreactor. The term “wall” refers to the solid/liquid interface within the bioreactor. By solid phase we mean the glass tube and the construct inside, i.e. the packed bed of glass beads and the growing cellular tissue. In the bioreactor, the mean direction of the fluid flow is parallel to the tube axis, denoted z-axis. Σ is the glass tube internal cross-section area, q is the volumetric flow rate feeding the bioreactor and u_s = q/Σ is the so-called superficial velocity. We denote ε the porosity of the construct, i.e. the volume fraction occupied by the culture medium, and K the Darcy permeability (or intrinsic permeability) of the construct.

Darcy’s permeability can be conveniently estimated with Carman–Kozeny phenomenological law [37]:

$$K=\epsilon r_h^2/k$$ 1

where r_h is the hydraulic radius defined as the ratio between the porosity and the wetted area:

$$r_h=\epsilon /s$$ 2

with s the specific wetted area. ε and s can be both determined from image analysis of bioreactor slices.

k is the so-called Kozeny constant. Typically, packed beds of porosity ε between 0.26 and 0.8 have a Kozeny constant of about 5, independently of the particles shape [38]. All our experiments being in this range of porosity, in the following, we assume that k = 5 independently of the construct history, i.e. perfused, static or T₀.

The flow regime within the bioreactor is characterized by the Reynolds number based on the permeability:

$${\text{Re}}_K=\rho u_s{K}^{1/2}/\mu$$ 3

When Re_K is typically lower than 10⁻²–10⁻¹ [39–41], Darcy’s regime holds, i.e. the gradient of the average fluid pressure $\widehat{p}$ depends linearly on the superficial velocity:

$$\frac{d\widehat{p}}{\mathit{dz}}=\frac{-\mu }{K}{u}_s$$ 4

As Re_K increases, inertial effects become non-negligible, and the linear dependence of the pressure gradient on the superficial velocity does not hold anymore. Two inertial regimes are usually distinguished: the Forchheimer regime at moderate Re_K and the turbulent regime at large Re_K. In the Forchheimer regime, the flow in the pores is still laminar. The breakdown in linearity is due to the increased contribution of pressure drag with respect to the surface drag due to friction. According to Bağcı et al. [39] who studied the flow regimes in packed beds of identical spheres (1- and 3-mm diameters), the transition from Darcy to Forchheimer regimes occurs at about Re_K = 1 and the transition from Forchheimer to turbulent regimes at about Re_K = 6–7.

When inertial effects are not negligible, Eq. 4 must be extended to include the Forchheimer correction, leading to the Darcy–Forchheimer equation [42]:

$$\frac{d\widehat{p}}{\mathit{dz}}=\frac{-\mu }{K}{u}_s-c_F{K}^{-1/2}\rho u_s^2=\frac{-\mu }{K}{u}_s\left(1+c_F{\text{Re}}_K\right)$$ 5

where c_f is a dimensionless form-drag constant. c_f is equal to 0.55 for a packed bed of identical spheres [42].

Let us focus on a bioreactor slice of thickness dz. The mean drag force dF_d exerted by the fluid is directly related to the driving pressure difference $d\widehat{p}$ across the slice:

$$d{f}_d=-\epsilon \Sigma d\widehat{p}$$ 6

We define f_d, the mean drag force per unit of wetted area, as:

$$f_d=\frac{d{f}_d}{s\Sigma dz}$$ 7

From Eqs. 1–7, we obtain:

$$f_d=\mu \left(k\frac{s}{{\epsilon }^2}\right)\left(1+c_F{\text{Re}}_K\right)u_s$$ 8

We infer that the mean modulus of the wall shear stress τ_m follows a similar analytical law:

$${\tau }_m=\mu \left(\alpha \frac{s}{{\epsilon }^2}\right)\left(1+\beta {\text{Re}}_K\right)u_s$$ 9

where α and β are expected to depend solely on the packed bed morphology. We emphasize that in Eq. 9 the dependence of τ_m on u_s is quadratic (since Re_K is proportional to u_s).

In the Darcy’s regime, Re_K <<1 and Eq. 9 reduces to the linear law obtained by Warren and Stepanek [43]:

$${\tau }_m=\mu \left(\alpha \frac{s}{{\epsilon }^2}\right)u_s$$ 10

In order to validate Eq. 9 and identify α and β, we consider the numerical data of Cruel et al. [44]: they simulated the flow in a packed column bioreactor (of inner diameter d_t = 13.1 mm) without cells using computational fluid dynamics (CFD) and obtained the wall shear stress distribution for different packing configurations at various superficial velocities. One of the configurations is a packed bed of identical beads: Cruel et al. generated four random stacks of 71 beads (3.5-mm diameter). The average height of the stacks is equal to h = 23.6 mm. They performed numerical simulations for each stack, with superficial velocities ranging from 1.2 to 24.7 mm s⁻¹.

From the geometric data reported by Cruel et al., we can easily calculate the porosity and the specific wetted area of their bioreactors, i.e. ε = 0.498 and s = 1.16 mm⁻¹. The calculation of s includes the contribution of the stack, i.e. 6(1 − ε)/d_p, and the contribution of the cylindrical inner wall, i.e. 4/d_t, the latter represents about 25% of the wetted area in the packed bioreactor. Using Eqs. 1–2, we estimate the permeability of the bioreactor at K = 1.82 × 10⁻² mm².

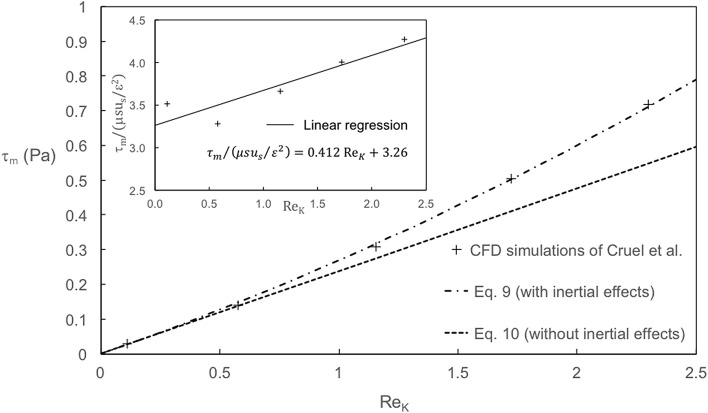
The average values of the wall shear stress τ_m calculated by Cruel et al. are reported in Fig. 2 as a function of the Reynolds number Re_K. α and β are determined by linear regression of ${\tau }_m/\left(\mu s{u}_s/{\epsilon }^2\right)$ versus Re_K using least squares method (see the inset in Fig. 2). We find α = 3.26 in good agreement with the value α = 3.07 obtained by Warren and Stepanek from Stokes flow simulations in random sphere packings at porosity ε = 0.5. We point out that the value of α is significantly lower than the value of the Kozeny constant k appearing in Eq. 8, equal to about 5. This may be explained by simply considering the drag force experienced by an isolated sphere: in this case, the viscous shear stress represents actually 2/3 of the drag force whereas the pressure contribution represents 1/3 of the drag force. We find β = 0.13. β is lower than its analog in Eq. 8, i.e. the dimensionless form-drag constant equal to c_F = 0.55. This is consistent with the fact that the friction drag grows at a slower rate than the pressure drag as Re_K increases [42].

Fig. 2.

Variations of the wall shear stress τ_m as a function of the permeability-based Reynolds number Re_K: comparison between the CFD calculations of Cruel et al. and the analytical expressions proposed in the present paper (Eqs. 9–10). Inset: linear regression of Cruel et al. data ${\tau }_m/\left(\mu s{u}_s/{\epsilon }^2\right)$ versus Re_K

The resulting analytical laws (Eqs. 9 and 10) are plotted on Fig. 2. It appears that Eq. 10 is in good agreement with Cruel et al. numerical data as long as the Reynolds number Re_K is lower than 1 (corresponding to the Darcy regime). For Re_K greater than 1, inertial effects are not negligible anymore and the dependence of the wall shear stress on the superficial velocity is no more linear. In this case, the numerical data of Cruel et al. are better described by Eq. 9.

Estimation of glucose and oxygen characteristic consumption time in the bioreactor

We estimated the consumption characteristic time of glucose and oxygen in static conditions. This time reads:

$${\tau }_i=\frac{C_0^i{l}_c}{\sigma V_m^i}$$ 11

where l_c = ε/s is a characteristic length of the pores within the construct, σ is the cell density, Cⁱ₀ is the initial concentration in species i and Vⁱ_m is the maximum consumption rate of species i. Equation 11 is relevant if τ_i ≫ l²_c/D_i, with D_i the diffusion coefficient of species i in the culture medium [45]. This condition is fulfilled since l²_c/D_i is presently in the order of 1 min or less.

In static conditions, f_tissue remains negligible and l_c ~ 200 µm. Based on the experimental values of f_cells, we estimate the cell density at T₀ and 3 weeks of static culture as σ = 10⁷ cells m⁻² and 10⁸ cells m⁻² respectively. The glucose uptake rate is equal to about 10⁻¹⁶ mol cell⁻¹ s⁻¹ [46], the oxygen uptake rate to 6 × 10⁻¹⁷ mol cell⁻¹ s⁻¹ [47]. The glucose initial concentration of the culture medium is equal to C^gl₀ = 2.5 × 10¹ mol m⁻³, the oxygen initial concentration to $C_0^{{\text{O}}_2}$ = 0.21 mol m⁻³. We find that the characteristic time of glucose consumption in static conditions, i.e. τ_gl = 1–8 weeks, is systematically higher than the time between two renewals of the culture medium: glucose is not a limited factor. The characteristic time of oxygen consumption in static conditions is in the order of ${\tau }_{{\text{O}}_2}$ = 3–20 h: cells located in the core of the bead stack will probably be in hypoxia after a few hours following the renewal of the medium.

In dynamic conditions, an estimate of the relative decrease in concentration in species i between the bioreactor inlet and outlet is given by:

$$\frac{\mathrm{\Delta }{C}_i}{C_0^i}=\frac{N_{\mathit{cells}}{V}_m^i}{q{C}_0^i}$$ 12

where N_cells is the number of cells within the bioreactor at the time considered. Although we do not have an experimental value of the number of cell in the bioreactor after 3 weeks of perfusion, we estimate it based on the values of the cell volume fraction at 2 and 3 weeks and the number of cells at 2 weeks, such as N_cells (3 weeks) = N_cells (2 weeks) × f_cells (3 weeks)/f_cells (2 weeks). After 3 weeks of culture, the relative decrease in glucose concentration between the bioreactor inlet and outlet is negligible (less than 1%). The relative decrease in oxygen concentration is up to 20%, suggesting the development of slight hypoxic conditions at the exit of the bioreactor after 3 weeks of culture.

Results

Histological analysis

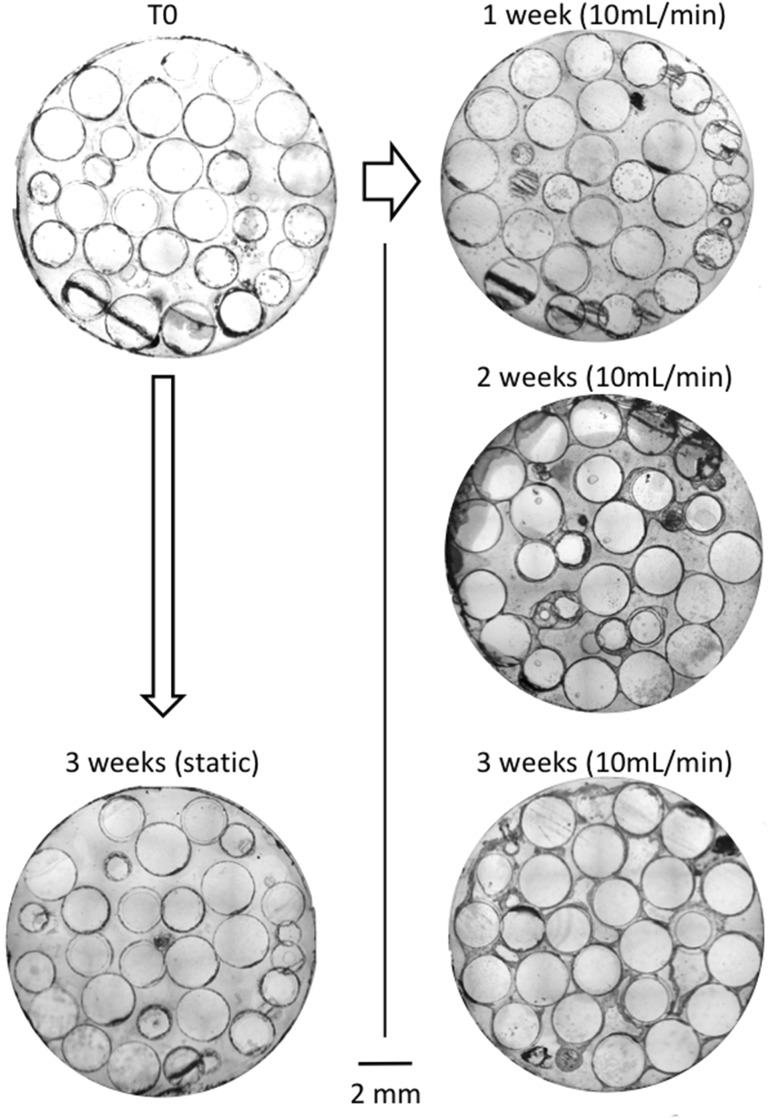
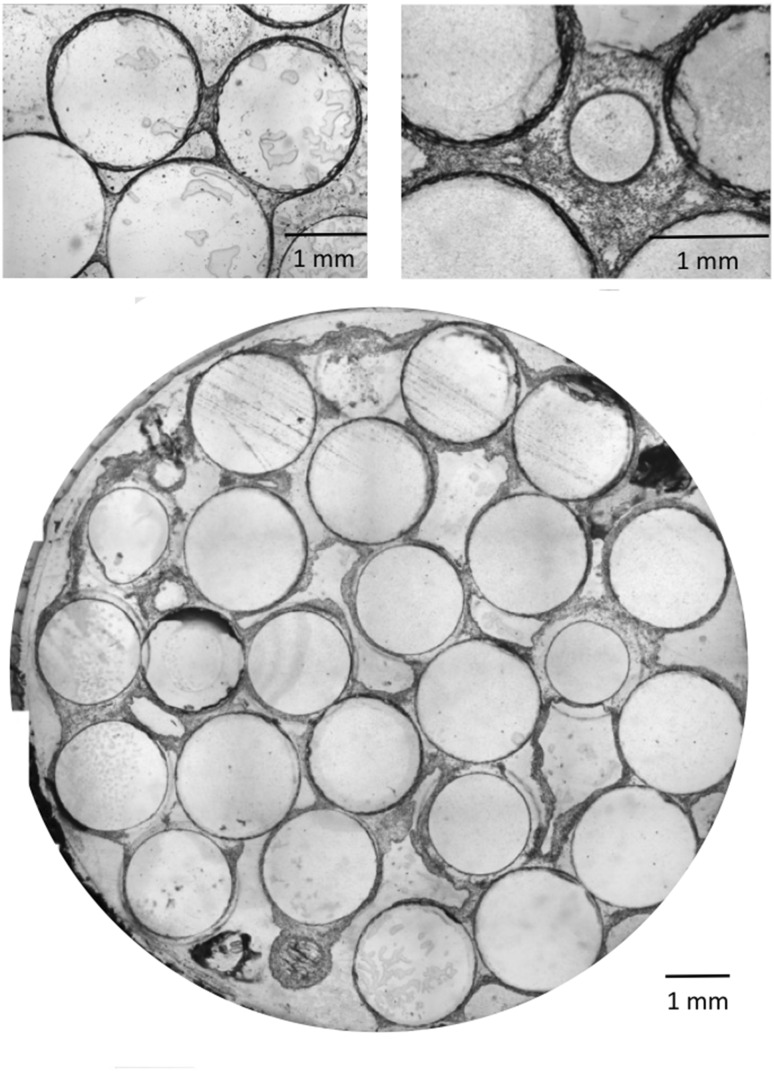
Histological cross-sections of the bioreactor in static and perfusion conditions are shown in Fig. 3. Glass beads appear as transparent discs, while cells are colored in blue. At T₀ and after 3 weeks of static conditions, blue lines are visible around the beads surface, although too thin to distinguish attached cells from residual stain infiltrations. In contrast, after 1, 2, and 3 weeks of perfusion, blue lines and uniform blue regions of increasing thickness are visible, revealing the presence of multilayered cell structures. Particularly large blue regions are observed bridging two to three beads, reaching up to 100 μm at 2 weeks, and 600 μm at 3 weeks of perfusion. The continuity of these regions suggests the formation of tissue enabled by the cells production of extracellular matrix (ECM). These bridge-like tissue structures are initiated at contact points between beads (Fig. 4, top left). At 3 weeks of perfusion, above a tissue thickness of about 200 μm, a decrease in cellular density is observed away from the proliferating edges, sometimes leading to an apparent detachment of tissue strips from the beads (Fig. 4, bottom).

Fig. 3.

Representative cross section of the construct cultured in static (left side) and dynamic (right side) conditions for 1, 2, and 3 weeks. Cells are stained with Stevenel Blue. All slices are taken at 15 mm from the chamber entrance (inner diameter of the bioreactor is 12 mm)

Fig. 4.

Histological images of stained slices in dynamic cell culture conditions (10 mL/min). Focus on the cellular bridge between two beads after 2 weeks (top left) and continuous cellular phase between beads after 3 weeks (top right). Cross section of a 3 weeks dynamic cell culture within the perfusion bioreactor (bottom)

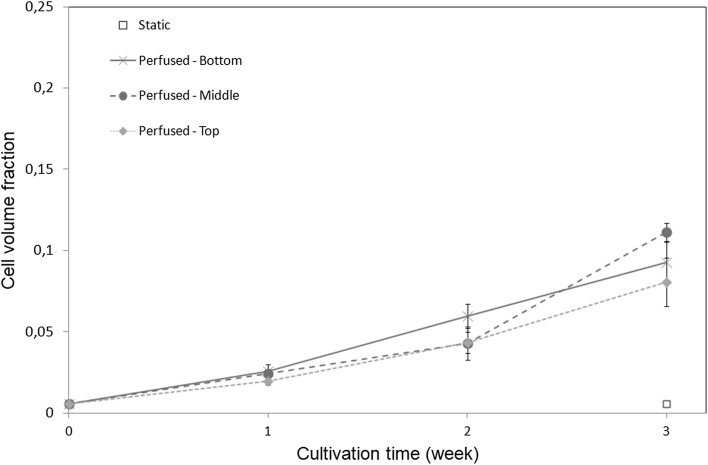
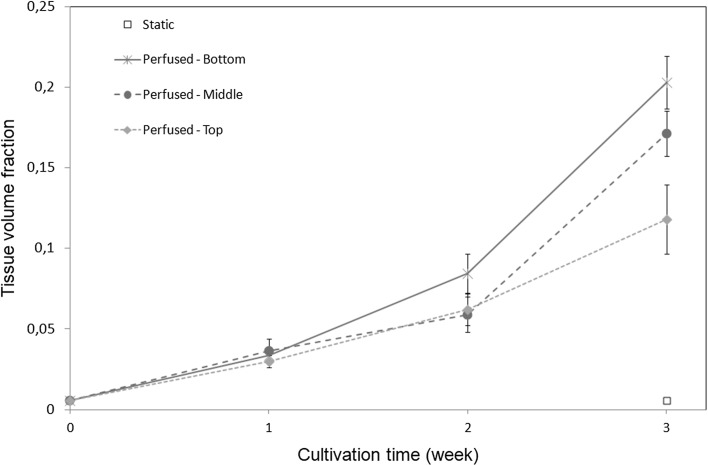
Cell (f_cells) and tissue (f_tissue) volume fractions are respectively shown in Figs. 5 and 6 as a function of culture time for different positions along the bioreactor height. Each point corresponds to an average of nine histological slices originating from three independent experiments. Consistently with direct observations (Fig. 2), constructs cultured in static conditions do not show any significant evolution in cell or tissue volume fraction. In contrast, after 3 weeks of perfusion, a ten to 20-fold increase in cell volume fraction is observed compared to initial and static constructs. In dynamic conditions, both cell and tissue volume fractions follow a similar non-linear increase with culture time. Overall, the tissue volume fraction is ten times higher than the cell volume fraction, suggesting that the tissue cell density decreases with time, in accordance with histological observations. No significant difference in cell volume fraction along the bioreactor height is found, although the mean value of cell and tissue fraction is slightly lower at the top of the bioreactor than at the bottom. However, at 3 weeks of culture we observe a decrease of the tissue volume fraction with the distance to the entrance of the perfusion chamber, suggesting that tissue cell density is larger at the bottom than at the top of the bioreactor. This trend is in agreement with our estimate of progressive oxygen depletion along the bioreactor length (see Sect. 2.7). Bead volume fraction is homogeneous along the bioreactor with a mean value and standard deviation of 0.55 and 0.03 respectively (data not shown).

Fig. 5.

Cell volume fraction f_cells as a function of the culture time at different locations within the bioreactor (bottom, medium and top part), in static and dynamic conditions. Bar length represents standard deviation

Fig. 6.

Tissue volume fraction f_tissue as a function of the culture time at different locations within the bioreactor (bottom, medium and top part), in static and dynamic conditions. Bar length represents standard deviation

Cell count

For each culture conditions, the number of cells in the bioreactor was assessed (n = 2 per condition). Cell count at 24 h after seeding and after 3 weeks of static culture were 0.1 ± 0.01 millions and 0.8 ± 0.1 millions respectively. After 1 and 2 weeks of perfusion, the cell count was 2.5 ± 0.1 millions and 60 ± 5 millions respectively. Cell count after 3 weeks of perfusion could not be assessed with this method, presumably due to the increased production of ECM preventing cell detachment.

Mean wall shear stress estimation

The mean wall shear stress exerted by culture medium flow on the cells depends on the superficial flow velocity and the scaffold geometry, including its porosity and specific wetted area. The superficial velocity (ratio between the volumetric flow rate and bioreactor internal cross-section) is constant for each experiment. However, the porosity of the construct and its specific wetted area may vary with time due to cell proliferation. Therefore, the mean wall shear stress is expected to change over time.

Based on the mean values measured for the tissue volume fraction (see Fig. 6), the bioreactor porosity ε = 1 − f_beads− f_tissue decreases from 0.45 ± 0.03 at T₀, to 0.28 ± 0.06 at 3 weeks of culture, while the specific wetted area varies from 1.98 ± 0.09 to 1.7 ± 0.10 mm⁻¹ in the same period. Here we assumed for simplicity the tissue volume to be homogeneous along the bioreactor. We estimate the bioreactor permeability K using Eqs. 1–2. We find that K decreases from (4.6 ± 1.3) × 10⁻³ mm² at T₀ to (1.5 ± 1.1) × 10⁻³ mm² at 3 weeks. We deduce from Eq. 3 that the Reynolds number remains lower than 0.1, and therefore that the flow is Darcian for the duration of experiments. The inertial correction to the mean wall shear stress is therefore negligible in Eq. 9. We finally obtain the mean wall shear stress τ_m exerted by the fluid: it increases from 48 ± 8 mPa at T₀ to 110 ± 50 mPa after 3 weeks of perfusion.

Discussion

Tissue growth in a 3D porous scaffold under culture medium flow

In this study, we combined histological and image analysis to analyze and quantify cell and tissue growth on a stack of glass beads under constant culture medium flow. Based on these observations, we identify four stages of fibroblast proliferation in a 3D porous scaffold under perfusion:

• Stage 1 Starting from a random and homogeneous cell seeding, cells divide and remain as a monolayer on the beads surface, eventually forming scattered cell clusters toward the end of the first week of culture.

• Stage 2 During the second week of culture, 3D continuous tissue structures develop from the cell clusters, forming multilayer structures. Assuming the surface of a spread fibroblast from 400 to 1000 µm², about 30 million cells in monolayer are required to cover the total surface of the beads. Based on our cell count, this value is reached between the first and second week of culture, suggesting that the transition from mono to multilayer structures occurs when cell confluence is reached. Interestingly, bridge-like tissue structures initiate at contact points between beads, the only “real” 3D environments within the bioreactor.

• Stage 3 After 2 weeks of culture, tissue structures grow thicker (100 to 600 µm), with higher cell density close to the tissue/fluid interface than at the center of the tissue. This observation can be explained by two non-exclusive scenarios: (1) cells migrate toward the peripheral tissue layer, likely driven by a gradient of nutrient; (2) cell death rate is higher at the center of the tissue due to a depletion of nutrients. In both cases, tissue growth is supported by important matrix production and remodeling allowing cells to evolve in 3D.

• Stage 4 Between week 2 and 3, tissue structures start to partially peel off from the beads. Although the ruptures of tissue strips might be favored by the important flow shear stress imposed by the reduction of volume available to the culture medium, ECM contraction might also contribute to an increase stress in the tissue layers.

Over all, these tissue growth mechanisms are consistent with recent 3D wound healing observations of fibroblast seeded on collagen matrix, where tissue invasion was found to be driven by tissue contraction, matrix assembly, and cell migration at the wound edge [48]. Importantly, such morphogenetic events involve spatial reorganization and deformation of ECM that cannot be captured on planar substrates.

Effect of shear stress on biomass production

In order to evaluate the effect of shear stress on cell proliferation in the bioreactor and determine the respective contribution of fluid mechanics and tissue contraction on the observed tissue detachment at Stage 4, we proposed an expression related wall-shear stress, scaffold porosity, and perfusion rate (Eq. 2). At the initial stage where tissue volume fraction is negligible, we find that the average wall shear stress for a 10 mL/min flow rate is about 50 mPa in our bioreactor, in the range of values reported to promote osteocompetent cell proliferation and differentiation [6, 8, 16, 49–51]. In contrast, in the absence of culture medium flow, cell proliferation is minimal, in agreement with reported perfusion bioreactor studies [4, 52]. At 3 weeks of culture at 10 mL/min perfusion, tissue growth induces a 38% reduction in bioreactor porosity, leading to a two-fold increase of the average wall shear stress reaching about 110 mPa (increase of 130% over the initial value). This result is in good agreement with Williams et al. [31] who found a 116% increase in mean shear stress over 16 days of culture in similar conditions. This value is below the 600 mPa threshold above which shear stress has been reported to be detrimental to osteocondictive cells [7, 14, 16, 53, 54]. Overall, we find that fibroblast growth is promoted at shear stress values consistent with those reported in bone tissue engineering applications for osteoblasts [6, 51]. However, given that fibroblasts might not be able to sustain shear stresses as high as osteoblast cells, we cannot conclude on the respective role of shear stress and matrix contraction on the observed tissue detachment at 3 weeks.

Spatial distribution of cell and tissue in the bioreactor

A requirement for the production clinically relevant volume of tissue constructs is the homogeneous cell and matrix deposition along the bioreactor length. As seen from Figs. 5 and 6, the cell volume fraction is approximately constant along the bioreactor, while the tissue volume fraction at 3 weeks is smaller toward the exit of the bioreactor, suggesting a lower tissue cell density. To evaluate if this effect is due to nutrient or oxygen depletion, we estimate their respective characteristic consumption time in perfusion and static conditions (see Sect. 2.7). In perfusion culture, we find that between the inlet and outlet of the bioreactor, the relative depletion in glucose and oxygen concentration is about 1% and 20% respectively at 3 weeks. This suggests the development of mild hypoxic conditions at the exit of the bioreactor after 3 weeks of culture, in agreement with the observed trend of lower tissue volume fraction in the top region of the bioreactor (Figs. 5 and 6). In static conditions, the characteristic time of glucose and oxygen consumption in the bioreactor is 1–8 weeks and 3–20 h respectively. We conclude that although glucose is not a limiting factor for cell growth, in static conditions, cells located in the core of the bead stack are in hypoxia few hours following culture medium renewal. We also observe an overall reduction of the tissue cell density with time, as shown from the faster increase of tissue volume fraction than cell volume fraction (Figs. 5 and 6). This suggests a remodeling of the tissue with time, enhanced by hydrodynamic mechanical stimuli.

Comparison with a perfusion bioreactor for bone tissue engineering and expected implications

In this work, we proposed a cell culture model inspired from the perfusion bioreactor for bone tissue engineering from David et al. [4]. To facilitate the analysis of cell and tissue growth under perfusion, we made two main simplifications to the design. First, the scaffold initially made of a stack of 3 mm porous coral cubes was replaced by a stack of 2 mm glass beads, therefore reducing the “double porosity” to a single one. This choice is motivated by: (1) porous media composed of spheres are well characterized in terms of architecture and transport properties [43, 44, 55, 56]; and (2) glass is known for its excellent biocompatibility, enabling mammalian cell adhesion and spreading. Second, instead of osteoinductive cells, we chose to use fibroblast for their known mechanosensitivity [57], rapid division time, and simple cultivation procedure. Because osteoblast cells have a proliferation rate that is twice slower than fibroblasts (about 48 h compared to 24 respectively), we expect that one main difference for a bioreactor with osteoblast cells would be a longer culture time required to reach the same degree of confluence than what is observed at 3 weeks with fibroblasts.

This work presents an essential step toward a better understanding of tissue growth in a perfusion bioreactor. In the future, further analysis would be required to relate the local culture conditions to local cell and tissue growth, in particular in terms of local fluid flow in specific scaffold geometry. This could be done for instance by combining X-ray micro-tomography imaging of the scaffold and tissue to reconstruct the three-dimensional geometry and evaluate the local shear stress by computational fluid dynamics [33].

We anticipate that our results will help the development and calibration of predictive models, which rely on estimates and morphological description of cell proliferation under shear stress. Such modeling approaches will require the accurate coupling between cell proliferation, species transport, and fluid flow, in order to design and optimize more complex scaffold geometries and culture conditions for the production of functional substitutes.

Compliance with ethical standards

Conflict of interest

The authors have no conflict of interest to declare and all co-authors confirm agreement with the final statement. All authors have been appropriately disclosed according to the policy of the Journal.

Ethical statement

There are no animal experiments carried out for this article.