Strain Relief during Ice Growth on a Hexagonal Template

Abstract

Heterogeneous ice nucleation at solid surfaces impacts many areas of science, from environmental processes, such as precipitation, to microbiological systems and food processing, but the microscopic mechanisms underpinning nucleation remain unclear. Discussion of ice growth has often focused around the role of the surface in templating the structure of water, forcing the first layer to adopt the registry of the underlying substrate rather than that of ice. To grow a thick ice film, water in the first few ice layers must accommodate this strain, but understanding how this occurs requires detailed molecular-scale information that is lacking. Here we combine scanning tunneling microscopy, low-energy electron diffraction, and work-function measurements with electronic structure calculations to investigate the initial stages of ice growth on a Pt alloy surface, having a lattice spacing 6% larger than ice. Although the first layer of water forms a strictly commensurate hexagonal network, this behavior does not extend to the second layer. Instead, water forms a 2D structure containing extended defect rows made from face-sharing pentamer and octamer rings. The defect rows allow the majority of second-layer water to remain commensurate with the solid surface while compensating lateral strain by increasing the water density close to that of an ice surface. The observation of octamer–pentamer rows in ice films formed on several surfaces suggests that the octamer–pentamer defect motif acts as a flexible strain relief mechanism in thin ice films, providing a mechanism that is not available during the growth of strained films in other materials, such as semiconductors.

Introduction

Heterogeneous growth of an ice film on a solid surface requires the surface to bind to water, creating the initial nucleus from which an extended ice film can grow. Although this process is common in nature, being a key step in atmospheric precipitation¹ and surface icing,² the buried solid–ice interface is difficult to probe directly and remains largely uncharacterized.³ The free energy of this interface depends both on the interaction between first-layer water and the solid surface and on the degree of hydrogen bonding that can be maintained between the first water layer and the ice film. Because water–solid bonding (by direct physisorption or by hydrogen bonding to a polar species^3,4) typically has a similar bond strength as a water–water hydrogen bond, the first water layer must adapt its structure to optimize both the water–solid interaction and the water H-bonding arrangement,⁵ creating hydrogen-bond structures that are quite specific to the surface in question. Various complex single-layer water structures are observed at different interfaces, including both low-dimensional linear chains⁶⁻⁹ and 2D structures containing some mixture of pentamer, hexamer, heptamer, and octamer rings.¹⁰⁻¹³ Invariably, these stable first-layer structures bear little similarity to bulk water or ice phases, making them ill suited to stabilize a water multilayer or act as a template for ice growth.

Whereas the recent work in this field has led to a good understanding of how the solid surface directs the formation of different monolayer ice structures,^3,4 very little is known about how ice structures evolve beyond a monolayer, and there are very few experimental studies that examine this question directly.¹⁴⁻¹⁷ Macroscopic icing requires water to form a thick ice film and, just as the first layer of water responds to the solid surface by forming unique phases, multilayer formation can be expected to relax the first layer as further water adsorbs. The extent of this rearrangement will depend on the binding energy of water to the solid relative to the cohesive energy of water,¹⁸ as well as the symmetry and lattice spacing of the surface,⁵ but exactly how the buried interface restructures is largely unknown. One surface on which wetting has received considerable attention is Pt(111), which is widely used as a water redox electrocatalyst,^19,20 making a molecular-level picture of this interface extremely desirable.²¹ Initially water forms a complex network, made up of hexamer, pentamer, and heptamer rings arranged in a large unit cell.¹⁰ Further water adsorption creates small two-layer islands with a commensurate arrangement,¹⁵ but the lattice mismatch to ice Ih(0001) disfavors extended structures. Instead, the multilayer dewets, forming monolayer water and multilayer clusters several layers thick.^14,22−24 Dewetting reflects the energetic cost of forming an interface between Pt(111) and the ice film, but the complex nature of the first layer makes it challenging to study how water restructures to create the buried Pt–ice interface.

In this Article, we target a molecular-level understanding of multilayer ice growth at a Pt surface alloy, aiming to explore the effect of lattice mismatch and strain on the growth of an ice film beyond the first layer. SnPt(111) is a CO-tolerant electrocatalyst for the oxygen reduction reaction,²⁵ on which water forms a commensurate hexagonal first-layer network.²⁶ This wetting layer provides a simple structure on which multilayer growth can be examined, allowing the mechanisms underpinning film growth to be examined free from some of the complexity present on the parent Pt(111) surface.

Using low-energy electron diffraction (LEED), scanning tunneling microscopy (STM), and electronic structure calculations, we examine how the second layer of water arranges to relieve lateral stress in the film as multilayer ice starts to grow on the hexagonal first layer. Second-layer water forms domains of a rectangular structure, consisting of hexagonal, face-sharing water rings separated by a regular array of linear defects. These defect rows consist of pairs of face-sharing water pentamers linked by an octamer ring, with each defect row separated from the next by a hexagonal water network to form a weakly ordered superstructure. This arrangement increases the density of water in the second layer from 0.67 to 0.75 monolayer, just 1% less than that in the ice Ih(0001) surface. Each rectangular (2√3 × 4√3)R30° domain relieves strain perpendicular to the defect rows while leaving the water film commensurate with the first layer in the other direction, with the three symmetry-related domains packing together to relieve the 2D stress. Although thicker structures were not imaged with STM, LEED shows that the additional order persists from 2 up to ca. 30 layers and is slowly replaced by a diffuse hexagonal LEED pattern. This behavior is consistent with thicker water films slowly relaxing from this domain structure to form an incommensurate ice film, similar to the behavior found in thick films on Pt(111).²⁷ These results suggest that linear chains of face-sharing pentamer rings linked by octamer units provide a common relaxation mechanism during thin film growth of water, allowing the lateral density of water to adapt from that which suits the solid surface to the lateral density of a bulk ice film. On the basis of these results, we contrast the uniquely plastic ability of water ice to restructure its H-bond network during thin-film growth with the elastic strain behavior found in other materials, such as semiconductor and graphene films.

Results and Discussion

First-Layer Water Growth

An STM image of the Pt(111)–Sn surface alloy, formed by depositing ≥0.33 ML Sn on the Pt(111) surface and annealing to 1000 K, is shown in Figure 1a, along with a structural model of this surface (Figure 1b). In these images, Sn appears as an increased tunnel current, but changing the tip condition can reverse this contrast. STM images confirm that Sn forms an ordered substitutional alloy, with only occasional vacancies in the (√3 × √3)R30° Sn lattice. The alloy surface is slightly buckled, and LEED finds that Sn sits 0.30 Å above Pt, with density functional theory (DFT) calculations giving a similar value (0.40 Å). STM images (Figure 1c) show that the water monolayer forms extended commensurate islands made up of interconnected hexagonal rings, with the edge of the islands aligned along the 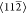directions. Each hexagonal ring images with a dark center, with alternate water sites showing slightly higher contrast than their neighbors. From images of water islands at low coverage, where the structures of both the first-layer water and the underlying SnPt substrate are resolved, we find that water is adsorbed on three Sn and three Pt atoms, with the center of the ring above a Pt site and Sn beneath the fainter of the two water sites (see Supporting Information, Figure S1).

Figure 1.

STM images and calculated structures for the SnPt(111) surface and the first water layer. (a) STM image of SnPt surface showing Sn imaging as bright features within the Pt(111) matrix (77 K, 201 mV, 807 pA). (b) Model for the SnPt surface showing Sn atoms (dark gray) surrounded by Pt (light gray), with the (√3 × √3)R30° unit cell shown in yellow. (c) STM image of a water monolayer after annealing to 120 K (77 K, 268 mV, 101 pA). (d) Lowest energy structure calculated for a single layer of water on SnPt, showing water adsorbed flat above Sn and a H-down configuration above Pt. (e) Simulation of the STM image for a H-down water layer, with the H-down site highlighted in blue. (f) STM simulation for water arranged in the alternative H-up structure, showing the H-up site in blue. The simulated voltage is +1 V, and the tip–surface distance is 6 Å.

The calculated structure for the water layer is shown in Figure 1d, with water forming an “H-down” structure with one water bound flat above Sn and the free H on the other water pointing down toward Pt.²⁶ Our calculations give a binding energy of E_ads = −0.76 eV/water (using the optB86b-vdW functional and the setup described in the Methods section), which is 0.14 eV/water more stable than the H-up arrangement, similar to the previous conclusions.²⁶ The stability of this structure is driven by a strong interaction between the electropositive Sn and the O atom of the flat-lying water. The water–Sn bond causes Sn to buckle out from the Pt surface layer, allowing the H-down water molecules to bind to their flat-lying neighbors in an almost planar arrangement.^26,28 A simulation of the STM images for the H-up and H-down structures is shown in Figure 1e,f. Although both structures correctly site the higher contrast site above Pt, as found in the STM images (see Figure S1), STM simulations for the H-up structure are dominated by the H atom that points out from the surface, such that the flat-lying water is barely visible. In contrast, STM images find only a small difference in contrast between the two water sites (Figure 1c), similar to that for the H-down simulation (Figure 1e) and supporting the original LEED I–V and work-function assignment of the structure to an H-down water layer.²⁶

Hexagonal islands of commensurate water have been previously imaged by STM on several surfaces,^29,30 but the two different binding arrangements expected (with one water bound flat to the surface via the O atom and the second water aligned with H pointing either up or down toward the surface) could not be distinguished. Maier et al.¹⁵ found islands with a hexagonal structure form on Ru(0001) and on Pt(111) in the presence of H, but STM images of the first water layer did not show any internal structure, presumably because the two water arrangements can interchange on the time scale of the STM measurement. In contrast with these systems, water on the SnPt surface (Figure 1c) shows a clear three-fold structure, implying that water on the Sn and Pt sites has a different binding arrangement and does not interconvert, even in the presence of the STM tip.

Second-Layer Ice Growth

Figure 2 shows large-area STM images of the first stages of multilayer water growth, along with detail from these images. The second water layer forms extended 2D islands above the first layer (Figure 2a), with the second layer completing before further multilayer adsorption occurs (Figure 2b). The second-layer network is built from three domains of a rectangular structure (marked α, β, and γ in Figure 2), with the domains aligned along the nearest-neighbor Sn directions (the 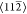symmetry directions). Individual domains are ca. 10 to 20 nm across and are characterized by defect rows, containing large, prominent rings that have a repeat unit of 2√3a_Pt along the rows (where a_Pt is the atomic spacing in Pt, 2.78 Å). Each row of large rings is separated from the next row by a network of water, with a repeat between rows of 6a_Pt or occasionally 7.5a_Pt. Small regions of hexagonal second-layer water sometimes appear between neighboring domains, in particular, where three different domains intersect, forming the triangular patches shown in Figure 2d,e. These regions are commensurate with the SnPt surface and closely resemble the hexagonal water network found for the first layer. The edge of these hexagonal regions aligns along the rows of large rings (see Figure 2d), allowing two or three symmetry-related domains to link seamlessly together (see Figure 2e). In other regions, the boundary between two domains can display less order, as shown by the regions marked by ellipses in Figure 2b.

Figure 2.

STM images showing second-layer water growth. (a) Large-area image (−173 mV, 22 pA) showing second-layer water growing on the hexagonal first layer (marked M for monolayer). The second layer consists of three interlocking rectangular domains (marked α, β, γ), aligned to the 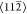symmetry directions. (b) Section from a complete two-layer film showing three intersecting domains (−167 mV, 22 pA). (c–e) Detail from the 40 Å square regions indicated in yellow in panel a. All images recorded at 99 K after growth of (a) 1.7 and (b) 2 layers of water at 135 K, where water is mobile on the surface. The features highlighted by arrows or ellipses are discussed in the text.

Increasing the STM current and bias voltage, to zoom in and examine the water network more closely, results in the images shown in Figure 3a–c. Although these images reveal more detail in the structure, the tip begins to interact with the water, and the contrast becomes sensitive to scan conditions, with different features being picked out depending on the domain orientation. The combination of variable imaging contrast, weak lateral ordering of the second layer, and contrast variation between images, presumably partially caused by disorder in the hydrogen atom positions at particular water sites, makes it difficult to immediately assign the second-layer water structure.

Figure 3.

Images of second-layer water domains aligned along the three different symmetry directions. The defect rows are indicated by an overlay showing the large and small rings as an octamer face-sharing pentamer row, with the (2√3 × 4√3)R30° repeat marked. A row of face-sharing hexamer rings that runs alongside the defect row is indicated in panel c; see the text for more details. Recorded at (a) 77 K, −845 mV, 26 pA; (b) 77 K, −727 mV, 26 pA; and (c) 99 K, −748 mV, 30 pA with a horizontal scan direction.

Despite these issues, a closer look at the STM images reveals several clues to the structure of the second layer. An examination of the defect rows shows that the large water rings are separated by an additional structure to form a 2√3a_Pt repeat along the directions (see regions marked by ellipses in Figure 2c,d). Whereas the structure between the large rings typically images as an elongated narrow ring in large-area images, it can be resolved in some high-resolution images (e.g., as highlighted in Figures 2c and 3a), where it is identified as two small face-sharing rings. 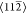On the basis of the STM images, and supported by the calculations described in the next section, we identify the defect rows as water octamer rings separated by two face-sharing pentamer rings, forming an extended 1D defect row with a 2√3a_Pt repeat along the directions. This arrangement is indicated schematically on the STM images in Figure 3. The defect rows display sites with high contrast decorating the rows, suggesting water at these sites protrudes above the second-layer plane. A well-defined chain of face-sharing hexagonal rings is found running along one edge of the octamer–pentamer rows (see Figure 3c and the rows marked by yellow arrows in Figure 2c,d). The water structure is typically less distinct on the other side of the defect rows, where the network shows lower contrast and is more difficult to resolve, with particular features appearing prominent depending on the image conditions. This region between the linear defects images with a simple √3a_Pt periodicity that matches the first water layer and underlying SnPt surface and contrasts with the doubled periodicity of the octamer–pentamer defect rows along the same direction.

Although the majority of the second-layer octamer–pentamer rows are separated from each other by 6a_Pt (three rows of hexagonal water), forming the (2√3 × 4√3)R30° repeat shown in Figure 3a,b, this ordering is weak and incomplete. In particular, the spacing of the defect rows is occasionally increased to 7.5a_Pt, equivalent to four rows of hexagonal water, or the octamer–pentamer chains are displaced by one unit (√3a_Pt) along the short repeat direction, as shown in more detail in Figure S2. Importantly, both types of disorder preserve the commensurate registry between the second-layer water and the (√3 × √3)R30° structure of the first water layer and the solid surface, implying a well-defined alignment between the second-layer water, the underlying water layer, and the SnPt surface. STM images of the two-layer structure can be directly related to the LEED patterns previously reported for thin multilayer water films,³¹ a Fourier transform of the image reproducing the 4√3 diffraction features, and streaking observed in LEED (see Figures S3 and S4).

The registry between the second-layer water and the first layer can be determined by extrapolating across the edge of second-layer islands, with measurements finding that the rows of hexagonal rings lie directly above first-layer water rings, as shown in Figure S5. A final constraint on the structure of the second layer is provided by the work-function change as the multilayer film grows, which is sensitive to the average orientation of water. The formation of the first water layer gives a work-function change Δϕ = −0.34 eV compared with the bare surface, consistent with the −0.5 eV calculated for an H-down water layer but not with other models for the water arrangement.²⁶ The work-function change increases to −0.68 eV as the second layer is formed, reaching a limiting value of Δϕ = −0.75 eV for >2 layers of water (see Figure S6). Being a global measurement, Δϕ will be influenced by areas that are not ordered, but it can be used to rule out structural models that orient too much water either H-up or H-down to create large work-function changes that are inconsistent with experiment.

Structural Models for Second-Layer Ice Growth

A structural interpretation of the second water layer has several key features to explain: the formation of rectangular (2√3 × ca. 4√3)R30° domains in preference to a biaxial reconstruction, the presence of defect rows containing large and small water rings separated by hexagonal chains, and the overall work-function and registry to the surface. Several fundamentally different models can be proposed for the structures observed. The first possibility is that the coverage in the second layer is the same as the first-layer water, in which case the rectangular domains represent a particular hydrogen arrangement that generates a (2√3 × 4√3)R30° distortion and rings of different appearance. Alternatively, the density of water may be different from the first layer; either a low-coverage domain structure will be formed in response to the lateral strain imposed by the first water layer or else the density may be increased to relax the surface toward the density of a bulk ice film. We investigated this question by simulating different types of second-layer structures: commensurate hexagonal water networks with protons oriented to create a (√3 × 4√3)R30° superstructure (Figure S7), missing row structures where one row of water molecules is removed to form linear second-layer domains (Figure S8), and, finally, a dense structure where an additional two water molecules are added to the (2√3 × 4√3)R30° unit cell (Figure S9) to give a coverage of 0.75 ML, just 1% less than the density of an ice Ih(0001) surface. Although a complete hexagonal second layer was the most stable structure we found, none of the hexagonal or missing row structures we simulated was able to reproduce the experimentally observed STM images, ruling out these structures. The stability of the two-layer hexagonal structure relative to the observed defect structure is discussed in the final section; first, we will describe the defect structure in more detail.

Because the appearance of the (2√3 × 4√3)R30° domains cannot be reproduced either by simple hexagonal networks or by linear defect structures, we focused our attention on structures with additional water in the top layer, and, in particular, on octamer–pentamer-containing structures similar to those discussed above to explain the STM results. Figure 4 shows calculated structures of this type, formed by inserting a pair of water molecules into alternate face-sharing hexamers to create a row of octamer rings separated by face-sharing pentamers. Using the chosen computational setup, these defect row structures have a similar binding energy to the commensurate hexagonal network, being just 13 to 28 meV/water less stable (Figure S9) depending on the precise proton arrangement chosen. However, the STM simulations now reproduce many of the characteristics observed in the experimental images. In particular, structures containing octamer–pentamer rows are able to reproduce the rows of alternating large and narrow rings (Figure 4e) as well as other aspects of the structure. Similar to the images, the STM simulations display high contrast sites that decorate the defect rows (see Figure 3) and are associated with water sites that are buckled above the second-layer plane. Moreover, the defect row structures also show an increased contrast of the hexagonal chain along one side of the structure but not the other (e.g., see Figure 4a), as seen in many of the STM images (e.g., see Figure 3c). The work function of the defect row structures depends on the detailed H arrangement but lies in the experimental range (Δϕ = −0.68 to −0.75 eV), with calculated structures having Δϕ between −0.35 and −0.41 eV (no H pointing toward the vacuum, Figure 4a,d), increasing to −1.04 eV as an increasing number of H atoms point into the vacuum; see Figure S9 for more details.

Figure 4.

Calculated structures for narrow domains of hexagonal ice separated by octamer face-sharing pentamer rows, similar to the structures observed in experiment. The structures shown panels a–d all have the same overall water H-bond arrangement and differ only in the location of the H atoms between the O atoms. The structures are formed by inserting a water dimer into alternate rings along a face-sharing hexagonal row using a (2√3 × 4√3)R30° unit cell with a coverage of 0.75 ML. Water molecules that protrude above the second layer are marked by blue circles and image with a high contrast in the STM simulations. Panel e shows a (2√3 × 4√3)R30° water network superimposed schematically on the experimental STM image from Figure 3b. Full details of all of the structures considered and their binding energies are given in Figure S9.

Discussion

The electronic structure calculations find that the most stable two-layer structure consists of a fully H-bonded, commensurate hexagonal sandwich structure, with each water molecule having three in-plane H bonds and one to the other layer, forming the highly symmetric arrangement shown in Figure 5a. This structure has all of the uncoordinated H atoms in the bottom layer rotated out of the first-layer arrangement to align H-up, losing the H-down arrangement favored for a single layer of water (Figure 1). STM images of water on SnPt do show small triangular regions of commensurate hexagonal second-layer water, but these are minority structures and do not grow more than four or five units (∼20 Å) across before a defect row is formed (see Figure 5d). The hexagonal patches show an intensity alternation similar to that found for STM simulations of the sandwich structure, where the flat second-layer water images with an increased contrast over its H-down neighbor. An analogous two-layer, hexagonal sandwich structure has been proposed previously for water on Au(111)³² and graphite,³³ but the water–surface interaction is very weak on these nonwetting surfaces and water does not form commensurate structures. Although the hexagonal (√3 × √3)R30° first-layer water network formed on SnPt has the correct symmetry to bind to a hexagonal ice multilayer, the lattice spacing of Pt(111) is 6% greater than expected for a bulk ice structure, creating lateral strain in any multilayer ice film that grows entirely commensurate with the surface. The absence of extended hexagonal domains of two-layer water suggests that this lateral strain is sufficient to destabilize this structure on SnPt.

Figure 5.

(a,b) Calculated structure for the symmetric, two-layer sandwich structure with the same water density as the first layer (0.67 ML) and a binding energy E_ads = −0.70 eV/water. (c) STM simulation with the high-contrast site marked. (d) Experimental image showing one of the small, minority hexagonal domains of second-layer water with the same (√3 × √3)R30° alternation in site contrast (30 Ų, −173 mV, 22 pA).

The majority of the second-layer structure we find on SnPt consists not of commensurate hexagonal water but of rectangular domains containing regularly spaced defect rows separated by a hexagonal water network (Figure 2). Calculations for water in a commensurate hexagonal network are not able to reproduce this arrangement despite the high stability of two-layer hexagonal sandwich structures in DFT (Figure S7). On the basis of the STM images, we propose that the defect rows consist of a high-density structure, formed by inserting a water dimer into alternate hexagons along a face-sharing row to create octamer rings separated by face-sharing pentamers. Calculated octamer structures of this type (Figure 4) correctly reproduce the alternation in ring size found in the STM images but are less stable than the sandwich structure, although by a small amount (≥13 meV/water). Different DFT functionals (PBE, PBE-D3) give similar results (see Table S1), although the relative stability of the structures changes slightly (by ca. 10 meV) depending on the functional used. However, calculations for different lattice parameters find that the octamer structures become favorable when the substrate is strained by ∼5% in the present DFT calculations (see Figure 6), becoming more stable than the double-layer sandwich structure (black line). The same occurs for the PBE and PBE-D3 functionals (Figure S10), so this trend is not functional-dependent. This trend suggests that relaxation of tensile stress in the second-layer ice structure by increasing the coverage is the driving force stabilizing these defect structures. Although it should be noted that DFT predicts this inversion in stability to occur at rather large tensile strains, this is likely a consequence of the DFT error in estimating the lattice constant of Pt and the H-bond length of the water network,³⁴ and it might appear at a different value of the biaxial strain in experiments.

Figure 6.

Change of the adsorption energy for the structures shown in Figures 4a–d and 5 as a function of the lattice constant of the substrate, a. Most of the defect row structures containing octamer–pentamer rows become more stable than the sandwich structure (black line) within the strain range that has been tested (up to 6%). Significant values of the substrate biaxial strain are indicated with black dotted lines. For the structure in Figure 4b, the sandwich structure is still more stable at 6% strain; however, the energy difference between the two goes from 17 meV down to 2 meV as strain is increased, signaling a similar trend as the other defect structures.

Further support for this idea comes from the recent observation of rows of face-sharing pentamers separated by octamer rings in several other water structures. Rows of octamer and pentamer rings were observed on Ru(0001), linking between out-of-phase hexagonal domains of two-layer water.¹⁵ In this case, second-layer water forms large hexagonal domains ∼10 units wide, crossed by occasional octamer–pentamer rows. The defect rows were attributed to either stacking faults associated with the formation of cubic ice or to domain boundaries between two crystals that nucleate out of registry, but the observation of regularly spaced octamer–pentamer rows on SnPt(111) suggests a different interpretation. The Ru surface has a smaller (3.7%) mismatch to ice than Pt (6.3%), reducing the lateral strain in a commensurate hexagonal water network on Ru compared with Pt. A smaller mismatch allows larger commensurate hexagonal domains to form on Ru before lateral stress becomes sufficient to favor forming an octamer–pentamer defect row to relax the tensile stress. Whereas this occurs after three hexagonal rows on Pt, the defect rows on Ru are more widely separated,¹⁵ which is consistent with the reduced lateral strain between Ru and bulk ice. Rows of octamer and face-sharing pentamer rings have also been observed recently in the first water layer on stepped Cu(511), creating a planar network that wets the surface.¹³ In this case, the defect row structure has a lower density than the buckled hexagonal structure that replaces it at higher coverage.¹⁷ Because a degree of mismatch between ice and any nucleating surface is inevitable when wetting solid surfaces, it appears that the formation of octamer–pentamer rows within a hexagonal network offers a generic strain relief mechanism to vary the density of thin ice films above a solid surface and may be anticipated as a common feature during wetting of solid surfaces.

Control of the surface strain is a key aspect of engineering the properties of semiconductor heterostructures^35,36 and other thin-film materials,³⁷ but it requires the adlayer to be sufficiently strongly coupled to the substrate to distort the film.³⁸ Despite this, even weak van der Waals (vdW) interactions can be used to manipulate material properties;^39,40 for example, the local registry between graphene and a suitable substrate can generate complex strain structures,³⁷ with strain levels as high as 7.5%,⁴¹ without restructuring the film. A defect-free thin-film heterostructure is needed to preserve material properties in technological applications, and common challenges faced to grow single crystals on strained substrates include phase transitions,^42,43 island formation,^38,44 and reconstruction of the interface layers with, for example, misfit dislocations.⁴⁵ Thin water films, despite not distorting elastically, show some similarities to solid films in the way they respond to the strain of the substrate. Indeed, the pentamer–octamer linear defects shown in the present work bear similarities to misfit dislocations, as their function is to restore the bulk density. However, misfit dislocations appear only after a critical (a few nanometers) thickness of the film, in a balance between the elastic energy and the cost of creating a defect. In contrast, water’s remarkable ability to distort its H-bond network allows these “linear defects” to form straight away in the second layer, as soon as it is deposited; therefore, ice cannot be strain-engineered at any thickness, which is quite different from thin films of covalent solids. This may also be true for other hydrogen-bonded solids of high technological relevance, such as the ferroelectric KH₂PO₄⁴⁶ or donor–acceptor ferroelectrics,⁴⁷ which would thus require well-matching substrates to be grown defect-free. In view of the difference in structure and H-bond strength to ice, this would warrant direct study.

The adsorption system presented here reveals how a very specific interfacial reconstruction is created in the first deposited layer of water and is relaxed in the subsequent multilayer film. Despite having a surface binding energy that is comparable to the water–water interaction energy,⁴⁸ the first layer of water is pinned into close registry with the substrate, creating a flat, H-down structure that suits this particular substrate. However, rather than growing commensurate with this template, the second-layer water already adapts its H-bond network to adopt the same lateral density as a bulk ice surface. Instead of distorting the ice structure by straining the water–water H-bond lengths, the water film adapts the H-bond network and geometrical arrangement to suit the specific environment. This remarkable ability to distort the H-bond geometry away from a tetrahedral arrangement with minimal energy cost allows water to form low-energy H-bond networks tailored to the surface periodicity, in a similar way as occurs around polar species to give water its unique solvation properties.^49,50 Because some degree of mismatch between ice and a nucleating surface is inevitable during heterogeneous nucleation, it appears that restructuring to form octamer–pentamer rows will provide a common, low-energy strain relief mechanism to allow the density of water to adapt from that which matches the solid surface to that of an ice film.

Conclusions

The growth of ice on a SnPt(111) template has been investigated using STM to reveal how thin water films reconstruct to accommodate the 6% lateral expansion of the first water layer. Second-layer water forms a network that is in close registry with the first-layer water but contains 12% more water, giving a density that is similar to that of a bulk ice surface. The additional water is incorporated as linear defects, made up of octamer rings linked by face-sharing water pentamers. The defect rows are linked by stripes of hexagonal water, three or four rows wide, forming a complete 2D hydrogen-bonding network in registry with the first layer. The formation of octamer–pentamer chains provides a low-energy mechanism to increase the density of the layer toward that of an ice surface, allowing the defect structure to bridge between the solid surface and a bulk ice film. These results demonstrate clearly that an understanding of how solid surfaces wet requires us to go beyond a description of the first water layer and develop techniques to examine how the first few layers of water restructure during adsorption.

Methods

Experiment

A Pt(111) crystal (99.999% Surface Preparation Laboratory) was polished to within 0.25° of the (111) face and cleaned by cycles of Ar⁺ ion sputtering at 0.9 keV and annealing to ∼1200 K. The surface was repeatedly treated in an oxygen atmosphere (5 × 10^–7 mbar), followed by annealing to remove carbon contamination. Tin (99.995%) was deposited from a thermal source to adsorb slightly in excess of 0.33 ML, and the surface was annealed to ∼1000 K to form the (√3 × √3)R30° substitutional surface alloy.⁵¹ The surface quality was determined by STM and using a low current MCP LEED system to characterize the adlayer and water film. Water adsorption was studied in an ultrahigh vacuum (UHV) chamber with a base pressure of 4 × 10^–11 mbar using a CreaTec low-temperature STM with a separate preparation chamber. Water films were grown using a molecular beam directed at the sample surface, held at 130 K. All experiments were performed in constant-current mode at T < 100 K. Images were recorded using a low tunnel current to prevent tip-induced restructuring or dissociation of the water structures, with the exact I_t and V_t values quoted in the figure captions. Applying a negative bias voltage to the sample gave the best resolution for the second wetting layer, imaging the occupied states of the water molecules.

Theory

DFT calculations were carried out with VASP⁵²⁻⁵⁴ using the optB86b-vdW functional.⁵⁵ The optB86b-vdW functional is a revised version of the vdW density functional of Dion et al.,⁵⁶ which has shown good agreement with experimental data for water adsorption on metals.⁵⁷⁻⁶¹ Further tests were performed with the PBE functional⁶² without and with the D3 vdW correction.⁶³ Core electrons were replaced by projector augmented wave potentials,⁶⁴ whereas the valence states were expanded in plane waves with a cutoff energy of 500 eV. All calculations were performed using a four-layer-thick (4 × 3) Pt(111) slab. In the top layer, 1/3 of the surface Pt atoms have been substituted with a Sn atom. Periodic images were separated by ∼15 Å of vacuum in the direction perpendicular to the surface. The metal atoms in the bottom layer were fixed to the bulk optB86b-vdW optimal positions (a_optB86b-vdW^Pt = 3.950 Å), whereas all other atoms were allowed to relax. A Monkhorst–Pack k-point grid of (3 × 6 × 1) was used in all calculations. A dipole correction along the direction perpendicular to the metal surface was applied, and geometry optimizations were performed with a residual force threshold of 0.005 eV/Å. STM images were simulated using the Tersoff–Hamann approach,⁶⁵ with a voltage of −500 mV and at a height of 8 Å above the metal surface for the two-layer structures and with a voltage of +1 eV and at a height of 6 Å for the one-layer structure. Simulated images for different voltages and tip heights show similar results, demonstrating that the conclusion does not depend on the choice of parameters. Adsorption energies per molecule, E_ads, were computed with a standard definition: E_ads = (E_water/PtSn – E_PtSn – n × E_H2O)/n, where the total energies of the n–water system, relaxed bare metal slab, and an isolated gas-phase water molecule are, respectively, E_water/PtSn, E_PtSn, and E_H2O. Favorable (exothermic) adsorption corresponds to negative values of the adsorption energy. It should be noted that energy differences between different adsorbed systems can be rather small, that is, <10 meV, which is generally considered the lower limit of reliability of DFT calculations. Therefore, to identify the experimental structure, comparisons between experimental and DFT-calculated work-function changes have also been considered as well as the compatibility of the STM images. The work function for the bare metal slab and the adsorbed system was determined by computing the total local potential along the direction perpendicular to the surface and considering the value for the vacuum above the slab. The work-function difference was then obtained by subtracting the two.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b03311.

• Additional characterization of the first- and second-layer water structures and a complete list of the binding energies and structures calculated for the monolayer and multilayer ice films (PDF)

• 3D molecular models of chemical structures in Figures 4 and 5 (ZIP)

The authors declare no competing financial interest.