Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Apr 11;13(5):5686–5692. doi: 10.1021/acsnano.9b01006

Lasing in Ni Nanodisk Arrays

Sara Pourjamal †, Tommi K Hakala †,‡,*, Marek Nečada †, Francisco Freire-Fernández †, Mikko Kataja †,§, Heikki Rekola ⊥, Jani-Petri Martikainen †, Päivi Törmä †, Sebastiaan van Dijken †,*
PMCID: PMC6543507  PMID: 30973219

Abstract

graphic file with name nn-2019-01006g_0005.jpg

We report on lasing at visible wavelengths in arrays of ferromagnetic Ni nanodisks overlaid with an organic gain medium. We demonstrate that by placing an organic gain material within the mode volume of the plasmonic nanoparticles both the radiative and, in particular, the high ohmic losses of Ni nanodisk resonances can be compensated. Under increasing pump fluence, the systems exhibit a transition from lattice-modified spontaneous emission to lasing, the latter being characterized by highly directional and sub-nanometer line width emission. By breaking the symmetry of the array, we observe tunable multimode lasing at two wavelengths corresponding to the particle periodicity along the two principal directions of the lattice. Our results are relevant for loss-compensated magnetoplasmonic devices and topological photonics.

Keywords: plasmonics, nanolasing, Ni nanodisk array, surface lattice resonance, loss-compensated magnetoplasmonics

Plasmonic resonators and cavities provide small mode volumes and ultrafast light–matter interactions at the nanoscale. Interactions between emitters and plasmonic modes have been studied in both weak and strong coupling regimes.1,2 Theoretical and experimental investigations on lasing in plasmonic systems have demonstrated the feasibility of compensating losses typical for metallic nanostructures3−23 and providing ultrafast operation speeds.8,24 Lasing as a loss-compensation mechanism would be particularly attractive for magnetoplasmonics, which enables active light manipulation at the nanoscale via field-controlled breaking of time-reversal symmetry25 and versatile design of magneto-optical responses.26 Potential applications of magnetoplasmonic nanostructures include nonreciprocal optical devices,27 label-free biosensors,28,29 metrology,30 and ultrafast all-optical magnetic switching.31 However, ohmic losses in ferromagnetic metals are considerably larger than those in noble metals, and the narrowing of intrinsically broad resonances via a transition to lasing has not been demonstrated yet.

Periodic arrays of metallic nanoparticles support collective surface lattice resonances (SLRs) that originate from radiative coupling of lossy single particle plasmon resonances with low-loss diffracted orders (DOs) of the lattice.32−37 In optical transmission spectra, the DOs of an array appear as maxima at λ ≈ np, where n is the refractive index of the surrounding medium and p is the particle periodicity. Hybridized Fano-like SLR modes reduce the signal, causing minimum transmission at a wavelength that deviates from the DO.33−37 Despite the plasmonic component, SLRs in arrays of noble metal nanodisks have particularly narrow line widths that can be utilized in lasing13−17,19,20,22 and Bose–Einstein condensation.38 Recently, it was demonstrated that collective SLR modes can be excited also in arrays of higher-loss ferromagnetic nanoparticles.39,40

Here, we report on lasing in a lattice of ferromagnetic nanodisks overlaid with optically pumped organic Rhodamine 6G (R6G) dye solution. Reduced line widths provided by the SLRs together with a carefully optimized lattice geometry and gain medium produce lasing at visible wavelengths, despite the broad plasmonic resonances of the individual nanodisks. Lasing is characterized by a highly directional and nonlinear increase of sub-nanometer line width emission by more than 2 orders of magnitude. Within the limits set by the gain profile of R6G, the lasing wavelength can be tuned by varying the particle periodicity. In rectangular arrays, we observe lasing at two wavelengths corresponding to λ ≈ n × pi for different particle periodicities (px and py) along the two principle axes of the lattice.

Results and Discussion

In our study, we used Ni as a ferromagnetic plasmonic material. We fabricated various arrays of Ni nanodisks on glass substrates using electron-beam evaporation and lift-off in an electron-beam lithography process. The nominal diameter and height of the nanodisks were 60 nm, and the size of the total array was 300 μm × 300 μm. As a reference, we considered a square array with px = py = 380 nm. In rectangular arrays with broken symmetry, px was kept constant and py was varied from 370 to 390 nm in 5 nm steps. The gain medium consisting of 35 mM R6G in 1:2 dimethyl sulfoxide (DMSO)/benzyl alcohol (BA) was inserted between the substrate with Ni nanodisk arrays and a cover glass.

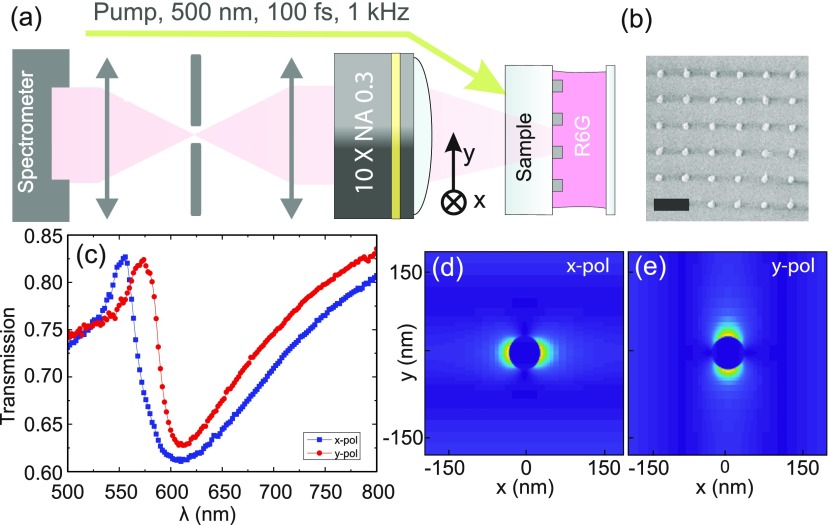
A schematic of the measurement setup including excitation and detection lines is depicted in Figure 1a. The sample was excited by 100 fs laser pulses with a wavelength of 500 nm at a 1 kHz repetition rate and from a 45° angle. The diameter of the pump spot was approximately 100 μm. Emitted light from the sample was collected with a 10× 0.3 NA objective lens. The back focal plane of the objective lens was focused to the entrance slit of a spectrometer. The long axis of the slit was aligned along the y-axis of the sample. From 2D intensity data collected by the CCD camera of the spectrometer, the wavelength and in-plane ky vector were calculated using ky = k0 sin (θ).19 Here k0 = 2π/λ and θ is the angle with respect to the sample normal. We note that we did not apply a magnetic field during the lasing experiments. A scanning electron microscopy image of the square 380 nm × 380 nm reference array is shown in Figure 1b.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic of the measurement setup. Emission spectra are measured by focusing the back focal plane of the objective lens to the entrance slit of the spectrometer. The gain medium is pumped by x-polarized 100 fs laser pulses with a wavelength of 500 nm and a 1 kHz repetition rate. The gain medium is inserted between the substrate with Ni nanodisk arrays and a cover glass. (b) Scanning electron microscopy image of the 380 nm × 380 nm array. In all experiments, the diameter and height of the Ni nanodisks are 60 nm. The scale bar corresponds to 500 nm. (c) Experimental transmission curves for the Ni nanodisk array with px = 380 nm and py = 370 nm. Data for incident polarization along the x and y directions of the array are shown. (d,e) Finite-difference time-domain simulations of near-field distributions in the same array. The simulations are performed for x- and y-polarized plane-wave excitation at the SLR wavelength.

Figure 1c shows experimental transmission curves of the Ni nanodisk array with px = 380 nm and py = 370 nm for incident polarization along x and y (see Supporting Information, Figure S1 for measurements on other arrays). The intensity maxima are close to the DOs of the lattice. Because the DO wavelength depends on the particle periodicity perpendicular to the polarization axis, the transmission curve for x-polarized light is blue-shifted with respect to the spectrum measured with y-polarization. Coupling of a narrow DO to a broad localized surface plasmon resonance (LSPR) in the Ni nanodisks produces a collective SLR mode.39 The SLR wavelength (minimum transmission in Figure 1c) corresponds to the wavelength where 1/α – S is 0.34,35 Here, S is the so-called array factor and α is the polarizability of a single Ni nanodisk. Damping of the SLR mode depends sensitively on the imaginary part of 1/α. Consequently, noble metal nanodisks with large polarizability produce narrow SLR modes with a line width of <10 nm when ordered into periodic arrays.32−37 Because of larger ohmic losses in Ni (i.e., small α), the SLRs in our plasmonic arrays are much broader (>100 nm; see Figure 1c). Finite-difference time-domain (FDTD) simulations of the 380 nm × 370 nm Ni nanodisk array at the SLR wavelengths (Figure 1d,e) show intense electric near fields in the particle plane, confirming the plasmonic character of this collective mode. Next, we demonstrate that despite the large line width of SLR excitations, it is possible to realize lasing in Ni nanostructures.

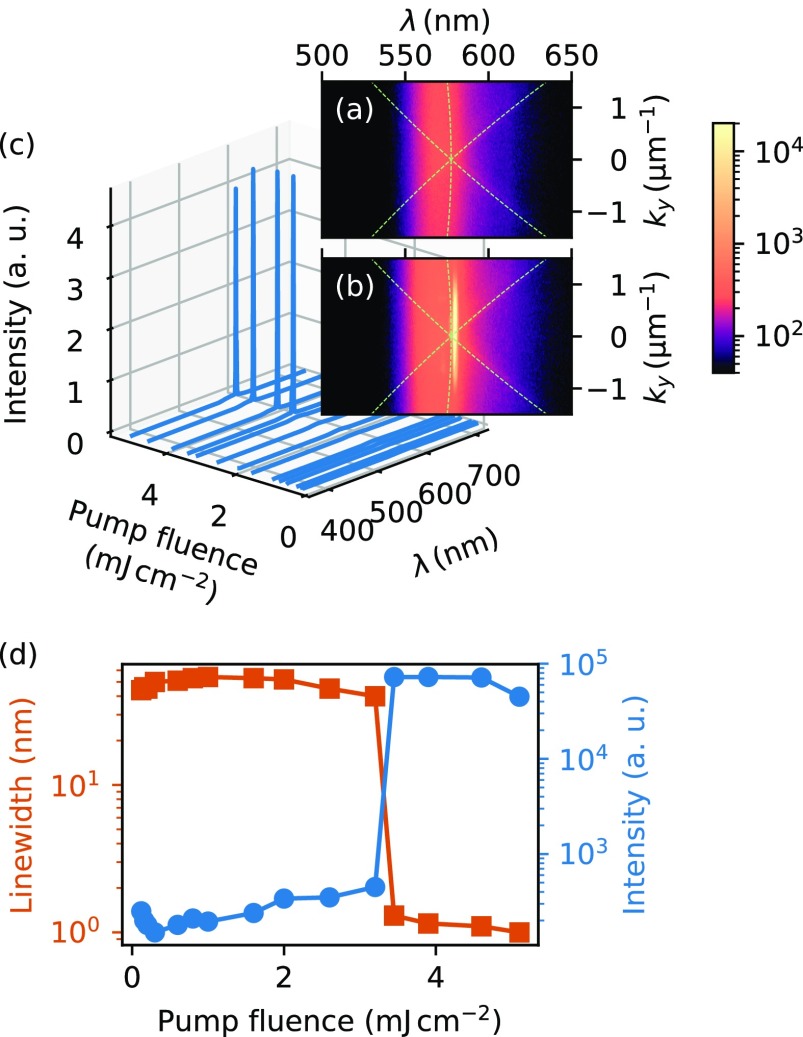
Figure 2a,b shows the ky and wavelength-resolved emission from the sample with a 380 nm × 380 nm Ni nanodisk array for a pump fluence below and above the lasing threshold (Pth ≈ 3.3 mJ cm–2). Below the threshold, the emission consists of two contributions. The first contribution has no angular dependence and originates from the R6G molecules. Because the molecules are spatially far away from the nanoparticles (and outside the SLR mode volume), they do not emit to the SLR mode. Their emission spectrum has a line width of ∼60 nm, which is the same as that for the R6G dye solution in the absence of the nanodisk array. The second emission contribution follows the ⟨+1,0⟩ and ⟨−1,0⟩ DOs of the array (crossed dashed lines) and, thus, depicts spontaneous emission of the molecules to the SLR modes. As expected from λ = n × pi and the transmission curves of Figure 1c, the DOs related to the periodicity py cross at λ = 578 nm if py = 380 nm and n = 1.52. At a higher pump fluence of 1.3Pth, we observe an intense single emission peak at λ ≈ 580 nm with a narrow line width of <1 nm and a small beam divergence of 5.7°. The lasing peak is slightly red-shifted from the DOs to a wavelength where the R6G dye solution can emit to the SLR modes of the Ni nanodisk array. The transition from spontaneous emission to lasing is manifested as an abrupt change in the emission spectrum (Figure 2c). Figure 2d summarizes the variation of the emission intensity and line width with increasing pump fluence. Most notably, we measure a strongly nonlinear increase of the emission intensity from ∼2 × 102 to ∼105 if the pump fluence is enhanced from 3.2 to 3.45 mJ cm–2. Simultaneously, the line width of the emission peak decreases from ∼60 to <1 nm. We note that the lasing peak line width of our Ni system is similar to those obtained with 2D arrays of Au, Ag, or Al nanoparticles (values range from 0.1 to 1.5 nm in refs (13, 18, 19, 21, and 22)). Thus, despite much larger losses in Ni nanodisk arrays (SLR line width >100 nm compared to 4–10 nm in noble metal lattices), intense and narrow line width lasing is still attained if enough gain is provided. This finding demonstrates that lasing can be used as a powerful tool to circumvent losses in magnetoplasmonic systems.

Figure 2.

Figure 2

Open in a new tab

Angle and wavelength resolved emission of a symmetric 380 nm × 380 nm Ni nanodisk array below (a) and above (b) the lasing threshold. The dashed lines indicate the DOs of the array. Because the momentum direction ky is monitored here, the ⟨+1,0⟩ and ⟨−1,0⟩ DOs related to the periodicity py appear as a cross feature, whereas the one related to px (at 578 nm) has a parabolic shape. The former is sometimes called TE and the latter TM mode in the literature.2 (c) Emission intensity at ky = 0 as a function of pump fluence. (d) Line width (squares) and intensity (circles) of the emission peak showing an abrupt nonlinear change of these parameters at a threshold pump fluence Pth ≈ 3.3 mJ cm–2.

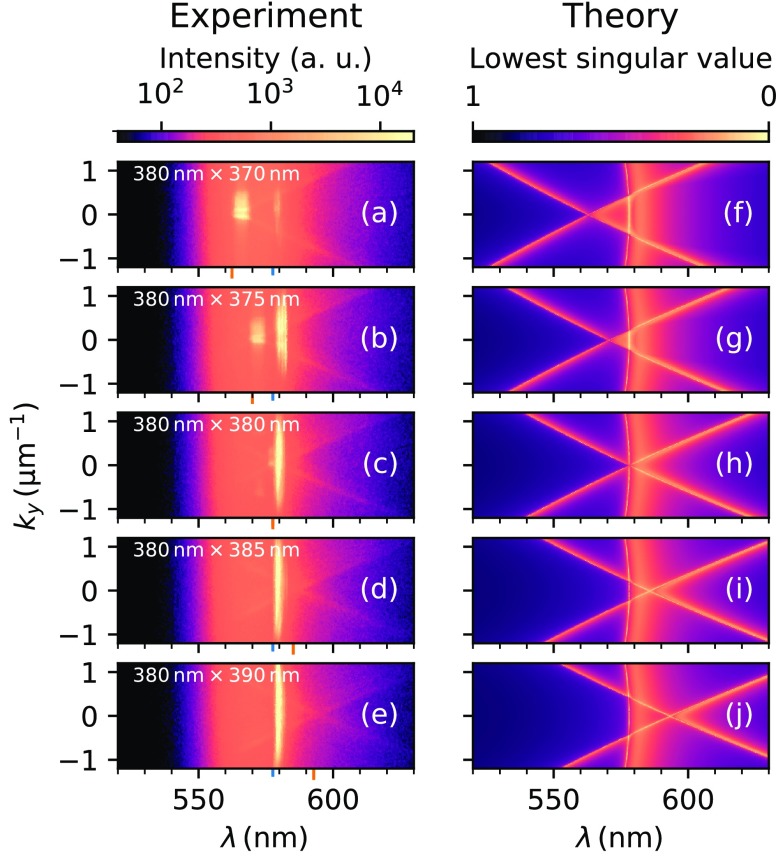
Next, we break the symmetry of the Ni nanodisk array by keeping px constant and increasing py from 370 to 390 nm in 5 nm steps. Figure 3 shows emission spectra of these samples for a pump fluence of 4.6 mJ cm–2. In (a), we observe two emission maxima, one at the same wavelength, λ ≈ 580 nm, as that for the square array (see Figure 3c) and the other at λ ≈ 565 nm. Threshold behavior and line width imply lasing action for both peaks. We note that the maximum at 565 nm is 15 nm blue-shifted from the other lasing peak. We associate this emission with the reduced particle periodicity along the y direction. The expected 15 nm blue-shift based on Δλ = n × Δpy supports this argument, as well as the FDTD simulations of Supporting Information, Figure S3. The emission maximum at 580 nm is associated with the larger periodicity of the rectangular Ni nanodisk array along the x direction.

Figure 3.

Figure 3

Open in a new tab

(a–e) Angle- and wavelength-resolved emission data for samples having px = 380 nm and py ranging from 370 to 390 nm at a pump fluence of 4.6 mJ cm–2. The red ticks label the crossing wavelength of the ⟨−1,0⟩ and ⟨+1,0⟩ diffracted orders related to the periodicity py of the array. (f–j) Dispersions of respective ideal infinite arrays computed using the T-matrix method for E in-plane modes. Dispersion bands of the array are characterized by singular values of the underlying scattering problem (1) reaching near 0.

In agreement with the dependence of the two lasing peaks on particle periodicity, the lower-wavelength emission maximum red shifts when py increases to 375 nm, whereas the other peak remains fixed at 580 nm (Figure 3b). A further increase of py to 380 nm results in a square nanodisk lattice, and consequently, the two emissions merge into one intense lasing peak (Figure 3c). For py > 380 nm, one would expect a second lasing peak to appear at λ > 580 nm. As can be seen from the emission data in Figure 3d,e, this is not the case. We explain the absence of the anticipated second peak by a reduced overlap of the SLR mode with the wavelength-dependent gain profile of the R6G dye solution. At wavelengths corresponding to py > 380 nm, the R6G gain is insufficient to compensate for the lossy SLR mode of the Ni nanodisk array, resulting in much weaker spontaneous emission instead of lasing. For py < 380 nm, the spectrum of the R6G gain medium overlaps more with the energy of the py-related SLR mode, and consequently, multimode lasing is observed. Two-mode lasing has been observed previously for noble metals.19,21 Moreover, for Al nanoparticles, it has been shown that highly asymmetric 1D arrays do also lase.22

To understand the mode properties, we employ a multiple-scattering T-matrix approach

graphic file with name nn-2019-01006g_m001.jpg 1

where M(ω, k) is a matrix depending on scattering and wave propagation properties of the array at a given frequency ω and aν(ω, k) is a vector of coefficients describing multipole nanoparticle excitations of a given mode. The problem (1) has a nontrivial solution; that is, a mode exists if the matrix M(ω, k) has a 0 singular value (SV). Therefore, to find modes supported by the array, we scan ω, k space to search for SV minima of M(ω, k). Due to losses, SV minima are not exactly 0 for real ω, k, but near 0 SVs nevertheless provide valuable information about the dispersion of the array. Figure 3f–j illustrates calculated modes with the lowest SVs of M(ω, k), resembling the experimental data of Figure 3a–e. The Materials and Methods section provides more details on the numerical model.

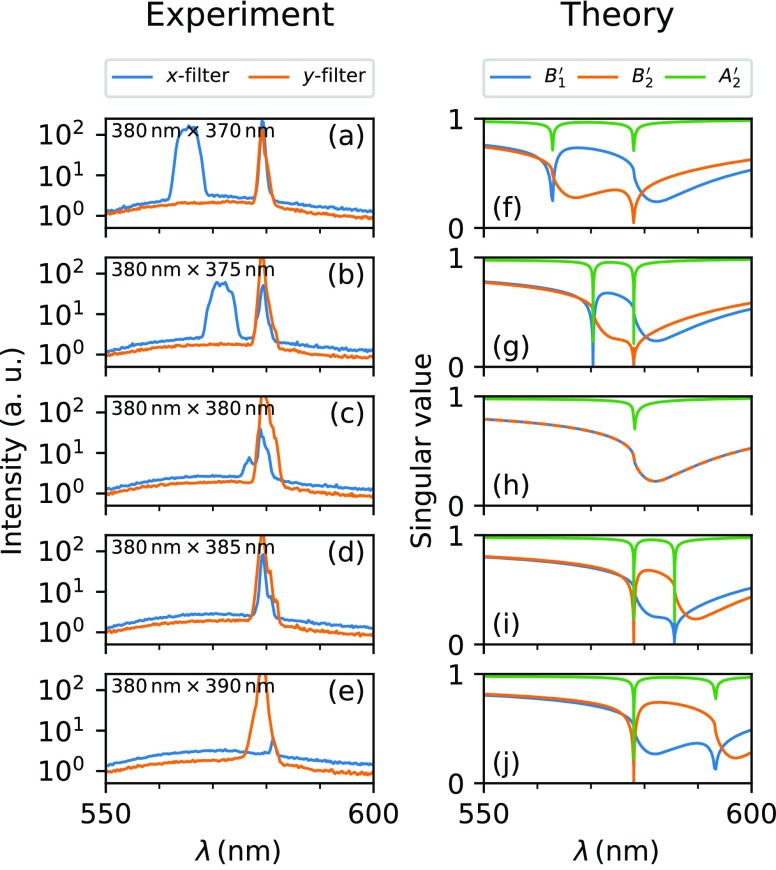
Finally, we analyze the polarization properties of the lasing modes in our Ni nanodisk samples with a R6G gain medium. Experimentally, this was done by placing a polarizer between the sample and spectrometer to determine the emission intensity with polarization along the x and y directions of the arrays. Figure 4a–e presents emission spectra for both polarization states at ky = 0 and a pump fluence of 4.6 mJ cm–2. In (a), the low wavelength emission related to py is x-polarized, whereas the px-related lasing peak at 580 nm exhibits both polarizations. We note that the x-polarization of this peak disappears at higher pump fluence (see Supporting Information, Figures S4 and S5). We observe similar behavior in (b), with a red shift in the lower wavelength lasing peak because of larger py. For the square array (c), we observe lasing at a single wavelength due to mode degeneracy. In (d), lasing takes place at the wavelength of the px-related SLR mode only. The lasing peak in this emission spectrum exhibits both polarizations. Finally, in (e), single mode lasing with reduced x-polarization is measured.

Figure 4.

Figure 4

Open in a new tab

(a–e) Emission spectra at ky = 0 for samples having px = 380 nm and py ranging from 370 to 390 nm. The pump fluence is 4.6 mJ cm–2. (f–j) Calculated singular values for arrays with the same particle periodicities. The blue and orange colors correspond to x- and y-polarized dipolar modes (B1,2′), respectively, and the green color corresponds to a quadrupolar mode (A2).

The polarization properties are also studied by the T-matrix method, which can uncover both x- and y-polarized dipolar as well as quadrupolar contributions at each wavelength. Figure 4f–j summarizes the results for the different Ni nanodisk arrays. In (f), SV minima are calculated for two dipolar modes corresponding to the experimentally observed wavelengths in (a) and polarizations at high pump fluence. The same applies for (g). In (h), the square array exhibits degeneracy of the dipolar modes. This raises the question whether the experimental observations in (c) are caused by lasing action of two perpendicular dipolar modes or a quadrupolar mode. Finally, in (i) and (j), we note that the model predicts a large quadrupolar weight at the measured lasing wavelength in (d) and (e). In (d), the experimental lasing peak exhibits both polarizations, and hence, the mode is indeed quadrupolar. In contrast, lasing in (e) is almost purely y-polarized, suggesting dipolar mode lasing. To rationalize this, we point out that a priori predictions of preferred lasing modes are difficult because mode dynamics, mode competition at available gain, and mode Q-factors all play a role. Furthermore, we observe a dependence of lasing behavior on pump fluence (see Supporting Information, Figure S4 for a complete set of emission spectra at different pump fluence). A more detailed understanding of mode competition in Ni nanodisk arrays requires further studies.

Conclusions

In summary, we demonstrate lasing in a high-loss ferromagnetic plasmonic system. In rectangular Ni nanodisk arrays, we observe multimode lasing and the coexistence of dipolar and quadrupolar modes. The results of this paper can be used for incorporating gain into magnetoplasmonic devices and realizing concepts for topological photonics. Notably, topological lasing has been demonstrated recently.42−44 In topological photonics,45−48 most lattice systems are based on nearest or next-nearest neighbor coupling via overlapping optical near-fields. Our Ni nanodisk arrays represent a radiatively coupled system where long-range couplings produce collective SLR modes. The symmetry properties of the array dictate the existence of energy degenerate modes at high-symmetry points of the Brillouin zone,41 for which the lifting of the degeneracy by a symmetry breaking mechanism can lead to topological features. The magnetic moment of nanodisks in a ferromagnetic array can be exploited for time-reversal symmetry breaking in such lattices. The Ni nanodisk arrays discussed in this paper show a magnetic circular dichroism effect of up to 0.5% in a saturating magnetic field of 150 mT.49

Materials and Methods

Sample Preparation

We fabricated the samples on glass substrates using electron-beam lithography. After a poly(methyl methacrylate) (PMMA) layer was spin-coated and baked at 180 °C for 1 min, the pattern was defined by exposing the resist layer to the electron beam. We developed the PMMA in a 1:3 methyl isobutyl ketone/isopropyl alcohol solution. Ni nanodisk arrays were fabricated by e-beam evaporation of a 60 nm thick film, followed by lift-off. After being patterned, the nanodisk arrays were covered by 2 nm Al2O3 using atomic layer deposition to protect Ni from degrading when contacted by R6G molecules.

Sample Characterization

We measured optical transmission curves using a spectrometer with a broad-band supercontinuum laser. For lasing measurements, the R6G gain medium was inserted between the glass substrate with Ni nanodisk arrays and a cover glass. The gain medium was pumped with a femtosecond laser (45° incident angle, 500 nm center wavelength, 100 fs pulse width, 1 kHz repetition rate, x-polarization). Emission spectra were recorded as a function of wavelength and in-plane ky-vector by focusing the back focal plane of a 10× 0.3 NA objective onto the slit of a spectrometer (Figure 1a). The lasing peaks were measured with three settings of the output polarization filter (x filter, y filter, no filter).

Simulations

The dispersion calculations in Figures 3f–j and 4f–j were performed using a multiple-scattering T-matrix approach. Here, we briefly introduce the model. A more detailed description can be found in the Supporting Information of ref (41).

The scattering properties of a single nanoparticle are first described in terms of vector spherical wave functions (VSWFs), giving the T-matrix of the nanoparticle at a given frequency. In the next step, electromagnetic interactions between nanoparticles are calculated as translation operators Sn,n′, which describe how VSWFs with one coordinate origin (located inside the nanoparticle n′) can be decomposed in a VSWF basis at another origin (corresponding to the location of nanoparticle n). This yields a set of linear equations describing the scattering properties of a system with many nanoparticles, which, in a per-particle matrix form, can be written as

graphic file with name nn-2019-01006g_m002.jpg 2

Here, the pext(n) column vectors contain the VSWF expansion coefficients of the external electromagnetic radiation incident onto the nth nanoparticle, and an is the vector of the unknown VSWF expansion coefficients of the scattered field created by the nth nanoparticle.

For periodic systems, the field expansion coefficients at different nanoparticle sites attain the Bloch waveform of 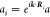Inline graphic, where Ri are the lattice vectors and k is the Bloch wave vector. If there is only one nanoparticle per unit cell and the T-matrices are the same for all particles, eq 2 can be rewritten as

graphic file with name nn-2019-01006g_m004.jpg

Labeling W = ∑i′ ≠ iSi, i′eik·(Ri′ – Ri) = ∑i′ ≠ 0S0, i′eik·Ri′, this gives

graphic file with name nn-2019-01006g_m005.jpg 3

where the only challenge remains in calculating the infinite lattice sums contained in the operator W, which in general diverge. One can work around this using Ewald-type summation techniques.

Equation 3 with a nonzero right-hand side describes the electromagnetic response of a periodic array on external periodic driving. Putting the right-hand side to 0 gives an equation for the electromagnetic modes supported by the array. The electromagnetic bands are then given for points (ω, k) in the frequency-quasimomentum space where the matrix M(ω, k) ≡ I – T(ω)W(ω, k) is singular. In other words, the dispersion of the array can be calculated by finding a set of (ω, k) pairs for which M(ω, k) has a 0 singular value. This usually does not exactly happen for real (ω, k) in lossy systems like our Ni nanodisk arrays. However, the complex lossy bands are typically located near the real (ω, k) points for which some singular value of M(ω, k) reaches a small enough minimum.

Point-group symmetries of nanoparticle arrays provide a lot of a priori information about the modes and enable us to simplify the calculations.50,51 All of the modes have to belong to the irreducible representations of the respective symmetry group. As a result, the M(ω, k = 0) matrix can be written in block-diagonal form, where each block corresponds to one irreducible representation of the symmetry group. Singular values can then be searched for in each block separately. This is what we did to obtain the results of Figure 4f–j.

At the Γ point (where the band edges responsible for lasing typically appear), our system exhibits D2h symmetry (or even D4h for the square array). The transformation properties of the irreducible representations under symmetry operations, encoded in the character tables, also determine which multipole excitations are allowed in each of the irreducible representations. In this way, we can determine which irreducible representations contain x and y dipolar nanoparticle polarizations or quadrupolar polarizations.

The T-matrix can be obtained using various numerical methods. For reliability reasons and due to the fact that the aspect ratio of our nanodisks is close to 1, we used a spherical approximation and calculated the T-matrix analytically using the Lorenz–Mie solution, assuming a nanoparticle radius of 42 nm, a homogeneous background medium with refractive index n = 1.52, and nanoparticles made of Ni with interpolated optical properties from Johnson and Christy.52

Electric field distributions in the Ni nanodisk arrays were modeled using the Lumerical FDTD software.

Acknowledgments

This work was supported by the Academy of Finland under Project Nos. 303351, 307419, 318987, and 316857, by the European Research Council (ERC-2013-AdG-340748-CODE), and by the Aalto Centre for Quantum Engineering. Lithography was performed at the Micronova Nanofabrication Centre, supported by Aalto University.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.9b01006.

  • Transmission curves for all Ni nanodisk arrays; FDTD lasing simulations; dependence of emission spectra on the laser pump fluence; polarization analysis of the lasing peaks (PDF)

The authors declare no competing financial interest.

Supplementary Material

nn9b01006_si_001.pdf (1.4MB, pdf)

References

  1. Törmä P.; Barnes W. L. Strong Coupling Between Surface Plasmon Polaritons and Emitters: A Review. Rep. Prog. Phys. 2015, 78, 013901 10.1088/0034-4885/78/1/013901. [DOI] [PubMed] [Google Scholar]
  2. Moerland R. J.; Hakala T. K.; Martikainen J.-P.; Rekola H. T.; Törmä P. In Quantum Plasmonics; Bozhevolnyi S., Martin-Moreno L., Garcia-Vidal F., Eds.; Springer: Berlin, 2017; pp 121–150. [Google Scholar]
  3. Bergman D. J.; Stockman M. I. Surface Plasmon Amplification by Stimulated Emission of Radiation: Quantum Generation of Coherent Surface Plasmons in Nanosystems. Phys. Rev. Lett. 2003, 90, 027402 10.1103/PhysRevLett.90.027402. [DOI] [PubMed] [Google Scholar]
  4. Hill M. T.; Oei Y.-S.; Smalbrugge B.; Zhu Y.; de Vries T.; van Veldhoven P. J.; van Otten F. W. M.; Eijkemans T. J.; Turkiewicz J. P.; de Waardt H.; Geluk E. J.; Kwon S.-H.; Lee Y.-H.; Nötzel R.; Smit M. K. Lasing in Metallic-Coated Nanocavities. Nat. Photonics 2007, 1, 589–594. 10.1038/nphoton.2007.171. [DOI] [Google Scholar]
  5. Stockman M. I. Spasers Explained. Nat. Photonics 2008, 2, 327–329. 10.1038/nphoton.2008.85. [DOI] [Google Scholar]
  6. Zheludev N. I.; Prosvirnin S. L.; Papasimakis N.; Fedotov V. A. Lasing Spaser. Nat. Photonics 2008, 2, 351–354. 10.1038/nphoton.2008.82. [DOI] [Google Scholar]
  7. Noginov M. A.; Zhu G.; Belgrave A. M.; Bakker R.; Shalaev V. M.; Narimanov E. E.; Stout S.; Herz E.; Suteewong T.; Wiesner U. Demonstration of a Spaser-Based Nanolaser. Nature 2009, 460, 1110–1112. 10.1038/nature08318. [DOI] [PubMed] [Google Scholar]
  8. Oulton R. F.; Sorger V. J.; Zentgraf T.; Ma R.-M.; Gladden C.; Dai L.; Bartal G.; Zhang X. Plasmon Lasers at Deep Subwavelength Scale. Nature 2009, 461, 629–632. 10.1038/nature08364. [DOI] [PubMed] [Google Scholar]
  9. Wuestner S.; Pusch A.; Tsakmakidis K. L.; Hamm J. M.; Hess O. Overcoming Losses with Gain in a Negative Refractive Index Metamaterial. Phys. Rev. Lett. 2010, 105, 127401. 10.1103/PhysRevLett.105.127401. [DOI] [PubMed] [Google Scholar]
  10. Ma R.-M.; Oulton R. F.; Sorger V. J.; Bartal G.; Zhang X. Room-Temperature Sub-Diffraction-Limited Plasmon Laser by Total Internal Reflection. Nat. Mater. 2011, 10, 110–113. 10.1038/nmat2919. [DOI] [PubMed] [Google Scholar]
  11. Khajavikhan M.; Simic A.; Katz M.; Lee J. H.; Slutsky B.; Mizrahi A.; Lomakin V.; Fainman Y. Thresholdless Nanoscale Coaxial Lasers. Nature 2012, 482, 204–207. 10.1038/nature10840. [DOI] [PubMed] [Google Scholar]
  12. Lu Y.-J.; Kim J.; Chen H.-Y.; Wu C.; Dabidian N.; Sanders C. E.; Wang C.-Y.; Lu M.-Y.; Li B.-H.; Qiu X.; Chang W.-H.; Chen L.-J.; Shvets G.; Shih C.-K.; Gwo S. Plasmonic Nanolaser Using Epitaxially Grown Silver Film. Science 2012, 337, 450–453. 10.1126/science.1223504. [DOI] [PubMed] [Google Scholar]
  13. Zhou W.; Dridi M.; Suh J. Y.; Kim C. H.; Co D. T.; Wasielewski M. R.; Schatz G. C.; Odom T. W. Lasing Action in Strongly Coupled Plasmonic Nanocavity Arrays. Nat. Nanotechnol. 2013, 8, 506–511. 10.1038/nnano.2013.99. [DOI] [PubMed] [Google Scholar]
  14. van Beijnum F.; van Veldhoven P. J.; Geluk E. J.; de Dood M. J. A.; ‘t Hooft G. W.; van Exter M. P. Surface Plasmon Lasing Observed in Metal Hole Arrays. Phys. Rev. Lett. 2013, 110, 206802. 10.1103/PhysRevLett.110.206802. [DOI] [PubMed] [Google Scholar]
  15. Meng X.; Kildishev A. V.; Fujita K.; Tanaka K.; Shalaev V. M. Wavelength-Tunable Spasing in the Visible. Nano Lett. 2013, 13, 4106–4112. 10.1021/nl4015827. [DOI] [PubMed] [Google Scholar]
  16. Schokker A. H.; Koenderink A. F. Statistics of Randomized Plasmonic Lattice Lasers. ACS Photonics 2015, 2, 1289–1297. 10.1021/acsphotonics.5b00226. [DOI] [Google Scholar]
  17. Dridi M.; Schatz G. C. Lasing Action in Periodic Arrays of Nanoparticles. J. Opt. Soc. Am. B 2015, 32, 818–823. 10.1364/JOSAB.32.000818. [DOI] [Google Scholar]
  18. Yang A.; Hoang T. B.; Dridi M.; Deeb C.; Mikkelsen M. H.; Schatz G. C.; Odom T. W. Real-Time Tunable Lasing From Plasmonic Nanocavity Arrays. Nat. Commun. 2015, 6, 6939. 10.1038/ncomms7939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hakala T. K.; Rekola H. T.; Väkeväinen A. I.; Martikainen J.-P.; Necada M.; Moilanen A. J.; Törmä P. Lasing in Dark and Bright Modes of a Finite-Sized Plasmonic Lattice. Nat. Commun. 2017, 8, 13687. 10.1038/ncomms13687. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ramezani M.; Halpin A.; Fernández-Domínguez A. I.; Feist J.; Rodriguez S. R.-K.; Garcia-Vidal F. J.; Gomez Rivas J. Plasmon-Exciton-Polariton Lasing. Optica 2017, 4, 31–37. 10.1364/OPTICA.4.000031. [DOI] [Google Scholar]
  21. Wang D.; Yang A.; Wang W.; Hua Y.; Schaller R. D.; Schatz G. C.; Odom T. W. Band-Edge Engineering for Controlled Multi-Modal Nanolasing in Plasmonic Superlattices. Nat. Nanotechnol. 2017, 12, 889–894. 10.1038/nnano.2017.126. [DOI] [PubMed] [Google Scholar]
  22. Rekola H. T.; Hakala T. K.; Törmä P. One-Dimensional Plasmonic Nanoparticle Chain Lasers. ACS Photonics 2018, 5, 1822–1826. 10.1021/acsphotonics.8b00001. [DOI] [Google Scholar]
  23. Wang D.; Wang W.; Knudson M. P.; Schatz G. C.; Odom T. W. Structural Engineering in Plasmon Nanolasers. Chem. Rev. 2018, 118, 2865–2881. 10.1021/acs.chemrev.7b00424. [DOI] [PubMed] [Google Scholar]
  24. Daskalakis K. S.; Väkeväinen A. I.; Martikainen J.-P.; Hakala T. K.; Törmä P. Ultrafast Pulse Generation in an Organic Nanoparticle-Array Laser. Nano Lett. 2018, 18, 2658–2665. 10.1021/acs.nanolett.8b00531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Temnov V. V.; Armelles G.; Woggon U.; Guzatov D.; Cebollada A.; Garcia-Martin A.; Garcia-Martin J.-M.; Thomay T.; Leitenstorfer A.; Bratschitsch R. Active Magneto-Plasmonics in Hybrid Metal-Ferromagnet Structures. Nat. Photonics 2010, 4, 107–111. 10.1038/nphoton.2009.265. [DOI] [Google Scholar]
  26. Armelles G.; Cebollada G.; García-Martín A.; González M. U. Magnetoplasmonics: Combining Magnetic and Plasmonic Functionalities. Adv. Opt. Mater. 2013, 1, 10–35. 10.1002/adom.201200011. [DOI] [Google Scholar]
  27. Floess D.; Giessen H. Nonreciprocal Hybrid Magnetoplasmonics. Rep. Prog. Phys. 2018, 81, 116401. 10.1088/1361-6633/aad6a8. [DOI] [PubMed] [Google Scholar]
  28. Maccaferri N.; Gregorczyk K. E.; de Oliveira T. V. A. G.; Kataja M.; van Dijken S.; Pirzadeh Z.; Dmitriev A.; Åkerman J.; Knez M.; Vavassori P. Ultrasensitive and Label-Free Molecular-Level Detection Enabled by Light Phase Control in Magnetoplasmonic Nanoantennas. Nat. Commun. 2015, 6, 6150. 10.1038/ncomms7150. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pourjamal S.; Kataja M.; Maccaferri N.; Vavassori P.; van Dijken S. Hybrid Ni/SiO2/Au Dimer Arrays for High-Resolution Refractive Index Sensing. Nanophotonics 2018, 7, 905–912. 10.1515/nanoph-2018-0013. [DOI] [Google Scholar]
  30. Zubritskaya I.; Lodewijks K.; Maccaferri N.; Mekonnen A.; Dumas R. K.; Åkerman J.; Vavassori P.; Dmitriev A. Active Magnetoplasmonic Ruler. Nano Lett. 2015, 15, 3204–3211. 10.1021/acs.nanolett.5b00372. [DOI] [PubMed] [Google Scholar]
  31. Kataja M.; Freire-Fernández F.; Witteveen J.; Hakala T.; Törmä P.; van Dijken S. Plasmon-Induced Demagnetization and Magnetic Switching in Nickel Nanoparticle Arrays. Appl. Phys. Lett. 2018, 112, 072406 10.1063/1.5012857. [DOI] [Google Scholar]
  32. Zou S.; Schatz G. C. Silver Nanoparticle Array Structures That Produce Giant Enhancements in Electromagnetic Fields. Chem. Phys. Lett. 2005, 403, 62–67. 10.1016/j.cplett.2004.12.107. [DOI] [Google Scholar]
  33. Kravets V. G.; Schedin F.; Grigorenko A. N. Extremely Narrow Plasmon Resonances Based on Di_raction Coupling of Localized Plasmons in Arrays of Metallic Nanoparticles. Phys. Rev. Lett. 2008, 101, 087403 10.1103/PhysRevLett.101.087403. [DOI] [PubMed] [Google Scholar]
  34. Auguié B.; Barnes W. L. Collective Resonances in Gold Nanoparticle Arrays. Phys. Rev. Lett. 2008, 101, 143902. 10.1103/PhysRevLett.101.143902. [DOI] [PubMed] [Google Scholar]
  35. Humphrey A. D.; Barnes W. L. Plasmonic Surface Lattice Resonances on Arrays of Different Lattice Symmetry. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 075404 10.1103/PhysRevB.90.075404. [DOI] [Google Scholar]
  36. Wang W.; Ramezani M.; Väkeväinen A. I.; Törmä P.; Gómez Rivas J.; Odom T. W. The Rich Photonic World of Plasmonic Nanoparticle Arrays. Mater. Today 2018, 21, 303–314. 10.1016/j.mattod.2017.09.002. [DOI] [Google Scholar]
  37. Kravets V. G.; Kabashin A. V.; Barnes W. L.; Grigorenko A. N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. 10.1021/acs.chemrev.8b00243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Hakala T. K.; Moilanen A. J.; Väkeväinen A. I.; Guo R.; Martikainen J.-P.; Daskalakis K. S.; Rekola H. T.; Julku A.; Törmä P. Bose–Einstein Condensation in a Plasmonic Lattice. Nat. Phys. 2018, 14, 739–744. 10.1038/s41567-018-0109-9. [DOI] [Google Scholar]
  39. Kataja M.; Hakala T. K.; Julku A.; Huttunen M. J.; van Dijken S.; Törmä P. Surface Lattice Resonances and Magneto-Optical Response in Magnetic Nanoparticle Arrays. Nat. Commun. 2015, 6, 7072. 10.1038/ncomms8072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Maccaferri N.; Bergamini L.; Pancaldi M.; Schmidt M. K.; Kataja M.; van Dijken S.; Zabala N.; Aizpurua J.; Vavassori P. Anisotropic Nanoantenna-Based Magnetoplasmonic Crystals for Highly Enhanced and Tunable Magneto-Optical Activity. Nano Lett. 2016, 16, 2533–2542. 10.1021/acs.nanolett.6b00084. [DOI] [PubMed] [Google Scholar]
  41. Guo R.; Necada M.; Hakala T. K.; Väkeväinen A. I.; Törmä P. Lasing at K Points of a Honeycomb Plasmonic Lattice. Phys. Rev. Lett. 2019, 122, 013901 10.1103/PhysRevLett.122.013901. [DOI] [PubMed] [Google Scholar]
  42. Bahari B.; Ndao A.; Vallini F.; El Amili A.; Fainman Y.; Kanté B. Nonreciprocal Lasing in Topological Cavities of Arbitrary Geometries. Science 2017, 358, 636–640. 10.1126/science.aao4551. [DOI] [PubMed] [Google Scholar]
  43. Harari G.; Bandres M. A.; Lumer Y.; Rechtsman M. C.; Chong Y. D.; Khajavikhan M.; Christodoulides D. N.; Segev M. Topological Insulator Laser: Theory. Science 2018, 359, eaar4003. 10.1126/science.aar4003. [DOI] [PubMed] [Google Scholar]
  44. Bandres M. A.; Wittek S.; Harari G.; Parto M.; Ren J.; Segev M.; Christodoulides D. N.; Khajavikhan M. Topological Insulator Laser: Experiments. Science 2018, 359, eaar4005. 10.1126/science.aar4005. [DOI] [PubMed] [Google Scholar]
  45. Khanikaev A. B.; Shvets G. Two-Dimensional Topological Photonics. Nat. Photonics 2017, 11, 763–773. 10.1038/s41566-017-0048-5. [DOI] [Google Scholar]
  46. Haldane F. D. M.; Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 2008, 100, 013904 10.1103/PhysRevLett.100.013904. [DOI] [PubMed] [Google Scholar]
  47. Lu L.; Joannopoulos J. D.; Soljacic M. Topological States in Photonic Systems. Nat. Phys. 2016, 12, 626–629. 10.1038/nphys3796. [DOI] [Google Scholar]
  48. Klembt S.; Harder T. H.; Egorov O. A.; Winkler K.; Ge R.; Bandres M. A.; Emmerling M.; Worschech L.; Liew T. C. H.; Segev M.; Schneider C.; Höfling S. Exciton-Polariton Topological Insulator. Nature 2018, 562, 552–556. 10.1038/s41586-018-0601-5. [DOI] [PubMed] [Google Scholar]
  49. Kataja M.; Pourjamal S.; van Dijken S. Magnetic Circular Dichroism of Non-Local Surface Lattice Resonances in Magnetic Nanoparticle Arrays. Opt. Express 2016, 24, 3562–3571. 10.1364/OE.24.003562. [DOI] [PubMed] [Google Scholar]
  50. Dresselhaus M. S.; Dresselhaus G.; Jorio A.. Group Theory: Application to the Physics of Condensed Matter; Springer-Verlag: Berlin, 2008. [Google Scholar]
  51. Bradley C. J.; Cracknell A. P.. The Mathematical Theory of Symmetry in Solids; Representation Theory for Point Groups and Space Groups; Clarendon Press: Oxford, 1972. [Google Scholar]
  52. Johnson P. B.; Christy R. W. Optical Constants of Transition Metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056–5070. 10.1103/PhysRevB.9.5056. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn9b01006_si_001.pdf (1.4MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES