Fast admixture analysis and population tree estimation for SNP and NGS data

Abstract

Motivation

Structure methods are highly used population genetic methods for classifying individuals in a sample fractionally into discrete ancestry components.

Contribution

We introduce a new optimization algorithm for the classical STRUCTURE model in a maximum likelihood framework. Using analyses of real data we show that the new method finds solutions with higher likelihoods than the state-of-the-art method in the same computational time. The optimization algorithm is also applicable to models based on genotype likelihoods, that can account for the uncertainty in genotype-calling associated with Next Generation Sequencing (NGS) data. We also present a new method for estimating population trees from ancestry components using a Gaussian approximation. Using coalescence simulations of diverging populations, we explore the adequacy of the STRUCTURE-style models and the Gaussian assumption for identifying ancestry components correctly and for inferring the correct tree. In most cases, ancestry components are inferred correctly, although sample sizes and times since admixture can influence the results. We show that the popular Gaussian approximation tends to perform poorly under extreme divergence scenarios e.g. with very long branch lengths, but the topologies of the population trees are accurately inferred in all scenarios explored. The new methods are implemented together with appropriate visualization tools in the software package Ohana.

Availability and Implementation

Ohana is publicly available at https://github.com/jade-cheng/ohana. In addition to source code and installation instructions, we also provide example work-flows in the project wiki site.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

To quantify population structure, researchers often use methods based on the STRUCTURE model (Pritchard et al., 2000). The basic assumption in this model is that individuals belong to a set of K discrete groups, each with unique allele frequencies and obeying Hardy-Weinberg Equilibrium, although the latter assumption can be relaxed (Gao et al., 2007). Furthermore, individuals are allowed to have fractional memberships of each group. The groups are often termed ‘ancestry components’ and are sometimes interpreted to represent ancestral populations. This interpretation may be correct in some scenarios, for example when analyzing balanced samples of recently admixed individuals from otherwise highly divergent groups, such as major human continental groups. However, if basic model assumptions are violated, for example if populations truly are not discrete units, such as in species that have geographic structure that varies continuously, the interpretation is more unclear. Nonetheless, inference under STRUCTURE-style models has proven highly popular for quantifying population genetic variation and for exploring the basic structure and divisions of genetic diversity in a sample.

STRUCTURE (Pritchard et al., 2000), FRAPPE (Tang et al., 2005) and ADMIXTURE (Alexander et al., 2009) are arguably the three most commonly used programs that apply the classical STRUCTURE model. STRUCTURE uses a Bayesian approach and relies on a Markov Chain Monte Carlo (MCMC) algorithm to jointly sample the posterior distribution of allele frequencies and fractional group memberships. FRAPPE uses a maximum likelihood estimate (MLE) approach and optimizes the likelihood for both allele frequencies and fractional group memberships using an expectation-maximization (EM) algorithm. ADMIXTURE uses the same model and statistical framework as FRAPPE but uses a faster optimization algorithm. ADMIXTURE executes a two-stage process, first taking a few fast EM steps and then executing a sequential quadratic programming (QP) algorithm. ADMIXTURE uses a pivoting algorithm to solve each QP problem and applies a quasi-Newton acceleration to each iteration. This acceleration does not respect parameter bounds. ADMIXTURE projects an illegal update to the nearest feasible point, and the acceleration step contributes only when it results in a better likelihood; otherwise the original QP update is used.

The interpretation of parameter estimates under the STRUCTURE model is somewhat contentious (Royal et al., 2010; Weiss and Long, 2009). It is not clear exactly what the groups, or ancestry components, represent, but in the most simple interpretation we can think of them as estimates of some idealized ancestral populations. If a researcher has inferred the existence of K ancestral populations and knows the fractional memberships of each individual in these populations, a next question would be to explore their evolutionary history. The estimated allele frequencies can provide information about this.

The first approaches for using allele frequencies to estimate population histories dates back to the seminal work by Edwards and Cavalli-Sforza (Cavalli-Sforza et al., 1964, 1967). They used Gaussian models for the joint distribution of allele frequencies of multiple populations to estimate genetic distances and to infer population trees. The use of Gaussian models to approximate genetic drift has recently had a resurgence after the availability of large Single Nucleotide Polymorphism (SNP) datasets. It is used in numerous methods and studies, including tests of local adaptation e.g. (Coop et al., 2010; Gunther et al., 2013) and the popular TREEMIX program developed by (Pickrell and Pritchard, 2012). The basic idea in these methods is that one can define the joint allele frequencies among populations in terms of a Gaussian distribution with a covariance matrix dictated by a tree (or admixture graph). Under the Gaussian model, a tree corresponds to exactly one unique covariance matrix, and each covariance matrix corresponds to at most one tree. Furthermore, the likelihood function can be calculated very fast numerically without any need for pruning. The assumption of a Gaussian model for the allele frequencies corresponds to an assumption of a Brownian motion process to model genetic drift instead of, say, a Wright-Fisher diffusion. For small time intervals, the Brownian motion process can provide a close approximation to the Wright-Fisher diffusion. However, for longer time intervals, especially when the allele frequency is close to either of the boundaries (0 and 1), the Brownian motion model is clearly not a very accurate approximation to the Wright-Fisher diffusion. Nonetheless, the Gaussian models provide useful frameworks for inference because of the distinct computational advantages.

A natural extension of the STRUCTURE-style inference framework is to use similar models on the inferred ancestry groups to explore their evolutionary histories. A primary objective of this paper is to provide a computational tool for doing just this and to examine the performance of the Gaussian model in this context.

We present ‘Ohana’, a tool suite for inferring global ancestry, population covariances and constructing population trees using Gaussian models. The Ohana tool suite includes the following innovations:

• A new optimization method for STRUCTURE-style modeling for inferring admixture in an MLE framework. Our method is applicable both to called genotypes and to NGS data with uncertainty regarding the true genotypes. The method solves the sequential QP problem based on the Active Set (Murty and Feng-Tien, 1988) algorithm, and tends, as we will show in the Results section, to find higher maximum likelihood values than ADMIXTURE in similar computational time.

• A new method for estimating population relationships from ancestry components using a Gaussian approximation. We estimate the best covariance matrix compatible with a tree, thereby estimating a tree, and we provide simple algorithms and visualization tools to obtain the evolutionary trees.

We evaluate the performance of the methods on real and simulated data, and we also present results on the limitations of the popular Gaussian model. We show, perhaps unsurprisingly, that the assumption of a Gaussian model in some cases can lead to severely biased branch lengths of population trees that have evolved under a Wright-Fisher diffusion process. This is a limitation of the approach implemented in Ohana and in other approaches that use Brownian motion models to approximate the Wright-Fisher diffusion.

2 Materials and methods

2.1 Statistical models

The familiar likelihood model, using genotype observations, from STRUCTURE, FRAPPE, ADMIXTURE, SPA (Yang et al., 2012) and other similar methods, is given by:

$$\ln [P_1^O(Q,\hspace{0.17em}F)]=\sum _i^I\sum _j^J\left\{g_{ij}·\ln \left[\sum _k^K{q}_{ik}·f_{kj}\right]+(2-g_{ij})·\ln \left[\sum _k^K{q}_{ik}·(1-f_{kj})\right]\right\}.$$

where K is the number of ancestry components, I is the number of individuals, and J is the number of polymorphic sites. The model can be extended to be applicable to NGS data without called genotypes, but with genotype likelihoods, using the method by (Korneliussen et al., 2014):

$$\ln [P_1^L(Q,\hspace{0.17em}F)]=\sum _i^I\sum _j^J\ln (g_{ij}^{AA}·A_{ij}^2+g_{ij}^{aa}{B}_{ij}^2+g_{ij}^{Aa}·2A_{ij}{B}_{ij}).$$

$$A_{ij}=\sum _k^K{q}_{ik}·f_{kj}.$$

$$B_{ij}=\sum _k^K{q}_{ik}·(1-f_{kj})$$

where $g_{ij}^{AA},\hspace{0.17em}{g}_{ij}^{Aa}$ and $g_{ij}^{aa}$ are the probabilities of observing the sequence data at the ith individual’s jth marker, conditioned on genotypes AA, Aa (or aA) and aa, respectively. This representation assumes markers with two alleles, although it could easily be generalized to multiple alleles.

To infer population histories, we model the joint distribution of allele frequencies across all ancestry components as a multivariate Gaussian similar to TREEMIX (Pickrell and Pritchard, 2012) and Bayenv (Gunther et al., 2013). The covariance matrix Ω of dimension K × K is assumed to be constant among all sites. We use the sample allele frequency to approximate the ancestral allele frequency, μ_j at site j. For genotype observations, we simply count and calculate the percentage of the major allele for each site. For genotype likelihoods, we use an EM algorithm (Korneliussen et al., 2014) to estimate the pooled sample allele frequency for each site. The joint distribution of allele frequencies is then given by:

$$P(f_j|\Omega ,\hspace{0.17em}{\mu }_j)\sim \mathcal{N}({\mu }_j,\hspace{0.17em}{\mu }_j(1-{\mu }_j)\Omega ).$$

This system is under-determined (see e.g. Felsenstein, 1985), i.e. multiple covariance matrices induce the same probability distribution on the allele frequencies. To circumvent this issue, we root the tree in one of the observations. This corresponds to conditioning on the allele frequencies in one of the populations when calculating the joint distribution of allele frequencies in the other populations. This idea is similar to Felsenstein’s restricted maximum likelihood approach (Felsenstein, 1985). We emphasize that the rooting is arbitrary but that it does not imply any assumptions of this population actually being ancestral (for time reversible models). We then obtain a new covariance matrix ${\Omega }^{\prime }$, which has size $(K-1)\times (K-1)$ and a joint density of the form:

$$\begin{array}{c}\ln \left[P_2\left(F\right)\right]=\ln \left\{\prod _j^J\left[\frac{1}{\sqrt{\left|2\pi c_j{\Omega }^{\prime }\right|}}\text{exp}\hspace{0.17em}\left(-\frac{1}{2}·f_j^{\prime T}·{\left(c_j{\Omega }^{\prime }\right)}^{-1}·f_j^{\prime }\right)\right]\right\}\\ =-\frac{1}{2}·\sum _j^J\left\{\left(K-1\right)·\ln \left(2\pi c_j\right)+\ln \left[\det \left({\Omega }^{\prime }\right)\right]+\frac{1}{c_j}·f_j^{\prime T}·{\Omega }^{\prime -1}·f_j^{\prime }\right\}\end{array}$$

where $c_j={\mu }_j(1-{\mu }_j)$

$$f_j^{\prime }=f_j-f_{j_0}.$$

2.2 Parameter inference

2.2.1 Inference for individual ancestries

To estimate Q and F, we use Newton’s approach. In general, we can approximate a function $F(x)$ by its second order Taylor expansion. We proceed to minimize this second-order approximation by solving $\Delta x$. In our problem, $\Delta Q$ and $\Delta F$ are constrained by $\forall \Delta q_{ik},\hspace{0.17em}{q}_{ik}+\Delta q_{ik}\in [0,\hspace{0.17em}1],\hspace{0.17em}\forall \Delta f_{kj},\hspace{0.17em}{f}_{kj}+\Delta f_{kj}\in [0,\hspace{0.17em}1]$ and ${\sum }_k^K\Delta q_{ik}=0$ because ${\sum }_k^K{q}_{ik}=1$. The analytical forms of the differential for $\ln [P_1^O(Q,\hspace{0.17em}F)]$ are presented below:

$$\begin{array}{l}\frac{\partial \left(\ln P_1^O\right)}{\partial q_{ik}}=\sum _j^J\left[\frac{g_{ij}·f_{kj}}{\sum _m^K{q}_{im}·f_{mj}}+\frac{\left(2-g_{ij}\right)·\left(1-f_{kj}\right)}{\sum _m^K{q}_{im}·\left(1-f_{mj}\right)}\right]\\ \frac{{\partial }^2\left(\ln P_1^O\right)}{\partial q_{ik}\partial q_{i^{\prime }{k}^{\prime }}}=\{\begin{array}{cc}-\sum _j^J\left\{\frac{g_{ij}·f_{kj}·f_{k^{\prime }j}}{{\left(\sum _m^K{q}_{im}·f_{mj}\right)}^2}+\frac{\left(2-g_{ij}\right)·\left(1-f_{kj}\right)·\left(1-f_{k^{\prime }j}\right)}{{\left[\sum _m^K{q}_{im}·\left(1-f_{mj}\right)\right]}^2}\right\}\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i=i^{\prime }\hfill \\ 0\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i\ne i^{\prime }\hfill \end{array}\\ \frac{\partial \left(\ln P_1^O\right)}{\partial f_{kj}}=\sum _i^I\left[\frac{g_{ij}·q_{ik}}{\sum _m^K{q}_{im}·f_{mj}}-\frac{\left(2-g_{ij}\right)·q_{ik}}{\sum _m^K{q}_{im}·\left(1-f_{mj}\right)}\right]\\ \frac{{\partial }^2\left(\ln P_1^O\right)}{\partial f_{kj}\partial f_{k^{\prime }{j}^{\prime }}}=\{\begin{array}{cc}-\sum _i^I\left\{\frac{g_{ij}·q_{ik}·q_{i{k}^{\prime }}}{{\left(\sum _m^K{q}_{im}·f_{mj}\right)}^2}+\frac{\left(2-g_{ij}\right)·q_{ik}·q_{i{k}^{\prime }}}{{\left[\sum _m^K{q}_{im}·\left(1-f_{mj}\right)\right]}^2}\right\}\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}j=j^{\prime }\hfill \\ 0\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}j\ne j^{\prime }\hfill \end{array}.\end{array}$$

The analytical forms of the differential for $\ln [P_1^L(Q,F)]$ can be found below:

$$\begin{array}{l}\frac{\partial \left(\ln P_1^L\right)}{\partial q_{ik}}=\sum _j^J\left[\frac{G_Q\left(i,j,k\right)}{F\left(i,j\right)}\right]\\ \frac{{\partial }^2\left(\ln P_1^L\right)}{\partial q_{ik}\partial q_{i^{\prime }{k}^{\prime }}}=\{\begin{array}{cc}\sum _j^J\left[\frac{F\left(i,j\right)·H_Q\left(i,j,k,k^{\prime }\right)-G_Q\left(i,j,k\right)·G_Q\left(i,j,k^{\prime }\right)}{F^2\left(i,j\right)}\right]\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i=i^{\prime }\hfill \\ 0\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i\ne i^{\prime }\hfill \end{array}\\ F\left(i,j\right)=g_{ij}^{AA}·A_{ij}^2+g_{ij}^{aa}·B_{ij}^2+g_{ij}^{Aa}·2A_{ij}{B}_{ij}\\ G_Q\left(i,j,k\right)=\frac{\partial F\left(i,j\right)}{\partial q_{ik}}\\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}=2g_{ij}^{AA}·f_{kj}·A_{ij}+2g_{ij}^{aa}·\left(1-f_{kj}\right)·B_{ij}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\hspace{0.17em}2g_{ij}^{Aa}·\left[A_{ij}·\left(1-f_{kj}\right)+B_{ij}·f_{kj}\right]\\ H_Q\left(i,j,k,k^{\prime }\right)=\frac{\partial G\left(i,j,k\right)}{\partial q_{i{k}^{\prime }}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =2g_{ij}^{AA}·f_{kj}·f_{k^{\prime }j}+2g_{ij}^{aa}·\left(1-f_{kj}\right)·\left(1-f_{k^{\prime }j}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\hspace{0.17em}2g_{ij}^{Aa}\left[f_{k^{\prime }j}·\left(1-f_{kj}\right)+\left(1-f_{k^{\prime }j}\right)·f_{kj}\right].\end{array}$$

$$\begin{array}{l}\frac{\partial \left(\ln P_1^L\right)}{\partial f_{kj}}=\sum _i^I\left[\frac{G_F\left(i,j,k\right)}{F\left(i,j\right)}\right]\\ \frac{{\partial }^2\left(\ln P_1^L\right)}{\partial f_{kj}\partial f_{k^{\prime }{j}^{\prime }}}=\{\begin{array}{cc}\sum _i^I\left[\frac{F\left(i,j\right)·H_F\left(i,j,k,k^{\prime }\right)-G_F\left(i,j,k\right)·G_F\left(i,j,k^{\prime }\right)}{F^2\left(i,j\right)}\right]\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}j=j^{\prime }\hfill \\ 0\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}j\ne j^{\prime }\hfill \end{array}\\ F\left(i,j\right)=g_{ij}^{AA}·A_{ij}^2+g_{ij}^{aa}·B_{ij}^2+g_{ij}^{Aa}·2A_{ij}{B}_{ij}\\ G_F\left(i,j,k\right)=\frac{\partial F\left(i,j\right)}{\partial f_{kj}}\\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}=2g_{ij}{\mathrm{}}^{AA}·q_{ik}·A_{ij}-2g_{ij}^{aa}·q_{ik}·B_{ij}\\ \hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}+\hspace{0.17em}2g_{ij}^{Aa}·\left(B_{ij}·q_{ik}-A_{ij}·q_{ik}\right)\\ H_F\left(i,j,k,k^{\prime }\right)=\frac{\partial G\left(i,j,k\right)}{\partial f_{k^{\prime }j}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =2g_{ij}^{AA}·q_{ik}·q_{i{k}^{\prime }}+2g_{ij}^{aa}·q_{ik}·q_{i{k}^{\prime }}-4g_{ij}^{Aa}·q_{ik}·q_{i{k}^{\prime }}.\end{array}$$

To solve these inequality- and equality-constrained quadratic optimization problems, we use an adaptation of the Active Set Algorithm (Murty and Feng-Tien, 1988). To solve the equality problem defined by the active set and to compute the Lagrange multipliers of the active set, we use the Karush-Kuhn-Tucker (KKT) approach (Karush, 1939; Kuhn and Tucker, 1951). In each iteration, the algorithm searches for a better solution by considering the active constraints as equality constraints. It deviates from the bounds when the Lagrange multipliers signal a better solution toward the feasible region. These procedures are implemented in the qpas program of Ohana. In Section S6 of the Supplementary Information (SI), we provide algorithm details, its application within STRUCTURE-style models, concrete examples, and comparisons with other solving strategies for the STRUCTURE-style modeling. Readers unfamiliar with KKT, QP, or active set optimization, and/or interested in the algorithmic details should refer to this section.

We convert the problem of manipulating huge matrices into sequences of small matrix operations of size K by K as in (Alexander et al., 2009). We do so by taking advantage of the fact that most off-diagonal values in the Hessian diminish. Only sub-matrices of size K by K are populated, and these off-diagonal zeros do not contribute to the solutions at the KKT step when solving linear systems. Further explanation and a concrete example of this matrix conversion can be found in Section S7 of the SI.

2.2.2 Inference for population covariances

To optimize the likelihood model defined in the last equation of Section 2.1, we use a black-box style of optimizer, the Nelder-Mead (NM) simplex method (Nelder and Mead, 1965). We use sample covariances, $S_c=\frac{1}{n}·{\sum }_i^n\left(x_i-{\overline{x}}_i\right){\left(x_i-{\overline{x}}_i\right)}^T$, as the initial starting point for the NM optimizer, and we use Cholesky decomposition (Cholesky, 2005) to determine the positive semi-definiteness and to compute matrix inverses and determinants. The nemeco program in Ohana performs this analysis. More detail on this algorithm can be found in Section S8 of the SI.

2.3 Estimation of phylogenetic trees

The algorithm described above estimates a covariance matrix compatible with exactly one tree. This covariance matrix can then be used to construct a (phylogenetic) tree using the Neighbor-Joining (NJ) method. We note that the NJ theorem (Saitou and Nei, 1987) states that when a distance matrix is accurately estimated for data evolved under a tree with positive branch lengths, the matrix will be compatible with exactly one phylogentic tree, and this tree will be accurately reconstructed by the NJ method. The covariance matrix has a one-to-one mapping to a distance matrix given by $\hspace{0.17em}\text{Dist}\hspace{0.17em}(p_1,p_2)=\text{Var}\hspace{0.17em}(p_1)+\text{Var}\hspace{0.17em}(p_2)-2\times \text{Cov}\hspace{0.17em}(p_1,p_2)$. If the covariance matrix is accurately estimated, the resulting tree will therefore also be estimated accurately. Our software implementation also allows for rendering of the estimated tree using the convert program.

2.4 Implementation

The qpas program in Ohana implements sequential QP based on the Active Set algorithm to solve the classical STRUCTURE model and the model used in NGSADMIX. It infers admixture from called genotype data, i.e. genotype observations, stored in the ped format from Plink (Purcell et al., 2007) and genotype likelihoods in the bgl format from beagle (Browning and Browning, 2007). Ohana’s nemeco program implements the NM optimization on the Gaussian modeling, and it infers population covariances. The convert program in Ohana facilitates different stages of the analysis by providing file conversions, fast approximations and visualizations. The source code, installation instructions and example workflows are available on GitHub at https://github.com/jade-cheng/ohana.

2.5 Simulated data

We used the software fastsimcoal2 (Excoffier et al., 2013) to produce genetic data using the Sequential Markov Coalescence (SMC) model (Marjoram and Tavaré, 2006; McVean and Cardin, 2005). We simulated populations of nucleotide sequences according to a given demographic scenario. For each ancestry component, we simulated 100 sequences of size 20 000 000 bp under an identical population size of 50 000 for all components. We simulated demographic topologies with certain branch lengths by controlling population splits and effective population sizes.

We simulated admixture proportions for un-admixed and admixed scenarios. For un-admixed cases, we simply assigned a fraction of the sample to each population. For admixed cases, we simulated Q_i independently from Dirichlet distributions $\hspace{0.17em}\text{Dir}\hspace{0.17em}(\alpha ,\hspace{0.17em}\alpha ,\hspace{0.17em}\alpha )$, similarly to the simulations used in (Pritchard et al., 2000) and (Alexander et al., 2009).

Finally, we simulated genotype observations by first calculating the major allele frequency f_ij for each individual at each marker location and then sampling genotypes under the assumption of Hardy-Weinberg Equilibrium, i.e. $p_{ij}^{AA}=f_{ij}^2,\hspace{0.17em}{p}_{ij}^{Aa}=2·f_{ij}·(1-f_{ij})$, $p_{ij}^{aa}={(1-f_{ij})}^2$, where $f_{ij}={\sum }_k^K{q}_{ik}·f_{kj}$, and p^AA, p^Aa and p^aa are the probabilities of observing major-major, major-minor, or minor–minor genotypes for the locus (Fig. 1).

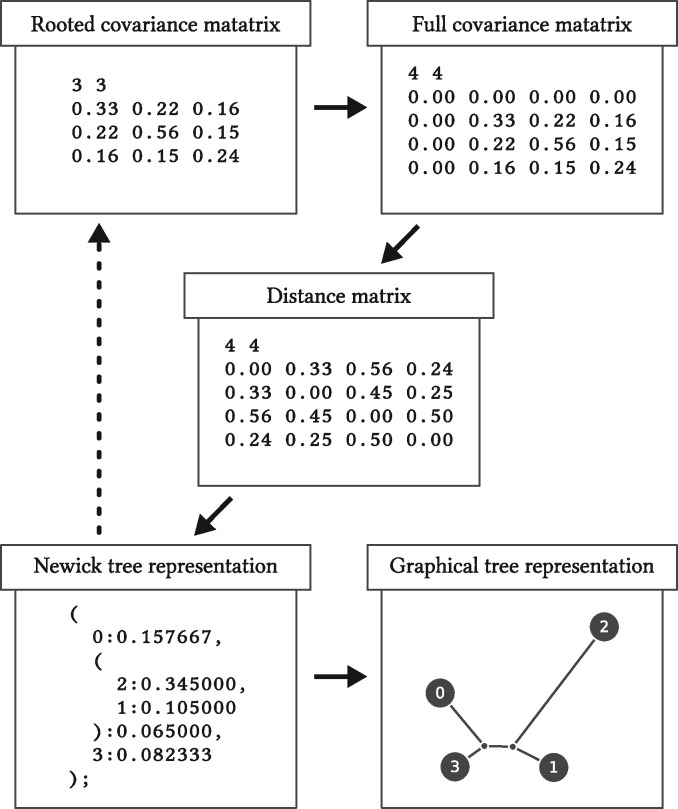
Fig. 1.

Phylogenetic tree construction pipeline. We estimate a rooted covariance matrix, where the root is arbitrarily chosen. We then recover the full covariance matrix, compute the distance matrix, and approximate the distance matrix as a tree structure using the NJ algorithm. Optionally, by supplying the estimated tree into the covariance inference process, we refine the estimated covariances to be most tree-compatible. Finally, we render the Newick tree in SVG format. For better control of the graphics, we recommend using our web service: http://www.jade-cheng.com/graphs/

2.6 Real data

We used four datasets for the comparison with ADMIXTURE shown in Figure 2 and Table 1:

• Dataset #1, a compilation of Europeans containing 17 507 markers and 118 individuals; this data was obtained from the POPRES (Nelson et al., 2008), ALS (Laaksovirta et al., 2010), Swedish Schizophrenia (Ripke et al., 2013) and NCNG (Espeseth et al., 2012) projects. It is a subset of data compiled for a study of Danish genetics (Athanasiadis et al., 2016)

• Dataset #2, a compilation of HapMap (2005) CEU, YRI, MEX and ASW individuals containing 13 928 markers and 324 individuals. This is the benchmark dataset used in the original ADMIXTURE paper (Alexander et al., 2009)

• Dataset #3, a compilation of Han Chinese samples from the HapMap project (2005) containing 9822 markers and 171 individuals.

• Dataset #4, a compilation of HapMap (2005) world population of 4695 markers 60 individuals of 10 North European, 10 Japanese, 10 Guaharati, 10 Luhya, 10 Maasai Kinyawa and 10 Tuscan.

Fig. 2.

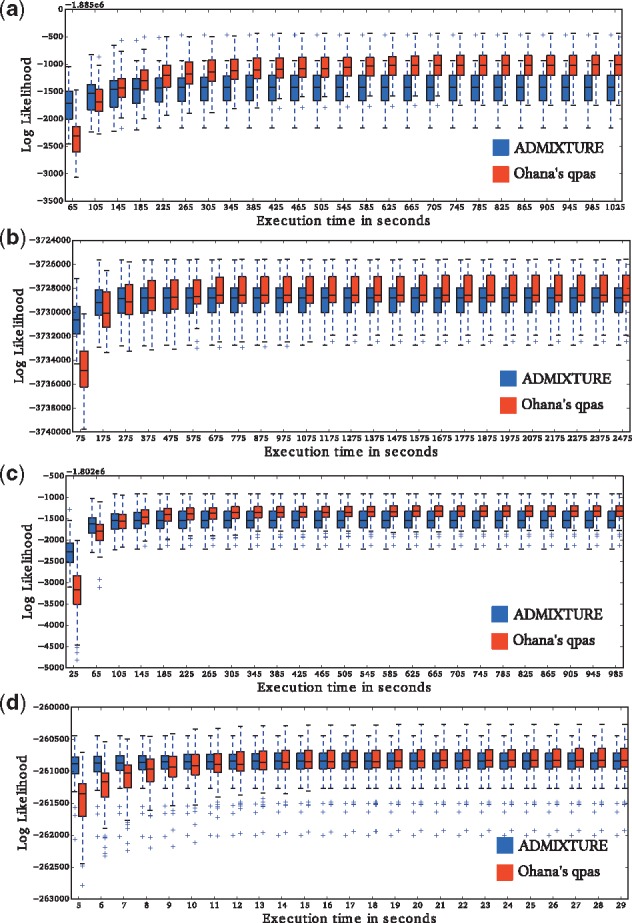
Comparison of computational speed and efficacy with ADMIXTURE. The plots show the change in the distribution of log likelihood values, produced from the two programs over time. Our method produces lower likelihood values initially, but it generally outperforms ADMIXTURE after relatively few iterations. For each dataset, each program was executed 100 times using random seeds ($0,1,\dots ,99$) and K = 9. (a, b, c, d) are four different datasets, same as in Table 1

Table 1.

A table of the highest log likelihoods achieved from ADMIXTURE and our method for a range K values

	Dataset #1			Dataset #2			Dataset #3			Dataset #4
K	Ohana	ADMIXTURE	Diff	Ohana	ADMIXTURE	Diff	Ohana	ADMIXTURE	Diff	Ohana	ADMIXTURE	Diff
2	−1967733	−1967733	0	−3835358	−3835365	7	−1857263	−1857263	0	−288991	−288991	0
3	−1956785	−1956799	14	−3799873	−3799887	14	−1848450	−1848451	1	−279462	−279463	1
4	−1946218	−1946244	26	−3788598	−3788607	10	−1841198	−1841199	1	−275212	−275213	1
5	−1935775	−1936025	250	−3777351	−3777361	11	−1834377	−1834378	1	−271807	−271808	1
6	−1925636	−1925877	241	−3766558	−3766540	−18	−1827829	−1827830	2	−268837	−268832	−5
7	−1915552	−1915743	191	−3755851	−3755860	9	−1821445	−1821458	13	−265907	−265923	17
8	−1905430	−1905638	209	−3746227	−3745412	−815	−1815214	−1815214	0	−263052	−263096	44
9	−1895372	−1895879	507	−3735240	−3736079	839	−1809084	−1809101	18	−260268	−260440	172
10	−1885306	−1885466	160	−3725558	−3725624	66	−1802911	−1802906	−5	−257539	−257736	197
11	−1875503	−1875853	350	−3715543	−3715157	−385	−1796763	−1796847	84	−254920	−254961	41
12	−1865492	−1865965	474	−3706069	−3707715	1646	−1790671	−1790811	140	−252196	−252266	70
13	−1855502	−1856262	760	−3697531	−3698519	987	−1784688	−1784765	77	−249456	−249468	12
14	−1845732	−1846490	758	−3688970	−3689124	154	−1778599	−1778671	73	−246760	−246817	56
15	−1836315	−1836775	460	−3681092	−3680829	−263	−1772555	−1772669	114	−244058	−244298	240

Note: For each dataset, each program, and each value of of K, we executed 100 times using random seeds $0,1,\dots ,99$ and chose the highest value found in any run. This mimics the procedure often used for real data analysis. In the vast majority of cases, our method found significantly higher likelihood values than ADMIXTURE. Dataset #1 is a compilation of Europeans containing 17 507 markers and 118 individuals. Dataset #2 is the benchmark dataset used in ADMIXTURE (Alexander et al., 2009) containing 324 CEU, YRI, MEX, and ASW individuals and 13 928 markers. Dataset #3 is a compilation of 171 Han Chinese samples and 9822 markers. Dataset #4 is a worldwide population of 60 individuals and 4695 markers.

For the admixture and covariance data analysis shown in Figure 5, we used a combination of world-wide samples containing 127 855 markers and 80 individuals from the HGDP project. We pruned for minor allele frequencies and Linkage Disequilibrium (LD) with Plink (Purcell et al., 2007) using the options –indep 50 5 2 –geno 0.0 –maf 0.05.

Fig. 5.

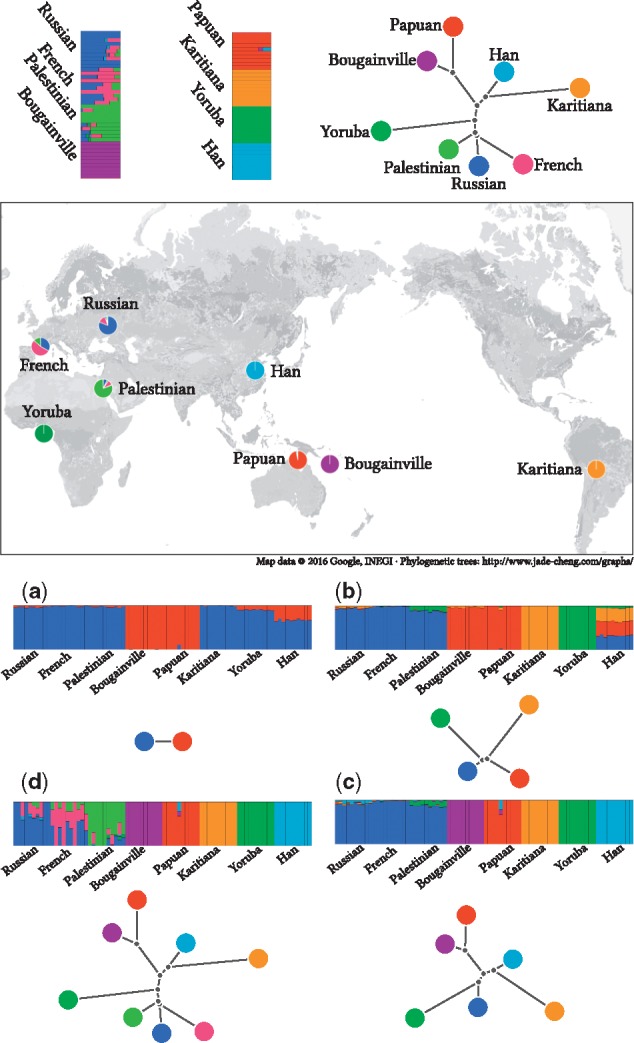
Analysis of human global data. We used a dataset compiled from the HGDP project containing 80 individuals from 8 populations, 10 per population. We filtered markers using Plink (Purcell et al., 2007) with options –indep 50 5 2 –geno 0.0 –maf 0.05. A total of 125 787 markers survived the filtration and were used for the analysis. For each K value, we dispatched 32 executions with random seeds from 0 to 31. We report only results from the execution that reached the best likelihood for each K. The plots show individual admixture proportions and population trees for several different values of K. The map combines the admixture results and geographical records of the HGDP samples. Each slice of each pie chart shows the sum of one component estimated in samples collected at that region. (a, b, c and d) show the admixture and tree estimates for $K=2,4,6,8$, respectively

3 Results

3.1 Computational speed

ADMIXTURE has previously been shown to have the most efficient optimization algorithm among the previously published methods for the classical STRUCTURE model (Alexander et al., 2009). We therefore compare our optimization algorithm to the algorithms implemented in ADMIXTURE. For a fair comparison, we show the distribution of likelihood values for the two methods, obtained after a fixed amount of computational time, for multiple different runs of Ohana and ADMIXTURE (Fig. 2 and Table 1). We verify that the likelihood values are comparable between the two programs by calculating likelihood values for the same parameter values for both programs. We use four different real datasets described in the Materials and methods section and explore a range of different values of K. For a very short amount of computational time, ADMIXTURE tends to find higher likelihood values. ADMIXTURE may possibly use better initial values for the optimization. However, after a relative short amount of time, our method tends to find higher likelihood values than ADMIXTURE for the same computational time.

3.2 Estimation of admixture and tree on simulated data

We simulated data on a tree using coalescence simulations as described in the Materials and methods section and estimated for different values of K (Fig. 3). This mimics the procedure often used in real data analyses in which multiple values of K are explored and presented without knowing the true value of K, although this value can be estimated using a variety of methods (Alexander and Lange, 2011; Scheet and Stephens, 2006; Wold, 1978).

Fig. 3.

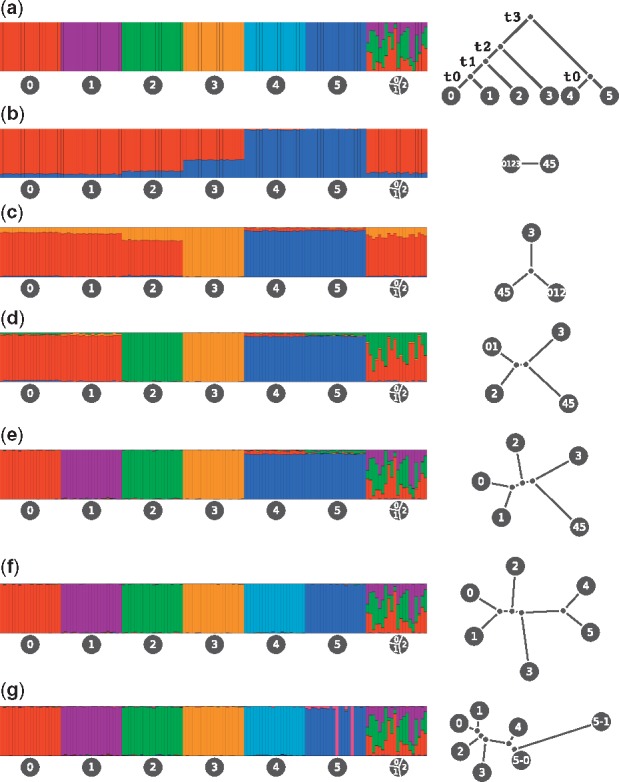
An evaluation of the tree inference procedure using coalescence simulations. We simulated 140 individuals in 7 groups, 20 individuals per group. The first 6 groups were un-admixed. The last group was an equal mixture of the first 3 groups. (a) Simulated admixture (left) and simulated demography (right). (b, c, d, e, f, g) Estimated admixture (left) and estimated demography (right) for $K=2,3,4,5,6,7$, respectively. For each of the 6 populations, we simulated 100 sequences of size 20 000 000 bp using fastsimcoal2 (Excoffier et al., 2013). We used a mutation rate of $2\times {10}^{-8}$ per generation, a recombination rate of ${10}^{-8}$ per generation, and a population size of 50 000. The time parameters were 1000, 2000, 3000, and 4000 generations for t₀, t₁, t₂ and t₃, respectively. A total of 125 787 markers survived filtration for being polymorphic, di-allelic, and with minor allele frequency greater than 5%. We then estimated admixture fractions and population trees using values of K ranging from 2 to 7

The plots show good correspondence between the true and the estimated values, for both admixture proportions and demography. Furthermore, the changes in tree topology as K changes reflect the hierarchical structure of the tree. For example, at K = 4 the internal branch reflects the split between populations (0, 1, 2) and (3, 4, 5).

3.3 Model limitations

There are at least three reasons why tree estimation using a Gaussian model based on estimated allele frequencies may face challenges. First, the allele frequencies are treated as observed data, but they are truly estimates. This has the potential for introducing a variety of biases. Second, the use of a Brownian motion model to approximate genetic drift is inaccurate near the boundaries and for long divergence times, likely leading to underestimates of the lengths of long branches. Third, due to differences in sample sizes for different populations, the STRUCTURE model may not identify groups that correspond to natural units of a tree, even when the populations truly have evolved in a tree-like fashion.

We explore some of these issues in the following simulation study (Fig. 4) by simulating trees with different divergence times: short, medium and long. For very short divergence times (Fig. 4a), the covariance matrix was estimated poorly because of the small differences in allele frequencies across populations. This in turn leads to reduced accuracy in the estimation of the tree. While the topology is recovered correctly, the lengths of the external branches are overestimated. This likely happens because the STRUCTURE-style modeling tends to maximize allele frequency differences for finite sample sizes, i.e. the estimated difference in allele frequencies between pairs of populations tends to be larger than the true difference. This is an issue that can be mitigated with larger sample sizes and tends to be a problem only when branch lengths are very small. Nonetheless, it will likely affect many real data analyses.

Fig. 4.

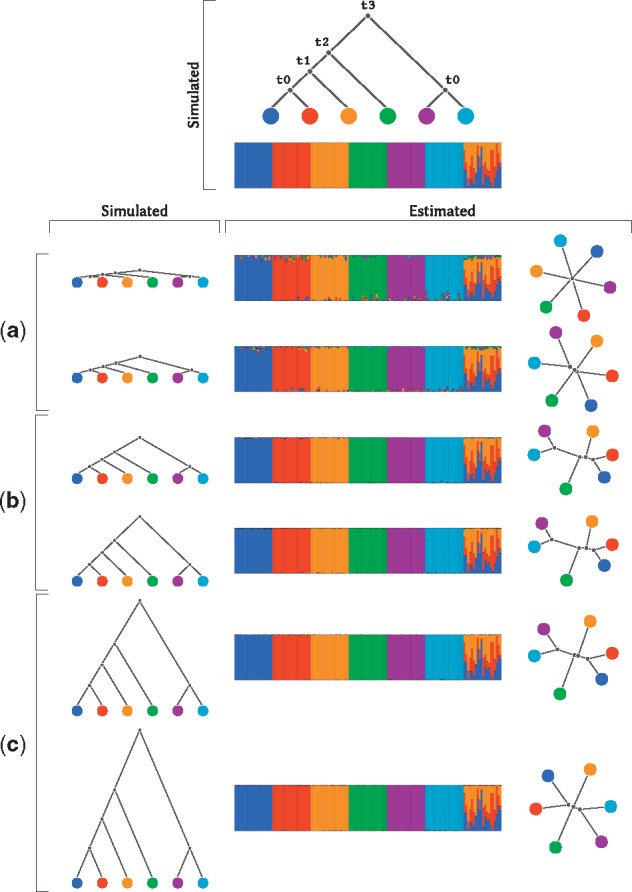
A simulation study for different divergence times. We simulated 140 individuals in 7 groups, 20 individuals per group. The first 6 groups were un-admixed. The last group was an equal mixture of the first 3 groups. We illustrate the simulated demography on the top. We simulated 6 divergence scenarios, 2 short shown in (a), 2 medium shown in (b) and 2 long shown in (c). From the shortest to the longest divergence scenario (top to bottom), the split times (t₀, t₁, t₂, t₃) in generation were: (10, 20, 30, 40), (100, 200, 300, 400), (1000, 2000, 3000, 4000), (1500, 3000, 4500, 6000), (10000, 20000, 30000, 40000), (20000, 40000, 60000, 80000)

In the long divergence scenario (Fig. 4c) another problem arises. For such long branches, the Brownian motion model is a poor approximation to genetic drift, and the mapping between the two transition probability functions (i.e. Wright-Fisher diffusion versus Brownian motion) is such that divergence times tend to be underestimated when they are long. The consequence is that the branch lengths of the tree are underestimated. We verify that this is the source of the bias by also simulating data under a Gaussian model directly and showing that under this model there is no significant bias for long branch lengths. This is described in SI Section S1. We note that the poor approximation of the Brownian motion model to the Wright-Fisher diffusion for long divergence times is a limitation for any inference system using similar statistical models such as TREEMIX (Pickrell and Pritchard, 2012) and Bayenv (Gunther and Coop, 2013), and it might be worthwhile in future work to explore the consequence of this effect for those methods as well.

In the medium-length divergence scenario (Fig. 4b), neither of the two previously mention sources of bias affect the inference, and the estimates of the branch lengths are therefore quite close to the true values. In all three divergence scenarios, the tree topologies were always estimated accurately.

3.4 Other simulation scenarios

We also evaluated the performance of the method under several other simulation scenarios, and the results are presented in SI Section S2–S5. A few noteworthy observations include:

• In more than one simulation scenario with ancient admixture, the population was not inferred to be admixed but received a unique admixture component, e.g. Supplementary Section S2 Figure S4 and Section S3 Figure S5. The probability of inferring admixture likely depends on the amount of drift since admixture. In the context of much human data showing evidence of ancient admixture, it might be worthwhile in future studies to explore how much drift after admixture is required to erase the signal of admixture.

• When K is smaller than the true number of ancestry components, populations with few individuals represented in the sample tend to be (wrongly) inferred as admixed, e.g. Supplementary Section S5 Figure S7. There is a clear dependence on sample size in inference of admixture components in STRUCTURE-style models. Similarly, the outgroup tends to be identified as the first admixture component that splits from the rest of the individuals, only when the outgroup is well-represented in the sample in terms of the number of individuals.

3.5 Real data analysis

We apply our method to analyze a panel of global human data using a range of K values. Figure 5 summarizes the results. The topologies of the trees largely mimic what is already known about human ancestry (e.g. Reich et al., 2012), i.e. using a root in Africa, Asians and Native Americans cluster together, the European and middle Eastern groups cluster together, etc. In addition to Yorubans having a long branch because this group is an outgroup to the rest, we also notice a relatively long branch leading to Native Americans, reflecting the increased drift in this group due to the bottleneck into the Americas and possibly small population sizes thereafter.

4 Discussion

In this paper, we introduce a new optimization method for the classical STRUCTURE model in an MLE framework. We compared the new optimization algorithm to the one implemented in the hitherto fastest program, ADMIXTURE. Our method generally outperformed ADMIXTURE by obtaining estimates with higher likelihood values in similar computational time. The difference between our method applied to called genotypes and ADMIXTURE is the algorithm used to solve sequential QP. Our method uses an adaptation of the Active Set algorithm while ADMIXTURE uses a pivoting method plus a quasi-newton acceleration. We implemented a pivoting-based QP solver, which is also published in Ohana under the name cpax. We also tested the quasi-newton accelerator as well as three other similar accelerators in the family of squared iterative methods, SQUAREM, (Varadhan and Roland, 2008). In our benchmark tests, these techniques did not perform as well. Section S6 in the SI provides more details on this topic.

We extend our new optimization algorithm to a similar model (Skotte et al., 2013) that allows us to infer population structure from genotype likelihoods. The advantage of working on genotype likelihoods instead of called genotypes is that genotype likelihoods incorporate the uncertainty regarding genotype calls inherent in much NGS data, and this makes it more applicable to low- or medium-coverage data (see e.g. Skotte et al., 2013).

In addition, we presented a new approach for estimating trees from ancestry components. Using coalescence simulations, we showed that when the trees are interpreted as reflecting true population trees, external branch lengths tend to be overestimated for small divergence times. However, for long divergence times, the use of a Gaussian model and its inaccuracy in approximating genetic drift cause branch length estimates to be downward biased. Nonetheless, the estimates of tree topology appear reasonably robust. The tree estimation and visualization tool should be of use to other researchers as an additional possible component of STRUCTURE-style analyses. The tree is a visualization of the covariance structure of the admixture components, and it may as such be useful even if a strict interpretation of a evolutionary tree may not be warranted. There might be several reasons why such an interpretation may not be appropriate, most of all because the true nature of the evolution of the ancestry components may not be well-described by a tree. Ancestry components are constructions that may or may not reflect true ancestral populations.

Funding

This work was funded by the Danish Council of Independent Research Sapere Aude grant 12-125062.

Conflict of Interest: none declared.