An evolutionary framework for measuring epigenomic information and estimating cell-type specific fitness consequences

Abstract

Here, we ask the question, “How much information do epigenomic data sets provide about human genomic function?” We consider nine epigenomic features across 115 cell types and measure information about function as a reduction in entropy under a probabilistic evolutionary model fitted to human and nonhuman primate genomes. Several epigenomic features yield more information in combination than they do individually. We find that the entropy in human genetic variation predominantly reflects a balance between mutation and neutral drift. Our cell-type specific FitCons scores reveal relationships among cell types and suggest that ~8% of nucleotide sites are constrained by natural selection.

Editorial Summary:

FitCons2 is a new framework that simultaneously clusters genomic sites by epigenomic features and evaluates the strength of natural selection on these sites. FitCons2 scores are used to generate fitness-consequence maps for 115 human cell types.

Recent technological advances have enabled the generation of massive quantities of genomic data describing natural genetic variation as well as diverse epigenomic features such as chromatin accessibility, histone modifications, transcription factor binding, DNA methylation, and RNA expression^1-4. However, the capability to gain insight into key cellular functions from this noisy, high-dimensional data has considerably lagged behind the capacity for data generation. Indeed, while the available data allows the vast majority of the human¹ and mouse² genomes to be associated with some type of “biochemical function,” often in a cell-type specific fashion, it is unclear—and highly controversial^5,6—to what degree this biochemical function reflects critical roles in cellular processes that have bearing on evolutionary fitness, as opposed to representing, say, noisy or incidental chromatin accessibility, protein/DNA binding, or transcription. This uncertainty about the true biological significance of many high-throughput epigenomic measurements is a critical barrier not only for interpretation of the available data, but also for prospective decisions about how much new data to collect, of what type, and in what combinations.

In this article, we attempt to address the question of how much information about genomic function is provided by general epigenomic “features,” including both genome annotations and high-throughput epigenomic data sets. The premise of our approach is that signatures of natural selection in DNA sequences can serve as a proxy for genomic function by reflecting fitness constraints imposed by cellular functions. We develop a novel information-theoretic framework for simultaneously clustering genomic sites by combinations of epigenomic features and evaluating the strength of natural selection on these sites. In addition to allowing us to measure relative amounts of global information provided by these epigenomic features, individually and in combination, this approach produces a collection of 115 cell-type specific genome-wide maps of probabilities that mutations at individual nucleotides have fitness consequences (FitCons maps), which we demonstrate are illuminating in various ways. Together, our analyses not only provide a guide for data interpretation and experimental design, but they also shed light on the fundamental manner in which biological information is stored in the genome.

Our approach to quantifying the information in epigenomic data builds on a growing collection of computational methods that attempt to extract biological meaning from large, heterogeneous collections of high-throughput genomic data. These include methods that cluster genomic sites based on epigenomic patterns^7,8, machine-learning predictors of pathogenic variants^9,10 or molecular phenotypes^11,12, and methods that combine epigenomic data with patterns of polymorphism or cross-species divergence to identify regions under evolutionary constraint^13,14. Our contribution to this literature has been to develop a probabilistic framework, called INSIGHT ^15,16, for measuring the bulk influence of natural selection from patterns of polymorphism and divergence at collections of target sites, and methods, called FitCons²³ and LINSIGHT ²⁴, that combine this framework with epigenomic data to estimate the probability that a mutation at any position in the genome will have fitness consequences. As we have previously discussed^17,18, the usefulness of these methods in predicting regulatory sequences or disease-associated variants depends on the imperfect assumption that local signatures of natural selection are informative about phenotypes of interest. Nevertheless, these evolution-based methods perform well at these tasks, in part owing to the crucial advantage of measuring the importance of genetic variants in real organisms in their natural environments. Our strategy here is to extend the INSIGHT framework to a new method, called FitCons2, that measures epigenomic “information” in terms of selective constraint, and allows us to address questions such as, “How much did epigenomic data set X reveal about genomic function?” or “Are data sets Y and Z more informative in combination than they are individually?”

RESULTS

FitCons2 clusters sites to maximize information

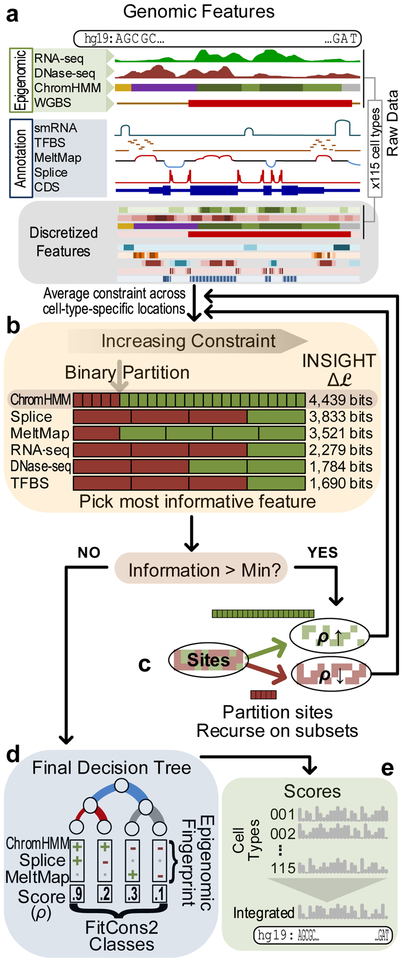
The original FitCons algorithm¹⁷ used a preprocessing step to partition the genome into hundreds of clusters on the basis of epigenomic and annotation data alone, without consideration of their evolutionary properties. By contrast, FitCons2 simultaneously addresses the clustering and evolutionary model-fitting steps, finding clusters of sites that are distinct both in their epigenomic and evolutionary properties.

More specifically, the FitCons2 algorithm works by recursively partitioning sets of genomic sites into two subsets, according to their associated epigenomic and annotation features (Figure 1). For example, at a particular step the algorithm might subdivide a given set of genomic sites into sites showing high and low transcriptional activity, based on counts of aligned RNA-seq reads, or those showing high and low chromatin accessibility, based on DNase-seq data. At each step in the algorithm, all candidate partitions of all current sets are considered, based on a collection of pre-discretized data types (Figure 1a&b). The algorithm selects the decision rule for partitioning that most improves the goodness of fit of the INSIGHT evolutionary model to the set of genomic sites under consideration when the model is fitted separately to the two proposed subsets rather than once to the entire set (see Methods). The procedure terminates when no partition improves the fit of the model by more than a predefined constant threshold (Figure 1c). In this way, the recursive algorithm produces a K-leaf binary decision tree that applies to each genomic site, causing the site to be assigned one of K labels based on its combination of local features (Figure 1d). When applied to all sites, the algorithm defines K clusters of genomic sites that reflect the natural correlation structure of both the epigenomic and the population genomic data. The identified clusters tend to be distinct from one other in terms of their influence from natural selection on the relatively recent time scales measured by INSIGHT, based on both human polymorphism and divergence with nonhuman primates. The overall influence of natural selection on each cluster is summarized by the associated estimate of the INSIGHT parameter ρ, which can be interpreted as the probability that a point mutation will have fitness consequences. As in the original FitCons algorithm, these ρ estimates are mapped back to the corresponding genomic sites and treated as nucleotide-specific fitness-consequence (FitCons) scores (Figure 1e).

Figure 1. Conceptual diagram of FitCons2 algorithm.

(a) Two types of genomic features are considered: four cell-type specific Epigenomic features (×115 cell types) and five Annotations (Table 1). In pre-processing, the raw data sets are discretized into 2–25 classes, which are ordered by estimates of ρ (Methods, Table 1). (b) The algorithm builds a decision tree by recursively partitioning “active sets” of genomic positions. Each binary partition is defined by applying a threshold to an ordered, discretized feature (gray arrow). The algorithm selects the active set (leaf) and binary partition that are maximally informative about selection. Information is measured by the increase in log likelihood ($\Delta \mathcal{L}$) under the INSIGHT model (Methods). The algorithm averages over cell-type specific locations for the Epigenomic features. (c) The recursive process is repeated until the improvement in information fails to exceed a minimal threshold. (d) The end result is a K-leaf decision tree such that each internal node represents a binary decision rule and each leaf corresponds to a combination of decision rules that can be applied to each nucleotide site in the genome. Each of these K combinations of decision rules induces a cluster of genomic sites that share a particular epigenomic “fingerprint”. Each of these K clusters is also associated with an estimate of ρ (its FitCons2 score). (e) These estimates of ρ can be mapped back to the genome sequence separately for each cell type. An “integrated” score that summarizes all cell types is also computed (Methods).

When evaluating candidate decision rules, the FitCons2 algorithm measures the goodness of fit of the INSIGHT model in terms of its log likelihood. The negated log likelihood, however, can be viewed as an estimate of the entropy of the probability distribution induced by the model, which in this case can in turn be viewed as a measure of the genetic entropy in a human population, generated and maintained since our divergence from our non-human primate ancestors (see Discussion, Methods, and Supplementary Text). Therefore, the increase in log likelihood associated with a decision rule in the FitCons2 algorithm can be interpreted as a reduction in entropy, or equivalently, as a measure of the information gain associated with the corresponding bi-partition of genomic sites and the epigenomic data that defines the bi-partition.

Decision tree and maps for 115 cell types

We applied FitCons2 to epigenomic data for human cells from the Roadmap Epigenomic Project⁴, together with population genomic data previously compiled for INSIGHT ^16-18, consisting of polymorphism data from 54 unrelated humans and phylogenetic divergence data from alignments of the chimpanzee, orangutan and rhesus macaque genomes to the human reference genome. (Larger data sets of human polymorphism data are now available but have negligible impact in this setting; see Methods.) To summarize the Roadmap data and associated genomic annotations, we made use of nine feature types spanning a broad range of biological processes, levels of genomic resolution, and degrees of cell-type specificity, including RNA-seq, DNase-seq, small RNAs (smRNA), chromatin states (ChromHMM), annotated coding sequences (CDS) and splice sites (Splice), transcription factor binding sites (TFBS), and predicted DNA melting temperatures (MeltMap) (see Table 1). The cell-type specific “Epigenomic” features were collected separately for each of the 115 karyotype-normal cell types represented in the Roadmap Epigenomic Project.

Table 1:

Summary of Epigenomic and Annotation Features Used by FitCons2

Name	Description	Type1	Levels2	Source
CDS	Coding sequences	Annotation	5: Start, Codon pos. 1,2,3, Non	GENCODE27
Splice	Splice sites	Annotation	4: Core, Prox, Dist, Non	GENCODE27
MeltMap3	Predicted DNA melting temperature	Annotation	5: VHi, Hi, Med, Lo, VLo	ref. 28
TFBS	Transcription factor binding sites	Annotation4	4: Hi, Med, Lo, None5	Ensembl29 & ref. 16
smRNA	Small RNAs	Annotation4	4: Hi, Med, Lo, None	ENCODE & Human Epigenome Atlas6.
RNA-seq	Transcription	Epigenomic	4: Hi, Med, Lo, None	Roadmap
DNase-seq	Chromatin accessibility	Epigenomic	4: Hi, Med, Lo, None	Roadmap
ChromHMM7	Chromatin modifications	Epigenomic	25: (see ref. 4)	Roadmap
WGBS	DNA methylation	Epigenomic	2: Hypo, non-Hypo	Roadmap

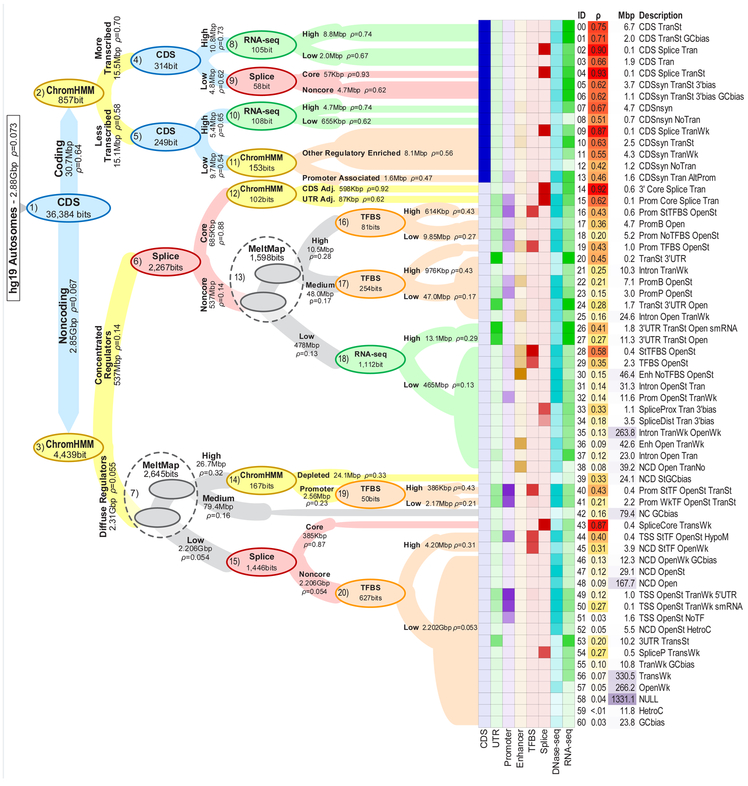
The recursive FitCons2 algorithm was applied to these data as described above, except that a single decision tree was estimated by averaging across all cell types when evaluating candidate decision rules (see Methods). The algorithm identified 61 classes, each defined by a distinct combination of epigenetic features and selective pressure (Figure 2 and Supplementary Tables 1 & 2). The estimated tree was robust, changing only in minor details when re-estimated from random samples of 50% of cell types (Supplementary Figure 1). Importantly, while each of the 61 identified classes is associated with a single estimate of ρ (representing its FitCons2 score), each class corresponds to a different set of genomic sites in each cell type, owing to differences in the cell-type specific features. Therefore, when these class-specific estimates of ρ are mapped to the genome, 115 cell-type specific FitCons2 maps are obtained. (These maps are available as genome-browser tracks; see URLs).

Figure 2. Decision tree and clusters for the human genome.

The decision tree obtained by applying FitCons2 to the human genome sequence (hg19 assembly; autosomes only). Nodes (ovals) represent decision rules (bi-partitions) and are labeled with the feature on which each rule is based as well as the associated increase in information (in bits). Nodes are colored by feature type. Edges extending from parent nodes to children are labeled with descriptions of partitions, their sizes in millions of basepairs (Mbp), and corresponding estimates of ρ. Edge widths are proportional to log(size). Dashed circles indicate successive binary partitions based on MeltMap that effectively create three-way splits. For simplicity, only the first 4–5 levels of the tree are shown in detail. The 61 leaves of the tree (at right) are labeled by unique identifiers, estimates of ρ, sizes in Mbp, and brief descriptions of the associated clusters (see Supplementary Tables 1 & 2 for additional details). Heatmap to left of cluster IDs displays relative enrichments for several annotations (Coding Sequences [CDS], Untranslated Regions [UTRs], Promoters, Enhancers, annotated Transcription Factor Binding Sites [TFBS], Splice sites, DNase-seq, and RNA-seq data).

The decision tree estimated by FitCons2 (Figure 2) is richly descriptive about the distribution of evolutionarily relevant information across the human genome. The first partition (node #1 in Figure 2) is between about 31 Mbp of protein-coding sequences (CDS; ρ = 0.641) and the noncoding sites (ρ = 0.067) in the genome. In noncoding regions, the second split (node #3) is between a collection of 20 chromatin states associated with regulatory and transcriptional activity (ρ = 0.14) and the remaining five states (ρ = 0.055). In coding regions, the second split (node #2) is between chromatin states associated with active transcription (ρ = 0.70) and ones that are not (ρ = 0.58). In noncoding regions labeled with regulation-associated chromatin states, which tend to fall near exons, the next split (node #6) distinguishes a small set of nucleotides (685 kbp) associated with splicing (ρ = 0.88) from the remaining nucleotides (ρ = 0.14). Subsequent splits make use of MeltMap (node #13), RNA-seq (node #18), chromatin states that identify CDS- and UTR-adjacent sites (node #12), and annotated TFBSs (nodes #16 & #17). Outside concentrated regulators in noncoding regions, MeltMap is used earlier (node #7; in part as a guide to promoters and UTRs), splice sites show up later (node #15), chromatin states are used to identify promoters (node #14), and RNA-seq does not appear, presumably because these regions tend to be farther from exon boundaries. Interestingly, TFBSs are particularly informative in combination with promoter-associated chromatin states (nodes #14 & #19), which signal cell-type specific activity. In coding regions, the third level in the tree distinguishes “high information” positions (such as start codons and 1st and/or 2nd codon positions) from “low information” positions (nodes #4 & #5). Subsequent splits make use of features such as RNA-seq and overlap with splice sites. Altogether, FitCons2 identifies a diverse collection of clusters in the genome, ranging in size from very small (~60 kbp) to very large (the “NULL” class [58] accounts for over 1 Gbp), and with ρ values from <1% to 93%.

A few genomic features contribute most information

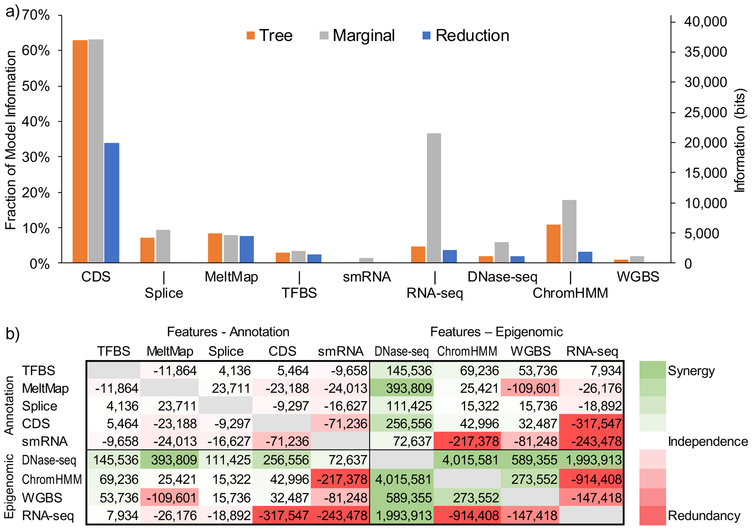
The reduction in entropy across the entire decision tree, measured at 58,759 bits, can be interpreted as the total information about selection provided by all of the available functional genomic data and annotations. Moreover, feature-specific contributions to this total can be obtained by summing over all nodes (decision rules) that make use of each feature. These estimates (Figure 3a, orange bars) suggest that 62.9% of all of the available information is attributable to CDS annotations, followed by 11.0% from ChromHMM, 8.4% from MeltMap, 7.2% from Splice, 4.8% from RNA-seq, 2.9% from TFBSs, and < 2% from each of DNase-seq, WGBS, and smRNA.

Figure 3. Information and synergy.

(a) Information about natural selection is attributed to each individual genomic feature by three methods: (1) summing over the associated decision rules in the tree (tree, orange); (2) measuring the information of the feature in isolation (marginal, gray); and (3) measuring the reduction in total information when that feature is excluded from the complete tree (reduction, blue). These measures are similar when a feature is largely orthogonal to other features (e.g., MeltMap) but different in the presence of strong correlations with other features (e.g., RNA-seq, ChromHMM). All estimates are based on log likelihoods computed from genome-wide data (Methods). (b) Synergy between all pairs of features measured as the excess in information obtained by considering a pair of features together relative to the information obtained by considering the two features separately (Methods). Each cell gives a value in bits. Cells are colored on a spectrum from red (large negative values, indicating redundancy) to green (large positive values, indicating synergy). Note that the matrix is symmetric.

The greedy algorithm used to construct the tree, however, will tend to overestimate the information attributable to features selected early in the process at the cost of features selected later. Therefore, we also considered (1) the marginal contribution of each feature in the absence of all others (gray bars in Figure 3a); and (2) the reduction in the total information when each feature is individually removed from the analysis (blue bars). The marginal method attributes 36.6% of all available information to RNA-seq, whereas the reduction method finds that only 3.7% of the available information is specific to RNA-seq. This difference reflects the strong correlation of RNA-seq with CDS annotations. Under the marginal method, the contribution of ChromHMM rises to 17.7% (from 11.0%) and that of DNase-seq to 5.9% (from 1.8%), suggesting substantial correlation of these covariates with one another and/or CDS and RNA-seq. Under the reduction method, the contribution of ChromHMM falls to 3.3%, that of DNase-seq to 2.0%, and that of Splice to 0.3%, with other features being less dramatically affected. Altogether, this analysis shows that the largest share of information about sites that are under selection comes from CDS annotations and RNA-seq data, with ChromHMM coming next and DNase-seq third, but these features are highly correlated with one another. The other features contribute smaller amounts of total information but are less correlated.

Entropy is primarily determined by mutation and drift

The entropy measured by FitCons2 reflects a balance of mutation (which acts to increase entropy) with drift and natural selection (which act to reduce entropy)^19,20. We attempted to separate the contributions of natural selection and the neutral processes of mutation and drift by applying FitCons2 to a subset of sites assumed to be free from selection for our INSIGHT analyses. To allow for heterogeneity across the genome in mutation rates and selection at linked sites, we separately considered such “neutral” sites in each of the 61 clusters identified by FitCons2 (Methods). By contrasting the entropy per nucleotide site for these neutral sites with the entropy per site for all nucleotides in each cluster, we were able to quantify the reduction in entropy (gain in information) specifically associated with natural selection per cluster.

Across the entire genome, we estimated the neutral entropy per site to be 0.1234 bits, but the actual entropy per site to be 0.1189 bits, indicating a reduction of 0.0045 bits per site from natural selection (Supplementary Table 3). Thus, according to the INSIGHT model, natural selection only reduces the entropy in genetic variation that derives from neutral processes by ~3.6%. However, the relative contributions of neutral processes and natural selection differ considerably by cluster. For example, in cluster 04, which represents splice sites in strongly transcribed coding regions, the neutral entropy per site is estimated at 0.0783 bits, and the observed entropy at 0.0237 bits, a reduction of ~70%. By contrast, in cluster 58, the “NULL” class, the neutral entropy per site is 0.1282 bits and the observed entropy is 0.1248 bits, a reduction of only 2.7%. In general, the reductions in entropy per site due to natural selection are well correlated with estimates of ρ (Supplementary Figure 2).

Some genomic features exhibit synergy

The FitCons2 framework also allows us to ask if there are combinations of features that exhibit synergy, in the sense that they yield more total information about natural selection in combination than they do individually. We looked for synergy using a simple pairwise measure defined as the excess in information, in bits, obtained by considering a pair of features together in comparison to the information obtained by considering each feature separately (see Methods). This measure is positive when the combination of two features allows for a better explanation of genome-wide variation as measured by INSIGHT, and it is equal to zero when this combination offers no improvement over the individual features (as when the features are nonoverlapping). This measure can be negative if two features provide redundant information about how the genome should be partitioned to account for patterns of variation (as when they are strongly correlated along the genome).

We found that most pairs of annotations displayed at most weak synergy (Figure 3b), probably because they tend to identify largely nonoverlapping regions of the genome, and/or to account for few bases overall (as with TFBS, smRNA, and Splice). By contrast, pairs of cell-type specific epigenomic features often displayed substantial synergy, with DNase-seq, in particular, showing synergy with all other epigenomic features. When pairs of annotations and cell-type specific epigenomic features were considered, synergy was generally negative or weakly positive, with the exception of DNase-seq, which showed strong positive synergy with all annotations, likely because it signals cell-type specific activity (see Discussion). Altogether, DNase-seq stands out in this analysis as the largest single contributor to synergy, with respect to both annotations and other epigenomic features. ChromHMM and WGBS show some similar trends but to a lesser degree, whereas RNA-seq appears to be the most redundant with other features. These observations have implications for future efforts in data collection and analysis (see Discussion).

Applications of cell-type specific FitCons2 scores

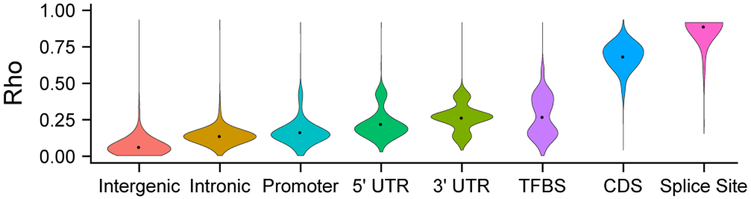
The average FitCons2 score per site, across cell types and positions, is 0.082, indicating that an expected ~8% of nucleotide sites are subject to natural selection, in reasonable agreement with previous measures based on population genetic and phylogenetic data^17,21. These selected sites include an expected 64% of all protein-coding bases (CDS) and 7.6% of all noncoding bases, with more than 90% of sites expected to be under selection falling in noncoding regions. Overall, the highest-scoring positions are in splice sites of annotated genes, followed by protein-coding sequences (CDS), TFBSs, 3’ and 5’ untranslated regions (UTRs), and promoters, with only slight elevations above the background in other annotated elements (Figure 4). These annotation-specific score distributions are often multimodal in a manner that reflects informative combinations of features in the decision tree. For example, the distribution for TFBSs has modes that reflect the partitioning of individual motif positions by information content and the combination with DNase-seq data. Similarly, the UTR and promoter distributions have modes reflecting locally elevated scores, from binding sites, DNase-seq, RNA-seq, WGBS, and related features. Interestingly, the annotation-specific bulk distributions are highly similar across cell types (Supplementary Figure 3). Nevertheless, the position-specific scores differ considerably across cell types and are informative about cell-type relationships, owing to differences in cell-type specific activity. We find that hierarchical clustering of cell types based on their FitCons2 scores recovers many known relationships among them (Supplementary Figure 4, Supplementary Text).

Figure 4. Annotation-specific distributions of FitCons2 scores.

Violin plots showing genome-wide score distributions for annotated coding regions (CDS), 5’ and 3’ untranslated regions (UTRs), splice sites, transcription factor binding sites (TFBS), core promoters, and remaining intronic and intergenic regions. Scores are for GM12878 cells and reflect regions “active” in that cell type (see Methods). These annotation-specific marginal score distributions are highly similar across cell types, despite differences in regions of the genome they summarize owing to cell-type specific activity (see Supplementary Figure 3). Splice sites were defined as the two intronic bases immediately adjacent to exon boundaries. Promoters were defined as 1,000 bp upstream of annotated transcription start sites. TFBS annotations based on ENCODE ChIP-seq data were obtained from ref. ¹⁶. Violin plots were generated with the R command ggplot2∷geom_violin(), with parameter adjust=0.50. The dots represent the means of the distributions. The numbers of nucleotide sites considered for each class are 1.782 billion (Intergenic), 117.9 million (Intronic), 8.236 million (Promoter), 816.8 thousand (5’ UTR), 3.872 million (3’ UTR), 4.810 million (TFBS), 5.222 million (CDS), and 424.3 thousand (Splice Site).

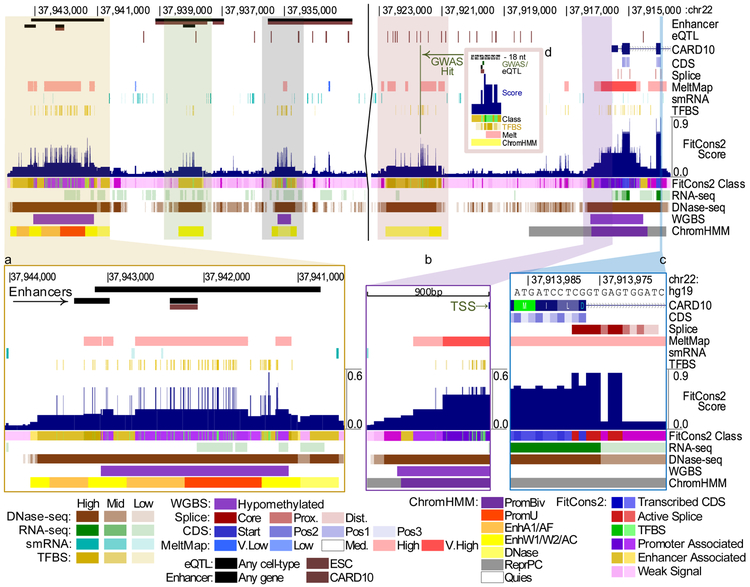
The FitCons2 scores across the human genome can be viewed and downloaded via a UCSC Genome Browser track. This track reveals elevated scores at many enhancers and promoters as well as genes and it often highlights unannotated regulatory elements (Figure 5; see also Supplementary Figures 5–9). Indeed, despite being designed as an evolutionary measure, the FitCons2 scores are useful as predictors of genomic function at individual nucleotides, comparing reasonably well to other computational methods in the identification of bound TFBSs and pathogenetic single-nucleotide variants (Supplementary Text and Supplementary Figures 10–13). By zooming into the base level in the browser, it is possible to observe high-resolution texture corresponding to features such as individual codon positions, TFBSs, and splice sites (Figure 5a-d). The browser track includes subtracks for the FitCons2 scores in each of the 115 cell types, which can easily be compared to assess cell-type specificity. In addition, the track includes an “integrated” score that summarizes the scores across all cell types (see Methods) and highlights both cell-type specific activity and activity shared across cell types (Supplementary Figure 7). This score provides a useful summary when it is not clear to the user what cell type is most relevant in evaluating the functional significance or evolutionary importance of a given site, or when scores are needed for a known cell type that is not among those for which epigenomic data is available.

Figure 5. Genome Browser display.

UCSC Genome Browser display for a region of chromosome 22 overlapping the 5’ end of the gene encoding caspase recruitment domain-containing protein 10 (CARD10), which participates in apoptosis signaling and activates NF-KB via BCL10. FitCons2 scores (dark blue, near middle) are shown for the ES-WA7 (embryonic stem cell from blastocyst) cell type. Annotation features are shown above the FitCons2 scores and cell-type specific epigenomic features are shown at bottom. For reference, predicted enhancers from EnhancerAtlas²³ (longer bars) and FANTOM5^24,25 (shorter bars; in both cases, brown indicates enhancers specifically associated with CARD10), eQTL from GTEx²⁶ (brown indicates specific association with CARD10), and the gene annotation from GENCODE²⁷ (top) are also shown. Insets show zoomed-in displays of (a) an apparent cluster of enhancers showing a high DNase-seq signal, ChromHMM states suggesting regulatory activity (orange: enhancer; red: promoter), and a high concentration of TFBSs; (b) the core promoter and transcription start site showing similar indications of regulatory activity; (c) a 5’ splice site and adjoining CDS and intronic sequences; and (d) GWAS and eQTL hits coinciding with a TFBS. Additional examples are shown in Supplementary Figures 5–7. A more detailed legend is provided in Supplementary Figures 8–9.

DISCUSSION

In this article, we have presented a method for simultaneously clustering genomic sites based on epigenomic features and estimating the probabilities that mutations at those sites will have fitness consequences. Our recursive bi-partitioning algorithm finds clusters of genomic sites that not only share epigenomic features but at which mutations also have similar fitness effects. This procedure produces interpretable maximum-likelihood estimates of key evolutionary parameters for each cluster, including the FitCons2 score, ρ. The interpretability of the FitCons2 scores represents a key advantage in comparison with other available scores for functional relevance or pathogenicity^9-14. Another major advantage is that these scores can be separately computed for many cell types to reflect differences in epigenomic features.

Importantly, FitCons2 also allows us to evaluate how informative these features are, both individually and in combination. The individual contributions to information, predictably, are dominated by CDS annotations, but broad, diffuse cell-type specific epigenomic features (e.g., ChromHMM, RNA-seq, and WGBS) and more focused annotations (e.g., Splice and TFBS) also make substantial contributions. The RNA-seq feature stands out as being highly informative by itself but only weakly informative when conditioning on other features, owing to its high degree of redundancy. DNase-seq shows, by far, the most synergy with other features, including both annotations and other cell-type specific epigenomic features, apparently because it can distinguish between “active” and “inactive” elements in a cell-type specific fashion. For example, the combination of DNase-seq and our cell-type general annotations of TFBSs provides information about which binding sites are, and are not, occupied in each cell type. This property of DNase-seq suggests that it is a particularly valuable data type to collect in studies in which the budget for functional genomics is limited, because it will enhance the value of other features.

A strength of our method is that it nominally provides cell-type specific FitCons2 scores. It is worth emphasizing, however, that the notion of cell-type specific “fitness” must be interpreted cautiously. Strictly speaking, a cell-type specific score ρ indicates that a nucleotide has an epigenomic “signature” in that cell type that, on average, is associated with a probability ρ of mutational fitness consequences. That measure, however, is based on patterns of genetic variation across a population and ultimately reflects natural selection at the level of whole organisms not individual cell types. Thus, differences across cell types in FitCons2 scores really represent differences across cell types in the way sites are grouped by their epigenomic fingerprints, and capture differences in cell-type specific “importance” only through these groupings. Nevertheless, these cell-type specific maps are useful in that they effectively capture cell-type specific activity, allow for sensitive detection of cell-type specific elements, and reflect the global correlation structure of epigenomic data across cell types.

The question of how much information is contained in the human genome is not a new one, but that question is typically taken to mean how many bits would be required to encode a single “reference” genome. The answer for the human genome (hg19) is roughly 5.7 billion bits for a simple single-base encoding, or as few as 5.2 billion bits if dependencies between neighboring bases are considered (see Supplementary Text). From an evolutionary perspective, however, this method of measuring information produces a vast overestimate, because most nucleotides in the human genome apparently have no effect on fitness and therefore are not truly “informative” (see also ref. ²²). In addition, human genomes are highly correlated with one another and with the genomes of other primates; given one human genome, another human genome contains much less information that it does alone. For these reasons, we use a population-based measure of information, and condition on the genome sequences of nonhuman primate outgroups. By making use of a set of putatively neutral sites, we can further decompose the information in a human population into a neutral component (due to a balance between mutation and drift) and component specifically associated with natural selection. Thus, we obtain an approximate measure of the fitness-relevant genetic information in a population of humans, generated and maintained since the human/chimpanzee divergence.

This decomposition reveals that the population-genetic entropy in a collection of human genome sequences, given their primate relatives, is primarily determined by a balance between mutation and genetic drift, with a small reduction from natural selection. This qualitative observation is not surprising, since it is well known that a small minority of nucleotides in the genome are under selection, but it is nevertheless striking that the absolute reduction in entropy, or the information, associated with natural selection is only ~13 million bits, or ~1.6 MB—about the size of a typical smartphone snapshot or email attachment. Thus, the fitness-relevant genetic information in a human population, given nonhuman primate genomes, is minimal on the scale of modern digital information, and dramatically smaller than the storage requirements for a single human genome sequence.

ONLINE METHODS

Comparative and population genomic data

We measured natural selection using INSIGHT and data describing both genetic divergence across primates and polymorphism within human populations. We reused the same data from several previous INSIGHT-based analyses^15-18 (see ref. ¹⁶ for complete details). Briefly, these data consist of genome assemblies for chimpanzee (panTro2), orangutan (ponAbe2), and rhesus macaque (rheMac2) aligned to the human reference genome (hg19), together with human polymorphism data extracted from the high-coverage “69 Genomes” data set from Complete Genomics, which was reduced to 54 unrelated samples. Genomic sites were rigorously filtered to eliminate repetitive sequences, recent duplications, CpG sites, and regions not showing conserved synteny across primates. Our analysis considered only the autosomes (chromosomes 1–22) because of substantial differences in mutation rates and distributions of selective effects on the sex chromosomes (X and Y). INSIGHT was run using putatively neutral regions identified by starting with all noncoding sites and excluding annotated RNA genes, TFBSs, phastCons-predicted evolutionarily conserved elements, and immediate flanking regions^15,16. Notably, while much larger population genomic data sets are now available^30-33, our experiments have shown that the use of even ~20 times more human individuals makes a negligible difference in estimates of the key parameter ρ, owing to the efficiency with which INSIGHT pools information across sites in the genome and the property that much of the information about natural selection derives from divergence rather than polymorphism (data not shown). Therefore, we opted to reuse a data set that has already been extensively processed and validated, and whose properties are well known to us.

Genomic features

We considered the nine genomic features described in Table 1 (ee also the Life Sciences Reporting Summary). For the four epigenomic features, we obtained the imputed RNA-seq, DNase-seq, WGBS, and ChromHMM data sets for each of the 127 cell types (numbered E001–E129, with E060 and E064 omitted) represented in the Roadmap Epigenomic Project data⁴ (see URLs). After initial processing, seven cell types were discarded due to deficiencies in data quality (E001, E003, E017, E027, E098, E104, and E113), and five additional cell types were discarded due to abnormal karyotypes (E114, E115, E117, E118, and E123), which could lead to alignment difficulties and major epigenomic perturbations. For each of the remaining 115 cell types, the “consolidated imputed” RNA-seq and DNase-seq data (representing log RPKM and p-values, respectively) were discretized into 4 levels each, using an exhaustive search over possible partition boundaries with an entropy-based objective function (see Supplementary Text for details). The labels from the 25-state version of the Roadmap ChromHMM analysis⁴ were used directly as feature values. The raw WGBS data was partitioned into two classes, corresponding to hypomethylated and non-hypomethylated regions, using the HMR program from the MethPipe package³⁴.

The five annotations were defined as follows for all cell types. The protein-coding gene (CDS) and Splice annotations were derived from the GENCODE V19 database²⁷, considering only “KNOWN” “protein_coding” transcripts with a single annotated start and stop codon. Based on CDS annotations, we labeled positions as falling in start codons, codon position 1, codon position 2, codon position 3, and noncoding positions. A position belonging to more than one class across isoforms was assigned to the class under greatest constraint (start > 2 > 1 > 3 > noncoding). For the splice feature, we considered the fifty intronic sites flanking each annotated CDS exon boundary and labeled them, by distance from the exon boundary, as under high, medium, low, or no average constraint, based on pooled data from all splice sites (Supplementary Text). The two positions within CDS immediately adjacent to the exon boundary displayed similar levels of constraint to the “high” intronic class and were included with them. Based on an initial exploratory analysis of potentially relevant genomic features, we also identified predicted DNA melting temperature (MeltMap) as a feature that correlates significantly with selective constraint, although it is likely that this relationship is at least partially explained by the strong correlation of melting temperature with G+C content, which in turn correlates strongly with the presence of functional elements in the genome. In particular, we observed minimal selective pressure at intermediate melting temperatures and elevated selective pressure at more extreme melting temperatures (Supplementary Text). Based on these observations, we discretized the predicted melting temperature into five levels ranging from “very low” to “very high”, with constraint levels such that {very low, very high} > {low, high} > medium.

Because they were available for only a limited collection of cell types, the transcription factor binding site (TFBS) and small RNA-seq (smRNA) features were based on pooled data and treated as annotations. For the TFBSs, we combined 588,958 binding sites from Ensembl Regulatory build V75 (ref. ³⁵) with 2,595,018 predicted sites we had previously assembled using ENCODE data¹⁶. Both sets were derived from ChIP-seq peaks, with bioinformatic motif-matching to identify likely TFBSs under the peaks (see ref. ¹⁶). After merging overlapping predictions, the final set consisted of 1,994,905 TFBSs spanning 23.6Mbp and representing 86 TFs. We partitioned nucleotides into four constraint classes based on the information content of the corresponding position in the position weight matrix for the TF in question (Supplementary Text). The smRNA data set was based on a combination of the UCSF-4Star composite, the UCSF Brain Germinal Matrix, the UCSC Penis Foreskin Keratinocyte (PFK) composite, and smRNA data from ENCODE for the CD20 and HUVEC cell types. Sites were also partitioned into four levels of constraint based on smRNA data (Supplementary Text).

Recursive bi-partitioning algorithm

The FitCons2 algorithm begins with the complete set of genomic sites and an associated collection of D functional genomic and annotation-based features. Each genomic site is labeled with a particular combination of features, a D-dimensional vector known as that site’s functional genomic fingerprint. As described above, each of the D feature types i is discretized into m_i possible values, where m_i ranges between 2 and 25. If these possible values do not have a natural ordering, they are ordered according to their marginal information about natural selection, as measured by the ρ parameter from INSIGHT. (This ordering by ρ is actually performed dynamically at every node in the tree, to allow for changes conditional on previous partitions; see Supplementary Text.) Thus, each nucleotide is assigned one of k_i possible ordered values for each of D feature types, i ∈ {1, …, D}.

The algorithm then considers a family of possible decision rules for splitting the set of genomic sites into two subsets. Each candidate decision rule is based on a single feature type and a threshold. For example, RNA-seq read counts are summarized by four feature values, corresponding to (1) no reads, and (2) low, (3) medium, or (4) high read counts. The algorithm considers partitioning the genome by the decision rules 1∣234, 12∣34 and 123∣4, where uv ∣ xy indicates a partitioning between sites labeled u or v and sites labeled x or y. Because the feature labels are ordered, the number of possible decision rules for each feature type i is always linear in m_i. These possible rules must be considered for each of the D feature types.

The algorithm selects the decision rule that maximizes the gain in information about natural selection. This choice is made by fitting the INSIGHT model separately to the two subsets of genomic sites defined by each candidate decision rule, and deriving a measurement of gain in information from the likelihoods of these models (see below). Choosing partitions that maximize this gain in information has the effect of maximizing the degree to which the resulting two subsets of sites are homogeneous and distinct from one other in terms of their influence from natural selection. Importantly, the gain in information associated with each candidate decision rule is computed as an average over all cell types, that is, by weighting each genomic position by the number of cell types displaying the specified feature value (or range of values) in the INSIGHT likelihood function. In this way, the decision tree is fitted to all cell-type specific data sets simultaneously.

The same procedure is then applied recursively to each of the two subsets of sites, and in turn, to subsets of those subsets, until no subset meets the criterion for further partitioning. Thus, a binary tree is defined with internal nodes representing decision rules and leaves representing particular combinations of decision rules (Figure 1). Furthermore, these leaves define genomic clusters that are maximally homogeneous and distinct in selective pressure. (This greedy algorithm finds a local maximum, but not necessarily a global maximum, according to the objective function used.) Because the algorithm is driven both by the genomic features and the patterns of genetic variation, it tends to find clusters that reflect the natural correlation structure of both the functional genomic and population genomic data.

In practice, we initially had the recursive algorithm terminate when no remaining candidate decision rule provided more than 5 bits of information, which produced a tree with 195 leaves. To obtain a smaller and more interpretable tree, however, we then pruned the tips of the tree based on a 50-bit threshold (meaning that we eliminated external branches until all corresponded to increase of information of at least 50 bits, as if we had used that as our original stopping criterion). Each step of the recursive algorithm can be viewed as a likelihood ratio test with four degrees of freedom (three free parameters and an addition degree of freedom for the choice of partition), so a 50-bit (69.4-nat) threshold corresponds to a nominal p-value of approximately 3 × 10⁻¹⁴. Even allowing for the hundreds of tests carried out by the algorithm, this threshold is still conservative. For efficiency, at each step of the algorithm, all internal nodes at a given tree depth are examined in parallel. Execution of the full algorithm completed in about 57 hours of wall clock time on a shared computer cluster.

This algorithm was additionally adapted for use in computing the “cell-type integrated” scores, as described in the Supplementary Text.

Statistics and Data Analysis

Measuring entropy with INSIGHT

As detailed in the Supplementary Text, we measure “information” in terms of the entropy of a distribution, P(X ∣ θ), where X is a collection of human genome sequences and θ is a parameter set that governs the distribution, implicitly conditioning also on O, a collection of closely related nonhuman primate “outgroups”. We use the INSIGHT probabilistic evolutionary model¹⁵ to define P(X ∣ θ). Importantly, INSIGHT provides an approximate measure of the genetic entropy not only of the sample X but of the population from which X is drawn (Supplementary Text).

The INSIGHT model is fitted to a collection of genomic sites by maximum likelihood. In the limit of a large number of sites, the maximized log likelihood of the model is closely related to the entropy of the distribution P(X ∣ θ), as follows. Conditional on the parameter set, θ, and the assumed block structure, INSIGHT assumes independence of nucleotide sites, with P(X ∣ θ) = ∏_i P(X_i∣θ). Thus, the maximized log likelihood can be written $\mathcal{L}(\widehat{\theta },X)={\max }_{\theta }\log P(X\mid \theta )={\max }_{\theta }{\sum }_i\log P(X_i\mid \theta )$. The entropy of $X\mid \widehat{\theta }$, in turn, can be written, $H(X)=-C{\sum }_{x}P(x\mid \widehat{\theta })\log P(x\mid \widehat{\theta })$, where the sum is over all possible alignment columns x and C is the number of columns in the actual alignment X. Assuming the model fits the data well, in the sense that the distribution of alignment columns under the model is close to the empirical distribution in X, then as C grows large,

$$\mathcal{L}(\widehat{\theta };X)=\sum _{i}logP(X_i\mid \widehat{\theta })\approx C\sum _{x}P(x\mid \widehat{\theta })logP(x\mid \widehat{\theta })=-H(X).$$

In other words, the negative log likelihood under INSIGHT is an estimator for the population genetic entropy. Throughout this article, we assume base-2 logarithms and express entropy in bits. The estimated entropy can be partitioned into neutral and selective components, as detailed in the Supplementary Text.

In practice, we often compute the log likelihood as an average across cell types, which can be interpreted as the expected complete data log likelihood under a mixture model with a uniform prior. Specifically, for a collection of sites X, we assume,

$$\mathcal{L}(\widehat{\theta };X)=\sum _i\left(\frac{{\sum }_{j\in J_i}\log P(X_i\mid {\widehat{\theta }}_{i,j})}{\mid J_i\mid }\right),$$

where J_i is the set of cell types for which data is available at genomic position i and ${\widehat{\theta }}_{i,j}$ denotes the INSIGHT model parameters associated with the features in cell type j at position i.

Information associated with features

Suppose a genomic feature F allows sites to be partitioned into those having a label (or set of possible labels) A, X_F=A = {X_i∣F(X_i)=A}, and the complement of that set, X_F≠A = {X_i∣F(X_i)≠A}. A new entropy can be computed based on this partitioning by fitting the INSIGHT model separately to X_F=A and X_F≠A, with two separate sets of free parameters: $H(X;F∕A)\approx -\mathcal{L}({\widehat{\theta }}_{F=A};X_{F=A})-\mathcal{L}({\widehat{\theta }}_{F\ne A};X_{F\ne A})$. This entropy, H(X;F/A), must always be less than or equal to the original entropy, H(X) (modulo optimization error). The reason is that the pair of INSIGHT models for the two subsets, X_F=A and X_F≠A, directly generalizes the single model applied to all sites and must fit the data at least as well, meaning that it will yield a maximized log likelihood at least as large. Thus, $\mathcal{L}({\widehat{\theta }}_{F=A};X_{F=A})+\mathcal{L}({\widehat{\theta }}_{F\ne A};X_{F\ne A})\ge \mathcal{L}(\widehat{\theta };X)$, which implies H(X; F/A) ≤ H(X). We can therefore define the nonnegative quantity, $\Delta H(X;F∕A)≔H(X)-H(X;F∕A)\approx \mathcal{L}({\widehat{\theta }}_{F=A};X_{F=A})+\mathcal{L}({\widehat{\theta }}_{F\ne A};X_{F\ne A})-\mathcal{L}(\widehat{\theta };X)=\Delta \mathcal{L}(F∕A;X)$, as the “information” associated with feature F having label A. This is the measure used for the information associated with each decision rule in our recursive bi-partitioning algorithm.

In some cases, it is also useful to have a measure of the overall “marginal” information associated with a feature F, considering all of its possible values (e.g., see Synergy, below). For this measure, we use:

$$\Delta H(X;F)\approx \left(\sum _a\mathcal{L}({\widehat{\theta }}_{F=a};X_{F=a})\right)-\mathcal{L}(\widehat{\theta };X).$$

Synergy

We define the pairwise synergy between features F and G as,

$$S(F,G)≔\Delta H(X;F,G)-[\Delta H(X;F)+\Delta H(X;G)],$$

where ΔH(X;F) and ΔH(X;G) represent the marginal information associated with F and G, respectively, and ΔH(X; F, G) is computed analogously by considering the Cartesian product of feature values for F and G. S(F, G) is positive when there is synergy between F and G, meaning that more information can be obtained by considering them together than by considering each of them separately; negative when they are “redundant” or highly correlated; and zero when they are, in a sense, orthogonal or “independent”. Notice that S(F, G) is similar in spirit to mutual information but conceptually distinct, because it is based on probabilities of a fixed data set X conditional on various values of the features F and G, rather than being based on a probability distribution for F and G.

In computing S(F, G), some special handling is required for sites at which features have a “null” value (meaning a signal that is absent or at background levels), as detailed in the Supplementary Text.

Annotation-specific distributions of FitCons2 Scores

The cell-type specific bulk distributions of scores for various annotation types (Figure 4 and Supplementary Figure 3) were based on regions “active” in each cell type of interest. For annotations associated with protein-coding genes (CDS, splice site, 5’ & 3’ UTR, promoter, and intronic), we defined “active” elements as ones associated with the top third of all annotated genes after ranking them by RPKM based on cell-type matched RNA-seq data. TFBSs were considered active if they coincided with ChIP-seq peaks in the matched cell type. The notion of cell-type specific “activity” was not applied to intergenic sites. We took care to exclude any positions that overlapped annotated CDSs from all other categories.

Code availability

The source code for FitCons2 is available on GitHub at https://github.com/CshlSiepelLab/FitCons2 under the simplified BSD license.

Data availability

All raw data for this study is publicly available from sources detailed in the Supplementary Text. The cell-type specific and integrated FitCons2 scores are available as UCSC Genome Browser tracks at http://compgen.cshl.edu/fitCons2/. Additional data generated during the course of our analyses can be obtained from the corresponding author [AS] by request.