Acoustic tweezers with frequency multiplexing enable dynamic manipulation of micro-objects using dual-channel excitation.
Abstract
Acoustic tweezers have recently raised great interest across many fields including biology, chemistry, engineering, and medicine, as they can perform contactless, label-free, biocompatible, and precise manipulation of particles and cells. Here, we present wave number–spiral acoustic tweezers, which are capable of dynamically reshaping surface acoustic wave (SAW) wavefields to various pressure distributions to facilitate dynamic and programmable particle/cell manipulation. SAWs propagating in multiple directions can be simultaneously and independently controlled by simply modulating the multitone excitation signals. This allows for dynamic reshaping of SAW wavefields to desired distributions, thus achieving programmable particle/cell manipulation. We experimentally demonstrated the multiple functions of wave number–spiral acoustic tweezers, among which are multiconfiguration patterning; parallel merging; pattern translation, transformation, and rotation; and dynamic translation of single microparticles along complex paths. This wave number–spiral design has the potential to revolutionize future acoustic tweezers development and advance many applications, including microscale assembly, bioprinting, and cell-cell interaction research.
INTRODUCTION
Manipulating micro/nano-objects, such as cells and extracellular vesicles, plays an important role in many disciplines, including biology, chemistry, engineering, and medicine (1, 2). Among various manipulation techniques, such as optical (3), electrical (4), magnetic (5), and acoustic tweezers (6–16), the acoustic tweezers have recently seen increased interest due to their ability to achieve contactless, label-free, and biocompatible manipulation (17–25). In particular, surface acoustic wave (SAW) tweezers have additional advantages in terms of precision, versatility, and suitability for point-of-care applications (17, 18). SAW tweezers are capable of manipulating micro/nano-objects for a wide range of applications, including patterning particles and cells (26, 27), controlling cell-cell interactions (28), cell printing (16, 29), particle/cell separation and sorting (30, 31), manipulating organisms (10), generating and translating droplets (32–35), and isolating extracellular vesicles (36).
Despite tremendous progress in this field, current SAW tweezers can only generate a limited array of wavefield distributions, which, in turn, limits the maneuverability, reconfigurability, degrees of freedom, and functionality for particle/cell manipulation. Ideal acoustic tweezers would contain more independently controlled transducers with different configurations and orientations, allowing for more dynamic features, better performance, and the ability to reshape the wavefields to more distributions. However, developing such SAW tweezers is challenging. SAWs in piezoelectric substrates are usually direction-dependent because of the anisotropic properties of piezoelectric substrates (37). Moreover, high-end delicate programmable multichannel electronics with high expense are required to independently control a large number of interdigital transducers (IDTs) at high frequencies (38, 39). In addition, although analytical models exist for simple cases (16, 28), there is no general model that considers multiple SAWs with different frequency–wave number components propagating in different directions, generated by a group of acoustic transducers. This analytical model is critical for rapid simulations of SAW wavefield, Gor’kov potential field, and acoustic radiation force, as well as for exploring the capabilities and guiding the design of acoustic tweezers.
Dynamic acoustic wavefields lead to time-variant acoustic radiation forces and thus open up the possibility of dynamic and reconfigurable particle/cell manipulation for multiple functions in a single device. In this work, we present wave number–spiral acoustic tweezers, a form of SAW tweezers capable of performing dynamic and reconfigurable particle/cell manipulation through the modulation of multitone excitation signals encoded with the desired phases and amplitudes at different frequencies. Wave number–spiral acoustic tweezers are composed of multiple IDTs with different configurations, designed in such a way that the wave numbers of generated SAWs vary gradually with respect to directions, tracing two spirals in the wave number space. This wave number–spiral design offers frequency-based steering, allowing one to steer the direction and adjust the wave number of standing SAWs by tuning the excitation frequency. Furthermore, in this design, a group of IDTs can be controlled simultaneously yet independently by modulating a multitone excitation signal. These features make it possible to dynamically reshape the SAW wavefield and Gor’kov potential field to various distributions, achieving dynamic and reconfigurable particle manipulation by modulating phases and amplitudes at different frequencies in multitone excitation signals. In addition, we develop a general analytical model that considers multiple SAWs with different frequency–wave number components propagating in different directions. Through analytical simulations and experiments, we demonstrate that with a single device, the wave number–spiral acoustic tweezers can achieve multiple functions, including multiconfiguration one-dimensional (1D) and 2D patterning, on-chip cell patterning and culture, dynamic manipulation and reconfiguration of 2D patterns, and dynamic translation of single microparticles along complex paths.
RESULTS
Principles of wave number–spiral acoustic tweezers
Wave number–spiral acoustic tweezers are composed of M pairs of IDTs, evenly distributed around the coordinate origin O (Fig. 1A). The detailed configuration is given in fig. S1. The devices are designed in such a way that the wave numbers of SAWs generated by IDTs gradually change with respect to directions, tracing two central symmetric spirals in the wave number space (Fig. 1B). The frequencies are also direction dependent (Fig. 1C), which can be derived theoretically, as , where k(θ) and s(θ) are the direction-dependent wave number and slowness of SAWs, respectively.
Fig. 1. Principle of wave number–spiral acoustic tweezers.
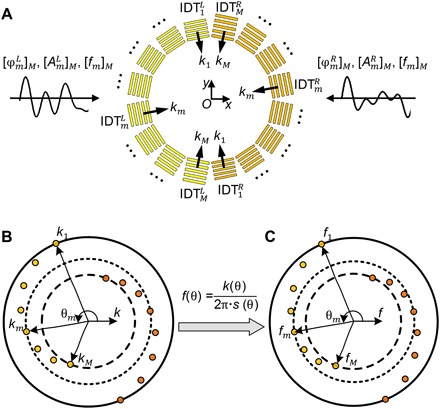
(A) A schematic of wave number–spiral acoustic tweezers. The acoustic tweezers are composed of M pairs of IDTs, evenly distributed around the coordinate origin O. In each pair, two IDTs [denoted as and (m = 1, 2, ⋯, M)] are symmetrically arranged on different sides of the origin O. One multitone signal encoded with phases and amplitudes at frequencies [fm]M is the excitation for M IDTs (denoted as ) on the left side; another signal with phases and amplitudes at frequencies [fm]M is for M IDTs (denoted as ) on the right side. (B) The wave numbers k of SAWs generated by IDTs gradually change with respect to direction θ, tracing two central symmetric spirals in the wave number space. (C) The wave frequencies f also gradually change with respect to direction θ, as derived by , where s(θ) is the slowness of SAWs.
The wave number–spiral design enables a new dynamic feature: frequency-based steering of standing SAWs. The direction and wave number of standing SAWs can be adjusted by tuning the excitation frequency. For example, when an input electrical signal contains a single frequency fm, the mth pair of IDTs in the wave number–spiral acoustic tweezers will be excited and will generate counterpropagating SAWs with the wave number km. The interference of counterpropagating SAWs will create standing SAWs with pressure node lines perpendicular to the direction θm.
The wave number–spiral design allows all the IDTs in the acoustic tweezers to be controlled simultaneously and independently with only two multitone excitation signals. This allows the resultant SAW wavefields to be dynamically reshaped without using complex and costly electronics like multiple-channel function generators and high-end programmable electronics. As shown in Fig. 1A, two independent multitone signals are adopted to control two groups: and on the left and right sides, respectively. The principle of controlling multiple IDTs with multitone signals is presented in section S1 and fig. S2. In this method, the phases and amplitudes of SAWs generated by different IDTs can be adjusted independently by modulating the phases and amplitudes at the corresponding frequencies in the multitone excitation signals. As a result, by carefully designing the multitone excitation signals, we are able to manipulate the SAW wavefield generated by the wave number–spiral acoustic tweezers and, thus, the resultant Gor’kov potential field and acoustic radiation force on particles/cells in the system.
To explore the capability of wave number–spiral acoustic tweezers, we developed a general analytical model (section S2). This model considers multiple SAWs with different frequency–wave number components propagating in different directions, allowing rapid simulations of the SAW wavefield, Gor’kov potential field, and acoustic radiation force generated by wave number–spiral acoustic tweezers. Through analytical studies, we derived the solutions for potential well distributions, as well as the relation between phase change and spatial translation vector (section S3 and fig. S3). Moreover, we demonstrated a new form of single potential wells, named “multitone potential wells,” which can be generated by minimizing SAWs at multiple frequencies (section S4 and fig. S4). By further introducing the subarray concept (40) to the wave number–spiral acoustic tweezers, we discovered that two independent multitone potential wells can be generated with two subarrays (section S4 and fig. S5). The position of each potential well can be independently controlled by properly modulating the phase differences of the corresponding subarray.
Compared to the IDT array–based acoustic tweezers recently proposed by Baudoin and colleagues (37–39), our wave number–spiral acoustic tweezers offer the following three advantages: (i) Our design introduces the frequency multiplexing concept by taking advantage of the frequency–wave number filtering capability of IDTs. SAWs propagating in multiple directions can be simultaneously and independently controlled simply by using an excitation signal with multiple frequency components. Hence, our design reduces the system complexity and does not require delicate programmable electronics with complex wiring and connections. (ii) Our tweezers can easily control wavelengths of SAWs for generating potential well patterns with different periods. (iii) Our frequency-multiplexed IDT arrays can generate and modulate continuous SAWs propagating in multiple directions by using continuous multitone excitation signals.
Device design and characterization
Wave number–spiral acoustic tweezers with five pairs of IDTs were designed and fabricated for proof-of-concept experiments. Figure 2 (A and B) shows a schematic (Fig. 2A) and a photo (Fig. 2B) of the fabricated wave number–spiral acoustic tweezers. Five pairs of IDTs are deposited onto an X-cut lithium niobate (LiNbO3) substrate, with each IDT covering 30°. No IDTs are designed in the ranges of −60° to −30° and 120° to 150° because SAWs are very weak in these directions. All the IDTs are divided into two groups, and in each group, five IDTs are linked to form a rosette-shaped IDT cluster. Hence, only two input channels are needed for powering and controlling all the IDTs. At the center of wave number–spiral acoustic tweezers, a two-layer polydimethylsiloxane (PDMS) device containing a microfluidic chamber is directly attached onto the substrate. Since the bottom layer of the PDMS device is only ~30 μm thick, the energy of SAWs propagating in the substrate can transmit through the thin bottom layer and then enter the microfluidic chamber with negligible loss. After use, the PDMS chamber can be easily peeled off and disposed, and the substrate with IDTs can be recycled.
Fig. 2. Device design and characterization of the wave number–spiral acoustic tweezers.
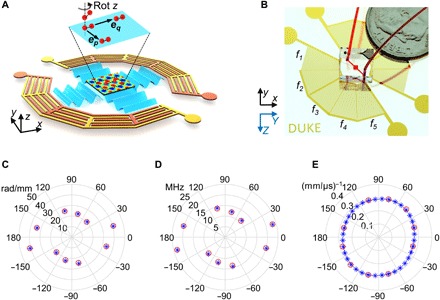
(A) A schematic of the designed proof-of-concept wave number–spiral acoustic tweezers, which are composed of five pairs of IDTs divided into two groups. In each group, five IDTs are interlinked so that only two input channels are needed for powering and controlling all the IDTs. If 2D standing SAWs are generated by two pairs of IDTs, then the resultant acoustic radiation force will trap micro-objects in the potential wells. By adjusting the phases, amplitudes, and frequencies of excitation signals, we can dynamically reshape the wavefields of standing SAWs, thus achieving dynamic and reconfigurable particle manipulation. (B) A photo of a fabricated chip with five pairs of IDTs deposited on an X-cut LiNbO3 substrate. A disposable microfluidic chamber is bonded on top of the substrate and filled with red dye for visualization. Y and Z are crystallographic axes for illustrating the orientation of the X-cut LiNbO3 substrate; x, y, and z are local coordinate axes as references for the wave number–spiral acoustic tweezers. The wave numbers (C), frequencies (D), and slowness values (E) at different angles obtained from the experiment (red circles) agree well with their theoretical values (blue asterisks).
The fabricated wave number–spiral acoustic tweezers were experimentally characterized by first tuning the excitation frequency and examining the standing SAW wavefields with 10-μm polystyrene beads. Resonant frequencies (denoted as f1 to f5) of the five IDT pairs were determined: 20.1, 23.3, 10.8, 12.1, and 13.9 MHz, respectively. The wave numbers and slowness values of SAWs generated at the five frequencies were also determined. As shown in Fig. 2 (C to E), the wave numbers, frequencies, and slowness values at different angles obtained from the experiment agree with the theoretical values.
When standing SAWs are generated by two pairs of IDTs, the resultant acoustic radiation force will move micro-objects to potential wells (at local minima of Gor’kov potential fields) and trap them there, as illustrated in Fig. 2A. The strength of the acoustic radiation force can be determined by the gradient of the potential field, which depends on several parameters including sizes and material properties of the micro-objects being manipulated, properties of the fluid, SAW frequencies, and input power of IDTs. To effectively manipulate micro-objects (e.g., 10-μm polystyrene beads), the applied acoustic radiation force is usually greater than 5 pN (10). By tuning the input power applied to the IDTs, the generated acoustic radiation force can be increased to 150 pN, which is limited by the capability of our power amplifier. Moreover, by adjusting the phases and frequencies of the excitation signals, we can dynamically reshape the wavefields of standing SAWs, achieving dynamic and reconfigurable particle/cell manipulation. For example, two trapped particles can be translated in-plane simultaneously along the direction of vector ep (or eq) by tuning the phase differences between two IDTs in the pth (or qth) pair (p ≠ q and p, q ∈ [1,2,⋯,5]). The two particles can also be rotated around their z axis by switching the excitation frequency. More functions are experimentally demonstrated in the subsections below, including multiconfiguration 1D and 2D patterning, dynamic manipulation and reconfiguration of 2D patterns, and dynamic translation of single microparticles along complex paths.
Multiconfiguration 1D and 2D patterning
Wave number–spiral acoustic tweezers allow independent generation and control of SAWs in multiple directions by properly designing the excitation signals. As SAWs in more directions are independently controlled, it becomes possible to generate more standing wave patterns and thus pattern particles/cells in more configurations. To explore the particle patterns that can be achieved by the fabricated acoustic tweezers chip with five pairs of IDTs, we performed both analytical simulations and microparticle patterning experiments.
Wave number–spiral acoustic tweezers can generate 2D standing SAWs by using modulated excitation signals with two frequencies. For example, when the modulated excitation signals contain two frequencies [f1, f4], the first and fourth pairs of IDTs will be excited and then generate orthogonal standing SAWs with wave numbers of k1 and k4 in directions of e1 and e4. As predicted by the analytical simulation (Fig. 3A), the interference of orthogonal standing SAWs generates a Gor’kov potential field with 2D periodic peaks (at pressure antinodes) and valleys (at pressure nodes). The pressure nodes are distributed in the form of a 2D rectangular grid array, which can also be considered as a 2D rectangular lattice having a rectangular unit cell with periods of π/k1 and π/k4 in directions of e1 and e4.
Fig. 3. Multiconfiguration 2D patterning of microparticles via wave number–spiral acoustic tweezers.
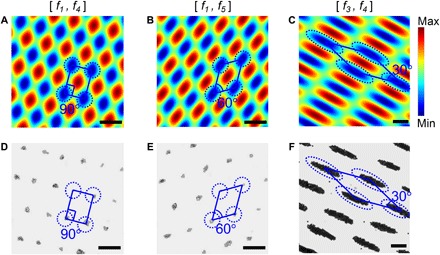
(A to C) Simulated Gor’kov potential fields for wave number–spiral acoustic tweezers, when excitation signals contain different frequency combinations [f1, f4], [f1, f5], and [f3, f4], respectively. (D to F) Experimental results (optical microscopy images) taken for the three frequency combinations [f1, f4], [f1, f5], and [f3, f4], respectively. The experimental results show that microparticles are patterned on 2D lattices with different spatial periods, edge lengths, and interior angles. The blue parallelograms are used for illustrating unit cells of 2D lattices. Scale bars, 100 μm.
More lattice configurations than the 2D rectangular lattice can be achieved by using modulated excitation signals with other frequency combinations. Figure 3 (B and C) plots analytical Gor’kov potential fields of two other representative cases: when the modulated excitations contain frequency combinations [f1, f5] (Fig. 3B) and [f3, f4] (Fig. 3C). For these two combinations, the angles between generated standing SAWs are 60° and 30°, respectively. The resultant potential fields are on oblique lattices with different parallelogram unit cells that have different edge lengths and interior angles. Microparticles in the potential fields shown in Fig. 3 (A to C) can be expected to move to potential valleys and become trapped there. Microparticle patterns in multiple 2D lattice configurations can be expected to form by using modulated excitations with different frequency combinations.
Figure 3 (D to F) shows experimental results for three representative frequency combinations [f1, f4] (Fig. 3D), [f1, f5] (Fig. 3E), and [f3, f4] (Fig. 3F). As expected, different 2D microparticle patterns are formed at potential valleys in different 2D lattice configurations. The density of microparticles in Fig. 3F is higher than those in Fig. 3D and Fig. 3E, which could be caused by the larger size of potential wells in Fig. 3F and variations of seeding densities. The experimental results in panels D to F of Fig. 3 agree well with analytical predictions in panels A to C of Fig. 3 from the perspective of lattice configurations. The agreement of analytical and experimental results verifies that the wave number–spiral acoustic tweezers can pattern microparticles in 2D lattice configurations simply by using excitations with two frequency components. Meanwhile, wave number–spiral acoustic tweezers can control the 2D lattice configuration (such as edge lengths and interior angles of unit cells) and achieve multiconfiguration 1D (section S5 and fig. S6) and 2D patterning by properly selecting the frequency combination. In addition, for any frequency combinations, the lattice configurations can be analytically predicted (section S3).
On-chip cell patterning and culture
In addition to 1D and 2D multiconfiguration patterning of microparticles, experiments were performed to explore the potential applications of the wave number–spiral acoustic tweezers for on-chip cell patterning and culture. For the proof of concept, two types of cells, U937 and HeLa cells, were patterned using the fabricated device. To maintain the optimal environment for cells, we placed the device in a customized cell culture chamber mounted on the stage of an inverted optical microscope (see Materials and Methods).
The experimental results in Fig. 4 (A and B) show that the U937 cells suspended in fresh RPMI 1640 medium were successfully patterned in 1D parallel and 2D rectangular lattice configurations. As shown in Fig. 4A, cells can be patterned in parallel chains of single cells. At some locations of Fig. 4B, it is also possible to distribute only one cell per potential well. In addition to patterning U937 cells, we performed experiments to pattern HeLa cells and then culture the patterned cells in a disposable microfluidic chamber attached on top of the SAW substrate. We injected the HeLa cells suspended in fresh Dulbecco’s Modified Eagle Medium (DMEM) into the disposable microfluidic chamber. After the cells were patterned under 1D standing SAWs, the amplitude of SAWs was gradually decreased to zero so that the patterned cells could settle down on the bottom PDMS layer of the disposable microfluidic chamber. The cells gradually adhered to the bottom PDMS layer while maintaining the original 1D parallel pattern with some slight cell movements, as shown in the optical microscopy images captured after 1 and 3 hours (Fig. 4, D and E). At the end of 6 hours, the captured image (Fig. 4F) shows an expanded cell pattern indicating the spreading of adhered cells, which is caused by cell movement.
Fig. 4. Cell patterning via wave number–spiral acoustic tweezers.
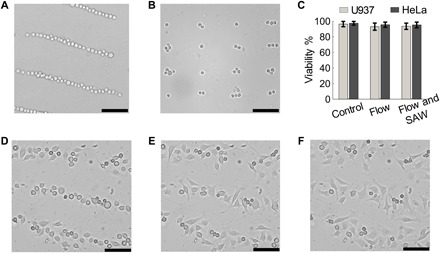
The experimental results (optical microscopy images) show that U937 cells are successfully arranged in (A) a 1D parallel pattern at the frequency f4, and (B) a 2D rectangular lattice with the frequency combination [f1, f4]. (C) For both U937 and HeLa cells, viabilities are nearly the same among three conditions: without any treatment (“Control”), flowing through the device (10 μl/min) without SAWs (“Flow”), and flowing through the device with SAWs with an excitation of 15 Vpp at 12 MHz (“Flow and SAW”). (D to F) Experimental results (optical microscopy images) after HeLa cells have been patterned and cultured for 1, 3, and 6 hours. These results show that cells patterned by SAWs can be cultured in the disposable microfluidic chamber. Meanwhile, the original pattern can be maintained with slight cell movements. Scale bars, 100 μm.
To examine the biocompatibility of our method, we performed cell viability assays on cells under three conditions: without any treatment (control), flowing through the acoustic tweezers (10 μl/min) without SAWs, and flowing through the acoustic tweezers with SAWs [with an excitation of 15 peak-to-peak voltage (Vpp) at 12 MHz]. Cell viabilities were obtained by counting live/dead cells stained with calcein AM (acetoxymethyl) and SYTOX orange (see Materials and Methods). The test results in Fig. 4C indicate that viabilities are nearly identical among these three conditions for both U937 and HeLa cells.
Dynamic manipulation and reconfiguration of 2D patterns
Dynamic, time-variant acoustic fields enable dynamic and reconfigurable particle/cell manipulation. With the capability to simultaneously and independently control both the phases and amplitudes of SAWs with multiple wave numbers in different directions, wave number–spiral acoustic tweezers make it possible to dynamically manipulate SAW wavefields and, thus, particle positions. Experiments were performed using wave number–spiral acoustic tweezers to dynamically manipulate and reconfigure 2D patterns of 10-μm polystyrene beads. Figure 5 (A to D) shows experimental results of four powerful dynamic capabilities, including pattern translation (Fig. 5A), pattern transformation (Fig. 5B), pattern rotation (Fig. 5C), and parallel merging (Fig. 5D).
Fig. 5. Experimental results (optical microscopy images) for dynamic manipulation and reconfiguration of 2D microparticle patterns via wave number–spiral acoustic tweezers.
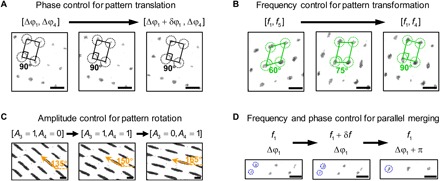
(A) Through phase control, microparticles on a 2D rectangular lattice are gradually translated in-plane, with the rectangular lattice configuration unaffected. (B) Through frequency control, a 2D microparticle pattern on an oblique lattice is gradually transformed to a different pattern on a rectangular lattice. (C) Through amplitude control, multiple beam-shaped microparticle agglomerates are simultaneously rotated from 135° to 165°. (D) Through frequency and phase control, three pairs of microparticle agglomerates are merged in parallel and become three larger agglomerates. Scale bars, 100 μm.
Figure 5A shows that microparticles patterned on a 2D rectangular lattice are gradually translated in-plane (movie S1). The pattern translation is carried out by gradually changing the phase difference Δφ1 at frequency f1 in the modulated excitation signals with frequency combination [f1, f2] (fig. S7A). In addition, the 2D translation of other patterns on oblique lattices is also possible, as proved by the analytical study (section S3). Figure 5B shows that a 2D microparticle pattern on an oblique lattice with an interior angle of 60° is gradually transformed to a different pattern on a rectangular lattice with an interior angle of 90° (movie S2). The pattern transformation is achieved by switching the frequency combination from [f1, f5] to [f1, f4] (fig. S7B). Figure 5C shows that the oblique angles of multiple beam-shaped microparticle agglomerates on a 2D oblique lattice are rotated from 135° to 165° simultaneously (movie S3). The pattern rotation is achieved by gradually increasing the amplitude at frequency f4 and then decreasing the amplitude at frequency f3 in modulated excitation signals with the frequency combination [f3, f4] (fig. S7C). Figure 5D shows that three pairs of microparticle agglomerates on an oblique lattice are merged in parallel and become three larger particle agglomerates (movie S4). The parallel merging is conducted through two steps (fig. S7D). First, the frequency f1 is slightly increased by a small perturbation δf so that standing SAWs with a smaller wavelength can be generated and bring the three pairs of agglomerates closer. Then, the frequency is restored back to f1 with the phase difference shifted to Δφ1 + π so that the three pairs can be merged in parallel and become three larger agglomerates. The maximum allowable velocity of moving a 10-μm polystyrene bead using our SAW-based acoustic tweezers is nearly 1600 μm/s (10), which is limited by the capability of our power amplifier. For switching patterns of multiple particles, the fastest switching action needs about 0.5 s using our acoustic tweezers. In the above, we have achieved four dynamic behaviors, including pattern translation, pattern transformation, pattern rotation, and parallel merging, simply by modulating the excitation signals of the wave number–spiral acoustic tweezers.
Dynamic manipulation of single microparticles
Wave number–spiral acoustic tweezers can control phases of SAWs propagating in different directions, precisely, rapidly, and automatically, thus enabling dynamic manipulation of single microparticles with high precision, flexibility, and robustness. The principle for dynamic manipulation of single microparticles is illustrated in Fig. 6A. The Gor’kov potential fields with acoustic radiation forces (small arrows) generated by two orthogonal pairs of IDTs (denoted as pth and qth pairs) are simulated for illustration purposes (Fig. 6A, top). When phase differences change from Δφ to Δφ + δφ, the potential well is shifted by a vector δx, and thus, a single microparticle in the well can be translated by δx. For two orthogonal pairs of IDTs, the relationship between phase change δφ and spatial translation vector δx is derived analytically (section S3) and summarized in Fig. 6A (bottom). For two pairs of IDTs not orthogonal to each other, a more general relation between δφ and δx is also derived (section S3).
Fig. 6. Dynamic manipulation of single microparticles via wave number–spiral acoustic tweezers.
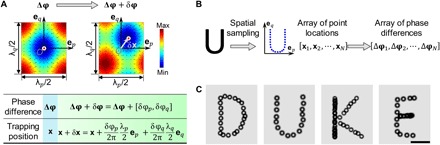
(A) The principle for dynamic manipulation of single microparticles. The Gor’kov potential fields with acoustic radiation forces (small arrows) generated by two orthogonal pairs of IDTs are simulated (top). When phase differences change from Δφ to Δφ + δφ, where Δφ = [Δφp, Δφq] and δφ = [δφp, δφq], the potential well is shifted by a vector δx, and thus, a single microparticle trapped in the well is translated by δx. The relation of phase difference and trapping position is summarized in a table (bottom). (B) Dynamic single-particle translation along desired paths can be performed through three steps. First, through spatial sampling, the desired path is converted to an array of points at coordinates [xn]N. Second, the coordinates are transformed to an array of phase differences [Δφn]N. Third, the dynamic single-particle translation is executed by following the predetermined phase differences and gradually modulating them in excitation signals. (C) Stacked optical images acquired during dynamic manipulation show that microparticles can be translated along complex paths, and their trajectories precisely depict four letters: “D,” “U,” “K,” and “E.” Scale bar, 50 μm.
On the basis of the relation of phase difference and trapping position described in Fig. 6A, single microparticles can be moved along any desired path. When two orthogonal pairs of IDTs are turned on, potential wells are generated in a 2D grid-like pattern and the target microparticle will be driven to the closest potential well, where it is then trapped. The trapped particle’s position is set as the coordinate origin. The following dynamic single-particle translation can be performed in three steps, as illustrated in Fig. 6B. First, the desired path is spatially sampled to generate an array of points at coordinates [x1, x2, ⋯, xN]. Second, the coordinates are transformed to phase differences [Δφ1, Δφ2, ⋯, ΔφN] according to the relation given in Fig. 6A. Third, the dynamic single-particle translation is executed by following the predetermined phase differences and gradually modulating them in excitation signals. We performed experiments using the wave number–spiral acoustic tweezers to translate a 10-μm polystyrene bead along four different paths and write the letters “D,” “U,” “K,” and “E” (movie S5). Figure 6C presents stacked optical images acquired during the dynamic manipulation. The images show that the particle trajectories precisely depict the four letters, even accounting for the curvature of the letters “D” and “U.” In our experiment, the dynamic manipulation is automatically performed by sequentially applying the predetermined phase differences through a function generator controlled by a MATLAB program. Since changing the phase through a programmable function generator is very fast (less than 0.1 s), the speed of moving a microparticle along a desired path is mainly determined by the particle velocity driven by the acoustic radiation force. In addition, in order to ensure that the particle movement closely follows the desired trajectory, the moving velocity should be stable. Our experimental investigation shows that the allowable velocity with an error less than 10% is nearly 15 μm/s for moving a 10-μm polystyrene bead. The experimental results demonstrate that wave number–spiral acoustic tweezers can achieve precise dynamic manipulation of single microparticles simply by modulating the phase differences encoded in the excitation signals.
DISCUSSION
In this study, we developed wave number–spiral acoustic tweezers that can dynamically reshape SAW wavefields and thus achieve dynamic and reconfigurable particle/cell manipulation simply by modulating multitone excitation signals. The wave number–spiral design offers frequency-based steerability, which allows the direction and wave number of standing SAWs to be adjusted by tuning the excitation frequency. Moreover, the wave number–spiral design introduces another feature: SAWs with distinct frequency–wave number components propagating in multiple directions can be controlled simultaneously and independently by using multitone excitation signals. Both the phase and amplitude of SAWs in each direction can be precisely controlled by modulating the phase and amplitude at the corresponding frequency encoded in the multitone excitation signal. With these features, multiconfiguration patterning, dynamic and reconfigurable manipulation, and many other functions are available in a single device. Moreover, wave number–spiral acoustic tweezers have automatic, robust, and flexible control simply by modulating multitone excitation signals without using complex and costly electronics like multichannel function generators and high-end programmable electronics.
We developed an analytical model for wave number–spiral acoustic tweezers. This model considers multiple SAWs with different frequency–wave number components propagating in different directions, allowing rapid simulations of the SAW wavefield, Gor’kov potential field, and acoustic radiation force generated by the wave number–spiral acoustic tweezers. As a result, this model can be used as an efficient tool to explore the potential capabilities and design possibilities of acoustic tweezers. The solutions for potential well distributions were derived through analytical studies, along with the relation between phase change and spatial translation vector. The analytical solutions can be used not only for predicting the potential well patterns but also for guiding the dynamic manipulation process and design of acoustic tweezers. Moreover, using our analytical model, we found a new type of single potential well, multitone potential wells, which are formed by minimizing the multitone SAWs. The single well is present at the global potential minimum, which is surrounded by other local potential minima. Because the potential gradient toward the global minimum is steeper than the gradients toward local minima, the acoustic radiation force driving particles to the global potential minimum is higher than the forces driving particles to the local potential minima. This means that particles are easier to trap at the global minimum by using the same input power for exciting IDTs. As the acoustic radiation forces toward the local minima become stronger with larger input power, the chance that particles fall into local minima will increase. By introducing the subarray concept to wave number–spiral acoustic tweezers, our acoustic tweezers are able to generate two independent multitone potential wells using two subarrays. The position of each potential well can be independently controlled by properly modulating the phase differences of the corresponding subarray.
Through proof-of-concept experiments, we demonstrated multiple functions using a single device, including multiconfiguration 1D and 2D patterning, on-chip cell patterning and culture, dynamic manipulation and reconfiguration of 2D patterns, and dynamic translation of single microparticles along complex paths. Wave number–spiral acoustic tweezers also increase the functionality of a single device because of the ability to dynamically reshape the SAW wavefields to various distributions. In addition, the fabricated device used in our experiments provides two more attractive features for practical implementations. A rosette-shaped IDT cluster with multiple interlinked IDTs only requires one input channel for powering and independently controlling all the IDTs in the cluster. Moreover, we designed a disposable microfluidic chamber with two-layer PDMS that can be peeled off and disposed of after each test, allowing reuse of the substrate to avoid cross contamination between different tests. The energy of SAWs in the substrate can directly transmit into the microfluidic chamber without coupling agents like water, oil, or other ultrasonic couplants.
Our work with wave number–spiral acoustic tweezers moves one step forward toward developing dynamic acoustic tweezers that can achieve more sophisticated operations and functionalities with lower requirements on system complexity and electronics. We believe that the wave number–spiral design will advance a wide range of applications, like bioprinting, fabrication of cell assemblies, cell-cell interactions, single-cell analysis, biosensing, and microscale assembly.
MATERIALS AND METHODS
Device fabrication
A schematic and a photo of the fabricated wave number–spiral acoustic tweezers are given in Fig. 2 (A and B). Five pairs of IDTs were deposited on an X-cut LiNbO3 substrate (thickness, 500 μm and double side polished) using standard lithography, evaporation, and lift-off techniques (16). As shown in Fig. 2, each IDT covers 30°. In the directions −60° to −30° and 120° to 150°, there are no IDTs, since SAWs are very weak in these directions because of the anisotropic properties of the LiNbO3 substrate. In addition, all the IDTs are divided into two groups. In each group, five IDTs are linked, forming a rosette-shaped IDT cluster, such that only two input channels are needed for powering and controlling all the IDTs.
The disposable microfluidic chamber (fig. S8A) is composed of two layers of PDMS, including a top layer with a microfluidic chamber (height, ~60 μm) and a thin bottom layer (thickness, ~30 μm) for sealing the chamber. The top layer was fabricated through standard soft lithography and mold-replica techniques (fig. S9, A to D). To fabricate the bottom layer, a thin layer of PDMS mixture was coated on a silicon wafer through spin coating (fig. S9E) and then baked at 65°C for 20 min. After that, the top layer was placed on the bottom layer with the open chamber facing downward and baked at 65°C for 40 min to bond the two layers together and seal the chamber (fig. S9F). The sealed chamber was peeled off from the silicon wafer and cut to the desired size for use (fig. S9G).
Before each test, a sealed microfluidic chamber was bonded on the LiNbO3 substrate with IDTs (fig. S8B). The bonding was performed in three steps. First, a drop of ethanol was added on the substrate. Then, the chamber was placed at the desired location. Last, the substrate with a chamber on top was baked at 65°C for 10 min. After these three steps, the chamber was successfully bonded on the substrate but could also be peeled off without damaging the substrate (fig. S8C). Hence, after each test, we removed and disposed the chamber to make it possible to reuse the substrate and avoid cross contamination between different tests. In addition, the energy of SAWs in the substrate could directly transmit into the microfluidic chamber through the thin bottom PDMS layer without using any additional coupling agents such as water, oil, or other ultrasonic couplants.
Experimental setup
The fabricated acoustic tweezers chip was mounted on the stage of an inverted optical microscope (TE2000-U, Nikon) with a disposable microfluidic chamber attached on top. Microparticles/cells were infused into the chamber through a 1-ml syringe (309659, Becton Dickinson) by an automated syringe pump (neMESYS, CETONI). The SAW excitation signals were generated by a two-channel arbitrary function generator (AFG3102C, Tektronix), amplified to 15 Vpp through power amplifiers (25A250A, Amplifier Research), and then sent to the IDTs to generate SAWs. Note that the function generator was controlled by a MATLAB program to achieve rapid, precise, and automatic manipulation of SAW wavefields, along with manipulation of microparticles/cells in the microfluidic chamber. In addition, the MATLAB program made it possible to generate a multitone signal in which the amplitude, phase, and delay time of each tone could be precisely modulated. Images and videos were taken by Nikon imaging software (NIS-Advanced, Nikon) through a charge-coupled device digital camera (CoolSNAP HQ2, Photometrics).
Microparticle and cell sample preparation
Polystyrene beads (10 μm; Bangs Laboratories Inc.) were suspended in deionized water to an approximate concentration of 1 × 106 ml−1. U937 cells [purchased from the American Type Culture Collection (ATCC)] were cultured in RPMI 1640 medium (Gibco, Life Technologies) containing 10% fetal bovine serum (Gibco, Life Technologies) and 1% penicillin-streptomycin (Mediatech). HeLa cells (purchased from ATCC) were cultured in DMEM (Gibco, Life Technologies) containing 10% fetal bovine serum (Gibco, Life Technologies) and 1% penicillin-streptomycin (Mediatech). Both the U937 and HeLa cells were maintained in a cell culture incubator (Nu-4750, NuAire) with a temperature of 37°C and a CO2 level of 5%. Before each experiment, U937 (or HeLa) cells were harvested and resuspended in fresh RPMI 1640 medium (or DMEM) to an approximate concentration of 1 × 106 ml−1.
On-chip cell culture
A fabricated acoustic tweezers device with a microfluidic chamber attached on top was placed in a customized cell culture chamber (INUBTFP-WSKM-GM2000A, Prior Scientific) mounted on the stage of an inverted optical microscope (TE2000-U, Nikon). For better adhesion of HeLa cells, the microfluidic chamber was precoated with fibronectin (50 μg/ml; Extracellular Matrices, Corning) at 4°C for 24 hours. Throughout the experiment, the temperature and CO2 level inside the cell culture chamber were maintained at 37°C and 5%, respectively. A humid environment necessary for cell culture was maintained by evaporating deionized water in the chamber.
Cell viability
Cell viability assays were performed on cells under three conditions: without any treatment (control), flowing through the device (10 μl/min) without SAWs, and flowing through the device with SAWs (with an excitation of 15 Vpp at 12 MHz). For each condition, live/dead cell staining was conducted using calcein AM for live cells and SYTOX orange for dead cells (Molecular Probes, Life Technologies). The cell viability was obtained by counting live and dead cells. Cells were counted as dead if they showed any amount of SYTOX orange stain.
Supplementary Material
Acknowledgments
Funding: We acknowledge support from the NIH (R01 HD086325, R01 AI120560, R33CA223908, and R01GM127714) and NSF (ECCS-1807601). Author contributions: Z.T. and S.Y. conceived the idea. Z.T., S.Y., P.-H.H., Z.W., P.Z., Y.G., H.B., M.W., and Y.X. contributed to the experimental design and scientific presentation. Z.T. and S.Y. performed all the experiments and data analysis. Z.T., Y.G., and C.C. contributed to the analytical simulations. S.Y. fabricated the SAW devices. Z.W. cultured and prepared cells. All the authors wrote the paper. T.J.H. provided overall guidance and contributed to the experimental design and scientific presentation. Competing interests: T.J.H. is an inventor on four U.S. patents related to this work filed by Penn State Research Foundation (no. 8573060, filed 4 December 2009; no. 9608547, filed 31 January 2013; no. 9606086, filed 31 July 2013; no. 9757699, filed 27 November 2013). He has also cofounded a start-up company, Ascent Bio-Nano Technologies Inc., to commercialize technologies involving acoustofluidics and acoustic tweezers. The authors declare no other competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/5/eaau6062/DC1
Section S1. Controlling multiple IDTs with a multitone excitation signal
Section S2. An analytical model for the wave number–spiral acoustic tweezers
Section S3. Analytical solutions for 2D potential well distributions
Section S4. Multitone potential wells
Section S5. Multiconfiguration 1D patterning
Fig. S1. A schematic of the wave number–spiral acoustic tweezers with detailed geometric relations.
Fig. S2. The principle of controlling multiple IDTs with a multitone excitation signal.
Fig. S3. Graphical illustrations for in-plane translation of 2D patterns.
Fig. S4. Single multitone potential wells generated by minimizing SAWs at multiple frequencies.
Fig. S5. Two independent multitone potential wells generated with independently controlled subarrays.
Fig. S6. Multiconfiguration 1D patterning of microparticles via wave number–spiral acoustic tweezers.
Fig. S7. Graphical illustrations for dynamic manipulation and reconfiguration of 2D microparticle patterns.
Fig. S8. Photos of a fabricated chip with a disposable PDMS chamber.
Fig. S9. Fabrication steps for a disposable microfluidic chamber.
Movie S1. Pattern translation.
Movie S2. Pattern transformation.
Movie S3. Pattern rotation.
Movie S4. Parallel merging.
Movie S5. Translation of single microparticles along complex paths.
REFERENCES AND NOTES
- 1.Bao G., Suresh S., Cell and molecular mechanics of biological materials. Nat. Mater. 2, 715–725 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Ozcelik A., Rufo J., Guo F., Gu Y., Li P., Lata J., Huang T. J., Acoustic tweezers for the life sciences. Nat. Methods 15, 1021–1028 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ashkin A., Dziedzic J. M., Yamane T., Optical trapping and manipulation of single cells using infrared-laser beams. Nature 330, 769–771 (1987). [DOI] [PubMed] [Google Scholar]
- 4.Voldman J., Electrical forces for microscale cell manipulation. Annu. Rev. Biomed. Eng. 8, 425–454 (2006). [DOI] [PubMed] [Google Scholar]
- 5.De Vlaminck I., Dekker C., Recent advances in magnetic tweezers. Annu. Rev. Biophys. 41, 453–472 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Wu J. R., Acoustical tweezers. J. Acoust. Soc. Am. 89, 2140–2143 (1991). [DOI] [PubMed] [Google Scholar]
- 7.Oberti S., Neild A., Dual J., Manipulation of micrometer sized particles within a micromachined fluidic device to form two-dimensional patterns using ultrasound. J. Acoust. Soc. Am. 121, 778–785 (2007). [DOI] [PubMed] [Google Scholar]
- 8.Shi J., Ahmed D., Mao X., Lin S.-C. S., Lawit A., Huang T. J., Acoustic tweezers: Patterning cells and microparticles using standing surface acoustic waves (SSAW). Lab Chip 9, 2890–2895 (2009). [DOI] [PubMed] [Google Scholar]
- 9.Lee J., Teh S.-Y., Lee A., Kim H. H., Lee C., Shung K. K., Single beam acoustic trapping. Appl. Phys. Lett. 95, 073701 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ding X., Lin S.-C. S., Kiraly B., Yue H. J., Li S. X., Chiang I. K., Shi J. J., Benkovic S. J., Huang T. J., On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. Proc. Natl. Acad. Sci. U.S.A. 109, 11105–11109 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dual J., Schwarz T., Acoustofluidics 3: Continuum mechanics for ultrasonic particle manipulation. Lab Chip 12, 244–252 (2012). [DOI] [PubMed] [Google Scholar]
- 12.Foresti D., Nabavi M., Klingauf M., Ferrari A., Poulikakos D., Acoustophoretic contactless transport and handling of matter in air. Proc. Natl. Acad. Sci. U.S.A. 110, 12549–12554 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carugo D., Octon T., Messaoudi W., Fisher A. L., Carboni M., Harris N. R., Hill M., Glynne-Jones P., A thin-reflector microfluidic resonator for continuous-flow concentration of microorganisms: A new approach to water quality analysis using acoustofluidics. Lab Chip 14, 3830–3842 (2014). [DOI] [PubMed] [Google Scholar]
- 14.Marzo A., Seah S. A., Drinkwater B. W., Sahoo D. R., Long B., Subramanian S., Holographic acoustic elements for manipulation of levitated objects. Nat. Commun. 6, 8661 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Melde K., Mark A. G., Qiu T., Fischer P., Holograms for acoustics. Nature 537, 518–522 (2016). [DOI] [PubMed] [Google Scholar]
- 16.Guo F., Mao Z., Chen Y., Xie Z., Lata J. P., Li P., Ren L., Liu J., Yang J., Dao M., Suresh S., Huang T. J., Three-dimensional manipulation of single cells using surface acoustic waves. Proc. Natl. Acad. Sci. U.S.A. 113, 1522–1527 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Friend J., Yeo L. Y., Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 83, 647–704 (2011). [Google Scholar]
- 18.Reboud J., Bourquin Y., Wilson R., Pall G. S., Jiwaji M., Pitt A. R., Graham A., Waters A. P., Cooper J. M., Shaping acoustic fields as a toolset for microfluidic manipulations in diagnostic technologies. Proc. Natl. Acad. Sci. U.S.A. 109, 15162–15167 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Drinkwater B. W., Dynamic-field devices for the ultrasonic manipulation of microparticles. Lab Chip 16, 2360–2375 (2016). [DOI] [PubMed] [Google Scholar]
- 20.Wiklund M., Acoustofluidics 12: Biocompatibility and cell viability in microfluidic acoustic resonators. Lab Chip 12, 2018–2028 (2012). [DOI] [PubMed] [Google Scholar]
- 21.Garg N., Westerhof T. M., Liu V., Liu R., Nelson E. L., Lee A. P., Whole-blood sorting, enrichment and in situ immunolabeling of cellular subsets using acoustic microstreaming. Microsyst. Nanoeng. 4, 17085 (2018). [Google Scholar]
- 22.Patel M. V., Tovar A. R., Lee A. P., Lateral cavity acoustic transducer as an on-chip cell/particle microfluidic switch. Lab Chip 12, 139–145 (2012). [DOI] [PubMed] [Google Scholar]
- 23.Antfolk M., Magnusson C., Augustsson P., Lilja H., Laurell T., Acoustofluidic, label-free separation and simultaneous concentration of rare tumor cells from white blood cells. Anal. Chem. 87, 9322–9328 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Jakobsson O., Antfolk M., Laurell T., Continuous flow two-dimensional acoustic orientation of nonspherical cells. Anal. Chem. 86, 6111–6114 (2014). [DOI] [PubMed] [Google Scholar]
- 25.Courtney C. R. P., Ong C.-K., Drinkwater B. W., Bernassau A. L., Wilcox P. D., Cumming D. R. S., Manipulation of particles in two dimensions using phase controllable ultrasonic standing waves. P. R. Soc. A 468, 337–360 (2011). [Google Scholar]
- 26.Collins D. J., Morahan B., Garcia-Bustos J., Doerig C., Plebanski M., Neild A., Two-dimensional single-cell patterning with one cell per well driven by surface acoustic waves. Nat. Commun. 6, 8686 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Collins D. J., Devendran C., Ma Z., Ng J. W., Neild A., Ai Y., Acoustic tweezers via sub–time-of-flight regime surface acoustic waves. Sci. Adv. 2, e1600089 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Guo F., Li P., French J. B., Mao Z., Zhao H., Li S., Nama N., Fick J. R., Benkovic S. J., Huang T. J., Controlling cell-cell interactions using surface acoustic waves. Proc. Natl. Acad. Sci. U.S.A. 112, 43–48 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Naseer S. M., Manbachi A., Samandari M., Walch P., Gao Y., Zhang Y. S., Davoudi F., Wang W., Abrinia K., Cooper J. M., Khademhosseini A., Shin S. R., Surface acoustic waves induced micropatterning of cells in gelatin methacryloyl (GeLMA) hydrogels. Biofabrication 9, 015020 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ai Y., Sanders C. K., Marrone B. L., Separation of Escherichia coli bacteria from peripheral blood mononuclear cells using standing surface acoustic waves. Anal. Chem. 85, 9126–9134 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ren L., Yang S., Zhang P. R., Qu Z., Mao Z., Huang P.-H., Chen Y., Wu M., Wang L., Li P., Huang T. J., Standing surface acoustic wave (SSAW)-based fluorescence-activated cell sorter. Small 14, 1801996 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tan M. K., Friend J. R., Yeo L. Y., Interfacial jetting phenomena induced by focused surface vibrations. Phys. Rev. Lett. 103, 024501 (2009). [DOI] [PubMed] [Google Scholar]
- 33.Demirci U., Picoliter droplets for spinless photoresist deposition. Rev. Sci. Instrum. 76, 065103 (2005). [Google Scholar]
- 34.Franke T., Abate A. R., Weitz D. A., Wixforth A., Surface acoustic wave (SAW) directed droplet flow in microfluidics for pdms devices. Lab Chip 9, 2625–2627 (2009). [DOI] [PubMed] [Google Scholar]
- 35.Zhang S. P., Lata J., Chen C., Mai J., Guo F., Tian Z., Ren L., Mao Z., Huang P.-H., Li P., Yang S., Huang T. J., Digital acoustofluidics enables contactless and programmable liquid handling. Nat. Commun. 9, 2928 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu M., Ouyang Y., Wang Z., Zhang R., Huang P.-H., Chen C., Li H., Li P., Quinn D., Dao M., Suresh S., Sadovsky Y., Huang T. J., Isolation of exosomes from whole blood by integrating acoustics and microfluidics. Proc. Natl. Acad. Sci. U.S.A. 114, 10584–10589 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Riaud A., Thomas J.-L., Charron E., Bussonnière A., Matar O. B., Baudoin M., Anisotropic swirling surface acoustic waves from inverse filtering for on-chip generation of acoustic vortices. Phys. Rev. Appl. 4, 034004 (2015). [Google Scholar]
- 38.Riaud A., Baudoin M., Thomas J.-L., Matar O. B., Saw synthesis with idts array and the inverse filter: Toward a versatile saw toolbox for microfluidics and biological applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63, 1601–1607 (2016). [DOI] [PubMed] [Google Scholar]
- 39.Riaud A., Thomas J.-L., Baudoin M., Matar O. B., Taming the degeneration of bessel beams at an anisotropic-isotropic interface: Toward three-dimensional control of confined vortical waves. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 92, 063201 (2015). [DOI] [PubMed] [Google Scholar]
- 40.Engholm M., Stepinski T., Olofsson T., Imaging and suppression of lamb modes using adaptive beamforming. Smart Mater. Struct. 20, 085024 (2011). [Google Scholar]
- 41.Bruus H., Acoustofluidics 7: The acoustic radiation force on small particles. Lab Chip 12, 1014–1021 (2012). [DOI] [PubMed] [Google Scholar]
- 42.Baresch D., Thomas J.-L., Marchiano R., Observation of a single-beam gradient force acoustical trap for elastic particles: Acoustical tweezers. Phys. Rev. Lett. 116, 024301 (2016). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/5/eaau6062/DC1
Section S1. Controlling multiple IDTs with a multitone excitation signal
Section S2. An analytical model for the wave number–spiral acoustic tweezers
Section S3. Analytical solutions for 2D potential well distributions
Section S4. Multitone potential wells
Section S5. Multiconfiguration 1D patterning
Fig. S1. A schematic of the wave number–spiral acoustic tweezers with detailed geometric relations.
Fig. S2. The principle of controlling multiple IDTs with a multitone excitation signal.
Fig. S3. Graphical illustrations for in-plane translation of 2D patterns.
Fig. S4. Single multitone potential wells generated by minimizing SAWs at multiple frequencies.
Fig. S5. Two independent multitone potential wells generated with independently controlled subarrays.
Fig. S6. Multiconfiguration 1D patterning of microparticles via wave number–spiral acoustic tweezers.
Fig. S7. Graphical illustrations for dynamic manipulation and reconfiguration of 2D microparticle patterns.
Fig. S8. Photos of a fabricated chip with a disposable PDMS chamber.
Fig. S9. Fabrication steps for a disposable microfluidic chamber.
Movie S1. Pattern translation.
Movie S2. Pattern transformation.
Movie S3. Pattern rotation.
Movie S4. Parallel merging.
Movie S5. Translation of single microparticles along complex paths.


