Two-dimensional hybrid perovskites sustaining strong polariton interactions at room temperature

Large single-crystal flakes of 2D perovskite are able to sustain strong polariton nonlinearities at room temperature.

Abstract

Polaritonic devices exploit the coherent coupling between excitonic and photonic degrees of freedom to perform highly nonlinear operations with low input powers. Most of the current results exploit excitons in epitaxially grown quantum wells and require low-temperature operation, while viable alternatives have yet to be found at room temperature. We show that large single-crystal flakes of two-dimensional layered perovskite are able to sustain strong polariton nonlinearities at room temperature without the need to be embedded in an optical cavity formed by highly reflecting mirrors. In particular, exciton-exciton interaction energies are shown to be spin dependent, remarkably similar to the ones known for inorganic quantum wells at cryogenic temperatures, and more than one order of magnitude larger than alternative room temperature polariton devices reported so far. Because of their easy fabrication, large dipolar oscillator strengths, and strong nonlinearities, these materials pave the way for realization of polariton devices at room temperature.

INTRODUCTION

In efficient communication and computing systems, information carriers are required to both travel long distances without losing coherence and simultaneously interact between them to implement logic functions such as switches or logic gates. Microcavity polaritons, quasiparticles that form in a semiconductor when an elementary excitation field interacts sufficiently strongly with the electromagnetic radiation field, could, in principle, fulfill these requirements and are promising candidates for a new generation of optoelectronic devices. These “dressed” photons exhibit enhanced nonlinearities due to their electronic component (1, 2), allowing many-body effects to be studied in optical systems and appearing as building blocks for integrated photonic circuits and electro-optic applications (3, 4). However, to bring strong nonlinearities and good optical properties to room temperature (RT) is a real challenge. Recently, polariton condensation and superfluidity have been observed at RT in organic semiconductors due to the very large binding energy and oscillator strength of Frenkel excitons (5). Nevertheless, interactions among excitons in organic materials are usually at least two orders of magnitude lower than the ones observed for typical Wannier-Mott excitons, and the spin degree of freedom, which is of paramount importance for photonic applications, is quickly averaged out. On the other hand, polaritons in layered transition metal dichalcogenide (TMD) materials have been anticipated as a possible approach to resolving this problem, as recently demonstrated (6), showing interactions at least 10 times higher than organic materials. However, these must be in single monolayers to function, are difficult to control, and barely achieve extensions of more than several tens of micrometers. Here, we demonstrate that polariton-polariton interactions at RT in two-dimensional (2D) single-crystal perovskites are as high as those measured at cryogenic temperatures in inorganic semiconductors.

Hybrid organic-inorganic perovskite systems have recently attracted a considerable attention driven by exceptional progress in photovoltaics, photonics, and optoelectronics (7–10). In particular, 2D perovskites are spontaneous realizations of multiple layered quantum well (QW) heterostructures made of (PbX₆)2− tetrahedral inorganic layers, with X indicating a halide, sandwiched between bilayers of organic cations (see Fig. 1A) (11, 12). The lowest-energy electronic excitations are associated with the inorganic sheet, the organic part acting as a potential barrier (7, 8, 13, 14).

Fig. 1. 2D perovskite single crystal embedded in an optical cavity.

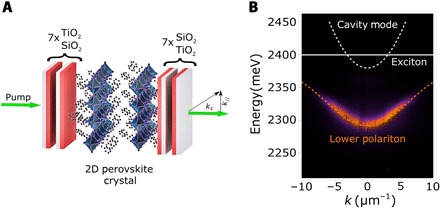
(A) Schematic representation of a 2D perovskite single crystal embedded in an optical cavity formed by two DBRs; in 2D perovskite, inorganic layers are separated by organic ligands realizing an effective multiple layered QW structure. (B) Energy versus in-plane momentum k photoluminescence emission from the sample represented in (A), with $k=\frac{2\mathrm{\pi }}{\mathrm{\lambda }}\text{sinθ}$, θ being the emission angle; the white dashed and solid lines represent the cavity and the exciton uncoupled modes, respectively, and the orange line is a fit to the polariton lower mode with E_X = 2.395 eV, E_C = 2.385 eV, and ℏΩ = 170 meV.

These 2D layered structures share strong similarities with multi-QW heterostructures made of epitaxially grown inorganic semiconductors, but they have larger binding energies and display stronger dielectric confinement in the inorganic layers. 2D hybrid perovskites also show enhanced collective effects due to the large number of layers stacked in a single crystal, which is an advantage over TMD monolayers. Strong light-matter coupling has already been observed in MAPbBr₃ microwire/nanowire cavities (15); in particular, evidence for exciton-polariton condensation has recently been reported in all-inorganic perovskite CsPbX₃ nanoplatelets (16, 17) and in spin-coated layered hybrid organic-inorganic perovskite thin films (18–20). Su et al. (21) have also shown polariton propagation in a CsPbBr₃ microcavity wire over a distance of 60 μm. These results indicate huge room for substantial advancements in realization of low-threshold coherent light sources and polaritonic devices with this kind of hybrid organic-inorganic semiconductor (22).

In this study, using single crystal of 2D hybrid perovskites, we were able to directly estimate an exciton-exciton interaction constant as high as $3\mathrm{\mu eV}{\mathrm{\mu m}}^2$. This value is more than one order of magnitude larger than the alternative RT polariton systems reported thus far and is comparable to the system used in all-optical transistors, switches, and gates currently shown to be operable only at cryogenic temperatures in GaAs-based semiconductors.

It is worth noting the strong recent interest in evaluation of such parameters in GaAs- or InGaAs-based polaritons. One of the main difficulties is estimation of the proper density of polaritons and the exciton reservoir that could lead to very diverse values, sometimes differing by many orders of magnitude (23–25).

To avoid possible overestimation of the interaction constant, we make sure in this study to deal only with polariton states by using a short resonant pulse excitation (50 fs) and a low repetition rate (10 kHz) to avoid the possible effect of dark exciton states persisting longer than the time between pulses. Moreover, we use very conservative quantities to estimate the polariton density. The 2D single-crystal perovskite we use is a large single-crystal flake of high quality to avoid nonradiative losses and grain-to-grain heterogeneity usually present in polycrystalline films.

At RT, we find the exciton oscillator strengths to be much larger than in epitaxial GaAs QWs at cryogenic temperatures and with comparable nonlinearities. Because of the large oscillator strength of the excitons and the very good crystal structure of the flakes, formation of polaritonic bands and strong nonlinearities are observed even when these structures are not embedded in a microcavity comprising highly reflecting mirrors. This finding is an important step toward realization of polaritonic devices working at RT with easy fabrication and minimal processing, avoiding complex heterostructures comprising top and bottom Bragg mirrors and prohibitive ultralow temperature of operation.

RESULTS AND DISCUSSION

We synthesize phenethylammonium lead iodide (C₆H₅(CH₂)₂NH₃)₂PbI₄ (PEAI) using an anti-solvent vapor-assisted crystallization method (26) and subsequent mechanical exfoliation (11). The 2D perovskite single crystals we use are large single-crystal flakes of high quality to avoid nonradiative losses and grain-to-grain heterogeneity usually present in polycrystalline films. In this study, we investigate both PEAI single crystals embedded in an optical cavity formed by two distributed Bragg reflectors (DBRs) acting as bottom/top mirrors and bare single crystals. Figure 1A shows a sketch of a single 2D PEAI crystal grown on a DBR formed by seven Si0₂/Ti0₂ pairs. A second DBR also formed by seven Si0₂/Ti0₂ pairs is sputtered on the single crystal to give rise to an optical Fabry-Perot cavity, where the PEAI 2D crystal is embedded. The optical response of the sample is measured in transmission geometry, where the excitation is provided by a nonresonant continuous-wave laser or a femtosecond pulsed laser resonant on the low polariton branch (see also the Supplementary Materials).

Figure 1B shows the energy and in-plane momentum-resolved emission from this sample under nonresonant excitation. Because of the strong coupling between the cavity mode and the exciton in the PEAI single crystal, a lower polariton mode is clearly visible with an emission energy of about 2.31 eV at k = 0. By fitting the experimental dispersion, we obtain a Rabi splitting ℏΩ = 170 meV, with an energy minimum of the cavity mode at E_C = 2.385 eV and an exciton energy E_X = 2.395 eV.

To test the polarization-dependent polariton-polariton interaction in this sample, we measure the resonant transmission of a 50-fs pulsed excitation laser through the sample at normal incidence (k = 0). The laser repetition rate is 10 kHz. The large time interval between laser pulses excludes the possibility that the observed dynamics are influenced by reservoir states, which usually have a lifetime no longer than 1 ns. Figure 2A shows the transmission when the laser is linearly polarized, and Fig. 2B shows the transmission when the laser is circularly polarized. Each spectrum in Fig. 2 (A and B) corresponds to different excitation powers, P. As the excitation power increases, we observe a shift of the transmission peak toward higher energies. The energy blueshift of the transmission peaks is plotted in Fig. 2C against the excitation power. As the excitation power increases, we observe a shift of the transmission peak toward higher energies, as expected for a system of interacting particles (16, 27), where the polariton density inside the active medium is proportional to the incident power. Moreover, Fig. 2C shows that the energy blueshift obtained with a circularly polarized laser (blue dots) is higher than the blueshift measured with a linearly polarized laser (red dots). That is, the observed energy blueshift is sensitively larger when all the polaritons are created with the same spin (28–31). Instead, by using a linear polarized laser (i.e., a coherent superposition of two counter-polarized circular components), only half of the excited polaritons share the same spin, thus roughly halving the interaction energy. We notice that the polarization properties of the elementary excitations in these materials arise from the optical transitions connecting the valence band s-type states with total angular momentum quantum numbers (J = 1/2, J_z = ±1/2) to p-type conduction band states with the same symmetry (because of the spin-orbit splitting in the conduction band) (32, 33). Hence, bright exciton states correspond to optical transitions satisfying the condition ΔJ_z = ±1, which can be excited by using either clockwise or counterclockwise circularly polarized radiation. As a consequence, polariton states are formed with ±1 spin polarization, in close analogy to inorganic semiconductor exciton polaritons in microcavities with embedded QWs.

Fig. 2. Nonlinearities in a cavity-embedded perovskite single crystal.

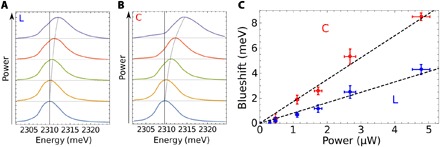
(A) Transmittivity spectra obtained by cutting the dispersion in Fig. 1B in k = 0 and corresponding to different resonant excitation power for linear (A) and circular (B) polarized excitation laser. (C) Blueshift of the polariton modes in the case of a linear (L) and a circular (C) polarized laser; the dashed lines are linear fit to the experimental data with slopes of 1.75 and 0.83 $\text{meV}/\mathrm{\mu W}$ for C and L, respectively.

Thus, the observed spin dependence strongly indicates not only that polariton-polariton interactions are the dominant effect responsible for the energy shift of the modes upon optical excitation but also that 2D perovskites can be used for polariton spintronics. The dashed lines in Fig. 2C are obtained as a linear fit to the experimental points. The ratio between the two slopes is L/C = 0.47 ± 0.06. By following Vladimirova et al. (29), we can extract the ratio α₂/α₁ from the data of Fig. 2C, in which α₂ is the interaction strength between polaritons with opposite spin and α₁ is the interaction strength between polaritons with the same spin. We then deduce from Fig. 2C a ratio ∣α₂/α₁∣ ∼ 0.05. This value is consistent with the picture of polariton-polariton interactions in standard semiconductors at cryogenic temperature, i.e., a strong repulsive interaction for polaritons with the same spin (α₁ > 0) and a weaker interaction for polaritons with opposite spin (∣α₁∣ ≫ ∣α₂∣). We observe spin-dependent nonlinearities similar to those observed in GaAs-based systems at cryogenic temperatures (29).

In the mean-field approximation and at low particle density, the blueshift ΔE_pol depends linearly on the polariton density n_pol: ΔE_pol = g_poln_pol. The polariton density n_pol is proportional to the excitation power incident on the sample. By analyzing the power dependence of the blueshift, it is possible to measure the polariton interaction constant and then, knowing the polariton excitonic fraction (or Hopfield coefficient), one can finally infer the excitonic interaction constant g_exc per layer under circularly polarized excitation. The estimated excitonic interaction constant values for the microcavity sample are g_exc ∼ 3 ± 0.5 $\mathrm{\mu eV}{\mathrm{\mu m}}^2$. This value is comparable with the one typically estimated for a single GaAs QW (24, 25), and it is the largest measured value at RT so far (see also the Supplementary Materials for details on the calculation of the excitonic interaction constant).

We also note that a small broadening is visible in the spectra of Fig. 2 (A and B) as the incident power increases. This effect can be explained by a time-dependent blueshift given by the exponential decay of the polariton population over time after the passage of the pump pulse. The broadening could result in a small underestimation of g_exc. However, we checked its contribution to be negligible, and the spectra of Fig. 2 (A and B) are consistent with the value of the exciton interaction constants obtained by taking the linear blueshift of the peak maxima (6). High values of polariton-polariton interaction constants have recently been suggested by numerical simulation of 1D condensate propagation in 3D perovskites (21).

The observation of polaritonic nonlinearities at RT in organic-inorganic hybrid materials is a fundamental step to assess their potential for real-world polariton devices. The structure of the sample in Fig. 1A is complex and requires at least a three-step fabrication process: growth of the bottom DBR mirror, growth of the single-crystal flake, and finally growth of the top DBR mirror. Further developments could involve additional fabrication steps like electrical contacts for carrier injection or interconnecting several devices to provide the different functionalities associated with network-on-chip technology. These further steps would result in an even more complex fabrication process, possibly hindering the technological appeal of RT polaritonic devices. However, RT polaritons in 2D single-crystal PEAI flakes have been observed even if the crystal flake is not embedded in an optical cavity formed by highly reflecting mirrors (32). Single bare PEAI crystal flakes without cavity are a relatively simpler system to grow. Moreover, the active region can be readily accessed for electrical connections, patterning, or interconnecting several devices. From a technological point of view, assessing RT polariton nonlinearities in single 2D crystals with no cavity is of utmost importance and would lift the complication to embed the perovskite between two mirrors.

Figure 3A shows a sketch of a single 2D PEAI crystal flake grown on a glass substrate. Figure 3B shows in-plane momentum and energy-resolved reflectivity spectra obtained from the single 2D PEAI crystal slab under white light illumination. The optical response of the sample is measured with an oil-immersion microscope objective, which allows us to capture, from the glass substrate side, the signal from the total internal reflection (TIR) at the air-crystal interface (see the Supplementary Materials for details). The measured reflectivity shows a manifold of lower polariton modes (visible as dips in the reflectivity spectra) arising from the coupling of the bare excitonic resonance (white line) with the optical resonances arising from multiple reflections at the top and bottom interfaces of the perovskite slab (32). The red dashed lines of Fig. 3B are fits to the lower polariton modes, giving a value of energy coupling between the optical modes and the excitonic transition of ℏΩ ∼ 170 meV. This value is larger than the linewidths of the different resonances involved, and it is thus fully consistent with the strong exciton-photon coupling regime (32). In particular, strong coupling between the exciton mode and the optical resonances of the slab is obtained at RT due to the optical confinement given by the refractive index contrast at the interface between the crystal and the surrounding media (air and glass substrate, respectively) and the high value of the excitonic oscillator strength in 2D perovskites.

Fig. 3. 2D perovskite single crystal grown on a glass substrate.

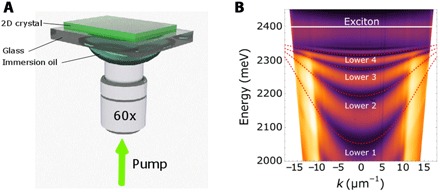
(A) Schematic representation of the TIR configuration adopted for resonant blueshift measurements: An immersion oil objective (60×) is used to focus the excitation beam on a 2D PEAI single-crystal flake grown on a glass substrate; the same objective is used to collect the reflected light. (B) Energy and in-plane momentum k resolved reflectivity spectra of a thick single-crystal slab of PEAI; the dips in reflectivity correspond to lower polariton modes resulting from the coupling of the exciton mode to different optical modes; the white line represents the energy of the bare exciton mode; the red dashed lines represent lower polariton modes; the enhanced intensity for k ⩾ 10 ${\mathrm{\mu m}}^{-1}$ corresponds to angles of incidence beyond the light line between air and the perovskite slab.

To understand whether the observed polariton modes of the bare 2D PEAI crystal can sustain nonlinearities at RT, we resonantly excite the single-crystal slab with a femtosecond pulsed laser. The excitation beam forms a finite angle with the surface of the slab, corresponding to an in-plane momentum of about k ∼ 12.7 ${\mathrm{\mu m}}^{-1}$. This value of in-plane momentum corresponds to an angle that is beyond the crystal-air TIR angle, which means that all the incident laser power is absorbed or reflected by the sample, where the transmitted part is negligible. The green oval region in Fig. 4A shows the energy and momentum spread of the laser used in resonant excitation. Figure 4B represents a vertical cut of the dispersion of Fig. 4A corresponding to the green region.

Fig. 4. Nonlinearities in a 2D perovskite single crystal.

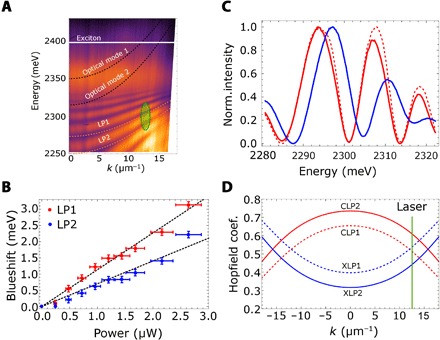
(A) Reflectivity spectra obtained for a PEAI single-crystal slab; the same excitonic mode is coupled to several optical modes of the slab; the two lower polariton modes highlighted by orange dashed lines originate from the coupling of the two optical modes (black dashed lines) to the excitonic mode (white solid line). (B) Energy shift of the lower polariton modes of (A) as a function of the incident power; the energy shift is measured at k ∼ 12.7 ${\mathrm{\mu m}}^{-1}$ corresponding to the green region of (A). (C) Reversibility of the observed blueshift of the polariton modes; the red continuous curve corresponds to the energy of the polariton modes for low excitation power P = 10 $\mathrm{\mu J}/{\text{cm}}^2$; the continuous blue curve shows the blueshifted modes at high excitation power P = 150 $\mathrm{\mu J}/{\text{cm}}^2$; when the excitation power is reduced, the polariton modes recover the original energy (dashed red curve). (D) Hopfield coefficients showing the exciton (XLP1, XLP2) and photon (CLP1, CLP2) fraction of the two lower polariton modes of (A); the green vertical line represents the in-plane momentum of the resonantly created polariton, where LP1 has a larger exciton fraction than LP2.

This choice of the incident angle, in addition to being in the highest reflectivity region, also allows us to probe polariton modes with a higher excitonic fraction and smaller linewidth. The bandwidth of the femtosecond laser is large enough to resonantly excite essentially three adjacent lower polariton branches. Figure 4B shows that the reflectivity spectra change when the incident power is increased: The low-power resonances (red continuous lines) are shifted at high incident power (blue continuous lines) and then recover their initial energy (red dashed lines) when the incident power is lowered, which guarantees that the blueshift is not due to degradation of the material upon optical excitation. This evidence shows that the observed blueshift arises from interparticle interactions, as observed in low-temperature inorganic polariton systems (28–30) and in the cavity-embedded single crystal in Fig. 2.

The TIR geometry chosen to perform resonant excitation allows us to neglect the transmission through the sample, simplifying the estimation of the incident power (see also the Supplementary Materials). The two lower polariton branches fitted by the dashed orange lines (LP1 and LP2) originate from the two optical modes highlighted by the two black dashed lines. Polariton modes originating from different cavity modes and coupled to the same excitonic transition have a different excitonic fraction at a given excitation angle. Figure 4C shows the blueshift measured for the lower polariton branches LP1 and LP2 in Fig. 4A as a function of the polariton density by using a linearly polarized pulsed laser. We observe that, for a given incident power (i.e., a given polariton density), the measured blueshift is higher for the polariton branch with the higher excitonic fraction, LP1, which confirms that the energy blueshift increases as the excitonic component increases. By fitting the data in Fig. 4C with a straight line and considering the relation between ΔE_pol and n_pol, we can obtain the excitonic interaction constant per layer $g_{\text{exc},\mathrm{L}}$ under linearly polarized excitation. Given the incident power values and considering that all the absorbed light is transformed into polaritons (which is a very conservative approximation, see the Supplementary Materials), the upper density limit for the exciton density per layer is about $n_{\text{exc},\text{layer}}={10}^{12}$ cm⁻². Accounting for the different excitonic fraction of the two lower polariton branches, we obtain a value of the excitonic interaction constant $g_{\text{exc},\mathrm{L}}\sim 1\pm 0.2$ $\mathrm{\mu eV}{\mathrm{\mu m}}^2$ per inorganic layer. This value is comparable with that obtained for the 2D single crystal embedded in a microcavity, as shown in Figs. 1 and 2. In both cases, we used a pulsed resonant laser to estimate the interaction constants, thus avoiding the effects of the polariton-reservoir interactions that would contribute to the blueshift observed and would forbid a direct probe of the polariton-polariton interaction constants. Moreover, we would like to stress that by neglecting any loss in the material, we overestimate the number of excitons in the system; therefore, much larger interaction strengths should be expected, and the reported value of g_exc should be taken as a lower bound. Nevertheless, this lower bound is already at least two orders of magnitude higher than typical interaction constants of organic excitons at RT (34) and about 20 times larger than the values recently measured in a WS₂ monolayer (6).

In summary, we have observed highly interacting polaritons in hybrid organic-inorganic 2D perovskite single crystals at RT. These materials spontaneously crystallize in a multiple layered QW-like structure, and because of the high oscillator strength of the excitonic transition, strong coupling is achieved at RT even without highly reflecting mirrors. The resulting polaritons are highly interacting with an excitonic interaction constant $g_{\text{exc}}\sim 3\pm 0.5\mathrm{\mu eV}{\mathrm{\mu m}}^2$. This value is two orders of magnitude higher than the values measured for organic excitons, and it is the highest measured at RT so far. Moreover, we observe that polariton-polariton interactions in our sample are spin dependent, where the repulsive interaction between polaritons with the same spin is the dominant effect. These results demonstrate that 2D hybrid organic-inorganic perovskites sustain highly interacting polaritons working with interaction constants, which are very promising for future polaritonic and spintronic devices at RT. We observe highly interacting polaritons at RT without embedding the active medium in an optical cavity. These findings are extremely important and promise to greatly reduce the cost and the complexity of fabrication and postprocessing of polaritonic devices.

METHODS

Synthesis of 2D perovskite flakes

PEAI solutions were prepared by dissolving equimolar amounts of PbI₂ and phenethylammonium iodide in γ-butyrolactone and stirring at 70°C for 1 hour. 2D perovskite single crystals were synthesized using an anti-solvent vapor-assisted crystallization method as follows: 5 μl of the perovskite solution was deposited on a glass cover slip and then covered by a second cover slip. Next, a small vial containing 2 ml of dichloromethane was placed on the top of the two sandwiched substrates. Substrates and vial were placed in a larger Teflon vial, closed with a screw cap, and left undisturbed for some hours. After this time, millimeter-sized crystals, with thicknesses varying from few to tens of micrometers, appeared in between the two substrates. Single crystals were mechanically exfoliated with the SPV 224PR-M Nitto Tape and transferred onto glass substrates. The exfoliated flakes, with thicknesses of tens of nanometers, appeared smooth and uniform over tens of square micrometers, as observed by scanning electron microscopy and atomic force microscopy.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/5/eaav9967/DC1

Section S1. Material synthesis

Section S2. Microcavity fabrication

Section S3. Absorption and photoluminescence

Section S4. Optical setup

Section S5. Interaction constant

Fig. S1. Absorption (blue) and photoluminescence (green) spectra measured on top of a PEAI single crystal with a 488-nm continuous-wave laser.

Fig. S2. Optical setup used to measure the microcavity sample.

Fig. S3. Exciton blueshift as a function of exciton density per QW obtained with a linearly polarized laser.

Fig. S4. Microcavity-embedded single crystal.