Statistical methods for evaluating the correlation between timeline followback data and daily process data with applications to research on alcohol and marijuana use

Abstract

Background:

Retrospective timeline follow-back (TLFB) data and prospective daily process data have been frequently collected in addiction research to characterize behavioral patterns. Although previous validity studies have demonstrated high correlations between these two types of data, the conventional method adopted in those studies was based on summary measures that may lose critical information and the Pearson’s correlation coefficient that has an undesirable property. This study proposes the functional concordance correlation coefficient to address these issues.

Methods:

We use real data collected from a randomized experiment to demonstrate the applications of the proposed method and compare its analytical results with those of the conventional method. We also conduct a simulation study based on the real data to evaluate the level of overestimation associated with the conventional method.

Results:

The results of the real data example indicate that the correlation between these two types of data varies across substances (alcohol vs. marijuana) and assessment schedules (daily vs. weekly). Additionally, the correlations estimated by the conventional method tend to be higher than those estimated by the proposed method. The simulation results further show that the magnitude of overestimation associated with the conventional method is greatest when the true correlation is medium.

Conclusions:

The findings of the real data example imply that daily assessments are particularly beneficial for characterizing more variable behaviors like alcohol use, whereas weekly assessments may be sufficient for low variation events such as marijuana use. The proposed method is a better approach for evaluating the validity of TLFB data.

1. Introduction

The timeline follow-back (TLFB; Sobell & Sobell, 1992) is a technique which uses a calendar and structured interview to assist retrospective recall of daily alcohol consumption over a specified time period (e.g., 90 days). It has also been adopted to assess a variety of health risk behaviors such as smoking (e.g., Sobell et al., 2017), drug use (e.g., Giasson-Gariepy, Potvin, Ghabrash, Bruneau, & Jutras-Aswad, 2017), violence (e.g., Epstein-Ngo et al., 2014), sexual behavior (e.g., Schroder, Johnson, & Wiebe, 2007), and eating behavior (e.g., Bardone, Krahn, Goodman, & Searles, 2000). In fact, TLFB is a popular measure in the substance abuse field because it can characterize the day-to-day patterns of substance use behaviors better than conventional questionnaires which usually inquire about an average or typical amount of substance use. In recent decades, health communication technology such as interactive voice response (IVR) and short message service (SMS) has made it possible to collect prospective daily process data, which record physiological or behavioral processes such as symptoms or mood daily over a period of time (Tennen, Affleck, Armeli, & Carney, 2000). In these data, retrospection bias and selectivity in describing experiences are both minimized. More importantly, because these technology systems can be delivered through participants’ mobile phones in real time and natural contexts, daily process data tend to have greater ecological validity (Reis, 2012). As a result, the number of researchers collecting daily process data has increased dramatically in the last decade (Gunthert & Wenze, 2012). Sophisticated statistical methods for examining the temporal association between precursors, target behaviors or consequences have also been applied to analyze these rich data (e.g., Testa & Derrick, 2014).

In spite of the many strengths of daily process data, TLFB is still more practical in some clinical and research settings, because it is less costly and demanding than daily data collection (Searles, Helzer, & Walter, 2000). The prospective daily process data could serve as an ideal criterion to validate the use of retrospective TLFB data in such settings. Researchers have demonstrated high correlations between TLFB data and daily process data based on summary measures such as an average number of drinks per day (Bardone et al., 2000; Kranzler, Abu-Hasaballah, Tennen, Feinn, & Young, 2004; Searles, Helzer, Rose, & Badger, 2002; Simpson et al., 2010; Simpson, Xie, Blum, & Tucker, 2011; Suffoletto, Callaway, Kristan, Kraemer, & Clark, 2012; Tucker, Foushee, Black, & Roth, 2007). Yet, summary measures are known to leave out clinically meaningful information (Wang, Winchell, McCormick, Nevius, & O’Neill, 2002). For example, an average number of drinks per day may not differentiate between one participant who drinks moderately every day and another one who only binges on the weekend. Furthermore, previous studies showed that the day-to-day correspondence measured by within-subject correlations between TLFB and daily process data could vary widely from −1 to +1 across individuals (Perrine, Mundt, Searles, & Lester, 1995; Searles et al., 2000; Simpson et al., 2011; Tucker et al., 2007). Thus, given that a major objective of collecting this type of data is characterizing behavior patterns over time, the potential loss of critical information due to aggregation and the possibility of reporting inflated correlations across validity studies are both legitimate concerns.

Even though the Pearson’s correlation coefficient has been commonly adopted in validity studies, it may not be an ideal method to evaluate the correlation between TLFB and daily process data. In the statistics literature, the Pearson’s correlation coefficient has been known to be a poor measure for agreement between two sets of data with location or scale shifts (Lin, 1989). This means that when two sets of data have different means or variances, the Pearson’s correlation coefficient could still be close to the value of +1 or − 1 as long as they have a strong linear relationship (In Section 2.1, we provide the mathematical definition of location or scale shifts and also demonstrate this issue with an example on self-reported quantity of alcohol consumption). This shortcoming of the Pearson’s correlation coefficient raises a real concern in the current research context, because the literature consistently shows that the level of health risk behaviors reported in daily process data tends to be higher than that in TLFB data (e.g., Patrick & Lee, 2010; Tucker et al., 2007). To deal with this issue, Lin (1989) proposed an alternative measure, the concordance correlation coefficient (CCC), and demonstrated its great statistical properties based on mathematical work and Monte Carlo simulations, including consistency, asymptotic normality, and robustness against samples from non-normal distributions even with small sample sizes. Another issue with existing validity studies is their heavy reliance on summary measures instead of the original daily data, which can be modeled as functional data because they are collected in many adjacent time points and can be characterized by nonparametric smooth functions (Ramsay & Silverman, 2005). In fact, Li and Chow (2005) have developed a new CCC for measuring agreement between paired functional data by extending Lin’s work, which is only applicable to paired data collected at a single time point. This functional CCC is, therefore, a better method to quantify the correlation between TLFB and daily process data.

The present study is the first application of the technical work of Li and Chow (2005) in the statistics literature to an important practical problem in addiction science. We provide a less technical introduction of this proposed method. We also use real data collected from a randomized experiment to demonstrate the applications of the proposed method (based on functional data), as well as compare its analytical results with those of the conventional method (based on summary measures). Further, the observations in the real data example serve as a motivator for a simulation study which is designed to evaluate the level of inflation associated with the conventional method across different settings. Moreover, we provide a comprehensive discussion of the application implications as well as an R package for carrying out the proposed method (see the Appendix).

2. Concordance correlation coefficient (CCC)

2.1. Cross-sectional data

Although the classical work of Lin (1989) only applies to cross sectional data, we briefly review it here to (1) illustrate the difference between the concordance correlation coefficient (CCC) and the Pearson correlation coefficient (Pearson’s r); and (2) provide a foundation for understanding its extension to functional data. The Pearson’s r (ρ) measures the linear relationship between two random variables X and Y but it fails to detect any location or scale shift. This is because ρ(aX + b,Y) = ρ(X,aY + b) = ρ(X,Y), where a > 0 and b are constants. To overcome this drawback, Lin (1989) proposed the CCC:

$${\rho }_c=\frac{2 \text{cov} (X,Y)}{ \text{var} (X)+ \text{var} (Y)+{(E(X)-E(Y))}^2},$$

which possesses the following properties:

1. −1≤ρ_c≤1 and |ρ_c|≤|ρ|.

2. ρ_c=0 if and only if ρ = 0.

3. ρ_c=ρ if and only if E(X) = E(Y) and var(X) = var (Y).

4. ρ_c= ± 1 if and only if ρ= ± 1, E(X)=E(Y) and var (X)= var (Y).

The Pearson’s r (ρ) measures how close the observations are to the best-fit line, whereas the CCC (ρ_c) measures how close the observations are to the identity line (i.e., 45° line). The former is always greater than or equal to the latter. When ρ_c = 1, each pair of measurements is in perfect agreement, for example, the data would look like (1,1), (2,2), (3,3), (4,4), (5,5). On the other hand, when ρ = 1, the data could be as discordant as (1,3), (2,5), (3,7), (4,9), (5,11). Suppose that the latter data reflect the number of drinks reported by five participants using both the TLFB and the daily process method, ρ would be an undesirable measure.

2.2. Functional data

Li and Chow (2005) extended the Pearson’s r and CCC to handle paired functional data. The original application was to evaluate the overall agreement between two methods for measuring body core temperature every minute over 90 min of an experimental period. Suppose that X(t) and Y(t) are a pair of measurements from the same subject with the time t ∈ T which is a finite closed real interval. The inner product is defined as.

$$\langle X(\cdot ),Y(\cdot )\rangle =E{\int }_{\text{T}}X(t)Y(t)w(t)dt,$$

where w(t) is a weight function and takes non-negative values over T. To simplify the notation, let X = X(t) and Y = Y(t). Li and Chow (2005) proposed the Pearson’s r for paired functional data as.

$$\rho (X,Y)=\frac{\langle X-E(X),Y-E(Y)\rangle }{\Vert X-E(X)\Vert \cdot \Vert Y-E(Y)\Vert },$$

Where $\Vert X\Vert =\sqrt{\langle X,X\rangle }$; both E(X) = E(X(t))and E(Y) = E(Y(t)) are functions of t. They also proposed the CCC for paired functional data as.

$${\rho }_c(X,Y)=\frac{2\langle X-E(X),Y-E(Y)\rangle }{\Vert E(X)-E(Y){\Vert }^2+\Vert X-E(X){\Vert }^2+\Vert Y-E(Y){\Vert }^2}.$$

Note that when X and Y are two univariate random variables (i.e., not functions of t) and w(t) = 1, the above two equations are reduced to the original Pearson’s r and CCC for cross-sectional data, respectively. Furthermore, no matter what the weight function is, this new CCC retains all the good properties of the original CCC proposed by Lin (1989). In practice, the true parameters ρ and ρ_c are unknown and can only be estimated based on the data from the whole sample. Li and Chow (2005) proposed estimators for both parameters (the technical details are omitted here) and established the consistency and asymptotic normality of the proposed estimators. Building upon the theorem, they further derived asymptotic confidence intervals for these estimators.

A unique strength of the method proposed by Li and Chow (2005) for estimating ρ and ρ_c in paired functional data is that the weight function w(·) allows researchers to assign more weight on the data collected during critical time points (given prior information). This is highly relevant to substance use related data, as it is well known that the consumption level tends to be higher on weekend days (Buu et al., 2014). When no prior information is available, however, common practices are to adopt equal weights across time or choose the weight function based on the patterns of empirical data. In Section 3.3, we provide a data analysis example to demonstrate how we assign different weights based on the weekday-weekend patterns of substance use empirically derived from the real data. We also provide a scientific reason for our approach. In the Appendix, we describe how to use the free R package developed by our team to assign equal weights (the default) or different weights for different time points using the example in Section 3.3.

3. A real data example

3.1. Design and sample

The Measurement and Methodology (M&M) Study (Buu et al., 2017) is a randomized experiment that was designed to examine the validity of TLFB data, as well as the properties of daily process data (e.g., measurement reactivity) as a function of assessment methods and schedules. The study focused on two assessment methods, IVR and SMS, which have been commonly used to collect daily process data and yet their relative compliance, response patterns, and user experiences were unknown. Further, the study was designed to test out a hybrid weekly protocol that requires recall of behaviors in the past week right after the weekend, in order to reduce the concerns about low compliance and measurement reactivity associated with daily data collection and also provide high quality data on the peak of use (i.e., during weekend). Participants of the M&M Study were recruited by re-contacting 600 drug users who enrolled in a previous observational study, the Flint Youth Injury Study (Bohnert et al., 2015), while seeking care in an emergency department (50% for assault injury) about 4 years before the M&M Study. Three hundred and seven participants aged 18–29 (mean = 24) were recruited into the M&M Study and randomized to four (2 × 2) assessment groups with different combinations of assessment methods (IVR or SMS) and schedules (daily or weekly). About 50% of the participants were male; 60% Black; 26% White; and 66% under public assistance.

At baseline, a 20–30 min staff-administered TLFB interview was conducted to collect retrospective data on substance use related behaviors including alcohol use, drug use, violence and sexual behaviors for each day in the past 90 days. Participants in the daily groups reported daily by IVR/SMS about their behaviors on the previous day for 90 days, starting from the next day of the baseline assessment. The weekly groups retrospectively reported about their behaviors in the previous 7 days on Sunday or Monday after the baseline; for those whose baseline was on a Sunday, Monday, or Tuesday, the duration was 13 weeks, whereas the others had the duration of 14 weeks. This protocol ensured that the IVR/SMS data collection fully covered the 90 days after baseline (i.e., the experimental period) for both the daily and weekly groups. After the experimental period, a 90-day TLFB interview was conducted to collect retrospective data on relevant behaviors so the correlation between TLFB and daily process data can be evaluated. The correlation was calculated for the daily and weekly groups separately for the purpose of comparison. We only include a brief description of the protocol that is directly related to the topic of this manuscript. Interested readers may refer to Buu et al. (2017) for other details of the M&M Study.

In this study, we analyzed the TLFB and daily process data on daily consumption of alcohol and marijuana using both the conventional method (summary measures) and the proposed method (functional data). The corresponding questions and responses are: “How many drinks containing alcohol did you have yesterday?” (0–60); “How many times did you use marijuana yesterday?” (0 = “none”; 1 =“once”; 2 = “twice”; 3 = “3–4 times”; 4 = “5–6 times”; 5 = “7–9 times”; 6=“10 or more times”). The following inclusion criteria based on participants’ retrospective reports at baseline were used to ensure that the analysis only included current substance users: alcohol use 2–4 times/month, 2–3 times/week, or 4+ times/week in past 6 months; marijuana use weekly or daily in past 6 months. These criteria identi-fied 112 current alcohol users and 146 current marijuana users. The statistical analysis on the real data from the M&M Study aimed to examine three research hypotheses. First, we hypothesized that the level of correlation between daily process and TLFB data for marijuana consumption would be higher than that for alcohol consumption, because the level of day-to-day fluctuation in marijuana consumption tends to be lower. Second, the level of correlation between the weekly protocol and the TLFB was hypothesized to be higher than that between the daily protocol and the TLFB, because of the retrospective nature of the weekly protocol. Third, we hypothesized that the level of correlation between daily process and TLFB data would be higher when the recall window is closer to the assessment time of TFLB, because the degree of memory decay would be lower.

3.2. Statistical analysis based on summary measures

Three commonly adopted summary measures were calculated for alcohol consumption: 1) the average number of drinks per day; 2) the percentage of days involving drinking; and 3) the maximum number of drinks. A similar set of three summary measures was computed for marijuana consumption except that the frequency rather than the quantity was the focus: 1) the average frequency of marijuana use per day; 2) the percentage of days involving marijuana use; and 3) the maximum frequency of marijuana use. Each summary measure was generated under three recall windows from the recent to the past: Days 1–30; Days 31–60; and Days 61–90.

Table 1 shows the Pearson’s correlation coefficient (Pearson’s r) and concordance correlation coefficient (CCC) for the correlation between TLFB and daily process data based on summary measures of alcohol consumption. These indices were calculated for the daily group and the weekly group separately for the purpose of comparison. Table 2 depicts the corresponding results on marijuana consumption. As expected, the level of correlation between TLFB and daily process data for marijuana consumption was higher than that for alcohol consumption. The correlations between TLFB and daily process data on the percentage of days involving drinking were higher than the corresponding correlations on the other two summary measures, indicating that drinking quantity was not approximated as well by TLFB. Moreover, our hypothesis that the TLFB would be more highly correlated with the weekly protocol than the daily protocol was only supported by the data on alcohol consumption. In terms of marijuana consumption, the correlation was at about the same level under both protocols. Although one would expect the correlation to decrease as the recall window moved from recent (i.e., 1–30) to past (61–90), the results did not show a clear pattern of changes to support this hypothesis. Furthermore, the CCC was consistently lower than Pearson’s r on summary measures of alcohol consumption, whereas the values of these two indices were very similar on summary measures of marijuana consumption.

Table 1.

The conventional Pearson’s correlation coefficients and concordance correlation coefficients based on summary measures of alcohol use in the real data example by assessment schedules and recall windows.

Composite scores with three recall windows	Daily		Weekly
	Pearson’s r	CCC	Pearson’s r	CCC
Average number of drinks per day
Days 1 −30	0.2395	0.0624	0.4486	0.3598
Days 31 −60	0.2736	0.1279	0.4408	0.3022
Days 61 −90	0.2606	0.2125	0.1949	0.1466
Percentage of days involving drinking
Days 1 −30	0.4205	0.3280	0.7331	0.6884
Days 31 −60	0.4414	0.2878	0.5969	0.5351
Days 61 −90	0.3493	0.2859	0.6032	0.5518
Maximum number of drinks
Days 1 −30	0.2743	0.2261	0.3531	0.3487
Days 31 −60	0.1969	0.1605	0.2562	0.2274
Days 61 −90	0.1209	0.1156	0.2334	0.1741

Table 2.

The conventional Pearson’s correlation coefficients and concordance correlation coefficients based on summary measures of marijuana use in the real data example by assessment schedules and recall windows.

Composite scores with three recall windows	Daily		Weekly
	Pearson’s r	CCC	Pearson’s r	CCC
Average frequency of marijuana use per day
Days 1–30	0.6972	0.6927	0.6716	0.6703
Days 31–60	0.6748	0.6594	0.6612	0.6565
Days 61–90	0.7159	0.7020	0.5506	0.5437
Percentage of days involving marijuana use
Days 1 −30	0.6452	0.6354	0.6109	0.6059
Days 31 −60	0.6316	0.6091	0.4730	0.4681
Days 61 −90	0.6844	0.6340	0.4324	0.4125
Maximum frequency of marijuana use
Days 1 −30	0.5258	0.5146	0.5559	0.5219
Days 31 −60	0.5941	0.5283	0.5226	0.4804
Days 61 −90	0.6009	0.5165	0.3993	0.3729

3.3. Statistical analysis based on functional data

As demonstrated in Tables 1 to 2, results of the conventional method could vary a lot across different summary measures, especially concerning alcohol consumption. The proposed method that treats both TLFB and daily process data as functional data not only avoids this issue but also preserves most of the information in the original data. Another important strength of the proposed method is that different weights could be assigned to different observed days, based on the likelihood of involvement in the target behavior. On those days with lower risk, perfect agreement in the data is more likely to occur (0 matches with 0). Thus, they do not contain as much information as the data collected on other days with higher risk, when some discrepancy in two reports about the quantity/frequency is usually expected. For this reason, the former days are assigned lower weight when the correlation is estimated. In this real data example, we weighted the seven days during a week based on the weekday-weekend patterns of substance use empirically derived from the daily process data. Table 3 lists the weight for each weekday by the type of substance use, which was estimated by the percentage of use events (response > 0) for the corresponding substance among all the reports collected on the particular weekday. The distributions indicate that alcohol use was more likely to occur during the weekend, whereas the likelihood of marijuana use only slightly increased on weekend days. Table 4 shows the Pearson’s r and CCC with 95% confidence intervals by assessment schedules and recall windows based on alcohol consumption data. Table 5 depicts the parallel results based on marijuana consumption data. As expected, the correlation between TLFB and daily process data for marijuana consumption was higher than that for alcohol consumption. Moreover, our hypothesis that TLFB would be more highly correlated with the weekly protocol than the daily protocol was only supported by the data on alcohol consumption. Although it was generally observed that the correlation decreased from Days 1–30 to Days 31–60, the expected decrease from Days 31–60 to Days 61–90 was not observed. Furthermore, the CCC was only slightly lower than Pearson’s r even with respect to alcohol consumption.

Table 3.

The weight functions of weekdays for calculating the functional Pearson’s correlation coefficients and concordance correlation coefficients by the type of substance use.

Weekday	Alcohol use	Marijuana use
Sunday	0.2544081	0.6463944
Monday	0.2347066	0.6446918
Tuesday	0.2325301	0.6526493
Wednesday	0.2152691	0.6492729
Thursday	0.2729498	0.6635828
Friday	0.3854819	0.6846615
Saturday	0.4182927	0.7048760

Table 4.

The functional Pearson’s correlation coefficient and concordance correlation coefficient with 95% confidence intervals based on functional data of alcohol use in the real data example by assessment schedules and recall windows.

		Daily		Weekly
		Pearson’s r	CCC	Pearson’s r	CCC
Days 1–30	Estimate 95% CI	0.1470 (0.0671, 0.2269)	0.1296 (0.034, 0.2252)	0.3628 (0.1233, 0.6023)	0.3271 (− 0.1107, 0.7648)
Days 31–60	Estimate 95% CI	0.0640 (− 0.0044, 0.1324)	0.0492 (− 0.0085, 0.1068)	0.1076 (0.0143, 0.2009)	0.0912 (− 0.0099, 0.1923)
Days 61–90	Estimate 95% CI	0.1131 (0.0326, 0.1936)	0.1047 (0.0181, 0.1914)	0.1866 (0.0254, 0.3479)	0.1437 (− 0.0487, 0.3362)

Table 5.

The functional Pearson’s correlation coefficient and concordance correlation coefficient with 95% confidence intervals based on functional data of marijuana use in the real data example by assessment schedules and recall windows.

		Daily		Weekly
		Pearson’s r	CCC	Pearson’s r	CCC
Days 1–30	Estimate 95% CI	0.556 (0.4257, 0.6863)	0.5435 (0.2671, 0.8199)	0.5439 (0.3846, 0.7033)	0.5325 (0.1902, 0.8749)
Days 31–60	Estimate 95% CI	0.4888 (0.3387, 0.6389)	0.4677 (0.1825, 0.7528)	0.5285 (0.3609, 0.6962)	0.5208 (0.1735, 0.8681)
Days 61–90	Estimate 95% CI	0.5219 (0.3861, 0.6577)	0.5112 (0.2201, 0.8023)	0.4797 (0.3022, 0.6572)	0.4711 (0.1371, 0.805)

4. Simulation study

The results of the real data example indicate that the correlations based on summary measures (Tables 1–2) tend to be higher than those based on functional data (Tables 4–5). These observations coupled with the concerns of information loss and correlation overestimation associated with summary measures compelled us to conduct a simulation study to further investigate this issue. In this simulation study, we manipulated the true value of the correlation and compared the estimation of the conventional method (based on a summary measure) with that of the proposed method (based on functional data).

4.1. Design of the experiment

Suppose we have n subjects from whom data are collected at time points t₁, …, t_T. Let D be the n × T data matrix with each row representing a subject and each column representing a time point:

$$D=\left(\begin{array}{cccc}{D}_{11}& D_{12}& \cdots & D_{1T}\\ D_{21}& D_{22}& \cdots & D_{2T}\\ ⋮& ⋮& \ddots & ⋮\\ D_{n1}& D_{n2}& \cdots & D_{nT}\end{array}\right).$$

In this simulation study, the TLFB data from the motivating example were designated as D, which was used as a template to generate another data set E. Particularly, we considered the following two cases:

Case 1: D is the TLFB data set on the quantity of alcohol consumption;

Case 2: D is the TLFB data set on the frequency of marijuana consumption.

In each case, we manipulated the Pearson’s r between D and E (ρ = 0.1, 0.2,…,1.0). Given the correlation ρ, we generated E column by column as follows. Let D_t and E_t(1 ≤ t ≤ T) denote the t-th column of D and E, respectively. We first generated a vector X_t of the same size as D_t, with each element in X_t being independent from the empirical distribution of D_t. Thus, X_t was independent of D_t. Then, we defined $E_t=\rho D_t+\sqrt{1-{\rho }^2}{X}_t\text{ for }1\le t\le T$. Under this setting, the Pearson’s r between D_t and E_t was ρ for any t; consequently, the functional Pearson’s r between D and E was ρ. We also computed the true values of the functional CCC between D and E (denoted by ρ_c) which depended on the true values of ρ and the empirical distribution of D_t. Tables 6–7 show the true values of ρand ρ_c under Cases 1–2, respectively.

Table 6.

The true functional Pearson’s correlation coefficients (ρ) and the corresponding functional concordance correlation coefficients (ρ_c) for the alcohol use data in the simulation study.

ρ	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
ρc	0.1	0.1997	0.299	0.398	0.4966	0.5951	0.6939	0.7935	0.8948	1

Table 7.

The true functional Pearson’s correlation coefficients (ρ) and the corresponding functional concordance correlation coefficients (ρ_c) for the marijuana use data in the simulation study.

ρ	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
ρc	0.0995	0.1962	0.2889	0.3776	0.4632	0.548	0.6354	0.7307	0.8435	1

We also made some adjustments to the simulated data set E to ensure that it had the same measurement scale as D. For Case 1, the alcohol consumption measure can only take values 0,1, …,60. Thus, we first rounded all the data in E to their nearest integers and then set any values > 60 to 60. For Case 2, the marijuana consumption measure can only take values 0, 1, 2, 3, 4, 5, 6. We first rounded all the data in E to their nearest integers and then set any values larger than 6 to 6. Using the real data D and simulated data E, we applied the method by Li and Chow (2005) to estimate the functional Pearson’s r and the functional CCC. For the purpose of methodological comparison, we also applied the conventional method to estimate Pearson’s r and CCC based on summary measures. Let ${\overline{D}}_i$ and $\overline{E_i}$ denote the sample mean of the i-th row of D and E, respectively. Using $\left({\overline{D}}_1,\dots ,{\overline{D}}_n\right)$ and $\left({\overline{E}}_1,\dots ,{\overline{E}}_n\right)$, the Pear son’s r and CCC for cross-sectional data could be calculated. The experiment was repeated 100 times. Then, the average values of the resulting four estimates (i.e., two functional indices and two conventional indices) over the 100 replications were compared with the true values to evaluate the performance of these estimates.

4.2. Simulation results

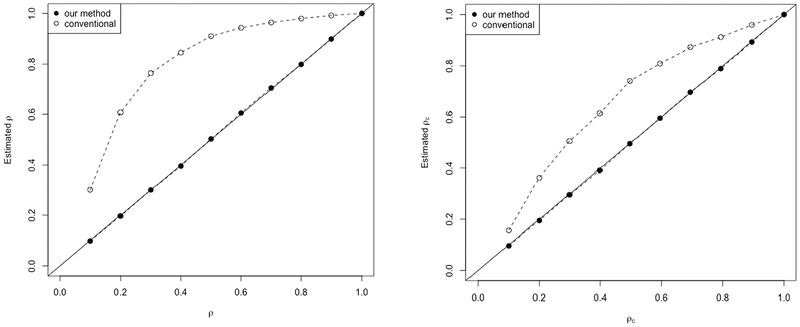
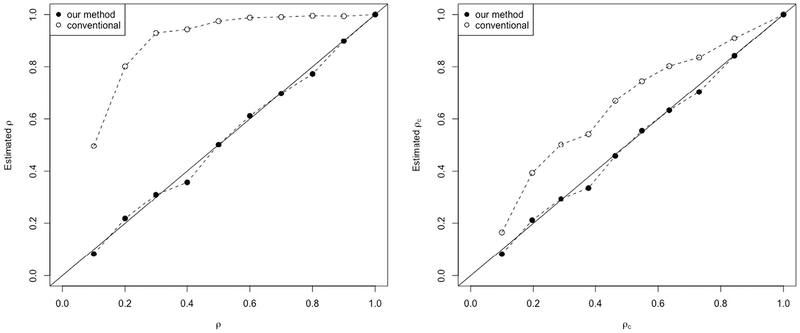
The simulation results are summarized in Figs. 1 to 2 for Cases 1–2, respectively. In each figure, the x-axis denotes the true correlation and the y-axis denotes the estimated correlation. The left panel compares the true ρand the estimated ρ, whereas the right panel compares the true ρ_c and the estimated ρ_c. Each dot represents the average of the corresponding estimates from the 100 replications. The solid diagonal line is the 45° line (y = x), which serves as the reference line. The closer a dot is to this line, the better the estimator performs. Both figures suggest that the proposed methods outperform the conventional methods that tend to overestimate the true correlations. Additionally, the magnitude of overestimation for the Pearson’s r is greater than that for the CCC (comparing the left panel with the right panel). Furthermore, the degree of deviation of the conventional estimates from the true values is characterized as a bell curve with the peak around the middle of the 0–1 scale.

Fig. 1.

Evaluating the two methods for estimating the Pearson’s correlation coefficient ρ (the left panel) and the concordance correlation coefficient ρ_c (the right panel) using the simulated data of alcohol use.

Fig. 2.

Evaluating the two methods for estimating the Pearson’s correlation coefficient ρ (the left panel) and the concordance correlation coefficient ρ_c (the right panel) using the simulated data of marijuana use.

5. Discussion

This study applies both the conventional and proposed methods to analyze the novel data collected from the M&M Study, with the objective of validating TLFB data using daily process data as the criterion. Specifically, we examine whether the correlation between these two types of data varies across substances (alcohol vs. marijuana), assessment schedules (daily vs. weekly), and recall windows (Days 1–30; Days 31–60; and Days 61–90). The first research hypothesis that the correlation between daily process and TLFB data would be higher for marijuana consumption than for alcohol consumption is based on previous research, which indicated that alcohol use behaviors are more likely to vary across days during a week than marijuana use behaviors (Buu et al., 2014). In fact, the empirical data collected from the M&M Study support this point, as alcohol use is more likely to occur on weekend days, whereas the likelihood of marijuana use does not change across days during a week. Further, both the conventional measures and functional measures indicate that the correlation between daily process and TLFB data is consistently higher for marijuana use. In fact, a previous study showed that self-report TLFB data and collateral TLFB data were more consistent for the frequency of marijuana use than for the frequency of alcohol use during a period of 6 months (Donohue et al., 2004). This implies that the TLFB assessment may be a better approach to delineating marijuana use, which does not have as much variation across days as compared to alcohol use. On the contrary, alcohol use tends to be influenced by social events (Finlay, Ram, Maggs, & Caldwell, 2012) and thus may fluctuate within a week and across weeks, making it less precise in characterizing the daily pattern of such behaviors using a retrospective method like the TLFB. In this regard, our findings are consistent with previous results (Hoeppner, Stout, Jackson, & Barnett, 2010) showing that 7-day TLFB reports resulted in greater estimates of alcohol consumption than 30-day TLFB reports.

The second research hypothesis that the TLFB would correlate more highly with the weekly protocol than the daily protocol is only supported by the alcohol consumption data, but not by the marijuana consumption data. For alcohol use, the weekly protocol appears to be more similar to the retrospective TLFB approach than the daily protocol, resulting in some loss of detailed information. This finding again demonstrates the relatively stable pattern of marijuana use. Taken together, the results suggest that daily assessments are particularly beneficial for measuring alcohol use with greater precision than retrospective TLFB interviews. Although weekly assessments are somewhat less precise for alcohol use, they may be sufficient for delineating marijuana use.

The third research hypothesis that the correlation between daily process and TLFB data would be higher when the recall window is closer to the assessment time of TLFB is not generally supported by the M&M data. Although this hypothesis is intuitively reasonable and consistent with the literature, our data do not show a clear decreasing trend from the recent to the past recall windows to support it. Although the way TLFB is administered aims to encourage the access of episodic memory (defined as the retrieval of information about specific episodes of a behavior), participants may tend to switch to sematic memory (referring to generalization about behavior that is stored in memory) as the reported date goes back in time. Such a switch may already occur sometime during the first 30-day recall window (Buu et al., 2014) and thus results in no consistent change across the three recall windows.

Statistical analysis on the M&M data demonstrates that the conventional methods in general produce higher estimates than those generated by the proposed methods. The simulation study further characterizes the degree of overestimation associated with the conventional method as a function of the true values. Specifically, the magnitude of deviation from the true value is relatively small when the true correlation is small (near 0) or large (near 1), whereas it is greatest when the true correlation is around the middle of the scale (around 0.5). This implies that the large correlation between TLFB data and daily process data reported in existing validity studies could possibly be a somewhat inflated estimate of just a medium correlation between the two. On the contrary, the proposed method is able to consistently produce an accurate estimate no matter what the true value is. Another important result of the simulation study is that the degree of overestimation by the conventional Pearson’s r is much greater than that by the conventional CCC. This finding, therefore, suggests that the Pearson’s r is a less desirable approach for validating TLFB data by daily process data.

The CCC has three major strengths that are particularly applicable to data collected in the substance abuse field. First, it can detect any location or scale shifts. Thus, if participants tend to report a higher level of addictive behaviors on one measure than the other, the value of CCC would decrease whereas the value of Pearson’s r would remain unchanged. Second, because CCC does not assume that the data follow any underlying distribution (Li & Chow, 2005), it can handle any data including skewed or zero-inflated data. Thus, CCC is highly applicable to substance use related data that are often dichotomous, ordinal, or count with zero-inflation. Third, the functional CCC was designed to handle a pair of any functional data, and thus has many practical applications beyond what was demonstrated by the analysis on daily data from the M&M Study. Particularly, in tobacco research, the ecological momentary assessment (EMA) involving multiple assessments within each day over a study period (Shiffman, 2009) has been commonly adopted to collect real-time data on mood swings and smoking episodes. The proposed method is also applicable to such data although they are more intensive than daily data. Furthermore, it is not uncommon to assess reports of substance use through multiple raters (e.g., self-report vs. collateral report), multiple modes (e.g., on-line vs. in-person), and multiple timeframes (e.g., test-retest). Thus, although the proposed method was originally motivated by the research question of validating TLFB data using daily process data as the criterion, it can also be applied to these settings. In spite of the wide applications reviewed above, the CCC has a notable limitation: it cannot be applied to analyze multivariate outcomes (e.g., analyzing the alcohol and marijuana data together). In the setting involving both functional data and multivariate outcomes, interested readers may refer to the distance correlation proposed by Gorecki et al. (2016). This alternative approach, however, is location-scale invariant just like Pearson’s r (Li, Zhong, & Zhu, 2012).

There are some limitations of the real data example that warrant future research. First, the randomized experiment was conducted among emerging adults who were originally recruited by a previous observational study on drug users, when they sought care in an emergency department (half for assault injury) about 4 years before the current study. Although the community sample of drug users with high proportion of minorities is a strength, findings nonetheless require validation with other samples. Second, the assessment did not include questions about the quantity of marijuana use, which is an important and yet challenging characteristic of marijuana consumption because of the wide variation in administration (smoking, edible, vaping) and potency (Norberg, Mackenzie, & Copeland, 2012). Instead, our study did assess the frequency of marijuana use that does not depend on the type of products. Future studies examining feasible methods to assess quantity particularly comparable across products are urgently needed for marijuana use, given national trends towards legalization of medical and recreational marijuana.

In conclusion, this study has made unique contributions to the addiction literature. First, we introduce a functional data approach to deal with the issues of the conventional method for validating TLFB data, as well as provide a free software to carry out this analytic approach (see the Appendix). Particularly, this new approach addresses the overestimation associated with the conventional method as characterized by the results of the simulation study. Second, we apply both the conventional and proposed approaches to analyze real data from a randomized experiment, as well as examine important research questions associated with the validity of TLFB data. The findings imply that daily assessments are particularly beneficial for characterizing more variable behaviors like alcohol use, whereas weekly assessments may be sufficient for low variation events such as marijuana use, if a higher precision (than that of the TLFB approach) is desirable. Researchers choosing an assessment methodology will need to balance feasibility and validity issues, with prospective approaches (preferably daily assessments followed by weekly assessments) having greater sensitivity to variations in behavioral patterns than retrospective TLFB approaches. Finally, such prospective approaches are important for measuring alcohol consumption as opposed to marijuana consumption, particularly given severe consequences likely associated with binge or high intensity drinking (Hingson, Zha, & White, 2017; Patrick & Terry-McElrath, 2017).

HIGHLIGHTS.

• Functional concordance correlation coefficient is the recommended method.

• Validity of timeline followback varies by substances and assessment schedules.

• Daily assessments are beneficial for more variable behaviors like alcohol use.

• Weekly assessments are sufficient for low variation events like marijuana use.

Appendix A. Appendix

We developed an R package, fccc, which is an abbreviation of functional concordance correlation coefficient and distributed it via Github. To install the package, please use the following commands:

> devtools::install_github(“TwoLittle/fccc”)

> library(fccc)

The package includes an introduction about the functions that can be used to carry out the conventional and proposed methods, as well as a simple example that demonstrates the usage. To check out the introduction and example, please use the following commands:

> help(package = ‘fccc’)

There are two functions in the package:

1. get.con.cor(X, Y): calculates the conventional Pearson’s correlation coefficient and the conventional concordance correlation coefficient.

2. get.fun.cor(X, Y, W): calculates the functional Pearson’s correlation coefficient and the functional concordance correlation coefficient.

The input data X and Y should be prepared in a matrix form with each row being a subject and each column being a time point. X and Y should be of the same size. Missing values should be coded as NaN.

The function, get.fun.cor(X, Y, W), also allows the user to specify the weight function, W, based on the research context. If the user does not specify the weight function W, get.fun.cor uses equal weights for each time point by default. For example,

> x = matrix(norm(12), 3, 4)

> y = matrix(norm(12), 3, 4)

> get.fun.cor(x, y)

Without the weight function, get.fun.cor(x, y)assumes equal weights, which produce exactly the same result as.

> w = matrix(1, 3, 4) # equal weight

> get.fun.cor(x, y, w)

One can also assign different weights to different time points. For example, suppose that we use the weight function for alcohol use listed in Table 3 to assign weights for each data point. Let W_ij be the (i,j)element of W. Then the value of the weight W_ij is determined by the weekday corresponding to the data point (i,j). For example, W_ij equals 0.2544081 if the corresponding weekday is Sunday; and W_ij equals 0.3854819 if the corresponding weekday is Friday.