Real-world Performance of Meta-analysis Methods for Double-Zero-Event Studies with Dichotomous Outcomes Using the Cochrane Database of Systematic Reviews

Yanan Ren; Lifeng Lin; Qinshu Lian; Hui Zou; Haitao Chu

doi:10.1007/s11606-019-04925-8

. 2019 Mar 18;34(6):960–968. doi: 10.1007/s11606-019-04925-8

Real-world Performance of Meta-analysis Methods for Double-Zero-Event Studies with Dichotomous Outcomes Using the Cochrane Database of Systematic Reviews

Yanan Ren ¹, Lifeng Lin ², Qinshu Lian ¹, Hui Zou ³, Haitao Chu ^1,^✉

PMCID: PMC6544742 PMID: 30887438

Abstract

Background

Meta-analysis combines multiple independent studies, which can increase power and provide better estimates. However, it is unclear how best to deal with studies with zero events; such studies are also known as double-zero-event studies (DZS). Several statistical methods have been proposed, but the agreement among different approaches has not been systematically assessed using real-world published systematic reviews.

Methods

The agreement of five commonly used methods (i.e., the inverse-variance, Mantel–Haenszel, Peto, Bayesian, and exact methods) was assessed using the Cohen’s κ coefficients using 368 meta-analyses with rare events selected from the Cochrane Database of Systematic Reviews. Three continuity corrections, including the correction of a constant 0.5, the treatment arm continuity correction (TACC), and the empirical (EMP) correction, were used to handle DZS when applying inverse-variance and Mantel–Haenszel methods.

Results

When the proportion of DZS studies was lower than 50% in a meta-analysis, different methods had moderately high agreement. However, when this proportion was increased to be over 50%, the agreement among the methods decreased to different extents. For the Bayesian, exact, and Peto methods and the inverse-variance and Mantel–Haenszel methods using the EMP correction, their agreement coefficients with the inverse-variance and Mantel–Haenszel methods using a constant 0.5 and TACC decreased from larger than 0.70 to smaller than 0.30. In contrast, the agreement coefficients only decreased slightly among the Bayesian, exact, and Peto methods and the inverse-variance and Mantel–Haenszel methods using the EMP correction.

Conclusions

To utilize all available information and reduce research waste and avoid overestimating the effect, meta-analysts should incorporate DZS, rather than simply removing them. The Peto and other conventional methods with continuity correction should be avoided when the proportion of DZS is extremely high. The exact and Bayesian methods are highly recommended, except when none of the included studies have an event in one or both treatment arms.

Electronic supplementary material

The online version of this article (10.1007/s11606-019-04925-8) contains supplementary material, which is available to authorized users.

KEY WORDS: Cochrane Database of Systematic Reviews, Cohen’s κ coefficient, double-zero-event studies, meta-analysis, rare event

INTRODUCTION

In pharmaceutical industry, it is important to evaluate drug safety during drug development and after approval.¹ Adverse events caused by side effects of new drugs are often rare; thus, it is hard to accurately estimate their rates in a single study. Meta-analysis can integrate quantitative information from multiple clinical trials to provide a more reliable and powerful assessment, which can be used to underpin guidelines, aid patients’ decision-making, and validate healthcare products.^2,3 However, there are potential methodological challenges for meta-analyses of adverse events due to sparse outcome data.⁴

Previous studies have demonstrated that conventional meta-analysis methods are not suitable when applied to the rare events studies, because they are mostly based on large-sample theories to make inferences.^5–8 Another concern of the conventional methods is that the log odds ratio and log risk ratio are either infinite or undefined if no event occurred in one or both treatment arms.⁹ In most available software packages, a continuity correction (usually 0.5) is often added to zero cells in single-zero-event studies by default while double-zero-events studies (DZS) are excluded from the analysis.^9,10 However, when a meta-analysis contains a relatively high proportion of DZS, excluding these studies may lead to fairly different conclusions and waste useful resources.^11,12

To overcome the problems of conventional methods caused by rare events, some methods including DZS without continuity correction have been proposed. Focusing on the risk difference, Tian et al.⁵ suggested an exact method of combining confidence intervals (CIs). Liu et al.⁷ developed an exact method by combing the so-called p value functions using several different effect sizes. Yang et al.⁸ pointed out that these two exact methods can be well combined under the framework of combining confidence distributions, and an R package “gmeta” has been developed for performing these methods. Besides the well-discussed frequentist methods, a variety of “exact” Bayesian methods based on the fixed and random effects models for the odds ratio or relative risk have also been proposed.^6,13,14

The three most commonly used effect sizes include the odds ratio, relative risk, and risk difference. Another effect measure, arcsine difference, can handle zero events naturally but is seldom used possibly because of its indirect interpretation.¹⁵ Because the odds ratio and relative risk have similar values when the event is rare and the odds ratio has some advantages over the relative risk (e.g., consistency to events labeling and valid inferences under different sampling methods), we focus on statistical methods which use the odds ratios as the primary measure in this article.^16,17

Different from previous studies which compared the performance of various statistical methods in meta-analysis with rare events through simulation studies,^9–11 this article evaluates the performance empirically using a large collection of published meta-analyses in the Cochrane Database of Systematic Reviews (CDSR). Specifically, Cohen’s κ coefficient is used to estimate chance-adjusted pairwise agreement among these statistical methods.¹⁸ In addition, we evaluate the impact of DZS on the agreement. A meta-analysis of 13 comparative trials of haloperidol versus chlorpromazine for schizophrenia is used as a worked example of comparing the selected methods.¹⁹

METHODS

Data Source

To empirically evaluate the performance of the various meta-analysis methods for rare events, we downloaded all systematic reviews published on all issues in the CDSR available by January 2016 using the Cochrane scraper software,²⁰ and we selected meta-analyses with binary outcomes and at least 5 studies from all reviews. Because the meta-analyses from the same systematic review likely contained some common studies, we selected the meta-analysis with the largest number of studies from each systematic review to avoid possible association between meta-analyses. The event in a meta-analysis was considered rare if the overall crude prevalence (the ratio of the cumulative number of events over the total sample size across studies) was less than 5%. Note that rare events might be defined differently (e.g., less than 1%) by different researchers²¹; we used the relatively large cutoff 5% because it could yield a relatively large number of meta-analyses for our empirical study. Finally, we excluded meta-analyses without any DZS or in which all studies were DZS.

Continuity Corrections

The log odds ratio is infinite or undefined if the study contains no events in one or both treatment arms. To avoid this problem, the commonly used methods add an artificial continuity correction to the studies with zero cells. Sweeting et al.⁹ have comprehensively compared the performance of a variety of continuity corrections, and three corrections, including the constant 0.5 correction, the treatment arm continuity correction (TACC), and the empirical correction (EMP), have been recommended. Table B.2 in the Supplementary Material presents detailed illustrations for TACC and EMP corrections.

Conventional Methods

The inverse-variance method, Mantel–Haenszel method, and Peto method were the three most frequently used methods for combining effect sizes in a fixed effect meta-analysis.^22,23 For the inverse-variance and Mantel–Haenszel methods, we applied the above three continuity corrections to studies with zero event in one treatment arm (single-zero-event studies, SZS) or both (double-zero-event studies, DZS). Table B.3 in the Supplementary Material summarizes software packages for handling zero events in a meta-analysis. The Peto method, in contrast, can combine single-zero-event studies without continuity correction.

The Mantel–Haenszel method is the default fixed effects method in RevMan 5 (which is the software specially designed to prepare and maintain Cochrane reviews)²⁴ and the “metabin” function in the R package “meta”.²⁵ Also, it is an option of function “metan” in STATA.²⁶ The Peto method can provide the least bias and most powerful results with rare events and balanced studies. However, it may not perform well when applied to studies with unbalanced designs or when the log odds ratio significantly differs from zero.²⁷ Besides conducting the fixed effect meta-analyses via the above three methods, the DerSimonian–Laird method was used to implement the random effects meta-analyses.²⁸

Exact Method

Liu et al.⁷ proposed an exact method which can use the information from all studies, including those having no event in a single or both arms, without any continuity correction. To implement the exact method, the so-called p value functions for the odds ratio are first obtained for individual studies from the mid-p adaption of Fisher’s exact test. Then, the confidence distribution combination method is used to integrate the individual p value functions to obtain the combined p value function. Finally, the point estimate, CI, and p value are obtained through the combined p value function. We used the R package “gmeta” to perform the exact method for the Cochrane meta-analyses.²⁹

Tian et al.⁵ proposed another exact method, but they focused on the risk difference while we primarily considered the odds ratio; therefore, their method was not used in this article.

Bayesian Method

In addition to the exact method by Liu et al.⁷ under the frequentist framework, the Bayesian approach can alternatively handle studies with no events in a meta-analysis without any artificial continuity correction. We implemented the Bayesian method for each Cochrane meta-analysis under both the fixed and random effects settings via WinBUGS with a burn-in period of 1000 iterations followed by 100,000 further iterations for posterior inference.³⁰ The posterior median and 95% equal-tail posterior credible interval (CrI) were summarized to estimate the odds ratio. Appendix A in the Supplementary Material provides more details of the methods used in our empirical study.

Agreement Among Different Methods

We used Cohen’s κ coefficient to assess the agreement between the results produced by different methods for rare events. This coefficient is a popular measure of the agreement between two categorical variables.¹⁸ By convention, κ value smaller than 0.2 suggests slight agreement; a κ value between 0.2 and 0.4 suggests fair agreement; 0.4 to 0.6 suggests moderate agreement, between 0.61 and 0.80 suggests substantial agreement, and from 0.81 to 1.00 suggests almost perfect agreement.³¹ Specifically, the p value of the overall effect estimate was obtained for each Cochrane meta-analysis using each method discussed above, and the significance level was set to 0.05. Based on the dichotomous results (significant or not) from the p values, Cohen’s κ coefficient was calculated for each pair of the methods, and the impact of DZS on the agreement was also examined.

RESULTS

Performance of Meta-analysis Methods for Rare Events in the CDSR

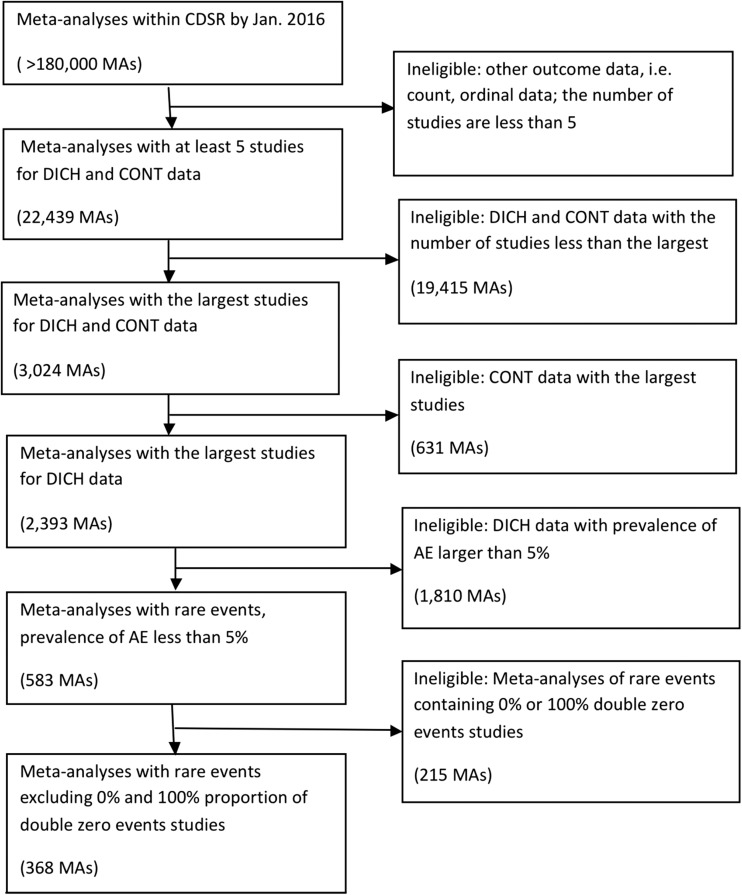
We collected a total of 5677 systematic reviews from the CDSR, which contained more than 180,000 meta-analyses. After selecting the largest meta-analyses from the reviews with binary outcomes and at least 5 studies, 2393 meta-analyses were retained, among which 583 had rare events. After excluding 215 meta-analyses without any DZS or any event, our final analysis data set consisted of 368 meta-analyses. The flow chart of our data collection is presented in Figure 1.

Flow chart of the selection criteria for the eligible meta-analyses from the CDSR. AE, adverse events; CDSR, Cochrane Database of Systematic Reviews; CONT, continuous; DICH, dichotomous; MA, meta-analysis.

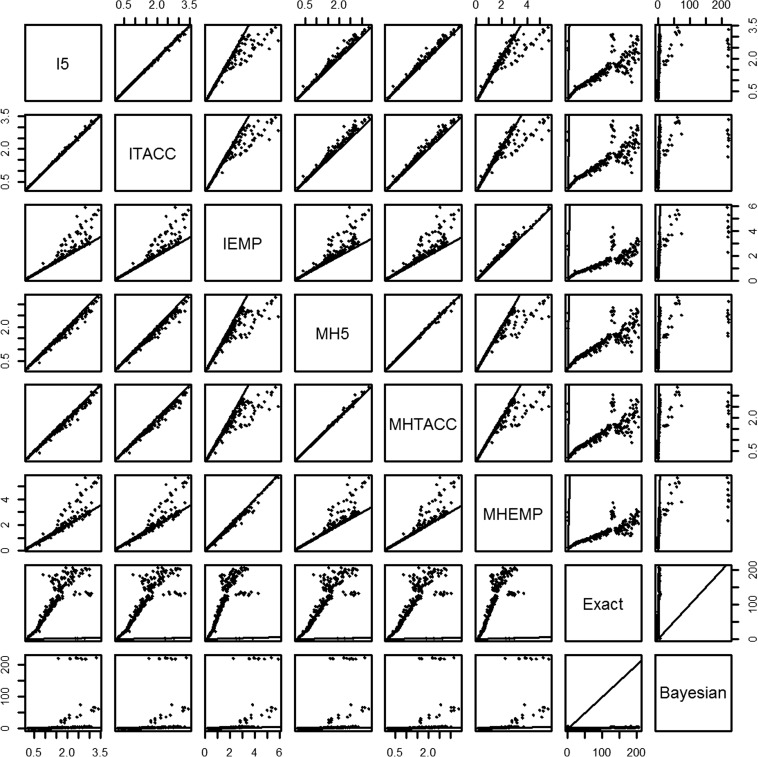
Figures 2 and 3 show the scatter plots for the agreement of log odds ratios and its associated CI/CrI length between different methods including DZS, respectively. Both figures illustrate that the best agreement was achieved between the inverse-variance method and Mantel–Haenszel method using the continuity correction of 0.5 and TACC. Their agreement with the exact method was intermediate and even weak with the methods using the EMP correction for the log odds ratio. For example, when the log odds ratio was far away from zero, the exact method and the methods using the EMP correction tended to produce larger estimates than other methods. Considerable disagreement patterns were seen between the associated CI/CrI lengths. For example, the CI/CrI length was generally wider using the exact method and the methods using the EMP correction, compared with the 0.5 correction and TACC. The agreement between the Bayesian and other methods was weak for both the log odds ratio and its CI/CrI length, which was due to some considerably large estimates for some meta-analyses with a high proportion of DZS and no events in one arm for all studies. For such meta-analyses, the exact method failed to produce a summary estimate. A similar agreement pattern was observed between the methods adding different continuity corrections only to studies with zero event in a single arm. Note that the agreements between the Peto method and the methods with different continuity corrections for the log odds ratio were moderately strong, particularly when the log odds ratio was not heavily departed from zero, and the Peto method is likely to result in narrower CI length comparing with methods with EMP (Figure C. 1 and Figure C. 2 in the Supplementary Material).

Scatter plot matrix of the agreement between the estimated overall log odds ratios produced by the fixed effect methods that include double-zero-event studies. I5, inverse-variance method with 0.5 continuity correction; ITACC, inverse-variance method with treatment arm continuity correction; IEMP, inverse-variance method with empirical continuity correction; MH5, Mantel–Haenszel method with 0.5 continuity correction; MHTACC, Mantel–Haenszel method with treatment arm continuity correction; MHEMP, Mantel–Haenszel method with empirical continuity correction.

Scatter plot matrix of the agreement between the lengths of 95% confidence intervals produced by the fixed effect methods that include double-zero-event studies. I5, inverse-variance method with 0.5 continuity correction; ITACC, inverse-variance method with treatment arm continuity correction; IEMP, inverse-variance method with empirical continuity correction; MH5, Mantel–Haenszel method with 0.5 continuity correction; MHTACC, Mantel–Haenszel method with treatment arm continuity correction; MHEMP, Mantel–Haenszel method with empirical continuity correction.

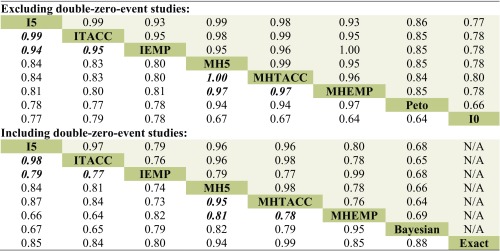
Table 1 shows Cohen’s κ coefficients for assessing the agreement among the different methods. The top sub-table shows the agreement among the methods excluding DZS while the bottom one is for the agreement including DZS. The lower and upper shaded triangular results are based on the outcomes from the fixed and random effects models, respectively. We focused on interpreting the results from the fixed effect models; the conclusions about the results from the random effects models can be similarly drawn.

Table 1.

Cohen’s κ Coefficients of the Agreement Among the Various Methods Based on Cochrane Meta-analyses with Rare Events

Open in a new tab

The lower and upper triangular results are based on the fixed and random effects models, respectively

Cohen’s κ coefficients from inverse-variance and MH methods are in bold italics

I0, inverse-variance method without continuity correction; I5, inverse-variance method with 0.5 continuity correction; ITACC, inverse-variance method with treatment arm continuity correction; IEMP, inverse-variance method with empirical continuity correction; MH5, Mantel–Haenszel method with 0.5 continuity correction; MHTACC, Mantel–Haenszel method with treatment arm continuity correction; MHEMP, Mantel–Haenszel method with empirical continuity correction; N/A, not applicable

Generally, the discrepancy between the methods with different continuity corrections was more significant when including DZS for analysis compared with excluding DZS. In particular, the agreement between the methods using the 0.5 correction (or TACC) and that with the EMP correction was considerably decreased when including DZS in the analyses. For example, κ was 0.97 for the agreement between the Mantel–Haenszel methods with the TACC and EMP corrections, and it decreased to 0.78 after including DZS. This implies that the inclusion and exclusion of DZS might lead to inconsistent conclusions from these methods for some meta-analyses. However, the decrease of the agreement between the methods with the continuity correction of 0.5 and TACC was ignorable. For example, κ was 1 for the Mantel–Haenszel method using the continuity correction of 0.5 and TACC when excluding DZS, and it decreased to 0.95 when including DZS. The slight impact of DZS was probably due to the roughly equal allocation sample size between the two treatment arms.

In addition, the exact method, Bayesian method, and Peto method achieved better agreement with the Mantel–Haenszel method than the inverse-variance method under the fixed effect framework. The Bayesian method agreed better with the methods with the EMP correction than the TACC or 0.5 correction, while the exact method had better agreement with the methods using the TACC or 0.5 correction than the EMP correction. Note that there was no obvious difference between the methods with different continuity corrections and the Peto method. For example, the agreement was fairly strong between the Peto method and the Mantel–Haenszel method with different corrections (κ > 0.9).

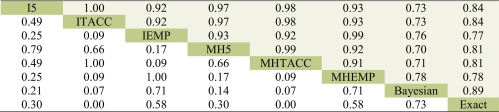
Table 2 shows the impact of DZS on the agreement among the selected fixed effect methods including DZS. The upper shaded and lower triangular results were based on the outcomes from meta-analyses with the proportion of DZS less or equal to 50% and greater than 50%, respectively. The coefficients in the upper triangular results were generally larger than those in the lower triangular, suggesting that the selected methods agreed with each other better when the proportions of DZS were less than 50%. For example, κ = 0.81 between the exact and Mantel–Haenszel methods with the TACC decreased to zero when the proportion of DZS was higher than 50%. Note that the proportion of DZS had ignorable impact on the agreement between some of the selected methods. For example, the agreement between the inverse-variance method and the Mantel–Haenszel method with the TACC or the EMP correction was almost perfect, even when the proportion of DZS was higher than 50%. Another example is that κ was 0.78 between the Bayesian and Mantel–Haenszel methods with the EMP correction, and it decreased slightly to 0.71.

Table 2.

Cohen’s κ Coefficients for the Agreement Among the Various Fixed Effect Methods Including DZS

Open in a new tab

The lower and upper triangular results are based on the meta-analyses with the proportion of double-zero-events studies ≥ 50% and < 50%, respectively

I5, inverse-variance method with 0.5 continuity correction; ITACC, inverse-variance method with treatment arm continuity correction; IEMP, inverse-variance method with empirical continuity correction; MH5, Mantel–Haenszel method with 0.5 continuity correction; MHTACC, Mantel–Haenszel method with treatment arm continuity correction; MHEMP, Mantel–Haenszel method with empirical continuity correction

Table 3 shows Cohen’s κ coefficients for the agreement between methods excluding and including DZS. A better agreement was achieved when the proportion of DZS was less than 50%. For example, the almost perfect agreement between the Peto and Bayesian methods decreased considerably (κ changed from 1 to 0.77) when the proportion of DZS was higher than 50%. Note that the agreement between the Peto method and the exact method was relatively robust to the proportion of DZS; only a slight decrease was observed (from 0.89 to 0.80) when the proportion of DZS was higher than 50%.

Table 3.

Cohen’s κ Coefficients for the Agreement Among the Various Methods Excluding and Including DZS

Fixed effect method		Cohen’s κ coefficients
Excluding DZS	Including DZS	All MA	DZS% ≤ 50%	DZS% > 50%
I0	Exact	0.71	0.74	0.00
I0	Bayesian	0.63	0.67	0.00
Peto	Exact	0.89	0.89	0.80
Peto	Bayesian	0.95	1.00	0.77
I5	I5	0.89	0.95	0.45
ITACC	ITACC	0.88	0.95	0.19
IEMP	IEMP	0.86	0.92	0.60
MH5	MH5	0.70	0.75	0.26
MHTACC	MHTACC	0.70	0.75	0.14
MHEMP	MHEMP	0.73	0.77	0.57

Open in a new tab

DZS, double-zero-event study; I0, inverse-variance method without continuity correction; I5, inverse-variance method with 0.5 continuity correction; ITACC, inverse-variance method with treatment arm continuity correction; IEMP, inverse-variance method with empirical continuity correction; MH5, Mantel–Haenszel method with 0.5 continuity correction; MHTACC, Mantel–Haenszel method with treatment arm continuity correction; MHEMP, Mantel–Haenszel method with empirical continuity correction; MA, meta-analysis

The impact of the proportion of DZS on the log odds ratio and its associated CI/CrI length was also investigated; the results are in Figures C.3 and C.4 in the Supplementary Material. Generally, as the proportion of DZS increased, the variability of the estimates by the selected methods also increased, which was consistent with the impact of DZS on the agreement between the methods.

Case Study

A meta-analysis of 13 comparative trials compared two drugs, haloperidol and chlorpromazine, which are commonly used to treat schizophrenia.¹⁹ Patients leaving studies because of adverse events were recorded as outcomes. In this meta-analysis, 8 studies (62%) contained no events in any treatment arm, and events only occurred in one treatment arm in the other 5 (38%) studies. The sample sizes from both treatment arms were comparable for most of the studies, and only one study contained almost three times sample sizes in the haloperidol group than that in the chlorpromazine group. Table B.4 in the Supplementary Material presents the data.

Table 4 shows the summary odds ratio, 95% CI/CrI, and p values from the various methods. p values less than 0.05 are shown in bold. Because it had been suggested that the Peto method was unbiased when the group size was balanced, the estimates by this method were used as the benchmark for the other methods. Its point estimate was 0.18 with 95% CI (0.04, 0.75), which suggested a significant difference between the two treatment arms. It is of interest to note the impact of inclusion of DZS on the point and confidence interval estimates of all these fixed effects methods. Overall, the methods with the EMP correction tended to pull the results away from the null, producing narrower confidence intervals and more significant p values, while the methods with the 0.5 or TACC tended to pull the results toward the null. For example, without DZS, the point estimate and 95% CI from the inverse-variance method with the EMP correction were 0.17 (0.02, 1.23); with DZS, they were 0.18 (0.04, 0.71). For the Mantel–Haenszel method with a continuity correction of 0.5, the estimates were 0.26 (0.07, 0.99) and 0.48 (0.19, 1.21) when excluding and including DZS, respectively. The exact method yielded in a non-significant conservative result with the widest CI due to the inclusion of DZS, while the Bayesian method resulted in the smallest point estimate 0.06 with a considerable narrow CI (0.00, 0.53). In summary, the estimate was inconsistent across the various methods because of differences in dealing with DZS.

Table 4.

Results Produced by Different Fixed Effect Methods in the Schizophrenia Comparative Study

Method	Excluding DZS		Including DZS
Method	OR [95% CI]	p	OR [95% CI]	p
Inverse-variance
I5	0.27 [0.07, 1.14]	0.07	0.53 [0.19, 1.44]	0.21
ITACC	0.27 [0.06, 1.19]	0.08	0.54 [0.19, 1.49]	0.23
IEMP	0.17 [0.02, 1.23]	0.08	0.18 [0.04, 0.71]	0.02
Mantel–Haenszel
MH5	0.26 [0.07, 0.99]	0.05	0.48 [0.19, 1.21]	0.12
MHTACC	0.28 [0.08, 1.06]	0.06	0.50 [0.20, 1.26]	0.14
MHEMP	0.12 [0.02, 0.63]	0.01	0.14 [0.04, 0.51]	0.003
Peto	0.18 [0.04, 0.75]	0.02	N/A	N/A
Exact	N/A	N/A	0.15 [0.00, 2.04]	N/A
Bayesian	N/A	N/A	0.06 [0.00, 0.53]	N/A

Open in a new tab

CI, confidence interval; DZS, double-zero-event study; I5, inverse-variance method with 0.5 continuity correction; ITACC, inverse-variance method with treatment arm continuity correction; IEMP, inverse-variance method with empirical continuity correction; MH5, Mantel–Haenszel method with 0.5 continuity correction; MHTACC, Mantel–Haenszel method with treatment arm continuity correction; MHEMP, Mantel–Haenszel method with empirical continuity correction; OR, odds ratio; N/A, not applicable

p = < 0.05 are in italics

DISCUSSION

Main Findings and Recommendations

Using 368 meta-analyses with DZS selected from the CDSR, this study illustrated that with a large proportion of DZS (i.e., when the adverse event was typically rare²¹), the agreement among the meta-analysis methods was low, which suggested that researchers should not rely on only a particular statistical method to make inference on the impact of treatments on adverse events.

No method is suitable for all sparse data scenarios. The Peto method which requires excluding DZS may not be a good choice, because it cannot fully utilize the information from all studies. On the other hand, to account for all available data including DZS,³² the exact and Bayesian methods may be preferable methods. However, if there is no event in one treatment arm across all studies, the exact method cannot be implemented, and the Bayesian method usually yields unreasonably large estimates.

The methods with different continuity corrections can be conveniently implemented through some existing statistical software. For example, the “metabin” function in the R package “meta” can include DZS or SZS and the metan function in STATA can include SZS by adding the 0.5 or TACC to all studies; however, the impact of constant 0.5 correction is hard to estimate, especially when the ratios of group size are unbalanced across studies and the TACC is prone to pull the estimates toward the null. Alternatively, the EMP correction borrows information about the odds ratio from other non-zero event studies under the frequentist framework. It has been suggested as a counterpart of the Bayesian method and may help researchers make reliable inferences. However, as publication bias often exists in meta-analyses,^33–35 applying the EMP correction may introduce bias that leads the results away from the null when there is no treatment effect on adverse events.

In summary, when adverse events are particularly rare (i.e., a large proportion of DZS), to give a more reliable conclusion, we recommend to apply the exact or Bayesian method for utilizing the information from all the studies. In the situation of no event in one arm for all studies, if the sample sizes between two groups are roughly balanced and the odds ratio is not heavily deviated from 1, the Peto method is recommended as a reliable reference approach because it generally does not incur large bias. We recommend not using continuity corrections when the proportion of DZS is high, because even a small continuity correction may lead to distorted inferences. However, the Mantel–Haenszel method with the EMP correction may be considered if external evidence indicates a substantial treatment effect. Generally, we should avoid applying continuity correction with 0.5 or TACC because it may result in considerable bias when zero events are common in one or both arms, especially when sample sizes vary between studies. Therefore, it might be informative to apply several methods with low agreement as a sensitivity analysis, and the results should be interpreted cautiously.

Limitations

In this study, we did not comprehensively discuss the difference between the fixed and random effects models, because we were interested in the impact of DZS on the estimated effect sizes rather than comparing the effects of the fixed and random effects models. Also, we evaluated only the agreement among some commonly used methods for synthesizing the odds ratios; the agreement of other methods for other types of effect sizes may be an interesting topic for future research. Meanwhile, the agreement was based on the meta-analyses from the CDSR which were related primarily to healthcare, so our conclusions may not be representative for all published meta-analyses with rare adverse events. It has been suggested that well-conducted observational studies can be combined with randomized clinical trials appropriately without incurring bias, and the benefits of including observational studies in systematic reviews of adverse events may overcome the disadvantages of wasting their information.^36,37 Therefore, evaluating the agreement among a more comprehensive pool of statistical methods in the context of rare events with a larger database (including observational studies) may help healthcare researchers estimate treatment effects on adverse events in a more reliable way.

Electronic Supplementary Material

ESM 1^{(258.5KB, docx)}

(DOCX 258 kb)

Acknowledgements

We thank Guang Yang and Guido Schwarzer for helpful discussion.

Funding Information

This research was supported in part by NIH (R21LM012744, R03HS024743, R21LM012197, and R03DE024750).

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they do not have a conflict of interest.

Footnotes

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

1.Barnes J. Drug safety. Nat Rev Drug Discov. 2007;6(11):937–937. doi: 10.1038/nrd2461. [DOI] [Google Scholar]
2.Sutton AJ, Higgins JP. Recent developments in meta-analysis. Stat Med. 2008;27(5):625–650. doi: 10.1002/sim.2934. [DOI] [PubMed] [Google Scholar]
3.Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to meta-analysis. New York: Wiley; 2009. [Google Scholar]
4.Sutton AJ, Cooper NJ, Lambert PC, Jones DR, Abrams KR, Sweeting MJ. Meta-analysis of rare and adverse event data. Expert Rev Pharmacoecon Outcomes Res. 2002;2(4):367–379. doi: 10.1586/14737167.2.4.367. [DOI] [PubMed] [Google Scholar]
5.Tian L, Cai TX, Pfeffer MA, Piankov N, Cremieux PY, Wei LJ. Exact and efficient inference procedure for meta-analysis and its application to the analysis of independent 2 x 2 tables with all available data but without artificial continuity correction. Biostatistics. 2009;10(2):275–281. doi: 10.1093/biostatistics/kxn034. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Cai T, Parast L, Ryan L. Meta-analysis for rare events. Stat Med. 2010;29(20):2078–2089. doi: 10.1002/sim.3964. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Liu D, Liu RY, Xie M. Exact meta-analysis approach for discrete data and its application to 2 x 2 tables with rare events. J Am Stat Assoc. 2014;109(508):1450–1465. doi: 10.1080/01621459.2014.946318. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Yang G, Liu D, Wang J, Xie MG. Meta-analysis framework for exact inferences with application to the analysis of rare events. Biometrics. 2016;72(4):1378–1386. doi: 10.1111/biom.12497. [DOI] [PubMed] [Google Scholar]
9.Sweeting MJ, Sutton AJ, Lambert PC. What to add to nothing? Use and avoidance of continuity corrections in meta-analysis of sparse data. Stat Med. 2004;23:1351–1375. doi: 10.1002/sim.1761. [DOI] [PubMed] [Google Scholar]
10.Bradburn MJ, Deeks JJ, Berlin JA, Localio AR. Much ado about nothing: a comparison of the performance of meta-analytical methods with rare events. Stat Med. 2007;26(1):53–77. doi: 10.1002/sim.2528. [DOI] [PubMed] [Google Scholar]
11.Cheng J, Pullenayegum E, Marshall JK, Iorio A, Thabane L. Impact of including or excluding both-armed zero-event studies on using standard meta-analysis methods for rare event outcome: a simulation study. BMJ Open. 2016;6(8):e010983. doi: 10.1136/bmjopen-2015-010983. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Chalmers I, Bracken MB, Djulbegovic B, et al. How to increase value and reduce waste when research priorities are set. Lancet. 2014;383(9912):156–165. doi: 10.1016/S0140-6736(13)62229-1. [DOI] [PubMed] [Google Scholar]
13.Smith TC, Spiegelhalter DJ, Thomas A. Bayesian approaches to random-effects meta-analysis: a comparative study. Stat Med. 1995;14(24):2685–2699. doi: 10.1002/sim.4780142408. [DOI] [PubMed] [Google Scholar]
14.Bai O, Chen M, Wang X. Bayesian Estimation and Testing in Random Effects Meta-analysis of Rare Binary Adverse Events. Stat Biopharm Res. 2016;8(1):49–59. doi: 10.1080/19466315.2015.1096823. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Rucker G, Schwarzer G, Carpenter J, Olkin I. Why add anything to nothing? The arcsine difference as a measure of treatment effect in meta-analysis with zero cells. Stat Med. 2009;28(5):721–738. doi: 10.1002/sim.3511. [DOI] [PubMed] [Google Scholar]
16.Egger M, Smith GD, Phillips AN. Meta-analysis: Principles and procedures. Br Med J. 1997;315(7121):1533–1537. doi: 10.1136/bmj.315.7121.1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Grimes DA, Schulz KF. Making sense of odds and odds ratios. Obstet Gynecol. 2008;111(2):423–426. doi: 10.1097/01.AOG.0000297304.32187.5d. [DOI] [PubMed] [Google Scholar]
18.Cohen J. A Coefficient of Agreement for Nominal Scales. Educ Psychol Meas. 1960;20(1):37–46. doi: 10.1177/001316446002000104. [DOI] [Google Scholar]
19.Leucht C, Kitzmantel M, Chua L, Kane J, Leucht S. Haloperidol versus chlorpromazine for treatment of schizophrenia. Schizophr Bull. 2008;34(5):813–815. doi: 10.1093/schbul/sbn087. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Springate DA, Kontopantelis E. Cochrane_scraper: tools for downloading data from the Cochrane Library of Systematic Reviews. 2014:Version 1.1.0.
21.Marodin G, Goldim JR. Confusions and Ambiguities in the Classification of Adverse Events in the Clinical Research. Revista Da Escola De Enfermagem Da Usp. 2009;43(3):690–696. doi: 10.1590/S0080-62342009000300027. [DOI] [PubMed] [Google Scholar]
22.Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst. 1959;22(4):719–748. [PubMed] [Google Scholar]
23.Yusuf S, Peto R, Lewis J, Collins R, Sleight P. Beta-blockade during and after myocardial-infarction - an overview of the randomized trials. Prog Cardiovasc Dis. 1985;27(5):335–371. doi: 10.1016/S0033-0620(85)80003-7. [DOI] [PubMed] [Google Scholar]
24.Higgins JPT, Green S. Cochrane handbook for systematic reviews of interventions. Chichester: John Wiley & Sons; 2008. [Google Scholar]
25.Schwarzer G. Meta: meta-analysis with R. 2014. https://cran.r-project.org/web/packages=meta. R package version 4.8-2.
26.Harris RJ, Bradburn MJ, Deeks JJ, Harbord RM, Altman DG, Sterne JAC. metan: fixed- and random-effects meta-analysis. Stata J. 2008;8(1):3–28. doi: 10.1177/1536867X0800800102. [DOI] [Google Scholar]
27.Greenland S, Salvan A. Bias in the one-step method for pooling study results. Stat Med. 1990;9(3):247–252. doi: 10.1002/sim.4780090307. [DOI] [PubMed] [Google Scholar]
28.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7(3):177–188. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
29.Yang G, Xie M. gmeta: meta-analysis via a unified framework of confidence distribution. R package version 2.2–4. http://CRAN.R-project.org/package=gmeta. Accessed 05 Feb 2016.
30.Lane PW. Meta-analysis of incidence of rare events. Stat Methods Med Res. 2013;22(2):117–132. doi: 10.1177/0962280211432218. [DOI] [PubMed] [Google Scholar]
31.Landis JR, Koch GG. Measurement of Observer Agreement for Categorical Data. Biometrics. 1977;33(1):159–174. doi: 10.2307/2529310. [DOI] [PubMed] [Google Scholar]
32.Friedrich JO, Adhikari NK, Beyene J. Inclusion of zero total event trials in meta-analyses maintains analytic consistency and incorporates all available data. BMC Med Res Methodol. 2007; 7 (5). [DOI] [PMC free article] [PubMed]
33.Rhodes S. Publication bias in meta-analysis. J R Stat Soc A Stat Soc. 2006;169:1012–1012. doi: 10.1111/j.1467-985X.2006.00446_14.x. [DOI] [Google Scholar]
34.Lin L, Chu H. Quantifying publication bias in meta-analysis. Biometrics. 2017;74(3):785–794. [DOI] [PMC free article] [PubMed]
35.Thornton A, Lee P. Publication bias in meta-analysis: its causes and consequences. J Clin Epidemiol. 2000;53(2):207–216. doi: 10.1016/S0895-4356(99)00161-4. [DOI] [PubMed] [Google Scholar]
36.Shrier I, Boivin J-F, Steele RJ, et al. Should meta-analyses of interventions include observational studies in addition to randomized controlled trials? a critical examination of underlying principles. Am J Epidemiol. 2007;166(10):1203–1209. doi: 10.1093/aje/kwm189. [DOI] [PubMed] [Google Scholar]
37.Golder S, Loke YK, Bland M. Meta-analyses of adverse effects data derived from randomised controlled trials as compared to observational studies: methodological overview. PLoS Med. 2011;8:e1001026. doi: 10.1371/journal.pmed.1001026. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ESM 1^{(258.5KB, docx)}

(DOCX 258 kb)

[CR1] 1.Barnes J. Drug safety. Nat Rev Drug Discov. 2007;6(11):937–937. doi: 10.1038/nrd2461. [DOI] [Google Scholar]

[CR2] 2.Sutton AJ, Higgins JP. Recent developments in meta-analysis. Stat Med. 2008;27(5):625–650. doi: 10.1002/sim.2934. [DOI] [PubMed] [Google Scholar]

[CR3] 3.Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to meta-analysis. New York: Wiley; 2009. [Google Scholar]

[CR4] 4.Sutton AJ, Cooper NJ, Lambert PC, Jones DR, Abrams KR, Sweeting MJ. Meta-analysis of rare and adverse event data. Expert Rev Pharmacoecon Outcomes Res. 2002;2(4):367–379. doi: 10.1586/14737167.2.4.367. [DOI] [PubMed] [Google Scholar]

[CR5] 5.Tian L, Cai TX, Pfeffer MA, Piankov N, Cremieux PY, Wei LJ. Exact and efficient inference procedure for meta-analysis and its application to the analysis of independent 2 x 2 tables with all available data but without artificial continuity correction. Biostatistics. 2009;10(2):275–281. doi: 10.1093/biostatistics/kxn034. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR6] 6.Cai T, Parast L, Ryan L. Meta-analysis for rare events. Stat Med. 2010;29(20):2078–2089. doi: 10.1002/sim.3964. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR7] 7.Liu D, Liu RY, Xie M. Exact meta-analysis approach for discrete data and its application to 2 x 2 tables with rare events. J Am Stat Assoc. 2014;109(508):1450–1465. doi: 10.1080/01621459.2014.946318. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR8] 8.Yang G, Liu D, Wang J, Xie MG. Meta-analysis framework for exact inferences with application to the analysis of rare events. Biometrics. 2016;72(4):1378–1386. doi: 10.1111/biom.12497. [DOI] [PubMed] [Google Scholar]

[CR9] 9.Sweeting MJ, Sutton AJ, Lambert PC. What to add to nothing? Use and avoidance of continuity corrections in meta-analysis of sparse data. Stat Med. 2004;23:1351–1375. doi: 10.1002/sim.1761. [DOI] [PubMed] [Google Scholar]

[CR10] 10.Bradburn MJ, Deeks JJ, Berlin JA, Localio AR. Much ado about nothing: a comparison of the performance of meta-analytical methods with rare events. Stat Med. 2007;26(1):53–77. doi: 10.1002/sim.2528. [DOI] [PubMed] [Google Scholar]

[CR11] 11.Cheng J, Pullenayegum E, Marshall JK, Iorio A, Thabane L. Impact of including or excluding both-armed zero-event studies on using standard meta-analysis methods for rare event outcome: a simulation study. BMJ Open. 2016;6(8):e010983. doi: 10.1136/bmjopen-2015-010983. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR12] 12.Chalmers I, Bracken MB, Djulbegovic B, et al. How to increase value and reduce waste when research priorities are set. Lancet. 2014;383(9912):156–165. doi: 10.1016/S0140-6736(13)62229-1. [DOI] [PubMed] [Google Scholar]

[CR13] 13.Smith TC, Spiegelhalter DJ, Thomas A. Bayesian approaches to random-effects meta-analysis: a comparative study. Stat Med. 1995;14(24):2685–2699. doi: 10.1002/sim.4780142408. [DOI] [PubMed] [Google Scholar]

[CR14] 14.Bai O, Chen M, Wang X. Bayesian Estimation and Testing in Random Effects Meta-analysis of Rare Binary Adverse Events. Stat Biopharm Res. 2016;8(1):49–59. doi: 10.1080/19466315.2015.1096823. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR15] 15.Rucker G, Schwarzer G, Carpenter J, Olkin I. Why add anything to nothing? The arcsine difference as a measure of treatment effect in meta-analysis with zero cells. Stat Med. 2009;28(5):721–738. doi: 10.1002/sim.3511. [DOI] [PubMed] [Google Scholar]

[CR16] 16.Egger M, Smith GD, Phillips AN. Meta-analysis: Principles and procedures. Br Med J. 1997;315(7121):1533–1537. doi: 10.1136/bmj.315.7121.1533. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR17] 17.Grimes DA, Schulz KF. Making sense of odds and odds ratios. Obstet Gynecol. 2008;111(2):423–426. doi: 10.1097/01.AOG.0000297304.32187.5d. [DOI] [PubMed] [Google Scholar]

[CR18] 18.Cohen J. A Coefficient of Agreement for Nominal Scales. Educ Psychol Meas. 1960;20(1):37–46. doi: 10.1177/001316446002000104. [DOI] [Google Scholar]

[CR19] 19.Leucht C, Kitzmantel M, Chua L, Kane J, Leucht S. Haloperidol versus chlorpromazine for treatment of schizophrenia. Schizophr Bull. 2008;34(5):813–815. doi: 10.1093/schbul/sbn087. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR20] 20.Springate DA, Kontopantelis E. Cochrane_scraper: tools for downloading data from the Cochrane Library of Systematic Reviews. 2014:Version 1.1.0.

[CR21] 21.Marodin G, Goldim JR. Confusions and Ambiguities in the Classification of Adverse Events in the Clinical Research. Revista Da Escola De Enfermagem Da Usp. 2009;43(3):690–696. doi: 10.1590/S0080-62342009000300027. [DOI] [PubMed] [Google Scholar]

[CR22] 22.Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst. 1959;22(4):719–748. [PubMed] [Google Scholar]

[CR23] 23.Yusuf S, Peto R, Lewis J, Collins R, Sleight P. Beta-blockade during and after myocardial-infarction - an overview of the randomized trials. Prog Cardiovasc Dis. 1985;27(5):335–371. doi: 10.1016/S0033-0620(85)80003-7. [DOI] [PubMed] [Google Scholar]

[CR24] 24.Higgins JPT, Green S. Cochrane handbook for systematic reviews of interventions. Chichester: John Wiley & Sons; 2008. [Google Scholar]

[CR25] 25.Schwarzer G. Meta: meta-analysis with R. 2014. https://cran.r-project.org/web/packages=meta. R package version 4.8-2.

[CR26] 26.Harris RJ, Bradburn MJ, Deeks JJ, Harbord RM, Altman DG, Sterne JAC. metan: fixed- and random-effects meta-analysis. Stata J. 2008;8(1):3–28. doi: 10.1177/1536867X0800800102. [DOI] [Google Scholar]

[CR27] 27.Greenland S, Salvan A. Bias in the one-step method for pooling study results. Stat Med. 1990;9(3):247–252. doi: 10.1002/sim.4780090307. [DOI] [PubMed] [Google Scholar]

[CR28] 28.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7(3):177–188. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]

[CR29] 29.Yang G, Xie M. gmeta: meta-analysis via a unified framework of confidence distribution. R package version 2.2–4. http://CRAN.R-project.org/package=gmeta. Accessed 05 Feb 2016.

[CR30] 30.Lane PW. Meta-analysis of incidence of rare events. Stat Methods Med Res. 2013;22(2):117–132. doi: 10.1177/0962280211432218. [DOI] [PubMed] [Google Scholar]

[CR31] 31.Landis JR, Koch GG. Measurement of Observer Agreement for Categorical Data. Biometrics. 1977;33(1):159–174. doi: 10.2307/2529310. [DOI] [PubMed] [Google Scholar]

[CR32] 32.Friedrich JO, Adhikari NK, Beyene J. Inclusion of zero total event trials in meta-analyses maintains analytic consistency and incorporates all available data. BMC Med Res Methodol. 2007; 7 (5). [DOI] [PMC free article] [PubMed]

[CR33] 33.Rhodes S. Publication bias in meta-analysis. J R Stat Soc A Stat Soc. 2006;169:1012–1012. doi: 10.1111/j.1467-985X.2006.00446_14.x. [DOI] [Google Scholar]

[CR34] 34.Lin L, Chu H. Quantifying publication bias in meta-analysis. Biometrics. 2017;74(3):785–794. [DOI] [PMC free article] [PubMed]

[CR35] 35.Thornton A, Lee P. Publication bias in meta-analysis: its causes and consequences. J Clin Epidemiol. 2000;53(2):207–216. doi: 10.1016/S0895-4356(99)00161-4. [DOI] [PubMed] [Google Scholar]

[CR36] 36.Shrier I, Boivin J-F, Steele RJ, et al. Should meta-analyses of interventions include observational studies in addition to randomized controlled trials? a critical examination of underlying principles. Am J Epidemiol. 2007;166(10):1203–1209. doi: 10.1093/aje/kwm189. [DOI] [PubMed] [Google Scholar]

[CR37] 37.Golder S, Loke YK, Bland M. Meta-analyses of adverse effects data derived from randomised controlled trials as compared to observational studies: methodological overview. PLoS Med. 2011;8:e1001026. doi: 10.1371/journal.pmed.1001026. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Real-world Performance of Meta-analysis Methods for Double-Zero-Event Studies with Dichotomous Outcomes Using the Cochrane Database of Systematic Reviews

Yanan Ren, PhD

Lifeng Lin, PhD

Qinshu Lian, PhD

Hui Zou, PhD

Haitao Chu, MD, PhD

Abstract

Background

Methods

Results

Conclusions

Electronic supplementary material

INTRODUCTION

METHODS

Data Source

Continuity Corrections

Conventional Methods

Exact Method

Bayesian Method

Agreement Among Different Methods

RESULTS

Performance of Meta-analysis Methods for Rare Events in the CDSR

Figure 1.

Figure 2.

Figure 3.

Table 1.

Table 2.

Table 3.

Case Study

Table 4.

DISCUSSION

Main Findings and Recommendations

Limitations

Electronic Supplementary Material

Acknowledgements

Funding Information

Compliance with Ethical Standards

Conflict of Interest

Footnotes

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases