Microstructure-based numerical simulation of the mechanical behaviour of ocular tissue

Abstract

This paper aims to present a novel full-eye biomechanical material model that incorporates the characteristics of ocular tissues at microstructural level, and use the model to analyse the age-related stiffening in tissue behaviour. The collagen content in ocular tissues, as obtained using X-ray scattering measurements, was represented by sets of Zernike polynomials that covered both the cornea and sclera, then used to reconstruct maps of collagen fibril magnitude and orientation on the three-dimensional geometry of the eye globe. Fine-mesh finite-element (FE) models with eye-specific geometry were built and supported by a user-defined material model (UMAT), which considered the regional variation of fibril density and orientation. The models were then used in an iterative inverse modelling study to derive the material parameters that represent the experimental behaviour of ocular tissues from donors aged between 50 and 90 years obtained in earlier ex vivo studies. Sensitivity analysis showed that reducing the number of directions that represented the anisotropy of collagen fibril orientation at each X-ray scattering measurement point from 180 to 16 would have limited and insignificant effect on the FE solution (0.08%). Inverse analysis resulted in material parameters that provided a close match with experimental intraocular pressure–deformation behaviour with a root mean square of error between 3.6% and 4.3%. The results also demonstrated a steady increase in mechanical stiffness in all ocular regions with age. A constitutive material model based on distributions of collagen fibril density and orientation has been developed to enable the accurate representation of the biomechanical behaviour of ocular tissues. The model offers a high level of control of stiffness and anisotropy across ocular globe, and therefore has the potential for use in planning surgical and medical procedures.

1. Introduction

Ocular numerical models have been widely used in a variety of biomechanical applications including medical device development and disease management [1–5]. Computer based simulations also have several advantages over laboratory experiments such as much reduced cost and more rapid evaluation. However, the effectiveness of numerical models relies on their ability to accurately represent the eye's geometry, loading, boundary conditions and biomechanical properties, the last of which is usually the most demanding feature in terms of characterization and embedding in numerical models [3,4,6–8].

Both the cornea and the sclera have complex material behaviour that is hyperelastic, viscoelastic, dependent on age and medical history and have significant regional variation of stiffness [9–13]. In addition, the tissue of ocular globe is known to retain a high degree of anisotropy as its mechanical behaviour is dependent on the distribution of collagen fibrils, the main load carrying components of the tissue [14]. With collagen fibrils showing significant regional variations in density and orientation, the biomechanical behaviour of the tissue changes accordingly, exhibiting stiffness levels that vary with location and direction, and making ocular biomechanics highly complex [15,16].

Computational finite-element (FE) models of corneal tissue have been developed over the last few decades especially in terms of material representation. At an early stage, linear elastic and homogeneous material models were employed [17,18], but later anisotropy and nonlinearity were introduced [6,7,19–24]. More recently, constitutive models that accounted for the nonlinear, viscoelastic and anisotropic material behaviour through consideration of fibril arrangements in the cornea and laboratory experiments of tissue mechanical performance have been developed [25]. These developments have made corneal numerical models increasingly reliable through more accurate representation of material behaviour.

The present study aimed to take important steps towards the goal of multiscale modelling of the full eye globe, in which the regional variations of both stiffness and anisotropy were derived from reliable microstructure data. While earlier studies have relied on idealizations of microstructure data that assumed mainly orthogonal and circumferential fibril orientations in the central cornea and limbus, the purpose of this study was to directly link the modelling process to raw X-ray scattering data in an effective way that took into account the realistic regional variation in collagen fibril density and arrangement of fibrils [7,24–26]. Further, the study aimed to extend microstructure-based models beyond the cornea to cover the full eye globe. This step is now possible with the availability of fibril arrangement data across the whole globe that have been reported in an earlier study [27].

2. Methods

2.1. Constitutive material model

The material model adopted in this study followed phenomenological formulation that fitted the microstructure data on collagen fibril distribution reported earlier [24]. A strain energy function, representing nonlinear, anisotropic, and incompressible material behaviour, was defined by means of additive terms for non-collagen material or tissue matrix (Ψ_m), collagen fibrils (Ψ_A) and incompressibility or volume dilation Ψ_U:

$$\mathit{\Psi }\hspace{0.17em}=\hspace{0.17em}{\overline{\mathit{\Psi }}}_m(\overline{\mathbf{F}})+\hspace{0.17em}{\overline{\mathit{\Psi }}}_A(\overline{\mathbf{F}},{\mathbf{a}}_{\mathbf{0}},{\mathbf{b}}_{\mathbf{0}})+{\mathit{\Psi }}_U(J),$$ 2.1

where F is the deformation gradient at any material point with a decoupled form of $\overline{\mathbf{F}}=J^{-1/3}\mathbf{I}\mathbf{F}$, I is an identity tensor, a₀ and b₀ are the vectors defining the orientations of fibrils as tangential and out of tangential to the ocular surface, and J is the determinant of deformation gradient F. Ψ_U(J) was introduced to control the volume dilation (compressibility):

$${\mathit{\Psi }}_U(J)=\frac{1}{D}{(J-1)}^2,$$ 2.2

where D is a material constant that must have a small value (10⁻⁵) to preserve the material incompressibility [24].

The combination of the decoupled $\hspace{0.17em}{\overline{\mathit{\Psi }}}_m$ and $\hspace{0.17em}{\overline{\mathit{\Psi }}}_A$ aimed to ensure that both ground substance matrix and collagen fibrils were contributing to the volume-distortional strain energy density. Following a study by Studer et al. [24], the neo-Hookean law was chosen for this application because of its ability to represent the hyperelasticity of ocular tissue and account for isotropic non-collagen material behaviour ($\hspace{0.17em}{\overline{\mathit{\Psi }}}_m$):

$$\hspace{0.17em}{\overline{\mathit{\Psi }}}_m(\overline{\mathbf{F}})=C_{10}({\overline{I}}_1-3),$$ 2.3

where C₁₀ is a material constant, ${\overline{I}}_1=tr(\overline{\mathbf{C}})$ is the first strain invariant after energy isochoric split of the volume contribution, and the decoupled form of right Cauchy deformation gradient $\overline{\mathbf{C}}={\overline{\mathbf{F}}}^{\mathbf{T}}\overline{\mathbf{F}}$.

The anisotropy term $\hspace{0.17em}{\overline{\mathit{\Psi }}}_A$ was modelled by considering two families of fibrils: the in-lamella fibrils $(\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Lam}})$ and the inter-lamella fibrils which create interactions between adjacent lamellae $(\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Int}}).$ Regarding the second fibril family, an out-of-plane angle of 15° was used following earlier studies [7,24]. In addition, a weighted average function Κ(r, φ, α, θ_i) was employed to describe fibril distribution over 180° at a general point and to allow the inclusion of both fibril families:

$$\hspace{0.17em}{\overline{\mathit{\Psi }}}_A(\overline{\mathbf{F}},{\mathbf{a}}_{\mathbf{0}},{\mathbf{b}}_{\mathbf{0}})=\frac{1}{N}\sum _{i=0}^N\mathrm{K}(r,\phi ,\alpha ,{\theta }_i)({\hspace{0.17em}\overline{\mathit{\Psi }}}_{A,\mathrm{Lam}}({\overline{I}}_4)+{\hspace{0.17em}\overline{\mathit{\Psi }}}_{A,\mathrm{Int}}({\overline{I}}_6)).$$ 2.4

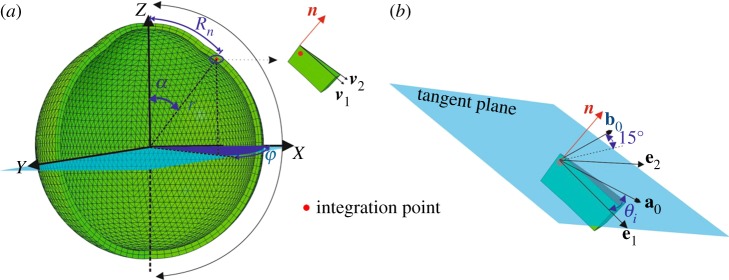
Equation (2.4) did not apply the probability density function [7,24] as the fibril density represented by $\mathrm{K}(r,\phi ,\alpha ,{\theta }_i)$ in this study was given by Zernike polynomials where (r, φ, α) define the spherical coordinates at any point in a global coordinate system, while θ_i is the azimuthal angle that controls fibril orientation in a local coordinate system (figure 1). The fourth and sixth invariants ${\overline{I}}_4,{\overline{I}}_6$ represent stretches in specific fibril directions where ${\overline{I}}_4={\mathbf{a}}_{\mathbf{0}}\overline{\mathbf{C}}{\mathbf{a}}_{\mathbf{0}}$ and ${\overline{I}}_6={\mathbf{b}}_{\mathbf{0}}\overline{\mathbf{C}}{\mathbf{b}}_{\mathbf{0}}.$ Total anisotropic strain energy was calculated as the sum of the contribution of all discretized fibrils at N orientations. These orientations numbered from 1 to N had the equal spacing over the continuous 180° from the local axis of e₁ that was defined in the meridional tangent direction. Therefore, the discretized fibril orientations specified by θ_i were decided in the established local coordinate system once a reasonable number of orientations N was suggested. $\mathrm{K}(r,\phi ,\alpha ,{\theta }_i)$ at one orientation specified by θ_i can form a density field function across all the spatial points with coordinates (r, φ, α). In order to select a representative value for N, a parametric study was performed and considered values between 3 and 180 where the effect of this variation was determined by assessing the apical displacement and reaching compromise between accuracy of model prediction and computational cost. Apical displacement was chosen in this parametric study as a result of the combined effects of both the cornea and sclera in the current eye model where the equator was prevented from movement in the Z direction. The results indicated that both accuracy and computational cost increase with higher values of N.

Figure 1.

A schematic of fibril recruitment. (a) The global coordinate system was defined by (X, Y, Z), a general integration point was located by the spherical coordinates (r, α, φ), and the normal vector was calculated by two vectors v₁ and v₂ for each element. (b) Two orthogonal vectors are located on the tangent plane with the unit vector e₁ aligned in the meridional tangent direction. The two unit vectors e₁, e₂ form the local coordinate system together with the normal vector n. The in-plane fibril family, represented by a₀, has the discretized orientation defined by azimuthal angle θ_i. The out-of-plane fibril family, represented by b₀, has an orientation defined by θ_i and an out-of-plane rotation angle 15°. (Online version in colour.)

Further, the specific forms of $\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Lam}}$ and $\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Int}}$ (equation (2.4)) were defined by Markert et al. [28] as

$$\begin{array}{rl}{\hspace{0.17em}\overline{\mathit{\Psi }}}_{A,\mathrm{Lam}}({\overline{I}}_4)& =\frac{{\mu }_1}{{\gamma }_1}\left({\overline{I}}_4^{{\gamma }_1/2}-1\right)-{\mu }_1\ln {\overline{I}}_4^{1/2}\\ \mathrm{and}{\overline{\mathit{\Psi }}}_{A,\mathrm{Int}}({\overline{I}}_6)& =\frac{{\mu }_2}{{\gamma }_2}\left({\overline{I}}_6^{{\gamma }_2/2}-1\right)-{\mu }_2\ln {\overline{I}}_6^{1/2},\end{array}\}$$ 2.5

where μ₁, γ₁ and μ₂, γ₂ are the material parameters for the two families of in-plane $\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Lam}}({\overline{I}}_4)$ and out-of-plane $\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Int}}({\overline{I}}_6)\hspace{0.17em}$ fibrils. Parameters μ controlled the initial stiffness of collagen fibrils and γ controlled the nonlinearity in the stress–strain material behaviour [7]. As the strain energy parameters, $\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Lam}}$ and $\hspace{0.17em}{\overline{\mathit{\Psi }}}_{A,\mathrm{Int}}$ existed only when the fibrils were subjected to tension, i.e. when stretch parameters ${\overline{I}}_4$ and ${\overline{I}}_6$ were larger than 1, the crimping state of the fibrils was not considered. It was expected that the fibrils would cease contributing to the tissue's mechanical action once subjected to compression.

2.2. Fitting of fibril distribution

Wide-angle X-ray scattering technique has been used to investigate the eye tissue in this study [16]. Experiments have been carried out at the IO2 unit of the UK's national synchrotron facility Diamond Light Source (Oxfordshire, UK) where a 40 µm width by 20 µm height micro-focus beam with λ = 0.979 Å wavelength and 0.5 s exposure time was used. A vacuum-compatible Pilatus detector sensor was placed at 350 mm behind the specimen to collect the X-ray reflections and a lead beam stop was located between the specimen and the detector to prevent any diffracted beam from damaging the detector's sensitive area.

A collagen fibril map of a healthy right eye without surgical or pathological history belonging to a 69-year-old donor was obtained and detailed in a previous study [27]. The tissue of the ocular globe was scanned using X-ray scattering facility at Station I02, Diamond Light Source Synchrotron (Oxford, UK). For each scanned point, the fibril content in each of equally spaced 360 orientations covering 360° was measured. A challenge is caused by the mismatch between the locations of the X-ray scanned points and the locations of the FE integration points, at which the fibril density microstructure data are required for the numerical models. This mismatch was addressed by fitting the microstructure X-ray data to surface polynomials that can then be used to estimate corresponding data at the integration points. The fibril density at an X-ray scanned point was discretized into N values in the N orientations considered based on the specific local coordinate system with a meridional axis e₁, and angles θ_i(i = 1 : N) representing the fibril orientations. The fibril densities in each orientation θ_i and in different scanning points were treated as the Z (height) values in polynomials, while the locations of scanning points provided the X and Y coordinates. Zernike, Gaussian–Hermite and orthogonal Fourier–Mellin polynomials were investigated with orders ranging between 5 and 25, and this step led to the use of Zernike polynomials as they provided the lowest fitting error on the collagen density across the full eye. The root mean square (RMS) of fit errors were 28.6%, 20.1% and 16.5% with Zernike orders 5, 15 and 25, respectively, while corresponding RMS errors (when the same number of polynomials were used) with Gaussian–Hermite were 30.8%, 25.4% and 23.3%, and with orthogonal Fourier–Mellin were 27.7%, 21.4% and 18.5%, respectively.

Further, in order to maintain the main features of fibril distribution and keep to a minimum the difference between measured data and the data provided by the Zernike polynomials, the fitting process was conducted separately for four ocular zones: the central cornea, the limbus, the anterior and equatorial sclera, and the posterior sclera. An overlap area with width of 2.4 mm was allowed between each two adjacent zones to ensure smooth transition of data from one zone to the next, and this process was repeated for each fibril orientation angle. The values of Zernike polynomial coefficients were calculated using the least-squares minimization method [29] for each of the four ocular zones considered (see the electronic supplementary material). The least-squares method was adopted in this analysis as it has been used successfully in the past in similar applications [30] and for its low computational cost; 5 s to calculate order 25 Zernike coefficients using a PC with Intel Core I7-4790 and 16GB RAM.

A study was conducted with Zernike orders between 5 and 25 to select a reasonable order that increased the fitting accuracy but avoided overfitting. In this study, the 10-fold cross-validation method was adopted in the overfitting analysis by dividing the total dataset in each ocular zone and in each orientation into ten subsets with approximately equal sizes [31,32]. For each data subset, the mean prediction error was calculated while adopting the coefficients of Zernike polynomials calculated based on the other nine data subsets and while considering Zernike orders between 5 and 25. After repeating this process for all 10 data subsets, the order of Zernike polynomials that provided the most accurate data predictions (and hence least prediction errors) was determined for all fibril orientations and all ocular zones. And once the order of Zernike polynomials was determined, all the measured data were used in a final exercise to determine values of the polynomial coefficients (using the least-squares method), which were then used to estimate the fibril content in each fibril orientation and each integration point.

This process was preceded by converting the XYZ coordinates of integration points into polar coordinates (R_n, φ), figure 1, to be compatible with the polar basis of Zernike polynomials. The term R_n was normalized by α/α_l to the range 0 to 1 for the cornea and normalized by 1 + (α − α_l)/(π − α_l) to the range 1 to 2 for the sclera where α_l was the complementary angle α of the elevation angle of the limbus.

2.3. Implementation of constitutive model in numerical simulation

A constitutive model was implemented in numerical simulation using Abaqus v. 6.14 standard solver^® (Dassault Systemes Simulia Corp., Rhode Island, USA) where two user subroutines (SDVINI and UMAT) were used to locate the model integration points, apply Zernike parameters and calculate stress and elasticity tensors that incorporate distribution of fibril content. Stress and elasticity tensors were derived based on the second Piola–Kirchhoff stress in the form [33]

$$\begin{array}{rl}\mathbf{S}& =2\frac{\mathrm{\partial }\mathit{\Psi }}{\mathrm{\partial }\mathbf{C}}\hspace{0.17em}=2\sum _{i=1}^6\frac{\mathrm{\partial }\mathit{\Psi }}{\mathrm{\partial }{I}_i}\frac{\mathrm{\partial }{I}_i}{\mathrm{\partial }\mathbf{C}}\\ \mathrm{and}\mathbf{E}& =4\frac{{\mathrm{\partial }}^2\mathit{\Psi }}{\mathrm{\partial }\mathbf{C}\mathrm{\partial }\mathbf{C}}=2\sum _{i=1}^6\frac{\mathrm{\partial }\mathbf{S}}{\mathrm{\partial }{I}_i}\frac{\mathrm{\partial }{I}_i}{\mathrm{\partial }\mathbf{C}}.\end{array}\}$$ 2.6

Subroutine SDVINI was programmed such that the pre-determined Zernike coefficients were used to estimate the fibril density at each integration point for each of the N orientations at the start of FE modelling analysis. The other subroutine, UMAT, was used to define a specific material model to control material behaviour by calculating the spatial version of elasticity tensor during each increment in loading. The fibril information calculated in SDVINI was passed to UMAT as location-based properties for each integration point.

2.4. Mesh density analysis

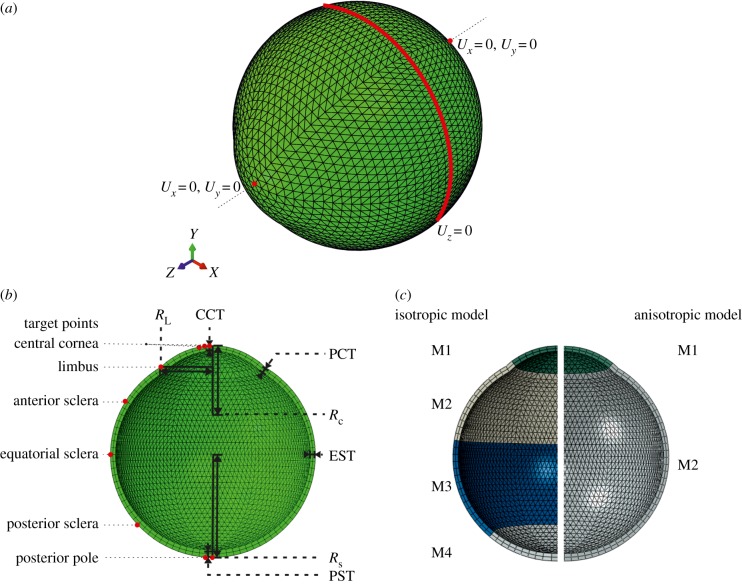
As mesh density can affect the convergence rate and accuracy of numerical models, a full eye model, whose geometry parameters were chosen based on earlier studies, was generated and used in a mesh density study (figure 2a). The study included 10 models with a number of corneal elements between 432 and 2700, and a number of scleral elements between 6504 and 43 764. All elements were 15-noded, solid, hybrid, and with quadratic formulation (C3D15H). The convergence was assessed by comparing the apical displacement and equator's radial expansion under 20 mm Hg of intraocular pressure (IOP), which lies at the high end of the normal range of IOP; between 12 and 21 mm Hg [41].

Figure 2.

Schematic views of an FE model showing geometry and material sections used in inverse analysis. (a) Constraint conditions illustrated on three-dimensional geometry. (b) Geometric parameters used to create numerical models including R_c, central corneal radius = 7.8 mm [34,35]; CCT, central corneal thickness = 0.545 mm [36]; PCT, peripheral corneal thickness = 0.695 mm; R_L, limbal radius = 5.85 mm [37,38]; R_s, scleral radius = 11.5 mm [39]; EST, equatorial thickness = 0.556 mm [40]; PST, posterior pole thickness = 0.834 mm; and p, corneal shape factor = 0.82; some target points are shown by red dots on one meridian in (b). The ocular model is shown with regions in (c); each has a separate set of Zernike polynomials at each fibril orientation. (Online version in colour.)

The material parameters adopted in this analysis were derived for ocular tissue with age 50 years [7]. Boundary conditions were set in a way in which the equatorial nodes were restrained in the Z direction, while the corneal apex and posterior pole nodes were restrained in both the X and Y directions.

2.5. Inverse analysis

Fibril densities were measured in arbitrary units and used initially as figures indicating the regional variation of stiffness across the ocular globe. The stiffness variation map was then calibrated (by determining values of the material parameters used in the strain energy model) through matching the numerical predictions of deformation under IOP with earlier experimental results. This matching was achieved through an inverse analysis process that was conducted to determine values of the six constitutive model parameters, D, C₁₀, μ₁, γ₁, μ₂ and γ₂, that were compatible with the material behaviour as determined experimentally in previous studies for ocular tissue aged between 50 and 90 years and subjected to IOP up to 30 mm Hg [9,10]. The experimental pressure–deformation behaviour obtained at 44 surface points on the ocular surface, and uniformly distributed on six meridians, figure 2b, acted as the target behaviour in the inverse analysis process.

The inverse analysis included an optimization process to determine the values of the six parameters that would provide deformation predictions with the best possible match with the target behaviour recorded at the 44 points. During this process, the cornea and the sclera were allowed to have different material parameters in order to account for the possible variation in fibril size and packing manner—cornea had thinner fibrils uniformly arranged in stromal lamellae while sclera had thicker fibrils arranged less orderly in interwoven bundles [42,43] (figure 2c).

The process benefitted from the results of earlier shear tests carried out on square 3 × 3 mm tissue specimens extracted from the central corneas of 12 human donors with ages between 30 and 100 years [3]. The specimens were subjected to shear stresses caused by two opposite loads applied on the specimen's top and bottom surfaces. Analysis of the results of these tests in our earlier study resulted in values of 0.009 MPa, 0.319 MPa and 2.0 for C₁₀, μ₂ and γ₂, respectively, for corneas over this age range [7]. These three inputs meant that the iterative inverse analysis process conducted in this study concentrated on μ₁ and γ₁ for both the cornea and the sclera, and μ₂ and γ₂ for the sclera.

2.6. Optimization tool

The particle swarm optimization (PSO) method was used in the optimization part of the inverse analysis process. The algorithm was developed by Eberhart & Kennedy [44] and has been widely applied in engineering applications [45–47]. In this study, the algorithm was implemented in MATLAB (R2018b) in conjunction with the Abaqus FE solver. The iterative analysis was set to be automatically terminated when the RMS of the absolute error (err) in equation (2.7), in the pressure–deformation curves between the target performance and the model behaviour became lower than a pre-set threshold of 5% of the maximum displacement of target curves. The absolute RMS error could be expressed as

$$\mathrm{err}=\frac{1}{N_{ld}}\sum _{\hspace{0.17em}{j}_{tc}=1}^{N_{ld}}{\left[\sqrt{\frac{{\sum }_{i=1}^{n_p}(u_i-U_i)}{n_p}}/U_{\max }\right]}_{\hspace{0.17em}{j}_{tc}},$$ 2.7

where n_p is the number of points on each pressure–deformation target curve, N_ld the number of pressure–deformation plots (31), u_i, U_i the displacement values at each specific pressure in the FE analysis and the target curve, respectively, and U_max the displacement under the maximum pressure as obtained from the target curve. The term $\sqrt{{(\sum }_{i=1}^n(u_i-U_i)/n_p)}$ is the RMS value for each target curve considered and err the average error value. All FE simulation runs were performed on a parallel Linux high performance computing cluster with eight cores and 4000 Mb RAM each.

3. Results

3.1. Analysis of Zernike fitting

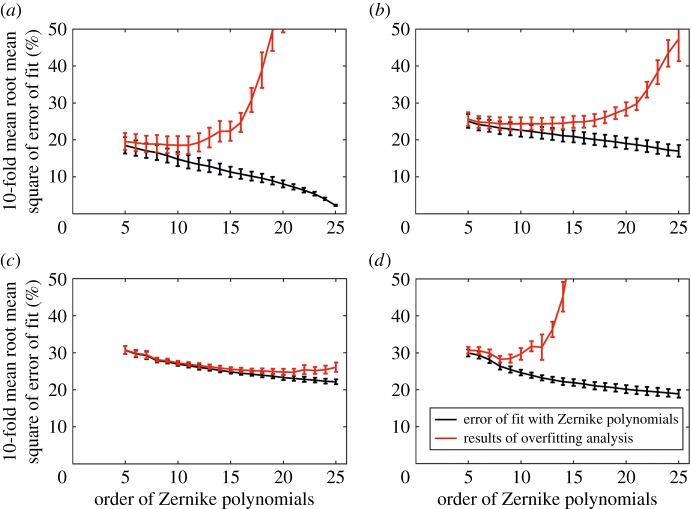
Zernike polynomials with orders between 5 and 25 were assessed and found to perform differently in the four ocular zones. In the central cornea, the fitting error decreased from 22.8 ± 2.4% at order 5 to 2.3 ± 0.18% at order 25 (figure 3a). The overfitting error initially decreased from 19.6 ± 3.2% with order 5 to 18.6 ± 2.4% with order 10, then increased sharply to 3068.9 ± 439.0% at order 25 (figure 3a). In comparison, the limbus, anterior and equatorial sclera, and posterior sclera showed smaller reductions in the fitting error with increased order from 5 to 25 (from 25.1 ± 1.8% to 17.0 ± 1.6%, from 30.7 ± 1.1% to 22.2 ± 0.7%, and from 30.0 ± 1.0% to 18.9 ± 1.1% in the three regions, respectively) (figure 3b–d). However, overfitting became significant for the limbus and posterior sclera. The limbus experienced an increase in overfitting error from 24.4 ± 1.6% to 47.3 ± 6.0% with increasing order from 13 to 25 (figure 3b). On the other hand, overfitting increase occurred earlier in the posterior sclera; at order 8 and increased by only 1.5% at order 10 but then kept rising from 28.3 ± 1.6% at order 10 to 36 766.0 ± 8941.5% at order 25 (figure 3d). These results pointed at order 10 as being suitable for all four zones.

Figure 3.

Errors of fit (black line) and overfitting (red line) with Zernike polynomials with orders between 5 and 25 in (a) zone 1: the cornea, (b) zone 2: the limbus, (c) zone 3: the equatorial sclera, and (d) zone 4: the posterior sclera. The mean fitting error relative to the average fibril density was calculated by the 10-fold cross-validation and its standard deviation for 180 orientation.

3.2. Optimum number of fibril orientations

Starting from 180 orientations (with an angular step of 1°), in which the raw X-ray scattering data were provided, a study was carried out to determine the optimum number of orientations that can be used in building numerical models with a reasonable compromise between analysis accuracy and cost [7,24,26]. As expected, decreasing the number of orientations led to gradual increases in the model prediction errors, which became exponential when fewer than 16 orientations were adopted (figure 4). Meanwhile, the analysis cost showed an opposite trend with significant cost reductions with fewer orientations. Based on these results, subsequent work adopted 16 fibril orientations in building ocular numerical models in this study.

Figure 4.

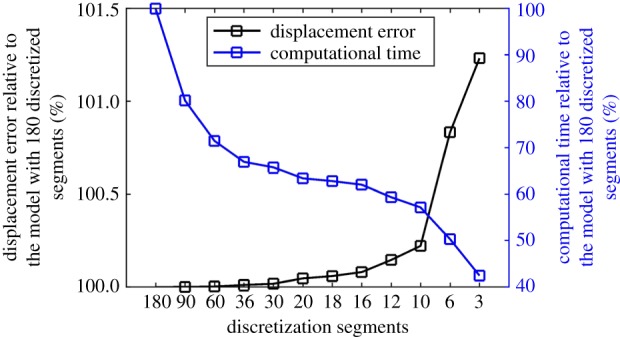
Variations in apical displacement predictions and analysis cost relative to the case with 180 fibril orientations when considering different orientation numbers between 3 and 180. (Online version in colour.)

3.3. Mesh convergence study

Figure 5 shows that significant reductions in the mesh density of FE models by up to 36% (from 46 464 elements to 29 400 elements), which led to 47% reductions in numerical analysis cost, caused only a 0.2% change in apical displacement prediction. A further reduction in the number of model elements from 29 400 to 12 696 caused a change in output by 0.8%, and this increased to 5.0% when the number of elements was cut down from 12 696 to 6936. Based on these results, a mesh density with 12 696 elements was selected for use in this study.

Figure 5.

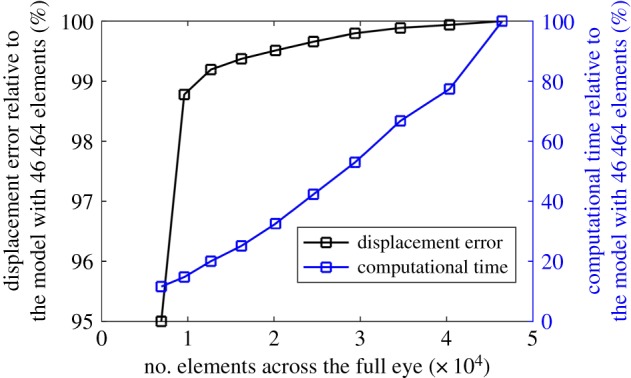
Apical displacement outputs and CPU computation time of numerical models with different mesh densities. (Online version in colour.)

3.4. Inverse analysis

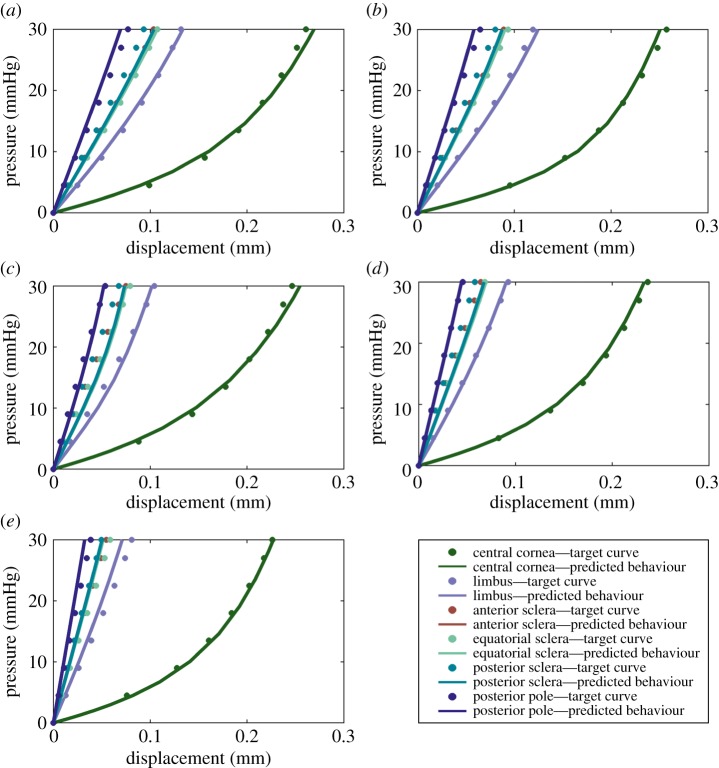
Inverse analysis was carried out to determine the parameters of the material model that provide the best match for numerical predictions of behaviour with the tissue behaviour obtained in earlier experimental studies in which cornea and sclera specimens (from donors aged between 50 and 90 years) were loaded under inflation conditions while monitoring their deformation [9,10]. The match between the numerical predictions and the experimental measurements was assessed using the PSO method, which has been used previously, with success, in solving optimization problems [47]. The inverse analysis process continued until the RMS of error between predicted and target pressure–deformation behaviour became lower than a pre-set threshold of 5%. At the end of the analysis, the output performance was as presented in figure 6, with the corresponding values of material parameters included in table 1. The central cornea exhibited larger axial and lateral displacements, both experimentally and numerically, compared with the sclera and the limbus. Displacements of all regions decreased with age, which was consistent with the expected age-related stiffening [10,48]. Of particular note, the material parameters, produced by the optimization process, accurately reproduced the experimental displacement curves of the central cornea, limbus and posterior pole.

Figure 6.

Target curves based on experimental material behaviour obtained for different regions of ocular globe (figure 2) and for different ages are compared with the predicted behaviour following conclusion of the inverse analysis procedure. (a–e) Behaviour of tissue aged 50, 60, 70, 80 and 90 years, respectively. (Online version in colour.)

Table 1.

Values of material parameters obtained by inverse analysis for ocular tissues with ages between 50 and 90 years.

age (years)		D	C10 (MPa)	μ1 (MPa)	γ1	μ2 (MPa)	γ2	err (%)
50	cornea	1 × 10−5	0.009	1.16 × 10−3	121.2	0.319	2.0	3.7
	sclera			4.44 × 10−5	532.6	1.48	10.0
60	cornea	1 × 10−5	0.009	1.24 × 10−3	124.2	0.319	2.0	4.1
	sclera			4.90 × 10−5	535.6	1.68	5.87
70	cornea	1 × 10−5	0.009	1.44 × 10−3	125.7	0.319	2.0	4.3
	sclera			6.02 × 10−5	535.6	2.7	3.6
80	cornea	1 × 10−5	0.009	1.46 × 10−3	132.2	0.319	2.0	3.6
	sclera			7.52 × 10−5	524.6	1.48	10.0
90	cornea	1 × 10−5	0.009	1.49 × 10−3	134.1	0.319	2.0	3.9
	sclera			8.74 × 10−5	536.9	2.43	9.98

A uniqueness test was also carried out within the inverse analysis exercise to assess the reliability of the material parameters obtained. Three inverse analysis attempts were conducted with different initial values assigned to the material parameters in the case for tissue with age 50 years. The results, shown in table 2, illustrated the independence of the inverse analysis output from the initial material parameter values. The results in table 1 show that the material parameters underwent consistent changes with age with the cornea's μ₁ and γ₁ both undergoing gradual increases. From 50 years old to 90, the value of μ₁ increased from 1.16 × 10⁻³ to 1.49 × 10⁻³, and the value of γ₁ from 121.2 to 134.1. On the other hand, the value of μ₁ increased with age in the sclera from 4.44 × 10⁻⁵ at 50 years old to 8.74 × 10⁻⁵ at 90, and γ₁ almost remained at the same level in all ages. The increase in the values of parameters μ₁ and γ₁ indicates greater tangent modulus of fibrils on the tangential plane of ocular surface and thus the stiffening of ocular tissue.

Table 2.

Results of a uniqueness test showing material parameters obtained from three inverse analyses using the 50-year-old deformation profile.

inverse analysis	age (years)		D	C10 (MPa)	μ1 (MPa)	γ1	μ2 (MPa)	γ2	err (%)
1	50	cornea	1 × 10−5	0.009	1.16 × 10−3	121.2	0.319	2.0	3.7
		sclera			4.44 × 10−5	532.6	1.48	10.0
2	50	cornea	1 × 10−5	0.009	1.15 × 10−3	121.4	0.319	2.0	3.6
		sclera			4.45 × 10−5	532.7	1.22	8.94
3	50	cornea	1 × 10−5	0.009	1.16 × 10−3	121.6	0.319	2.0	3.7
		sclera			4.44 × 10−5	532.3	1.24	10

4. Discussion

In recognition of the collagen fibrils' role as the main load-carrying component in ocular tissue, research has progressed to develop numerical models of ocular mechanical behaviour that rely on microstructural, fibril distribution maps in controlling the distribution of tissue stiffness and anisotropy [6,7,20,23,24,26,49,50]. This study aimed to extend this work in two significant ways; to cover the full ocular globe, instead of limiting coverage to the cornea or the posterior sclera, and to rely on raw, eye-specific X-ray scattering data instead of idealizations of fibril distribution maps. Data at each measurement point, which included fibril content estimates in 180 directions, were grouped into 16 segments to significantly reduce computational time. The data within each of these segments were then fitted to Zernike polynomials to enable the estimate of values of fibril content at the FE integration points, which have different locations from the X-ray measurement points. With the fibril data on content and orientation represented by Zernike polynomials, the constitutive model could rely on these data in reproducing the regional variation of both stiffness and anisotropy. A further exercise was then conducted to use this model, along with the experimentally observed ocular mechanical response to laboratory loading under IOP up to 30 mm Hg, to estimate values for the model's material parameters that represent behaviour of tissue aged 50–90 years.

This study was built on available corneal microstructure mathematical models and extended the constitutive material model to full-eye application [7,24]. The X-ray scattering data in the form of fitted Zernike polynomial parameters were used to provide precise fibril distribution at each integration point and to account for the tissue's strong anisotropy. The material model used produced stable behaviour even with reasonable variations in mesh density and during the inverse analysis study.

The iterative inverse analysis procedure provided a distinctive set of material parameters for each of the cornea and sclera. This approach was adopted because of fundamental variations in fibril diameter and arrangement in the two regions. While fibril diameter in the cornea ranged between 25 and 35 nm, it was between 25 and 230 nm in the sclera [42]. Moreover, whereas fibrils were packed in a mainly parallel manner in the cornea, they were more interwoven in the sclera. These variations would affect the material behaviour even with the same collagen content.

The increase of both material parameters μ₁ and γ₁ in the cornea and only μ₁ in the sclera led to reductions in displacement values across the ocular globe with age (figure 6). The stiffening of the cornea and sclera with age was studied earlier and evidenced through increases in tangent modulus [9,10]. In our study, μ₁ in the cornea increased by 28.5% from 50 years old to 90 while the value of γ₁ increased slightly by 10.6%. The corresponding increase in μ₁ in the sclera was significantly higher, at 96.8%, while γ₁ remained almost constant. The variation in values of parameters μ and γ points at distinctive behaviour differences between the cornea and sclera. While μ controls the initial stiffness, or initial gradient of the stress–strain relationship, γ controls how this initial stiffness varies with further stress. The results show that the cornea had higher initial stiffness of in-plane fibrils but lower rate of stiffness growth than the sclera. For out-of-plane fibrils, the cornea showed both lower initial stiffness and lower rate of stiffness growth than the sclera.

While previous studies adopted 180 discretized orientations for the angular fibril distribution [7,24,51], this study investigated the effect of reducing number of discretization segments on numerical model predictions. Having fewer fibril orientations would simplify the process to integrate fibril contribution in the numerical implementation of the strain energy function—reducing the number of Zernike polynomials needed to describe fibril distribution in each orientation, and subsequently simplify the construction of the element stiffness matrices. The optimum number of fibril orientations in our study was 16, at which there was a 0.08% change in numerical model output associated with a 40.0% reduction in analysis cost.

The study has a number of limitations, which should be noted. First, the lack of information on the out-of-plane orientation and density of inter-lamella fibrils made it necessary to assume an out-of-plane fibril elevation angle of 15° and the same angular density distribution as lamella fibrils, both of which were adopted in earlier studies of Studer et al. [24] and Whitford et al. [7]. This assumption could affect the model behaviour under shear, which would be important in applications subjecting the tissue to flexural effects such as tonometry loading. Second, the material model assumed that the ground substance matrix had the same composition across the whole eye, allowing C₁₀ to have the same value in both the cornea and sclera. Future research should explore the validity of this assumption and its effect on ocular behaviour predictions. Third, variations in fibril distribution through tissue thickness were disregarded in model construction as they could not be characterized using X-ray scattering technique. The assumption of uniform fibril distribution across tissue thickness, which was necessary in this study, should be explored in future work while bearing in mind that this will be a challenging, expensive and time-consuming task.

In conclusion, this study presented a constitutive material model that covered the whole eye surface and incorporated the X-ray microstructure characteristics measured for seven ex-vivo human eyes. By considering experimental pressure–deformation behaviour and using an inverse analysis procedure, the model's parameters could be determined to represent tissue behaviour and its age-related stiffening. The current full-eye constitutive model can be used for assessment of clinical challenges including simulation of medical or surgical procedures that interact or interfere mechanically with the eye.

Data accessibility

All the data have been included in the electronic supplementary material.

Authors' contributions

D.Z. carried out data analysis, designed the numerical model and drafted the manuscript. A.A. critically revised the manuscript and contributed to the data analysis. As.E. participated in data analysis. H.P.S. participated in the modelling of ocular globe. A.M. and N.M. revised the manuscript. Ah.E. provided the idea, supervised the study and critically revised the manuscript.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.