Abstract
It has been suggested that neck muscle strength and anticipatory cocontraction can decrease head motions during head impacts. Here, we quantify the relative angular impulse contributions of neck soft tissue to head stabilization using an OpenSim musculoskeletal model with Hill-type muscles and rate-dependent ligaments. We simulated sagittal extension and lateral flexion mild experimental head impacts performed on 10 subjects with relaxed or cocontracted muscles, and median American football head impacts. We estimated angular impulses from active muscle, passive muscle and ligaments during head impact acceleration and deceleration phases. During the acceleration phase, active musculature produced resistive angular impulses that were 30% of the impact angular impulse in experimental impacts with cocontracted muscles. This was reduced below 20% in football impacts. During the deceleration phase, active musculature stabilized the head with 50% of the impact angular impulse in experimental impacts with cocontracted muscles. However, passive ligaments provided greater stabilizing angular impulses in football impacts. The redistribution of stabilizing angular impulses results from ligament and muscle dependence on lengthening rate, where ligaments stiffen substantially compared to active muscle at high lengthening rates. Thus, ligaments provide relatively greater deceleration impulses in these impacts, which limit the effectiveness of muscle strengthening or anticipated activations.
Keywords: ligament, head impacts, cervical spine, muscle strength
1. Introduction and background
Anecdotally, muscle strength and muscle cocontraction in anticipation of an impact are thought to reduce head motions during a head impact, which in turn is thought to reduce risk of brain injury. Clinicians, athletic trainers and coaches have thus been recommending neck muscle strength training and field awareness exercises for contact sports athletes to protect themselves on the field [1].
Research studies have been less conclusive about the correlation between muscle strength or anticipatory muscle cocontraction with a reduction in head motion. Laboratory studies applying low-severity external loads to human subjects have demonstrated that anticipated muscle cocontraction significantly reduces head motion following impacts [2]. However, impact forces in these studies are of the order of maximal neck muscle isometric force production, and it is unclear how effective neck muscles are at resisting more severe impact forces.
One prospective field study found a correlation between neck muscle strength and reduced brain injury incidence in high school athletes [3]. This represented the first field evidence that a correlation exists between muscle strength and reduction of brain injury, which the authors postulated was due to a reduction in head motion following impacts. However, the study neglected to account for factors such as athlete mass which have also been implicated in head impact kinematics [4]. Other prospective field studies have also failed to identify similar correlations between neck muscle strength or anticipatory preparation and brain injury risk or head kinematic severities [5,6].
Researchers have also investigated the effect of neck strengthening regimens on head motion, which are more useful for suggesting preventative measures for individuals [7,8]. These studies have found that while strengthening regimens can increase neck strength, there was little evidence that such techniques reduced head motions. However, many of these studies were limited by relatively small subject populations, and a large prospective study relating neck strengthening exercises and reduction of head motion following an impact is a current gap in the literature.
The studies discussed thus far have focused on drawing correlations between neck muscle strength or anticipated cocontraction with decreases in head motion following an impact. To determine an anatomical mechanism by which neck muscle strength or anticipated cocontraction might reduce head motions following an impact, a more controlled or model-based approach is required.
Recently, several researchers have sought to uncover this mechanism by simulating head impacts while varying neck muscle strength or activity [9–12]. However, researchers have reached varying conclusions due to differences in study design, such as choice of model (finite-element, anthropomorphic test dummy surrogate, rigid linkage model) or choice of impact conditions (severity, direction, impact surface). Furthermore, these studies have focused primarily on the effect of active muscles, and typically neglect the role of other soft tissue in stabilizing the head.
Thus, the role of neck muscles in head impacts remains an active area of research. In this study, we approach this problem by quantifying the moment and angular impulse contributions of active musculature, passive muscle structure, ligaments and external loads to study their relative roles during head impacts using musculoskeletal head and neck models developed in OpenSim. We simulated experimental head motions performed in 10 subjects during mild head impacts and extrapolated to median American football head impacts. The moment production of individual elements is dictated by their constitutive material models, which shed light on the underlying biomechanical mechanisms of head stabilization during impacts.
2. Results
To determine the relative contributions of muscle activity, passive muscle structures and passive ligaments during head stabilization, we modified a previously developed OpenSim head and neck musculoskeletal model [13,14]. We performed forward dynamics simulations of previously published mild experimental head impacts in 10 subjects [4]. In the experiments, loads were applied to induce head motion in two directions (sagittal plane extension and coronal plane lateral flexion towards the non-dominant side) and with two muscle activity conditions. For the first muscle activity condition, we instructed subjects to minimally activate neck muscles while maintaining an upright posture (gravity balance), which we consider a relaxed condition. For the second muscle activity condition, we instructed subjects to maximally activate muscles while maintaining an upright posture, which we consider a cocontracted muscle condition.
Subject-specific models were generated for these simulations scaled to subject height, mass and isometric strength in sagittal plane flexion and coronal plane lateral flexion. In each simulation, the motion was restricted to the primary motion plane (sagittal plane or coronal plane). From the simulations, we determined the relative moments and angular impulses responsible for head stabilization. We also simulated median severity of American football head impacts with cocontracted muscles in the 10 subject-specific models using extrapolated force profiles to observe differences in relative moment and angular impulse contributions.
2.1. Experimental angular impulse and moment contributions
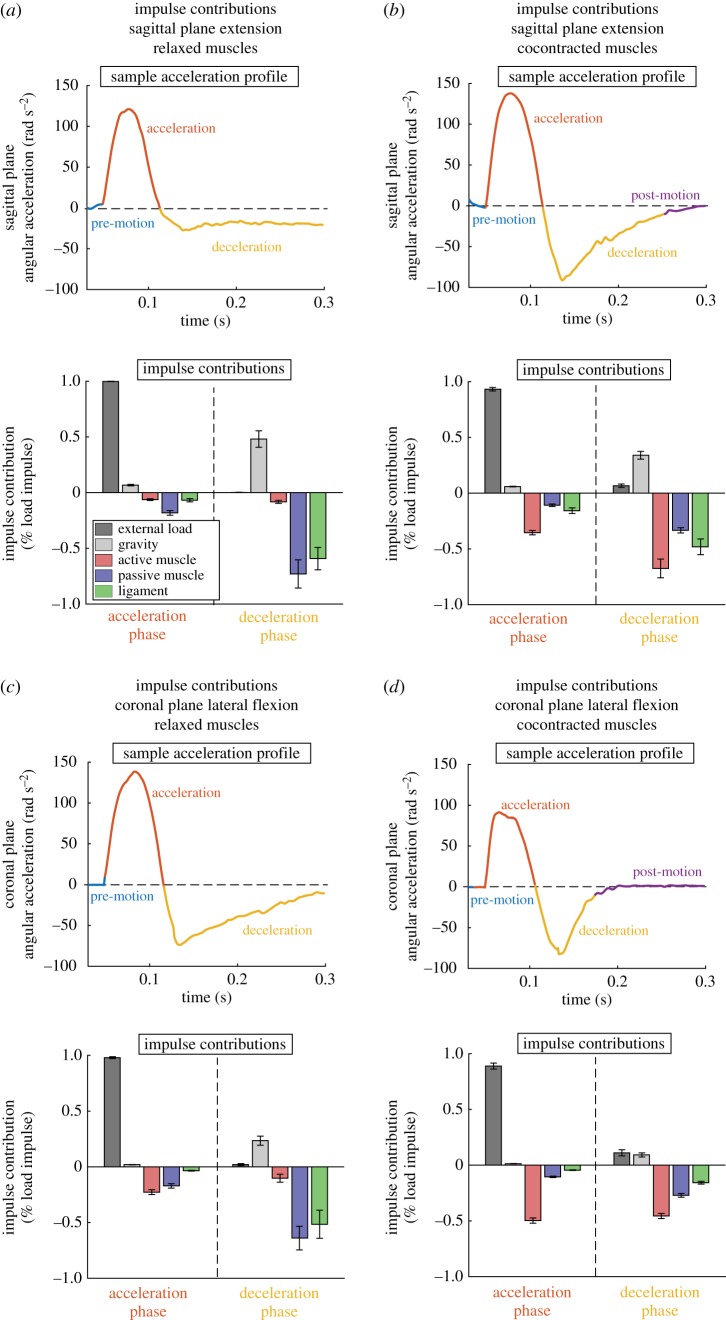
To demonstrate contributions to stabilization during mild experimental head impacts, we first show relative angular impulse contributions of the external force, gravity, all muscles (active component), all muscles (passive component) and all ligaments during acceleration and deceleration phases (figure 1). Contributions were normalized by the total angular impulse provided by the external load and aggregated over all 10 subjects for each condition. Angular impulses were obtained by integrating moments over periods of acceleration and deceleration.
Figure 1.
Angular impulse contributions during simulated mild head impacts. Impacts were divided into an acceleration and deceleration phase based on the planar angular acceleration time history (positive acceleration is the sagittal extension of lateral flexion towards the non-dominant side). We included a short 30 ms of zero force pre-load to allow the model to reach a balanced steady state (pre-motion). In some conditions, head stabilization was achieved before the end of the 300 ms impact simulation, resulting in a post-motion period with low angular accelerations (|α| < 10 rad s−2). Impulse contributions during acceleration and deceleration phases were computed for external load, gravity, all muscles (active component), all muscles (passive component) and all ligaments for each condition and aggregated over all subjects. Angular impulse contributions were also normalized by total angular impulse produced by the external force. When neck muscles were relaxed, ligaments and passive muscles had the largest angular impulse contribution in deceleration for (a) sagittal extension and (c) coronal lateral flexion, respectively. When neck muscles were cocontracted, the active muscle had the largest angular impulse contribution in deceleration for both (b) sagittal extension and (d) coronal lateral flexion. In all cases, external load provided the angular impulse that accelerated the head, with active muscles providing over 30% resistive angular impulse during cocontracted muscle cases. (Online version in colour.)
In all conditions, the acceleration phase was dominated by the angular impulse provided by the external load. When muscles were relaxed, there were no substantial resistive angular impulses provided by any soft tissue structures during the acceleration phase. However, when the muscles were cocontracted, the active muscles provided resistive angular impulses that were 30% of the total impact angular impulse.
During the deceleration phase, soft tissue structures were responsible for providing angular impulses that stabilized the head. When subjects relaxed neck muscles, angular impulse was dominated by the ligaments and passive muscle in both sagittal extension and coronal lateral flexion. When muscles were cocontracted, angular impulse contributions were dominated by the active muscle.
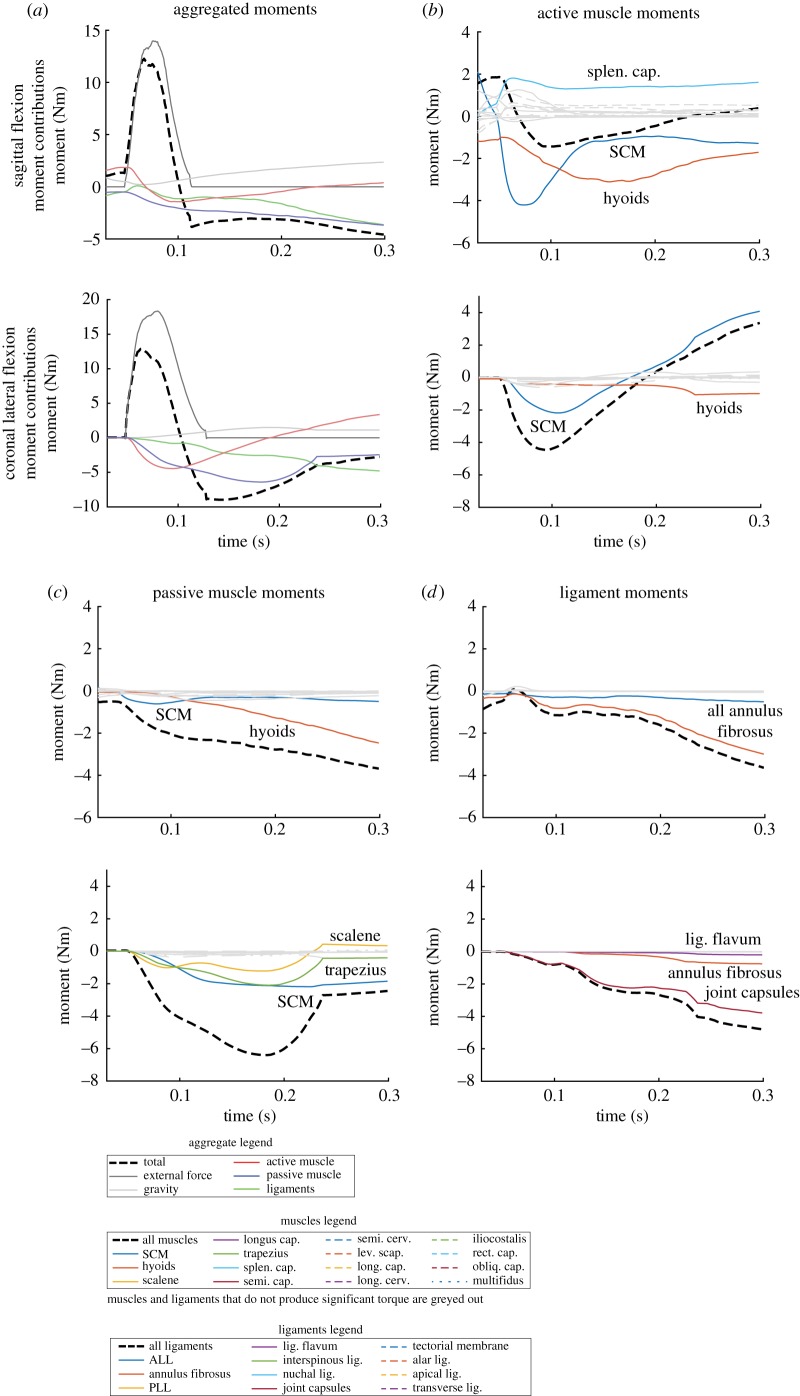
We next show a breakdown of moments generated over time by external load, gravity, muscle groups (active component), muscle groups (passive component) and ligament groups (figure 2). These were produced for a single subject with relaxed neck musculature in sagittal extension and coronal lateral flexion to pinpoint the structures most responsible for head stabilization and to demonstrate the time evolution of moment generation.
Figure 2.
Moments produced by model forces demonstrate important structures for stabilization. Moments over the impact period from force elements in the simulation are presented (positive moments are moments in sagittal extension or lateral flexion to the non-dominant side). We show samples from a sagittal extension and coronal lateral flexion simulation with relaxed neck muscle activations. (a) Moments from external load, gravity, aggregated active muscle, passive muscle and ligaments are shown first to demonstrate how moments from each group change with time. Moments from (b) active muscle component and (c) passive muscle component show that the SCM produces large negative moments resisting impact motion in both directions. Moments from (d) ligaments show that AF fibres and capsular ligaments dominate in sagittal extension and coronal lateral flexion, respectively. (Online version in colour.)
In sagittal extension, both active and passive components of the hyoid muscles and sternocleidomastoid (SCM) muscles had large negative moment contributions resisting impact motion. Annulus fibrosus (AF) fibres produced significantly greater negative moments among the ligaments. While both AF fibres and active SCM muscles produced similar negative moments, there were some muscles, such as the splenius capitis, providing positive moments that reduced the overall contribution from the active muscles. These positive moments were due to the initial activation that was necessary to maintain an upright posture (gravity balance) and was held through the duration of the impact.
In coronal lateral flexion, the SCM produced the greatest negative moment of the muscles (active and passive components), with substantial contributions from the passive component of the trapezius and scalene muscles as well. Of the ligaments, the joint capsules provided the greatest negative moments, with minor contributions from the AF fibres and the ligamentum flavum.
2.2. Extrapolated median football impact
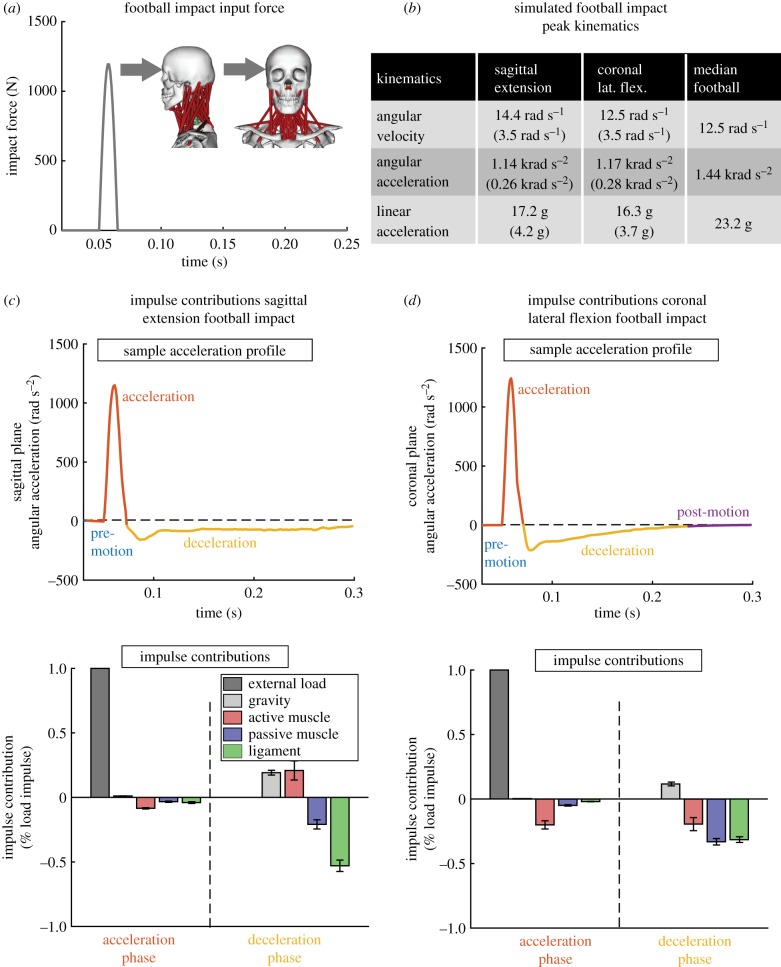
Finally, we show results from the median severity American football head impacts simulated using an extrapolated force profile aggregated over the 10 subjects (figure 3). The force profile was generated to produce median American football kinematics over the 10 subject-specific models with cocontracted muscle activations. Median kinematics were taken from a previous exposure study of American football athletes wearing instrumented mouthguards over several games [15,16]. Simulated kinematics were within 20% of the median values in both sagittal extension and coronal lateral flexion.
Figure 3.
Extrapolated American football median impact shows a change in stabilization contributions. (a) We applied a simulated American football impact force in sagittal extension and coronal lateral flexion to our strongest subject with cocontracted neck muscle activations. (b) Simulation kinematics were within 20% of the median American football impact kinematics. Angular impulse contributions in (c) sagittal extension and (d) coronal lateral flexion show that the active muscle has less relative contribution than in the experimental trials. In sagittal extension, the ligaments provide the most angular impulse in deceleration. (Online version in colour.)
Angular impulse analysis (similar to figure 1) shows a decrease in resistive active muscle angular impulse contribution during the acceleration phase in both sagittal plane extension and coronal plane lateral flexion directions. While active muscles produced a resistive angular impulse that was 30% of the total impact angular impulse in mild experimental loads, this is reduced to below 20% in median American football head impacts.
During the deceleration phase, there is a relative decrease in active muscle angular impulse contribution despite using cocontracted muscle activations. In sagittal extension, active muscles in fact provide a positive angular impulse, whereas the ligaments now provide the largest resistive angular impulse contribution. The positive angular impulse is likely due to the SCM providing an extension moment at large extension angles as reported previously [13]. In coronal lateral flexion, both the passive ligaments and passive muscle structures provide larger resistive angular impulse contributions than the active muscles.
3. Discussion
In this study, we estimate the relative angular impulse contribution of active muscle, passive muscle and passive ligament structures to head stabilization during experimental mild head impacts and extrapolated median American football head impacts using a musculoskeletal OpenSim model. While many previous studies have focused on the ability of neck musculature to resist head impacts and stabilize motion, we sought to quantify the contributions of the various cervical spine tissue structures (including the active and passive components of muscles).
We have demonstrated that in experimental mild head impacts, cocontraction of neck muscles resulted in large stabilization moments from the active component of the muscles, in particular, the SCM muscle. While there was a significant increase in active muscle impulse contribution, we only observed a significant decrease in simulated head kinematics during lateral flexion impacts. This differs somewhat from previous experiments where there is an overall decrease in kinematics with muscle cocontraction [2], though we note that in our experimental trials, the load impulse during cocontracted muscles cases is significantly higher than in relaxed muscle cases despite having the same input energy (equivalent mass dropped from equivalent height) [4]. When we extrapolate to median severity American football impacts, active muscle contributions decrease relative to other elements (ligaments and passive muscles). In sagittal extension, one of the more common impact scenarios in American football [15], the passive ligaments provide the most angular impulse stabilizing the head.
This indicates that the relative distribution of loads in the cervical spine among muscles and passive structures is dependent on impact direction and severity. In coronal lateral flexion, it has been previously reported that muscle moment arms for neck lateral flexors are larger than for neck sagittal flexors [13]. The SCM, which contributed the most muscle moments and angular impulses in our study, had a nearly five times larger moment arm in coronal lateral flexion than sagittal flexion [13]. Thus, the muscle angular impulse contributions remain relatively large in lateral flexion.
For severity dependence, we focus on the constitutive models for the muscle (Hill-type) and ligaments (figure 4). At higher severities, the lengthening rates of both the muscles and ligaments increase substantially. Previous studies of whiplash simulations report that ligaments can experience over 1000 mm s−1 lengthening rates [17–19]. While the velocity relationship for Hill-type active muscle plateaus at a relatively low lengthening rate (one optimal fibre length per second), which we achieved during our mild experimental head impacts, it has been suggested that the ligaments have a log-stiffening behaviour with respect to lengthening rate [19–21]. Thus, with increased impact severity, the active muscles did not produce substantially greater moments than the mild experimental head impacts. However, due to the strong ligament dependence on lengthening rate, the ligament moments scaled with impact severity.
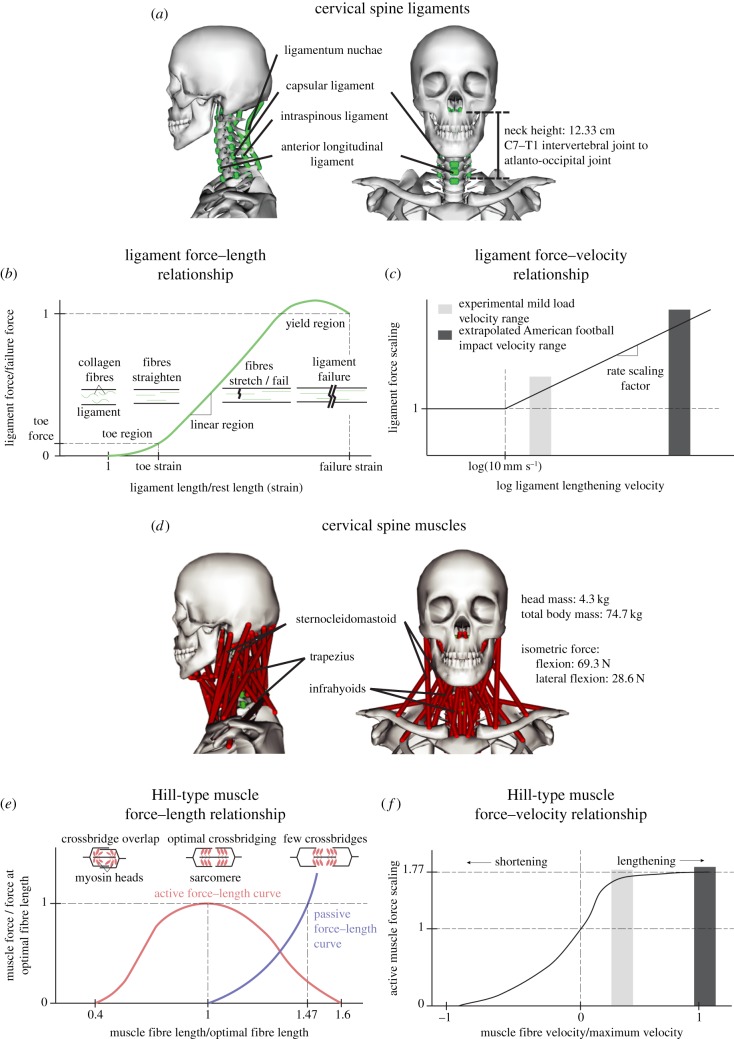
Figure 4.
OpenSim head and neck impact model. The OpenSim musculoskeletal model is a 20 degree-of-freedom model that was based on the Mortensen 2018 model. (a) We added 80 individual cervical spine ligament sections representing 11 ligament groups to represent soft tissue stabilization force elements. The constitutive material model for the ligaments was represented with a (b) force–length and (c) force–velocity curve, which were identified previously in the literature. The force–length relationship of ligaments has a characteristic shape corresponding to the straightening (toe region), stretching (linear region) and breaking (yield region) of collagen fibres. Our constitutive model does not include a yield region, similar to how passive tendon is modelled. (d) The model also contains 84 muscle subvolumes over 15 muscle groups, which were defined in the original Mortensen 2018 model. Muscles were represented using the Hill-type muscle model, with a (e) force–length curve modelling myosin cross bridges in sarcomere functional units and a (f) force–velocity curve scaling force output depending on muscle fibre velocities. Ligament and muscle peak lengthening velocities are marked in (c,e) during experimental mild external loads and extrapolated median American football impacts. While the (e) muscle force–velocity scaling is similar in both load regimes, the (c) ligament force–velocity scaling is substantially larger during median American football impacts, resulting in greater moments produced by ligaments in the high-severity regime. (Online version in colour.)
While we were able to simulate experimental mild head impacts using an OpenSim model and analyse muscle and ligament contributions to stability, this study has a number of limitations. First, our findings are dependent on our chosen constitutive muscle and ligament models, and the properties for each muscle and ligament. However, we note that the Hill-type muscle model is a standard model used in countless musculoskeletal modelling platforms to model all aspects of the human body [20,22,23]. The ligament model, particularly the force–length relationship, is also well established in the literature and used in many finite-element models [20,21]. We note, however, that muscles typically are not evaluated at extremely high lengthening rates, and while force–velocity scaling plateaus in the current Hill-type muscle model implementation, the scaling may continue to increase at extremely high rates.
The OpenSim model also only includes structures representing the skeletal structure, ligaments and muscles. However, the cervical spine contains other structures (such as the trachea) that could also contribute to angular impulses during impact. We included only muscles and ligaments as they are the most ubiquitous in the cervical spine, but other structures should be properly modelled and analysed further. We note, however, that muscles represent the only active structure in the cervical spine, so the addition of additional tissue structures will only add to impulses from passive components that are not affected by muscle strengthening or pre-activation.
More broadly, we must also discuss the implications of using the OpenSim musculoskeletal framework for simulating head impacts compared to previously presented models. Unlike some prior work [9–12] which relied on complex finite-element models, OpenSim is a rigid multibody simulation platform. The limitation of such modelling frameworks is that they do not necessarily accurately represent geometric dependencies. Indeed, muscles and ligaments in the OpenSim model are represented as linear elements with the exception of the SCM muscles which wrap around the omohyoid muscle.
However, such simplifications allow OpenSim to run with orders of magnitude less computational power and give accurate estimates of gross relationships. OpenSim, in particular, has been used extensively to assess moment and force production in locomotion as the rigid multibody representation accurately captures gross measurements such as intersegmental forces or muscle–tendon forces [22,24,25]. Similarly here, we believe that an OpenSim model accurately captures the gross elements that contribute to head and neck stabilization, but a finite-element simulation will be required to capture fine details such as localized strains and stresses within muscles and ligaments.
Previous modelling work has also focused primarily on studying inertial whiplash loading scenarios, which are relevant to automotive impacts [23,26–30], and are thus not necessarily applicable to direct head loads which are more representative of contact sports scenarios. As a result, most previous models are specifically validated in whiplash scenarios. Previous experimental work has shown that muscle cocontraction can reduce head kinematics in laboratory direct head loading scenarios but has not used models to study the relative moments of the contributing soft tissue structures [2].
While we demonstrate that muscle cocontraction can indeed produce significant stabilizing moments in mild laboratory head impacts, we caution that this does not necessarily extend to more severe impacts seen in contact sports that cannot be effectively evaluated in the laboratory. Thus, the need for a model evaluated specifically for direct head loading scenarios is necessary to extrapolate the effect of muscle cocontraction to more severe head impacts.
For the OpenSim simulations, we chose to fix the torso to ground (Material and methods). We did this because in the experimental mild head impact study, we attempted to fix the torso by seating subjects in a rigid back chair [4]. However, as was reported in the previous study, there was some torso motion, particularly in the coronal lateral flexion trials. We note that linear accelerations had the largest errors between OpenSim simulations and experimental head impacts (electronic supplementary material, D), and it is possible this was because of the torso motion. However, we note that our other analyses focused on angular impulses and moments (angular metrics).
For coronal lateral flexion experiments, we had to constrain the OpenSim model to planar rotations by locking out-of-plane joints. It has been previously reported and it was observed in the experimental dataset that there is significant coupling between coronal lateral flexion and axial rotations [31]. While these out-of-plane rotations were observed experimentally, we previously reported that the in-plane motion dominated the head motion response experimentally [4].
Other methods for computing intervertebral moments were previously presented for a finite-element model in whiplash scenarios [32]. These methods involved computing moments in a planar cross-section, and were thus sensitive to the choice of cross-section and did not account for moments from forces not captured within the cross-section (specifically intervertebral discs as is noted in the study) [32].
In conclusion, we have quantified the relative contribution of muscles and ligaments to head stabilization during impacts. While there is no doubt the muscles play a role in stabilizing the head, their relative contribution depends on impact severity and direction and is not always greatest. Thus, claims that neck muscle strengthening and anticipatory cocontraction reduce head motions following impact must be made cautiously and should be compared against other factors such as head and neck orientation [4,33]. Cervical spine ligaments are well studied in whiplash injuries and automotive crashes, and despite playing a large role in head and neck stability, they have received relatively little attention in head impact biomechanics.
Our OpenSim model and analysis represent a step towards uncovering the nuanced roles of the cervical spine structures in head impacts. However, further improvements can and should be made. To facilitate collaborative efforts and dissemination of our simulations and datasets, we have provided experimental data, models and simulations on the public SimTK repository: https://simtk.org/projects/kuo-head-neck.
4. Material and methods
4.1. OpenSim musculoskeletal model
The musculoskeletal model was developed in OpenSim and is derived from a previous head and neck model used to quantify moments of the neck muscles [13,14]. Details of the model are provided in electronic supplementary material, A and B. Our main contribution was the addition of passive ligaments in the cervical spine (this included the AF fibres of the intervertebral disc). We included 80 individual sections representing 11 ligament groups (described in electronic supplementary material, B). The constitutive material model for the ligaments consisted of a force–length () and force–velocity () relationship as a function of the element length () and element loading rate ():
| 4.1 |
The ligament force–length relationship has been extensively described in the literature and consists of a toe region of relatively low force production, a linear region where ligaments exhibit elastic behaviour, and a yield region where the ligament begins to mechanically fail [21,34–36]. We represent ligaments here with a piece-wise linear function representing the toe and linear regions and parametrized by a toe modulus (), a toe strain (), a linear modulus (), ligament rest length () and ligament cross-sectional area (, equations (4.2) and (4.3)):
| 4.2 |
and
| 4.3 |
The ligament force–velocity relationship is also particularly well studied in cervical spine ligaments as these ligaments experience high loading rates in injury scenarios [17–19]. It has been suggested that beyond a representative quasi-static loading rate (we chose 10 mm s−1), ligament force linearly scales with a slope () against the log loading rate (equation (4.4)) [19,20]:
| 4.4 |
Parameters for each ligament at each intervertebral joint were defined and validated from previous literature (electronic supplementary material, B and C). Geometrical muscle and ligament attachments and bony articulations were defined visually. We additionally confirmed ligament lengths against previous literature (electronic supplementary material, B).
Besides the newly added ligaments, the model consists of 84 muscle subvolumes representing 15 distinct muscle groups, including hyoid muscles and multifidus muscles. These muscles were modelled as Hill-type muscles in OpenSim (equations (4.5) and (4.6), figure 4) and parametrized by optimal muscle force (, activation (a), the active and passive force–length relationships ( and , respectively) as a function of muscle length () and the force–velocity relationship () as a function of muscle velocity () [25]. Muscle force transmission to rigid vertebral elements was parametrized by muscle fibre pennation angle () and tendon force–length relationship () as a function of tendon length (), and additionally constrained by geometrical muscle–tendon length (, equation (4.7)). Details of the muscle model can be found in Mortensen [14].
| 4.5 |
| 4.6 |
| 4.7 |
Seven cervical vertebrae (C7–C1) and the skull were represented with rigid elements. Cervical vertebrae C7 through C2 articulated with respect to the inferior vertebrae with a three degree-of-freedom rotational joint. The most inferior C7 cervical vertebrae articulated with respect to the torso with a three degree-of-freedom rotational joint. The torso was subsequently fixed to the inertial frame, though could be adjusted to articulate with full six degree-of-freedom motion. The C1–C2 (atlanto-axial) and skull–C1 (atlanto-occipital) joints are anatomically distinct and allow for substantial rotation about the inferior–superior axis and left–right axis, respectively [37]. Thus, we modelled these joints with single rotational degree-of-freedom joints about their respective rotational axes. In total, our model had 20 degrees of freedom. Further details of the model are presented in electronic supplementary material, A.
4.2. Simulating experimental head impacts
We collected a dataset of mild head impact loads in 10 human subjects (5 males and 5 females) published in a separate study with which to validate the model and quantify the relative moment contributors [4]. Briefly, we applied mild impacts to the head on subjects seated in a rigid back chair to restrict torso motion. Mild impacts were applied in two directions to produce planar head sagittal extension and head lateral flexion towards the non-dominant side to exercise primarily the dominant side SCM muscle. Subject was instructed to either minimally activate (relax) or maximally cocontract neck muscles during impact. For each set of conditions (direction and muscle activity), subjects performed up to six trials.
Before applying mild impact loads, subjects performed isometric contraction trials in sagittal flexion and coronal lateral flexion while upright. This provided a measure of subject neck strength, which was used to scale model muscle strengths in OpenSim. To estimate baseline OpenSim isometric strength, we added a constraint to the skull and measured the constraint force when sagittal flexion or coronal lateral flexion muscles were maximally activated (69.3 and 28.6 N isometric force in sagittal flexion and coronal lateral flexion, respectively). Subject mass and estimated neck lengths from the video (defined as the distance from the midpoint between the shoulders approximating the C7–T1 intervertebral joint to the atlanto-occipital joint) were also used to scale the mass and height of the OpenSim model.
Mild impact loads were delivered through the head mass centre via a wrestling headgear that was attached to a load plate (2 kg) upon which an impact plate (3 kg) was dropped from a height of 1 m. Loads were measured with an in-line tension meter (TLL-500) measuring at 1500 Hz and triggered data collection when a 50 N threshold was exceeded. The tension meter collected 80 ms pre-trigger and 720 ms post-trigger. We averaged impact force time histories over the six trials for each subject and each set of conditions. Average impact forces were used to apply external loads in OpenSim simulations.
We measured dominant side SCM muscle activity using a custom electromyograph. Muscle activity in isometric trials was treated as the maximal activation. We previously reported an average relaxed and cocontracted SCM muscle activity was 22.7 ± 1.6% and 79.0 ± 9.5% (mean ± s.e.) of isometric muscle activity [4]. Because we only measured SCM muscle activity, we had to estimate activity in the remaining neck muscles. Relaxed OpenSim neck muscle activations were found by minimizing the sum of all muscle activations while maintaining head and neck balance under gravity and with the constraint that SCM activation was 20%. Similarly, cocontracted OpenSim neck muscle activations were found by maximizing the sum of all muscle activations while maintaining head and neck balance under gravity with the constraint that SCM activation was 80%.
For each subject-scaled OpenSim model, we ran a forward dynamics simulation using relaxed or cocontracted muscle activations and applying averaged external loads [38]. Four sets of conditions (sagittal extension with relaxed neck muscles, sagittal extension with cocontracted neck muscles, coronal lateral flexion with relaxed neck muscles and coronal lateral flexion with cocontracted neck muscles) were tested for each subject, generating 40 forward dynamics simulations. For each simulation, the torso was fixed to the ground to represent the rigid back chair. In sagittal extension, the symmetry of the head and neck maintained planar motion. However, in coronal lateral flexion, we had to restrict out-of-plane rotations to maintain planar motion. Detailed analysis of the simulations against the experiments is presented in electronic supplementary material, D.
4.3. Moment and angular impulse analysis
After validating simulations, we computed the moments applied to the head from muscle activity, passive muscle, ligaments, external load and gravity during the simulated experimental mild impacts. As these were all linear forces, we needed to define a moment arm for each linear force. Because the cervical spine has many degrees of freedom and several muscles cross multiple intervertebral joints, we defined the moment arm () as the ratio between the change in length of a linear force () and the change in rotation of the head (, equation (4.8)) [13,39]:
| 4.8 |
The moment applied by the linear force to the head is then simply the force provided by the linear force scaled by the moment arm. Moments were first computed for each linear force element, compounded by muscle or ligament group (e.g. hyoids), and finally aggregated by type (impact load, gravity, active muscle, passive muscle and passive soft tissue).
To further define contributions to head stabilization, we integrated the moments to obtain angular impulses. We noted that for our controlled experimental impact, there was a distinct acceleration and deceleration phase wherein the head was set into motion (acceleration) and returned to rest (deceleration). These phases were defined using the simulated angular acceleration traces, and moments were integrated into each phase to define the angular impulse over each phase. Angular impulses were normalized by the total external load angular impulse.
4.4. Extrapolated median football impact
Finally, we extrapolated this analysis to a more relevant American football head impact scenario. To simulate American football head impacts, we generated an extrapolated force profile that produced head kinematics similar to those previously measured from the field [15,16]. We applied a 15 ms half-sine force pulse with peak 2000 N to the head mass centre resulting in sagittal extension and coronal lateral flexion for each of the 10 subject-specific OpenSim models (figure 3). In addition, we used the cocontracted muscle activation profile and computed relative moment and angular impulse contributions in the acceleration and deceleration phases.
Supplementary Material
Acknowledgements
We would also like to acknowledge Jon Mortensen and Andrew Merryweather for their help with the OpenSim musculoskeletal model.
Ethics
Our results are based on experimental data collected in a human subject study. The lead author obtained written consent from our subjects to participate in our study, which was approved by the Stanford Internal Review Board (IRB: 36466).
Data accessibility
Experimental data and simulation results are posted in a public repository through the OpenSim SimTK site: https://simtk.org/projects/kuo-head-neck.
Authors' contributions
C.K. was responsible for designing the study, collecting experimental data, developing the model, running simulations, analysing data and writing the final manuscript. J.S. helped develop the ligament model, run simulations and analyse data. M.F. helped collect experimental data, analyse data and write the final manuscript. I.Y. helped develop the ligament model, run simulations and analyse data. R.H. helped run simulations and analyse data. Finally, D.C. helped with study design and writing the manuscript.
Competing interests
The authors have no competing interests to declare.
Funding
We would like to acknowledge our funding sources, Office of Naval Research grant no. N00014-16-1-2949, the Stanford Bio-X Graduate Research Fellowship Program and the National Science Fellowship Graduate Science Fellowship.
References
- 1.Benson BW, et al. 2013. What are the most effective risk-reduction strategies in sport concussion? Br. J. Sports Med. 47, 321–326. ( 10.1136/bjsports-2013-092216) [DOI] [PubMed] [Google Scholar]
- 2.Eckner JT, Oh YK, Joshi MS, Richardson JK, Ashton-Miller JA. 2014. Effect of neck muscle strength and anticipatory cervical muscle activation on the kinematic response of the head to impulsive loads. Am. J. Sports Med. 42, 566–576. ( 10.1177/0363546513517869) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Collins CL, et al. 2014. Neck strength: a protective factor reducing risk for concussion in high school sports. J. Prim. Prev. 35, 309–319. ( 10.1007/s10935-014-0355-2). [DOI] [PubMed] [Google Scholar]
- 4.Kuo C, Fanton M, Wu L, Camarillo D. 2018. Spinal constraint modulates head instantaneous center of rotation and dictates head angular motion. J. Biomech. 76, 220–228. ( 10.1016/j.jbiomech.2018.05.024) [DOI] [PubMed] [Google Scholar]
- 5.Mihalik JP, et al. 2011. Does cervical muscle strength in youth ice hockey players affect head impact biomechanics? Clin. J. Sport Med. 21, 416–421. ( 10.1097/JSM.0B013E31822C8A5C) [DOI] [PubMed] [Google Scholar]
- 6.Mihalik JP, Moise KF, Ocwieja KE, Guskiewicz KM, Register-Mihalik JK. 2014. The effects of player anticipation and involvement on head impact biomechanics in college football body collisions. In Mechanism of concussion in sports (ed. Ashare A, Ziejewski M), pp. 41–55. West Conshohocken, PA: ASTM International; ( 10.1520/STP155220120108) [DOI] [Google Scholar]
- 7.Mansell J, Tierney RT, Sitler MR, Swanik KA, Stearne D. 2005. Resistance training and head-neck segment dynamic stabilization in male and female collegiate soccer players. J. Athl. Train. 40, 310–319. [PMC free article] [PubMed] [Google Scholar]
- 8.Naish R, Burnett A. 2013. Can a specific neck strengthening program decrease cervical spine injuries in a men's professional rugby union team? A retrospective analysis. J. Sports Sci. Med.12, 542–550.
- 9.Eckersley CP, Nightingale RW, Luck JF, Bass CR. 2017. Effect of neck musculature on head kinematic response following blunt impact. In Proc. IRCOBI Conf., Antwerp, Belgium, 13–15 September 2017, pp. 674–676. [Google Scholar]
- 10.Shewchenko N, Withnall C, Keown M, Gittens R, Dvorak J. 2005. Heading in football. Part 2: biomechanics of ball heading and head response. Br. J. Sports Med. 39(Suppl. 1), 26–33. ( 10.1136/bjsm.2005.019042) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jin X, et al. 2017. The role of neck muscle activities on the risk of mild traumatic brain injury in American football. J. Biomech. Eng. 139, 101002 ( 10.1115/1.4037399) [DOI] [PubMed] [Google Scholar]
- 12.Bruneau D, Cronin DS, Panzer M, Vilar JSG, Kent R. 2018. Comparison of the hybrid III head and neck to a detailed head and neck finite element model with active musculature, in a football impact scenario. In Proc. IRCOBI Conf., Athens, Greece, 12–14 September, 2018, pp. 322–323. [Google Scholar]
- 13.Vasavada AN, Li S, Delp SL. 1998. Influence of muscle morphometry and moment arms on the moment-generating capacity of human neck muscles. Spine (Phila Pa 1976) 23, 412–422. ( 10.1097/00007632-199802150-00002) [DOI] [PubMed] [Google Scholar]
- 14.Mortensen JD, Vasavada AN, Merryweather AS. 2018. The inclusion of hyoid muscles improve moment generating capacity and dynamic simulations in musculoskeletal models of the head and neck. PLoS ONE 13, e0199912 ( 10.1371/journal.pone.0199912) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kuo C, et al. 2018. Comparison of video-based and sensor-based head impact exposure. PLoS ONE 13, e0199238 ( 10.1371/journal.pone.0199238) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wu LC, et al. 2018. Detection of American football head impacts using biomechanical features and support vector machine classification. Sci. Rep. 8, 1 ( 10.1038/s41598-017-17765-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ivancic PC, et al. 2007. Dynamic mechanical properties of intact human cervical spine ligaments. Spine J. 7, 659–665. ( 10.1016/j.spinee.2006.10.014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shim VPW, Liu JF, Lee VS. 2006. A technique for dynamic tensile testing of human cervical spine ligaments. Exp. Mech. 46, 77–89. ( 10.1007/s11340-006-5865-2) [DOI] [Google Scholar]
- 19.Yoganandan N, Cusick J, Maiman D, Myers T, Sances A. 1989. Dynamic response of human cervical spine ligaments. Spine (Phila Pa 1976) 14, 1102–1110. ( 10.1097/00007632-198910000-00013) [DOI] [PubMed] [Google Scholar]
- 20.Panzer MB. 2006. Numerical modelling of the human cervical spine in frontal impact. Master's thesis, University of Waterloo, Ontario, Canada.
- 21.Pintar FA. 1987. The biomechanics of spinal elements. Dev. Implement. Eff. 6, 74839 ( 10.16953/deusbed.74839) [DOI] [Google Scholar]
- 22.Rajagopal A, et al. 2016. Full body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans. Biomed. Eng. 63, 2068–2079. ( 10.1109/TBME.2016.2586891) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Östh J, et al. 2017. A female head–neck model for rear impact simulations. J. Biomech. 51, 49–56. ( 10.1016/j.jbiomech.2016.11.066) [DOI] [PubMed] [Google Scholar]
- 24.Hamner SR, Delp SL. 2013. Muscle contributions to fore-aft and vertical body mass center accelerations over a range of running speeds. J. Biomech. 46, 780–787. ( 10.1016/j.jbiomech.2012.11.024) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Millard M, Uchida T, Seth A, Delp SL. 2013. Flexing computational muscle: modeling and simulation of musculotendon dynamics. J. Biomech. Eng. 135, 021005 ( 10.1115/1.4023390) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Grauer JN, Panjabi MM, Cholewicki J, Nibu K, Dvorak J. 1997. Whiplash produces an S-shaped curvature of the neck with hyperextension at lower levels. Spine (Phila Pa 1976) 22, 2489–2494. ( 10.1097/00007632-199711010-00005) [DOI] [PubMed] [Google Scholar]
- 27.Stemper BD, Yoganandan N, Pintar FA. 2003. Gender dependent cervical spine segmental kinematics during whiplash. J. Biomech. 36, 1281–1289. ( 10.1016/S0021-9290(03)00159-3) [DOI] [PubMed] [Google Scholar]
- 28.Fice JB, Cronin DS. 2012. Investigation of whiplash injuries in the upper cervical spine using a detailed neck model. J. Biomech. 45, 1098–1102. ( 10.1016/j.jbiomech.2012.01.016) [DOI] [PubMed] [Google Scholar]
- 29.Panjabi MM, Pearson AM, Ito S, Ivancic PC, Wang JL. 2004. Cervical spine curvature during simulated whiplash. Clin. Biomech. 19, 1–9. ( 10.1016/j.clinbiomech.2003.09.006) [DOI] [PubMed] [Google Scholar]
- 30.Deng YC, Goldsmith W. 1987. Response of a human head/neck/upper-torso replica to dynamic loading—II. Analytical/numerical model. J. Biomech. 20, 487–497. ( 10.1016/0021-9290(87)90249-1) [DOI] [PubMed] [Google Scholar]
- 31.Panjabi M, Brand R, White A. 2001. Mechanical properties of the human cervical spine as shown by three-dimensional load-displacement curves. Spine (Phila Pa 1976) 26, 2692–2700. ( 10.1097/00007632-200112150-00012) [DOI] [PubMed] [Google Scholar]
- 32.White NA, Moreno DP, Gayzik FS, Stitzel JD. 2015. Cross-sectional neck response of a total human body FE model during simulated frontal and side automobile impacts. Comput. Methods Biomech. Biomed. Eng. 18, 293–315. ( 10.1080/10255842.2013.792918) [DOI] [PubMed] [Google Scholar]
- 33.Fanton M, Kuo C, Sganga J, Hernandez F, Camarillo DB. 2018. Dependency of head impact rotation on head-neck positioning and soft tissue forces. IEEE Trans. Biomed. Eng.66, 988–999. ( 10.1109/tbme.2018.2866147) [DOI]
- 34.Yoganandan N, Kumaresan S, Pintar FA. 2000. Geometric and mechanical properties of human cervical spine ligaments. J. Biomech. Eng. 122, 623–629. ( 10.1115/1.1322034) [DOI] [PubMed] [Google Scholar]
- 35.Panjabi MM, Oxland TR, Parks EH. 1991. Quantitative anatomy of cervical spine ligaments. Part I. Upper cervical spine. J. Spin. Disord. 4, 275–276. ( 10.1097/00002517-199109000-00003) [DOI] [PubMed] [Google Scholar]
- 36.Panjabi MM, Oxland TR, Parks EH. 1991. Quantitative anatomy of cervical spine ligaments. Part II. Middle and lower cervical spine. J. Spin. Disord. 4, 277–285. ( 10.1097/00002517-199109000-00004) [DOI] [PubMed] [Google Scholar]
- 37.Panjabi MM, White AA. 1980. Basic biomechanics of the spine. Neurosurgery 7, 76–93. ( 10.1227/00006123-198007000-00014) [DOI] [PubMed] [Google Scholar]
- 38.DeMers MS, Hicks JL, Delp SL. 2017. Preparatory co-activation of the ankle muscles may prevent ankle inversion injuries. J. Biomech. 52, 17–23. ( 10.1016/j.jbiomech.2016.11.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sherman MA, Seth A, Delp SL. 2013. What is a moment arm? Calculating muscle effectiveness in biomechanical models using generalized coordinates. Proc. ASME Des. Eng. Tech. Conf. V07BT10A052 ( 10.1115/DETC2013-13633) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Experimental data and simulation results are posted in a public repository through the OpenSim SimTK site: https://simtk.org/projects/kuo-head-neck.