Spatio-temporal integration in plant tropisms

Abstract

Tropisms, growth-driven responses to environmental stimuli, cause plant organs to respond in space and time and reorient themselves. Classical experiments from nearly a century ago reveal that plant shoots respond to the integrated history of light and gravity stimuli rather than just responding instantaneously. We introduce a temporally non-local response function for the dynamics of shoot growth formulated as an integro-differential equation whose solution allows us to qualitatively reproduce experimental observations associated with intermittent and unsteady stimuli. Furthermore, an analytic solution for the case of a pulse stimulus expresses the response function as a function of experimentally tractable variables, which we calculate for the case of the phototropic response of Arabidopsis hypocotyls. All together, our model enables us to predict tropic responses to time-varying stimuli, manifested in temporal integration phenomena, and sets the stage for the incorporation of additional effects such as multiple stimuli, gravitational sagging, etc.

1. Introduction

Plant tropisms are the growth-driven responses of a plant organ which reorients itself in the direction of an environmental stimulus such as light, termed phototropism or gravity, termed gravitropism. Tropisms are driven by a directional stimulus, which leads to the asymmetric redistribution of a growth hormone such as auxin [1–5] which then directs growth. For example, in figure 1a we show snapshots of the negatively gravitropic response of a wheat seedling placed horizontally at time t = 0, where the seedling shoot detects the direction of gravity and grows to oppose it. This response is dynamical, and one might suspect that if the stimulus is changed intermittently, the spatio-temporal response itself will be complex. In the simple experiment described above, gravity acts continuously on the shoot with a constant magnitude. Thus, it is not possible to distinguish between a response that integrates the stimulus over time and one that acts instantaneously. However, experimental observations of gravitropism and phototropism dating back more than a century have shown that plants respond to time varying stimuli in a way that suggests that they do integrate the stimuli in time. For example, different combinations of stimuli that are intermittent in time [7–11] or which have reciprocal ratios of intensity and duration [12–19], so that the time-integrated stimulus is constant, lead to the same response, as shown in the insets in figures 2 and 3. Explanations of shoot phototropism assume that this follows from photobiology [21]. However, the fact that this phenomenon has also been observed in the context of gravitropism suggests that one must look for a common signal transduction pathway, naturally implicating the polar transport of the growth hormone auxin that is critical in mediating tissue growth, and is indeed driven by either gravity or light. Furthermore, these observations of responses to time-varying stimuli also naturally suggest that the plant retains a memory of the stimulus. To quantify this at a minimal level, we turn to linear response theory to characterize the relationship between the responsive geometry of growth and the exciting stimulus.

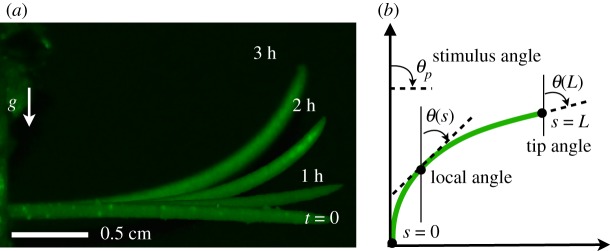
Figure 1.

(a) Time course of a gravitropic response of a single wheat seedling placed horizontally (perpendicular to the direction of gravity) at t = 0, and measured at 1 h intervals. (b) Mathematical definitions [6]. The angle θ(s, t) at point s along the organ at time t is defined from the vertical. The parameter s runs along the organ from s = 0 at the base, to s = L at the tip. The tip angle θ(L, t) is the quantity which is conventionally measured in experiments. (Online version in colour.)

Figure 2.

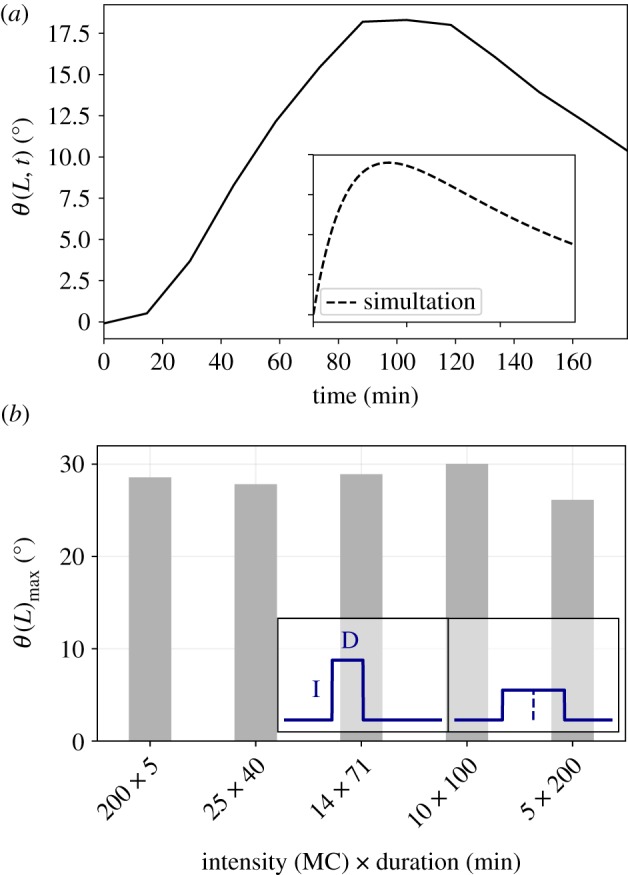
(a) Experimental observations made by Orbović & Poff [20] who recorded the time course of the tip angle θ(L, t) of Arabidopsis thaliana seedlings as a response to a 0.9 s pulse of blue light, observed hours after the pulse is gone. The inset shows the simulated response using our response theory approach described in equation (2.2), similarly exhibiting a response long after the stimulus has ended. Axes are identical to the main figure; however the time scale is arbitrary, providing a qualitative agreement. (b) Reciprocity experiment on the phototropic response of Avena coleoptiles, adapted from Briggs [13]. Inset shows lighting protocols in arbitrary units; one unilateral pulse of light versus another pulse with half the intensity and double the duration, i.e. identical total dose. The main figure shows the average maximal angle of the tip measured for different reciprocal ratios of intensity (ranging between 5 and 200 MC) and duration of exposure time (ranging between 200 and 5 s), yielding the same total dose of 1000 MC × s ∼ 1.46 W m⁻². (Online version in colour.)

Figure 3.

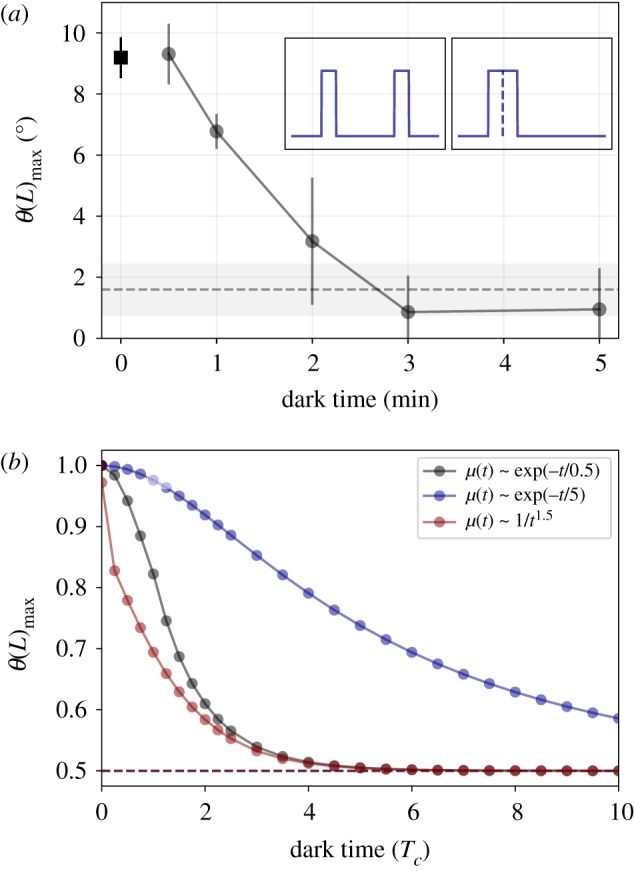
(a) Summation experiment on the phototropic response of Vaucheria geminata, adapted from Kataoka [11]. Inset shows lighting protocols in arbitrary units; two pulses of light separated by dark time, versus a single continuous pulse with double the duration. Circles are the average maximal tip angle (vertical bars indicate SE) measured for the response to two light pulses, each 10 s and 6 W m⁻², separated by a dark interval of various durations (x-axis). The square symbol is the response to a continuous pulse of 20 s (zero lag). The vertical dashed line is the average response to a single pulse of 10 s, where the grey bar indicates the SE. (b) Equivalent simulations of summation experiment with two pulses of duration 0.0025 T_c, using different response functions: two exponentials μ(t) ∼ exp(− t/τ) with τ = 5T_c (blue, top line) and τ = 0.5T_c (black, middle line), and a power law μ(t) ∼ 1/t^1.5 (red, bottom line). Maximal tip angles are normalized to allow comparison, so that the maximal angle for zero lag is always 1, and the control response to a single pulse is 0.5 (dashed line). (Online version in colour.)

The description of input–output relations of a signal transducer characterize the output y(t) as the weighted sum of the input signal x(t) convolved by a response function μ(t), so that we may write $y(t)={\int }_{-\mathrm{\infty }}^t\mu (t-t^{\mathrm{\prime }})\hspace{0.17em}\hspace{0.17em}x(t^{\mathrm{\prime }})\hspace{0.17em}\text{d}{t}^{\mathrm{\prime }}$. This approach has been used in a variety of problems concerning temporal responses of organisms to external stimuli, including bacterial chemotaxis [22,23], cellular chemotaxis [24] and the light-induced growth response in Phycomyces [25]. Extending this framework to the tropisms seen in plant shoots requires coupling the non-local temporal response to the growth-driven dynamical changes in the shape of the whole plant organ, leading to a spatio-temporal framework that is qualitatively different from previous purely temporal theories, as we will see.

2. Model

We start from a recent framework describing the kinematics of tropic responses that combines internal proprioception and external phototropism or gravitropism [6,26] to explain the growth kinematics of shoots subject to uniform and constant stimuli. The shape of a slender shoot growing in a single plane, figure 1b, can be described in terms of the local angle θ(s, t) of the tangent to the shoot from the vertical as a function of the arc-length along the centreline s at time t. The shoot actively grows only within its growth zone, of length L_gz which is smaller than the length of the entire organ L. Within the growth zone, L > s > L − L_gz, observations suggest [6] that the rate of change of the curvature in the growth zone is proportional to a weighted sum of the stimulus term associated with the environment, and the proprioceptive term that penalizes deviations from a straight shoot. Then the kinematics of shoot growth for L > s > L − L_gz follow the equation [6]:

$$\frac{{\mathrm{\partial }}^2\theta (s,t)}{\mathrm{\partial }t\mathrm{\partial }s}=-\beta \sin (\theta (s,t)-{\theta }_{\hspace{0.17em}p})-\gamma \frac{\mathrm{\partial }\theta (s,t)}{\mathrm{\partial }s},s\in [L-L_{\mathrm{gz}},L].$$ 2.1

Here θ_p is the angle of the stimulus (light or gravity) relative to the vertical, ($\mathrm{\partial }$θ(s, t)/$\mathrm{\partial }$s) is the local curvature, and the parameters β and γ are the sensitivities to gravity (or light) and proprioception. There is a characteristic length scale in the problem L_c = γ/β that results from the balance between graviception and proprioception, and two characteristic time scales determined by (i) the strength of the proprioceptive feedback given by the proprioceptive time T_c = 1/γ and (ii) the time required for the stimulus to make its influence felt over the entire growth zone, the growth time T_v = 1/βL_gz. The ratio of these two time scales results in a dimensionless response parameter B = βL_gz/γ, which determines the relative importance of proprioception and (gravi/photo) tropism. Biologically relevant values are B ∈ [0.9 − 9.3], displaying broad intraspecific and interspecific variability [6]. Outside of the growth zone, the shoot does not respond so that ($\mathrm{\partial }$²θ(s, t)/$\mathrm{\partial }$t$\mathrm{\partial }$s) = 0 in the region s < L − L_gz.

We note that although the model assumes that the response to the stimulus is a weighted sum of the proprioceptive, gravitropic and phototropic stimulus, it is linear and instantaneous, i.e. it cannot account for the experimental observations of temporal integration discussed earlier [7–11]. To allow for this, we introduce a convolution of the external stimulus term with a response function μ(t), leading to a modified form of the dynamic law for shoot reorientation:

$$\frac{{\mathrm{\partial }}^2\theta (s,t)}{\mathrm{\partial }t\mathrm{\partial }s}+\gamma \frac{\mathrm{\partial }\theta (s,t)}{\mathrm{\partial }s}=-{\int }_{-\mathrm{\infty }}^t\beta (\tau )\mu (t-\tau )\sin (\theta (s,\tau )-{\theta }_{\hspace{0.17em}p})\hspace{0.17em}\text{d}\tau .$$ 2.2

The convolution with the response function μ(t) represents the memory associated with the response to a temporal history of stimuli in a spatio-temporal setting associated with growth, and is the main theoretical contribution of this paper. As one might expect, the experimental observations of reciprocity and summation of stimuli are valid only within some time window, suggesting that the response function should decay with an equivalent characteristic time scale, and needs to be determined experimentally. We note that when μ(t) = δ(t), the Dirac-delta function, there is no memory in the system, and as expected, we recover the original model equation (2.1) corresponding to an instantaneous response.

We note that both in equations (2.1) and (2.2) sensing is assumed to occur along the entire growth zone, as exhibited by the species used in the experiments presented in this paper, Arabidopsis thaliana and Vaucheria geminata [27–29]. However, it is possible to also account for sensing purely at the apical tip alone by replacing the stimulus term sin(θ(s, t) − θ_p) with sin(θ(L, t) − θ_p), a topic that we will take up in the future.

3. Results

To see the utility of this modified law equation (2.2), we first turn to the results of an experiment [20] showing the response of Arabidopsis thaliana to a pulse of light, shown in figure 2a. We see that the response is observed hours after the pulse is gone, and so cannot be described by the instantaneous model equation (2.1) [6]. This becomes clear since after the stimulus ends, equation (2.1) simplifies to ($\mathrm{\partial }$²θ(s, t)/$\mathrm{\partial }$t$\mathrm{\partial }$s) = −γ($\mathrm{\partial }$θ(s, t)/$\mathrm{\partial }$s), i.e. only the restoring proprioceptive term remains and the angle ceases to increase, as opposed to what is observed. However, our modified response law in equation (2.2) can naturally account for a response occurring long after a stimulus has been switched off.

To make this clear in a concrete setting, we choose a unilateral stimulus acting at θ_p = π/2 and the kernel μ(t) = e^−t/10 along with initial conditions corresponding to a straight seedling, i.e. $\mathrm{\partial }$θ/$\mathrm{\partial }$s|_t=0 = 0, an initial angle from the vertical θ(s, 0) = θ₀ = 0, and boundary conditions corresponding to a clamped base, i.e. θ(0, t) = 0, and a free end ∂θ/∂s|_s=L = 0. To solve equation (2.2) with these conditions, we use a simple forward-Euler integration method, as described in the electronic supplementary material, with the following parameters: time step of dt = 0.005, length of the shoot L = 1.0, number of discrete elements N = 100, so that the spatial element is ds = L/N, and the gravi/photo-ceptive and proprioceptive sensitivities were taken to be β = 5.0 and γ = 0.5. The characteristic time and length scales are then T_c = 2 and L_c = 0.1. Our choice of parameters here simulates a higher sensitivity and thus a faster and larger simulated response (large angles). In the inset of figure 2a, we see the ability of the model to adequately capture the experimental phenomenology, leaving for later a discussion of the choice of relevant time scales and the qualitative dependence of the solutions on these choices.

Having shown that the integrated response function allows us to capture the delayed response of the growing shoot to a pulse of light, we now turn to explain the reciprocity experiments from more than a half-century ago [13] associated with the phototropic response of Avena coleoptiles. When the shoots where exposed to identical total doses of unilateral light, but with reciprocal ratios of intensity and exposure time, the response measured in terms of the maximal angle of the tip θ(L)_max remains identical for all these different combinations of stimuli. Thus, the coleoptiles respond to the integrated history of stimuli within this time range, rather than the instantaneous value of the stimuli. To explain these observations, we use equation (2.2) as a basis for numerical simulations, emulating the described reciprocity experiments, with the same initial and boundary conditions as for the pulsed light experiment, and show that our model does indeed capture this, as shown in figure 2b.

Expanding on this, in table 1 we show results for simulations employing an exponential response function of the form μ(t) ∼ exp(−t/0.5), where time is measured in units of characteristic time scale T_c = 2. The intensity of the stimulus was varied by changing the stimulus sensitivity β₀ over the period of stimulation. As expected, these simulations yield similar responses for stimuli with identical total doses but reciprocal ratios of intensity and duration, as long as the duration (the longest here being 0.125 T_c) is shorter than the natural decay built into the exponential memory kernel, i.e. τ = 0.5T_c.

Table 1.

Simulations of reciprocity experiments equivalent to figure 2b, employing an exponential response function of the form μ(t) ∼ exp(−t/0.5), in units of convergence time T_c = 2.

intensity	duration	maximal tip angle
2	0.125	71.2
4	0.0625	71.4
10	0.25	71.5
20	0.0125	71.5
25	0.01	71.5
50	0.005	71.5

Having seen that our modified dynamical response equation (2.2) can indeed capture the observations of both the delayed response and the reciprocity experiments, we now turn to understanding the qualitative nature of the form of the kernel and the length and time scales in our system. We do so by investigating the integration time scale and its dependence on the decay of the response function using a summation experiment in phototropism [11]. In figure 3a, we show the maximal angle of the tip θ(L)_max of a coenocytic alga Vaucheria geminata to light pulses of 10 s each, as a function of dark interval of various durations. We note that for lag times between 30 s and approximately 3 min the response decays, going from the response for the sum of both pulses, to that for a single pulse. This decay suggests a smoothly decaying response function with a memory time scale of about 2 min.

To test the effect of using different memory kernels, we now employ response functions of exponential and power law forms: exp(−t/τ) with τ = 0.5, 5 (in units of T_c), and μ(t) ∼ 1/t^1.5. In figure 3b, we show results for simulations using equation (2.2), where, in order to allow for a comparison, maximal tip angles are normalized so that the maximal angle for zero lag is always unity, and the control response to a single pulse is 0.5. We see that as the intervening dark time increases, the response decays relative to that for a single pulse. Furthermore, our choice of different kernel response functions leads to a different decay in the integrated response, clearly indicating its importance for the correct prediction of tropic responses to dynamic stimuli.

Given the qualitative difference in the results as a function of the kernel, we turn to extract the form of the response function from the kinematics of tropic responses for the case of a pulse stimulus, by substituting β(t) = β₀δ(t₀ = 0) in the linearized version of equation (2.2). When combined with the initial condition θ(s, t = 0) = 0, this leads to the result

$$\frac{{\mathrm{\partial }}^2\theta (s,t)}{\mathrm{\partial }t\mathrm{\partial }s}+\gamma \frac{\mathrm{\partial }\theta (s,t)}{\mathrm{\partial }s}=-{\beta }_0{\theta }_{\hspace{0.17em}p}\mu (t).$$ 3.1

As shown in detail in the electronic supplementary material, integrating equation (3.1) over s, and recalling the boundary condition θ(s = 0, t) = 0, leads to

$$\mu (t)=\frac{1}{L{\theta }_{\hspace{0.17em}p}{\beta }_0}\left(\frac{\mathrm{\partial }\theta (L,t)}{\mathrm{\partial }t}+\gamma \theta (L,t)\right),$$ 3.2

providing an experimentally tractable relation allowing us to extract the kernel response function from the experimentally observed dynamics of the angle at the tip as a response to a pulse stimulus.

Using the measured response of seedlings to a pulse of light [20] shown in figure 2a, we now apply equation (3.2) to determine bounds on the kernel response function. We note that in their experiment seedlings were rotated in a clinostat which effectively cancels their ability to sense gravity, meaning that the seedlings are only affected by the light pulse, in line with the assumptions made in equation (3.2). Though the values of β and γ were not measured in the original experiment, we can estimate the lower bound of the proprioceptive time T_c as the time at which the maximal angle is achieved (approx. 80 min), and the upper bound as the largest value that still yields positive values of the response function, given that the derivative ($\mathrm{\partial }$θ(L, t)/$\mathrm{\partial }$t) is negative for the relaxation regime (approx. 100 min). We therefore have $T_c\in [80,100]\hspace{0.17em}\text{min}$, so that γ ∈ [0.01, 0.0125]. Substituting the measured θ(L, t), the calculated ($\mathrm{\partial }$θ(L, t)/$\mathrm{\partial }$t) and the two bounds for γ into equation (3.2), we get two bounds for the functional form, up to a prefactor, of the response function μ(t), shown in figure 4.

Figure 4.

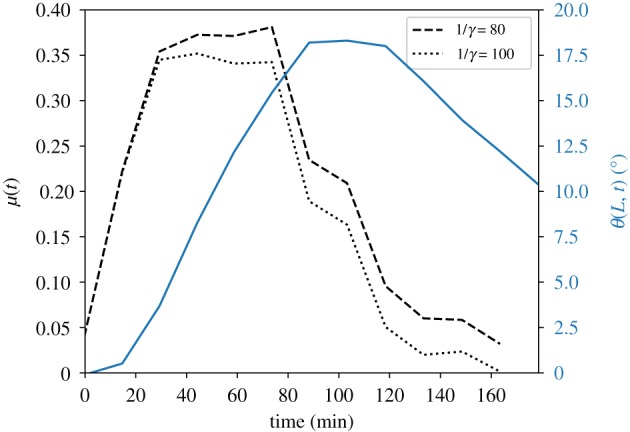
Time course of the tip angle θ(L, t) of Arabidopsis thaliana seedlings as a response to a pulse of blue light [20] (solid line, right y-axis), as also displayed in figure 2a. We numerically calculate the derivative ($\mathrm{\partial }$θ(L, t)/$\mathrm{\partial }$t), and substitute this, together with an estimated γ, in equation (3.2), yielding the functional form of the estimated response function, plotted against the left y-axis. The dashed and dotted lines represents μ(t) calculated with the upper and lower bound of γ, respectively, as detailed in the main text. (Online version in colour.)

4. Discussion and conclusion

Experimental observations of plant tropisms over a century ago show that growing plants respond by changing their shape identically to different combinations of stimuli—intermittent in time (termed summation experiments) or with reciprocal ratios of intensity and duration (reciprocity). This suggests a tropic response that is non-local in space–time. Here, we have provided a simple but general quantitative framework for the ability of growing shoots to integrate stimuli in space and time. Our theory takes the form of an integro-differential dynamical law for the growth response in terms of a memory kernel μ(t) and helps explain both the summation and reciprocity experiments. The novelty of this dynamical law lies in the fact that though response functions have been used previously in the context of organismal stimulus–response curves [22–25], they have always been limited to the temporal domain. Here we show a conceptually different response in coupled spatio-temporal systems; indeed, this approach may be more generally applied to diverse developmental systems. As this paper was in review, the authors became aware of a similar approach that has been recently taken [30] to explain the form of observed stimulus–response curves for transient constant force inclination stimuli, limited to an exponential response function.

Using the observed response to a pulse stimulus allows us to relate the form of the memory kernel μ(t) to experimentally tractable variables including the temporal evolution of the angle at the tip θ(L, t) and provide upper and lower bounds for the functional form of the response function. That the two estimates do not deviate significantly suggests that our result is robust.

More generally, since the behaviours associated with time-varying stimuli are observed both in phototropism and gravitropism, they cannot be due to the sensory system (as had previously been suggested for phototropism [21]). Instead we suggest that this is due to a common signal transduction pathway, naturally implicating polar transport of the growth hormone auxin, represented here by the response function. We particularly suggest that this memory may be due to the inherent stochasticity of signal transduction (e.g. lateral auxin transport), which effectively smears a signal over time. Following the example of summation experiments, the transduced signals of two consecutive short stimuli will spread over time, and eventually overlap. The plant organ will therefore effectively respond to both. This overlap is mathematically represented by the convolution of the stimulus with the response function, and the amount of overlap is a result of how much the signal has spread, dictated by both the dynamics of transport and the distance the signal had to cover. A direct consequence of this is that larger organs are expected to exhibit a larger integration time scale. If information (in the form of auxin) has to be physically transported from the receptor side to the other side of the plant organ, it means that larger distances (larger organs) will require longer times, and therefore greater spreading of the signal—and whence a longer time scale of the response function. This observation is in line with the two species discussed in this paper, Arabidopsis and Vaucheria geminata: their characteristic widths are approximately 500 μm [20], and approximately 40 μm [31,32], respectively, while their characteristic memory time scale is of the order of 200 min for Arabidopsis (shown in figure 2a) compared to 3 min for Vaucheria geminata (figure 3a).

Our theory is but the first step in understanding how growing systems respond to environmental stimuli. Natural questions that arise include testing the assumption of linear response experimentally, comparing the response functions for phototropic and gravitropic responses, which share many signal transduction processes, and incorporating additional effects such as internal cues [33], and the role of passive drooping of a growing shoot [34], all problems for the future.

Data accessibility

The digitized data as well as the code used in this work are openly available in the following link: https://github.com/merozlab/temṗintegration.

Authors' contributions

Y.M. conceived of the study, designed and coordinated the study, performed numerical simulations, analysed experimental data and drafted the manuscript. R.B. participated in conceiving and designing the study, and helped draft the manuscript. L.M. conceived of the study, participated in the design of the study and the underlying mathematical framework, and critically revised the manuscript. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

No funding has been received for this article.