Abstract
Crystallization is a fundamental and ubiquitous process that is well understood in case of atoms or small molecules, but its outcome is still hard to predict in the case of nanoparticles or macromolecular complexes. Controlling the organization of virus nanoparticles into a variety of 3D supramolecular architectures is often done by multivalent ions and is of great interest for biomedical applications like drug or gene delivery, biosensing as well as for bionanomaterials and catalysis. In this paper, we show that slow dialysis, over several hours, of wild type Simian Virus 40 (wt SV40) nanoparticle solution against salt solutions containing MgCl2, with or without added NaCl, results in wt SV40 nanoparticles arranged in a body cubic center (BCC) crystal structure with Im3m space group, as a thermodynamic product, in coexistence with soluble wt SV40 nanoparticles. The nanoparticle crystals formed above a critical MgCl2 concentrations. Reentrant melting and resolubilization of the virus nanoparticles took place when the MgCl2 concentrations passed a second threshold. Using synchrotron solution X-ray scattering we determined the structures and the mass fraction of the soluble and crystal phases as a function of MgCl2 and NaCl concentrations. A thermodynamic model, which balances the chemical potentials of the Mg2+ ions in each of the possible states, explains our observations. The model reveals the mechanism of both the crystallization and the reentrant melting and resolubilization and shows that counterion entropy is the main driving force for both processes.
Keywords: Small Angle X ray Scattering, reentrant condensation, crystallization, resolubilization, like charge attraction, bridging interactions, SV40
Graphical Abstract
Crystallization is a common fundamental process that is fairly understood in the case of atoms or small molecules. The conditions that lead to crystallization of nanoparticles and large supramolecualr assemblies, however, are still hard to predict. Assembly and crystallization of virus nanoparticles and other nanoparticles are of great interest owing to the potential use of the forming structures in bionanomedical and bionanomaterial applications.1 Virus nanoparticles may be fabricated into functional nanosanotructure devices, serve as protein nanocapsules, nanocarriers for metalic nanoparticles, drug or gene delivery, biosensors, or as nanoreactors for catalysis.2–5 Virus nanoparticles may assemble into a range of superstructure cages that are partially ordered or crystals.6–8 Virus crystals can serve as templates for porus materials or ordered solids containing nanoscopic order.9 The surfaces of virus nanoparticles display charges and the behavior of virus nanoparticles in salt solutions containing monovalent and/or multivalent ions is therefore of great interest for both fundamental and practical reasons.
Charged interfaces in water or monovalent aqueous salt solutions have counterions that dissociate from the surface into the solution. The counterions are attracted to the charged surface but owing to their thermal energy they dissociate from the surface and their density profile follows Boltzmann’s distribution.10,11 The number of positive and negative ions is equal and so does the number of attractive and repulsive electrostatic interactions. However, the fact that the counterions are distributed away from the charged surfaces results in a net repulsive interaction between two like-charged surfaces.12 When aqueous salt solutions contain multivalent ions, above some critical concentration, c*, counterion condensation and strong correlation effects may lead to net attraction between like-charged interfaces.13–16
Like-charged attraction can lead to nanoparticle or polymer condensation and formation of charged complexes or crystals. The factors that determine whether the net interaction is repulsive or attractive include the surface charge density, the flexibility of the interface or chains, the structure and charge-density of the multivalent counterions, the solution concentrations of the nanoparticles/molecules and salts, and the geometry of the interfaces; spherical (colloidal particles, for example), chain coated particles (for example, DNA-coated nanoparticles), cylindrical/rod-like (like microtubule or actin), flat (charged lipid bilayers), semiflexible chains (like DNA) or flexible chains (like sodium polystyrene sulfonate).17–39
When the concentration of the multivalent ions is further increased beyond a critical value, c** (where c** > c*), the total interaction switches from attractive to repulsive and leads to reentrant melting and resolubilization of the nanoparticles/molecules.34–38,40–44
Proteins surface, as opposed to polyelectrolytes or charged colloids, present a complex, nonuniform pattern of charged, polar, and hydrophobic residues, which can be tuned by pH.45 The charge patterns together with distinct local topologies may result in an involved phase behavior as a function of solution conditions.46 Both the chemical character of the charge groups on the surface of the protein and the specificity of the counterions have important implications for the interactions and the structures that form.40,47 Protein condensation and reentrant melting and resolubilization has also been observed in the presences of multivalent ions.43,44
Isolated nucleosome core particles (NCPs) contain negatively charged DNA and protein with positively charged groups. The condensation and reentrant phase diagram of NCPs had been systematically studied using different multivalent cations.48–50
Spherical virus nanoparticles can be considered as small colloids with a patchy (charged) outer surface. Virus microcrystals may also form when osmotic pressure is applied.51 The osmotic stress is needed to overcome the repulsive electrostatic interaction between the virus nanoparticles.
In this paper, we focus on the effect of divalent Mg2+ cations on the interactions and phase behavior of wild type Simian Virus 40 (wt SV40) nanoparticle solutions. SV40 is a small non enveloped, icosahedral virus and a member of the polyomavirus family. Its genome is a 5.2 kbp circular double stranded DNA (dsDNA) that is warped around host histones forming a minichrimosome structure.52,53 The virus external diameter is ca.48nm.54 The viral capsid is composed of three types of structural viral proteins (VPs): VP1, VP2 and VP3.54,55 The major capsid building block is a VP1 pentamer (VP15) where 72 VP15s form the outer surface of the capsid that posses a T=7d symmetry.54,56
We found that slow dialysis of wt SV40 nanoparticles solutions against MgCl2 solutions, with and without added NaCl, over several hours, gave a thermodynamic product of wt SV40 nanoparticles arranged in a body cubic center (BCC) crystal structure with Im3m space group. We explored the crystallization and reentrant melting and resolubilization phase diagram of wt SV40 nanoparticles solution that was coupled to a reservoir solution containing different concentrations of MgCl2, with or without added NaCl. The crystal structure and the mass fraction of soluble wt SV40 nanoparticle and wt SV40 crystals were determined using synchrotron solution Small Angle X ray Scattering (SAXS). We also present a thermodynamic model that accounts for both the crystallization and the reentrant melting and resolubilization, and is consistent with our experimental data. In this model, the virus crystal formation and reentrant melting and resolubilization are attributed to the balance between the Mg2+ adsorption and bridging interactions and the chemical potential of the Mg2+ ions in the bulk solution.
Results and discussion
MgCl2 induces crystallization of wt SV40 into a BCC (Im3m) crystal
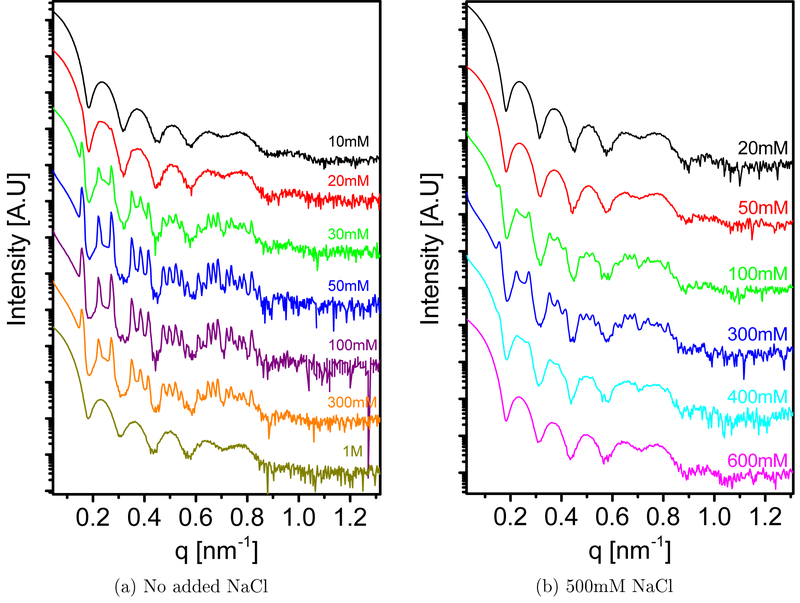
Figure 1 shows the scattering curve from wt SV40 at varying MgCl2 concentrations (0.01 – 1 M), with and without added 0.5 M NaCl. A BCC crystalline phase with space group Im3m appeared when the MgCl2 concentrations were between 20 and 300 mM, when no salt was added. When 0.5 M NaCl was added, BCC crystals were observed between 100 and 400 mM MgCl2. A similar BCC was published in the crystallographic data, protein data bank (PDB) ID 1SVA.54 In a BCC lattice, the observed peaks comes from crystal planes that the sum of their Miller indices is even. The indexation of the peaks and the assignment of the relevant planes are presented on a selected signal in Figure S6 and Table S1. The unit cell parameters and the symmetry space group did not change with MgCl2 or NaCl concentrations. To emphasis the structure factor contribution to the signal, the scattering curves were divided by the form-factor of the virus that was multiplied by a scaling factor to account for possible variations in the total virus concentrations.
Figure 1:
Azimuthally integrated small angle X-ray scattering intensity curves of wt SV40 solution, at different MgCl2 concentrations, as a function of the magnitude of the scattering vector, q. (a) When no NaCl was added to the dialysis solution, at 10 mM MgCl2 there was no indication for the presence of the crystalline phase. This signal was therefore used to determine the contribution of the form-factor to the scattering intensity curve that contained a coexisting crystalline phase (see Eq. 17). The crystalline phase first appeared at 20mM MgCl2 and completely disappeared at 1 M MgCl2. (b) The addition of 500 mM NaCl to the dialysis solution shifted the appearance of the crystalline phase to 100 mM MgCl2. This phase was not detected at 600 mM MgCl2. For this set of measurements, the scattering signal at 20 mM MaCl2 was considered as the form factor contribution.
For the data set with no added NaCl the line-shape of the peaks in Figure 2a suggests that there were two BCC crystalline phases with slightly different unit cells. Therefore, the fitting of the normalized signal to Eq. 21 included parameters of two slightly different BCC lattice unit cells. Our results indicate that there was a dense BCC phase with a unit cell vector of 55.9 nm, which is close to the unit cell (55.8 nm) obtain previously by crystallography, using different buffer conditions.54 The second phase has a slightly larger unit cell vector of 56.7nm. We attribute the existence of these two phases to the relatively short incubation time of the virus solution in the relevant MgCl2 bulk solution (10 ± 2 h), This time scale is probably too short for attaining full equilibrium. It is important to note that the differences in the q values of the peak centers between these two phases is above the measurement resolution (as explained and demonstrated in Section 3.1 in the Supporting Information (SI) and Figure S7).
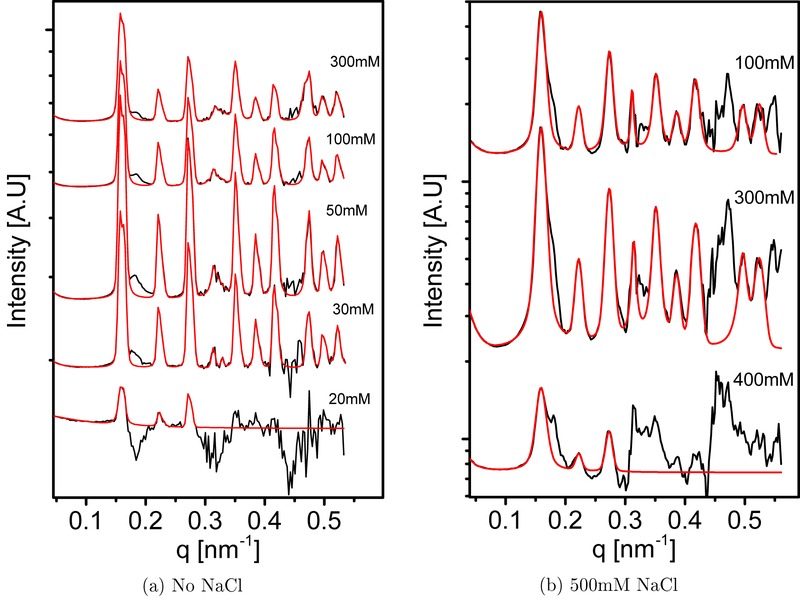
Figure 2:
The structure-factor contribution to the scattering curves in Figure 1, at each MgCl2 concentration, as a function of q for two sets of measurements: (a) With no added NaCl to the solution and (b) with 500 mM that were added to the dialysis solution. The black curves in each figure correspond to the normalized signals I([MgCl2]>q)/|FF(q)|2 and the red curves represents the best fitted g (q) function described in Eq. 21. The curves are separated by an arbitrary scale along the intensity axis, for clarity of presentation. The deviations from the structure factor model result from slight changes in the form factors with increasing the MgCl2 concentrations. The origin of these deviations is explained in Section 3.2 and Figure S8 in the SI.
We expect that at equilibrium condition only one BCC structure will be visible. In contrast, the structure factor results in the presence of NaCl, that are presented in Figure 2b, could be fitted by considering only one crystal phase with a unit cell vector of size 56.3 nm. It is of interest to note that this value happens to be the average of the two lattice vectors when no NaCl was added. The fitting results for the peaks positions for the three unit cells sizes are give in Table S2. The differences between the two experiments could have originated from slight differences in the crystal formation kinetics, in inter-virus interaction strength, slight variation of the form factor with or without added NaCl or differences in the measurement resolution between setups. It is important to note that the fraction of the crystalline phase was lower when NaCl was added and further limited the ability to distinguish between two adjacent peaks. The variation in the distance between the center of mass of two virus particles that are in contact within the BCC crystal was between 4 and 8 Å. This variation did not change the solubility results presented in Figure 3 (scattered points) and was not taken into account in the fitted model (solid curves in Figure 3).
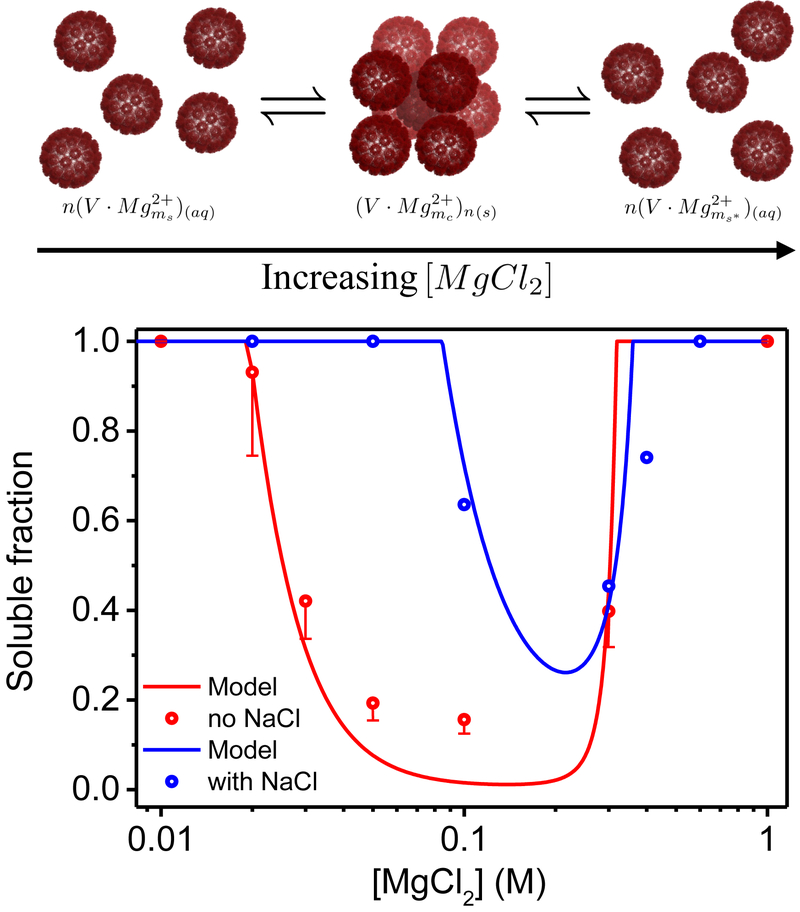
Figure 3:
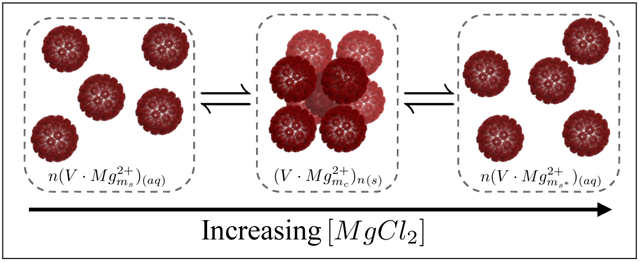
The fraction of soluble virus, χs, as a function of MgCl2 concentration. The scattered circles are the experimentally measured χs obtained from the fitting of the normalized scattering curves (Figure 2). The blue circles correspond to the data set with 500mM NaCl and the red circles correspond to the measurements without added NaCl. The error bars of the red circles represent the maximum possible deviation in the values of the solubility that result from multiplying the form factor by a scaling factor of 0.8 ± 0.01, as described in Material and Method. The red and blue curves represent the theoretically predicted soluble fractions based on our thermodynamic model, in which the Mg2+ adsorption energies ϵs = ϵnb and ϵb were −0.805 and −1.851 for the red curve and −0.260 and −1.262 for the blue curve. The number of possible binding sites per pentamer, N, was 20 and the fraction of pentamers that can form bridges in the BCC 10 lattice, fp, was in both cases. The cartoon illustrates crystallization and reentrant and resolubilization processes with increasing the MgCl2 concentration. The virus cartoon is based on PDB ID 1SVA54 and was created using PyMOL software.57
The solubility of wt SV40 changed nonmonotonically with MgCl2 concentration
The mass fraction of the soluble virus, χs, was obtained by fitting of the normalized scattering curves to Eq. 21. Figure 3 shows that χs changed nonmonotonically with the concentration of MgCl2 in the bulk solution. The crystalline phase first appeared when the bulk MgCl2 concentration was increased above a threshold concentration, c*. Further increase of the MgCl2 concentration increased the mass fraction of the crystalline phase, up to a maximal point (minimum solubility of the virus). Additional increase of the concentration reversed the process and resolubilized the virus particles in the crystal state, until a second threshold, c** was reached, above which all the virus particles were soluble. c* and c** defined the range of MgCl2 concentration where the two phases (soluble and crystalline) coexisted.
Addition of monovalent salt concentration changed c*
We can see from the experimental data in Figure 3 that the window of concentrations between c* and c** changed by adding monovalent salt in addition to the MgCl2. The value of c* increased from between 10 and 20 mM to somewhere between 50 and 100 mM. This shift is consistent with an effective weaker affinity of the Mg2+ ions to the exposed virus acidic sites, in the presence of Na+ ions that compete for the same sites.47 The data points are too sparse to determine if c** changed or not.
NaCl or spermine alone did not crystallize wt SV40
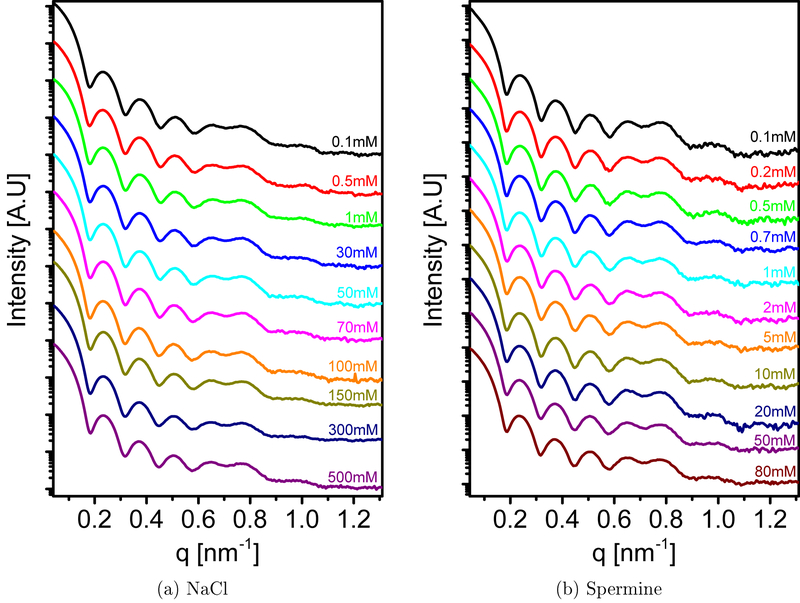
Figure 4 shows that when NaCl or spermine salt solutions were added to wt SV40, no virus crystals formed. NaCl has monovalent ions and therefore was unable to bridge virus particles. Spermine, however, has a tetravalent positively charged ion, which could bridge as it does, for example, with nucleosome core particles,48 DNA,26 microtubule,27–29 or actin.58 It is of interest to note that dipolar lipid bilayers with saturated tails, can adsorb a range of multivalent ions, like Ca2+ or Mg2+, but not NaCl or spermine.59–61 The electophoretic mobility of the virus particles was measured after dialysis against MgCl2 or spermine solutions at concentrations similar to the SAXS measurements (see Sec. 4 in the SI and Figure S9). The results show that both Mg2+ and Spm4+ can bind the virus surface and change its mobility, and hence it surface-charge sign, from negative to positive. Whereas the Mg2+ binding condensed the virus particle into a crystalline phase, the binding of spermine did not. These results suggest that some level of ion specificity controls the condensation of the viral particles rather than purely the net surface charge of the viral nanoparticles.
Figure 4:
Azimuthally integrated small angle X-ray scattering intensity curves of wt SV40 solution, at different NaCl concentrations (a) and Spermine concentrations (b) as indicated in the figure.
Chemical reaction
To explain our findings with MgCl2, we propose a simple model (illustrated in Figure 3) that is based on the specific adsorption of Mg2+ onto negatively charged sites on the outer surface of the virus capsid. We attribute the formation of the virus crystal to Mg2+ ions that act as bridging agents and connect between virus particles.62 The reaction is therefore:
| (1) |
V represent the virus, n is the mean number of virus particles in a crystal domain, ms and mc are the number of Mg2+ ions that adsorb per virus in the soluble and crystalline states, respectively. The MgCl2 concentration was fixed by the large volume of the dialysis solution. At equilibrium, the relative amounts of the virus at each state depend on the supersaturation state of the solution. Above the virus solubility threshold, Cs, the mass fractions of the two states (soluble and crystal) are defined as and , where Ctot refers to the total virus concentration. Cs is a function of the MgCl2 concentration. Our model predicts the solubility threshold as a function of MgCl2 concentration in the bulk, by minimizing the free energy of a solution containing the virus at the two states.
Thermodynamic model
In our model the total free energy of the system, Ftot is therefore the sum of the virus free energies in the crystal, Fc, and in the soluble, Fs, states
| (2) |
Fs has two contributions, the free energy of the adsorbed Mg2+ cations on the soluble virus, , and the solution entropy of the soluble virus. The following model suggests a very simple mean-field explanation to the observed crystallization and resolubilization of the spherical virus nanoparticles induced by bridging interaction of Mg2+ ions.
Crystallization and resolubilization of wt SV40 depend on the chemical potential of Mg2+
wt SV40 has a sphere-like structure with an outer surface that is tiled with negative (acidic), positive (basic) or neutral (polar or non-polar) residues. The negative patches are the potential Mg2+ binding sites where bridging interactions may occur. The model includes Ns potential surface binding sites per virus. These sites can be unoccupied (hydrated carboxylic group) or occupied by adsorbed Mg2+. Each site that adsorbs a Mg2+ ion may be in one of the following three possible states: an adsorbed cation on the surface of a soluble (s) virus, an adsorbed cation that bridges (b) two adjacent virus particles and an adsorbed cation on the surface of the virus in the crystal phase that does not participate directly in the bridging interaction (non-bridging, nb).
The model assumes fixed virus concentration (or volume fraction), temperature, and pressure. The solubility threshold, and therefore the partition between the two states, is a function of the difference in the virus standard chemical potentials between the soluble and crystallized states. We assumed that changes in the free energy are mainly owing to changes in the partition of the adsorbed Mg2+ cations in their different possible states. The partition between the soluble and crystalline states results from minimizing the excess free energy of the adsorbed Mg2+ cation with respect to is standard state under the constraint of a fixed Mg2+ chemical potential in the bulk. The total free energy change of the adsorbed Mg2+ cations is given by
| (3) |
The free energy change for the adsorbed Mg2+ cations on the surface of a soluble virus is given by the ideal lattice gas approximation63
| (4) |
, kB is Boltzmann’s constant, Ns is the total number of acidic binding sites on the outer surface of a virus, and θs is the Mg2+ coverage fraction of acidic sites on a surface of a soluble virus. ϵs is the free energy change for adsorption of one Mg2+ ion onto an acidic site of a soluble virus, namely replacing the sodium counter ion with the magnesium ion from its standard state in the bulk. The number of adsorbed ions per soluble virus is therefore .
In the same manner, we can write the free energy for the adsorbed Mg2+ cations on the surface of the virus in the crystal. In this case, the free energy change is divided into two terms; the first term describes the free energy change for the adsorbed cations on the contact surface where it acts as a bridging agent (b) and the second term is associated with adsorbed cations on the rest of the virus surface that do not take part in the bridging interaction (nb). According to our model the free energy change is given by
| (5) |
where the total number of binding sites on the surface is fixed Nb + Nnb = Ns. In our model we assume that only a fraction, fp, of the virus pentamers can participate in the bridging interaction to form the BCC crystal structure, therefore, we can write Nb = fpNs and Nnb = (1 – fp) Ns. The equilibrium occupation numbers for the different adsorption sites can be determine by minimizing the total free energy with respect to the different coverage fractions where i ∈ (s, b, nb), under a fixed chemical potential of the bulk. At equilibrium this is equivalent for demanding the equality of the chemical potentials of the Mg2+ at all states
| (6) |
where
| (7) |
and μ is the bulk chemical potential that is given by , where is the activity of Mg2+ cations in the bulk. Using the equilibrium condition (Eq. 6), we derived the different coverage fractions as a function of the bulk concentration of MgCl2,
| (8) |
We can now use this result to derive an expression for the chemical potential of the virus in its soluble and crystalline state as a function of the chemical potential of Mg2+ in the bulk. The chemical potential of the soluble virus is given by
| (9) |
The first term represents the contribution of the Nsθs adsorbed Mg2+ cations per virus and the second term represents the solution entropy of the virus. Cs is the solubility of the virus at a given MgCl2 concentration (in units of volume fraction) and Cs,o is a scaling parameter to set the solubility of the virus with no added MgCl2 (the reference state). Similar expression for the chemical potential of the virus in the crystal state is given by
| (10) |
where fp is the fraction of virus surface that participates in bridging interaction. In the last expression we neglected the entropy term of the crystal state. The factor of 0.5 accounts for the fact that each bridging ion interacts with two adjacent virus particles. At equilibrium μsoluble = μcrystal and the expression for the solubility is given by
| (11) |
where is the difference in the number of adsorbed Mg2+ cations per virus between the crystal and the soluble states that is equal to
| (12) |
The expected fraction of soluble virus as a function of the concentration of the bulk MgCl2 can then be derived by the supersaturation condition where the value of χs is between 0 and 1. Eq. 12 was plotted in Figure S10 and discussed in Sec. 5 in the SI.
Estimating the values of model parameters
To compare the prediction of the model with the experimental result one needs to estimate the values of the parameters. We set the interaction surface area per contact between two virus particles to be equal to the outer surface area of one pentamer. Therefore, fp, the surface fraction for the bridging interaction, was set to for the BCC lattice. The number of potential binding sites per pentamer was estimated by the number of the acidic residues (Asp and Glu) that are found on the outer surface of a pentamer and are accessible for interaction with adjacent pentamer. We estimated this number from the crystal structure of the VP1 pentamer (1SVA). The number of acidic resides was found using PvMol software57 and for estimating the protonation state we used H ++ server.64 From the crystal structure there are 3 or 4 acidic residues per monomer that are accessible for the interaction. The calculated pKa vales were between 0.74 and 3.38. Therefore, the number of available binding sites per pentamer, N, was estimated to be between 15 and 20. The solid curves in Figure 3 were obtained with N = 20. The results, however, did not change considerably when N was 15. The reference state, Cs,0, was set to 0.68 which is the volume fraction of spheres that form a BCC lattice geometry.65 The initial virus volume fraction was estimated by the following equation
| (13) |
where CVP1 is the VP1 monomer concentration (≈ 1 mg/ml), Mw,VP1 is the molecular weight of the monomer (40kDa), Nav is Avogadro number, and VSV40 is the volume of the virus that was calculated by assuming the virus to be a sphere with an outer diameter of ~50 nm. Inserting these parameters to Eq. 13 gave an initial volume fraction of 2.74 × 10−3. To estimate the chemical potential of Mg2+ we calculated the Mg2+ activity coefficient as a function of MgCl2 concentration using the Khoshkbarchi and Vera Eq.66 The activity coefficients are given for solutions of MgCl2 in water. We used the same values also when 0.5 M NaCl was added. Although added NaCl could have changed the activity of the Mg2+ ions, small variations in the activity results in a small scale prefactor on the Mg2+ adsorption energies (ϵi), without changing the overall dependence of the virus solubility on the MgCl2 concentrations. ϵi were fitted to describe the experimental results, assuming that ϵs = ϵnb.
The thermodynamic model reproduces the measured virus solubility
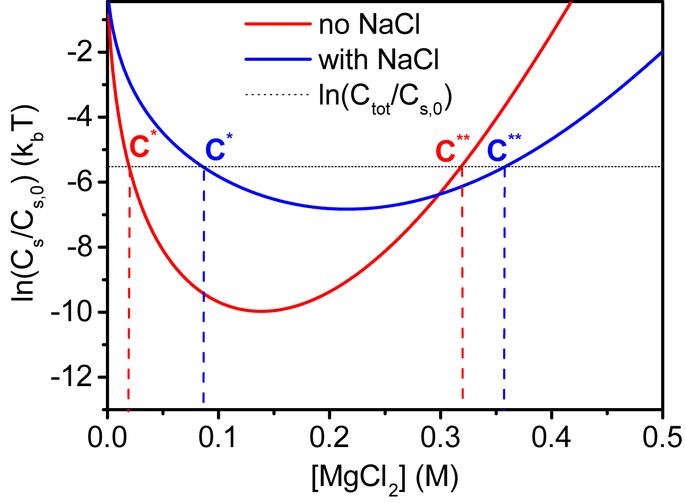
Figure 3 compares the experimental with the calculated virus solubility as a function of the MgCl2 concentration in the bulk. The binding free energies, ϵs and ϵb, were the only fitting parameters required to reproduce the experimental data. Figure 5 shows more clearly the shift in the calculated coexistence concentration window (c* and c**). The free energy change for the crystallization process, , is equivalent to the logarithm of the virus solubility ln . By plotting ln as a function of the concentration of MgCl2 in the bulk, we obtain the virus phase diagram, as was previously done for short dsDNA fragments.41 The horizontal line, ln , is solution entropy gain from dissolving the total virus concentration. At virus concentrations, where the solution entropy gain (horizontal line) is below the crystallization free energy curve, all the virus is in the soluble phase. At virus concentrations at which the horizontal line is above the crystallization curve, a coexisting state of the two phases is expected. In our model the change in the total free energy is controlled by the chemical potential of the bulk Mg2+ cations, μ, that acts as a generalized force. The response of the system to this force is to change , by controlling the relative fractions of the crystalline and soluble phases.
Figure 5:
Virus supersaturation criterion as a function MgCl2 concentration. The red and blue curves are given by (Eq. 12) for the two calculated models (0 and 500 mM NaCl concentrations). These curves represent the free energy change for crystallization as a function of MgCl2 concentration. The black horizontal line corresponds to the log of the experimental volume fraction of the virus, Ctot, divided by a reference volume fraction of a BCC packaging geometry, Cs,0. Whenever the black line is lower than the red or blue curves, the model predicts that only soluble virus is present in the solution. In the concentrations range between c* and c**, where the total volume fraction of virus is higher than the solubility threshold our model predicts the coexistence of a soluble and a crystalline phases with the relative mass fractions of and respectively.
The experimental results are explained by the model. The horizontal black line is the experimental ln as was estimated by Eq. 13. At low MgCl2 concentration this line is below the crystallization free energy curve and therefore the only visible phase is soluble virus. As the MgCl2 concentration increases the two lines intersect at concentration c*. At higher MgCl2 concentrations the black line is above the crystallization free energy curve and at this region the fraction of the crystalline phase is proportional to the distance between the black line and the crystallization curve. Above the second intersection point, c**, the stable state is again the soluble virus. At high MgCl2 concentrations, the bulk Mg2+ ion chemical potential increases (owing to the low solution entropy of the ions). The system reacts by increasing the number of Mg2+ ions that bind to the possible virus acidic sites and as result, resolubilizing the virus.
Figure 5 can be examined in order to predict the effect of changing the the total virus concentration and monovalent salt concentration. The thermodynamic model predicts that at constant concentration of monovalent salt, upon increasing the total concentration of the virus, c* and c** will be shifted so that the coexistence window will be wider. The point of maximum crystallization, however, will remain constant. At constant virus concentration, upon addition of monovalent ions, the point of maximal crystallization is shifted towards higher concentrations up to a point where crystallization will not be possible even at very high divalent salt concentrations. The minimum virus concentration that is required for the crystallization is increasing with the addition of NaCl. Similar observations were reported for DNA and nucleosome core particles.40,67
Binding free energy
In our mean field model we assumed that the main contribution to the free energy change in bringing two virus particles into contact, comes from short-ranged interaction of the Mg2+ cations with the carboxylic groups on the solvated outer surface of the virus. We did not include terms for the contribution of long-ranged electrostatic interactions in our model (the variation in the binding energies, ϵi, is effectively accounting for some of the contribution). As the observations were essentially similar in the presence of 500 mM NaCl, where the crystalline phase first appeared at 100 mM MgCl2, supports our assumption that the contribution of long-ranged electrostatic interactions was minimal. When 0.5 M NaCl was added, the screening length was very short (~3 Å), and diminished any contribution of this type of long-ranged electrostatic interactions.
Furthermore, without added NaCl, a crystalline phase appeared even at 300 mM MgCl2, where the screening length is small (~3Å). In addition, at MgCl2 concentrations where no crystals appeared we did not observed any positional correlations at low q in our SAXS curves that could have been resulted from long-ranged electrostatic interactions.
We attribute part of the short-ranged interactions to the entropy gain in releasing a pair of Na+ and Cl− ions to the solution upon binding of one Mg2+ cation to the soluble state of the virus and two pairs when the Mg2+ cation bridges two virus particles in the crystalline phase. Additional contribution for the free energy of binding may include the change in hydration of the binding site and of the Mg2+ cations as proposed previously for trivalent ions68 and for nonelectrostatic interactions between the Mg2+ cations and the carboxyl (rather than phosphate) groups.47 The adsorption of divalent cations may increase the hydrophobic character of the adsorption site, hence, bridging becomes more favorable.
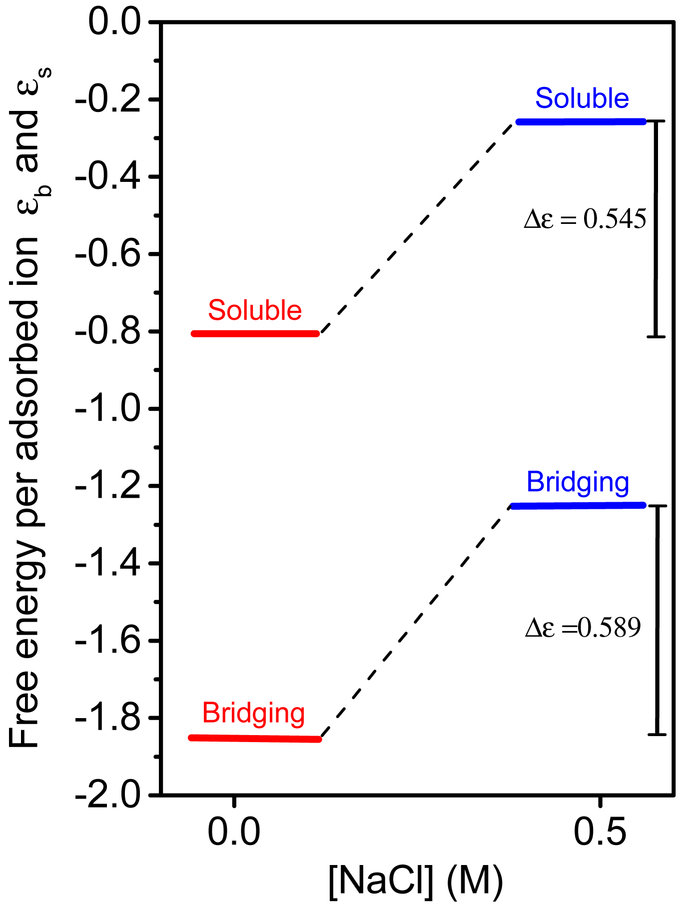
In this work we tested the effect of increasing the monovalent salt concentration in the reservoir. We expect that the free energy gain owing to Na+ and Cl− counterions release will be lower as the reservoir already contains a large amount of these ions. The influence of the added NaCl on the binding free energy, ϵb and ϵs, is illustrated in Figure 6. When the NaCl bulk concentration was higher, both ϵb and ϵs decreased, owing to competition between the Mg2+ and Na+ ions on the virus binding acidic sites.47 This effect is equivalent to a shift in the reference state of the Mg2+ chemical potential in the reservoir, based on which the binding free energy gain is obtained. As a result, higher MgCl2 concentrations were required to induce crystallization in the presence of 0.5 M NaCl. The change in the energy gap Δϵ = ϵb − ϵs, decreased by 5% when NaCl was added, as the net free energy gain from bridging does not depend on the above competition.
Figure 6:
The resultant adsorption energies in the absence and presence of added NaCl.
Conclusions
In this paper we showed how a slow dialysis of wild type Simian Virus 40 (wt SV40) nanoparticles against MgCl2 solutions, with or without added NaCl, can form BCC crystals (with space group Im3m) of wt SV40 nanoparticles in coexistence with soluble virus nanoparticles, when the MgCl2 concentration exceeded a critical concentration, c*. When the MgCl2 concentration was further increased and exceeded a second threshold, c** > c*, reentrant melting and resolubilization of the virus nanoparticles was observed. The window at which the crystals formed depended on the concentration of added NaCl. The observation can be explained by a simple thermodynamic model. The model balances the Mg2+ ion chemical potential in solution with the chemical potentials of the Mg2+ ions that adsorbed onto the virus nanoparticles or formed salt bridges between neighboring virus nanoparticles. The model shows that the entropy of the counterions is the dominant driving force for the entire process.
Methods
wt SV40 purification
A monolayer of CV1-PD cells was infected with wt SV40 at multiplicity of infection (MOI) = 0.05. The infected cells were incubated between 5 and 6 days at 37 °C until more than 50% of the cells were deformed and detached from the surface. Harvest was performed according to the di-detergent method69 in which cell lysis was induced by adding deoxycholate and TritonX-100 at final concentrations of and , respectively. Cell debris was precipitated by centrifuging the dispersion in 50 ml tubes at 4 °C and 3000 RPM for 30 min using Sorvall RT7 centrifuge and RTH-250 rotor. The supernatant was then transferred to 40 ml Beckman polyallomer tubes (cat# 331372) and the virus was precipitated by ultracentrifugation using TST-28 rotor at 25,000 RPM for 4h. The supernatant was discarded and 0.5 ml of phosphate-buffered saline (PBS) were added on top of the virus pellet. The tubes were then closed and left overnight for resuspention at 4 °C. Following resuspention, the pellets were transferred to 2 ml eppendorf tubes and suspended by sonication in ice cooled water using ultrasonic processor XL sonicator. The virus suspension was added to a 2.7 M CsCl solution and the refractive index was adjusted to 1.3655 using Abbe-3L refractometer. The virus suspension was then ultracentrifuged in 5 ml Beckman polyallomer tubes (cat# 326819), in SW50.1 rotor at 40,000RPM and 4 °C for 24 h. Following ultracentrifugation two blue bands were visible under scattered light along the tube. The lower band, at the middle of the tube, contained wt SV40 particles whereas the upper band had empty or partially empty capsids.
The lower band was pulled and re-banded. The fractions were analyzed to asses wt SV40 protein content using SDS-polyacrylamide gel electrophoresis (Novex WedgeWell 412% Tris-Glycine) with Coomassie-Blue staining (Instant blue stain, Expedeon) and the DNA content was estimated using 260:280nm absorption ratio70 measured by a nanodrop spectrophotometer (Nanodrop 2000c, Thermo Scientific).
Samples preparation for SAXS measurements
Wt SV40 samples were dialvzed against NaCl solutions, MgCl2 solutions with or without added 0.5 M NaCl or lower concentrations of spermine solutions. For the high spermine concentrations (above 5 mM) the samples were prepared by adding high concentration salt solutions to the 5mM sample. The dialysis was preformed at 4 °C using GeBa Mini dialysis tubes (Gene Bio Application Ltd, cat# D070–6). Two cycles of dialysis were conducted, 1.5 h each, against bulk solutions that their volumes were ×1000 the volume of the wt SV40 sample. The samples were then equilibrated at ambient room temperature for ca. 10 ± 2h, in the dialysis tube, before they were transferred to a flow cell capillary for solution SAXS measurements.
SAXS measurement setup and data reduction
SAXS measurements were preformed in the P12 beamline of the EMBL located at the PETRA III storage ring (DESY, Hamburg),71 the SWING beamline at Soleil Synchrotron (GIF-sur-YVETTE)72 and at the ID02 beamline at the European Synchrotron Radiation Facility (ESRF) in Grenoble.73 Measurements were taken at 25°C. The SAXS profiles shown in Figure 1a were measured at P12 beamline. The sample to detector distance was 3.1m and the X-ray wavelength was 1.24 Å, resulting in a q-range from qmin = 0.025 nm−1 to qmax = 4.8 nm−1, where q is the magnitude of the scattering vector. For each measurement, 30 μ1 of sample were injected to a 2 mm thick quartz capillary flow-cell by an automated sample changer.74 30 frames were recorded while the sample flew through the capillary. The acquisition time per frame was 50 msec and the scattered intensity was collected by a single-photon 2D PILATUS 2M pixel detector (DECTRIS). SAXS curves shown in Figure 1b were measured at ID02 beamline. The sample to detector distance was 3m and the X-ray wavelength was 0.92 Å, resulting in a q-range from qmin = 0.029 nm−1 to qmax = 2.8 nm −1. For each measurement, in the flow-through capillary cell, 40 μl of sample were manually pushed to the capillary position using a syringe and between 10 and 20 frames were taken while the sample was flowing. The exposure time was 50 msec per frame and the scattered intensity was recorded on a FReLoN 16M Kodak CCD detector. The scattering curves of SV40 in spermine and NaCl solutions, shown in Figure 4. were measured at SWING beamline. The sample to detector distance was 2.6m and the photons wavelength was 1.03 Å. The q-range for these measurements was between 0.039nm−1 and 4.2nm−1. For each measurement 30 μl of the sample were injected to the capillary at a flow rate of and 75 frames were recorded while flowing. The exposure time of each frame was 750 ms and the scattered intensity was recorded on a PCCD170170 (AVIEX) detector. Background measurements of each solution from the dialysis beakers were taken before and after each virus sample. The background measurements were required for subtracting the contribution of the solvent in the virus solution measurements and to ensure that no protein or virus precipitation was left on the walls of the capillary. Data reduction was perform by manually selecting between 10 and 40 frames for each virus sample and ~ 50 frames for the background measurements and averaging. The averaged background signals were then subtracted from the averaged virus signals.
SAXS analysis
In our analysis method we constrained the virus to be in one of the following two states; a soluble state and a crystallized state. The scattering from the soluble virus was considered within the limit of noninteracting dilute particle solutions. In this limit, we neglected any contribution to the scattering intensity that resulted from positional-correlations between virus particles. This approximation was justified by the low volume fraction (ca. 10−3) of the virus and by the scattering results at low MgCl2 concentrations (with no added NaCl) that showed negligible deviation from the expected scattering intensity from an ideal solution of noninteracting particles. Further details are provided in section 1 in SI and Figure S1. Under this approximation the scattering intensity from noninteracting N virus particles, INvirus particles (q) = NIvirus (q), where Ivirus (q) is the scattering intensity of a single soluble virus given by:
| (14) |
where the form factor, FF, is the Fourier transform of the electron density contrast of the virus with respect to the solvent, . is the elastic momentum transfer vector. In general, the brackets 〈…〉 represent average over time, virus orientations in the solution, and virus structure polydispersity. Since wild-type virus particles are generally stable and monodispersed we shall neglect the polydispersity and time terms in the averaging for the rest of this work.
In contrast to the soluble virus, the scattering intensity of the virus in the crystalline state depends both on the form-factor of a single virus, , and on the contribution from the positional correlations within the crystal lattice, usually called the lattice-sum or structure-factor, SF. The scattering intensity of the crystal of virus particles is given by
| (15) |
where is the position vector located at the center of the i-th virus in the crystal. In this equation, each directly depends on the orientation of the virus with respect to the chosen set of axes of the crystal as well as in its structural parameters. To simplify the calculation of this averaged sum, one can use the decoupling approximation.75 Under this approximation the scattering intensity of the crystalline phase is:
| (16) |
where β (q) is the ratio . The decoupling approximation is valid in either of the following two cases: the orientation of the particle is uncorrelated with its position in space (hypothesis H175); or if the particle can be approximately considered (up to some resolution threshold) as spherical. Within the spherical limit, β (q) = 1 and the intensity is reduced to
| (17) |
where is the orientationaly averaged structure-factor of a crystal with an average of N unit cells in positional correlation. As demonstrated in Figure S2, for the SV40 crystal Eq. 17 holds up to a resolution at which inter-pentamer correlations contribute significantly to the scattering intensity. As the characteristic distance between pentamers is ~ 10nm,76 we expect that the resolution limit for the spherical approximation will be at q ≈ 0.6 nm−1.
The structure-factor function was then modeled as a series of peak line-shape functions,
| (18) |
where Ci and fi (q) are the amplitude and the normalized peak line-shape of the ith correlation peak, respectively. n is the total number of peaks up to the q value where the spherical approximation holds. fi (q) is given by the pseudo-Voigt function77
| (19) |
where is a Gaussian function whose center is at and its full width at half maximum (FWHM) is Γi. is a Lorentzian function with the same center and FWHM. The parameter η varies between 0 and 1.
As there were no spatial correlations between the soluble and the crystalline states, the total scattering intensity profile from each measured sample should correspond to a simple summation of the scattering intensity from each state, multiplied by the amount of substance in each state. Therefore, the total scattering intensity (in units of mg · ml−1cm−1) as a function of MgCl2 concentration and q, is:
| (20) |
the coefficients Csoluble and Ccrystal are the concentrations of the soluble virus and the crystal with an averaged of N virus particles in positional correlation, respectively. The values of both Csoluble and Ccrystal depend on the bulk MgCl2 concentration. The scattering intensities Ivirus (q) and (q) are given in absolute units of cm−1. Therefore, to normalize the signal with respect to their form-factor contribution, each scattering signal was divided by the scattering signal from wt SV40 where no structure factor contributions were detected (10 mM MgCl2 or 20 mM MgCl2 with added 0.5 M NaCl). When no NaCl was added, the scale of the form-factor signal was further multiplied by a factor 0.8 ± 0.01 to ensure overlap of the scattering signals at high q, where no structure-factor features were detected. We attribute the latter factor to variations in the total virus concentration resulted from transferring the samples from the dialysis tubes to the measurement capillary flow cell. Partial precipitation of virus particles between loading the samples and measuring them may have also slighly contributed to the value of this factor. The normalized signals were then fitted to:
| (21) |
where χsol and χcrystal are the mass fraction of virus particles at the soluble and crystalline states, respectively. Using X + software developed in our lab,78–80 we minimized the following cost function
| (22) |
Peak indexation and crystal structure determination
We used X+ software,78–80 for correlation peak index assignment and for determining the crystal lattice structure. The fitting procedure included an initial scan for finding the crystal symmetry group that best represented the measured series of scattering peak center positions. After the crystal symmetry was established the size of the unit cell vectors was determined by minimizing the total distance between the expected peak center positions, , from a given size of a unit cell vectors and the vector of peak positions, , obtain from fitting Eq. 21 to the normalized signals.
Supplementary Material
Acknowlegement
We thank Daniel Harries for very helpful discussions. We acknowledge the European Synchrotron Radiation Facility (ESRF) beamline ID02 (T. Narayanan and his team), Desy synchrotron at Hamburg, beamline P12 (D. Svergun and his team), and Soleil synchrotron, Swing beamline (J. Perez and his team) for provision of synchrotron radiation facilities and for assistance in using the beamlines. We thank Ofra Moshel for her help with conducting the electrophoretic mobility measurements. RA acknowledges support from the Kaye-Einstein fellowship foundation. UR and RA acknowledge financial support from the Israel Science Foundation (grant 656/17), US-Israel binational Science Foundation (grant 2016311), the FTA-Hybrid Nanomaterials program of the Planning and Budgeting Committee of the Israel Council of Higher Education, and the NIH (Award Number 1R01AI118933).
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI:
Validation of the ideal gas approximation for the 10 mM MgCl2 signal; justification of the decoupling approximation with β = 1; peak indexing and shape, lattice planes, and phase fitting results; Electrophoretic mobility measurements; free energy for crystallization (PDF).
References
- 1.Auyeung E; Li TI; Senesi AJ; Schmucker AL; Pals BC; de La Cruz MO; Mirkin CA DNA-Mediated Nanoparticle Crystallization into Wulff Polyhedra. Nature 2014, 505, 73–77. [DOI] [PubMed] [Google Scholar]
- 2.Schwarz B; Uchida M; Douglas T Chapter One-Biomedical and Catalytic Opportunities of Virus-Like Particles in Nanotechnology. Adv. Virus Res 2017, 97, 1–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pokorski JK; Steinmetz NF The Art of Engineerings Viral Nanoparticles. Mol. Pharmaceutics 2011, 8, 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Loo L; Guenther RH; Basnayake VR; Lommel SA; Franzen S Controlled Encapsidation of Gold Nanoparticles by a Viral Protein Shell. J. Am. Chem. Soc 2006, 128, 4502–4503. [DOI] [PubMed] [Google Scholar]
- 5.Chen C; Daniel M-C; Quinkert ZT; De M; Stein B; Bowman VD; Chipman PR; Rotello VM; Kao CC; Dragnea B Nanoparticle-Templated Assembly of Viral Protein Cages. Nano Lett. 2006, 6, 611–615. [DOI] [PubMed] [Google Scholar]
- 6.Douglas T; Young M Viruses: Making Friends With Old Foes. Science 2006, 312, 873–875. [DOI] [PubMed] [Google Scholar]
- 7.Uchida M; Klem MT; Allen M; Suci P; Flenniken M; Gillitzer E; Varpness Z; Liepold LO; Young M; Douglas T Biological Containers: Protein Cages as Multifunctional Nanoplatforms. Adv. Mater 2007, 19, 1025–1042. [Google Scholar]
- 8.Jordan PC; Patterson DP; Saboda KN; Edwards EJ; Miettinen HM; Basu G; Thielges MC; Douglas T Self-Assembling Biomolecular Catalysts for Hydrogen Production. Nat. Chem 2015, 8, 179–185. [DOI] [PubMed] [Google Scholar]
- 9.Falkner JC; Turner ME; Bosworth JK; Trentler TJ; Johnson JE; Lin T; Colvin VL Virus Crystals as Nanocomposite Scaffolds. J. Am. Chem. Soc 2005, 127, 5274–5275, PMID: 15826137. [DOI] [PubMed] [Google Scholar]
- 10.Harries D; Podgornik R; Parsegian VA; Mar-Or E; Andelman D Ion Induced Lamellar-Lamellar Phase Transition in Charged Surfactant Systems. J. Chem. Phys 2006, 124, 224702. [DOI] [PubMed] [Google Scholar]
- 11.Harries D; Raviv U 1 Soft Matter Physics of Lipid Membrane–Based Assemblies. Liposomes, Lipid Bilayers and Model Membranes: From Basic Research to Application 2014, 3–26. [Google Scholar]
- 12.Loosley-Millman ME; Rand RP; Parsegian V Effects of Monovalent Ion binding and Screening on Measured Electrostatic Forces Between Charged Phospholipid Bilayers. Biophy. J 1982, 40, 221–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bloomfield VA DNA Condensation. Curr. Opin. Struct. Biol 1996, 6, 334–341. [DOI] [PubMed] [Google Scholar]
- 14.Wong GC; Pollack L Electrostatics of Strongly Charged Biological Polymers: Ion-Mediated Interactions and Self-Organization in Nucleic Acids and Proteins. Annu. Rev. Phys. Chem 2010, 61, 171–189. [DOI] [PubMed] [Google Scholar]
- 15.Kanduč M; Naji A; Podgornik R Counterion-Mediated Weak and Strong Coupling Electrostatic Interaction Between Like-Charged Cylindrical Dielectrics. J. Chem. Phys 2010, 132, 224703. [DOI] [PubMed] [Google Scholar]
- 16.Besteman K; Van Eijk K; Lemay S Charge Inversion Accompanies DNA Condensation by Multivalent Ions. Nat. Phys 2007, 3, 641–644. [Google Scholar]
- 17.Rouzina I; Bloomfield VA Macroion Attraction due to Electrostatic Correlation Between Screening Counterions. 1. Mobile Surface-Adsorbed Ions and Diffuse Ion Cloud. J. Phys. Chem 1996, 100, 9977–9989. [Google Scholar]
- 18.Nadler M; Steiner A; Dvir T; Szekely O; Szekely P; Ginsburg A; Asor R; Resh R; Tamburu C; Peres M; Raviv U Following the Structural Changes During Zinc-Induced Crystallization of Charged Membranes Using Time-Resolved Solution X-Ray Scattering. Soft Matter 2011, 7, 1512–1523. [Google Scholar]
- 19.Grønbech-Jensen N; Mashl RJ; Bruinsma RF; Gelbart WM Counterion-Induced Attraction Between Rigid Polyelectrolytes. Phys. Rev. Lett 1997, 78, 2477. [Google Scholar]
- 20.Ha B-Y; Liu AJ Counterion-Mediated Attraction Between Two Like-Charged Rods. Phys. Rev. Lett 1997, 79, 1289. [Google Scholar]
- 21.Javidpour L; Lošdorfer Božič A; Naji A; Podgornik R Multivalent Ion Effects on Electrostatic Stability of Virus-Like Nano-Shells. J. Chem. Phys 2013, 139, 154709. [DOI] [PubMed] [Google Scholar]
- 22.Sapir L; Harries D Macromolecular Compaction by Mixed Solutions: Bridging Versus Depletion Attraction. Curr. Opin. Colloid Interface Sci 2016, 22, 80–87. [Google Scholar]
- 23.Moshe L; Saper G; Szekely O; Linde Y; Gilon C; Harries D; Raviv U Modulating the Structure and Interactions of Lipid–Peptide Complexes by Varying Membrane Composition and Solution Conditions. Soft Matter 2013, 9, 7117–7126. [Google Scholar]
- 24.Bowen WR; Sharif AO Long-Range Electrostatic Attraction Between Like-Charge Spheres in a Charged Pore. Nature 1998, 393, 663–665. [Google Scholar]
- 25.Lee S; Le TT; Nguyen TT Reentrant Behavior of Divalent-Counterion-Mediated DNA-DNA Electrostatic Interaction. Phys. Rev. Lett 2010, 105, 248101. [DOI] [PubMed] [Google Scholar]
- 26.Raspaud E; De La Cruz MO; Sikorav J-L; Livolant F Precipitation of DNA by Polyamines: A Polyelectrolyte Behavior. Biophys. J 1998, 74, 381–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Needleman DJ; Ojeda-Lopez MA; Raviv U; Miller HP; Li Y; Song C; Feinstein SC; Wilson L; Choi MC; Safinya CR Ion Specific Effects in Bundling and Depolymerization of Taxol-Stabilized Microtubules. Faraday Discuss. 2013, 166, 31–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ojeda-Lopez MA; Needleman DJ; Song C; Ginsburg A; Kohl PA; Li Y; Miller HP; Wilson L; Raviv U; Choi MC; Safinya CR Transformation of Taxol-Stabilized Microtubules into Inverted Tubulin Tubules Triggered by a Tubulin Conformation Switch. Nat. Mater 2014, 13, 195–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Needleman DJ; Ojeda-Lopez MA; Raviv U; Miller HP; Wilson L; Safinya CR Higher-Order Assembly of Microtubules by Counterions: From Hexagonal Bundles to Living Necklaces. Proc. Natl. Acad. Sci. U. S. A 2004, 101, 16099–16103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rädler JO; Koltover I; Salditt T; Sa_nya, C. R. Structure of DNA-Cationic Liposome Complexes: DNA Intercalation in Multilamellar Membranes in Distinct Interhelical Packing Regimes. Science 1997, 275, 810–814. [DOI] [PubMed] [Google Scholar]
- 31.Wong GC; Tang JX; Lin A; Li Y; Janmey PA; Safinya CR Hierarchical Self-Assembly of F-Actin and Cationic Lipid Complexes: Stacked Three-Layer Tubule Networks. Science 2000, 288, 2035–2039. [DOI] [PubMed] [Google Scholar]
- 32.Huang C-I; Olvera de La Cruz M Polyelectrolytes in Multivalent Salt Solutions: Monomolecular Versus Multimolecular Aggregation. Macromolecules 2002, 35, 976–986. [Google Scholar]
- 33.Leung C-Y; Palmer LC; Kewalramani S; Qiao B; Stupp SI; De La Cruz MO; Bedzyk MJ Crystalline Polymorphism Induced by Charge Regulation in Ionic Membranes. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 16309–16314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.De La Cruz MO; Belloni L; Delsanti M; Dalbiez J; Spalla O; Drifford M Precipitation of Highly Charged Polyelectrolyte Solutions in the Presence of Multivalent Salts. J. Chem. Phys 1995, 103, 5781–5791. [Google Scholar]
- 35.Solis FJ; De La Cruz MO Attractive Interactions Between Rodlike Polyelectrolytes: Polarization, Crystallization, and Packing. Phys. Rev. E 1999, 60, 4496. [DOI] [PubMed] [Google Scholar]
- 36.Solis FJ; de la Cruz MO Collapse of Flexible Polyelectrolytes in Multivalent Salt Solutions. J. Chem. Phys 2000, 112, 2030–2035. [Google Scholar]
- 37.Kanai T; Boon N; Lu PJ; Sloutskin E; Schofield AB; Smallenburg F; van Roij R; Dijkstra M; Weitz DA Crystallization and Reentrant Melting of Charged Colloids in Nonpolar Solvents. Phys. Rev. E 2015, 91, 030301. [DOI] [PubMed] [Google Scholar]
- 38.Solis FJ; De La Cruz MO Flexible Linear Polyelectrolytes in Multivalent Salt Solutions: Solubility Conditions. EPJdirect 2000, 2, 1–18. [Google Scholar]
- 39.Kewalramani S; Guerrero-García GI; Moreau LM; Zwanikken JW; Mirkin CA; de la Cruz MO; Bedzyk MJ Electrolyte-Mediated Assembly of Charged Nanoparticles. ACS Cent. Sci 2016, 2, 219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.De Frutos M; Raspaud E; Leforestier A; Livolant F Aggregation of Nucleosomes by Divalent Cations. Biophys. J 2001, 81, 1127–1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nguyen T; Rouzina I; Shklovskii B Reentrant Condensation of DNA Induced by Multivalent Counterions. J. Chem. Phys 2000, 112, 2562–2568. [Google Scholar]
- 42.Nguyen TT; Shklovskii BI Complexation of DNA with Positive Spheres: Phase Diagram of Charge Inversion and Reentrant Condensation. J. Chem. Phys 2001, 115, 7298–7308. [Google Scholar]
- 43.Zhang F; Skoda M; Jacobs R; Zorn S; Martin RA; Martin C; Clark G; Weggler S; Hildebrandt A; Kohlbacher O; Schreiber F Reentrant Condensation of Proteins in Solution Induced by Multivalent Counterions. Phys. Rev. Lett 2008, 101, 148101. [DOI] [PubMed] [Google Scholar]
- 44.Zhang F; Weggler S; Ziller MJ; Ianeselli L; Heck BS; Hildebrandt A; Kohlbacher O; Skoda MW; Jacobs RM; Schreiber F Universality of Protein Reentrant Condensation in Solution Induced by Multivalent Metal Ions. Proteins: Struct., Funct., Bioinf 2010, 78, 3450–3457. [DOI] [PubMed] [Google Scholar]
- 45.Roosen-Runge F; Heck BS; Zhang F; Kohlbacher O; Schreiber F Interplay of pH and Binding of Multivalent Metal Ions: Charge Inversion and Reentrant Condensation in Protein Solutions. J. Phys. Chem. B 2013, 117, 5777–5787. [DOI] [PubMed] [Google Scholar]
- 46.Nicolai T; Durand D Protein Aggregation and Gel Formation Studied with Scattering Methods and Computer Simulations. Curr. Opin. Colloid Interface Sci 2007, 12, 23–28. [Google Scholar]
- 47.Sabbagh I; Delsanti M Solubility of Highly Charged Anionic Polyelectrolytes in Presence of Multivalent Cations: Specific Interaction Effect. Euro. Phys. J. E 2000, 1, 75–86. [Google Scholar]
- 48.Bertin A; Mangenot S; Renouard M; Durand D; Livolant F Structure and Phase Diagram of Nucleosome Core Particles Aggregated by Multivalent Cations. Biophys. J 2007, 93, 3652–3663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.De Frutos M; Raspaud E; Leforestier A; Livolant F Aggregation of Nucleosomes by Divalent Cations. Biophys. J 2001, 81, 1127–1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mangenot S; Leforestier A; Durand D; Livolant F Phase Diagram of Nucleosome Core Particles. J. Mol. Biol 2003, 333, 907–916. [DOI] [PubMed] [Google Scholar]
- 51.Casselyn M; Perez J; Tardieu A; Vachette P; Witz J; Delacroix H Spherical Plant Viruses: Interactions in Solution, Phase Diagrams and Crystallization of Brome Mosaic Virus. Acta Crystallogr., Sect. D: Biol. Crystallogr 2001, 57, 1799–1812. [DOI] [PubMed] [Google Scholar]
- 52.Griffith JD Chromatin Structure: Deduced from a Minichromosome. Science 1975, 187, 1202–1203. [DOI] [PubMed] [Google Scholar]
- 53.Cremisi C; Pignatti PF; Croissant O; Yaniv M Chromatin-Like Structures in Polyoma Virus and Simian Virus 40 Lytic Cycle. J. Virol 1976, 17, 204–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Stehle T; Gamblin SJ; Yan Y; Harrison SC The Structure of Simian Virus 40 Refined at 3.1 Å Resolution. Structure 1996, 4, 165–182. [DOI] [PubMed] [Google Scholar]
- 55.Baker TS; Drak J; Bina M Reconstruction of the Three-Dimensional Structure of Simian Virus 40 and Visualization of the Chromatin Core. Proc. Natl. Acad. Sci. U. S. A 1988, 85, 422–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Li PP; Nakanishi A; Clark SW; Kasamatsu H Formation of Transitory Intrachain and Interchain Disulfide Bonds Accompanies the Folding and Oligomerization of Simian Virus 40 Vp1 in the Cytoplasm. Proc. Natl. Acad. Sci. U. S. A 2002, 99, 1353–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Schrödinger LLC, The PyMOL Molecular Graphics System, Version 1.8.
- 58.Tang JX; Janmey PA The polyelectrolyte nature of F-actin and the mechanism of actin bundle formation. J. Biol. Chem 1996, 271, 8556–8563. [DOI] [PubMed] [Google Scholar]
- 59.Szekely O; Steiner A; Szekely P; Amit E; Asor R; Tamburu C; Raviv U The structure of ions and zwitterionic lipids regulates the charge of dipolar membranes. Langmuir 2011, 27, 7419–7438. [DOI] [PubMed] [Google Scholar]
- 60.Fink L; Feitelson J; Noff R; Dvir T; Tamburu C; Raviv U Osmotic stress induced desorption of calcium ions from dipolar lipid membranes. Langmuir 2017, [DOI] [PubMed] [Google Scholar]
- 61.Lotan O; Fink L; Shemesh A; Tamburu C; Raviv U Critical Conditions for Adsorption of Calcium Ions onto Dipolar Lipid Membranes. J. Phys. Chem. A 2016, 120, 3390–3396. [DOI] [PubMed] [Google Scholar]
- 62.Farbman-Yogev I; Bohbot-Raviv Y; Ben-Shaul A A Statistical Thermodynamic Model for Cross-Bridge Mediated Condensation of Vesicles. J. Phys. Chem. A 1998, 102, 9586–9592. [Google Scholar]
- 63.Hill TL An Introduction to Statistical thermodynamics; Dover Publication Inc., New York, 1986; pp 124–130. [Google Scholar]
- 64.Anandakrishnan R; Aguilar B; Onufriev AV H++ 3.0: Automating pK Prediction and the Preparation of Biomolecular Structures for Atomistic Molecular Modeling and Simulations. Nucleic Acids Res. 2012, 40, W537–W541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Chaikin PM; Lubensky TC Principles of Condensed Matter Physics; Cambridge university press, 2000. [Google Scholar]
- 66.Wilczek-Vera G; Rodil E; Vera JH On the Activity of Ions and the Junction Potential: Revised Values for All Data. AIChE J. 2004, 50, 445–462. [Google Scholar]
- 67.Raspaud E; Chaperon I; Leforestier A; Livolant F Spermine-induced aggregation of DNA, nucleosome, and chromatin. Biophys. J 1999, 77, 1547–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Matsarskaia O; Braun MK; Roosen-Runge F; Wolf M; Zhang F; Roth R; Schreiber F Cation-Induced Hydration E_ects Cause Lower Critical Solution Temperature Behavior in Protein Solutions. J. Phys. Chem. B 2016, 120, 7731–7736. [DOI] [PubMed] [Google Scholar]
- 69.Rosenberg B; Deutsch J; Ungers G Growth and Purification of SV40 Virus for Biochemical Studies. J. Virol. Methods 1981, 3, 167–176. [DOI] [PubMed] [Google Scholar]
- 70.Porterfield JZ; Zlotnick A A Simple and General Method for Determining the Protein and Nucleic Acid Content of Viruses by UV Absorbance. Virology 2010, 407, 281–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Blanchet CE; Spilotros A; Schwemmer F; Graewert MA; Kikhney A; Jeffries CM; Franke D; Mark D; Zengerle R; Cipriani F; Svergun D Versatile Sample Environments and Automation for Biological Solution X-Ray Scattering Experiments at the P12 Beamline (PETRA III, DESY). J. Appl. Crystallogr 2015, 48, 431–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.David G; Pérez J Combined Sampler Robot and High-Performance Liquid Chromatography: A Fully Automated System for Biological Small-Angle X-Ray Scattering Experiments at the Synchrotron SOLEIL SWING Beamline. J. Appl. Crystallogr 2009, 42, 892–900. [Google Scholar]
- 73.Vaerenbergh PV; LÃl’onardon J; Sztucki M; Boesecke P; Gorini J; Claustre L; Sever F; Morse J; Narayanan T An Upgrade Beamline for Combined Wide, Small and Ultra Small-Angle X-Ray Scattering at the ESRF. AIP Conf. Proc 2016, 1741, 030034-1-4. [Google Scholar]
- 74.Round A; Felisaz F; Fodinger L; Gobbo A; Huet J; Villard C; Blanchet CE; Pernot P; McSweeney S; Roessle M BioSAXS Sample Changer: a Robotic Sample Changer for Rapid and Reliable High-Throughput X-ray Solution Scattering Experiments. Acta Crystallogr., Sect. D: Biol. Crystallogr 2015, 71, 67–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Guinier A; Fournet G Small Angle Scattering of X-rays; J. Wiley & Sons, New York, 1955; p 30. [Google Scholar]
- 76.Saper G; Kler S; Asor R; Oppenheim A; Raviv U; Harries D Effect of Capsid Confinement on the Chromatin Organization of the SV40 Minichromosome. Nucleic acids Res. 2012, gks1270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Thompson P; Cox D; Hastings J Rietveld Refinement of Debye–Scherrer synchrotron X-ray Data from Al2O3. J. Appl. Crystallogr 1987, 20, 79–83. [Google Scholar]
- 78.Székely P; Ginsburg A; Ben-Nun T; Raviv U Solution X-ray Scattering form Factors of Supramolecular Self-Assembled Structures. Langmuir 2010, 26, 13110–13129. [DOI] [PubMed] [Google Scholar]
- 79.Ben-Nun T; Ginsburg A; Székely P; Raviv U X+: a Comprehensive Computationally Accelerated Structure Analysis Tool for Solution X-ray Scattering from Supramolecular Self-Assemblies. J. Appl. Crystallogr 2010, 43, 1522–1531. [Google Scholar]
- 80.Ben-Nun T; Asor R; Ginsburg A; Raviv U Solution X-ray Scattering Form-Factors with Arbitrary Electron Density Profiles and Polydispersity Distributions. Isr. J. Chem 2015, [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.