Evaluating Flexible Modeling of Continuous Covariates in Inverse-Weighted Estimators

Abstract

Correct specification of the exposure model is essential for unbiased estimation in marginal structural models with inverse-probability-of-treatment weights. However, although flexible modeling is commonplace when estimating effects of continuous covariates in outcome models, its use is less frequent in estimation of inverse probability weights. Using simulations, we assess the accuracy of the treatment effect estimates and covariate balance obtained with different exposure model specifications when the true relationship between a continuous, possibly time-varying covariate L_t and the logit of the probability of exposure is nonlinear. Specifically, we compare 4 approaches to modeling the effect of L_t when estimating inverse probability weights: a linear function, the covariate-balancing propensity score, and 2 easy-to-implement flexible methods that relax the assumption of linearity: cubic regression splines and fractional polynomials. Using data from 2 empirical studies, we compare linear exposure models with flexible exposure models to estimate the effect of sustained virological response to hepatitis C virus treatment on the progression of liver fibrosis. Our simulation results demonstrate that ignoring important nonlinear relationships when fitting the exposure model may provide poorer covariate balance and induce substantial bias in the estimated exposure-outcome associations. Analysts should routinely consider flexible modeling of continuous covariates when estimating inverse-probability-of-treatment weights.

Marginal structural models permit estimation of exposure effects in the presence of time-varying confounders that are also mediators (1, 2), and they are also useful in point-source treatment settings when the outcome model is difficult to specify (3). Marginal structural models are commonly fitted using inverse-probability-of-treatment–weighted regression (4). The resulting estimators of exposure effects are unbiased, provided that assumptions of consistency, correct model specification, exchangeability, no measurement error, and positivity are all met (1, 5). Inverse probability weighting produces a “pseudopopulation” in which covariate distributions are balanced, that is, similar between exposure groups (1, 5).

For dichotomous exposures, inverse probability weights are typically estimated using logistic regression, often with untransformed continuous covariates, which implicitly assumes linear associations with the logit of the probability of exposure (6, 7). Yet important deviations from linearity often occur. For example, the likelihood of initiating drug therapy may increase steeply only upon exceeding a threshold for disease activity (8, 9).

Ignoring nonlinear covariate effects could induce substantial inaccuracies in estimating inverse probability weights, which may result in poor balance, residual confounding, and biased effect estimates (1). For these reasons, many authors have advocated wider use of flexible modeling of continuous covariates (10–14). However, most of the recently published analyses which employed marginal structural models did not use flexible modeling (see Web Appendix 1 and Web Table 1, available at https://academic.oup.com/aje), and while explorations of the consequences of model misspecification in this context exist (5, 15–18), few have systematically investigated nonlinear covariate-treatment relationships in simulations (16, 18). Pirracchio et al. (16) evaluated ensemble learning for propensity score estimation and concluded that it improved covariate balance and reduced bias when the exposure model was incorrectly specified, although the computational burden was high and improvements were modest. Imai and Ratkovic (18) proposed and assessed the performance of the covariate-balancing propensity score (CBPS) approach. However, neither study compared the proposed methodology with less computationally intensive flexible modeling techniques that may be easier to implement in widely available software, such as regression splines (19) and fractional polynomials (FPs) (12) (Web Figure 1).

Accordingly, we performed comprehensive simulations to systematically compare several strategies for modeling continuous covariates in inverse-probability–weighted estimators, under a variety of clinically plausible assumptions. To illustrate the practical benefits of flexible modeling of real-life clinical data, we also present results from analyses of 2 empirical studies.

METHODS

Modeling strategies

The motivation for flexible modeling of covariate-outcome associations is to avoid constraining a priori the functional form of this relationship to a particular parametric family of functions, such as conventionally used linear functions. Many flexible modeling techniques developed over the past 4 decades help to avoid such constraints, although head-to-head comparisons are limited (20–22). In our simulations and empirical studies, we considered 2 simple, popular flexible techniques: 1) unpenalized polynomial regression splines and FPs and 2) a newer alternative, the CBPS (18, 23).

Regression splines are piecewise polynomials, joined smoothly at predefined points termed “knots” (19). Increasing the number of knots, or the degree of the polynomial, increases flexibility (24). However, even relatively simple quadratic or cubic splines with 1–2 knots offer a rich variety of curvilinear shapes (19, 25). We therefore rely on unpenalized cubic regression B-splines with a single knot at the median value of the observed covariate distribution.

FPs model the effects of continuous covariates using flexible parametric models by selecting 1 or 2 simple functions within a prespecified set, each of which is assigned its own regression coefficient (12). For a single continuous covariate X, the choice involves 8 power transformations $X^p$, where p = [−2, −1, −0.5, 0, 0.5, 1, 2, 3], with $X^0={\log }_{10}X$ (12). The single best-fitting function from this set is denoted FP1, the first-order FP, and it can represent only monotonic relationships (26). Second-order FPs (FP2), which select the best pair of functions from the same set of 8 choices, offer greater flexibility and can capture nonmonotonic relationships (26). FP2 models involve 2 transformations (powers p and q) and are defined (12) as follows.

$$\mathrm{If}p\ne q,{\mathrm{\beta }}_0+{\mathrm{\beta }}_1{x}^p+{\mathrm{\beta }}_2{x}^q.$$

$$\mathrm{If}p=q,{\mathrm{\beta }}_0+{\mathrm{\beta }}_1{x}^p+{\mathrm{\beta }}_2{x}^q\times {\log }_{10}x.$$

The best-fitting of the 36 possible combinations of p and q (including 8 with p = q) is then selected as the final FP2 model (26). In our analyses, the choice between best-fitting FP1 estimators and FP2 estimators was based on likelihood ratio tests (12, 26).

The CBPS approach estimates inverse-probability-of-treatment weights in a data-adaptive fashion with the goal of minimizing covariate imbalance (18, 23). The method prespecifies balancing conditions for exposure model covariates at each time point, within a method-of-moments framework (18, 23). This approach requires the analyst to prespecify a functional relationship between the covariates and exposure and, thus, is not inherently “flexible.” Nevertheless, we consider CBPS a potentially useful alternative to flexible modeling, because in other contexts it has been shown to be robust to mild misspecification of the exposure model (23). In the simulations described below, we evaluate the ability of the CBPS to handle nonlinear covariate effects.

Overview of simulation studies

In simulations, we assessed bias in treatment effect estimators resulting from various approaches to handling continuous covariates in the model used to estimate inverse probability weights, in a range of scenarios (see below). In each scenario, we simulated 300 data sets, with sample sizes of 250 or 500. We chose 300 replications to improve computational feasibility after we determined that the results were comparable to using 1,000 simulated data sets (Web Appendix 2, Web Figure 2). We analyzed each simulated sample using 5 alternative exposure models, in which the effect of a continuous covariate was estimated using, respectively, a linear function, regression splines, FP models, and the CBPS, as well as the true data-generating function, which provided a benchmark for evaluating the other approaches. For the spline-based estimates, we specified 4 degrees of freedom (implying 1 interior knot), which is roughly equivalent to the degrees of freedom in FP2 models (12). We approximated 95% confidence intervals using the 2.5th and 97.5th percentiles of the distribution of the respective treatment effect estimates across the 1,000 bootstrap resamples (27).

Throughout all simulation scenarios presented below, we assess bias and variance in exposure effect estimates from the inverse-probability–weighted outcome model, which is the parameter of interest when fitting marginal structural models. We also calculated the standardized mean difference (SMD) for each covariate, to assess covariate balance across the 2 exposure groups (28). We conducted our simulations and analyses in R, version 3.3.1 (R Development Core Team, Vienna, Austria), and used the “splines,” “mfp,” and “CBPS” packages (29).

Single-interval simulation study design

In efforts to enhance clinical relevance and plausibility, we designed our first simulation study on the basis of an earlier analysis of the effect of hepatitis C virus (HCV) cure (exposure; determined by sustained virological response after completion of HCV therapy) on liver fibrosis (outcome; assessed by computing the aspartate aminotransferase:platelet ratio index (APRI)) in the Canadian HIV–Hepatitis C Co-infection Cohort Study (30). Using a plasmode-like simulation and a point-treatment setting (31, 32), we sampled vectors of the following covariates from study participants, measured at the initial visit after HCV treatment discontinuation: antiretroviral treatment status for human immunodeficiency virus (HIV), sex, log-transformed γ-glutamyl transferase (GGT) level, and age.

We simulated values of exposure status and outcome for each participant, conditional on these covariates. In 3 distinct data-generating scenarios, the true functional form of the relationship between log₁₀(GGT) and the logit of the probability of exposure was assumed to be linear, quadratic, and exponential, respectively. For example, assuming linearity, we generated a dichotomous exposure X from the binomial distribution with P(X = 1) defined as

$$\begin{array}{c}P\left(X=1\right)={\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1\left(\mathrm{Antiretroviral\; treatment\; status}\right)\hfill \\ +{\mathrm{\alpha }}_2\left({\log }_{10}\mathrm{GGT}\right)+{\mathrm{\alpha }}_3\left(\mathrm{Female\; sex}\right)+{\mathrm{\alpha }}_4\left(\mathrm{Age}\right).\hfill \end{array}$$

For the 2 other scenarios, we replaced the original log₁₀(GGT) values by their quadratic or exponential transformations. We provide additional details in Web Table 2.

In the main scenarios, we generated the continuous outcome Y as follows, where $\mathrm{\epsilon }$ represents normally distributed N[0, 1] errors:

$$Y={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\left(X\right)+{\mathrm{\beta }}_2\left(\mathrm{Sex}\right)+{\mathrm{\beta }}_3\left(\mathrm{Age}\right)+{\mathrm{\beta }}_4\left({\log }_{\mathrm{10}}\mathrm{GGT}\right)+\mathrm{\epsilon }.$$

Web Appendix 2 outlines the design and methods of additional, similar simulations that focus on time-to-event outcomes.

Two-interval simulation study design

In the second study, we generated longitudinal trajectories across 2 time intervals, composed of (L₁, X₁, L₂, X₂, Y₂), where L represents a continuous time-varying covariate, X denotes time-varying exposure status, and Y₂ is a continuous outcome, measured at the second interval. Subscripts denote the interval.

Web Table 3 provides further details on data generation. Briefly, we first generated continuous covariates L₁ and L₂ by sampling from uniform distributions, in which L₂ was conditional on both X₁ and L₁. We then simulated the interval-specific exposure status X₁ and X₂ from the Bernoulli distribution, conditional on L₁ and on both L₂ and X₁, respectively. Finally, we generated the outcome Y₂ from a multivariable linear regression model, conditional on L₁, X₁, L₂, and X₂.

Empirical study 1: the Canadian HIV–Hepatitis C Co-infection Cohort Study

To illustrate a real-life application of the methods used in simulations, we analyzed data on 460 participants in the Canadian HIV–Hepatitis C Co-infection Cohort Study (2004–2016), for whom 1 or more visits occurred after HCV therapy (30). Participants were at least 16 years of age and had both documented HIV infection and chronic HCV infection or prior laboratory evidence of HCV exposure (30). As in a previous analysis (33), we focused on the association between HCV therapy and progression of liver disease.

Our exposure of interest was sustained virological response to HCV treatment, defined as undetectable HCV RNA 12 weeks after therapy discontinuation (34). Our continuous outcome was the log-transformed APRI, a noninvasive measure of liver fibrosis (35). We note that log-transformation of the response in a linear regression model implies that covariate effects are estimated on a multiplicative scale. Consequently, in both empirical studies, results reported on the original scale of APRI refer to the median rather than mean value of the outcome (36), with reductions in median APRI computed as $1-{10}^{\mathrm{\beta }}$, where β is the regression coefficient.

Empirical study 2: the Multicenter AIDS Cohort Study

In the second empirical analysis, we considered data from the Multicenter AIDS Cohort Study (37), corresponding to the initial 3 follow-up visits (March 1986–1992), after azidothymidine (AZT) had become available. In an earlier analysis of these data, investigators did not apply different flexible regression models (38, 39). Here, we consider the relationship between AZT treatment status (exposure: currently treated or untreated) and the continuous outcome, defined as log₁₀ CD4-positive T-lymphocyte (CD4+) count, in cells/mm³, measured at the third follow-up visit. We excluded all participants who reported acquired immunodeficiency syndrome (AIDS)-defining illnesses at their first visit.

RESULTS

Throughout the simulation sections, we focused on 1) accuracy of the estimation of the effect of the exposure on the outcome, as measured by the bias and variance of the corresponding regression coefficients, obtained using alternative modeling strategies to estimate inverse-probability-of-treatment weights, and 2) covariate balance in the pseudosamples that resulted from these alternative exposure modeling strategies.

Single-interval simulation study results

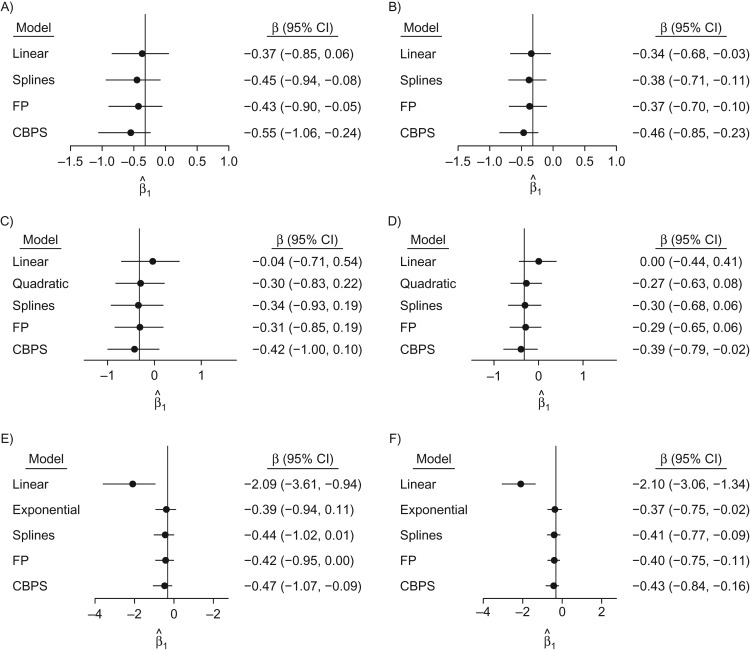
Figures 1 and 2 and Web Table 4 show results for the single-interval simulations, where the outcome model included exposure status, sex, and age. As expected, correctly specified inverse-probability-of-treatment weighting (IPTW) models yielded nearly unbiased estimates of the exposure effect. When the true covariate-exposure relationship was nonlinear, the linear IPTW models performed poorly, regardless of sample size. In the quadratic setting, the bias of the linear model was over an order of magnitude greater than that for each of the flexible models (Figure 1, Web Table 4); in the exponential scenario, the resulting bias and covariate imbalance for the model specifying a linear relationship also increased markedly.

Figure 1.

Effect estimates and their variability in single-interval simulations, as indicated by 95% bootstrap confidence intervals, for n = 250 (left column) and n = 500 (right column) when the true covariate-exposure relationship is linear (top row), quadratic (middle row), or exponential (bottom row). True values are denoted by the vertical line. CBPS, covariate-balancing propensity score; CI, confidence interval; FP, fractional polynomial.

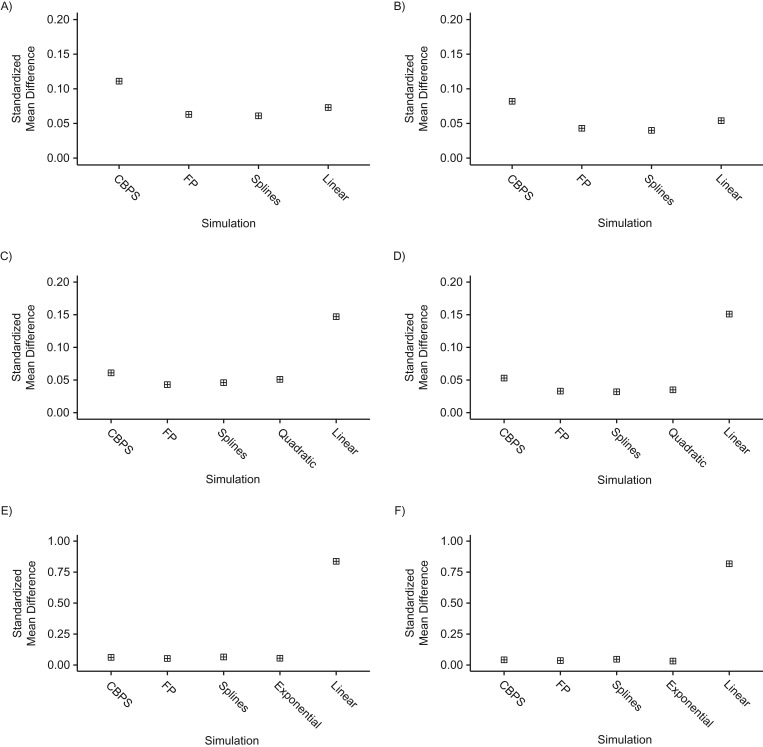
Figure 2.

Balance of covariates across treatment levels in single-interval simulations, as estimated by standardized mean differences, for n = 250 (left column) and n = 500 (right column) when the true covariate-exposure relationship is linear (top row), quadratic (middle row), or exponential (bottom row). CBPS, covariate-balancing propensity score; FP, fractional polynomial.

The spline- and FP-based exposure models yielded comparably small bias across all scenarios, with slightly more bias when the true relationship was linear or exponential and the sample contained 250 simulated observations (Web Table 4). In the linear scenario, the small additional bias for the spline and FP models probably reflects overfitting; however, these biases are much smaller than the bias of the linear model in truly nonlinear scenarios. Relative to the spline and FP specifications, CBPS estimates exhibited greater bias in each scenario (Figure 1, Web Table 4). In the linear setting, with n = 250, CBPS effect estimates were twice as biased on average as FPs or splines. Increasing sample size consistently reduced the bias of the CBPS estimates across scenarios; for n = 500, estimates were 30% less biased on average than for n = 250, and though still more biased than FPs or splines, they were considerably less biased than linear estimates when the true relationship was quadratic or exponential.

In the nonlinear settings, the spline and FP exposure models yielded similar root mean squared errors (RMSEs) for exposure status in the inverse-weighted outcome model. The resulting estimates were comparable to those from the marginal structural model fitted using weights from the correctly specified exposure model, with RMSEs nearly 2 times smaller than those for the linear models (Web Table 4). The RMSE for the CBPS estimates was higher relative to both flexible approaches by 30% in the linear scenarios and 8% higher in the nonlinear scenarios (Web Table 3).

The spline and FP estimators yielded similar coverage for the exposure effect estimate that approached the nominal 95% level (Web Table 4). Fitting linear terms for a continuous covariate in the exposure model reduced coverage, sometimes dramatically (to <15% when the true relationship was exponential).

The spline and FP exposure models slightly improved covariate balance even in the linear scenario, yielding smaller SMDs relative to the linear model (Figure 2, Web Table 4). We note, however, that improvements in covariate balance do not necessarily translate to reductions in bias or RMSE. FP and linear exposure models produced similar SMDs in both quadratic settings, yielding nearly equivalent balance on GGT. Spline models produced the best balance of all 4 methods, with SMDs only 11%–19% greater than those based on the true model (Figure 2). As anticipated, the linear model yielded poorer balance in this setting, with SMDs exceeding those in any of the alternative models, regardless of sample size. The CBPS provided slightly larger SMDs than either spline or FP estimators (Figure 2). In the exponential setting, SMDs were consistent across all exposure models except for the linear specification, whose performance was poor. The CBPS estimator produced balance comparable to that provided by the true model, while performance was slightly better for spline and FP models (Figure 2, Web Table 5).

The results of simulations with a time-to-event outcome were similar and confirmed that flexible modeling of continuous covariates improved covariate balance and avoided biased estimation of the exposure-outcome associations (data not shown).

Two-interval simulation study results

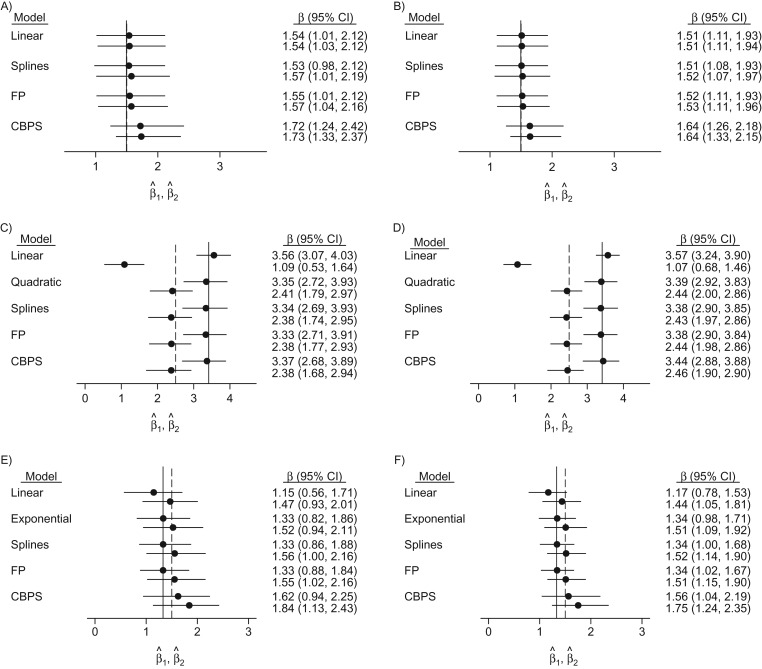
In the 2-interval simulation study, we performed analyses similar to those of the single-interval study, except that separate logistic models regressed 1) X₁ on L₁ and 2) X₂ on (X₁, L₂). We stabilized the inverse probability weights for the second interval.

As before, we observed considerably biased exposure effect estimates from conventional models that imposed linear effects of L₁ in the quadratic and exponential scenarios (Figure 3 and Web Table 5). RMSEs for first-interval estimates were comparable across linear, spline, and FP models in the linear scenario but slightly (about 30%) higher for the flexible approaches in the quadratic case. The RMSE for the CBPS estimates was consistently higher than that for spline or FP models, as in the single-interval study. In contrast, for the second interval in the quadratic setting, because of important bias in the linear model estimates, it yielded very high RMSEs, over 3 times larger than those for any other model (Web Table 5). The CBPS offered the worst bias-variance trade-off in the exponential setting, where the RMSE was nearly double that of other methods for both sample sizes (Web Table 5).

Figure 3.

Effect estimates and their variability in 2-interval simulations, as indicated by 95% bootstrap confidence intervals, for n = 250 (left column) and n = 500 (right column) when the true covariate-exposure relationship is linear (top row), quadratic (middle row), or exponential (bottom row). True values are denoted by the vertical lines. CBPS, covariate-balancing propensity score; CI, confidence interval; FP, fractional polynomial.

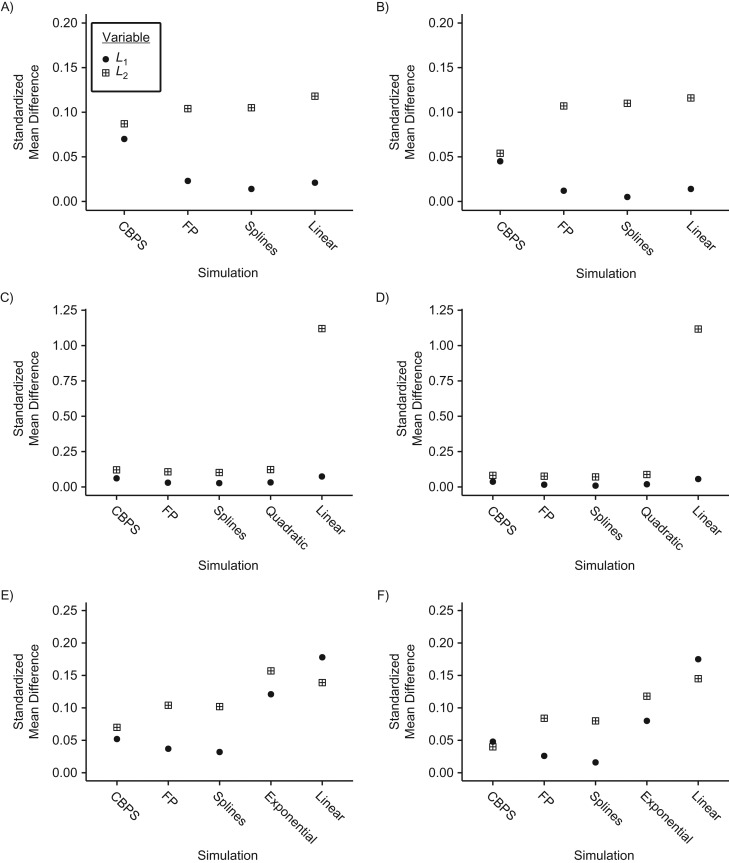
Spline and FP exposure models provided 87%–95% coverage of the 95% confidence intervals in all scenarios, with slightly better coverage in the first interval (Web Table 5). In the linear scenarios, the CBPS exposure model provided the poorest coverage, with only 76% coverage in the first interval and 67% coverage in the second interval for a sample with 250 observations. In the quadratic setting, spline and FP exposure models remained comparable, while the CBPS yielded 83%–88% coverage. In the exponential setting, flexible exposure models yielded near nominal coverage for X₁, whereas the CBPS provided lower 70%–87% coverage. Covariate balance remained comparable across all models in the linear scenarios, except for L₂ with n = 500, where CBPS presented the largest improvement (Figure 4 and Web Table 5). In both nonlinear scenarios, all nonlinear models markedly improved balance, relative to the conventional linear model, in both intervals.

Figure 4.

Balance of covariates across treatment levels in 2-interval simulations, as estimated by standardized mean differences, for n = 250 (left column) and n = 500 (right column) when the true covariate-exposure relationship is linear (top row), quadratic (middle row), or exponential (bottom row). CBPS, covariate-balancing propensity score; FP, fractional polynomial.

Empirical study 1 results

After weighting, covariate balance improved markedly regardless of the exposure model specification (Web Appendix 3, Web Figure 3). The linear IPTW model yielded SMDs of 0.05 and 0.10 for GGT and log₁₀(HIV RNA), respectively. The spline and FP models provided identical covariate balance on GGT and comparable balance on log₁₀(HIV RNA); both improved balance relative to the linear model (Table 1, Figure 2). In contrast, the CBPS specification resulted in slightly worse balance relative to the linear model.

Table 1.

Association Between Sustained Virological Response at 12 Weeks and Progression of Liver Disease as Measured by the Aspartate Aminotransferase:Platelet Ratio Index, Canadian HIV–Hepatitis C Co-infection Cohort Study, 2004–2016^a

Variable	Exposure Model Specification
	Linear		Splines		FP		CBPS
	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI
SVR12b status	−0.11	−0.20, −0.03	−0.11	−0.20, −0.03	−0.11	−0.19, −0.02	−0.13	−0.21, −0.04
Female sex	−0.09	−0.21, 0.05	−0.09	−0.22, 0.04	−0.09	−0.22, 0.04	−0.08	−0.21, 0.05
BMIc (per 10 units)	−0.01	−0.10, 0.07	−0.01	−0.11, 0.08	−0.01	−0.11, 0.08	−0.01	−0.11, 0.08
Age (per 10 years)	−0.01	−0.07, 0.04	−0.02	−0.08, 0.04	−0.02	−0.08, 0.04	−0.02	−0.08, 0.05
Injection drug use in preceding 6 months	−0.05	−0.17, 0.07	−0.05	−0.18, 0.07	−0.05	−0.17, 0.08	−0.04	−0.17, 0.09
Duration of HCV infection (per 10 years)	0.04	0.00, 0.08	0.04	−0.01, 0.08	0.04	−0.01, 0.08	0.04	−0.01, 0.08
HCV genotype of 2, 3, or 4 vs. HCV genotype 1	0.13	0.03, 0.25	0.14	0.03, 0.26	0.14	0.03, 0.26	0.13	0.03, 0.25

Abbreviations: BMI, body mass index; CBPS, covariate-balancing propensity score; CI, confidence interval; FP, fractional polynomial; HCV, hepatitis C virus; HIV, human immunodeficiency virus; SVR, sustained virological response.

^a 95% CIs were computed by means of the nonparametric bootstrap percentiles approach.

^b SVR 12 weeks after discontinuation of HCV therapy.

^c BMI was calculated as weight (kg)/height (m)².

The linear model estimated a 22% (95% confidence interval (CI): −0.20, −0.03) reduction in the outcome (median APRI following sustained virological response), similar to the 3 flexible models that estimated a 22%–26% decrease (Table 1). Overall, these results indicate meaningful improvements in liver health after successful HCV treatment and suggest that no substantial loss of accuracy (e.g., due to overfitting), except for a minor loss of precision, is incurred by applying a flexible approach when there is no evidence of nonlinearity in the covariate-treatment association.

Empirical study 2 results

We identified a nonlinear relationship between log₁₀(CD4+) and AZT. The FP algorithm selected p = 0 and q = 0 as providing the optimal fit in the first interval, corresponding to a logarithmic transformation of log₁₀(CD4+), with a P value of 0.02 for the test of linearity. In the second interval, p = 0.5 and q = 0.5 were selected; the best-fitting FP2 model suggested an inverse J-shaped relationship (data not shown) but was marginally nonsignificant (P = 0.14 relative to linear model), with a slightly improved Akaike’s Information Criterion value. However, we selected the best-fitting FP function regardless of the test of nonlinearity.

In the first interval (Web Figure 4), covariate balance was best for the spline-based exposure model (SMD = 0.03 for log₁₀(CD4+)) and second best for the linear model (SMD = 0.10). In the second interval, splines (SMD = 0.28) narrowly outperformed the linear and FP treatment models (SMDs were 0.32 and 0.30), while the CBPS offered by far the best balance (SMD = 0.03).

Regardless of the exposure model used, the inverse-probability-of-treatment–weighted outcome model estimated a 20%–40% decline in CD4+ cell count among persons initiating AZT therapy between the first and second study visits, relative to participants not treated with AZT during this time interval, and an increase in CD4+ cell count of 80%–200% associated with AZT treatment at the following visit (Table 2). The linear IPTW model yielded both the smallest reduction in CD4+ cell count (−0.10 log₁₀ cells/mm³, 95% CI: −0.89, 0.87) and the largest increase in CD4+ cell count between the 2 visits (0.47 log₁₀ cells/mm³, 95% CI: −0.12, 1.16). The 3 flexible exposure models yielded broadly comparable results, with the CBPS providing estimates slightly closer to the linear model but more precise at both visit 1 (−0.21 log₁₀ cells/mm³, 95% CI: −0.61, 0.20) and visit 2 (0.26 log₁₀ cells/mm³, 95% CI: −0.13, 0.65). Indeed, the CBPS approach yielded smaller standard errors than all other models (Table 2).

Table 2.

Association Between Treatment With Azidothymidine and CD4+ T-Lymphocyte Count (cells/mm³) Given 4 Exposure Model Specifications for log₁₀(CD4+), Multicenter AIDS Cohort Study, 1986–1992^a

Variable	Exposure Model Specification
	Linear		Splines		FP		CBPS
	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI	$\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}$	95% CI
Treated at visit 1	−0.10	−0.89, 0.87	−0.25	−0.99, 1.00	−0.23	−0.91, 0.40	−0.21	−0.61, 0.20
Treated at visit 2	0.47	−0.12, 1.16	0.26	−1.02, 1.03	0.24	−0.47, 1.02	0.26	−0.13, 0.65

Abbreviations: AIDS, acquired immunodeficiency syndrome; CBPS, covariate-balancing propensity score; CD4+, CD4-positive; CI, confidence interval; FP, fractional polynomial.

^a 95% CIs were computed by means of the nonparametric bootstrap percentiles approach.

Taken together, these results demonstrate the potential benefits of AZT treatment, while illustrating the possible variation between the estimates obtained using alternative approaches to model a potentially nonlinear relationship between time-varying covariate(s) and the treatment. Additional results for simulations given an accelerated failure time model are reported in Web Appendix 2, Web Tables 6 and 7.

DISCUSSION

We assessed the implications of different approaches to modeling continuous covariates in the exposure model for estimates of exposure effects in marginal structural models and for covariate balance after inverse probability weighting. Our simulation results indicated that failure to capture the correct functional form of the relationship between a continuous time-varying covariate and the logit of the probability of being treated/exposed may result in substantial bias, because of residual imbalance in the covariate distribution in the weighted pseudo-population.

These findings illustrate the benefits of flexible modeling of continuous covariates when fitting inverse-probability–weighted models. Our comparisons of RMSE suggest that increased flexibility is preferable to parsimony when fitting the exposure model, regardless of whether a nonlinear relationship exists.

In our simulations, flexible modeling improved the bias-variance trade-off over that of the linear model by yielding only minimal increases in the variance of effect estimates, relative to large reductions in bias if the true relationship diverged from linearity. Overall, the performance of the chosen flexible models remained comparable to that of the conventional linear model even when it was used to generate the data, but they yielded noticeable improvements in RMSE and covariate balance when the covariate-exposure relationship was nonlinear.

When applying the CBPS, we entered continuous covariates as linear terms and chose to evaluate the method’s performance when naively applied; such use is likely to result in model misspecification. This may partially explain the poorer balancing performance of the CBPS when compared with flexible approaches in the quadratic and exponential simulation settings. Consequently, in case of uncertainty regarding the true form of the underlying exposure-covariate relationship, we suggest fitting exposure models using splines and FPs, as these flexible techniques yield reasonably accurate estimates regardless of the true and unknown functional form. Finally, the important reduction in bias these 2 methods afford makes them attractive, especially given their limited computational costs in most settings. Several easily applied solutions to fit both FP and spline models are available in current statistical packages. However, as with other methods, users should carefully consider software defaults and their sensitivity to features in the data to be analyzed.

Our simulations were not exhaustive. We explored a range of plausible relationships between a confounder and an exposure, but other functions could have been considered. In our survey conducted to assess the frequency with which flexible modeling was used with inverse weighting, we found that recent applications of inverse weighting are predominantly used for continuous outcomes measured at a single time point or time-to-event outcomes (Web Appendix 1). The exposure model, from which inverse probability weights are obtained, is typically fitted by logistic regression. Our review of studies that used inverse weighting, published in 6 selected epidemiology or clinical journals in 2017, indicated that only 5 (31%) of these publications employed flexible modeling of continuous covariates, while in the remaining articles relationships with exposure were a priori constrained to be linear (Web Appendix 1). These findings, together with the tremendous computational burden of the simulations, led us to study only continuous and time-to-event outcomes. Because the focus of this investigation was on bias arising due to misspecification of the exposure model—a violation of the fundamental assumption of correct model specification required for unbiased estimation in inverse weighting—we would expect similar biases to result in the estimated exposure effect regardless of the chosen outcome type. Further, previous work has illustrated the use of polytomous logistic regression in estimating inverse-weighted models when exposures are categorized (40). Again, within this context, the consequences of ignoring nonlinearity are likely to be similar.

We focused on relatively well-known and easily implemented approaches to model-fitting. Other approaches to modeling of covariate-exposure relationships have been proposed, including ensemble methods (41); however, prior research suggests that estimation is highly computationally intensive without substantial reductions in bias or increases in precision (42). Further, because of concerns that ensemble methods may not be appropriate for modeling exposures in IPTW (16, 42), we chose not to pursue them here.

Discussions of potential consequences of ignoring nonlinearity in the exposure model are infrequent in the marginal structural model literature, with some notable exceptions (5, 16, 18). Using simulations, we have demonstrated the benefits of simple yet flexible approaches to addressing potentially nonlinear relationships that are widely applicable in analyses using marginal structural models.

Abbreviations

AIDS

acquired immunodeficiency syndrome

APRI

aspartate aminotransferase:platelet ratio index

AZT

azidothymidine

CBPS

covariate-balancing propensity score

CI

confidence interval

FP

fractional polynomial

GGT

γ-glutamyl transferase

HCV

hepatitis C virus

HIV

human immunodeficiency virus

IPTW

inverse-probability-of-treatment weighting

RMSE

root mean squared error

SMD

standardized mean difference