Abstract
This paper presents a deterministic model for Neisseria meningitidis, a bacterium that causes meningitis. The model was parameterized using data from the 2017 meningitis outbreak in Nigeria. Optimal control theory was applied to investigate the optimal strategy for curtailing the spread of the disease using control variables determined from sensitivity analysis. These control variables are personal-protection such as the use of facial masks, and vaccination. The results show that the two controls avert more infections at low costs. Furthermore, a reciprocal relationship exists between the use of facial masks and vaccine. That is, when the use of facial masks is high, the use of vaccine is low and vice versa.
Cost-effective analysis was applied to investigate the most cost-effective strategy from various combination of control strategies. The results show that strategy combining all the control variables is the most cost-effective strategy followed by the strategy involving both personal-protection, the vaccination-only strategy was the least cost-effective. Although vaccination strategy is not cost-effective in this study, it is as effective in curtailing the infection as the other two control strategies. The study suggests that governments of communities with limited resources should consider complementing the use of vaccine with the use of facial mask particularly in hard-to-reach places in their communities.
Keywords: Neisseria meningitidis, Sensitivity analysis, Optimal control, Cost-effective analysis
1. Introduction
Neisseria meningitidis is a gram-negative diplococcus bacterium that causes meningitis and other meningococcal diseases (Centers for Disease Contr, 2015; Rouphael & Stephens, 2012). The bacteria is transmitted person-to-person via droplets of respiratory or throat secretions from carriers (World Health Organization, 2017b). Healthy individuals who have had close and prolonged contact with an infected individual can be infected with the bacteria. For example, closed and prolonged contact such as kissing, sneezing, or coughing or living in close quarters (household crowding), sharing eating or drinking utensils can lead to infection (Centers for Disease Contr, 2015; World Health Organization, 2017b). The bacteria colonize the nasopharynx or pharyngeal of carriers (Centers for Disease Contr, 2015; Hitchcock, Robinson, & Neisseriae, 1993, p. 229; Rouphael & Stephens, 2012) and can sometimes overwhelm the body's defensive system, spreading into the bloodstream and reaching the brain (Centers for Disease Contr, 2015; World Health Organization, 2017b). It should be noted that meningococcemia infection state occurs when the bacteria cause a bloodstream infection. About 10% to 20 of individuals are estimated to be Neisseria meningitidis carriers, but this number may be higher during epidemics outbreaks (World Health Organization, 2017b). The incubation period of the diseases is about 3–4 days but may vary between 2 and 10 days (Centers for Disease Contr, 2015; World Health Organization, 2017b). The fatality rate is about 10%–15%, and the meningococcemia infections can reach up to 40% (Centers for Disease Contr, 2015).
The meningococcal disease is found worldwide; however, the “meningitis belt” of sub-Saharan Africa has the highest number of occurrences worldwide (Centers for Disease Contr, 2013). The “meningitis belt” stretches from Senegal to Ethiopia and include countries like Bénin, Burkina Faso, Burundi, Cameroon, Côte d’Ivoire Eritrea, Ethiopia, Gambia, Ghana, Guinea, Guinea Bissau, Kenya, Mali, Mauritania, Nigér, Nigeria, Uganda, Central African Republic, Democratic Republic of Congo, Rwanda, Sénégal, Sudan, South Sudan, Tanzania, Chad, and Togo (Centers for Disease Contr, 2013; World Health Organization, 2017b).
The highest incidence of meningitis occurs during the dry season from December to July when dry winds loaded with dust combine with the cold night and the occurrence of upper respiratory tract infection damage the nasopharyngeal mucosa. These combined events increase the risk of meningococcal disease (Centers for Disease Contr, 2012; Greenwood, Blakebrough, Wali, & Whittle, 1984; Sabatini et al., 2012; World Health Organization, 2017b). Also, N. meningitidis transmission could be facilitated by large population displacements and by pilgrimages and traditional markets at regional levels (Sabatini et al., 2012; World Health Organization, 2017b). All these factors put together may explain the large epidemics which occurs during the dry Harmattan season in the meningitis belt (Sabatini et al., 2012; World Health Organization, 2017b). Harmattan is a season in West African, which happens from November ending to mid-March (Encyclopdia Britannica and I, 2018; Minka & Ayo, 2014). The season is characterized by the dry and dusty northeasterly trade wind, which blows over West Africa from the Sahara Desert into the Gulf of Guinea (Encyclopdia Britannica and I, 2018).
There are 12 identified serogroups, 6 of which are known to cause epidemics, these are namely the A, B, C, W135, X and Y serogroups (Centers for Disease Contr, 2015; Rouphael & Stephens, 2012; World Health Organization, 2017b). In Nigeria, N. meningitidis strains A and C are the dominant subgroups. A major outbreak of strain A occurred in Nigeria in 2009 with over 55,000 cases which resulted in about 2500 deaths (World Health Organization, 2017d). And since 2013 Nigeria has been experiencing large outbreaks of meningitis C; in 2015, over 2500 cases of the disease were reported. The current 2017 outbreak has led to over 9902 cases with over 602 deaths (Nigeria Centre for Disease Control (NCDC), 2017b).
Neisseria meningitidis is treatable and preventable and vaccines are the cornerstone of prevention and control of the bacteria (Centers for Disease Contr, 2012). Capsular polysaccharide vaccines used to prevent N. meningitidis have been available and used since the 1970s (Centers for Disease Contr, 2012). These include a bivalent vaccine which prevents the serogroups A and C infections, a trivalent vaccine (against serogroups A, C, and Y) and a tetravalent vaccine (against serogroups A, C, Y, and W135). However, like with any vaccine, meningococcal vaccines are not 100% effective.
In this study, we develop a mathematical model with an imperfect vaccine. We use sensitivity analysis to detect the model parameters whose variability has the strongest impact on the diseases' reproduction number. From these parameters we select two (namely the use of facial masks and vaccination) and use them as time-dependent control variables. To the best of our knowledge, this study is the first work to uniquely identifies facial masks as means to control Neisseria meningitidis. The with the aid of optimal control theory, we investigate the impact of these two variables on diseases transmission, that is, we determine the associated optimal control pair. We also investigate the cost-effectiveness of these control variables using cost-effectiveness analysis.
2. Model formulation
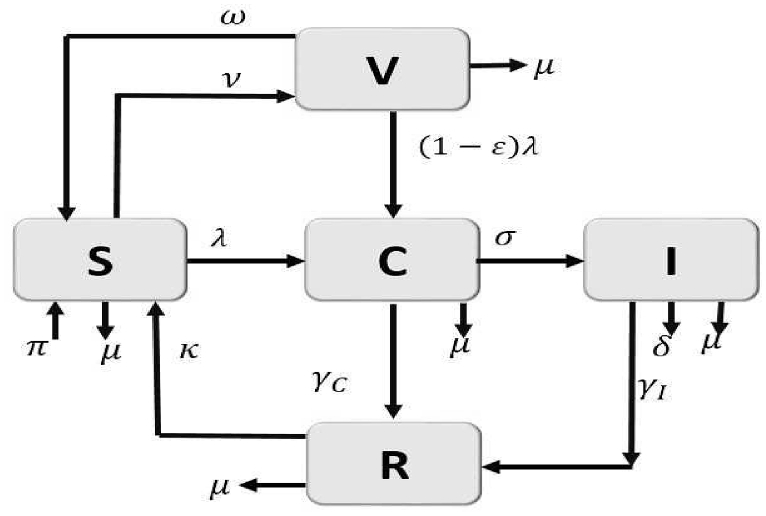
The model is derived as follows: the population is divided into susceptible (S), vaccinated (V), carrier (C), infectious (I), and Recovered (R) classes. Therefore, the total population at a given is time .
Individuals move from one class to the other as the disease progresses according to their disease status. The susceptible class (S) is populated by new recruits from three classes: 1) either via birth or immigration of susceptible individuals at the rate ; 2) from the recovered individuals with loss of immunity at the rate κ;; and 3) from those individuals whose vaccine had waned at the rate ω. We further assumed that there is no entry of the infectious into the population either by vertical transmission or immigration; thus, the new inflow into the population does not enter the infectious classes. All individuals, whatever their status, are subject to natural death, which occurs at the rate μ. The susceptible population is reduced by infection following effective contact with infected individuals at the rates , defined by
| (1) |
The parameter β is the effective transmission probability per contact and the parameters is a modification parameter that indicates the infectivity of individuals in the carrier class. The susceptible population is further reduced by constant vaccination. That is, susceptible individuals, move to the vaccinated class at the constant rate ν. Since the meningitis vaccine is highly effective but not 100% effective we assume that the vaccinated population is reduced by infection at the rates , where The parameter ε gives the measure of the vaccine efficacy. For example, indicates that the vaccine is 100% effective. The meningitis vaccine is highly effective but not 100% effective. Thus, we assume that the vaccinated population is reduced by infection at the rates , where The parameter ε gives the measure of the vaccine efficacy. For example, indicates that the vaccine is 100% effective.
When individuals in both susceptible and vaccinated classes are infected they move into the carrier class (). This class is reduced by disease progression to the infectious class () at the rate σ or by recovery at the rate to the recovered class () or by natural death at rate
Individuals in the infectious class increase due to disease activation in the carrier class, the population decreases by recovery at the rate and disease-induced death at the rate δ. The recovered class is populated by recoveries from both the carrier and infectious classes and reduced due to loss of immunity.
Hence, from the above descriptions and assumptions, the system of nonlinear differential equations describing the transmission dynamics of meningitis in the population is given as
| (2) |
The descriptions of the model parameters are given in Table 1 and the model flow-diagram is given in Fig. 1.
Table 1.
Description and values of the parameters of the meningitis models (2) and (3).
| Parameter | Definition | Baseline value | Reference |
|---|---|---|---|
| Recruitment rate | 3,253,607 year−1 | Estimated | |
| ν | Vaccination rate | 0.4868 day−1 | Assumed |
| ε | Vaccine efficacy | 85% | World Health Organization, (2017a) |
| ω | Vaccine waning rate | 1/5 day−1 | (Centers for Disease Contr, 2010; Hepkema, Pouwels, van der Ende, Westra, & Postma, 2013) |
| β | Transmission probability | 0.3345 day−1 | Fitted |
| η | Disease modification parameter | 1 | Assumed |
| Recovery rate for carrier | 0.1118 day−1 | Fitted | |
| Recovery rate for infected | 0.1128 day−1 | Fitted | |
| σ | Disease progression rate | 0.0438 day−1 | Fitted |
| κ | Immunity waning rate | 0.0032 day−1 | Fitted |
| μ | Natural death rate | 1/56 year−1 | World Health Organization, (2017c) |
| δ | Disease induced death rate | 0.1923 year−1 | (Irving, Blyuss, Colijn, & Trotter, 2012; Vereen, 2008) |
Fig. 1.
Flow diagram of the meningitis model (2).
2.1. The basic reproduction number
The basic reproduction number () of the meningitis model (2) is given below. The reproduction number, , is the number of secondary infections in an entirely susceptible population due to infections from one introduced infectious individual with meningitis. If , the disease will die out in the community and if it will persist. The theoretical study of the model basic properties are presented in Appendix A, and the calculations to derive the expression of are given in Appendix B.
The reproduction number is given as
In the absence of vaccine (i.e., ) reduces to given in equation (4) below. The quantity is the reproduction number in the worst-case scenario when intervention like vaccination is absent.
2.2. Backward bifurcation
Disease transmission models typically undergo a simple transcritical bifurcation at where there is an exchange of model's stability as the model equilibria move from the disease-free equilibrium (DFE) to an endemic equilibrium. Some models such as vaccination models, exhibit backward bifurcation where the stable DFE co-exists with a stable endemic equilibrium when the reproduction number is less than unity (see (Agusto, 2013; Agusto et al., 2013; Agusto & Gumel, 2010; Brauer, 2004; Dushoff, Huang, & Castillo-Chavez, 1998; Elbasha & Gumel, 2006; Garba, Gumel, & Bakar, 2008; Sharomi, Podder, Gumel, Elbasha, & Watmough, 2007; Sharomi, Podder, Gumel, & Song, 2008)). In a backward bifurcation setting, disease control is only feasible if is reduced further to values below another sub-threshold less than unity.
The important implication of this phenomenon on public health is that the classical requirement of having the reproduction number less than unity, although necessary, is no longer sufficient for disease control. This means that the effective disease control is dependent on the initial sizes of the sub-populations of the model. It is instructive, therefore, to explore whether or not the model (2) exhibits the phenomenon of backward bifurcation. In determining this possibility in the model (2), we use the Centre Manifold theory (Carr, 1981), as described in Theorem 4.1 by Castillo-Chavez and Song (Castillo-Chavez & Song, 2004).
The existence of the endemic equilibria of the meningitis model (2) is given in Appendix C, while the backward bifurcation analysis is given in Appendix D.
2.3. Parameter estimation
Here we parameterize meningitis model (2). We employ three strategies for obtaining parameter values: first we gather the parameter values from literature (see Table 1). Second, for those parameter not found in the literature we estimate their values when possible (see Table 1). For instance, the demographic parameter, μ, is estimated as per year, where 56 years is the average lifespan in Nigeria (World Health Organization, 2017c). The other demographic parameter, , is then estimated as follows. Since the total population of Nigeria as at 2015 was (World Health Organization, 2017c), we assumed that , which is the limiting total human population in the absence of the disease, is , so that per year.
For those parameters we could not obtain their values by either of the above processes we fitted them based on the 2017 Nigerian meningitis outbreak data obtained from the Nigeria Centre for Disease Control (NCDC) for weeks 5–27 (Nigeria Centre for Diseas, 2017). However, it should be noted that in the data set no public health interventions such as vaccination were used during weeks 5–27. Thus, to proceed with the parametrization, we develop in the subsection below the basic meningitis model (3) to reflect these conditions. Before we introduce the model, we describe the data set to be used.
2.3.1. The 2017 meningitis outbreak data
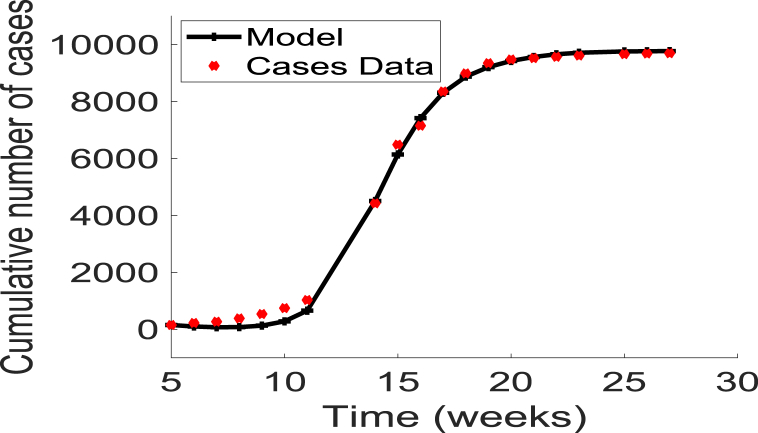
The data were obtained from the Nigeria Centre for Disease Control (NCDC) (Nigeria Centre for Diseas, 2017). The NCDC compiles weekly meningitis epidemiological report data from hospitals in affected States throughout the country. The data include the cumulative number of cases and deaths. Fig. 2 displays the cumulative number of cases from weeks 5 through 27. It should be noted that no public health interventions such as vaccination were used during this period of time.
Fig. 2.
Data fitting of the cumulative new cases and disease-induced mortality using the basic model (3), for the 2017 meningitis outbreaks in Nigeria (extracted from the Nigerian Centre for Disease Control (NCDC) website (Nigeria Centre for Diseas, 2017)). The parameters fitted are given as .
2.3.2. Basic meningitis model
To quantify the expected burden of the disease in the country, we fitted the 2017 meningitis data to a meningitis model of a worst-case scenario where public health interventions such as vaccination or facial masks are not implemented in the community. In the absence of such interventions, the model (2) reduces to the following basic model:
| (3) |
The meningitis pre-intervention model (3) is bounded and positively-invariant in the biologically-feasible region
with,
The reproduction number for model (3) is given as:
| (4) |
The method to derive this expression is similar to the one used to compute (see Appendix B) and the calculations are given in Appendix E. The global stability of the meningitis model (3) DFE is investigated in Appendix E and the existence of the endemic equilibrium is given in Appendix F.
To complete the parametrization of the meningitis model (2), we fit the model (3) to the 2017 Nigerian meningitis outbreak data obtained from NCDC for weeks 5–27 (Nigeria Centre for Diseas, 2017) using the classic least-squares method. Furthermore, The following values were taken for the initial conditions: the initial total population was taken as the population at the year 2015, i.e., the initially infected individuals as , which is the same as the initial number of infected in the data. We assumed and , so the initial susceptible are .
The resulting fitting is shown in Fig. 2. The resulting fitted parameter values are . Using these parameter estimates and the expression for the basic reproduction number in equation (4), we obtained the value of for the 2017 meningitis outbreak in Nigeria as .
2.4. Sensitivity analysis
The outputs of deterministic models are governed by the model input parameters, which may exhibit some uncertainty in their determination or selection. We employed a global sensitivity analysis to assess the impact of uncertainty and the sensitivity of the outcomes of the numerical simulations to variations in each parameter of the model (2) using Latin Hypercube Sampling (LHS) and partial rank correlation coefficients (PRCC). LHS is a stratified sampling without replacement technique which allows for an efficient analysis of parameter variations across simultaneous uncertainty ranges in each parameter (Blower & Dowlatabadi, 1994; Marino, Hogue, Ray, & Kirschner, 2008; McKay, Beckman, & Conover, 2000; Sanchez & Blower, 1997). PRCC measures the strength of the relationship between the model outcome and the parameters, stating the degree of the effect that each parameter has on the outcome (Blower & Dowlatabadi, 1994; Marino et al., 2008; McKay et al., 2000; Sanchez & Blower, 1997). Thus, sensitivity analysis determines the parameters with the most significant impact on the outcome of the numerical simulations of the model (Blower & Dowlatabadi, 1994; Marino et al., 2008; McLeod, Brewster, Gumel, & Slonowsky, 2006). To generate the LHS matrices, we assume that all the model parameters are uniformly distributed. Then a total of 1000 simulations of the models per LHS run were carried out. The initial conditions used are stated in Section 1.3, the baseline values are given in Table 1, and the ranges were chosen as 20% from the baseline values (in either direction). The response functions used are the basic reproduction numbers and , for model (2) and (3), respectively. The range for ε is taken as 85%–100% (World Health Organization, 2017a).
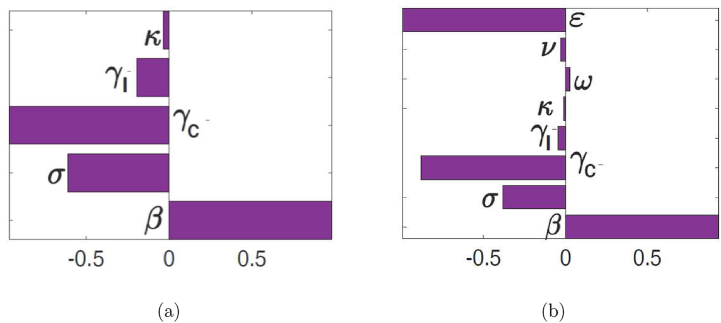
To identify the parameters with the most significant impact on the reproduction numbers ( and ), the model outcomes, we used Latin Hypercube Sampling (LHS) and partial rank correlation coefficients (PRCC) methods. From Fig. 3, it follows that the parameters that have the most influence on the reproduction numbers are the transmission probability per contact (β), the recovery rate of the carrier population (), the vaccine efficacy rate (ε), and the disease progression rate (σ). Identification of these critical parameters is essential to the formulation of effective control strategies for combating the spread of disease. In particular, the results of this sensitivity analysis suggest that a strategy that reduces the transmission probability per contact (i.e., reduces β), will adequately mitigate the spread of meningitis in the community. Furthermore, a strategy that increases the vaccine efficacy (increase ε) and increases the recovery rates (increase ) will be useful in curtailing the spread of meningitis in the community.
Fig. 3.
PRCC values for the meningitis models (3) and (2), using as response functions: (a) The reproduction number ; and (b) The reproduction number . Parameter values (ranges) used are as given in Table 1.
2.5. Quantifying the expected disease burden
To quantify the expected burden of the disease in the country (under the worst-case and vaccination scenarios), the distribution profile of and is generated, using the parameter values in Table 1 and the parameters in the parameter space generated from the sensitivity analysis.
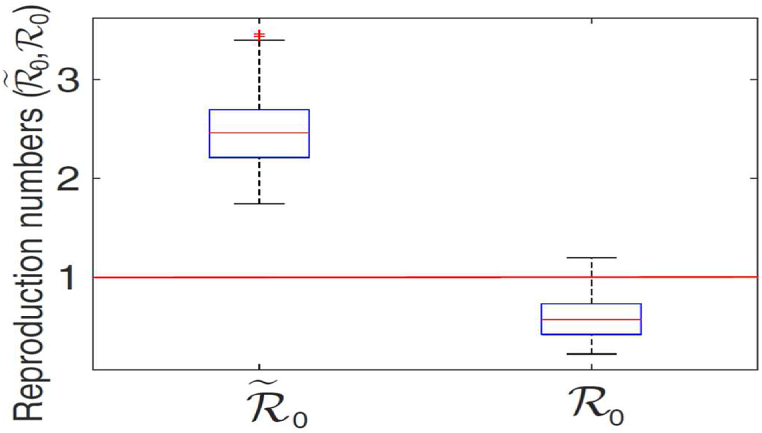
The results obtained, depicted in Fig. 4, show the distribution of the reproduction number in the range (with a mean , suggesting the potential for a larger meningitis outbreaks, where one infected case infects, on average, about 2.4754 others). However, when vaccination program is implemented, the distribution of , decreases to , with a mean of (indicating the possibility of eliminating the disease with the use of vaccination). It is evident from Fig. 4 that the disease burden associated with the worst-case scenario is three times more than the vaccination case. Furthermore, it is worth noting that for the worst-case scenario, the central 50% of the generated values are concentrated in the interval , with the median of close to the mean value. For the vaccination case, the central 50% of the generated values are concentrated in the interval , with the median around . These simulations emphasize the importance of vaccination in curtailing meningitis outbreak in Nigeria.
Fig. 4.
The box plot of the reproduction numbers ( and ) for the model (2) and (3). Parameter values (baseline) and ranges used are as given in Table 1.
Hence, we obtained in this study, that the value of for the 2017 meningitis outbreak in Nigeria is (see Section 1.3) and the distribution of the reproduction number is in the range (with a mean ) for the estimated worst-case scenario. Using the parameters in Table 1 with vaccination as a public health intervention, and the formula for in (1.1), we estimated the reproduction number as , which is within the estimated interval .
In the next section, we apply optimal control theory using results from the sensitivity analysis to determine the optimal vaccination control strategy that will effectively curtail the spread of meningitis in the community.
2.6. The optimal control problems
The result of the sensitivity analysis suggests that a control strategy capable of reducing the transmission probability per contact (i.e., reduces β) will adequately reduce the spread of meningitis in the community. Furthermore, a strategy that increases the vaccine efficacy (increase ε) and the recovery rates (increase and ) will be effective in curtailing the spread of meningitis in the community.
Among the parameters identified above, the transmission probability β is the one that can be easily manipulated. For example, it can be reduced by decreasing the contact between susceptible individuals and infected using personal protection such as wearing of facial mask. Thus, we introduce into the transmission model (2) a time-dependent control variable (representing the use of facial mask) that impacts the transmission probability Additionally, we assume that everyone in the community wears facial masks regardless of their vaccine status, which affects the transmission probability indirectly. This assumption is akin to the use of bed-nets in some malaria disease models (Agusto et al., 2013; Blayneh, Gumel, Lenhart, & Clayton, 2010; Okosun, Rachid, & Marcus, 2013).
However, ensuring adequate compliance might be challenging since these masks might not be too comfortable to wear particularly for long hours due to the “heat inside a facepiece” (Canini et al., 2010; Skaria & Smaldone, 2014). Nonetheless, these masks can be worn for as long as 8 h (Centers for Disease Contr, 1997), just as long as sleeping underneath a bednet in a typical night. On the other hand, there are comfortable masks that can be worn with ease and comfort.
We also consider as a time-dependent control variable the vaccination rate () which was previously taken as a constant parameter (ν). Although this parameter does not significantly impact the reproduction number , we nevertheless consider this parameter as time-dependent variable since the vaccine efficacy (ε) have a significant impact on the . The incorporation of the time-dependent control variable and into the model (2) yields:
| (5) |
where , and .Our goal is to minimize the cost function defined as
| (6) |
subject to the differential equation (5), where is the final time. This performance specification involves minimizing the numbers of carriers and infectious individuals, along with the cost of applying the controls (). In this paper, the controls , and in the objective functional are quadratic since the costs of these interventions are nonlinear. This assumption is based on previous works suggesting that there are no linear relationships between the effects of interventions and the cost of the intervention of the infective populations. Additionally, such quadratic costs have been frequently used (Joshi, 2002; Jung, Lenhart, & Feng, 2002; Kern, Lenhart, Miller, & Yong, 2007; Kirschner, Lenhart, & Serbin, 1997; Lenhart & Workman, 2007; Yan & Zou, 2008). The coefficients, , are balancing cost factors or weights on the costs.We seek to find the optimal controls , such that
with the control set defined as,
where are the lower and upper bounds of controls , and . The derivation of these bounds are discussed in Section 2.1.The controls () are a bounded Lebesgue integrable functions (Jung et al., 2002; Yan & Zou, 2008). The characterization of the controls are given in Appendix G and the study shows that the optimal control pair minimizing is given as
| (7) |
2.7. Setting bounds on the controls , and
The time dependent control represents personal protection. This control lies between . Observe that if , then the use of personal protection such as facial masks is ineffective while if such personal protection measures are 100% effective. Thus, we set the lower bound of the control to and the upper bound to .
The control represents vaccination rate. Vaccination rates for many diseases ranges from 0 to 100%. Zero is an indication of lack of vaccination, and 100% implies total vaccination. Although 100% total vaccination is hard to attain, there are instances when this could be possible. For instance, this could occur if available vaccine dosage is more than the targeted population (Lopalco & Carrillo Santisteve, 2014). Unfortunately, in some communities in sub-Saharan Africa, it is hard to attain coverage due to factors like economic reasons and displacement from wars. However, coverage has been achieved for most childhood diseases (Tsega et al., 2016). Hence, we assumed that control is bounded above at one (i.e., ) and below at zero (i.e., ); thus lies between zero and one, that is, where 1 indicates vaccination rate.
Next, we discuss the numerical solutions obtained from the corresponding optimal control problem consisting of (5) together with (6); the interpretations from various strategies considered and their corresponding implications for diseases control.
3. Numerical simulations
The computations of the optimal controls and state values were performed using a Runge-Kutta method of the fourth order. The algorithm is summarized as follows: first, an initial estimate for the control pair is made. Then the state variables are solved forward in time using the dynamics (5). The results obtained for the state variables are plugged into the adjoint equations (G-2). These adjoint equations with given final conditions (G-4) are then solved backward in time, employing the backward fourth-order Runge-Kutta method. Both the state and adjoint values are then used to update the control (7), and the process is repeated until the current state, adjoint, and controls values converge sufficiently, that is, convergence is achieved within a pre-set tolerance value (Lenhart & Workman, 2007).
To illustrate the optimal control strategies, we mimic a small village in one of the affect States in Nigeria. In particular, we consider the population of Zamfara State one of the worse hit states (Nigeria Centre for Diseas, 2017). The estimated 2011 total population of the state is (Wikipedia, 2018). We mimic a small village in this state by taking the statewide population and divide it by 1000. That is, the population of this small village is about . To set the initial conditions we split into the classes as follows. The initial infected population is , which is the value in the data set taken from NCDC. We assume that initial population of vaccinated individuals is . The initial population of carriers is , and the initial recovered population is . Hence, the initial susceptible population is calculated as . For the weight factors we choose . It should be pointed out that the values of the weights used in the simulations are theoretical as they were chosen only to illustrate the control strategies proposed in this paper.
On vaccine efficiency, the World Health Organization indicate that one dose of the vaccine has a short life efficacy ranging from 85% to 100% in older children and adults (World Health Organization, 2017a). Thus, we set the vaccine efficacy to be . Additionally, we set the waning rate to be five years post-vaccination because this is the value reported for young adolescents (Centers for Disease Contr, 2010; Hepkema et al., 2013). We assume a vaccination rate because this part of the country is experiencing violent attacks by arm bandits and Boko Haram the Islamist terrorist group; as a result, the vaccination rate may be within this range as the local folks and health officials fear for their lives (News24, 2017; Sahara Reporters, 2019). The reproduction number in the absence of intervention is , this was calculated in Section 1.4 using the estimated and fitted parameter values in Table 1. This value indicates the epidemic nature of the disease in the population.
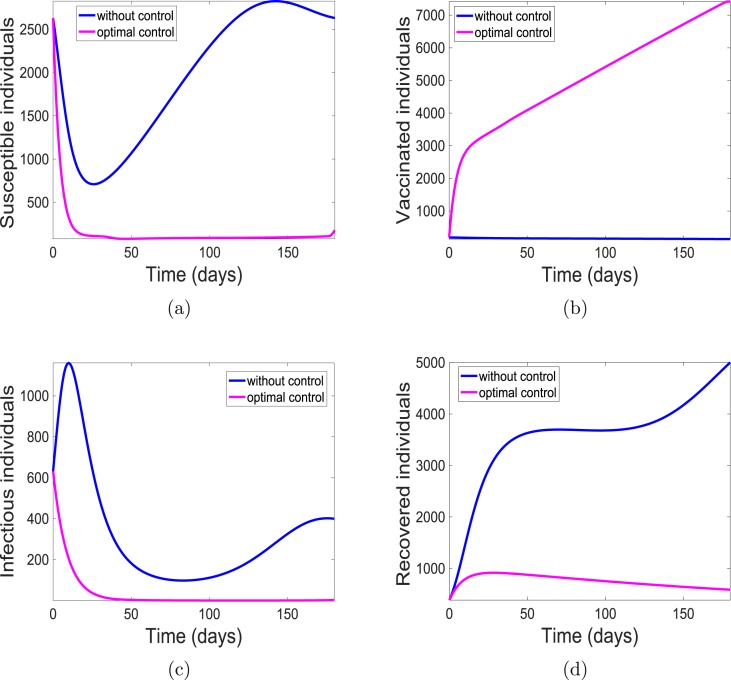
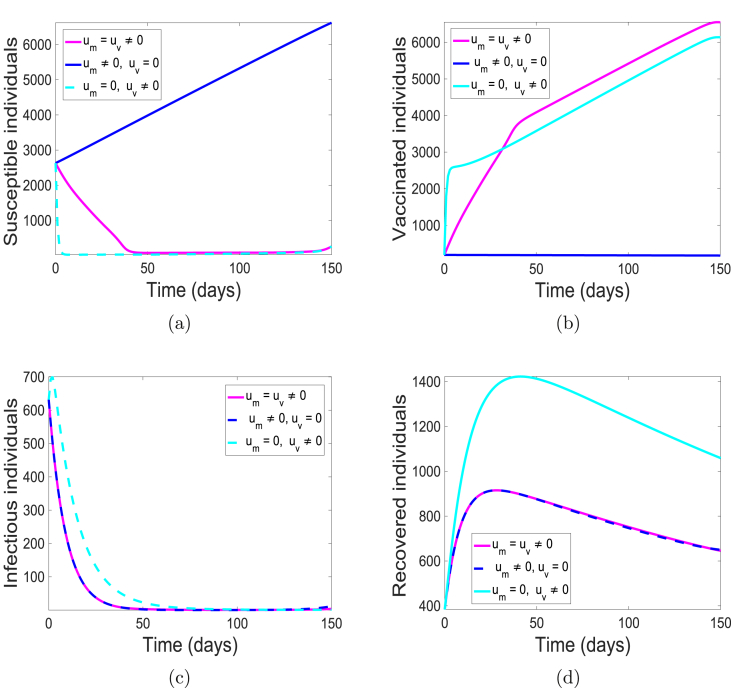
The simulations of the state variables of the meningitis model (5), with and without implementing the optimal control is given in Fig. 5. We have set the simulation period at 180 days to be consistent with the range of days in the data set we have used. Although, simulation period is 15 days more than the number of days from the data; the cumulative number of cases were obtained from the simulated weeks 5 through 27. With optimal control, most of the susceptible populace are either protected or vaccinated from the bacteria (see Fig. 5(a) and (b)) thereby leading to fewer individuals at the risk of infection (see Fig. 5(c)) and eventually resulting in fewer individuals recovering from the infection as shown in Fig. 5(d). This is not the case in the absence of the control strategy. There are more infectious (carrier and infected) individuals present due to the fact that more susceptible are unprotected, that is, they lack either the use of facial mask or vaccination. Consequently, there are more recovered individuals.
Fig. 5.
Simulation results of model (5) with controls. (a) Susceptible individuals; (b) Vaccinated individuals; (c) Infectious individuals (Carrier and Infected); and (d) Recovered individuals.
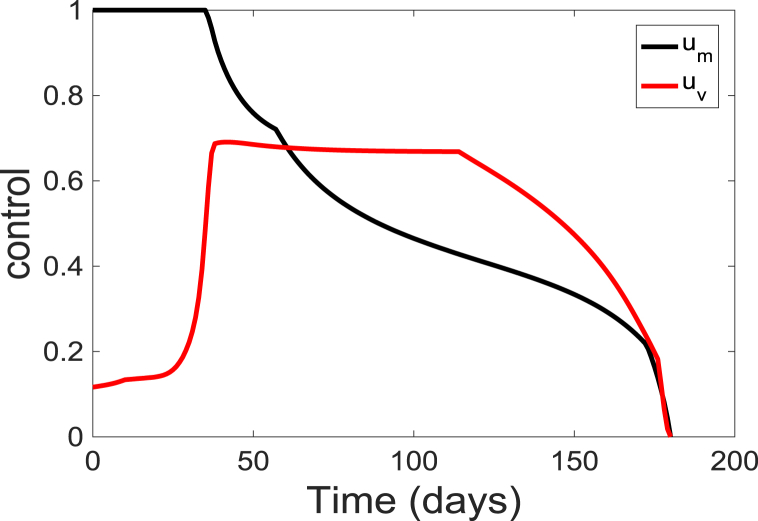
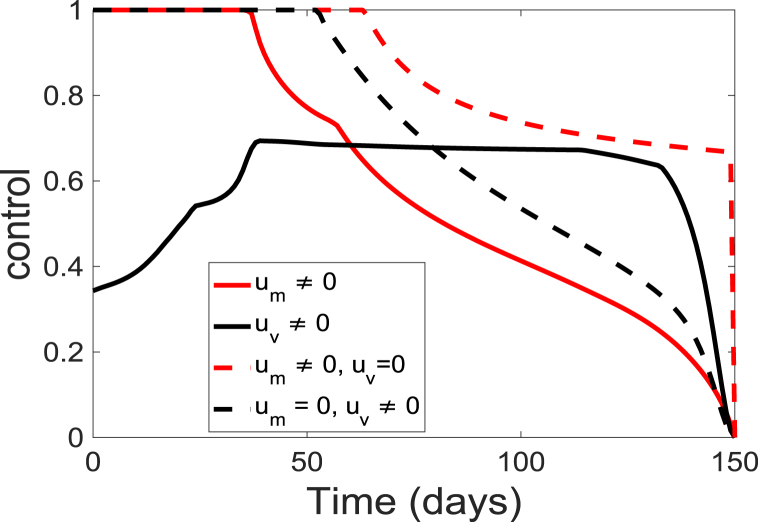
The corresponding simulated time-dependent controls ( and ) are depicted in Fig. 6. The time-dependent controls is at the upper bound, , for about 35 days before decreasing to the lower bound at the end of the simulation period; while the control starts at a lower rate of 0.12 and slowly increase to a maximum of about 0.67 at day 36 and gradually decreasing over time. These results suggest that to prevent an outbreak, individuals in the community should continually wear these facial or surgical masks at the beginning of the season but they should gradually get vaccinated. The result further suggests that vaccination of the populace should be maintained at a relatively low level of 0.67 for about 80 days of the simulation period. Additionally, the results indicate that to maintain the population protected from the diseases, both the vaccination and the personal protection need to be kept at a relatively high level.
Fig. 6.
Simulation results of the control profile of model (5).
In summary, we have introduced into the model two time-dependent control variables to represent the changes in time of personal protection like facial masks and vaccination. We found that the total number infectious (infected and carrier) individuals can be reduced in the community by the application of personal protection time-dependent controls.
3.1. Varying cost weight associated with controls and
In this section, we investigate the effect of varying and . These coefficients are the balancing cost factors or weights on the costs of implementing the controls and . Changes in them give a distinct cost of implementing the control strategies.
3.2. Varying the weight associated with control
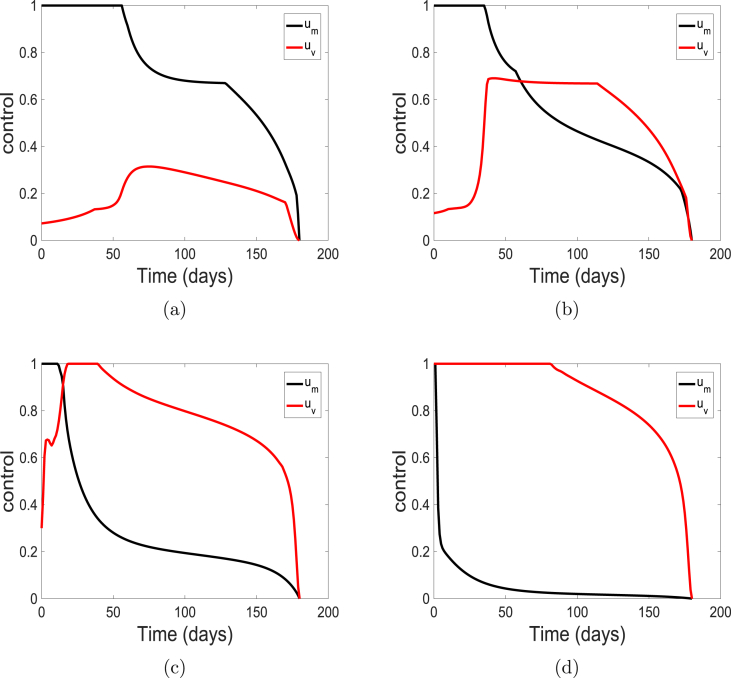
First, we vary the weight on the control representing the use of personal protection such as facial or surgical masks. We use the weights , , , and , the weight on control is kept at the baseline value of one (i.e., ). These costs correspond to the cases with very cheap, cheap, expensive and very expensive facial masks. The solution profiles for the state variables of the model (5) are similar to the profiles depicted in Fig. 5 and are therefore not shown here. The solution profiles are depicted in Fig. 7.
Fig. 7.
Simulation results of the control profile of model ((5)) using cost weights (a) ; (b) ; (c) ; and (d) .
Fig. 7 show that as the weight increases from low to high (i.e., from cheap to very expensive cost), control decreases from the upper bound to levels very close to the lower bound. Also, vaccine control increases to the upper bound when the weight are very high (i.e., very expensive cost). This reciprocal relationship between the weight and control help to keep the community protected and the infection low as observed in Fig. 5.
3.3. Varying the weight associated with control
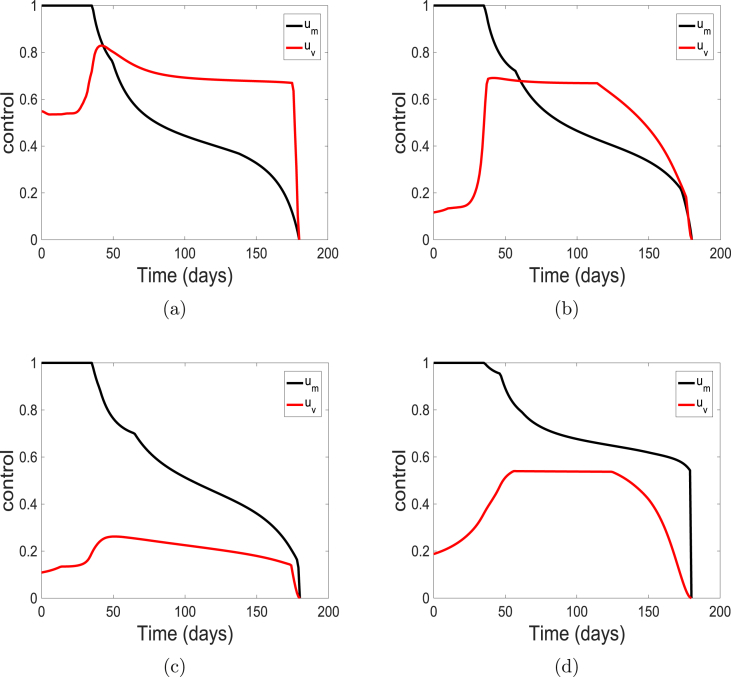
Next, we vary the weight on control and maintain the weight on control at the baseline value of one (i.e., ). We use the weights , , , and . These costs correspond to very cheap, cheap, expensive and very expensive vaccine, respectively. The profile of the control solutions are depicted in Fig. 8. The solution of the state variables are similar to those observed in Fig. 5 and are also not show here.
Fig. 8.
Simulation results of the control profile of model (5) using cost weights (a) ; (b) ; (c) ; and (d) .
At low values (i.e., ) which corresponds to a very low cost of applying the vaccination, the control is usually at the upper bound and above the control on facial mask. However, as increases (indicating more expensive vaccination process), the level of the control falls below the control .
This reciprocal relation between the weight and control is not as strong or obvious as the reciprocal relationship observed for and control (see Fig. 7). Note, this relationship helps to keep the community protected and the infection low as observed in Fig. 5.
4. Cost-effectiveness analysis
Controlling and eradicating diseases in a community can be both labor intensive and expensive. Hence, to determine the most cost-effective strategy to use, it is imperative to carry out a cost-effectiveness analysis. In this section, we apply cost-effectiveness analysis to investigate the cost-effectiveness associated with the use of vaccination and personal protection control strategies, and the associated benefits gained from implementing these controls (Agusto, 2013; Agusto & ELmojtaba, 2017). To this end, we consider the following combination of time-dependent controls making up three control strategies A-C:
1. Strategy A: combination of and
2. Strategy B: control -only while setting ; and
3. Strategy C: control -only while setting .
along with the baseline cost weights . The cost-effective analysis will be implemented using three approaches; namely, the infection averted ratio (IAR), the average cost-effectiveness ratio (ACER) and the incremental cost-effectiveness ratio (ICER) (Agusto, 2013; Agusto & ELmojtaba, 2017).
4.1. Infection averted ratio
The infection averted ratio (IAR) is stated as:
| (8) |
The number of infection averted is the difference between the total infectious individuals over the simulation period in the absences of control and the total infectious individuals with control. The strategy with the highest ratio is the most cost-effective.
4.2. Average cost-effectiveness ratio (ACER)
The average cost-effectiveness ratio (ACER) is calculated against the no intervention scenarios. The ACER is calculated as
| (9) |
The total cost produced by the intervention is estimated using the objective function given in (6).
4.3. Incremental cost-effectiveness ratio
The incremental cost-effectiveness ratio (ICER) is the additional cost per additional health outcome. We assume that the costs of the various control interventions are directly proportional to the number of controls deployed. To compare two or more competing intervention strategies incrementally, one intervention is compared with the next-less-effective alternative (Agusto, 2013; Agusto & ELmojtaba, 2017). Thus, the ICER is calculated as
| (10) |
The ICER numerator includes (where applicable) the differences in the costs of disease averted or cases prevented, the costs of intervention(s), and the costs of averting productivity losses among others. The ICER denominator, on the other hand, is the differences in health outcomes which may include the total number of infections averted or the number of susceptibility cases that are prevented from becoming carriers or infected.
4.4. Cost-effectiveness analysis: varying weights
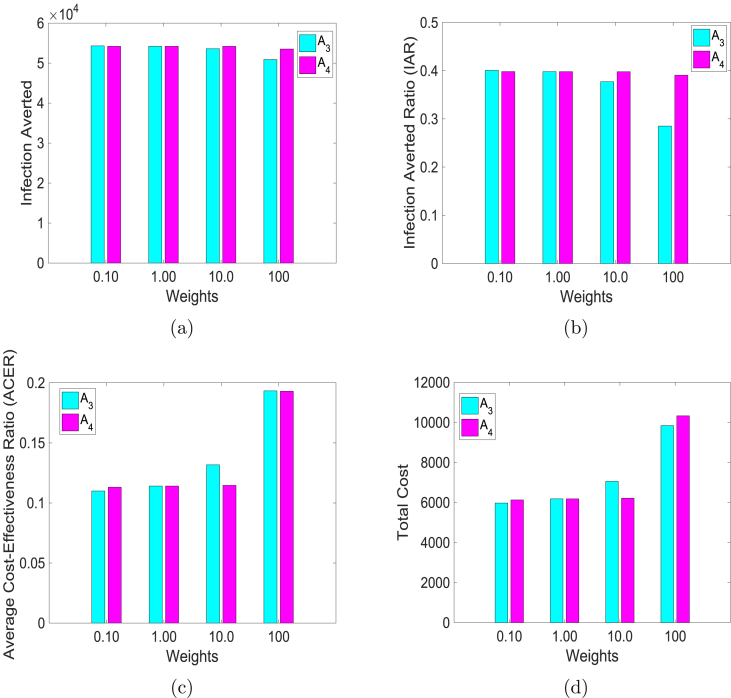
Next, we compare the impact of varying the weights on the infection averted ratio (IAR), average cost-effectiveness ratio (ACER), infection averted, and total cost. We use the control weights , , , and keeping , which is the baseline value. Similarly, we use , , , and at the baseline value of . The results of simulations are in Fig. 9, where the bar graphs of the two weights and for the different cost-effectiveness metric are plotted together.
Fig. 9.
Simulation results of model (5) using control weights , , , and when , the baseline value (the turquoise colored bars). Similarly, using , , , and at the baseline value of (the magenta colored bars). (a) Infection averted; (b) Infection averted ratio (IAR); (c) Average cost-effective ratio (ACER); and (d) Total cost.
When the weights are low, the two controls avert more infections (see Fig. 9(a), the blue bar in the first column of Fig. 9(a) corresponds to , while the magenta bar is ), but with vaccine averting slightly more infections than facial masks. This is clearly shown in Fig. 9(b), where the bar graph of the ratio of the infection averted is plotted for the different weights. Furthermore, from Fig. 9(a) and (b), we observed that higher weights led to fewer infections being averted.
The results depicted in Fig. 9(c) and (d) are expected, lower weights are more cost-effective than higher weights; surprisingly, vaccine led to lower cost at higher weights. This is because vaccination offers better protection with fewer infected at the end of the simulation period. Another factor that may explain such a result is our assumption that everyone in the community uses facial masks regardless of their vaccine status.
4.5. Cost-effectiveness analysis: control strategies A-C
The results of the optimal control simulations of problems (5), and (6) using Strategies A-C are depicted in Fig. 10. The three control strategies led to a situation in which most of the susceptible population is either protected or vaccinated from the bacteria (see Fig. 10(a) and (b)). Strategy A produced the most vaccinated; this is because the use of facial mask offers some level of protection to some vaccinated individuals in the population who would have been infected since the vaccine is not 100% effective.
Fig. 10.
Simulation results of model (5) with and without. (a) Susceptible individuals; (b) Vaccinated individuals; (c) Infectious individuals (Carrier and Infected); and (d) Recovered individuals.
Strategy A and B led to fewer infected and recovered while Strategy C resulted in more infected (infectious and carriers) and recovered (see Fig. 10(c) and (d)). This result shows the impact of the use of facial masks in protecting the entire populace during the outbreak.
The corresponding time-dependent controls ( and ) for strategies A-C are depicted in Fig. 11. To ensure the level of protection observed in Fig. 10, the control profiles for Strategy A are required to be complementary (see the red and black solid lines in Fig. 11) this is because control is required to start at the upper bound for about 37 days before gradually reducing to the lower bound, while control starts at 0.35 and slowly reaching 0.69 in about 39 days. Notice that after 60 days control is high while control is low, hence the reciprocal relationship earlier mentioned.
Fig. 11.
Simulation results of the control profile of model (5).
For Strategies B and C, the controls -only and -only are required to start and stay at the upper bounds for about 65 and 54 days respectively. Control stays higher at about 0.70 until the end of the simulation period. Thus, when either strategy B or strategy C is in place, to obtain the level of protection observed in the community while using Strategy A, high level of compliance is required for control .
4.5.1. Infection averted ratio
Using the parameter values in Table 1, the IAR for each intervention strategy was determined. Table 2 gives the IAR for the three strategies implemented.
Table 2.
Total infection averted, total cost, IAR and ACER for the intervention strategies A, B, and C.
| Strategies | Total infection averted | Total Cost | IAR | ACER |
|---|---|---|---|---|
| Strategy A | 0.3629 | 0.1445 | ||
| Strategy B | 0.3636 | 0.1451 | ||
| Strategy C | 0.2003 | 0.3167 |
According to this cost-effectiveness analysis method, Strategy B involving personal protection (-only with ) have the highest infection averted ratio and the least total cost; therefore it is the most cost-effective. The next less cost-effective measure is Strategy A involving the combination of personal protection () such as the use of facial or surgical masks and vaccination (). Strategy C involving vaccination of susceptible individuals in the community is the least cost-effective. This is due to the relatively low number of infection averted and a higher total cost (see Table 2).
4.5.2. Average cost-effectiveness ratio (ACER)
Based on this cost-effectiveness approach, the most cost-effective strategy is Strategy B, followed by Strategy A and the least cost-effective strategy is Strategy C (see Table 2).
Next, to further investigate the cost-effectiveness of the distinct control strategies, we evaluate the incremental cost-effectiveness ratio (ICER).
4.5.3. Incremental cost-effectiveness ratio.
To implement the ICER, we simulate the model for each of the three interventions strategies. Using these simulation results, we rank the control strategies in increasing order of effectiveness based on infection averted. This ranking procedure shows that Strategy C averted the least number of infections, followed by Strategy A, and Strategy B averts the most number of infections (see Table 3).
Table 3.
Total infection averted, total cost, and ICER for the intervention strategies A, B, and C.
| Strategies | Total infection averted | Total Cost | ICER | |
|---|---|---|---|---|
| Strategy C | 0.2003 | 0.3167 | ||
| Strategy B | 0.3636 | 0.1451 | ||
| Strategy A | 0.3629 | 0.1445 |
The ICER is computed as follows:
A look at Table 3 shows a cost saving of 0.3167 for Strategy B over Strategy C; this is obtained by comparing ICER(B) and ICER(C). The lower ICER obtained for Strategy B is an indication that Strategy C strongly dominate Strategy B; this simply indicates that Strategy C is more costly to implement than Strategy B. Therefore, it is better to exclude Strategy C from the set of control strategies and consider alternative interventions to implement in order to preserve limited resources. Therefore, Strategy C is left out, and Strategy A is further compared with Strategy B. Hence, we obtain the following numerical results.
The ICER is computed as follows:
From Table 4 we observe that Strategy B strongly dominate Strategy A. This merely implies that Strategy B is more costly and less effective compared to Strategy A. Thus, we exclude strategy B from further consideration.
Table 4.
Total infection averted, total cost, and ICER.
| Strategies | Total infection averted | Total Cost | ICER | |
|---|---|---|---|---|
| Strategy B | 0.3636 | 0.1451 | ||
| Strategy A | 0.3629 | 0.1445 |
Thus, following the above analysis, we conclude that Strategy A (control and ) is the most cost-effective strategy followed by Strategy B, the combination of all controls -only. Strategy C (control -only) is the least cost-effective strategy and should carefully be considered for implementation particularly in resource-limited places such as most of the communities in the meningitis belt of sub-Saharan Africa.
5. Discussions and conclusions
5.1. Discussions
There are several different serogroups of Neisseria meningitidis but only strain A, B, C, W135, X, and Y can cause epidemics (World Health Organization, 2017b). The dominant strains in Nigeria are strains A and C (Men A and C). Nigeria experienced a major outbreak of strain A in 2009 with over 55,000 cases which resulted in about 2500 deaths (World Health Organization, 2017d). And since 2013, there have been reported outbreaks of meningitis C in few local government areas of Kebbi and Sokoto States in Nigeria. However, in 2015, over 2500 cases of the disease were reported across three states of the country. And the current 2017 outbreak has led to over 9902 suspected cases and 602 deaths in 31 states of the country (Nigeria Centre for Disease Control (NCDC), 2017b). In future work, we will study the co-evolution of Men A and C in Nigeria and the possible displacement of Men A by Men C.
Vaccine is a highly effective control strategy against the disease, and “can drastically reduce the magnitude of the epidemic” (World Health Organization, 2017d). Individuals in the meningitis belt have seen some level of protection against Men A by the use of Men A conjugate vaccine (MACV) introduced in 2010 (World Health Organization, 2017d). Over 260 million people have been vaccinated across 19 countries leading to over 57% reduction in meningitis cases. Unfortunately, this is not the case with Men C (United Nations Children's Fund (UNICEF), 2017; World Health Organization, 2017d). The Men C vaccines are polysaccharide vaccines and are currently in short supply because they are being phased out in other parts of the world (World Health Organization, 2017d). And the more effective and long-lasting conjugate vaccines are not readily and promptly available (World Health Organization, 2017d).
Hence, it is not surprising to note that during the 2017 meningitis outbreak Nigeria experienced meningitis vaccine shortage (British Broascasting Cooperation (BBC), 2017; News24, 2017; Nigeria Centre for Disease Control (NCDC), 2017a; Voice of America (VOA), 2017). However, the Nigerian health ministry has been working closely with WHO, UNICEF and other partners to ensure timely access to the Men C vaccines needed to respond to the outbreak and prevent further cases (Nigeria Centre for Disease Control (NCDC), 2017a).
Thus, to ensure the protection of the population, particularly people living in hard-to-reach areas of the region, we propose the use of facial masks. This study is the first study to identify and use facial masks as a means to control Neisseria meningitidis. As observed from our sensitivity analysis to adequately reduce the spread of meningitis in the community, it is vital to reduce the transmission probability per contact (i.e., reduce β). This can be achieved through the use of measures like the wearing of facial or surgical masks. The idea of such control measure is analogous to the use of insecticide-treated bednets that has drastically reduced the number of malaria cases across sub-Sahara Africa.
The use of facial masks is a personal protection measure used as an infection-control strategy (Food and Drug Admini, 2017; Sim, Moey, & Tan, 2014). It creates a physical barrier against potential contaminants in the immediate environment and prevents liquid and airborne particles from contaminating the face (Food and Drug Admini, 2017). Facial masks can offer up to 45% protection under pseudo-steady concentration environment, while the protection varied from 33 to 100% under expiratory emissions (Lai, Poon, & Cheung, 2011). The use of surgical and N95 masks against the transmission of SARS has an effective level of about 68% and 91%, respectively (Jefferson et al., 2008; Sim et al., 2014).
Thus, in this study, we consider not only vaccination but also the use of personal protection like wearing facial masks. We model these control measures by introducing into the meningitis model two time-dependent control variables. We investigated the associated benefits of the control strategies using cost-effectiveness analysis. This was achieved, using three approaches, namely the infection averted ratio (IAR), the average cost-effectiveness ratio (ACER) and the incremental cost-effectiveness ratio (ICER).
Using these cost analysis techniques, we determine the impact of and (which are the weights on the cost of implementing the controls and respectively) on IAR, ACER, infection averted, and total cost. The following values of weights were used: , and . The results are summarized in Fig. 9. These costs represent very cheap, cheap, expensive and very expensive facial masks and vaccines respectively. From Fig. 9(a) and (b) we observed that lower weights could lead to fewer infections; with vaccine averting slightly more infections than the use of facial masks. Furthermore, both controls ( and ) are equally cost-effective at lower weights than higher weights (see Fig. 9(c) and (d)). It is surprising to see that facial mask control lead to higher ACER and total cost at higher weights. This is due to the model requirement that everyone in the population uses facial masks regardless of whether they are vaccinated or not. This requirement follows from the model assumption that the meningitis vaccine is imperfect.
According to the results from our analysis, the use of facial masks is comparable to a control strategy implementing vaccination, as it can avert a large number of infections in the communities most impacted by meningitis (See Fig. 10). The wearing of facial masks is not common in Africa as opposed to a common practice in Asia; nevertheless, the governments of communities in sub-Sahara Africa should consider complementing the use of vaccine with the use of facial masks. Particularly in hard-to-reach villages and especially during outbreaks like the 2017 outbreak in Nigeria. Furthermore, our study shows that the use of low-cost facial masks is very cost-effective (See Fig. 9). Therefore, the government of communities with limited resources should encourage their citizens to wear these masks, since they will benefit tremendously from saved resources that can be channeled into other projects of equal relevance for the communities.
Further cost analyzes were carried out on the three control strategies A-C using the baseline weights . Strategy A is a combination of time-dependent controls and representing the use of facial masks and vaccination. Strategy B involves control -only, that is, the use of facial mask only while setting ; and Strategy C is control -only, that is, only consider the implementation of vaccination with .
Based on the results of these cost analysis, Strategies A and B averted the most number of infection; Strategy C performed the least in averting the number of infections, which is not a surprising result. Similar conclusions follow from the result obtained using the ACER, the IAR, and the objective functional (see Fig. 9(d) at the baseline weights). Thus, our results suggest that Strategy A is the most cost-effective strategy to implement. Although this analysis shows that Strategy C is the least cost-effective strategy to implement, it still did an excellent job of averting infection in the community (see Fig. 9(a) and (b)).
In summary, the result of the cost-effectiveness analysis suggests that resource-limited communities such as those in the meningitis belt should consider using facial or surgical masks during the seasons when the prevalence of meningitis is high.
5.2. Conclusions
Next, we summarize some of the main theoretical and epidemiological findings of this study. In this work, we presented a deterministic model of a system of ordinary differential equations of meningitis infection transmission dynamics. The developed model was parameterized using data obtained from Nigerian centers for diseases and controls (NCDC). Optimal control theory was used to study the impact of personal protection (such as facial or surgical masks), and vaccination as effective control measures against the epidemics. The following results were observed from our analysis and numerical simulations:
-
(i)
The model has a disease-free equilibrium (DFE) that is locally asymptotically stable if the reproduction number is less than one () and unstable otherwise ();
-
(ii)
The application of time-dependent controls can reduce the total number of infected (infectious and carrier) individuals in the population;
-
(iii)
By investigating the effect of changes in the weights and which corresponds to changes in the costs of implementing the controls and we observed that
-
(a)
A reciprocal relation exist between the cost of facial mask use and vaccination coverage; as the cost of facial mask increases the use of vaccination increases and vice versa.
-
(b)
Lower weights are more cost-effective than higher weights.
-
(c)
When the weights on the costs are low, the two controls avert more infections, but vaccine averts slightly more infections than facial masks.
-
(iv)
The most efficient and cost-effective control strategy is the strategy involving both control variables (that is, Strategy A). This is followed by Strategy B (a strategy with the use of facial masks only). The Strategy C (a strategy with vaccination only) is the least cost-effective. Although vaccination strategy is not cost-effective, it performs just as well as the other two strategies when the ability to curtail the infection is assessed.
Data access statement
The authors confirm that the data supporting the findings of this study are available within the article and can be obtained at the Nigeria Centre for Disease Control (NCDC) http://www.ncdc.gov.ng/reports.
Conflict of interests
The authors declare that they have no conflict interests.
Acknowledgment
The authors acknowledge with thanks the reviewers for their comments and suggestions that have helped improve this final version.
Handling Editor: Y. Shao
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.idm.2019.05.003.
A. Analysis of the meningitis model (2)
Basic qualitative properties
Positivity and boundedness of solutions
For the meningitis model (2) to be epidemiologically meaningful, it is essential to prove that all its state variables are non-negative for all time. In other words, solutions of the model system (2) with non-negative initial data will remain non-negative for all time .
Lemma A.1
Let the initial data , where . Then the solutions of the meningitis model (2) are non-negative for all . Furthermore
where
Proof
Let . Thus, . It follows from the first equation of system (2), that
which can be re-written as
Hence,
so that,
Similarly, it can be shown that for all .
For the second part of the Proof, note that .
Adding components of the model (2) gives
| (A-1) |
Hence,
as required.
Invariant regions
The meningitis model (2) will be analyzed in a biologically-feasible region as follows. Consider the feasible region
with,
Lemma A.2
The region is positively-invariant for the model (2) with non-negative initial conditions in .
Proof
It follows from summing equations of model (2) that
Hence, , if . Thus, . In particular, .
Thus, the region is positively-invariant. Furthermore, if , then either the solutions enters in finite time, or approaches asymptotically. Hence, the region attracts all solutions in .
B. Stability of disease-free equilibrium (DFE) and the reproduction number of the meningitis model (2)
In this section, the conditions for the stability of the equilibria of the model (2) are stated. The meningitis model (2) has a disease free equilibrium (DFE). The DFE is obtained by setting the right-hand sides of the equations in the model (2) to zero, which is given by
The stability of can be established by calculating the reproduction number using the next generation operator method on system (2). Taking C, and I as the infected compartments and then using the notation in (Van den Driessche & Watmough, 2002), the Jacobian F and V matrices for new infectious terms and the remaining transfer terms, respectively, are defined as:
Therefore, the reproduction number is
where, ρ is the spectral radius.
The expression is the number of secondary infections in completely susceptible population due to infections from one introduced infectious individual with meningitis. Further, using Theorem 2 in (Van den Driessche & Watmough, 2002), the following result is established.
Lemma B.1
The disease-free equilibrium (DFE) of the meningitis model (2) is locally asymptotically stable (LAS) if and unstable if .
C. Existence of endemic equilibria of the meningitis model (2)
Let,
denote the endemic equilibrium of the meningitis model (2) where
| (C-1) |
where, , , , with and
| (C-2) |
Substituting the expression in (C-1) into (C-2), we obtain the following quadratic polynomial after some computations
| (C-3) |
where
From polynomial (C-3), we see that the coefficient . Further, coefficient whenever . Thus, the signs of determines the number of possible positive real roots the polynomial (C-3) can have. This can be investigated using the Descartes Rule of Signs on the quadratic polynomial , given in (C-3) (with ). The various possibilities for the roots of are tabulated in Table 5.
Table 5.
Number of Possible Positive Real Roots of when and .
| Cases | Number of sign changes | No of possible positive real roots | ||||
|---|---|---|---|---|---|---|
| (endemic equilibrium) | ||||||
| 1 | + | + | + | 0 | 0 | |
| + | + | – | 1 | 1 | ||
| 2 | + | – | + | 2 | 0,2 | |
| + | – | – | 1 | 1 |
The following results (Theorem C.1 and Lemma C.2) follow from the various possible combinations for the roots of in Table 5.
Theorem C.1
The meningitis model (2) has a unique endemic equilibrium if and whenever Cases 1 and 2 are satisfied.
The existence of multiple endemic equilibria when (shown in Table 5) indicates the possibility of backward bifurcation (Agusto et al., 2011, 2013; Brauer, 2004; Carr, 1981; Dushoff et al., 1998; Elbasha & Gumel, 2006; Garba et al., 2008; Sharomi et al., 2007, 2008), a phenomenon where the disease-free equilibrium co-exist with a stable endemic equilibrium when the associated reproduction number () is less than one.
Lemma C.2
The meningitis model (2) has at least one positive endemic equilibrium whenever , and could have zero or two positive endemic equilibria whenever .
D. Backward bifurcation analysis of the meningitis model (2)
The phenomenon of backward bifurcation is shown using the concept of centre manifold theory on system (2). First, we make the following changes in variables by setting , , , , and . Furthermore, employing the vector notation , the meningitis model (2) with vaccination can be reformulated in the form , with as given below
| (D-1) |
The Jacobian of system (D-1) evaluated at the disease-free equilibrium, , is given by
| (D-3) |
Consider the case . Suppose that β is chosen as a bifurcation parameter. Setting and solving for β using the expression for gives
The Jacobian matrix evaluated at has a simple zero eigenvalue with the other eigenvalues having negative real parts. Hence the centre manifold theorem can be applied to analyze the dynamics of (D-1) near .
Computing the right and the left eigenvector of , denoted respectively by and , we have
and
Using the result from Theorem 4.1 by Castillo-Chavez and Song (Castillo-Chavez & Song, 2004), we calculate the coefficients a and b as
The coefficient b is given as follows:
The coefficient b is positive since and ; the presence of backward bifurcation in model (2) is determined by the sign of coefficient a.
E. Stability analysis of the pre-intervention model (3)
Local stability of the DFE
The disease free equilibrium (DFE) of the meningitis pre-intervention model (3) is given by
The stability of is established by calculating the reproduction number using the next generation operator method on system (3) as in Appendix B. Taking C, and I as the infected compartments, the Jacobian and matrices for new infectious terms and the remaining transfer terms, respectively, are defined as:
Therefore, the reproduction number is
Using Theorem 2 in (Van den Driessche & Watmough, 2002), the following result is established.
Lemma E.1
The disease-free equilibrium (DFE) of the meningitis pre-intervention model (3) is locally asymptotically stable (LAS) if and unstable if .
Global stability of DFE
Theorem E.2
The DFE of the meningitis pre-intervention model (3) is globally asymptotically stable whenever .
Proof
The proof is based on using a comparison theorem. The equations for the infected components in (3) can be written in terms of
| (E-1) |
where, , the matrices , , and Q are non-negative matrices given, respectively, by
Thus, since in , for all , it follows from (E-1) that
| (E-1) |
Using the fact that the eigenvalues of the matrix all have negative real parts (see the local stability result given in Lemma E.1, where if which is equivalent to having eigenvalues with negative real parts when (Van den Driessche & Watmough, 2002)), it follows that the linearized differential inequality system (E-2) is stable whenever . Consequently, as . Thus, by comparison theorem (Lakshmikantham, Leela, & Martynyuk, 1989; Smith & Waltman, 1995), as . Substituting in the third, and fourth equations of the meningitis model (3) gives . Hence, as for . Hence, the DFE is GAS in if .
F. Existence of endemic equilibrium of the pre-intervention model (3)
Let,
denote the endemic equilibrium of the pre-intervention model (3) where
| (F-1) |
with
| (F-2) |
Substituting the expression in (F-2), (F-3), we obtain after some computations the polynomial
| (F-3) |
where
| (F-4) |
It follows from (F-0) that if and only if . Furthermore, if ( corresponds to the DFE, and is biologically meaningless). Thus, the model (3) has a unique EEP whenever . This result is summarized below:
Theorem F.1
The meningitis model (3) has a unique endemic equilibrium whenever , and no endemic equilibrium otherwise.
G. Characterization of optimal controls
We seek to find optimal controls , such that
| (G-1) |
where the control set,
Control characterizations
The necessary conditions that an optimal control pair must satisfy come from Pontryagin's Maximum Principle (Pontryagin, 1987). This principle converts (5) and (6) into a problem of minimizing pointwise a Hamiltonian H, with respect to the controls ( and ). First we formulate the Hamiltonian from the cost functional (6) and the governing dynamics (5) to obtain the optimality conditions.
where are the associated adjoints for the states . The system of adjoint equations is found by taking the appropriate partial derivatives of the Hamiltonian (G-2) with respect to the associated state and control variables.
Theorem G.1
Given an optimal control pair () and solutions of the corresponding state system (5) that minimizes over . Then there exists adjoint variables satisfying
| (G-2) |
and with transversality conditions
| (G-3) |
The optimality conditions is given as
in the interior of the control set . Furthermore, the control pair is given as
| (G-4) |
Proof
The existence of an optimal control is guaranteed using the result by Fleming and Rishel (Fleming & Rishel, 2012). Thus, the differential equations governing the adjoint variables are obtained by the differentiation of the Hamiltonian function, evaluated at the optimal controls. Thus, the adjoint system can be written as:
evaluated at the optimal controls and corresponding state variables, results in the stated adjoint system (G-2) and (G-3). Furthermore, differentiating the Hamiltonian function with respect to the control variables in the interior of the control set and then solving for controls result in the optimality conditions given as
Solving for and , we have,
(G-5)
Using the bounds on the controls, the characterization (G-4) can be derived. ∎
Remark 1
Due to the a priori boundedness of the state and adjoint functions and the resulting Lipschitz structure of the ODE's, the uniqueness of the optimal control for small time () was obtained. The uniqueness of the optimal control quintuple follows from the uniqueness of the optimality system, which consists of (5) and (G-2), (G-3) with characterization (G-4). The restriction on the length of the time interval is to guarantee the uniqueness of the optimality system, the smallness in the length of time is due to the opposite time orientations of (5), (G-2), and (G-3); the state problem has initial values, and the adjoint problem has final values. This restriction is very common in control problems (see (Agusto, 2013; Agusto, Marcus, & Okosun, 2012; Agusto & Lenhart, 2013; Joshi, 2002; Jung et al., 2002; Kern et al., 2007; Kirschner et al., 1997)).
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Agusto F.B. Optimal isolation control strategies and cost-effectiveness analysis of a two-strain avian influenza model. Biosystems. 2013;113(3):155–164. doi: 10.1016/j.biosystems.2013.06.004. [DOI] [PubMed] [Google Scholar]
- Agusto F.B., Del Valle S.Y., Blayneh K.W., Ngonghala C.N., Goncalves M.J., Li N. The impact of bed-net use on malaria prevalence. Journal of Theoretical Biology. 2013;320:58–65. doi: 10.1016/j.jtbi.2012.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agusto F.B., ELmojtaba I.M. Optimal control and cost-effective analysis of malaria/visceral leishmaniasis co-infection. PLoS One. 2017;12(2) doi: 10.1371/journal.pone.0171102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agusto F.B., Gumel A.B. Theoretical assessment of avian influenza vaccine. DCDS Series B. 2010;13(1):1–25. [Google Scholar]
- Agusto F.B., Gumel A.B., Lenhart S., Odoi A. Mathematical analysis of the transmission dynamics of bovine tuberculosis model. Journal of Mathematical Methods in Applied Sciences. 2011;34:1873–1887. [Google Scholar]
- Agusto F., Lenhart S. Optimal control of the spread of malaria superinfectivity. Journal of Biological Systems. 2013;21(04):1340002. [Google Scholar]
- Agusto F.B., Marcus N., Okosun K.O. Application of optimal control to the epidemiology of malaria. The Electronic Journal of Differential Equations. 2012;2012(81):1–22. [Google Scholar]
- Blayneh K.W., Gumel A.B., Lenhart S., Clayton T. Backward bifurcation and optimal control in transmission dynamics of west nile virus. Bulletin of Mathematical Biology. 2010;72(4):1006–1028. doi: 10.1007/s11538-009-9480-0. [DOI] [PubMed] [Google Scholar]
- Blower S.M., Dowlatabadi H.I. Sensitivity and uncertainty analysis of complex models of disease transmission: An hiv model, as an example. International Statistical Review/Revue Internationale de Statistique. 1994:229–243. [Google Scholar]
- Brauer F. Backward bifurcations in simple vaccination models. Journal of Mathematical Analysis and Applications. 2004;298(2):418–431. [Google Scholar]
- British Broascasting Cooperation (BBC) 2017. Nigeria meningitis: Vaccine cost cripples response to outbreak.http://www.bbc.com/news/world-africa-39479097 [Google Scholar]
- Canini L., Andréoletti L., Ferrari R., P., D'Angelo, Blanchon T. Surgical mask to prevent influenza transmission in households: A cluster randomized trial. PLoS One. 2010;5(11) doi: 10.1371/journal.pone.0013998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr J. Springer-Verlag; New York: 1981. Applications of centre manifold theory. [Google Scholar]
- Castillo-Chavez C., Song B. Dynamical models of tuberculosis and their applications. Mathematical Biosciences and Engineering. 2004;1(2):361–404. doi: 10.3934/mbe.2004.1.361. [DOI] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention . 1997. Niosh service time recommendations for pseries particulate respirators.https://www.cdc.gov/niosh/npptl/usernotices/notices/run-050297.html [Google Scholar]
- Centers for Disease Control and Prevention . Vol. 60. 2010. (Updated recommendations for use of meningococcal conjugate vaccines—advisory committee on immunization practices (ACIP)). MMWR. Morbidity and mortality weekly report. (3):72, 2011. [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention . 2012. Epidemiology of meningitis caused by neisseria meningitidis, streptococcus pneumoniae, and haemophilus influenza.https://www.cdc.gov/meningitis/lab-manual/chpt02-epi.html [Google Scholar]
- Centers for Disease Control and Prevention . 2013. Meningococcal disease (neisseria meningitidis)https://wwwnc.cdc.gov/travel/diseases/meningococcal-disease [Google Scholar]
- Centers for Disease Control and Prevention . 13th ed. 2015. Meningococcal disease. Epidemiology and Prevention of vaccine-preventable diseases. [Google Scholar]
- Dushoff J., Huang W., Castillo-Chavez C. Backwards bifurcations and catastrophe in simple models of fatal diseases. Journal of Mathematical Biology. 1998;36(3):227–248. doi: 10.1007/s002850050099. [DOI] [PubMed] [Google Scholar]
- Elbasha E.H., Gumel A.B. Theoretical assessment of public health impact of imperfect prophylactic hiv-1 vaccines with therapeutic benefits. Bulletin of Mathematical Biology. 2006;68(3):577. doi: 10.1007/s11538-005-9057-5. [DOI] [PubMed] [Google Scholar]
- Encyclopdia Britannica, Inc. Harmattan. 2018. https://www.britannica.com/science/harmattan [Google Scholar]
- Fleming W.H., Rishel R.W. Vol. 1. Springer Science & Business Media; 2012. (Deterministic and stochastic optimal control). [Google Scholar]
- Garba S.M., Gumel A.B., Bakar M.R.A. Backward bifurcations in dengue transmission dynamics. Mathematical Biosciences. 2008;215(1):11–25. doi: 10.1016/j.mbs.2008.05.002. [DOI] [PubMed] [Google Scholar]
- Greenwood B.M., Bradley, Blakebrough I.S., Wali S., Whittle H.C. Meningococcal disease and season in sub-saharan africa. The Lancet. 1984;323(8390):1339–1342. doi: 10.1016/s0140-6736(84)91830-0. [DOI] [PubMed] [Google Scholar]
- Hepkema H., Pouwels K.B., van der Ende A., Westra T.A., Postma M.J. Meningococcal serogroup a, c, w135 and y conjugated vaccine: A cost-effectiveness analysis in The Netherlands. PLoS One. 2013;8(5) doi: 10.1371/journal.pone.0065036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hitchcock P.J., Robinson E.N., Jr., Neisseriae Z.A.M.G. 2nd ed. Williams and Wilkins; Baltimore, Md: 1993. Gonococcus and meningococcus. Mechanisms of microbial Disease. [Google Scholar]
- Irving T.J., Blyuss K.B., Colijn C., Trotter C.L. Modelling meningococcal meningitis in the african meningitis belt. Epidemiology and Infection. 2012;140(05):897–905. doi: 10.1017/S0950268811001385. [DOI] [PubMed] [Google Scholar]
- Jefferson T., Foxlee R., Del Mar C., Dooley L., Ferroni E., Hewak A. Physical interventions to interrupt or reduce the spread of respiratory viruses: Systematic review. BMJ. 2008;336(7635):77–80. doi: 10.1136/bmj.39393.510347.BE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi H.R. Optimal control of an hiv immunology model. Optimal Control Applications and Methods. 2002;23(4):199–213. [Google Scholar]
- Jung E., Lenhart S., Feng Z. Optimal control of treatments in a two-strain tuberculosis model. Discrete and Continuous Dynamical Systems - Series B. 2002;2(4):473–482. [Google Scholar]
- Kern D.L., Lenhart S., Miller R., Yong J. Optimal control applied to native–invasive population dynamics. Journal of Biological Dynamics. 2007;1(4):413–426. doi: 10.1080/17513750701605556. [DOI] [PubMed] [Google Scholar]
- Kirschner D., Lenhart S., Serbin S. Optimal control of the chemotherapy of hiv. Journal of Mathematical Biology. 1997;35(7):775–792. doi: 10.1007/s002850050076. [DOI] [PubMed] [Google Scholar]
- Lai A.C.K., Poon C.K.M., Cheung A.C.T. Effectiveness of facemasks to reduce exposure hazards for airborne infections among general populations. Journal of The Royal Society Interface. 2011;9(70):938–948. doi: 10.1098/rsif.2011.0537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakshmikantham V., Leela S., Martynyuk A.A. Marcel Dekker, Inc.; New York and Basel.: 1989. Stability analysis of nonlinear systems. [Google Scholar]
- Lenhart S., Workman J.T. CRC Press; 2007. Optimal control applied to biological models. [Google Scholar]
- Lopalco P.L., Carrillo Santisteve P. Actual immunization coverage throughout europe: Are existing data sufficient? Clinical Microbiology and Infections. 2014;20(s5):7–11. doi: 10.1111/1469-0691.12453. [DOI] [PubMed] [Google Scholar]
- Marino S., Hogue I.B., Ray C.J., Kirschner D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. Journal of Theoretical Biology. 2008;254(1):178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKay M.D., Beckman R.J., Conover W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics. 2000;42(1):55–61. [Google Scholar]
- McLeod R.G., Brewster J.F., Gumel A.B., Slonowsky A. Sensitivity and uncertainty analyses for a sars model with time-varying inputs and outputs. Mathematical Biosciences and Engineering. 2006;3(3):527. doi: 10.3934/mbe.2006.3.527. [DOI] [PubMed] [Google Scholar]
- Minka N.S., Ayo J.O. Influence of cold–dry (harmattan) season on colonic temperature and the development of pulmonary hypertension in broiler chickens, and the modulating effect of ascorbic acid. Open Access Animal Physiology. 2014;6(1–11) [Google Scholar]
- News24 . 2017. Vaccine shortage for Nigeria meningitis outbreak.https://www.news24.com/Africa/News/vaccine-shortage-for-nigeria-meningitis-outbreak-20170330-2 [Google Scholar]
- Nigeria Centre for Disease Control Weekly epidemiological report. 2017. http://www.ncdc.gov.ng/reports/weekly
- Nigeria Centre for Disease Control (NCDC) 2017. Meningitis outbreak in Nigeria affects five states.http://www.ncdc.gov.ng/news/67/meningitis-outbreak-in-nigeria-affects-five-states [Google Scholar]
- Nigeria Centre for Disease Control (NCDC) Weekly epidemiological report. 2017. http://www.ncdc.gov.ng/reports/96/2017-november-week-47
- Okosun K.O., Rachid O., Marcus N. Optimal control strategies and cost-effectiveness analysis of a malaria model. Biosystems. 2013;111(2):83–101. doi: 10.1016/j.biosystems.2012.09.008. [DOI] [PubMed] [Google Scholar]
- Pontryagin L.S. CRC Press; 1987. Mathematical theory of optimal processes. [Google Scholar]
- Rouphael N.G., Stephens D.S. Neisseria meningitidis: Biology, microbiology, and epidemiology. Neisseria meningitidis: Advanced Methods and Protocols. 2012;1–20 doi: 10.1007/978-1-61779-346-2_1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatini C., Bosis S., Semino M., Senatore L., Principi N., Esposito S. Clinical presentation of meningococcal disease in childhood. Journal of Preventive Medicine and Hygiene. 2012;53(2) [PubMed] [Google Scholar]
- Sahara Reporters, Inc Zamfara killings, resurgence of boko haram attacks unacceptable, says jni. 2019. http://saharareporters.com/2019/01/02/zamfara-killings-resurgence-boko-haram-attacks-unacceptable-says-jni%E2%80%8B
- Sanchez M.A., Blower S.M. Uncertainty and sensitivity analysis of the basic reproductive rate: Tuberculosis as an example. American Journal of Epidemiology. 1997;145(12):1127–1137. doi: 10.1093/oxfordjournals.aje.a009076. [DOI] [PubMed] [Google Scholar]
- Sharomi O., Podder C.N., Gumel A.B., Elbasha E.H., Watmough J. Role of incidence function in vaccine-induced backward bifurcation in some hiv models. Mathematical Biosciences. 2007;210(2):436–463. doi: 10.1016/j.mbs.2007.05.012. [DOI] [PubMed] [Google Scholar]
- Sharomi O., Podder C., Gumel A., Song B. Mathematical analysis of the transmission dynamics of hiv/tb coinfection in the presence of treatment. Mathematical Biosciences and Engineering. 2008;5(1):145. doi: 10.3934/mbe.2008.5.145. [DOI] [PubMed] [Google Scholar]
- Sim S.W., Moey K.S.P., Tan N.C. The use of facemasks to prevent respiratory infection: A literature review in the context of the health belief model. Singapore Medical Journal. 2014;55(3):160. doi: 10.11622/smedj.2014037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skaria S.D., Smaldone G.C. Respiratory source control using surgical masks with nanofiber media. Annals of Occupational Hygiene. 2014;58(6):771–781. doi: 10.1093/annhyg/meu023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith H.L., Waltman P. Cambridge University Press; 1995. The theory of the chemostat. [Google Scholar]
- Tsega A., Hausi H., Chriwa G., Steinglass R., Smith D., Valle M. Vaccination coverage and timely vaccination with valid doses in Malawi. Vaccine Reports. 2016;6(8–12) [Google Scholar]
- United Nations Children's Fund (UNICEF) 2017. West africa on alert for meningitis epidemic.https://www.unicef.org/wcaro/english/45014872.html [Google Scholar]
- U.S. Food and Drug Administration . 2017. Masks and n95 respirators.https://www.fda.gov/MedicalDevices/ProductsandMedicalProcedures/GeneralHospitalDevicesandSupplies/PersonalProtectiveEquipment/ucm055977.htm [Google Scholar]
- Van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences. 2002;180(1):29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- Vereen K. Virginia Commonwealth University; 2008. An SCIR Model of meningococcal meningitis. PhD thesis. [Google Scholar]
- Voice of America (VOA) 2017. Nigeria tackles deadly meningitis outbreak amid vaccine scarcity.https://www.voanews.com/a/nigeria-tackles-deadly-meningitis-outbreak-amid-vaccine-scarcity/3806872.html [Google Scholar]
- Wikipedia Zamfara state. 2018. https://en.wikipedia.org/wiki/Zamfara_State
- World Health Organization . 2017. Meningococcal disease.http://www.who.int/ith/vaccines/meningococcal/en/ [Google Scholar]
- World Health Organization . 2017. Meningococcal meningitis.http://www.who.int/mediacentre/factsheets/fs141/en/ [Google Scholar]
- World Health Organization Nigeria. 2017. http://www.who.int/countries/nga/en//
- World Health Organization (WHO) 2017. Who and partners provide vaccines to control meningitis c in Nigeria.http://www.who.int/emergencies/nigeria/meningitis-c/en/ [Google Scholar]
- Yan X., Zou Y. Optimal and sub-optimal quarantine and isolation control in sars epidemics. Mathematical and Computer Modelling. 2008;47(1):235–245. doi: 10.1016/j.mcm.2007.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.