Optimization unit for real-time applications in unbalanced smart distribution networks

Graphical abstract

Highlights

• •This work proposes a new generalized formulation for the optimal power flow.
• •The proposed formulation is suitable for real-time energy management systems.
• •Unlike previous research, the proposed formulation tackles practical unbalanced systems.
• •Detailed analysis with simulation results of the proposed formulation are provided.
• •The proposed approach is characterized by scalability and low computational time.

Abstract

This paper presents a new generic approach for developing a Jacobian matrix for use with the optimization unit in real-time energy management systems (EMS) for unbalanced smart distribution systems. The proposed formulation can replace approximated calculations for real-time optimal power flow in an optimization unit while providing greater accuracy and requiring less computational time, which is critical for real-time EMS. The effectiveness and robustness of the proposed approach have been tested through simulations with different distribution networks. The simulation results demonstrate a significant reduction in the computational time with the new proposed formulation. Moreover, the results demonstrate the scalability of the proposed approach as the reduction in the computational time is more significant for large practical systems. The proposed approach is characterized by evaluating the scalability and low computational time; thus, it can be used by grid operators in real-time energy management applications for large-scale practical distribution systems.

Introduction

For a number of environmental and techno-economic reasons, smart grids have become the subject of significant interest over the last few years [1], [2]. A particular focus is related to the application of smart grids in distribution systems, where most power system losses and failures occur. For this reason, distribution systems are currently undergoing a significant transition to a new structure with respect to information, control, and power flow.

Power flow represents an essential engine in application software for distribution systems [3]. Power flow methods are divided into two categories based on the state variable that is employed for solving the power flow problem: either the node voltage or the branch current [3]. In the first category, numerous power flow methods have been developed since the 1960s, including network equivalence methods [4], Newton-Raphson methods [5], and fast decoupled methods [6]. The second category is associated with the development of techniques such as backward/forward sweep methods [7], which are widely used in commercial software [8], [9].

Optimizing distribution system assets is a fundamental functionality of smart distribution networks (SDNs). However, even if the convergence of power flow methods is guaranteed, they are not suitable for real-time applications that require an optimal power flow (OPF). These applications require not only a robust OPF but also a fast OPF algorithm, which is the main focus of this work.

The OPF problem involves solving for an optimal operating point for a distribution system that minimizes a predefined cost function, such as system losses or generation scenarios that are subject to specific techno-economic and/or environmental constraints on system variables [10]. The OPF usually involves two convergence problems: (1) the convergence of the power flow to a feasible solution and (2) the convergence of the optimization to a global optimum.

Many optimization techniques guarantee the feasibility of the solution, which in turn guarantees the convergence of the power flow problem [11]. However, with regard to the optimization and because the unbalance power flow problem is a nonlinear highly nonconvex problem [12], the convergence to a global optimum is not guaranteed. To address this limitation, several methods have been proposed for the global optimization of nonlinear problems, such as convexification [13] and branch-and-reduce [14] methods. OPF convergence problems have thus been adequately addressed in the research.

To perform a real-time process, such as energy storage system scheduling, the whole process should be completed in the range of half of a minute up to a few minutes. This process involves not only OPF but also other algorithms, such as topology processing, load allocation, and forecasting. These algorithms are components of the future smart grid energy management systems, which should be designed to address various grid and customer technologies. Most of the recent work in the area of smart grids utilizes optimization software for solving OPF problems, but a major aspect of real-time applications, the computational time required by the proposed algorithms, has not yet been examined.

Previous works [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27] proposed a variety of approaches for coordinating different SDN components/assets in real time: energy storage systems (charging/discharging), electric vehicle (EV) charging, distributed generation (DG), volt/var control equipment, and/or residential load consumption.

Some of the abovementioned research has failed to consider power flow [15], [16]. Other studies considered the power flow constraints for balanced distribution systems [17], [18], [19], [20], [21], [22]. Linearization of the power flow constraints was proposed elsewhere [23], [24], where the power flow formulas were linearized around an estimated operation point. This method can lead to inaccurate results, which in turn can have severe consequences in real time. For example, the voltage magnitude or the limits for voltage unbalance could be violated in the actual distribution system on unmonitored nodes but not in the linearized approximated model. The work presented by Maffei et al. [25] proposed a real-time OPF for energy management in smart grids utilizing the preceding horizon technique. The approaches reported previously [26], [27] are based on the real-time energy management of controllable loads and EVs in unbalanced distribution systems. However, the approaches described earlier [25], [26], [27] utilized commercial software for solving the required optimization problem, which cannot be relied upon in real-time applications, as explained in this section. Moreover, no mention is made of the computational time, which is a highly critical aspect and can be a barrier to the practical implementation of any energy management system.

Some work utilized different techniques to solve large scale OPF problems. In Ref. [28], the authors utilized Benders decomposition to reduce the problem size. The work in [29] proposed using a genetic algorithm (GA) and fuzzy clustering to increase the computational speed. Mostafa et al. [30] proposed a multi-objective technique for optimizing the unbalanced system operation under a high penetration of renewable DG by minimizing the system losses and improving the voltage profile. The work presented by others [29], [30] relied on the utilization of a GA to solve the mixed-integer nonlinear programming (MINLP) problem. However, meta-heuristic techniques are unsuitable for real-time applications in smart grids for two reasons: (1) the computational time required for these techniques is unpredictable, and (2) for large systems in which the decision variables might be in the range of hundreds or thousands, these techniques are likely to be slow compared to the gradient-based techniques.

To solve the unbalanced OPF problem, researchers usually employ optimization software tools, which normally find a solution for the optimization problem using a procedure that includes an evaluation of the approximated values for the constraint derivatives, which is known as the Jacobian matrix. For large networks, the use of an approximated Jacobian matrix, based, for example, on finite differences, significantly increases the computational time. It is well known that providing the derivatives of the constraints to the solver produces a more reliable solution and decreases the computational time. The solver can also find a feasible point for the problem; however, the finite differences around that feasible point may result in an infeasible solution that causes the solver to terminate prematurely without reaching an optimal feasible solution [31].

The work presented in this paper is focused on the optimization unit, which is a core element of any energy management system (EMS). The optimization unit is responsible for solving the assigned OPF problem by the EMS. In this work, we propose a new generalized Jacobian matrix formulation for improving accuracy and reducing the computational time in an unbalanced OPF for SDNs.

Energy management system for SDN

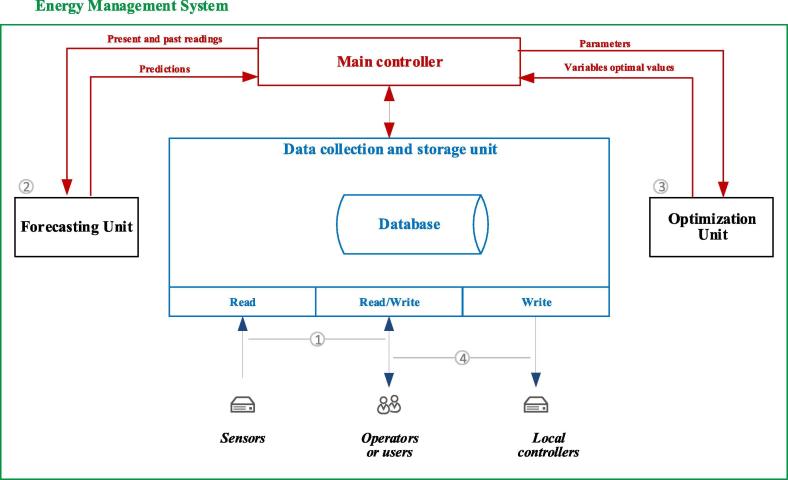
To optimize the SDN operation in real time, local distribution companies (LDCs) usually adopt a general procedure, whereby a central controller receives data from the users and the metering system via a communication infrastructure. This step is defined as stage 1 in Fig. 1. These data is preprocessed according to the measured values, type of measurement, and time stamp of the measurement; the data is then stored in the database (DB). Further, the data are processed in stage 2 by the forecasting unit to predict future consumptions or generations. In stage 3, all the parameters are sent to the optimization engine to process the real-time OPF to develop the optimal operation decisions of the SDN, which are returned back to the DB. These results are then used in stage 4 for (1) updating the situational awareness about the SDN conditions and (2) updating the control actions of the local controllers (LCs) within the SDN.

Fig. 1.

Main components of a real-time energy management system that utilizes the OPF in an SDN.

For real-time SDN system/market operations, this process should be completed as quickly as possible; a few seconds for small systems and up to a few minutes for large systems is considered an appropriate range. The computational time needed for solving the OPF problem represents a major challenge. This is the time it takes for the parameters to be sent to the optimization unit until when the optimal decisions are received, as shown in Fig. 1. The OPF run-time increases exponentially as the size of the system increases. The research presented in this paper addresses Jacobian matrix evaluation, which is a core element for solving the OPF problem. The derivation of the proposed form of the Jacobian matrix for unbalanced distribution systems is explained in the next section.

Proposed generalized OPF

This section presents the derivation of a Jacobian matrix for the proposed generalized OPF. In general, any OPF problem can be formulated as follows:

$$\mathrm{M}\mathrm{i}\mathrm{n}f(x_{\left(v\right)})$$ (1)

and is subject to

$$g_{(u)}(x_{\left(v\right)})=0$$ (2)

$$h_{(w)}(x_{\left(v\right)})\le 0$$ (3)

where $v$, $u$, and $w$ are the indices for the variables, equality constraints, and inequality constraints, respectively; $f\left(x_{\left(v\right)}\right)$ is the objective function; $g\left(x_{\left(v\right)}\right)$ and $h_{(w)}\left(x_{\left(v\right)}\right)$ are the equality and inequality constraints, respectively.

Any OPF problem includes the power flow mismatch constraints expressed in Eqs. (4), (5) as the equality constraints. The remaining equality and inequality constraints define other technical, environmental, and economical constraints, which are selected based on the system requirements. Eqs. (4), (5) are as follows:

$$P_{IN\left(i\right)}^{\left(p_1\right)}=P_{G\left(i\right)}^{\left(p_1\right)}-P_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\alpha }_{\left(i,p_1\right)}}-P_{L1\left(i\right)}^{\left(p_1\right)}=\sum _{j\in \mathcal{I}}\sum _{{\phi }_2}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)-V_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (4)

$$Q_{IN\left(i\right)}^{\left(p_1\right)}=Q_{G\left(i\right)}^{\left(p_1\right)}-Q_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\beta }_{\left(i,p_1\right)}}-Q_{L1\left(i\right)}^{\left(p_1\right)}=\sum _{j\in \mathcal{I}}\sum _{{\phi }_2}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)-V_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left({\phi }_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (5)

where $i$ and $j$ are the buses indices; $p_1$ and $p_2\in \mathrm{\Phi }$ are the buses indices; $P_{\mathit{IN}(i)}^{(p_1)}$ and $Q_{\mathit{IN}(i)}^{(p_1)}$ are the injected active and reactive power at bus $i$ for phase $p_1$, respectively; $P_{G(i)}^{(p_1)}$ and $Q_{G(i)}^{(p_1)}$ are the measured or known generated active and reactive power at bus $i$ for phase $p_1$, respectively; $P_{L0(i)}^{(p_1)}$ and $Q_{L0(i)}^{(p_1)}$ are the nominal measured or known active and reactive power of the load at bus $i$ for phase $p_1$, respectively; $P_{L1(i)}^{(p_1)}$ and $Q_{L1(i)}^{(p_1)}$ are the nominal unknown active and reactive power of the load at bus $i$ for phase $p_1$, respectively; ${\alpha }_{\left(i,p_1\right)}$ and ${\beta }_{\left(i,p_1\right)}$ are the active and reactive power exponents of the load at bus $i$, respectively; $V_{\left(i\right)}^{(p_1)}$ and ${\delta }_{\left(i\right)}^{(p_1)}$ are the magnitude and angle of the voltage at bus $i$ for phase $p_1$, respectively; $Y_{(i,j)}^{(p_1,p_2)}$ and ${\theta }_{(i,j)}^{(p_1,p_2)}$ are the magnitude and angle of the admittance element in the branch admittance matrix, respectively; $\mathcal{I}$ is the set of all system buses; $\mathrm{\Phi }=\{1,2,3\}$ is the set of phases; ${\mathcal{H}}_{\left(i\right)}\subset \mathrm{\Phi }$ is the subset of the existing phases at bus $i$.

The active and reactive power mismatch equations (4), (5), are formulated based on a branch admittance matrix, which can be calculated using Kron’s reduction on Carson’s equations for the self and mutual impedances [1]. Since some of the load bus quantities might be measured or known, while others are unknown, it is assumed that the measured or known quantities are voltage dependent. In contrast, the unknown quantities are assumed to be voltage independent because their values are unknown or variable in any case.

Solving this nonlinear programming problem requires three sets of derivatives: (1) the gradient, (2) the Jacobian matrix, and (3) the Hessian matrices. The focus of the research presented in this paper is the Jacobian matrix parametric definition and the fast numerical computation for the SDN OPF runs.

In this study, all the SDN active and reactive powers, voltages, and voltage angles are assumed as variables, and all variables and parameters are considered in per-unit values. It is assumed that the Jacobian matrix size is $m\times n$, where $m$ is the number of constraints and $n$ is the number of variables. Only the power flow constraints and variables are considered in this paper. The Jacobian matrix $\mathbb{J}$ can be given as in (6). Thus, each entry $J\left(u,v\right)$ in the Jacobian matrix is defined as in (7), which corresponds to the differentiation of constraint $u$ with respect to (w.r.t.) variable $v$. These considerations mean that each constraint must be differentiated w.r.t. all variables.

$${\mathbb{J}}_{\left(m\times n\right)}=\left[\begin{array}{ccc}\frac{d{g}_{(1)}}{d{x}_{(1)}}& \cdots & \frac{d{g}_{(1)}}{d{x}_{(n)}}\\ ⋮& \ddots & ⋮\\ \frac{d{g}_{(m)}}{d{x}_{(1)}}& \cdots & \frac{d{g}_{(m)}}{d{x}_{(n)}}\end{array}\right]$$ (6)

$$J\left(u,v\right)=J\left(g_{(u)},x_{(v)}\right)=\frac{d{g}_{(u)}}{d{x}_{(v)}}\forall u\le m,v\le n$$ (7)

Assuming the total number of buses in the system is $N_{\mathit{bus}}$, the total number of variables can be defined as $3\times 6\times N_{\mathit{bus}}$, where $3$ refers to the number of phases, and $6$ refers to $P_{L1(i)}^{(p_1)}$, $Q_{L1(i)}^{(p_1)}$, $P_{G\left(i\right)}^{\left(p_1\right)}$, $Q_{G(i)}^{(p_1)}$, $V_{\left(i\right)}^{(p_1)}$ and${\delta }_{\left(i\right)}^{(p_1)}$. Moreover, the number of constraints for any OPF can be identified as $3\times 2\times N_{\mathit{bus}}$, where $3$ refers to the number of phases, and $2$ refers to the two type of constraints: the active power mismatch $g_{(i)}^{P_{(p_1)}}$ and the reactive power mismatch $g_{(i)}^{Q_{(p_1)}}$. Therefore, the Jacobian matrix would have $6N_{\mathit{bus}}$ rows, corresponding to the constraints, and $18N_{\mathit{bus}}$ columns, corresponding to the variables. The Jacobian matrix thus can be defined as in (8), where the entry $J\left(g_{(u)},x_{(v)}\right)$ refers to $d{g}_{(u)}/d{x}_{(v)}$. The $6N_{\mathit{bus}}$ constraints and their derivatives, which represent the Jacobian matrix entries, are defined in (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20), (21), (22), (23), (24), (25), (26), (27), as explained below.

As a first step in forming the Jacobian matrix, the Jacobian entries are initialized to zero, i.e.$,J\left(g_{(u)},x_{(v)}\right)=0\forall u\le m,v\le n$. This step is included because most Jacobian entries are zeros due to the radial structure of distribution systems; each bus is usually connected to two or three buses. For example, assume that bus $i$ is connected only to buses $i+1$ and $i-1$. This arrangement means that all the entries for the power mismatch constraint for bus $i$ in the Jacobian matrix will be zeros except for those corresponding to buses $i-1,i,$and $i+1$.

After all the Jacobian entries have been initialized to zeros, as a second step, each entry is updated. The active power mismatch entries are derived first and followed by the reactive power mismatch entries.

Jacobian matrix entries for active power constraints

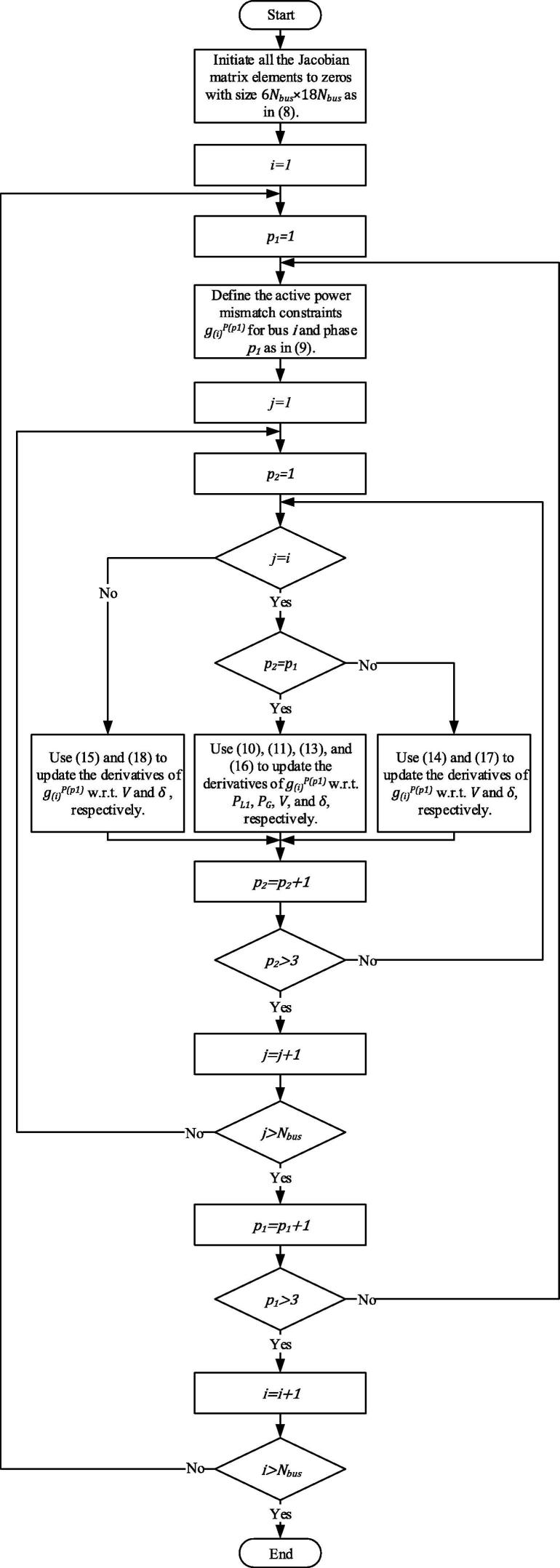
To update the Jacobian matrix entries for the active power constraints, i.e., $d{g}_{(i)}^{P_{(p_1)}}/d{x}_{(v)}$, the procedure shown in Fig. 2 can be used, which is explained as follows. Based on (4), each bus has up to three active power mismatch constraints, as in (9). The Jacobian matrix entries corresponding to the variables $P_{L1\left(i\right)}^{\left(p_1\right)}$ and $P_{G\left(i\right)}^{\left(p_1\right)}$ can thus be derived as in (10), (11).

Fig. 2.

The procedure to update the Jacobian matrix entries for the active power constraints.

As indicated in (9), $g_{(i)}^{P_{(p_1)}}$ is composed of two major terms: a positive double summation and a negative double summation. Each summation can be broken down into three components so that $g_{\left(i\right)}^{P_{\left(p_1\right)}}$ can be rewritten as in (12), where $g_{\left(i\right)}^{P_{\left(p_1\right)}}$ is composed of six terms. The third and sixth terms cancel each other out.

For the derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. the magnitude of the voltage, three different cases can be defined as follows:

• •The derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. the same bus $i$ and the same phase $p_1$voltage magnitude, as in (13);
• •The derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. the same bus $i$ and a different phase $p_2\ne p_1$voltage magnitude, as in (14);
• •The derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. a different bus voltage magnitude $j\ne i$, as in (15).

Similarly, for the derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. the voltage angle, three cases can be identified, as in (16)–(18):

• •The derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. the same bus $i$ and the same phase $p_1$ voltage angle, as in (16);
• •The derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. the same bus $i$ and a different phase $p_2\ne p_1$ voltage angle, as in (17);
• •The derivative of $g_{(i)}^{P_{(p_1)}}$ w.r.t. a different bus $j\ne i$ voltage angle, as in (18).

Jacobian matrix entries for reactive power constraints

The Jacobian matrix entries that correspond to the reactive power mismatch constraints $g_{(i)}^{Q_{(p_1)}}$ in (19) can be derived in a similar way since they are derived for the active power. These entries are defined by (20), (21), (22), (23), (24), (25), (26), (27).

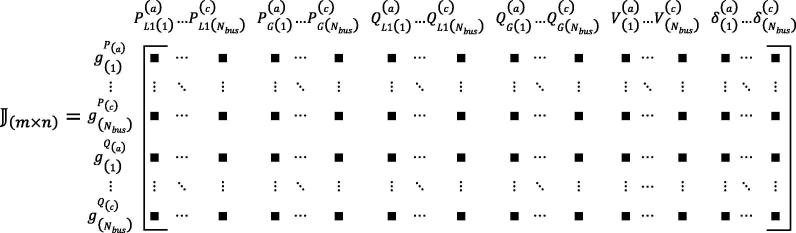(8)

$$g_{\left(i\right)}^{P_{\left(p_1\right)}}=P_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\alpha }_{\left(i,p_1\right)}}+P_{L1\left(i\right)}^{\left(p_1\right)}-P_{G\left(i\right)}^{\left(p_1\right)}+\left(\sum _{j\in \mathcal{I}}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{(p_1)}{V}_{\left(j\right)}^{(p_2)}{Y}_{(i,j)}^{(p_1,p_2)}\cos \left({\theta }_{(i,j)}^{(p_1,p_2)}+{\delta }_{\left(j\right)}^{(p_2)}-{\delta }_{\left(i\right)}^{(p_1)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (9)

$$J\left(g_{(i)}^{P_{(p_1)}},P_{L1\left(i\right)}^{\left(p_1\right)}\right)=1\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (10)

$$J\left(g_{(i)}^{P_{(p_1)}},P_{G(i)}^{(p_1)}\right)=-1\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (11)

$$g_{\left(i\right)}^{P_{\left(p_1\right)}}=P_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\alpha }_{\left(i,p_1\right)}}+P_{L1\left(i\right)}^{\left(p_1\right)}-P_{G\left(i\right)}^{\left(p_1\right)}+\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(\sum _{j\ne i}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}\right)\right)+\left(V_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_1\right)}\cos \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_1\right)}\right)\right)-\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{(p_1)}{V}_{\left(j\right)}^{(p_2)}{Y}_{(i,j)}^{(p_1,p_2)}\cos \left({\theta }_{(i,j)}^{(p_1,p_2)}+{\delta }_{\left(j\right)}^{(p_2)}-{\delta }_{\left(i\right)}^{(p_1)}\right)\right)-\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{(p_1)}{V}_{\left(i\right)}^{(p_2)}{Y}_{(i,i)}^{(p_1,p_2)}\cos \left({\theta }_{(i,i)}^{(p_1,p_2)}+{\delta }_{\left(i\right)}^{(p_2)}-{\delta }_{\left(i\right)}^{(p_1)}\right)\right)-\left(V_{\left(i\right)}^{(p_1)}{V}_{\left(i\right)}^{(p_1)}{Y}_{(i,i)}^{(p_1,p_1)}\cos \left({\theta }_{(i,i)}^{(p_1,p_1)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (12)

$$J\left(g_{\left(i\right)}^{P_{\left(p_1\right)}},V_{\left(i\right)}^{\left(p_1\right)}\right)={\alpha }_{\left(i,p_1\right)}{P}_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\alpha }_{\left(i,p_1\right)}-1}+\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(\sum _{j\ne i}2V_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}\right)\right)-\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (13)

$$J\left(g_{\left(i\right)}^{P_{\left(p_1\right)}},V_{\left(i\right)}^{\left(p_2\right)}\right)=\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}\left(V_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\right)-\left(\sum _{p_2\ne p_1}\left(V_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},p_2\ne p_1$$ (14)

$$J\left(g_{\left(i\right)}^{P_{\left(p_1\right)}},V_{\left(j\right)}^{\left(p_2\right)}\right)=-\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}\left(V_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},j\ne i$$ (15)

$$J\left(g_{\left(i\right)}^{P_{\left(p_1\right)}},{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)=\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (16)

$$J\left(g_{\left(i\right)}^{P_{\left(p_1\right)}},{\delta }_{\left(i\right)}^{\left(p_2\right)}\right)=-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},p_2\ne p_1$$ (17)

$$J\left(g_{\left(i\right)}^{P_{\left(p_1\right)}},{\delta }_{\left(j\right)}^{\left(p_2\right)}\right)=\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}\left(V_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},j\ne i$$ (18)

$$g_{\left(i\right)}^{Q_{\left(p_1\right)}}=Q_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\beta }_{\left(i,p_1\right)}}+Q_{L1\left(i\right)}^{\left(p_1\right)}-Q_{G\left(i\right)}^{\left(p_1\right)}+\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(V_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_1\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_1\right)}\right)\right)-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\ne i}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}\right)\right)-\left(V_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_1\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (19)

$$J\left(g_{(i)}^{Q_{(p_1)}},P_{L1\left(i\right)}^{\left(p_1\right)}\right)=1\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (20)

$$J\left(g_{(i)}^{Q_{(p_1)}},P_{G(i)}^{(p_1)}\right)=-1\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (21)

$$J\left(g_{(i)}^{Q_{(p_1)}},V_{\left(i\right)}^{(p_1)}\right)={\beta }_{\left(i,p_1\right)}{Q}_{L0\left(i\right)}^{\left(p_1\right)}{\left(V_{\left(i\right)}^{\left(p_1\right)}\right)}^{{\beta }_{\left(i,p_1\right)}-1}+\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(\sum _{p_2\ne p_1}2V_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\ne i}2V_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_1\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (22)

$$J\left(g_{\left(i\right)}^{Q_{\left(p_1\right)}},V_{\left(i\right)}^{\left(p_2\right)}\right)=\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},p_2\ne p_1$$ (23)

$$J\left(g_{\left(i\right)}^{Q_{\left(p_1\right)}},V_{\left(j\right)}^{\left(p_2\right)}\right)=\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\sin \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},j\ne i$$ (24)

$$J\left(g_{\left(i\right)}^{Q_{\left(p_1\right)}},{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)=-\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (25)

$$J\left(g_{\left(i\right)}^{Q_{\left(p_1\right)}},{\delta }_{\left(i\right)}^{\left(p_2\right)}\right)=\left(\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,i\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,i\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\ne p_1}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},p_2\ne p_1$$ (26)

$$J\left(g_{\left(i\right)}^{Q_{\left(p_1\right)}},{\delta }_{\left(j\right)}^{\left(p_2\right)}\right)=\left(\sum _{j\ne i}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)},j\ne i$$ (27)

Results and discussion

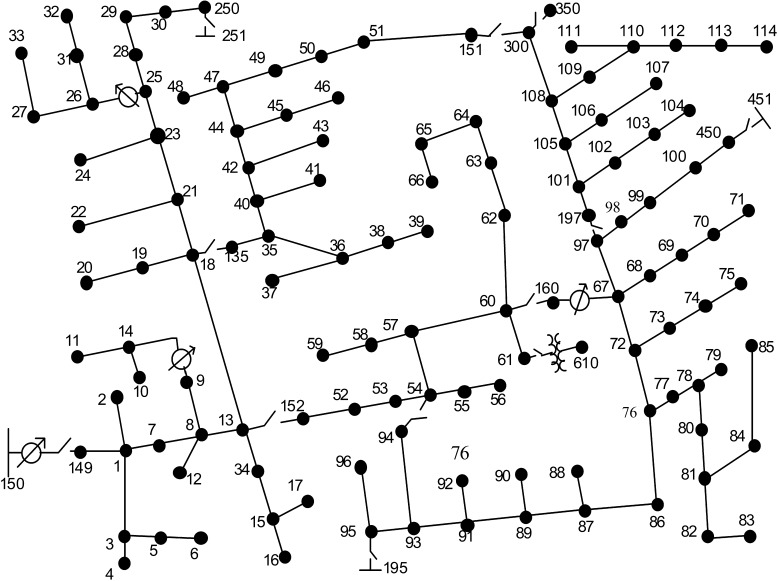
For the purpose of evaluation, the proposed Jacobian was tested on two systems. The first is a simple 4-bus radial system, which is a small part of a real system located in Ontario, Canada. The system has a simple structure, as shown in Fig. 3. The second system is the IEEE 123-bus system [32], which is illustrated in Fig. 4. The load and line data for the 4-bus system and the 123-bus system are shown in Table 1 and in [32], respectively. In both cases, it is assumed that the central controller that hosts the energy management system is located at the substation or main grid connection. For each case, the exact Jacobian ${\mathbb{J}}_{\mathit{exact}}$ was generated in a MATLAB® environment using symbolic differentiation of the power flow mismatch equations in (12), (19).

Fig. 3.

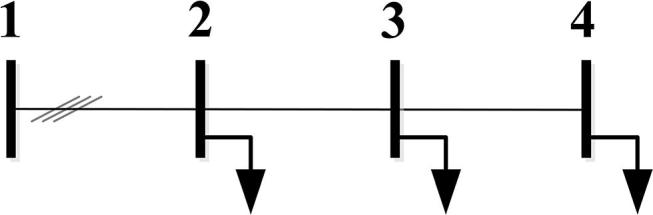
4-Bus distribution test system.

Fig. 4.

IEEE 123-bus distribution test system [32].

Table 1.

4-Bus system data in p.u.

From ($\mathit{i}$)	1	2	3
To ($\mathit{j}$)	2	3	4
${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(a,a\right)}$	$25.588\angle -64.25$	$34.118\angle -64.25$	$51.177\angle -64.25$
${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(b,b\right)}$	$26.924\angle -62.51$	$35.899\angle -62.51$	$53.849\angle -62.51$
${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(c,c\right)}$	$24.382\angle -65.82$	$32.510\angle -65.82$.	$48.764\angle -65.82$
${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(a,b\right)}$or${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(b,a\right)}$	$9.578\angle 124.31$	$12.771\angle 124.31$	$19.157\angle 124.31$
${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(a,c\right)}or{\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(c,a\right)}$	$5.496\angle 110.76$	$7.328\angle 110.76$	$10.992\angle 110.76$
${\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(c,b\right)}or{\stackrel{\rightharpoonup }{Y}}_{\left(i,j\right)}^{\left(b,c\right)}$	$7.091\angle 117.80$	$9.454\angle 117.80$	$14.182\angle 117.80$
$P_{L0\left(j\right)}^{\left(a\right)}$	0.309	0.175	0.175
$P_{L0\left(j\right)}^{\left(b\right)}$	0.287	0.175	0.175
$P_{L0\left(j\right)}^{\left(c\right)}$	0.079	0.175	0.175
$Q_{L0\left(j\right)}^{\left(a\right)}$	0.068	0.088	0.168
$Q_{L0\left(j\right)}^{\left(b\right)}$	0.231	0.088	0.071
$Q_{L0\left(j\right)}^{\left(c\right)}$	0.192	0.088	0.001

To develop the exact Jacobian, the symbolic differentiation deals with each single constraint as a whole mathematical formula while considering the derivatives w.r.t. all possible variables. On the other hand, the proposed Jacobian $J_{\mathit{proposed}}$ is customized to the structure of the distribution system and develops the derivatives as the sum of individual terms. Mathematically, both ${\mathbb{J}}_{\mathit{exact}}$ and $J_{\mathit{proposed}}$ are identical in their output.

The exact Jacobian development, which is performed off-line, took 1.5 min for the simple 4-bus system and 13.5 h for the 123-bus system. On the other hand, the proposed Jacobian can be implemented directly without the need for preprocessing. For large practical systems, the computer will run out of memory trying to perform symbolic differentiation. This was the case when a practical test-case of a 575-bus unbalanced system was tested.

Moreover, for any topology change due to fault clearing or seasonal reconfiguration, ${\mathbb{J}}_{\mathit{exact}}$ must be developed for the new topology, which is very time consuming for large systems and will cause a considerable delay in the EMS process.

For simplicity, a simple OPF case was considered, in which each bus had six variables: $P_G^{(a,b,c)}\mathrm{a}\mathrm{n}\mathrm{d}{Q}_G^{(a,b,c)}$ for the slack bus and $V^{(a,b,c)}$ and ${\delta }^{(a,b,c)}$ for all other buses. The slack bus is the reference bus where the voltage magnitude and the voltage angles are known. The Jacobian matrix contains the derivative of the power mismatch equations (six equations for each bus), making the Jacobian matrix a size of $6N_{\mathit{bus}}\times 6N_{\mathit{bus}}$. The reduction in the Jacobian matrix size compared to the size considered in the previous section ($6N_{\mathit{bus}}\times 18N_{\mathit{bus}}$) is due to the assumption that each bus has only 6 variables instead of 18. The simulations were performed on a 3.6 GHz dual core processor with 16 GB of RAM. The optimization problems for the two case studies were solved using the constrained nonlinear optimization tool based on the interior point method in the MATLAB® environment.

The proposed Jacobian $J_{\mathit{proposed}}$ was constructed for each case. ${\mathbb{J}}_{\mathit{exact}}$ and ${\mathbb{J}}_{\mathit{proposed}}$ were compared to an approximated Jacobian ${\mathbb{J}}_{\mathit{approx}}$, which was evaluated using a finite difference approximated derivative, as in (28), for low values of $\mathrm{\Delta }x.$ In each case, a battery storage system (BSS) is controlled via an online signal from a central controller that runs the OPF problem, whereby the optimal charging/discharging power is determined and the computational time is evaluated.

$$\frac{\mathit{df}}{\mathit{dx}}=\frac{f\left(x+\mathrm{\Delta }x\right)-f(x)}{\mathrm{\Delta }x}$$ (28)

4-Bus test system

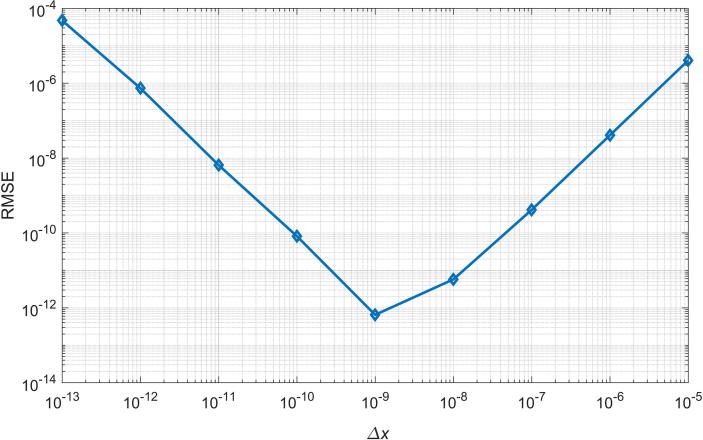
For the 4-bus test system, the Jacobian size is $24\times 24$. For the sake of comparison, the Jacobian is evaluated for the initial condition $x_0$, which corresponds to $V^{(a,b,c)}=1$ and ${\delta }^{(a,b,c)}=0,-2\pi /3,\mathrm{a}\mathrm{n}\mathrm{d}2\pi /3$. The root mean square error, $\mathit{RMSE}$, which is defined in (29), is used for comparing the results:

$$\mathit{RMSE}=\sqrt{\frac{1}{m\times n}\sum _{u\le m}\sum _{v\le n}{\left({\left[E_{\left(u,v\right)}\right]}_{x_{0(v)}}\right)}^2}$$ (29)

where$E_{\left(u,v\right)}$ is the difference between $J_{exact\left(u,v\right)}$ and either $J_{approx\left(u,v\right)}$ or $J_{\mathit{proposed}(u,v)}$.

As shown in Fig. 5, as $\mathrm{\Delta }x$ decreases, the value of the $\mathit{RMSE}$ for the approximate Jacobian is further reduced. However, reducing $\mathrm{\Delta }x$ is problematic because it approaches the precision limit of the software and hardware used for the computations. In this case, as $\mathrm{\Delta }x$ was reduced below 10⁻⁹, the value of the $\mathit{RMSE}$ increased to 1.396 × 10⁻⁹ at $x_0$. On the other hand, for ${\mathbb{J}}_{\mathit{proposed}}$, the error was zero, which shows that ${\mathbb{J}}_{\mathit{proposed}}$ is identical to ${\mathbb{J}}_{\mathit{exact}}$.

Fig. 5.

The $\mathit{RMSE}$ of the approximate Jacobian versus $\mathrm{\Delta }x$ for the 4-bus test system.

The three Jacobian matrices were evaluated at 1000 different values for $x_0$ w.r.t. the computation time, t. The computational time statistics are shown in Table 2.

Table 2.

Computation time (ms) for evaluating the Jacobian matrix for the 4-bus test system.

	${\mathbb{J}}_{\mathit{exact}}$	${\mathbb{J}}_{\mathit{proposed}}$	${\mathbb{J}}_{\mathit{approx}}$
Mean	0.6579	0.6423	7.4060
Minimum	0.6401	0.6250	7.278
Maximum	1.0095	0.9900	8.4856

As indicated, the proposed Jacobian computational time was much less than that for the approximate method but very close to the exact method. The mean computation time for the approximate Jacobian was 7.4 ms compared to 0.642 ms for the proposed Jacobian, which is almost 11 times faster. This discrepancy is attributable to two factors: (1) most of the derivatives are zeros, which is easily identified in ${\mathbb{J}}_{\mathit{proposed}}$ but must be evaluated for ${\mathbb{J}}_{\mathit{approx}}$; (2) for each term in the Jacobian matrix, ${\mathbb{J}}_{\mathit{approx}}$ must evaluate a function twice as in (28), while ${\mathbb{J}}_{\mathit{proposed}}$ evaluates only one function.

A comparison of the computational time of ${\mathbb{J}}_{\mathit{proposed}}$ to that of ${\mathbb{J}}_{\mathit{exact}}$ reveals a slightly faster performance for the proposed formulation, as identified by a 2.4% reduction in the mean computational time. This decrease is due to the complexity of the form of ${\mathbb{J}}_{\mathit{exact}}$, where symbolic differentiation is considered in comparison to the compact form of ${\mathbb{J}}_{\mathit{proposed}}$. As the size and complexity of the system increases, this difference is expected to be significant.

To test the proposed Jacobian for solving an OPF problem, a BSS is presumed to be located at bus 4. To simplify the analysis, the BSS optimal schedule (to charge and discharge) will be determined by the OPF run to minimize the overall system losses. The BSS is also assumed to operate at a unity power factor.

Although the test case study is simple, the proposed Jacobian formulation is applicable (and scalable) to any OPF case study, including DER optimal management in microgrids and distribution networks, transactive energy markets modeling, simulation and analysis.

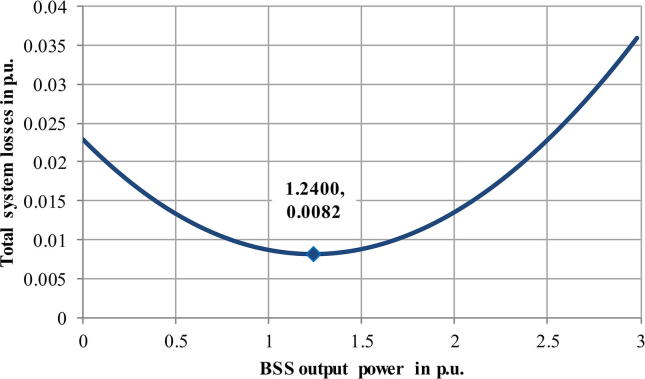
To determine the optimal power amount injected from the BSS $P_{\mathit{bat}}$, a simple test was performed before applying the OPF, in which the injected power from the BSS was varied and the system losses were evaluated. The test outcomes showed that the system loss for the base case ($P_{\mathit{bat}}=0$) was 0.0229 p.u., which corresponded to 1.33% of the total system demand. On the other hand, the minimum loss was 0.0082 p.u., or 0.48%, which occurred at $P_{\mathit{bat}}=1.24$ p.u., as shown in Fig. 6.

Fig. 6.

Total system losses for the 4-bus system versus the BSS output power.

To test the proposed Jacobian computation method, an OPF problem was formulated as follows:

$$\underset{P_{\mathit{bat}}}{\min }{P}_{\mathit{loss}}^{\mathit{Tot}}=\sum _{ph1}{P}_{\mathit{loss}}^{(p1)}$$ (30)

is subject to

$$P_{G\left(i\right)}^{\left(p_1\right)}+P_{bat\left(i\right)}^{\left(p_1\right)}-P_{L\left(i\right)}^{\left(p_1\right)}=\left(\sum _{j\in \mathcal{I}}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)-\left(\sum _{j\in \mathcal{I}}\sum _{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\cos \left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (31)

$$Q_{G\left(i\right)}^{\left(p_1\right)}-Q_{L\left(i\right)}^{\left(p_1\right)}=-\left({\sum }_{j\in \mathcal{I}}{\sum }_{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(i\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\mathit{sin}\left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(i\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)+\left({\sum }_{j\in \mathcal{I}}{\sum }_{p_2\in {\mathcal{H}}_{\left(j\right)}}{V}_{\left(i\right)}^{\left(p_1\right)}{V}_{\left(j\right)}^{\left(p_2\right)}{Y}_{\left(i,j\right)}^{\left(p_1,p_2\right)}\mathit{sin}\left({\theta }_{\left(i,j\right)}^{\left(p_1,p_2\right)}+{\delta }_{\left(j\right)}^{\left(p_2\right)}-{\delta }_{\left(i\right)}^{\left(p_1\right)}\right)\right)\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (32)

$$P_{\mathit{loss}}^{(p1)}=\sum _i{P}_{G\left(i\right)}^{\left(p_1\right)}+P_{bat\left(i\right)}^{\left(p_1\right)}-P_{L\left(i\right)}^{\left(p_1\right)}\forall p_1$$ (33)

$$V_{\mathit{min}}\le V_{\left(i\right)}^{\left(p_1\right)}\le V_{\mathit{max}}\forall i\in \mathcal{I},p_1\in {\mathcal{H}}_{\left(i\right)}$$ (34)

$$V_{\left(i\right)}^{\left(p_1\right)}=V_{\mathit{slack}},{\delta }_{\left(i\right)}^{\left(a\right)}=0,{\delta }_{\left(i\right)}^{\left(b\right)}=-\frac{2\pi }{3},{\delta }_{\left(i\right)}^{\left(c\right)}=\frac{2\pi }{3}\forall i\in I_{\mathit{slack}}$$ (35)

$$P_{G\left(i\right)}^{\left(p_1\right)},Q_{G\left(i\right)}^{\left(p_1\right)}=0\forall i\notin I_{\mathit{slack}}$$ (36)

$$P_{bat\left(i\right)}^{\left(p_1\right)}=\left\{\begin{array}{cc}{P}_{bat\left(i\right)}/3\hfill & \forall i\in I_{\mathit{bat}}\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right)$$ (37)

where $V_{\mathit{min}}\mathrm{a}\mathrm{n}\mathrm{d}{V}_{\mathit{max}}$ are the minimum and maximum voltage limits, respectively, which are set to 0.95 and 1.05, respectively;$V_{\mathit{slack}}$ is the slack bus voltage, which is set to 1.05 p.u.; $I_{\mathit{slack}}=\{1\}$ and $I_{\mathit{bat}}=\{4\}$ are the subsets of the slack bus and the BSS bus, respectively.

The nonlinear programming (NLP) OPF problem, defined in (30), (31), (32), (33), (34), (35), was solved using an interior-point algorithm in the MATLAB environment with default settings. The problem was first solved using finite differences. The optimal solution was $P_{\mathit{loss}}^{\mathit{Tot}}=0.0082$ p.u. at $P_{bat\left(4\right)}=1.2366$ p.u., which was very close to the values indicated in Fig. 6. The computational time was 100.81 ms.

On the other hand, when the gradient of the objective function and the Jacobian of the constraints were provided, the optimal solution was $P_{\mathit{loss}}^{\mathit{Tot}}=0.0082$ p.u. at $P_{bat\left(4\right)}=1.2366$ p.u., which was identical to the values derived from using finite differences. The process took 23.76 ms, which represents a 76.43% reduction in the computational time.

123-Bus test system

The 123-bus system is assumed to be moderately sized for a practical distribution system, which may contain more than 500 buses. Closing the switches and removing zero impedance lines reduces the 123-bus system to 119 buses, in which the size of the Jacobian matrix is $714\times 714$, which is equivalent to 509,796 entries in the matrix.

The time required for evaluating the Jacobian matrices was recorded for 100 different $x_0$ values. As shown in Table 3, the mean time for evaluating ${\mathbb{J}}_{\mathit{approx}}$ was 24% less than the mean time required for evaluating ${\mathbb{J}}_{\mathit{exact}}$ with a zero RMSE value. On the other hand, for$\mathrm{\Delta }x$ = 10⁻⁹, the $\mathit{RMSE}$ for ${\mathbb{J}}_{\mathit{approx}}$ was 4.806 × 10⁻⁶ at $x_0$; this differs significantly from the RMSE for the 4-bus system, which was 1.396 × 10⁻⁹. The mean computational time for ${\mathbb{J}}_{\mathit{approx}}$ was 4.72 s, which was 78 times higher than that for ${\mathbb{J}}_{\mathit{proposed}}$.

Table 3.

Computation time (ms) for evaluating the Jacobian matrix for the 123-Bus test system.

	${\mathbb{J}}_{\mathit{exact}}$	${\mathbb{J}}_{\mathit{proposed}}$	${\mathbb{J}}_{\mathit{approx}}$
Mean	80.22	60.35	4718.97
Minimum	78.68	59.95	4695.60
Maximum	82.90	63.50	4800.86

For a moderately sized system, evaluating ${\mathbb{J}}_{\mathit{approx}}$ for a single iteration may consume more than 4 s, depending on the hardware and software used to solve for OPF. Thus, for a practical distribution system with hundreds of buses, evaluating ${\mathbb{J}}_{\mathit{approx}}$ in real time is impractical, and the error increases dramatically as the system becomes larger. In addition, developing ${\mathbb{J}}_{\mathit{exact}}$ is very time consuming and may lead to memory limitation errors, as explained previously. These considerations provide strong evidence of the need for a closed form Jacobian matrix, which could be easily coded and applied to solving real-time optimization problems in distribution systems, such as DER optimal management, transactive energy market clearing and the optimal pricing of DERs.

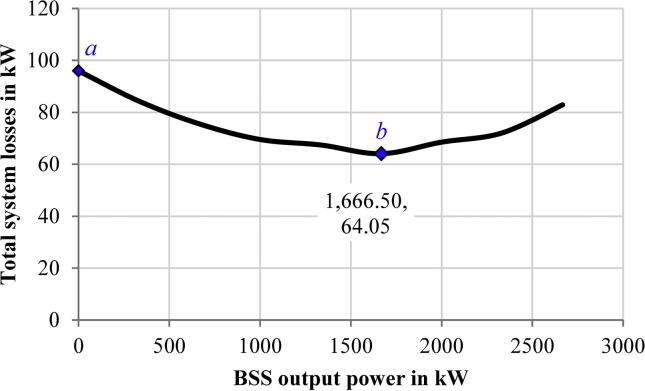
It is assumed that a BSS unit operating at a unity power factor is located at bus 49, which is chosen arbitrarily. Changing the output power of the BSS helps us in evaluating and minimizing the distribution system losses, as shown in Fig. 7. As indicated in the figure, the loss for the base case without the BSS was 95.94 kW at point a, which was very close to the value of the system loss reported in [32] (95.611 kW). As the injected power from the BESS increases, the system losses decrease, where the minimum loss was 64.05 kW at $P_{\mathit{bat}}$ = 1.667 MW, which is shown as point b in Fig. 7. The decrease in the system losses is attributed to the reduction in the current flowing from the grid to supply the loads, which are supplied partially by the BESS. For losses greater than 1.667 MW, increasing the injected power from the BESS causes an increase in the losses due to reverse power, where the excess current that flows from the BESS to the grid direction causes higher losses in the lines.

Fig. 7.

The total system losses for the 123-bus system versus the BSS output power.

To test the proposed Jacobian matrix computation method, the same NLP problem expressed in (30), (31), (32), (33), (34), (35) was used, with the BSS connected to bus 49. The minimum system loss was 61.045 kW at $P_{\mathit{bat}}$ = 1.6151 MW. Although the finite difference and the proposed Jacobian reached the same optimal solution, the computational times were 0.82158 and 25.57 s with and without applying the Jacobian method, respectively. The case study results clearly showed that applying the proposed Jacobian method could substantially reduce the OPF computational time.

Moreover, as the size of the system increases, the reduction becomes even greater, which emphasizes the necessity for providing the Jacobian of the constraints in real-time DER management or transactive energy market clearing; this may require solving a large OPF problem.

Conclusions

The work presented in this paper tackles a core element of any modern EMS, which is the optimization unit. The proposed approach targets the computational process for the optimization unit for real-time unbalanced SDN operations (e.g., smart grid applications). The proposed approach could help reduce the complexity and computational time associated with the SDN applications, which usually involve real-time optimal scheduling of the system assets (including DERs and demand response/DR). The paper includes a detailed formulation of the proposed generalized Jacobian matrix, which can be tailored according to the real-time measurements and available system data.

The formulation presented for unbalanced SDNs is based on three sets of derivatives for the power mismatch constraints: (1) the derivative w.r.t. the same bus and the same phase voltage magnitude, (2) the derivative w.r.t. the same bus and a different phase voltage magnitude, and (3) the derivative w.r.t. different bus voltage magnitudes. The proposed Jacobian matrix formulation can be applied to any distribution network after adjustments are made depending on the available equipment, such as voltage regulators and capacitor banks.

The simulation results demonstrated the effectiveness and scalability of the proposed formulation for evaluating the values of the Jacobian matrix entries in a timely manner and with zero RMSE error compared to the exact and approximated Jacobian evaluation methods. The results also provided enough evidence to support the need for using the proposed Jacobian matrix formulation in real-time OPF problem solving for smart grid applications, such as DER/DR optimal management and transactive energy market clearing.

Conflict of interest

The authors have declared no conflict of interest.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.