Abstract
Background:
The fractal dynamics of gait variability in people with Parkinson’s disease has been studied by applying the detrended fluctuations analysis (DFA) to short time series (<200 strides). However, DFA is sensitive to time series length, and it is unclear if DFA results from short time series are reliable and if they reflect the fractal dynamics of longer time series.
Research question:
Is DFA reliable when applied to short time series?
Methods:
We applied DFA to stride time series from five 3-min trials and one 15-min trial in 12 people with Parkinson’s disease, 14 healthy older adults and 14 healthy young adults walking overground. Within each group, intraclass correlations (ICC 3,1) were performed to assess the reliability of i) the five 3-min trials together, ii) each 3-min trials to the 15-min trial, and iii) the first 150 strides from the 15-min trial to the full 15-min trial.
Results:
Our three main findings are that 1) stride time α-DFA values are not consistent from trial-to-trial for short stride time series, 2) stride time α-DFA values from each 3-min trials are not consistent when compared to stride time α-DFA values from a 15-min trial, and 3) stride time α-DFA values from the first 150 strides of the 15-min trial are not consistent when compared to α-DFA values from the full 15-min trial.
Significance:
Our results confirm that α-DFA values from 3-min walking trials are not reliable, and that they do not reflect the scale invariant properties of longer time series. This suggests that previous studies assessing the fractal dynamics of gait variability from about 3-min walking must be interpreted with caution. A major clinical implication is that DFA cannot be used to study gait in people unable to perform 500 strides continuously.
Keywords: fractal fluctuations, gait variability, Parkinson’s disease, detrended fluctuation analysis, stride time series, overground walking
1. Introduction
Steady-state walking is characterized by the presence of subtle stride-to-stride variations, i.e., gait variability. The analysis of the temporal organization of gait variability has become an integral part of human gait research [1–5]. While many techniques exist to estimate the temporal organization of stride time series, the detrended fluctuation analysis (DFA) has been the most popular in recent years, mostly because it provides more accurate results from ‘short’ time series (e.g., between a few hundred and a thousand data points) [2–3, 6–9]. The outcome of the DFA is a scaling exponent α-DFA which informs about the statistical nature of fluctuations. In stationary time series, such as during steady-state human walking, random fluctuations correspond to α = 0.5, persistent fluctuations to α > 0.5 and anti-persistent fluctuations to α < 0.5. Persistence and anti-persistence refers to the likelihood that stride deviations will be followed by subsequent deviations in the same direction or in opposite direction, respectively. Healthy young adults walking overground produce persistent stride time fluctuations [4–5,10–11], but a drift toward randomness is observed with aging and neurological impairments, such as Parkinson’s disease (PD) [12–21]. A recent study evidenced a correlation between α-DFA and PD severity [20], supporting its importance in the study of gait dynamics, and in line with the hypothesis that α-DFA could be a marker for fall-risk and gait adaptability [22–23].
A significant limitation of DFA is its sensitivity to the length of the time series under consideration. Previous studies using either numerical or biological signals evidenced that time series shorter than 500 data points (e.g., corresponding to the number of stride intervals from about 10 minutes of self-paced walking) yield questionable results due to the high variance in the estimation of the scaling exponent [2–3, 9]. Despite these methodological considerations, the majority of previous research collected stride time series in people with neurological disorders for only two to five minutes (i.e., between 100 and 250 strides) [13–14, 16–19]. Further, comparing different groups or conditions based on a single observation implicitly assumes a high reliability of the variable of interest. Pierrynowski et al. [24] found a high within-day reliability of the scaling exponent collected during 3-min treadmill walking trials, but a relatively high standard error measurement. The authors acknowledged that their conclusions may not hold true during overground walking because stride time variability seems different between treadmill versus overground walking.
It is still unknown 1) if α-DFA from short time series is reliable in PD patients (and other populations) walking overground, and 2) if α-DFA from short stride time series represents α-DFA from longer stride time series. The purpose of this study was to estimate the within-day reliability of DFA from stride time series collected in people with PD walking overground for five trials of three minutes each. We collected stride time series from healthy young and older adults to estimate the effect of PD on the reliability of the measures. We also compared the reliability of each 3-min trials to a single 15-min trial. Our hypotheses were that i) there will be no significant differences between trials within each group for the stride time α-DFA values, and ii) the intraclass correlation coefficients will be poor for all three groups, suggesting that three minutes is not enough to obtain reliable scaling exponents of stride time series during overground walking.
2. Methods
This study is a re-analysis of data published in [25]. The study was approved prior to its conductance by the Institutional Review Board of the University of Nebraska Medical Center, and all participants gave written informed consent prior to their participation. Fifteen people with Parkinson’s disease (PD group; Hoehn & Yahr median and range: 1.5, 1-3), fifteen age-matched healthy elderly adults (HE group), and fifteen healthy young adults (HY group) participated in the experiment. One participant in the HE group, one participant in the HY group and three participants in the PD group were excluded from further analyses for different reasons (cf. Results). Therefore, analyses were applied to 14 HY (five female; age 23 ± 1.69 years old), 14 HE (nine female; age 67.71 ± 5.92 years old) and 12 PD (two female; age 71.31 ± 6.12 years old). All participants were able to ambulate independently for at least 20 minutes, and participants in the PD group must have been diagnosed with idiopathic PD as defined by the UK Brain Bank Criteria. Other eligibility criteria can be found in [25]. Participants in the PD group were assessed under their regular medication (‘on’-state). Welch’s t-test did not reveal any statistically significant differences between HE and PD groups for any variables. Other demographic information can be found in [25].
Participants were instructed to wear comfortable clothing and shoes. They walked with four force-sensitive footswitches (Trigno™ EMG System, Delsys Inc; 1942 Hz) placed directly under the heel and the forefoot of each foot, in order to collect initial contact (heel-strike) and final contact (toe-off) of each stride taken. Participants walked at a comfortable, self-selected speed around a 200-meter long indoor track. The entire protocol consisted of 45 minutes total of walking, divided into three blocks performed in a randomized order. The three blocks consisted of one 15-min trial, five 3-min trials, and thirty 30-sec trials. At least five minutes of rest was provided between blocks, and at least 30 seconds rest was provided between trials in the 3-min and 30-sec blocks. During the experiment, there was no visual evidence of freezing of gait nor festinating gait in any participant with PD. In the present study, we did not consider the ‘30-sec’ block, because 30 seconds of walking data is clearly not enough to apply DFA. We focused on each 3-min trials, and the full 15-min trial. We also analyzed the first 150 stride intervals from each full 15-min trial, to test if a short sample from a long time series provide α-DFA value similar to the longer time series itself (Figure 1)
Figure 1.
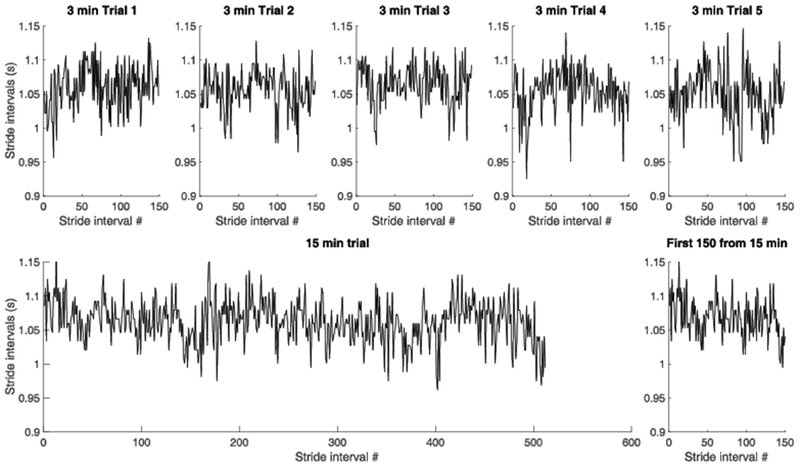
Representative example from one participant in the PD group of stride time series from each of the five 3-min trials (top), from the 15-min trial (bottom left) and from the first 150 strides in the 15-min trial (bottom right).
The main dependent variable in this study was the scaling exponent α-DFA of the series of stride intervals. Five strides were removed at the beginning and the end of each individual trial to reduce the effects of gait initiation and gait deceleration. The length of the stride time series – among every 3-min trials – ranged between 136 and 172 for the PD group, between 149 and 181 for the HE group, and between 135 and 187 for the HY group. The length of the stride time series for the 15-min trial was truncated to the first 512 stride time intervals for all participants (see [25] for details). Stride time series can be found in Supplementary data S1.
The scaling exponent α-DFA of stride time series was estimated using the evenly-spaced detrended fluctuation analysis (DFA) [26]. The methodology of DFA has been described in details elsewhere [2–5]. In this study, we used window sizes ranging from 10 to N/2 for the 3-min trials (and to N/8 for the 15-min trial), where N is the time series length. We made this choice because N/8 for shorter trials would result in estimating the slope based on only a dozen points. While increasing the maximum window size (from N/8 to N/2) may increase the variability of the slope estimation, evenly-spaced DFA tends to reduce the impact of the larger windows size on the slope estimation.
Two-way ANOVAs (3 groups × 5 trials) were used to compare the following measures from stride time intervals in the 3-min trials: mean, coefficient of variation (CV) and α-DFA. Post-hoc analysis entailed Tukey’s multiple comparison’s tests.
For each group, ICC estimates and their 95% confident intervals were calculated using SPSS statistical package version 23 (SPSS Inc, Chicago, IL) based on a single-measurement, absolute-agreement, two-way mixed-effects model (ICC 3,1) to determine the reliability of mean, CV and α-DFA. We compared 1) the five 3-min trials together, 2) each 3-min trials to the 15-min trial, and 3) the first 150 strides from the 15-min trial to the full 15-min trial. The reliability was graded based on the lower 95% CI values, with values less than 0.50 indicating poor reliability, values between 0.50 and 0.75 indicating moderate reliability, values between 0.75 and 0.90 indicating good reliability and values above 0.90 indicating excellent reliability [27–28]. Level of statistical significance was set at a p-value < 0.05.
3. Results
Three participants in the PD group and one participant in the HE group did not completed the fifth trial, and were therefore excluded from further analyses. One participant in the HY group was also excluded because of technical difficulties in the fifth trial.
The two-way ANOVA revealed no interaction effect (F(8,148)=0.4544, p=0.886), nor trial effect (F(4,148)=0.384, p=0.820) on stride time mean values. A group effect was detected (F(2,37)=4.525, p=0.017), and Tukey’s multiple comparisons test revealed that HE walked with significantly lower stride time intervals than HY (p=0.0136). The two-way ANOVA revealed no interaction effect (F(8,148)=0.714, p=0.680), but a trial effect (F(4,148)=2.442, p=0.049) and a group effect (F(2,37)=3.922, p=0.028) on stride time CV. Tukey’s multiple comparisons test revealed that stride time CV in PD was significantly greater than in HE (p=0.026), and significantly greater in trial 5 than in trial 2 (p=0.035). The two-way ANOVA revealed no interaction effect (F(8,148)=0.580, p=0.793), trial effect (F(4,148)=1.807, p=0.130), nor group effect (F(2,37)=2.089, p=0.138) on stride time α-DFA.
For the three groups, ICCs between the five 3-min trials were graded excellent for mean (Figure 2), but poor for CV and α-DFA (Table 1). ICCs between each 3-min trials and the 15-min trial were graded poor for mean, CV and α-DFA for the three groups (Figure 3), with the exception of mean in the HE group which were all graded between moderate and excellent (Table 2). ICCs between the first 150 strides from the 15-min trial and the full 15-min trial were graded as excellent for mean in the three groups; moderate for CV for the HY, but poor for the HE and PD groups; and poor for α-DFA for the three groups (Table 2).
Figure 2.
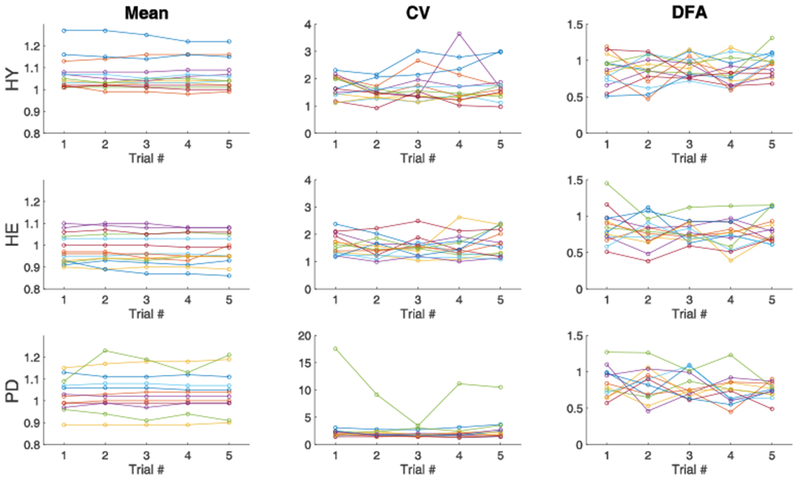
Comparison of the mean (left), coefficient of variation (middle) and α-DFA (right) from stride time series in the five 3-min trials in healthy young (top), healthy elderly (middle) and Parkinson’s disease (bottom) groups. Each color within a group represents a single participant.
Table 1.
Mean and standard deviation (SD) of stride time series means, coefficients of variation and α-DFA for each 3-min trials, and corresponding intraclass correlation coefficients (95 % confidence interval, CI). Means and standard deviations for the 15-min trial are also provided.
| Trial 1 Mean (SD) | Trial 2 Mean (SD) | Trial 3 Mean (SD) | Trial 4 Mean (SD) | Trial 5 Mean (SD) | ICC (95% CI) | 15 min trial Mean (SD) | ||
|---|---|---|---|---|---|---|---|---|
| HY | Mean (s) | 1.07 (0.07) | 1.06 (0.07) | 1.07 (0.07) | 1.07 (0.07) | 1.06 (0.07) | 0.98 (0.95-0.99) | 1.07 (0.07) |
| CV (%) | 1.69 (0.41) | 1.53 (0.31) | 1.71 (0.56) | 1.77 (0.73) | 1.73 (0.59) | 0.55 (0.31-0.78) | 1.76 (0.46) | |
| α-DFA | 0.86 (0.21) | 0.84 (0.20) | 0.91 (0.14) | 0.83 (0.19) | 0.95 (016) | 0.19 (0.01-0.50) | 0.89 (0.09) | |
| HE | Mean (s) | 0.98 (0.07) | 0.98 (0.07) | 0.98 (0.07) | 0.98 (0.07) | 0.98 (0.07) | 0.97 (0.96-0.99) | 0.99 (0.06) |
| CV (%) | 1.62 (0.38) | 1.50 (0.35) | 1.53 (0.36) | 1.54 (0.45) | 1.67 (0.50) | 0.50 (0.27-0.76) | 1.71 (0.49) | |
| α-DFA | 0.85 (0.24) | 0.78 (0.21) | 0.79 (0.14) | 0.75 (0.20) | 0.82 (0.20) | 0.46 (0.23-0.73) | 0.87 (0.16) | |
| PD | Mean (s) | 1.01 (0.08) | 1.01 (0.08) | 1.01 (0.09) | 1.02 (0.08) | 1.02 (0.09) | 0.95 (0.89-0.98) | 1.02 (0.08) |
| CV (%) | 2.07 (0.47) | 1.96 (0.40) | 1.90 (0.50) | 1.93 (0.54) | 2.21 (0.77) | 0.72 (0.50-0.89) | 2.20 (0.85) | |
| α-DFA | 0.84 (0.18) | 0.80 (0.19) | 0.82 (0.17) | 0.74 (0.18) | 0.78 (0.17) | 0.18 (−0.02-0.52) | 0.77 (0.12) |
HY Healthy young, HE Healthy elderly, PD Parkinson’s disease, CV Coefficient of variation, DFA Detrended fluctuation analysis, ICC Intraclass correlation.
Figure 3.
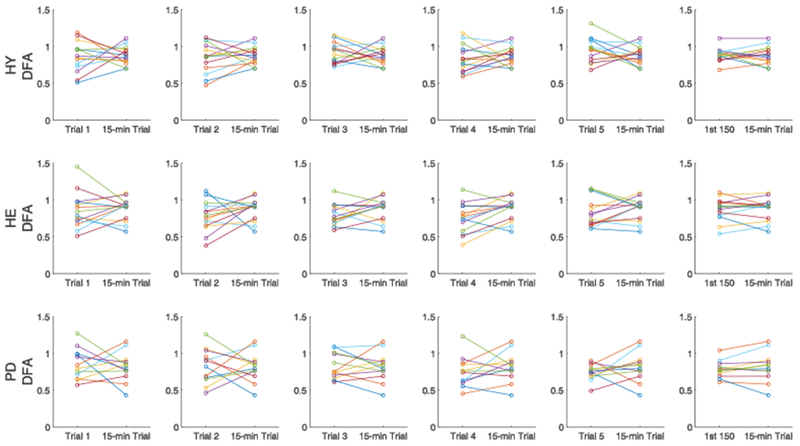
Comparison of α-DFA between each 3-min trials and the 15-min trial (five columns on the left), and between the first 150 strides from the 15-min trial and the full 15-min trial (right column) in healthy young (top), healthy elderly (middle) and Parkinson’s disease (bottom) groups. Each color within a group represents a single participant.
Table 2.
Intraclass correlation coefficients (95 % confidence interval, CI) of stride time series means, coefficients of variation and α-DFA between the 15-min trial and each 3-min trials (Trial 1 to Trial 5), and between the 15-min trial and the first 150 stride intervals from the 15-min trial.
| ICC (95 % CI) between each shorter trials and the 15 min trial | |||||||
|---|---|---|---|---|---|---|---|
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | First 150 from 15-min | ||
| HY | Mean | 0.35 (−0.22 – 0.73) | 0.34 (−0.25 – 0.73) | 0.34 (−0.25 – 0.73) | 0.24 (−0.35 – 0.66) | 0.23 (−0.36 – 0.68) | 0.99 (0.97 – 1.00) |
| CV | 0.37 (−0.21 – 0.75) | 0.31 (−0.17 – 0.70) | 0.53 (0.00 – 0.82) | 0.34 (−0.24 – 0.73) | 0.42 (−0.16 – 0.77) | 0.89 (0.63 – 0.96) | |
| α-DFA | −0.38 (−0.82 – 0.21) | 0.06 (−0.49 – 0.56) | −0.23 (−0.72 – 0.35) | 0.28 (−0.24 – 0.70) | −0.03 (−0.51 – 0.48) | 0.42 (−0.15 – 0.77) | |
| HE | Mean | 0.90 (0.72 – 0.97) | 0.96 (0.88 – 0.99) | 0.95 (0.85 – 0.98) | 0.94 (0.83 – 0.98) | 0.98 (0.95 – 0.99) | 0.99 (0.98 – 1.00) |
| CV | 0.52 (0.01 – 0.82) | 0.31 (−0.18 – 0.70) | 0.25 (−0.26 – 0.68) | 0.74 (0.35 – 0.91) | 0.52 (−0.01 – 0.82) | 0.90 (0.45 – 0.97) | |
| α-DFA | 0.30 (−0.30 – 0.71) | 0.07 (−0.40 – 0.55) | −0.07 (−0.53 – 0.44) | 0.46 (−0.03 – 0.78) | 0.33 (−0.21 – 0.72) | 0.77 (0.42 – 0.92) | |
| PD | Mean | 0.73 (0.30 – 0.91) | 0.41 (−0.20 – 0.79) | 0.52 (−0.06 – 0.83) | 0.65 (0.16 – 0.89) | 0.46 (−0.14 – 0.81) | 0.98 (0.93 – 0.99) |
| CV | 0.06 (−0.52 – 0.60) | 0.18 (−0.46 – 0.67) | 0.70 (0.27 – 0.90) | 0.14 (−0.49 – 0.65) | 0.21 (−0.38 – 0.69) | 0.58 (0.08 – 0.85) | |
| α-DFA | 0.10 (−0.47 – 0.61) | −0.17 (−0.73 – 0.45) | 0.36 (−0.25 – 0.76) | 0.23 (−0.41 – 0.70) | 0.04 (−0.54 – 0.59) | 0.76 (0.38 – 0.92) | |
HY Healthy young, HE Healthy elderly, PD Parkinson’s disease, CV Coefficient of variation, DFA Detrended fluctuation analysis, ICC Intraclass correlation.
4. Discussion
We tested the within-day reliability of α-DFA values of stride time series collected overground during five trials of three minutes in people with Parkinson’s disease, healthy elderly and healthy young adults. Our three main findings are that 1) there was poor absolute agreement of α-DFA values between the five 3min trials, independently of age and disease, 2) there was poor absolute agreement between stride time α-DFA values from each 3-min trials when compared to stride time α-DFA values from a longer, 15-min trial, and 3) there was poor absolute agreement between stride time α-DFA values from the first 150 strides of the 15-min trials when compared to α-DFA values from the full 15-min trial. Overall, these results confirm that α-DFA values from short walking trials are not consistent from trial-to-trial, and that they do not reflect the scale invariant properties of longer time series.
Applying DFA to stride time series collected during 3-min trials led to inconsistent results. This implies that α-DFA obtained during any of the 3-min trials may be completely different from α-DFA obtained from any other 3-min trials. This lack of reliability of α-DFA values from short stride time series was found not only in the PD group but also for healthy elderly and healthy young adults, suggesting this finding was not age- or disease-dependent. This finding is striking as the majority of studies ([20–21] being exceptions) assessed α-DFA in PD gait from a single short trial [13–19], due to the relatively long time needed to collect a few hundred strides or even multiple short trials. However, our results suggest that α-DFA obtained from one trial is not necessarily similar during another trial. This finding may challenge the conclusions drawn from previous studies collecting only 100 to 200 stride intervals [16–19]. This is consistent with previous literature assessing the precision of DFA in simulated and experimental time series, recommending to collect a minimum of 500 cycles [2–3, 8–9]. In contrast with previous literature, we did not find any statistically significant effect of groups on α-DFA. While beyond the scope of this paper, this tends to confirm that DFA applied on short time series is not sensitive enough to discriminate between groups. In particular, the dispersion of values within each group was very high (i.e., standard deviation of α-DFA for short trials between 0.14 and 0.24). Overall, these results suggest that one α-DFA value obtained during a single 3-min trial may be very different from another 3-min trial, even if collected just a few minutes after.
While α-DFA values were not reliable between short trials, we wanted to test if they could still provide a reliable estimation of α-DFA from a longer trial. Our results indicate that the scaling exponents obtained during any of the 3-min trials were not consistent with the scaling exponent from a longer 15-min trial (Table 2 and Figure 3). This lack of consistency was also evident for the mean and CV values, with the exception of mean values for the HE group. Overall, these results suggest that individual gait dynamics observed during (any) 3-min trial provide different information than gait dynamics during prolonged walking. Our findings challenge the potential clinical application of fractal analysis to clinical gait: the scaling exponent from short gait trials is not only not reliable from one trial to the next, but it also does not reflect the scale-invariant properties of stride-time fluctuations observed during longer (i.e., theoretically more reliable) walking trials.
We wanted to test if the low reliability between each 3-min trials and the 15-min trial mainly originated from the low precision of α-DFA from short time series, or from the fact that the stride time series were generated in different (independent) conditions. Our results show that α-DFA from the first 150 strides of the 15-min trial was not consistent when compared to a-DFA from the full 15-min trial. Notably, this result was found only for α-DFA, while mean and CV from the first 150 strides of the 15-min trial were very reliable to the full 15-min trial. This result confirms that the low between-trials consistency of α-DFA is mainly due to the time series lengths.
This study presents a number of limitations. The length of the time series from the 3-min trials were different from trial to trial, although each individual produced roughly the same amount of strides in each 3-min trials (cf. Supplementary Data S1). This choice made trial-to-trial comparisons more challenging, but in our opinion increased the ecological validity of our approach to answer the original research question, i.e., does DFA from two consecutive 3-min trials give similar scaling exponents? We also chose different maximum window sizes for DFA applied to 3-min or 15-min trials (N/2 vs. N/8, respectively). This choice was mainly driven by the necessity to obtain a sufficient number of values (i.e., number of windows of different sizes) to plot a line of best fit in log-log coordinates. The minimum time series length was 135, which would have led the analysis of only six different window sizes (i.e., from 10 to 135/8=16.875). It should also be stressed that people with PD in this study were primarily in the early-stage of the disease. Therefore, the conclusions of this study may not hold true for late-stage PD or even other neurological disorders. It is also important to remember that 15-min walking should not be considered a ‘gold-standard’ for applying DFA. This time series length was considered as the reference in the present study, but further studies should investigate the consistency of 15-min walking trials, and if they reflect similar dynamics as longer walking trials (e.g., one-hour walking). Finally, this study focused solely on evenly-spaced DFA, but other methods may improve the detection of the scaling exponent for very short time series (<200 strides), such as the adaptive fractal analysis [29–30]. These analyses are beyond the purpose of this study, which was to test the most commonly used method, not to determine which method would give the most reliable results.
5. Conclusions
This study evidenced that applying DFA to stride intervals collected during short trials is not reliable, and that the scaling exponents from short trials do not reflect gait dynamics on longer trials. This result was anticipated, based on numerous studies showing the necessity to apply DFA to longer time series (500 strides is typically recommended) [3, 8–9]. However, previous research studying PD gait dynamics applied DFA to shorter stride time series [16–19]. Our findings evidence that the results from such studies should be interpreted with extreme caution. Similar to other colleagues [9], we recommend that DFA should not be applied to time series shorter than 500 data points. While this constraint may reduce its applicability to clinical populations not capable of walking continuously for 15 minutes, it is necessary for meaningful interpretation of results.
Supplementary Material
Highlights.
We tested the reliability of fractal analysis on short stride time series.
Detrended fluctuations analysis was applied to five 3-min walking trials.
We compared people with Parkinson’s disease to older and young adults.
Between-trial reliability of scaling exponents from 3-min trials is poor.
Scaling exponents from 3-min trials do not reflect gait dynamics of longer trials.
Acknowledgements:
This work was supported by the University Committee on Research and Creative Activity of the University of Nebraska at Omaha, and by the Center for Research in Human Movement Variability of the University of Nebraska at Omaha, NIH (P20GM109090). The study sponsors were not involved in the collection, analysis and interpretation of data, in the writing of the manuscript, nor in the decision to submit the manuscript for publication. The views expressed are those of the authors and not necessarily those of the NIH. The authors thank Daniel Jaravata for his support with data processing.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest
The authors declared no potential conflict of interest with respect to the research, authorship, and publication of this article. This manuscript has not been published and is not under consideration for publication elsewhere.
References
- 1.Choi JS, Kang DW, Seo JW, and Tack GR (2015). Reliability of the walking speed and gait dynamics variables while walking on a feedback-controlled treadmill. J. Biomech 48, 1336–1339. doi: 10.1016/j.jbiomech.2015.02.047 [DOI] [PubMed] [Google Scholar]
- 2.Damouras S, Chang MD, Sejdić E, and Chau T (2010). An empirical examination of detrended fluctuation analysis for gait data. Gait Posture 31, 336–340. doi: 10.1016/j.gaitpost.2009.12.002 [DOI] [PubMed] [Google Scholar]
- 3.Delignières D, Ramdani S, Lemoine L, Torre K, Fortes M, and Ninot G (2006). Fractal analysis for short time series: a reassessement of classical methods. J. Math. Psychol 50, 525–544. doi: 10.1016/j.jmp.2006.07.004 [DOI] [Google Scholar]
- 4.Dingwell JB, and Cusumano JP (2010). Re-interpreting detrended fluctuation analyses of stride-to-stride variability in human walking. Gait Posture 32, 348–353. doi: 10.1016/j.gaitpost.2010.06.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hausdorff JM, Peng CK, Ladin Z, Wei JY, and Goldberger AL (1995). Is walking a random walk? Evidence for long-range correlations in the stride interval of human gait. J. Appl. Physiol 78, 349–358. doi: 10.1152/jappl.1995.78.1.349 [DOI] [PubMed] [Google Scholar]
- 6.Peng CK, Mietus J, Hausdorff JM, Havlin S, Stanley HE, and Goldberger AL (1993). Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett 70, 1343–1346. doi: 10.1103/PhysRevLett.70.1343 [DOI] [PubMed] [Google Scholar]
- 7.Chen Z, Ivanov PC, Hu K, and Stanley HE (2002). Effect of nonstationarities on detrended fluctuation analysis. Phys. Rev. E 65(4), 041107. doi: 10.1103/PhysRevE.65.041107 [DOI] [PubMed] [Google Scholar]
- 8.Kuznetsov NA, and Rhea CK (2017). Power considerations for the application of detrended fluctuation analysis in gait variability studies. PLoS ONE 12(3), e0174144. doi 10.1371/joumal.pone.0174144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Warlop T, Bollens B, Detrembleur C, Stoquart G, Lejeune T, and Crevecoeur F (2018). Impact of series length on statistical precision and sensitivity of autocorrelation assessment in human locomotion. Hum. Mov. Sci 55, 31–42. 10.1016/j.humov.2017.07.003 [DOI] [PubMed] [Google Scholar]
- 10.Marmelat V, Torre K, and Delignières D Relative roughness: an index for testing the suitability of the monofractal model. Front Physio 3, 208. doi: 10.3389/fphys.2012.00208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Terrier P, Turner V, and Schutz Y (2005). GPS analysis of human locomotion: Further evidence for long-range correlations in stride-to-stride fluctuations of gait parameters. Hum. Mov. Sci 24, 97–115. doi: 10.1016/j.humov.2005.03.002 [DOI] [PubMed] [Google Scholar]
- 12.Goldberger AL, Amaral LAN, Hausdorff JM, Ivanov PC, Peng CK, and Stanley HE. (2002). Fractal dynamics in physiology: alterations with disease and aging. Proc. Natl. Acad. Sci. USA. 99, 2466–2472. doi: 10.1073/pnas.012579499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hausdorff JM, Lertratanakul A, Cudkowicz ME, Peterson AL, Kaliton D, and Goldberger AL (2000). Dynamic markers of altered gait rhythm in amyotrophic lateral sclerosis. J. Appl. Physiol 88, 2045–2053. doi: 10.1152/jappl.2000.88.6.2045 [DOI] [PubMed] [Google Scholar]
- 14.Hausdorff JM, Mitchell SL, Firtion R, Peng CK, Cudkowicz ME, Wei JY, et al. (1997). Altered fractal dynamics of gait: Reduced stride-interval correlations with aging and Huntington’s disease. J. Appl. Physiol 82, 262–269. doi: 10.1152/jappl.1997.82.1.262 [DOI] [PubMed] [Google Scholar]
- 15.Hausdorff JM (2007). Gait dynamics, fractals and falls: Finding meaning in the stride-to-stride fluctuations of human walking. Hum. Mov. Sci 26, 555–589. doi: 10.1016/j.humov.2007.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hove MJ, Suzuki K, Uchitomi H, Orimo S, and Miyake Y (2012). Interactive rhythmic auditory stimulation reinstates natural 1/f timing in gait of Parkinson’s patients. PLoS ONE 7(3), e32600. doi: 10.1371/journal.pone.0032600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kirchner M, Schubert P, Liebherr M, and Haas CT (2014). Detrended Fluctuation Analysis and Adaptive Fractal Analysis of Stride Time Data in Parkinson’s Disease: Stitching Together Short Gait Trials. PLoS ONE 9(1), e85787. doi: 10.1371/joumal.pone.0085787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ota L, Uchitomi H, Ogawa KI, Orimo S, and Miyake Y (2014). Relationship between Neural Rhythm Generation Disorders and Physical Disabilities in Parkinson’s Disease Patients’ Walking. PLoS ONE 9(11), el 12952. doi: 10.1371/joumal.pone.0112952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Uchitomi H, Ota L, Ogawa KI, Orimo S, and Miyake Y (2013). Interactive rhythmic cue facilitates gait relearning in patients with Parkinson’s disease. PLoS ONE 8, e72176. doi: 10.1371/journal.pone.0072176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Warlop T, Detrembleur C, Bollens B, Stoquart G, Crevecoeur F, Jeanjean A, et al. (2016). Temporal organization of stride duration variability as a marker of gait instability in Parkinson’s disease. J. Rehab. Med 48, 865–871. doi: 10.2340/16501977-2158 [DOI] [PubMed] [Google Scholar]
- 21.Warlop T, Detrembleur C, Stoquart G, and Jeanjean A (2018). Gait complexity and regularity are differently modulated by treadmill walking in Parkinson’s disease and healthy population. Front. Physiol 9:68. doi: 10.3389/fphys.2018.00068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stergiou N, and Decker LM (2011). Human movement variability, nonlinear dynamics, and pathology: Is there a connection? Hum. Mov. Sci 30, 869–888. doi: 10.1016/j.humov.2011.06.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.van Orden G, Kloos H, and Wallot S (2009). Living in the pink: Intentionality, wellbeing, and complexity In: Hooker C (Ed.) Handbook of the Philosophy of Science Volume 10: Philosophy of Complex Systems (pp. 639–683). New York: Elsevier, doi: 10.1016/B978-0-444-52076-0.50022-5 [DOI] [Google Scholar]
- 24.Pierrynowski MR, Gross A, Miles M, Galea V, McLaughlin L, and McPhee C (2005). Reliability of the long-range power-law correlations obtained from the bilateral stride intervals in asymptomatic volunteers whilst treadmill walking. Gait Posture 22, 46–50. doi: 10.1016/j.gaitpost.2004.06.007 [DOI] [PubMed] [Google Scholar]
- 25.Marmelat V, Reynolds NR, and Heilman A (2018). Gait dynamics in Parkinson’s disease: short gait trials “stitched” together provide different fractal fluctuations compared to longer trials. Front. Physiol 9:861. doi: 10.3389/fphys.2018.00861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Almurad ZMH, and Delignières D (2016). Evenly spacing in Detrended Fluctuation Analysis. PhysicaA 451, 63–69. 10.1016/j.physa.2015.12.155 [DOI] [Google Scholar]
- 27.Cicchetti DV (1994). Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess 6(4), 284. doi: 10.1037/1040-3590.6.4.284 [DOI] [Google Scholar]
- 28.Koo TK, and Li MY (2016). A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropract. Med 15(2), 155–163. 10.1016/j.jcm.2016.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kuznetsov N, Bonnette S, Gao J, and Riley MA (2013). Adaptive fractal analysis reveals limits to fractal scaling in center of pressure trajectories. Ann. Biomed. Eng 41(8), 1646–60. doi: 10.1007/s10439-012-0646-9. [DOI] [PubMed] [Google Scholar]
- 30.Riley MA, Bonnette S, Kuznetsov N, Wallot S, and Gao J (2012). A tutorial introduction to adaptive fractal analysis. Front. Physiol, 3, 371 10.3389/fphys.2012.00371. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


