Body fat estimates from bioelectrical impedance equations in cardiovascular risk assessment: The PREVEND cohort study

Abstract

Aims

To investigate prospectively the association of body fat percentage (BF%) estimates using various equations from bioelectrical impedance analysis (BIA) with cardiovascular events, compared with body mass index (BMI) and waist circumference.

Methods and results

We used data of 34 BIA-BF%-equations that were used for estimation of BF% in 6486 (men = 3194, women = 3294) subjects. During a median follow-up of 8.3 years, 510 (7.9%) cardiovascular events (363 in men; 147 in women) occurred. In men, the crude hazard ratio (95% confidence interval) for BF% from the best predicting BIA-BF%-equation was 3.97 (3.30–4.78) against 2.13 (1.85–2.45) for BF% from the BIA device's BIA-BF%-equation, 1.34 (1.20–1.49) for BMI and 1.49 (1.40–1.73) for waist circumference per log-1-SD increase of all. In women, the hazard ratios for best predicting BIA-BF%-equation, BIA device estimation, BMI and waist circumference were 3.80 (2.85–4.99), 1.89 (1.57–2.28), 1.35 (1.21–1.51) and 1.52 (1.31–1.75), respectively. After adjustments for age, Framingham cardiovascular disease risk score and creatinine excretion – a marker of muscle mass – BF%s and BMI remained independently associated with cardiovascular events in both men and women, while waist circumference was independently associated with cardiovascular events in men, but not in women. According to discrimination ability (C-index) and additive predictive value (net reclassification index and integrated discrimination index) on obesity measures to the Framingham cardiovascular disease risk score, BF% was superior to BMI and waist circumference in both men and women.

Conclusions

BF% was independently associated with future cardiovascular events. Body fat estimates from the best-predicting BIA-BF%-equations can be a more predictive measurement in cardiovascular risk assessment than BMI or waist circumference.

Introduction

Cardiovascular disease (CVD) is a major cause of mortality in both men and women.¹ While men have the highest CVD incidence, CVD is increasing in women, especially younger women.² This creates a need to investigate whether CVD indicators in women differ from those in men. One potential candidate could be the risk related to adiposity.³ Although excess body fat is recognized as an important causal factor, the strength of its association with CVD may depend on the method used to measure adiposity, and there may be differences between men and women.^4,5

The most commonly used measures in CVD risk assessment to date are body mass index (BMI) and waist circumference.⁶ Importantly, these biometric measures do not differentiate between fat and fat-free mass, the latter of which includes muscle mass, which may be inversely associated with CVD risk.^7,8 Furthermore, the accurate evaluation of waist circumference could depend on measurement procedures, and it is also only a poor measure of the intra-abdominal fat mass it is supposed to measure, thereby weakening its association.⁹ Other methods used to measure adiposity more accurately, such as magnetic resonance imaging, dual-energy X-ray absorptiometry or computed tomography scan, are usually expensive, labour-intensive and require radiation exposure.^10,11 The exception may be bioelectrical impedance analysis (BIA). BIA is non-invasive, feasible, low cost and potentially useful, particularly in clinical evaluation.^11,12 The principle underpinning this method is that measurement is possible because lean body mass conducts electricity more efficiently than fat mass does. By placing electrodes on the hands and feet, for example, it is possible quickly to measure how efficiently electricity is conducted through the body or impeded.^10,12 Several BIA-body fat percentage (BF%)-equations are available which use impedance measures to calculate body fat, fat-free mass and total body water.^10,12,13

Previous studies have compared how various obesity measures are associated with individuals' cardiovascular risk profiles. Few have included BIA, and it is not clear which measure best predicts CVD.^5,13–15 Another issue is that, with the plethora of BIA-BF%-equations available for estimating BF%, it is not clear which equation is best.¹³ Therefore, we hypothesized that BF% estimated by the best fitted BIA-BF%-equation might be a better predictor of future cardiovascular events than BMI and waist circumference.

The aim of this study is to investigate prospectively the association between estimated body fat measured by bioelectrical impedance analysis with future cardiovascular events, compared with BMI and waist circumference, and particularly to assess the predictive value of body fat estimates using various BIA-BF%-equations and compare these differences between men and women.

Materials and methods

Study population

This study was conducted with participants from the Prevention of Renal and Vascular End-stage Disease (PREVEND) study. The PREVEND is a prospective Dutch cohort drawn from the general population, which began in 1997. The study design and recruitment processes are described in detail elsewhere.¹⁶ We used data from the second survey (2001–2002, n = 6894) as the baseline for the current analysis because the BIA measurement was only available from this period. We excluded participants with a history of CVD (n = 201) and missing BIA data (n = 168). Moreover, 39 participants were lost to follow-up between the baseline and the first cardiovascular event, leaving a total of 6486 participants.

The PREVEND study was approved by the local medical ethics committee of the University Medical Centre Groningen and conducted in accordance with the Declaration of Helsinki. All participants provided informed written consent.¹⁶

Measurements at baseline

Body weight and height were measured to calculate BMI as the ratio between weight (kilograms) and the square of height (metres). Minimum waist circumference was measured on bare skin at the natural indentation between the 10th rib and the iliac crest. When there was no indentation we measured it in the middle between navel and rib cage. Systolic and diastolic blood pressures were calculated as the mean of the last two measurements.¹⁶ A single frequency BIA device (BIA 101, RJL systems, Akern SRL, Italy) was used to measure whole-body electrical impedance at 50 kHz between the hand and the foot. The bioelectrical impedance measures obtained were used to estimate body fat percentages.¹⁶ Creatinine excretion – a marker of muscle mass – was calculated as the mean of the two 24-h urine collections.⁸ The analytical methods for urine collection and other fasting blood sample methods are described in greater detail elsewhere.^8,16

Baseline cardiovascular risk was evaluated using the Framingham 10-year CVD risk score including age, total and high-density lipoprotein (HDL) cholesterol level, current smoking status, systolic blood pressure, anti-hypertensive medication use and diabetes.¹⁷ Prevalent CVD was defined based on self-reported diagnosis by a physician of cardiac, cerebral and peripheral vascular morbidity.

Body fat estimation

The device we used to measure bioelectrical impedance provided an estimate of BF% using the manufacturer's unpublished BIA-BF%-equation. We also used 33 BIA-BF%-equations to estimate BF%s. The equations were selected based on their having been developed for adults (Supplementary Material Table S1 online).^10,12,13,18

BIA-BF%-equations are developed to estimate various aspects of the body composition, including lean body mass (LBM), fat-free mass (FFM), total body water (TBW) and body fat mass. We used the following conversions to estimate BF%: FFM = 0.97 * LBM for men and FFM = 0.92 * LBM for women; FFM = TBW/0.73; BF% = (body weight – FFM)/body weight.^10,13 After conversion, a total of 34 different body fat estimates were eligible for evaluation for the prediction of CVD.

Cardiovascular events

We used the combined incidence of cardiovascular morbidity and cardiovascular mortality as our outcome measure, which we term ‘cardiovascular event’ in the remaining analyses. Information on cardiovascular morbidity was obtained from PRISMANT, the Dutch national registry of hospital discharge diagnoses. Data on mortality were obtained from the municipal register. Outcome data were coded according to the International Classification of Diseases, Ninth Revision (ICD-9) until 1 January 2009 and after this date ICD-10 codes were used. Cardiovascular events were defined as follows: acute myocardial infarction, acute and subacute ischaemic heart disease, subarachnoid haemorrhage, intracerebral haemorrhage, other intracranial haemorrhage, occlusion or stenosis of the pre-cerebral or cerebral arteries, coronary artery bypass grafting or percutaneous transluminal coronary angioplasty, and other vascular interventions. Follow-up was defined in our study as the period from the second survey to the date of the first cardiovascular event, death or 1 January 2011.

Statistical analysis

All the analyses were performed separately for men and women. The study characteristics were expressed as means with a standard deviation (SD) for normally distributed variables, medians with interquartile range for non-normally distributed variables or numbers with percentages (%) according to the participants with and without cardiovascular events. The differences between groups were compared using Student's t-test or the Mann–Whitney U test and Chi-Square test. The age-adjusted Pearson partial correlation coefficient was calculated to evaluate associations of body fat estimates with baseline characteristics.

Cox proportional hazard regression analysis was used to examine the association between BF% from various BIA-BF%-equations and future cardiovascular events and to compare this association with BMI and waist circumference. After crude Cox regression analysis, we adjusted all the obesity measures for age (Model1), Framingham CVD Risk Score (Model2) and creatinine excretion – a marker of muscle mass –(Model3). The outcomes were presented as hazard ratio per standardized log (1-SD) unit increase, to enable better comparison between the obesity measures. To compare the hazard ratio for obesity measures, the z-statistic test was calculated and each BIA-BF%-equation was compared with the BMI and waist circumference respectively.¹⁹ Product-terms of obesity measures and gender were added to test for potential gender differences of the associations of obesity measures with CVD.

Harrell's C-index was used to compare the discrimination of the obesity measures by adding each obesity measure (extended models) to the Framingham CVD risk score (base model) for the CVD prediction^17,20 based on regression analysis. In addition, significance of the increases in C-index was tested by differences in -2 log likelihood of regression models with and without obesity measures. Furthermore, the net reclassification index (NRI) and integrated discrimination index (IDI) were used to assess the additive predictive value of obesity measures over the Framingham CVD risk score as the general CVD risk factor in assessing the improvement of obesity measures.²¹ Calculations were based on the movement of an individual ‘up’ or ‘down’ when reclassifying people with and without cardiovascular events through the addition of each obesity measure to the Framingham CVD risk score (NRI) and on the improvement in the mean sensitivity and any increase in 1-Specifity with obesity measures (IDI).²¹

Subgroup analysis was performed in age categories. The population was categorized as being over or under 55 years old, according to the World Health Organization guideline.²² The analysis was not performed for the female population, as the number of events was insufficient.

Data used to calculate the Framingham CVD risk score up to 3.0% was missing. We performed a single imputation with predictive mean matching for missing data. A two-sided statistical significance was set at p < 0.05 for all tests. All statistical analyses were performed using SPSS software V.22 (Chicago, IL, USA) and R software V.3.2.2 (http://www.r-project.org) and its libraries ‘survIDINRI’ and ‘CsChange’.

Results

The male and female participants who experienced a cardiovascular event were older and had worse cardiometabolic profiles with higher BMI but lower muscle mass compared with participants who had not experienced a cardiovascular event (Table 1). The BF% from BIA device and other BF%s from BIA-BF%-equations (Supplementary Table S2) were all significantly higher in both male and female participants with a cardiovascular event (p < 0.05). Age-adjusted Pearson correlation analysis yielded body fat estimates from different BIA-BF%-equations which were all significantly associated with other obesity measures and creatinine excretion (Supplementary Table S3) and CVD risk factors (Supplementary Table S4).

Table 1.

Baseline characteristics.

	Total	CV event
		Without	With	p value
Men
Number (%)	3194 (49.2)	2831 (47.7)	363 (71.2)	–
Age, years	53.8 ± 12.3	52.6 ± 12.0	63.5 ± 10.4	<0.0001
Obesity measures
Body fat mass, %a	26.9 ± 6.3	26.5 ± 6.2	30.1 ± 5.8	<0.0001
BMI, kg/m2	26.7 ± 3.7	26.6 ± 3.7	27.7 ± 3.5	<0.0001
Waist circumference, cm	97.0 ± 11.1	96.5 ± 11.0	101.3 ± 10.6	<0.0001
Creatinine excretion, µmol/L)	14.88 ± 3.27	14.98 ± 3.27	14.16 ± 3.18	<0.0001
Cardiovascular risk factors
Current smokers, n (%)	881 (27.6)	760 (26.8)	121 (33.3)	0.012
Alcohol drinkers, n (%)	2589 (81.1)	2319 (81.9)	270 (74.4)	<0.0001
SBP, mmHg	129.2 ± 16.8	129.2 ± 16.8	141.6 ± 20.1	<0.0001
Total cholesterol, mmol/L	5.41 ± 1.03	5.40 ± 1.01	5.52 ± 1.17	0.033
HDL cholesterol, mmol/L	1.12 ± 0.26	1.13 ± 0.26	1.08 ± 0.27	0.001
Triglycerides, mmol/L	1.52 ± 1.19	1.48 ± 1.13	1.80 ± 1.54	<0.0001
C-reactive protein, mmol/L	1.27 (0.61–2.74)	1.18 (0.58–2.61)	2.04 (0.97–4.55)	<0.0001
Framingham CVD risk score	13.9 ± 5.8	13.3 ± 5.7	17.1 ± 3.7	<0.0001
Type 2 diabetes, n (%)	116 (3.6)	83 (2.9)	33 (9.1)	<0.0001
Women
Number (%)	3292 (50.8)	3145 ( 52.6)	147 (28.8)	–
Age, years	52.3 ± 11.6	51.8 ± 11.4	62.5 ± 10.9	<0.0001
Obesity measures
Body fat mass, %a	36.3 ± 7.3	36.1 ± 7.3	40.2 ± 6.5	<0.0001
BMI, kg/m2	26.6 ± 4.9	26.5 ± 4.9	28.6 ± 5.2	<0.0001
Waist circumference, cm	87.3 ± 12.5	87.1 ± 12.4	93.0 ± 12.3	<0.0001
Creatinine excretion, µmol/L	10.5 ± 2.3	10.6 ± 2.3	9.73 ± 2.49	<0.0001
Cardiovascular risk factors
Current smokers, n (%)	933 (28.3)	880 (28.0)	53 (36.1)	0.040
Alcohol drinkers, n (%)	2207 (67.0)	2139 (68.0)	68 (46.3)	<0.0001
SBP, mmHg	122.2 ± 19.0	121.5 ± 18.6	138.4 ± 21.4	<0.0001
Total cholesterol, mmol/L	5.46 ± 1.05	5.45 ± 1.05	5.78 ± 1.04	<0.0001
HDL cholesterol, mmol/L	1.37 ± 0.32	1.38 ± 0.32	1.27 ± 0.32	<0.0001
Triglycerides, mmol/L	1.19 ± 0.72	1.18 ± 0.71	1.46 ± 0.87	<0.0001
C-reactive protein, mmol/L	1.41 (0.63–3.29)	1.39 (0.61–3.20)	2.75 (1.18–5.49)	<0.0001
Framingham CVD risk score	11.6 ± 6.2	11.3 ± 6.1	16.1 ± 3.8	<0.0001
Type 2 diabetes, n (%)	85 (2.6)	69 (2.2)	16 (10.9)	<0.0001

Data are presented as mean ± SD or median (interquartile range, 25th–75th percentile) and number (percentage).

^aDefault estimate for BF% using the device's unpublished BIA-BF%-equation.

CV: cardiovascular; BMI: body mass index; SBP: systolic blood pressure; HDL: high-density lipoprotein; CVD: cardiovascular disease; BF%: body fat percentage; BIA: bioelectrical impedance analysis

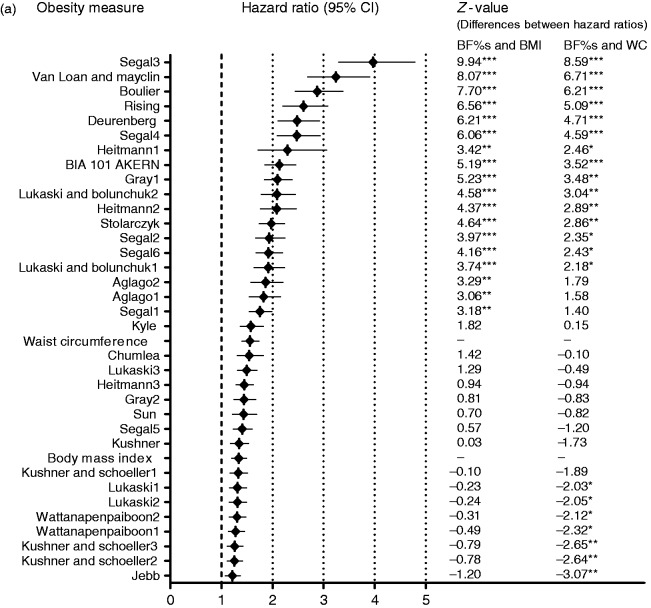
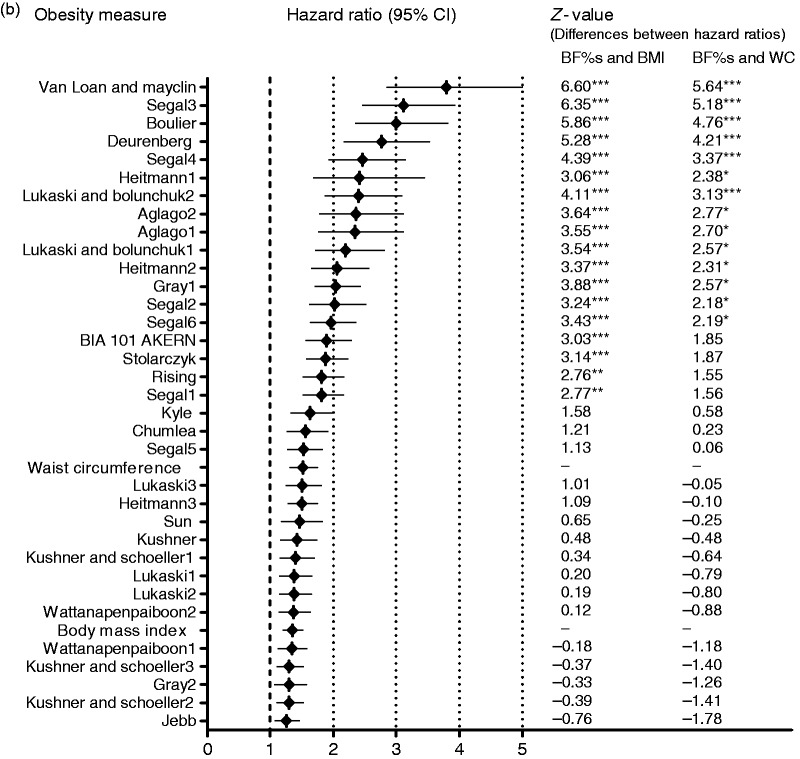
A total of 510 (7.9%) participants experienced a cardiovascular event (363 in men; 147 in women) after a median follow-up of 8.3 (7.8–8.9) years. The hazard ratio (95% confidence interval) for the BF% from the best predicting BIA-BF%-equation (Segal3) in men was 3.97 (3.30–4.78), against 1.34 (1.20–1.49) for BMI and 1.49 (1.40–1.73) for waist circumference. In women, these hazard ratios were 3.80 (2.85–4.99), 1.35 (1.21–1.51) and 1.52 (1.31–1.75) for the best predicting BIA-BF%-equation (Van-Loan-Mayclin), BMI and waist circumference respectively. All in all, crude hazard ratios for >10 BIA-BF%-equations were significantly higher than those for BMI and waist circumference (Figure 1; Supplementary Table S5). The prediction value of all 34 BIA-BF%-equations was attenuated, with 33 equations remaining statistically significant in men and one in women after adjustment for age and Framingham CVD risk score and creatinine excretion. For the other obesity measures, BMI and waist circumference were independently associated with CVD in men. In women, BMI association with CVD remained statistically significant while waist circumference was no longer related to CVD after adjustment for Framingham CVD risk score. On adding creatinine excretion, the predictions became slightly stronger for both men and women (p < 0.001; Tables 2 and 3). Formal testing for interaction between obesity measures and gender for associations with CVD did not yield significant p-values.

Figure 1.

Comparison of the crude hazard ratios per standardized log unit increase for obesity measures in CVD prediction in (a) men, (b) women. z-values indicate the differences between hazard ratios for BF% estimates and BMI or waist circumference. The z-value calculation was applied as z = (b[O1]-b[O2])/SE, where b[O1] and b[O2] are regression coefficients of the obesity measures, while SE is the standard error of the difference in the coefficients. This was computed as the square root of the sum of the squares of the standard errors for two coefficients. *p<0.05; **p<0.01; ***p<0.001.

CI: confidence interval; BF%: body fat percentage; BMI: body mass index; WC: waist circumference

Table 2.

Associations of BIA-BF%-equations, body mass index and waist circumference with cardiovascular events in men.

Obesity measures	Hazard ratio (95% CI)
	Model 1	Model 2	Model 3
Body mass index	1.26 (1.12–1.42)****	1.24 (1.10–1.40)**	1.28 (1.12–1.47)****
Waist circumference	1.30 (1.15–1.47)****	1.27 (1.12–1.44)****	1.32 (1.15–1.51)****
Body fat percentage
BIA 101 AKERN	1.23 (1.04–1.45)*	1.22 (1.03–1.44)*	1.23 (1.03–1.46)*
Heitmann1	1.76 (1.29–2.39)****	1.67 (1.22–2.28)**	1.77 (1.27–2.46)***
Heitmann2	1.41 (1.17–1.70)****	1.37 (1.13–1.65)**	1.41 (1.16–1.73)**
Segal1	1.32 (1.15–1.53)****	1.29 (1.12–1.49)**	1.34 (1.14–1.56)***
Segal2	1.36 (1.15–1.61)****	1.32 (1.12–1.56)**	1.35 (1.13–1.60)**
Segal3	1.68 (1.25–2.24)***	1.59 (1.19–2.14)**	1.58 (1.18–2.13)**
Segal4	1.45 (1.19–1.76)****	1.40 (1.15–1.71)**	1.41 (1.15–1.73)**
Segal5	1.29 (1.12–1.49)****	1.26 (1.10–1.45)**	1.31 (1.12–1.53)**
Segal6	1.36 (1.17–1.58)****	1.32 (1.14–1.54)****	1.37 (1.16–1.62)****
Van-Loan-Mayclin	1.60 (1.27–2.02)****	1.53 (1.21–1.94)****	1.59 (1.24–2.05)****
Kyle	1.28 (1.10–1.50)***	1.26 (1.08–1.46)**	1.28 (1.09–1.51)**
Aglago1	1.27 (1.06–1.53)*	1.24 (1.03–1.49)*	1.27 (1.04–1.54)*
Deurenberg	1.40 (1.15–1.69)****	1.35 (1.11–1.64)**	1.37 (1.12–1.68)**
Boulier	1.22 (0.98–1.53)
Chumlea	1.26 (1.06–1.49)***	1.23 (1.04–1.46)*	1.23 (1.03–1.47)*
Gray1	1.37 (1.17–1.60)****	1.33 (1.14–1.55)****	1.36 (1.16–1.61)****
Gray2	1.24 (1.06–1.45)**	1.21 (1.03–1.42)*	1.21 (1.03–1.42)*
Jebb	1.18 (1.04–1.3)*	1.16 (1.02–1.31)*	1.18 (1.03–1.35)*
Lukaski1	1.17 (1.03–1.34)*	1.15 (1.01–1.31)*	1.15 (1.01–1.32)*
Lukaski2	1.17 (1.03–1.34)*	1.15 (1.01–1.31)*	1.15 (1.01–1.32)*
Lukaski3	1.22 (1.07–1.40)**	1.20 (1.04–1.37)*	1.20 (1.05–1.38)*
Rising	1.31 (1.07–1.61)*	1.27 (1.03–1.56)*	1.29 (1.04–1.60)*
Stolarczyk	1.37 (1.18–1.59)****	1.34 (1.15–1.55)****	1.37 (1.18–1.61)****
Wattanapenpaiboon1	1.17 (1.03–1.33)*	1.16 (1.02–1.32)*	1.16 (1.02–1.32)*
Wattanapenpaiboon2	1.17 (1.03–1.33)*	1.15 (1.01–1.31)*	1.16 (1.01–1.32)*
Sun	1.22 (1.03–1.45)*	1.19 (1.01–1.42)*	1.19 (1.00–1.42)*
Aglago2	1.27 (1.06–1.52)*	1.24 (1.03–1.49)*	1.26 (1.04–1.53)*
Heitmann3	1.26 (1.11–1.42)****	1.23 (1.09–1.40)**	1.25 (1.09–1.42)**
Kushner	1.18 (1.02–1.34)*	1.15 (1.00–1.32)*	1.15 (1.00–1.32)*
Kushner_Schoeller1	1.17 (1.02–1.34)*	1.15 (1.00–1.31)*	1.15 (1.00–1.32)*
Kushner_Schoeller2	1.18 (1.04–1.33)*	1.16 (1.02–1.31)*	1.17 (1.02–1.33)*
Kushner_Schoeller3	1.17 (1.04–1.33)*	1.16 (1.02–1.31)*	1.17 (1.02–1.33)*
Lukaski_Bolunchuk1	1.24 (1.04–1.47)*	1.21 (1.02–1.44)*	1.22 (1.02–1.45)*
Lukaski_Bolunchuk2	1.24 (1.04–1.49)*	1.21 (1.01–1.45)*	1.22 (1.02–1.46)*

Model1: adjusted for age; Model2: adjusted for age, Framingham CVD risk score; Model3: adjusted for age, Framingham CVD risk score, creatinine excretion – a marker of muscle mass.

Data are presented if the measures remained significant after further adjustments.

^*p < 0.05

^**p < 0.01

^***p < 0.001

^****p < 0.0001

BIA: bioelectrical impedance analysis; BF%: body fat percentage; CI: confidence interval; CVD: cardiovascular disease

Table 3.

Associations of BIA-BF%-equations, body mass index and waist circumference with cardiovascular events in women.

Obesity measures	Hazard ratio (95% CI)
	Model 1	Model 2	Model 3
Body mass index	1.19 (1.04–1.37)*	1.16 (1.01–1.33)*	1.19 (1.03–1.38)*
Waist circumference	1.21 (1.02–1.43)*
Body fat percentage
BIA 101 AKERN	1.20 (0.96–1.50)
Heitmann1	1.46 (0.99–2.17)
Heitmann2	1.31 (1.01–1.69)*
Segal1	1.26 (1.02–1.55)*
Segal2	1.26 (0.99–1.62)
Segal3	1.40 (0.96–2.03)
Segal4	1.31 (0.98–1.75)
Segal5	1.21 (0.99–1.48)
Segal6	1.30 (1.05–1.62)*
Van-Loan-Mayclin	1.66 (1.10–2.49)*	1.53 (1.21–1.94)*	1.54 (1.02–2.32)*
Kyle	1.15 (0.91–1.44)
Aglago1	1.21 (0.88–1.68)
Deurenberg	1.40 (1.02–1.91)*
Boulier	1.17 (0.80–1.70)
Chumlea	1.18 (0.95–1.47)
Gray1	1.30 (1.04–1.61)*
Gray2	1.07 (0.87–1.31)
Jebb	1.09 (0.93–1.27)
Lukaski1	1.11 (0.91–1.35)
Lukaski2	1.11 (0.91–1.35)
Lukaski3	1.12 (0.92–1.37)
Rising	1.14 (0.92–1.41)
Stolarczyk	1.21 (0.98–1.49)
Wattanapenpaiboon1	1.09 (0.91–1.30)
Wattanapenpaiboon2	1.11 (0.92–1.34)
Sun	1.13 (0.90–1.43)
Aglago2	1.21 (0.88–1.67)
Heitmann3	1.19 (1.01–1.41)*
Kushner	1.11 (0.90–1.37)
Kushner_schoeller1	1.11 (0.91–1.36)
Kushner_schoeller2	1.10 (0.93–1.30)
Kushner_schoeller3	1.10 (0.93–1.30)
Lukaski_bolunchuk1	1.18 (0.89–1.57)
Lukaski_bolunchuk2	1.19 (0.88–1.60)

Model1: adjusted for age; Model2: adjusted for age, Framingham CVD risk score; Model3: adjusted for age, Framingham CVD risk score, creatinine excretion – a marker of muscle mass.

Data are presented if the measures remained significant after further adjustments.

^*p < 0.05

BIA: bioelectrical impedance analysis; BF%: body fat percentage; CI: confidence interval; CVD: cardiovascular disease

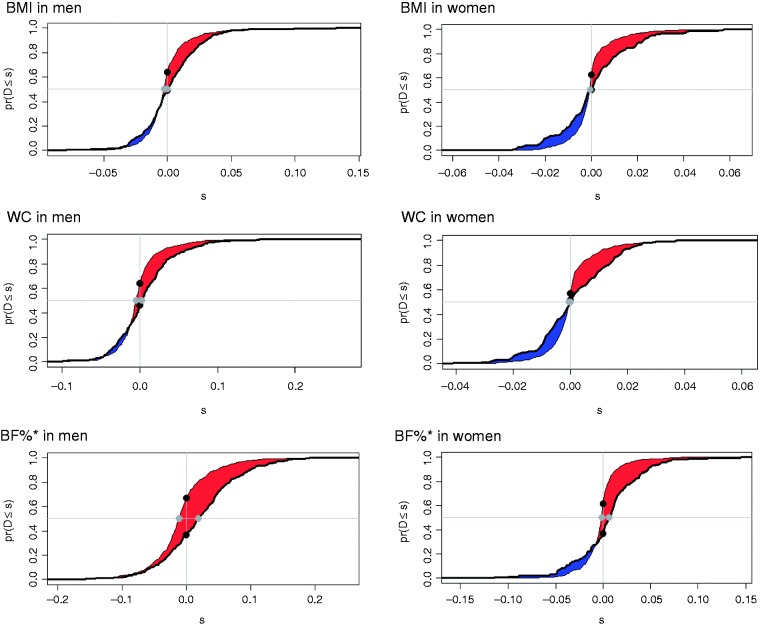
Based on the discrimination, the C-index for the CVD prediction was 0.700 and 0.751 in men and women using the base model (Framingham CVD risk score) and increased with the addition of each obesity measure. However, the only statistically significant increases in C-index were found for the extended model containing BIA (Table 4; Supplementary Table S6). To take the comparison further, Figure 2 depicts the effect of using the additional information from all the obesity measures on the CVD prediction based on NRI and IDI. The highest correct reclassification was 30.9% for a BIA-BF%-equation against 14.9% for BMI and 18.3% for waist circumference in men (p < 0.001). In women, only BIA showed significant improvements in reclassification, whereas BMI and waist circumference failed to improve NRI and IDI. An overall correct reclassification of BIA-BF%-equation was 24.8% in women (Figure 2; Supplementary Table S7).

Table 4.

C-index for the model containing different obesity measures in prediction of cardiovascular events.

	C-index (95% CI)	p value	C-index changes (95% CI)	p value
Male
Base model	0.700 (0.678; 0.723)	<0.0001	–	–
Extended models	–		–	–
Base + BMI	0.705 (0.683; 0.728)	<0.0001	0.005 (–0.002; 0.013)	0.17
Base + WC	0.711 (0.689; 0.734)	<0.0001	0.011 (–0.001; 0.023)	0.06
Base + BF%a	0.731 (0.709; 0.753)	<0.0001	0.031 (0.015; 0.047)	<0.0001
Female
Base model	0.751 (0.718; 0.784)	<0.0001	–	–
Extended models	–		–	–
Base + BMI	0.759 (0.728; 0.791)	<0.0001	0.009 (–0.004; 0.021)	0.18
Base + WC	0.758 (0.725; 0.790)	<0.0001	0.007 (–0.003; 0.017)	0.18
Base + BF%a	0.774 (0.742; 0.806)	<0.0001	0.023 (0.006; 0.041)	0.01

Base model: Framingham CVD risk score.

^aBody fat is estimated using the Van-Loan-Mayclin BIA-BF%-equation.

CI: confidence interval; BMI: body mass index; WC: waist circumference; BF%: body fat percentage; CVD: cardiovascular disease; BIA: bioelectrical impedance analysis

Figure 2.

The additive predictive value of obesity measures over the Framingham cardiovascular disease (CVD) risk score as assessed by the paired difference of risk scores in CVD prediction. Data are shown by paired difference between the risk scores estimated at t = 10 years on the probability scale using base and extended models by BMI, waist circumference and BF% (from top to bottom) in men and women. The difference between the areas (red) under the two curves indicates the integrated discrimination index. The difference between two black dots indicates the continuous net reclassification index. The difference between two grey dots indicates the median improvement. y-axis, pr(D≤s) = cumulative probability; x-axis, s = difference between base and extended model risk scores.

*BF% is estimated using the Van-Loan-Mayclin BIA-BF%-equation.

BMI: body mass index; WC: waist circumference; BF%: body fat percentage; BIA: bioelectrical impedance analysis

Subgroup analysis by age shows that BF% and waist circumference were independently associated with CVD in both younger and older men while BMI discriminates cardiovascular events better in younger men (Supplementary Figure S2).

Discussion

We identified that the association of BF% measured by BIA was independently associated with future cardiovascular events. The predictive value of BIA depends on the equation used. The body fat estimates from the best-predicting BIA-BF%-equations were strongly associated with future cardiovascular events, and this effect was stronger when compared with BMI and waist circumference in men and women. Furthermore, BIA was the best method among the obesity measures for improving cardiovascular risk assessment of Framingham CVD risk score in men, and the only method in women.

To the best of our knowledge, this is the first longitudinal study to compare different BIA-BF%-equations in the prediction of CVD. In a cross-sectional study by Willett et al., the predictive ability of BIA was shown to differ according to the equations used, in line with our study.¹³ Our study showed that the predictive value of BIA could be improved by using a BIA-BF%-equation fitted to a specific population. For instance, the predictive value of the body fat estimate based on our BIA device manufacturer's BIA-BF%-equation was lower than at least 10 other equations. Moreover, since the BIA devices' default algorithms are based on company equations and the information about these equations is not clear, we considered it would be better to investigate openly available algorithms as well. In addition, according to hazard ratios and C-indexes, the Van-Loan-Mayclin BIA-BF%-equation was the best-predicting equation in CVD prediction in men and women, making it worth investigating its predictive power in other populations.

Our second aim was to compare the association between BIA and cardiovascular events with other obesity measures, such as BMI and waist circumference. Several studies agree with our findings, which showed that BIA is better for CVD prediction than BMI and waist circumference.^5,14 For instance, a long-term population-based study of 26,942 participants identified that BF% was more strongly correlated with cardiovascular events when compared with BMI and waist circumference.⁵ Marques-Vidal et al. found that BIA-BF% permitted the capture of three times more participants with high estimated cardiovascular risk than BMI and almost twice as many as the waist-to-hip ratio in 10-year CVD risk estimation.¹⁴ Nevertheless, not all the studies reported that BIA is superior to BMI and waist circumference for estimating CVD risk.^13,15 One of the explanations for these controversial results might be that they used an unsuitable BIA-BF%-equation. Furthermore, Willett and colleagues' study findings reported that fewer than 10 of the 51 BIA-BF%-equations tested were close to but not superior to BMI in the prediction of obesity-related risk factors, such as fasting plasma glucose, HDL, triglyceride and systolic blood pressure. However, comparison between BIA and BMI was based only on the correlation coefficients and was not supported by any formal comparisons.¹³ In our prospective study, the superiority of BIA was supported by a number of tests, such as a z-test, C-index and NRI and IDI.

We found clear sex differences in CVD prediction using different obesity measures. This could be explained by different fat distributions in men and women, which have different roles in cardiovascular risk.^4,23 There is an indication that total fat expressed in BF% and BMI were independent predictors of cardiovascular events in both men and women, whereas an indication of abdominal fat such as waist circumference was associated with future cardiovascular events only in men. This finding aligns with previous studies reporting that abdominal fat distribution is more strongly related to CVD in men. Onat et al. identified that visceral adiposity is a better predictor of CVD risk in men, while total fat is more closely associated with CVD risk in women.⁴ Florath et al. found an overestimation of waist circumference for CVD risk in women but not in men.²³ Furthermore, the current CVD risk burden in men and women argues for improvements in the risk assessment and the prevention of CVD,^24,25 especially for women.² Our study suggests that a sex-specific CVD risk assessment could be improved by using BIA as one of the obesity measures; only BIA provided significant improvement in the prediction of Framingham CVD risk scores in women.

Since our hypothesis is based on the predictive power of body fat, we used creatinine excretion in our analysis to identify whether BIA-BF% is associated with future cardiovascular events independently of muscle mass. A study by Srikanthan et al. showed that a specific subgroup with high muscle mass and lower fat mass had a lower mortality rate than other groups.²⁶ For our study population, a previous analysis by Oterdoom et al. showed that muscle mass as reflected by creatinine excretion predicts the development of CVD.⁸ However, we found that the association between BIA and future cardiovascular events is independent of the creatinine excretion.

Several limitations apply to the methodology of BIA, including the theoretical assumptions that underlie the technique. For example, the assumption that the body has a uniform cylinder shape, that the body is homogeneous and that the conductive length is directly related to body height. Other limitations are due to differences in membrane conductivity among various cell types and the differences in the body's hydration.¹² These differences can vary with individual characteristics such as age and sex. Therefore, BIA-equations incorporate information on height, age, sex and other parameters.^10,12 Regarding the crude hazard ratios, equations in our study which incorporated age were more strongly associated with CVD compared with equations which did not incorporate age (Supplementary Figure S3). It is evident that age is an important factor in the association between body fat and CVD. After adjustments for age, we found no difference between equations which did and those which did not incorporate age. Furthermore, the equations based on a female population were also the best-predicting equations in men. Taken together, our results show that the predictive value of BIA is independent of the formula and is generated with or without taking age and sex into account.

The strengths of this study include the prospective community-based cohort, the large sample size, the long term follow-up and the extensive information on clinical characteristics. Furthermore, this study is the first longitudinal evaluation which has applied various bioelectrical impedance equations to CVD prediction. However, our study has some limitations. We did not perform external validation for the predictive value of the BIA-BF%-equations. Furthermore, the number of events recorded in women was limited.

Conclusion

The BF%s for most BIA-BF%-equations tested in men and at least one body fat estimate in women were independently associated with future cardiovascular events. The predictive value of BIA depends on the equation used to estimate body fat. The body fat estimates from the best-predicting BIA-BF%-equations were superior to BMI and waist circumference in how well they predicted future cardiovascular events in both men and women. Accordingly, of the various obesity measures, BF% is a better candidate measure for improving cardiovascular risk assessment in women.

Author contribution

All co-authors contributed to the conception or design of the work and contributed to the acquisition, analysis, or interpretation of data for the work. OB and EC drafted the manuscript. MFE, RTG, SJLB and EC critically revised the manuscript. All gave final approval and agree to be accountable for all aspects of work ensuring integrity and accuracy.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: the Dutch Kidney Foundation supported the infrastructure of the PREVEND program (grant E.033). The Dutch Heart Foundation supported studies on lipid metabolism (grant 2001–005).