BUMPy: A model-independent tool for constructing lipid bilayers of varying curvature and composition

Abstract

Molecular dynamics is a powerful tool to investigate atomistic and mesoscopic phenomenon in lipid bilayer systems. These studies have progressed with the advent of increased computational power and efforts are now increasing being directed toward investigating the role of curvature and bilayer morphology, as these are critical features of biological processes. Computational studies of lipid bilayers benefit from tools that can create starting configurations for molecular dynamics simulations, but the majority of such tools are restricted to generating flat bilayers. Generating curved bilayer configurations comes with practical complications and potential ramifications on physical properties in the simulated system if the bilayer is initiated in a high-strain state. We present a new tool for creating curved lipid bilayers that combines flexibility of shape, force field, model resolution and bilayer composition. A key aspect of our approach is the use of the monolayer pivotal plane location to accurately estimate interleaflet area differences in a curved bilayer. Our tool is named BUMPy (Building Unique Membranes in Python) is written in python, is fast and has a simple command line interface.

Graphical Abstract

Introduction

Molecular dynamics (MD) is an increasingly powerful computational tool for the study of structure and dynamics of biological macromolecular systems. MD studies of lipid membranes typically consist of periodically constrained lipid bilayers in a rectangular box simulated at constant pressure, which prevents the formation of high curvature or complex topological states, though some curvature-related properties such as the bilayer bending modulus^1–5 and the spontaneous curvature^6–8 can be estimated from equilibrium properties of a flat bilayer. However, biological membranes exist in complex configurations (e.g. the endoplasmic reticulum, mitochondrial inner membranes) and these configurations are often critical states in biological processes such as endocytosis, cell division, and chemotaxis. Hence, in recent years interest has grown in simulating curved lipid systems, which have included vesicles^9–12, cylinders^1,9,13, fusion intermediates^14–18, and membrane buckles^5,19–22.

While a number of useful tools exist for investigators to generate flat lipid bilayers at both atomistic and coarse-grained resolution to initiate MD simulations^23–30, the tools for generating curved lipid systems are more sparse. Simulations of vesicles can be set up using the CHARMM-GUI²⁶ coarsegrained vesicle builder, Packmol³¹, or LipidWrapper³². Packmol has the additional capacity for setting up ellipsoid shapes as well as cylinders, while in principal LipidWrapper can generate any curved topology, though the process for creating some complex shapes in LipidWrapper requires modeling in 3^rd party software. Of the above tools, the CHARMM-GUI Vesicle builder is limited to a subset of lipids in the Martini Force Field⁷, while LipidWrapper and Packmol are flexible both in force field and lipid composition. Other tools not discussed in detail here support forming nonbilayer structures such as micelles,^23,33,34 and inverted hexagonal phases³⁵.

An important consideration when assessing tools for generating curved lipid systems is the treatment of interleaflet ratios, as the outer leaflet in any curved bilayer will have a larger area (and therefore more lipids) than the inner leaflet. The extent of area mismatch between leaflets depends on the topology in question and the degree of curvature, and is not trivial to estimate. In a closed shape such as a vesicle, inaccuracies in interleaflet ratio estimation can lead to changes in shape and/or artifacts arising from nonequilibrium lipid packing. Of the tools listed above, only CHARMM-GUI directly addresses this concern, using an empirical model to estimate lipid counts and interleaflet ratios for vesicles. Even in this case, the CHARMM-GUI protocol recommends a lengthy equilibration process using artificial pores to account for errors in the initial estimates. Packmol and LipidWrapper do not directly control interleaflet ratios when building bilayers, and the resulting lipid ratios and densities are a result of the tools’ packing procedures.

The key to calculating correct interleaflet ratios is determining the respective surface areas of the inner and outer monolayers of the curved bilayer, at which point they can be populated according to the areas per lipid calculated in flat bilayers. However, the definition of a molecular surface cannot be unambiguously defined and the choice of atoms used to define the surface will ultimately affect the surface area calculated for a curved system. The approach we have taken is to calculate the surface area of the curved shape at the monolayer pivotal plane - a surface within the monolayer that has the same area in a flat or curved system³⁶. Therefore, we believe our approach removes a degree or arbitrariness to the surface area calculation and allows us to construct curved bilayer systems with optimal interleaflet number ratios.

We are motivated by our observation that current tools for creating curved starting structures for MD simulations are limited in the range of shapes that can be created, and do not properly address the problem of accurately predicting interleaflet area differences. Herein, we present a new approach for generating in silico curved lipid membranes for starting configurations for MD simulations called BUMPy (Building Unique Membranes in Python). BUMPy is a versatile tool that can create any number of shapes and is independent of both lipid type and forcefield. The current BUMPy repository includes commonly simulated shapes that lack implementations in other software packages, such as buckles, tethers, and elongated vesicles. Furthermore, we demonstrate that our approach accurately addresses the interleaflet ratio problem by determination of the monolayer pivotal plane.

Methods

Geometric transformations

In BUMPy, generation of different curved shapes is accomplished by geometric transformations to the coordinates of flat bilayer systems. To generate a cylindrical shape, a flat patch of bilayer is selected with lateral dimensions corresponding to the length and circumference of the desired cylinder (Figure 1A and 1B). The Cartesian coordinates along the axis with dimensions of the cylindrical circumference are projected as angles along a circle with the desired radius, with $\theta =x/R.$ The new coordinates in that dimension are then calculated according to a sine and cosine description of a circle, with $x^{\prime }=R*\sin (\theta )$ and $z^{\prime }=R*\cos (\theta ).$ Spherical shapes are generated using a similar procedure to that for cylinders. Rather than describing positions with Cartesian coordinates, the bilayer positions are transformed to polar coordinates, and the angles for transformation are calculated as a function of the radial coordinate, while retaining angular coordinates (Figure 1C).

Figure 1. The basic building blocks of BUMPy.

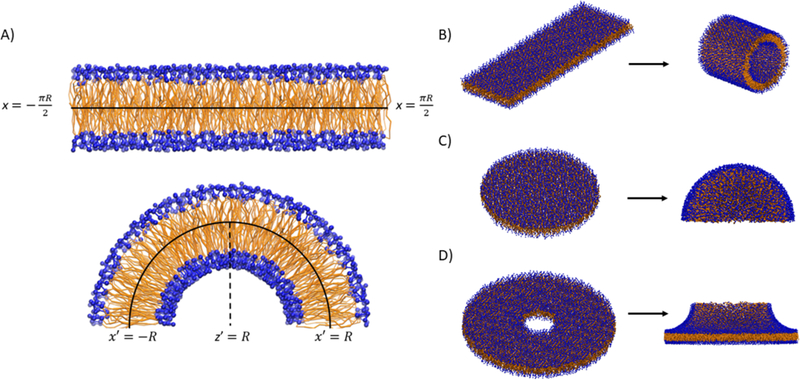
A) Transformation of a flat patch of bilayer into a cylindrical geometry. The x dimension of the flat bilayer corresponds to the circumference of the curved shape. B) Side view of the transformation from a rectangular patch of bilayer to a cylinder. C) Transformation of a circular patch of bilayer to a hemisphere. D) Transformation of a hollow disc into a toroidal junction.

It may be of interest to create geometries with radial symmetry (cylinders, spheres) and couple them to flat bilayer patches. The interface between the two systems is modeled by a toroidal junction (Figure 1D), the shape of which is determined both by the radius of the radially symmetric system being coupled, as well as a radius defining the sharpness of the junction.

Area Matching

Transformation of flat coordinates to curved shapes will create area strain if both monolayers have an equal number density of lipids. Consider the transformation of a flat patch of bilayer to a cylinder with a radius R, length L and thickness T. The inner leaflet will have a surface area of $A_{inner}=2\pi L(R-T/2),$ while the outer leaflet will have an area of $A_{outer}=2\pi L(R+T/2),$ but both leaflets have the same number of lipids as before the transformation, and therefore the resultant cylinder will have different areas/lipid in the inner and outer leaflet. Such a mismatch can only be equilibrated by interleaflet flip-flop, a process which takes place on time scales of minutes to hours³⁷, far beyond those accessible in typical equilibrium MD simulations.

To account for area mismatch, the leaflets of the flat bilayer are transformed separately. The size of the patch corresponding to the outer leaflet is chosen to satisfy the size of a cylinder with a given radius of $R_{outer}=(R+T/2)$, and likewise $R_{inner}=(R-T/2)$ for the inner leaflet. The coordinates of both leaflets are then scaled to fit into a box matching the original cylindrical dimensions (Figure 2). Thus, the flat bilayer patch has an uneven density of lipids, that when transformed exactly matches the correct areas for the inner and outer leaflets and maintains equilibrium area/lipid values (assuming the initial flat bilayer is well equilibrated). A similar procedure is performed for spheres and toroidal junctions: the initial outer and inner monolayer slices are chosen to be circles with different radii based on the thickness.

Figure 2. Area matching in BUMPy.

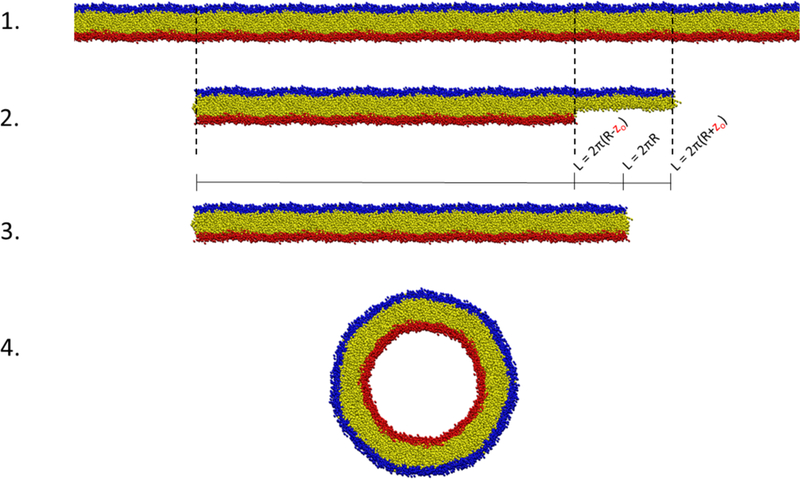
1) An initial bilayer patch is larger than the required dimensions. 2) Slices of the original bilayer are taken separately by the top and bottom leaflets to match their specific area requirements, dependent on the requested geometry and z_o location. 3) The top and bottom leaflets are scaled laterally to occupy the size corresponding to the requested geometry. At this point, the density of lipids in the top leaflet is higher than in the original bilayer, and the density in the bottom leaflet is lower than in the original bilayer. 4) The geometric transformation takes place.

Spheres and junctions require an additional rescaling step before transformations, as flat surfaces cannot be directly mapped onto morphologies with multiple non-zero principal curvatures without accruing local area strain. In other words, the total number of lipids can be accurately estimated, but a simple linear scaling of the flat region into a circle with correct dimensions would lead to local density imbalances upon transformation. To account for this, in spherical and toroidal junctions the flat coordinates are scaled nonlinearly to generate an even density on the spherical surface. Details on the scaling method are provided in the Supporting Information (SI).

To match areas in the manner described above, the choice of thickness must be carefully chosen. The pivotal plane (z_o) of a monolayer is the surface that does not deform when the monolayer undergoes a curvature deformation^36,38. Critically, this allows us to compare the areas of flat monolayers to curved monolayers by measuring the surface area of the curved bilayers at their monolayer pivotal planes. Therefore, given a bilayer shape with a desired radius R, the area of the outer monolayer can be estimated by calculating the surface area of a shape with radius $R+{\mathit{z}}_{\mathit{o}},$ and likewise $R-{\mathit{z}}_{\mathit{o}}$ for the inner monolayer. Throughout this work we will denote the pivotal plane of a monolayer as a distance z_o from the center of a bilayer. It should be noted that z_o is more correctly the pivotal plane of a flat monolayer, and that the actual pivotal plane (z) varies slightly with curvature. The curvature correction to the pivotal plane distance is small for moderately curved systems⁹ and is only relevant for very high curvatures as it falls off quadratically with curvature, so we will neglect the correction in our approach.

Software Implementation Details

BUMPy is implemented in Python as a command-line tool. It can be freely downloaded at www.github.com/MayLab-UConn/BUMPy, along with usage details and examples. NumPy is the only required dependency of BUMPy. BUMPy has been tested with Python 3.6.0 and NumPy 1.11.3. BUMPy is capable of building systems with upwards of 10 million particles on a typical desktop computer, and can create systems with over 500 million particles on a high-RAM machines. Performance details are provided in Supporting Information (Figure S1), as well as sample command line usages.

Simulation Methods

Force Fields and System Setups

The majority of simulations in this work were performed using the coarse-grained Martini forcefield with standard (nonpolarizable) water⁷. Additional simulations were performed using the atomistic CHARMM-36 additive forcefield³⁹. Flat bilayer systems were created using the insane bilayer builder²⁷ for the Martini systems, while the CHARMM-GUI Membrane Builder³⁰ was used to create atomistic bilayers compatible with the CHARMM-36 forcefield. Cylinders, spheres, and other shapes were then generated from flat systems using BUMPy and solvated using the gmx solvate tool in GROMACS.

Coarse-grained Simulation Parameters

All simulations were performed using GROMACS 2016⁴⁰. Energy minimization and initial equilibration followed the protocol suggested by the CHARMM-GUI Martini maker. Initial energy minimization was performed using the steep integrator with soft-core potentials for short-ranged interactions, allowing tolerance for overlapping particles. An additional round of energy minimization with the steep integrator was then performed with soft-core potentials turned off. The minimization steps were followed by several short simulations (10,000 steps) using the MD integrator, iteratively increasing the timestep from an initial step of 2 fs to a final timestep of 20 fs, while applying position restraints to the lipid phosphate beads. Simulation times here are reported without scaling.

All subsequent simulations used the MD integrator with a timestep of 20 fs. Electrostatic interactions were shifted to 0 at a distance of 1.1 nm using the reaction-field method with reaction field dielectric (ε_rf) set to infinity, and van der Waals interactions were directly cut off at the same distance using the Potential-shift-Verlet modifier, as suggested by de Jong and colleagues⁴¹. Temperature was maintained at either 300 K or 33 K using the v-rescale algorithm with a time constant of 1 ps, with the solvent and bilayers coupled separately.

Pressure coupling was accomplished using the Parrinello-Rahman barostat⁴² with a time constant of 12 ps and a compressibility of 3 * 10⁻⁴ bar^-1. Spherical systems were simulated using isotropic pressure coupling with a reference pressure of 1 bar. Cylindrical systems were simulated using semi-isotropic pressure coupling, with the long axis of the cylinder aligning with the z-dimension, using a reference pressure of 1 bar in both the z and x/y dimensions. Simulations of flat bilayers were performed with semi-isotropic pressure coupling with both the lateral and normal direction pressures coupled to a 1 bar pressure bath.

Atomistic Simulation Parameters

An all-atom vesicle composed of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine lipids (DPPC) was constructed with a radius of 5 nm and simulated with the CHARMM-36 forcefield. The equilibration procedure was similar to that of the coarse-grained systems, involving a short energy minimization using soft-core potentials, followed by a longer minimization without soft-core potentials, and then successive rounds of equilibration with restraints on the phosphorus atom. A time step of 2 fs was used, with the Verlet cutoff scheme. Lennard-Jones interactions were cut off at 1.2 nm and modified with the forceswitch option of GROMACS between 1.0 and 1.2 nm. Coulombic interactions were directly calculated within 1.2 nm and long-range electrostatics were treated with the Particle Mesh Ewald method. Temperature was maintained at 330 K using the Nose-Hoover thermostat, and isotropic pressure coupling was maintained using the Parrinello-Rahman barostat, with a time constant of 5 ps, a compressibility of 4.5 * 10⁻⁵ bar⁻¹, and a reference pressure of 1 bar.

Pore Formation Protocol

Pores were induced in cylinders and vesicles using the protocol of Qi and colleages²⁶, using flat-bottom potentials in GROMACS to allow for lipid flip-flop and equilibration between the bilayer leaflets. The Martini 2.0 lipid forcefield provided by CHARMM-GUI contains the relevant parameters and only requires an input in the GROMACS .mdp simulation parameter file to activate the potentials. Vesicles were equilibrated with 6 pores, two along each major axis, while cylinders were equilibrated with 4 pores (along two axes), all with a force constant of 1000 kJ mol⁻¹ nm^-2. A pore radius of 1 nm was found to be the smallest for which interleaflet flipflop was observed. Most simulations were simulated with a 1 nm radius pore for a brief (2 ns) equilibration period, followed by a 200 ns simulation with a pore radius of 2.0 nm for accelerated flipflop, then a 400 ns simulation with a 1.0 nm pore for data collection.

Dummy Particles

While BUMPy can generate bilayers of various shapes and curvatures, these systems may be unstable if the bilayer properties (e.g. spontaneous curvature, bending modulus) are discordant with the imposed geometry. Nonetheless, it can be useful to study lipid properties under these conditions and we demonstrate how a lipid bilayer can be made to maintain an otherwise unstable shape. A semicylinderplane system (see Figure 6 and Table 1) was bracketed on either side of the bilayer with a grid of dummy particles, which is a modified version of the protocol implemented by Yesylevskyy and coworkers⁴³. The dummy particle grid was created with lateral spacing of 0.5 nm and an interleaflet thickness of 4.6 nm, and particles were anchored in place with position restraints using a force constant of 1000 kJ mol⁻¹ nm^-2. The dummy particles only interacted with the hydrophobic tail beads of the bilayer, while all other interactions were turned off. The potential between dummy particles and tail beads was modeled with a purely repulsive interaction by using a Lennard Jones potential with the C⁽¹²⁾ parameter set to 0.0258 kJ mol⁻¹ nm¹² (corresponding to ε = 2.0 kJ mol⁻¹, and σ = 0.62 nm), and the attractive C⁽⁶⁾ parameter set to 0.

Figure 6. Examples of shapes in the BUMPy repository.

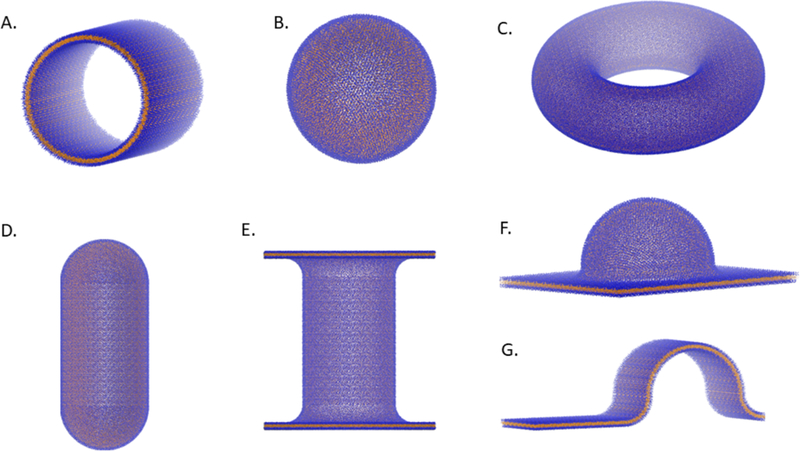
A) Cylinder. B) Sphere. C) Torus. D) Capped cylinder. E) Double-bilayer-cylinder. F) Semisphere-plane. G) Semicylinder-plane.

Table 1.

Current list of shapes available in BUMPy repository, with associated geometric parameters and shape-specific notes.

Shape	Parameters	Notes
Semisphere	R_sphere	basic building block
Cylinder	R_cylinder L_cylinder	-basic building block -quarter-cylinder used as a junction between orthogonal structures
partial_torus	R_torus R_tube	-basic building block -quarter-torus used as toroidal junction
Flat_bilayer	X_dimension Y_dimension	-basic building block
Sphere	R_sphere
Torus	R_torus R_tube	R_torus > R_tube
Capped_cylinder	R_cylinder L_cylinder	-cap radius is necessarily equal to the cylinder radius
Double_bilayer_cylinder	R_cylinder L_cylinder R_junction L_flat	L flat >= 2 * (R cylinder + R_junction)
Semicylinder_plane	R_cylinder L_cylinder R_junction L_flat	L flat > 2 * (R cylinder + R_junction)
Semisphere_plane	R_sphere R_junction L_flat	L flat > 2 * (R cylinder + R_junction)
Buckle	R_buckle L_buckle	L_buckle is the length in the flat dimension

Data Analysis

The pivotal plane of a lipid monolayer can be calculated from vesicles and cylinders that are in transverse (interleaflet) equilibrium. Wang and Deserno⁹ derived a relationship between z_o, radius (R), and the interleaflet lipid number ratio for cylinders

$$z_{o-cylinder}=\frac{\rho -1}{\rho +1}*R$$ Eq.1

where ρ is the outer to inner leaflet lipid number ratio. A similar relationship exists for spheres

$$z_{o-sphere}=\frac{\sqrt{\rho }-1}{\sqrt{\rho }+1}*\mathit{\text{R}}$$ Eq.2

Therefore, to calculate z₀, we need only to simulate a vesicle or cylinder to equilibrium by inducing pores, then measure the resulting radius and interleaflet ratio.

Calculating interleaflet ratios and radii

Simulation trajectories were processed in Python using MDTraj⁴⁴ To assign lipids to leaflets on a dynamic basis, cartesian coordinates were converted to cylindrical coordinates (in the case of cylinders) or spherical coordinates (in the case of vesicles). The radii of the phosphate beads (R_p) were then compared to the radial position of the terminal tail bead (Rt) in the same molecule, and lipids were either assigned as inner (Rp > R_t) or outer leaflets (R_p < R_t) on a frame-by-frame basis. In each frame, the radius of each leaflet was individually calculated as the average of the phosphate radii, and then the leaflet radii were averaged to obtain the bilayer radius.

Lateral Pressure Pro files

Lateral Pressure Profiles (LPPs) for flat bilayers were calculated using GROMACS-LS⁴⁵, a modified version of GROMACS 4.5.5. For analysis of LPPs, coordinates and velocities were saved every 5 ps for 100 ns, for a total of 20,000 frames per simulation. LPPs along the z axis of the bilayers were calculated with 0.01 resolution.

Diffusion coe fficients

Lipid diffusion coefficients were calculated for vesicle systems by calculating the mean squared displacements of lipids over a range of lag-times and calculating a linear fit to the equation MSD = 2dDτ, where MSD is the mean squared displacement at a time lag τ, d is the dimensionality and D is the diffusion coefficient. In this case, the vesicle was treated as a 2-dimensional surface (d=2). Mean squared displacements of individual lipids were calculated by calculating the arc length along the sphere between initial positions and positions after a lag time of τ. The measured displacements are therefore dependent on the radius of the vesicle. The use of the bilayer radius is inappropriate in this case, as the area of the outer monolayer is greater than that of the inner monolayer. We therefore calculated the displacements and diffusion coefficients of the inner and outer monolayers separately, and used the location of the pivotal plane of each monolayer as the radius for calculating arc lengths and displacements.

Results

Stability of BUMPy-generated systems

The geometric transformation procedure applied when creating shapes with BUMPy has several sources of potential problems that could create high energy states that cause numerical instabilities. First, since all coordinates are transformed, the mapping from a flat to a curved environment causes a change to the internal coordinates of each molecules. The extent of this change depends on the magnitude of curvature, and under high curvature conditions this effect could become energetically unfavorable. Second, BUMPy is able to combine multiple “building-block” shapes into complex geometries. At the interface between building block segments steric clashes between lipids can arise, which would be unfavorable. Third, since BUMPy performs transformations on monolayers and then reassembles the bilayer, this practice can lead to clashes at the inter-leaflet interface. Particularly in the second and third cases, overlap of particle van der Waals radii can lead to systems with potential energies with magnitudes beyond machine precision, in which case energy minimization can fail. This difficulty can be mitigated with the use of soft-core potentials^46,47, which scale down the magnitude of non-bonded interactions, reducing energies so that minimization proceeds. Indeed, this is the suggested protocol (for example) when minimizing a Martini system obtained from the CHARMM-GUI. We have found that a short (50 step) soft-core minimization in GROMACS with default parameters, followed by a typical equilibration scheme is sufficient for numerical stability with every shape in the repository, and for every lipid type we have tested.

Estimating Zo from spheres and cylinders

The pivotal plane of a monolayer can be calculated as a function of the radius and interleaflet lipid ratio for spherical and cylindrical bilayer systems using eq. 1 and eq. 2⁹. To allow for transverse equilibration of lipid packing densities on accessible timescales, we implemented a modified version of a relaxation protocol that has been used in several previous studies^10,13,26,48, in which pores are induced in the bilayer using cylindrical flat-bottom potentials. Lipids can then migrate between leaflets with their headgroups facing the hydrophilic channel.

Initially, we constructed a cylindrical bilayer with a 10 nm radius to test the feasibility of measuring Zo based on interleaflet ratios and radii. To our knowledge, the only in silico report of z_o location comes from the work of Wang and Deserno⁹, in which they calculated the z_o of a Martini DMPC bilayer to be 0.85 +/− 0.011 nm, via a buckling protocol. For comparison purposes, we adopted the same lipid composition and temperature (300 K) in our system, though we note some simulation parameter differences, notably in the timestep and pressure coupling schemes. Our initial system setup was generated using an initial guess of $z_o^i=1.0\text{nm}.$ Throughout this work we will denote initial estimates of pivotal plane locations used by BUMPy to create shapes as $Z_o^i,$ while actual observed values of the pivotal plane locations once equilibrated are denoted by z₀. With a 2.0 nm pore radius, the observed zo converged to ~0.85 nm within 50 ns (Figure S2). After 200 ns, the pore radius was reduced to 1.0 nm, and z_o remained constant at 0.85 nm within fluctuations.

To test the robustness of our z_o estimates with respect to geometry and curvature, we constructed vesicles and cylinders with radii ranging from 5 nm to 20 nm in 5 nm increments and calculated z_o values after allowing interleaflet equilibration through pore formation. Figure 3A shows the observed radii and interleaflet ratios (p) with reference lines fit to a z_o of 0.85 nm, and Figure 3B shows the resulting calculated z_o for each trial, with the reference of 0.85 nm drawn and shaded to the uncertainty reported by Wang and Deserno⁹. Observed z_o values for cylinders closely matched the reported value, falling within error for all radii. In the cylindrical systems, a slight drift towards higher radii was observed. The semi-isotropic pressure coupling scheme allows for volume and aspect ratio changes, resulting in the cylinders contracting in the longitudinal dimension and expanding in the circumferential dimension. However, the observed interleaflet ratios still lie along the contour defined by a z_o = 0.85 nm (Figure 3A, red), indicating that the relationship between R, ρ and z_o is well accounted for by eq. 1.

Figure 3. Validation of pivotal plane-based area calculations.

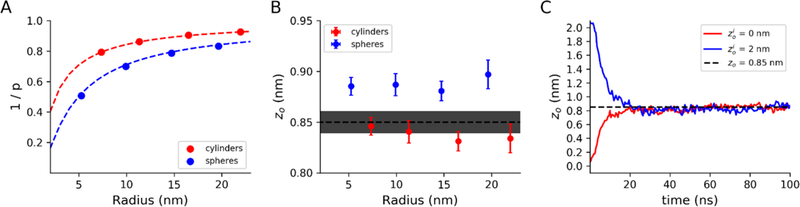
All bilayers were composed of 100% DMPC. Error bars represent 95% confidence intervals estimated from standard errors A) Relationship between interleaflet ratios and radii for spheres and vesicles. The red and blue dashed lines are theoretical contours to z_o=0.85 nm for cylinders and spheres, respectively. x and y error bars are smaller than markers. B) Calculated z_o locations after equilibration for vesicles and cylinders. The dotted line is set at z_o = 0.85 nm, with grey shading to indicate 95% confidence interval reported by Wang and Deserno. C) Time-course of observed z_os for 10 nm radius cylinders created with zⁱ_o parameters of 0.0 nm and 2.0 nm, equilibrated with 2.0 nm radius pores.

Likewise, eq. 2 appears to model the same relationship for vesicles (Figure 3A, blue). However, when determining the Zo for spherical systems, we observed a small but statistically significant and consistent difference, with Zo values for spherical systems consistently 0.03–0.05 nm higher than for cylinders of the same initial radii as the spheres (Figure 3B, blue). We are unsure as to the origin of this discrepancy, but speculate that the flat-bottom pore potential may play a role. Induction of pores in a vesicle introduces a lipid-excluded area to the vesicle surface. This must lead to either area strain in the vesicle or expansion to add more surface area. Inflating the vesicle may affect the apparent Zo on its own, but also may affect the interleaflet ratio, as the extent of curvature has changed. In contrast, the cylindrical systems can relax area strain through the pressure coupling mechanism (by expansion along the longitudinal direction at constant radius). The impact of z_o differences of this magnitude is explored below.

Convergence of pivotal plane from initial estimates

The previous systems were generated using BUMPy with an $z_o^i=1.0\text{nm}.$ We then generated DMPC cylinders with 10 nm radii using $z_o^i=0\text{nm}$ (equal lipid numbers between leaflets) and $z_o^i=2.0\text{nm}$ to assess the numerical stability of systems with an inaccurate estimate for z_o, as well as to confirm convergence to the actual z_o when subjected to pore-based equilibration. In both systems, the cylinders minimized and equilibrated without issue, and the final observed z_o values were in agreement with earlier measurements, converging within 40 ns (Figure 3C).

Effect of zⁱ₀ on bilayer properties

The results shown in Figure 3 demonstrate that a pivotal-plane based description of interleaflet area differences is consistent across a range of curvatures, and that given the ability to equilibrate, systems with different starting $z_o^i\text{s}$ will converge to the same value. However, the presence of a small but statistically significant difference between observed z_os in spheres and cylinders indicates some systematic error in the measurement of z_o. It is therefore important to determine to what extent an erroneous z_o estimate affects system properties, especially if one were to bypass the pore-based equilibration (which would be required when simulating bilayers with interleaflet compositional differences). To assess the potential impact of z_o-based interleaflet mismatches, we created spherical systems with initial radii of 10 nm, and used a range of $z_o^i\text{s}$ as inputs to BUMPy. A larger $z_o^i$ has the effect of increasing the ratio of outer leaflet to inner leaflet lipids. The effect of $z_o^i$ on lipid counts and areas is quantified for a 10 nm radius sphere composed of DMPC in Figure S3. The vesicles were then simulated without allowing pore-based relaxation, and several system observables were then compared between the systems. Figure 4A shows calculated radii for vesicles created with $z_o^i$ ranging between 0 (equal interleaflet numbers) and 1.8 nm. As $z_o^i$ is increased, the radius monotonically decreases, though between a $z_o^i$ of 0 and 1.8 nm, the spread is only 0.2 nm total, and differences in radii between systems constructed using $z_o^i$ values of 0.6 nm and 0.8 nm or between 0.8 nm and 1.0 nm are 0.021 nm and 0.031 nm respectively. Changing the $z_o^i$ estimate therefore has a measurable but quite small effect on the observed radius. In each case, the observed radius is larger than the target radius of 10.0 nm by 0.05 to 0. nm, the origin of which is speculated on below.

Figure 4. Effect of $z_o^i$ on vesicles properties.

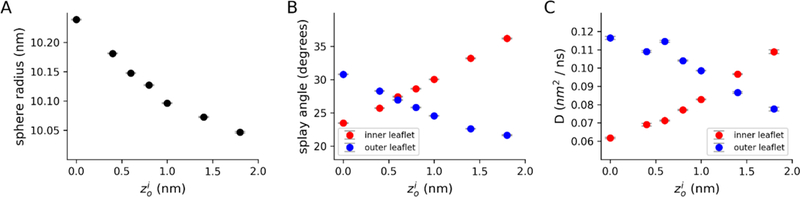
Spherical vesicles were created using a range of $z_o^i$ estimates, and simulated for 150 ns without allowing pore-based interleaflet equilibration. A) Equilibrated radius of vesicles. B) Splay angle between the phosphate beads and terminal tail beads. Splay is calculated as the angle between the outward normal vector and the vector pointing from the phosphate to the tail bead for the inner leaflet. For the outer leaflet, the inward normal vector is used. C) 2-dimensional diffusion coefficients for lipids in the inner and outer leaflets, calculated from the linear fit of a mean-squared displacement plot at various time lags.

To examine whether the differences in interleaflet ratios impact lipid structure and dynamics, we calculated the splay angles between the monolayer outward normal vector and the vector between the phosphate and a terminal tail bead (Figure 4B). With increasing $z_o^i$, the splay angles of the inner leaflets increase while the splays in the outer leaflets decrease. As the differences in radii between the systems are minor (Figure 4A), the findings can be interpreted simply as a result of area strain. Systems with higher $z_o^i\text{s}$ have more lipids in the outer leaflet, effectively decreasing the area per lipid in that leaflet (Figure S3A and S3C), while the opposite effect is observed in the inner leaflet. The increased splay of the inner leaflet is a result of each lipid having a larger area and less lateral area strain, and vice versa for the outer leaflet.

An intriguing feature of the leaflet splay analysis is the $z_o^i$ at which the splay angles of the inner and outer leaflets match each other does not coincide exactly with the correct z_o of 0.85 nm, as might be expected. Matching splay occurs around $z_o^i$ = 0.6 nm, while around $z_o^i$= 0.85 nm the splay angles of the inner leaflet lipids are larger than those of the outer leaflet. Such interleaflet lipid tail behaviors in equilibrated vesicles have been demonstrated before¹⁰, and indicate that the two leaflets have differences in lateral packing. In principal, this could be problematic, as the pivotal plane area-matching theory assumes equal areas per lipid between the two leaflets. However, the magnitude of the difference in splay at the correct z_o is small (less than 5^o), and such effects are expected to decrease with increasing radius. Nevertheless, the small differences observed here may indeed be responsible for the radius shifts observed in Figure 4A.

To measure the effect of $z_o^i$ on lipid dynamics, we calculated the 2-dimensional lateral diffusion coefficients of the inner and outer leaflets (Figure 4C). The diffusion coefficients (D) for the outer leaflet were found to decrease with increasing $z_o^i$, and the opposite trend was observed for the inner leaflet. Again, the trends can be explained in terms of area mismatch; as lipids are added to the outer leaflet, increased packing of lipids slows the diffusion rates, and vice versa for the inner leaflet. Unlike with splay angles, it is not expected that the outer and inner leaflet trends should overlap at the correct z_o. Diffusion rates in spherical systems are strongly attenuated by boundary effects, with the inner leaflet (with a smaller surface area) experiencing a larger reduction in diffusion compared to an infinite planar system⁴⁹.

In sum, the effects of using an incorrect are small but measurable, and are consistent with effects attributable to area per lipid mismatch. The range of values explored was between 0 and 2 nm, whereas the calculated zo values for 3, 4, and 5 tail-bead lipid models all fall within +/− 0.15 nm of a central value of roughly 1 nm, a range in which errors associated with Zo are exceedingly small (Figure 4). Therefore, an estimate of 1 nm will (at least for Martini systems) be sufficiently accurate for most simulation purposes, circumventing the need to directly calculate Zo. For those simulations requiring extreme precision of the area per lipid, or for investigations that directly involve pivotal plane theory, the following section may provide additional insight.

Predicting Zo from flat bilayer properties

Calculating z_o via interleaflet equilibration of curved membranes requires relatively large systems and some computational expense, so ideally one would like to be able to estimate z_o with reasonable accuracy from examining flat bilayer properties that are more easily assessed. To test this possibility, we calculated z_o locations for a number of phosphatidylethanolamine (PE) and phosphatidylcholine (PC) lipids in the Martini forcefield using our cylinder-based equilibration protocol and performed simulations of flat bilayers with lipids of the same composition (see list of simulated systems in Table S1). We calculated the average phosphate bead depths relative to the center of the bilayer, and compared them to our calculated z_o depths (Figure 5). We found a linear relationship between phosphate and z_o locations when comparing lipids with the same head group but varying acyl chain compositions. Figure 5B shows the z_o locations as fractional depths with respect to the phosphate location. We found that the z_o locations of PC lipids were consistently located at around ~50% of the phosphate depths, while the z_o of PE lipids were found closer to ~43% of the phosphate depth. The use of phosphates as an indicator of membrane thickness is common but arbitrary, so we performed the same analysis using the first acyl tail bead proximal to the glycerol groups (Figure S4A), and found a similar trend.

Figure 5. z_o for different lipids in the Martini force field.

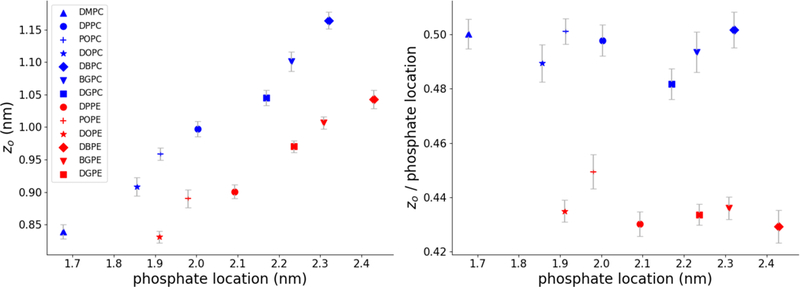
A) Relationship between phosphate positions and z_o positions. B) Same data as panel A, with the z_o locations plotted as fractions of the phosphate positions. In both figures error bars are 95% confidence intervals estimated from standard errors. Errors in the x dimension were smaller than the marker sizes.

Experimental work⁵⁰ and atomistic simulation⁵¹ of H_II phases suggest that the pivotal plane of lipids lies close to the level of the glycerol moiety, roughly 2/3 of the distance from the bilayer center to the phosphate coordinate. In contrast, we find that z_o values lie closer to the center of the monolayer (defined relative to phosphate depth), in agreement with Wang and Deserno’s calculation of z_o for DMPC. They suggested that such mismatch may be due to the coarse-grained nature of the Martini forcefield. The consistency of our results across a number of lipid types supports this suggestion.

Wang and Deserno noted that the Zo location of DMPC closely aligned with a specific peak in the lateral pressure profile (LPP), and suggested LPP features as potential predictors of Zo location⁹. To test this possibility, we calculated LPPs for all of our flat lipid systems (Figure S5). Each lipid’s Zo location was found in the general region of the first positive peak of the LPPs before the negative peak that represents interfacial tension. However, the shapes of the LPP peaks for many of the lipids are not as well-defined as that of DMPC, making a quantitative description of the positive peak unreliable. To quantify Zo location in the context of LPPs, we compared calculated Zo locations to two characteristics resolvable in all of the LPPs: i) the crossover point from positive pressure to negative pressure, and ii) the interfacial negative pressure peak (Figure S4B–C). As with the phosphate positions, we found that the z_o positions were located at certain fractions of the LPP features, but that the PC and PE trends were consistently different. Therefore, while z_o positions can be found in similar regions of the LPP, a consistent quantitative extraction of z_o location from LPPs suffers from the same head-group dependence as estimating z_o from simpler metrics such as phosphate positions.

Application to all-atom systems

To determine the suitability of BUMPy for application to atomistic systems, we constructed a vesicle composed of DPPC with a 5 nm radius and performed a simulation using the CHARMM36 force field. The vesicle was stable over the course of a 50 ns simulation (Figure S6), with an average radius of 5.32 +/– 0.26 nm. We note that determination of the pivotal plane using pore-based equilibration is likely computationally unfeasible for all-atom systems, and that the pivotal plane of an atomistic lipid likely does not match up with its CG counterpart. However, the pivotal plane of lipids can be calculated experimentally from inverted hexagonal phases⁵⁰, so using experimental estimates of z_o may be a plausible starting point.

Shape repository

The current list of shapes available in BUMPy are listed in Table 1 and selected images are shown in Figure 6. Once a template is created, users can apply it to build the specified geometry with any combination of size parameters and any lipid composition simply by specifying the parameters at the command line interface. The strategy of creating complex shapes from simple building blocks allows us to rapidly create these templates and add them to the repository.

The capabilities of BUMPy have some overlap with existing software. For example, the ability to generate vesicles is also available in the CHARMM-GUI (but only for Martini lipids), and cylinders can be generated with PackMol. BUMPy is able to generate shapes that have been used in previous simulations but were generated either using in-house scripts or by application of forces to the simulation. These include capped cylinders¹¹, buckles^5,19–21 and tethers^14,18 (similar to the double_bilayer_cylinder shape in the BUMPY repository). Additional shapes in the repository may not have a direct biological counterpart, but may be of interest in reductionist studies of curvature effects on membrane properties.

Enforcing geometry using dummy particles

The equilibrium shape that a bilayer adopts is governed by the minimization of bending energy, which has been accurately described by the Helfrich Hamiltonian that has parameters of spontaneous curvature, bending rigidity and Gaussian curvature modulus.⁵² Therefore if a bilayer is constructed into a shape which does not represent a minimum energy configuration, the initial configuration will be unstable . In an unrestrained system with high total or gaussian curvature, or those with lipid compositions whose intrinsic curvature preferences do not match the curvature environment, the shape will deviate from the initial configuration towards lower energy states. Indeed, a number of the shapes in our current repository either collapse upon release of position restraints, or have significant deviations in their equilibrium geometry, despite high accuracy in the estimate of the pivotal plane position.

Observation of the relative stability of various membrane geometries is an interesting topic of study in and of itself, but there may be scenarios in which it is desirable to enforce a geometry on a bilayer. Recently, Yesylevskyy and colleagues developed an approach to maintain curved lipid morphologies, in which membranes are bracketed on both sides of the bilayer by a grid of dummy particles, which only interact with the hydrophobic core of the bilayer⁴³. With judicious selection of the distance of the dummy particle grid with respect to the bilayer center, and selection of the distance at which the repulsive interaction occurs, one can set up a system in which the dummy particles only interact with the bilayer when it deviates from its ideal geometry.

We have added an option to BUMPy that allows the user to add a grid of dummy particles to each side of the bilayer with a desired grid spacing and distance from the bilayer center. We have tested this implementation in a coupled semicylinder-bilayer system, and confirmed that the dummy particle setup results in maintenance of the previously unstable geometry (Supplemental Video 1). We note that while Yesylevskyy and colleagues⁴³ observed no significant artifacts in bilayer properties when the dummy particle setup are applied to flat bilayers, there is as of yet no such study of the impact of dummy interactions in curved systems. We intend to test for any artifacts arising from the dummy particle protocol in future work.

Discussion

BUMPy is fast, versatile, and easy to use. To generate curved lipid systems with accurate lipid areas, the user must only provide an area-equilibrated flat bilayer and a value for the pivotal plane location. We note that this bilayer need not be minimized or equilibrated in the typical simulation sense, as the only quantity of the bilayer that must be accurately represented is the lateral area per lipid. Thus, if that quantity is known an unequilibrated bilayer with the correct area per lipid can be generated using insane.py²⁷ or some other tool and then used as an input for BUMPy.

Obtaining a reasonable estimate for z_o is therefore the largest obstacle to accurately creating curved systems. Importantly, we have demonstrated that the z_o values of a number of Martini lipids are clustered around 1 nm, and within that range, errors associated with misestimating z_o are quite small. Thus, for most cases (using Martini), no additional simulations are required to estimate z_o, and BUMPy users can proceed with an estimate of ~1nm. On the other hand, simulations for which extreme accuracy of area is required may need a more rigorous estimate z₀, in which case the pore-based equilibration protocol may be employed.

To calculate zo when using models that do not display fast transverse relaxation, one must observe equilibrium interleaflet ratios using pore-based protocols (Wang and Deserno put forward an additional method using buckled bilayers⁹). However, once z_o is known it can be applied to build systems with any shape or size. We have determined z_o for a small number of lipid types in the Martini forcefield (Table S2), and will add to the repository over time. In addition, as the pivotal plane of more lipids become available, a systematic analysis of the effect of chain length, saturation and head group size may reveal trends that one can use to predict z_o from chemical principles.

One system type for which pore-based z_o measurements cannot be directly made are membranes with intra-leaflet heterogeneity (i.e. systems with multicomponent monolayers). The calculation of z_o using the method of Wang and Deserno assumes that the intrinsic area per lipid is constant between the leaflets. In a heterogeneous system with pores, lipids will partition to minimize the curvature frustration energy, disrupting the desired component concentrations in each leaflet. In these cases, one can estimate the z_o as a concentration-weighted average of the individual components. Alternatively, one could estimate z_o from H_II phase simulations and different hydration levels^51,53.

If one has a reasonable estimate of z_o for a given system, the pore-based equilibration procedure can be skipped, which has advantages beyond simply minimizing computational expense. One potential benefit occurs when simulating heterogeneous and/or asymmetric bilayers. Lipids in heterogeneous vesicles have been demonstrated to partition differentially between the inner and outer leaflets to minimize curvature frustration, leading to asymmetric concentrations between the leaflets¹⁰. While this state represents the energy minimum of the system with respect to curvature energetics, it is sometimes the case that researchers wish to simulate systems with fixed lipid ratios, for instance when the simulation attempts to reproduce an asymmetric biological membrane composition⁵⁴. Allowing interleaflet flipflop in a heterogeneous system inevitably leads to changes to the desired leaflet compositions.

Similarly, some of the shapes that are of interest for simulations separate the solvent in the system into multiple compartments, such as a vesicle. It may be desirable to simulate the separate water compartments with different conditions, varying factors such as ionic strength, pH, or osmotic pressure. In such situations, adding a hdrophilic channel connecting the compartments complicates maintaining those differences.

One potentially limiting factor of BUMPy is the assumption that the equilibrium area of a lipid in a flat bilayer is equivalent to that in a curved system. The consistency of z_o measurements across a variety of curvatures (Figure 3) supports this assumption, but it may not hold at the most extreme curvatures. In addition, some lipids display unique characteristics in the presence of curvature. For example, polyunsaturated lipids in the outer membrane of vesicles have been shown to fold their acyl chains back up into the membrane, potentially affecting the area per lipid in that leaflet¹⁰. Such effects of individual lipid types are not accounted for in the area-matching implementation of BUMPy, and should be considered carefully when setting up simulations.

While the coordinate transformation-based implementation of BUMPy leads to complete flexibility of force field and lipid type, BUMPy currently only allows creation of bilayer-organized structures where individual molecules are assigned on a leaflet basis. In the future, BUMPy could be extended to applications involving monolayer-based phases such as micellar or inverted-hexagonal phases, as the concept of the monolayer pivotal plane still applies in these systems for estimating initial lipid densities. In principal, a monolayer based approach would allow for creation of non-lipid materials which the simulation field has explored, such as carbon nanotubes⁵⁵. A final consideration is that BUMPy does not currently support embedded proteins. A tool already exists with facility for embedding (single or multiple) proteins into both flat and curved membranes⁵⁶, which we suggest should be used for such purposes after generating curved lipid-only systems using BUMPy.

Conclusions

We have presented BUMPy, a tool for the creation of starting configurations for MD simulations of curved bilayers. In addition to being fast and easy to use, BUMPy allows for complete flexibility of membrane composition and is forcefield independent. The use of small, simple geometric building blocks to model more complex topologies allows for generation of a wide range of biophysically relevant morphologies, many of which (to our knowledge) lack any other published implementations, and is an easily extensible approach to adapt to future needs. Through zo-based area estimation we provide a quantitative approach to populating individual leaflets with the correct number of lipids, and in this work have elucidated the extent to which lipid packing inaccuracies affect some membrane properties.