Quantifying solid stress and elastic energy from excised or in situ tumors

Abstract

Solid stress, distinct from both tissue stiffness and fluid pressure, is a mechanical stress that is often elevated in both murine and human tumors. The importance of solid stress in tumor biology has been recognized in initial studies: solid stress promotes tumor progression and lowers the efficacy of anticancer therapies by compressing blood vessels and contributing to hypoxia. However, robust, reproducible, and objective methods that go beyond demonstration and bulk measurements have not yet been established. We have developed three new techniques to rigorously measure and map solid stress in both human and murine tumors that are able to account for heterogeneity in the tumor microenvironment. We describe here these methods and their independent advantages: 2D spatial mapping of solid stress (planar-cut method), sensitive estimation of solid stress in small tumors (slicing method), and in situ solid-stress quantification (needle-biopsy method). Furthermore, the preservation of tissue morphology and structure allows for subsequent histological analyses in matched tumor sections, facilitating quantitative correlations between solid stress and markers of interest. The three procedures each require ~2 h of experimental time per tumor. the required skill sets include basic experience in tumor resection and/or biopsy (in mice or humans), as well as in intravital imaging (e.g., ultrasonography).

INTRODUCTION

Solid stress is defined as the mechanical stress that is contained in—and transmitted by—the solid and elastic elements of the extracellular matrix and cells in the tumor microenvironment. We first described solid stress in 1997 (ref. 1) in vitro, and later confirmed its role and biological consequences in vivo^2,3. We investigated angiotensin system inhibitors (ASIs) as agents that target the origins of this abnormal physical force, demonstrating that alleviating solid stress (e.g., via stromal and cancer cell reprogramming, and reduction of extracellular matrix) can decompress collapsed vessels, improve tumor perfusion, reduce hypoxia (and its associated downstream tumor-promoting pathways), and improve drug delivery and efficacy^4,5. These preclinical findings have culminated in the initiation of a phase II clinical trial⁶, which is investigating the ASI losartan in combination with cytotoxic therapy in unresectable, locally advanced, pancreatic ductal adenocarcinoma (PDAC). Strikingly, an interim analysis of this trial indicates that adding this solid stress-reducing agent to cytotoxic therapy doubles the frequency of conversion to resectable tumors and improves overall survival (OS) in these PDAC patients^7,8.

Development of the protocol and initial results

Most recently, we developed three novel methods that accurately measure solid stress and its 2D spatial distribution in both tumors and the host tissues in which they reside, as well as the resulting stored elastic energy in murine and human tumors⁹. These three methods are described here in detail: (i) the planar-cut method, which provides 2D maps of solid stress in tumors; (ii) the slicing method, which provides sensitive measurements of solid stress (reported as expansion ratio) in small lesions; and (iii) the needle- biopsy method, which is a clinically adaptable in situ quantification method that does not require total tumor resection and preserves the effects of the surrounding host organ tissues on intratumoral forces. From our application of these methods to a variety of tumor types and host tissues, we were able to conclude that (i) the magnitude and distribution of solid stress are dictated not only by the cancer cells but also by the local host microenvironment, (ii) solid stress—and not stiffness—increases with tumor size, and (iii) the mechanical confinement of a tumor by the surrounding host tissue can substantially contribute to intratumoral solid-stress levels⁹.

Comparison with other methods of measuring solid mechanical force

In our previous efforts to characterize solid stress, we devised a simple ‘partial-cut’ method to enable bulk measurements of this abnormal force, based on measurements of tissue deformation upon release of stored compressive and tensile stresses at the plane of a partial cut³. Although this earlier method definitively proved the existence of solid stress in a simple manner, there were some inherent limitations: the resulting singular bulk measurement did not highlight the heterogeneity of these stresses within different areas of the tumor, the method could not be applied to small tumors or to in situ tumors, and the mathematical modeling relied on assuming elliptical tumor shapes and pre-assigning regions of tension and compression.

Another promising method for measuring residual stresses in biological tissues is based on the deformation of fluorescent oil microdroplets¹⁰. Although this unique method is capable of measuring cell-generated forces during morphogenesis and tissue development in embryos, there are some limitations of this method. The residual forces are reported based on the deformation of an incompressible oil droplet; hence, the droplet does not deform or change volume when exposed to isotropic forces, which are usually found in the central regions of tumors. Furthermore, because this method is based on optical measurements of the droplet geometry, the maximum depth of measurement is governed by the working distance of the optical microscope, which is typically on the order of 100–400 μm.

Level of expertise needed to implement the protocol

A major advantage of these newly developed methods is that the techniques and readouts can be specifically tailored based not only on the biological question of interest, but also on the expertise of the user as well. For example, a researcher who seeks to simply determine how much solid stress is present in a tumor/tissue of interest can do so easily with basic surgical techniques to remove the tumor and incise it (e.g., with the planar-cut method) and a standard camera to image the resulting deformation. One could measure the maximum height of the incised sample before and after tissue relaxation, and calculate a ‘normalized deformation’ factor as a quantitative representation of solid stress. A researcher with access to higher-resolution optical imaging (e.g., ultrasonography) and material property measurements (e.g., atomic force microscopy (AFM)), as well as knowledge of mathematical modeling and relevant software, can achieve more precise and accurate estimates of solid stress.

Limitations

These protocols allow for unprecedented analyses of the effects of solid stress on tumor biology. Many of the materials used are readily accessible to most laboratories, including agarose solutions, biopsy needles, drills, vibratomes, and simple computational software (MATLAB and ABAQUS) with publicly available codes⁹. Potential limitations could include the need for a high-resolution ultrasound (if a detailed 2D stress field is needed), as well as access to methods of measuring stiffness (e.g., optical or tissue-based measurements such as AFM). In the absence of tissue stiffness measurements, however, quantitative inferences of strain (i.e., normalized deformation) can be made simply from the deformation data obtained from solid-stress release without the need to calculate the value of the force.

As described above, the three methods each have their own associated advantages, but they also have distinct limitations (summarized in Table 1). The planar-cut method is restricted to ex vivo measurements and requires embedding of the tissues in agarose before cutting, which may not be possible in all clinical settings. The slicing method requires ex vivo agarose-embedded tissues as well, and although it is more sensitive than the planar-cut method, it provides only indirect or bulk estimations of solid stress. The needle-biopsy method, although performed in situ, is not as sensitive as the slicing method.

TABLE 1 |.

Comparisons of the three methods for solid-stress measurements.

Method	Advantages	Limitations	Key equipment/materials	Timing
Planar-cut method	Direct estimations of the solid-stress component perpendicular to the cut plane (in Pa) and elastic energy (in J), both at the plane of interest	Not as sensitive as the slice method; unable to detect minute solid-stress values	Agarose gel	5 min of ex vivo tissue prep
	High-resolution 2D spatial maps of solid-stress distribution across the entire planar surface	Unable to be performed in situ	Aluminum mold	4 min of casting in agarose
	Able to distinguish regions of compression versus tension and account for tumor heterogeneity across the entire planar surface	Unable to be performed on tissue samples <1.5 mm in diameter Unable to estimate in-plane solid-stress components	Imaging system (ultrasound or optical)	<1 min of cutting 10 min of stress relaxation 5 min of imaging 30 min of material property measurement 60 min postprocessing Total: 115 min
Slice method	Highly sensitive; able to quantify area of expansion due to small values of solid stress	Provides an indirect solid-stress estimation (area expansion ratio) that is a bulk estimation of the average strain in the tissue slice	Agarose gel	5 min of ex vivo tissue prep
	Able to measure the strain induced by an unrelaxed in-plane solid-stress component	Unable to be performed in situ	Vibratome (slicer)	4 min of casting in agarose
	Applicable to small tissue samples (>1 mm in diameter)	Cannot distinguish between regions of compression versus tension	Imaging system (ultrasound or optical)	<1 min of slicing 10 min of stress relaxation 5 min of imaging 30 min of material property measurement 30 min postprocessing Total: 85 min
Needle-biopsy method	Provides 1D radial solid-stress profiles (in Pa)	Not as sensitive as the slice method; unable to detect minute solid-stress values	Disposable biopsy punch	5 min of ex vivo tissue prep
	Able to distinguish regions of compression versus tension	Unable to be performed on tissue samples <1.5 mm in diameter	Electric drill	<1 min of punching
	Does not require total tumor resection and can be performed in situ	Cannot estimate non-radial stress components (vertical and circumferential) in nonsymmetric tumor geometries	Imaging system (ultrasound or optical)	10 min of stress relaxation
	Preserves the effects of the surrounding host-organ tissue on intratumoral solid stress		Agarose gel (optional)	5 min of imaging 30 min of material property measurement
	Rapidly translatable to the clinic			60 min postprocessing Total: 110 min

Applications of the procedure

Broad application of the methods described in this protocol by cancer researchers and clinicians will facilitate further understanding of how abnormal biomechanics impacts tumor biology, provide robust and reproducible quantifications of solid stress and elastic energy that can be correlated with clinical outcomes as future predictive or prognostic factors (similar to the way tissue stiffness has emerged as such a factor¹¹), and illuminate novel, clinically translatable targets for alleviating solid stress in order to enhance drug delivery and efficacy in the treatment of solid tumors.

For example, collagen architecture¹² and tumor stiffness^11,13 have been linked and also implicated as prognostic factors in breast cancer. It could be possible to use the needle-biopsy or planar-cut method to measure solid stress in human breast cancer tumors, correlate it with collagen and stiffness measurements, evaluate its applicability as a prognostic marker of patient survival, and correlate it to other outcomes such as disease progression, treatment response/resistance, and emergence of metastasis. Efforts such as these would reveal new relationships between mechanical forces and biological consequences in tumors that can be exploited via innovative therapeutic approaches. Given the ongoing clinical trials aimed at reducing mechanical stresses in tumors^6,14, new methods are needed that can robustly and accurately uncouple stiffness from solid stress so that these outputs may be used as predictive metrics of treatment efficacy.

These methodologies also hold great potential for developmental biologists interested in measuring tissue mechanics. The embryo is known to experience solid stress during the early phases of growth, and there have been recent efforts to quantify these residual forces¹⁰. The protocols described here are capable of mapping the residual solid stresses and elastic energy in developing tissues, which can then be correlated to histological markers of interest in normal and pathological development.

Thus, these protocols allow for rigorous and reproducible measurements of solid stress and elastic energy, which have important but not fully elucidated roles in developmental and tumor biology. These methods, applied preclinically and clinically, will reveal new insights into pathological tissue mechanics, and diagnostic and predictive markers for patients.

Experimental design

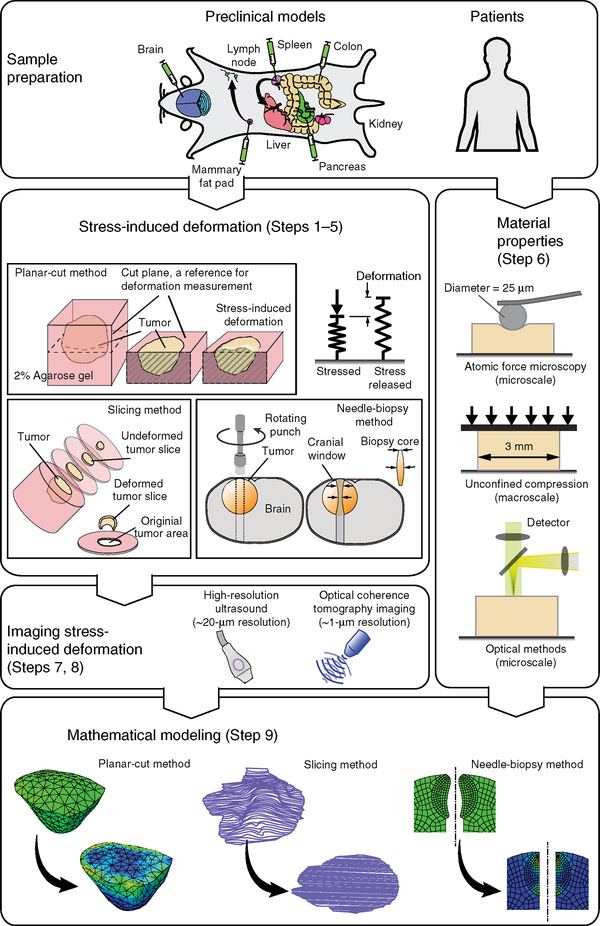
The protocols below (Fig. 1) are based on the observation that when tumor tissue is incised (whether a single planar cut, a slice, or a biopsy punch), some of the solid stresses are released, and the tumor mechanically relaxes near the incision (Fig. 1; Steps 1–5). The resulting topography of the sample preserves the spatial location of areas of compression (expanded tissue) and tension (contracted tissue). The deformation is mapped using high-resolution ultrasonography (Fig. 1; Steps 7 and 8), and then the magnitude and spatial distribution of solid stress, as well as its associated elastic energy, are calculated from the deformation information, coupled with tissue stiffness (Fig. 1, Step 6), measured via conventional methods, e.g., AFM and unconfined compression tests (Step 6) or by using the recently developed optical techniques^15,16 and mathematical computations (Fig. 1; Step 9).

Figure 1 |.

Overview of the procedure for estimation of solid stress in tumors. (Top left) Examples of clinically relevant tumor models are developed via orthotopic implantation of cancer cells into the desired organs (see Table 2 for details on tumor models). (Steps 1–5) Solid stress is released and the stress-induced deformation is obtained via three different methods: the planar-cut method, in which solid stress is released by a planar cut at the plane of interest; the slicing method, in which the stress is released by cutting the tumor in a thin slice; and the needle-biopsy method, in which the stress is released by punching a cylindrical void into the tissue of interest. (Steps 7 and 8) The stress-induced deformation is imaged in 3D by high-resolution ultrasound or optical modalities such as optical coherence tomography (OCT) techniques. (Step 6) The material properties, such as Young’s modulus, are obtained at the microscale via atomic force microscopy, and at the macroscale by the unconfined compression test. Recently developed optical methods, such as laser speckle rheology¹⁶ and Brillouin scattering¹⁵ can also be used to provide a 2D map of stiffness in the plane of the cut. (Step 9) In the cases of the planar-cut and needle-biopsy methods, the stress-induced deformation and material properties are incorporated into a finite-element model to estimate the solid-stress component that is fully released. In the case of the slicing method, the area expansion of the slice is considered to be a bulk measure of the in-plane solid stresses. Parts of the figure are adapted from ref. 9, Springer Nature.

The three methods were developed for specific applications. The planar-cut method (Fig. 2) is the most robust of the three methods. It provides a high-resolution 2D spatial distribution map of solid stress within the tissue, allows for easy differentiation between areas of tension and compression, and provides a direct estimation of solid stress and its associated elastic energy. The slicing method (Fig. 3) is the most sensitive of the three methods, allowing for the measurement of small values of solid stress in small tumors, such as tumors early in development or small metastases. Although all three methods can be used on human tumors, the needle-biopsy method (Fig. 4) is the most clinically relevant and translatable. The biopsy core, which can be obtained from routine tests in patients, contains valuable information about solid stress in tumors and does not require tumor resection. Mechanical information can be garnered, not only from deformation within the biopsy hole, but also from the biopsy core itself; furthermore, this method preserves the effects of the surrounding host organ tissues on intratumoral forces.

Figure 2 |.

Planar-cut method. (a) The tissue is embedded in agarose gel in a custom-made aluminum cast. (b) The tissue-gel construct is then cut at the plane of interest. (c,d) The solid stress-induced deformation is measured via high-resolution ultrasound (c) to provide the 2D stress-induced deformation map (d). (e) The stress-induced deformation map, the geometry, and the material properties of the tissue are incorporated into a 3D mathematical model to estimate solid stress at the cut plane in the direction perpendicular to the cut surface. It should be mentioned that the stress field can only be reported at the cut surface. The stresses at points deeper into the tissue are not fully released by this method, and hence the estimated values at these points do not represent the total stress. c adapted from ref. 9, Springer Nature. All animal procedures in this figure were carried out following the Public Health Service Policy on Humane Care of Laboratory Animals and approved by the Institutional Animal Care and Use Committee of Massachusetts General Hospital.

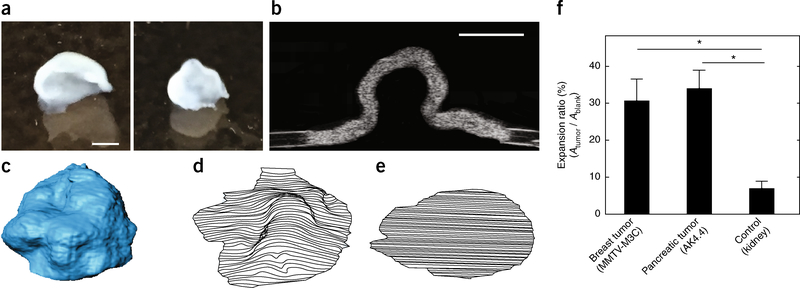
Figure 3 |.

Slicing method. The in-plane components of solid stress are released by cutting the tumor into thin slices. (a) Representative deformed slices from MMTV-MCa-M3C murine breast tumors (see Table 2 for details). (b) The ultrasound image of the section of the deformed slice. (c) The 3D reconstruction of a deformed slice. (d) Expanded slice. The ratio of the deformed and expanded slices to the original area of the slice provides a measure of the in-plane solid stresses. (e) The original area of the slice was obtained from the blank left in the agarose gel that was sliced with the tissue. (f) The slicing method is applied to breast and pancreas tumors, which show 30 and 35% increases in surface area, respectively, after the stress relaxation by slicing. The expansion ratio is significantly higher in these tumors as compared with that of the normal kidney (negative control), which results in 5% expansion ratio. The data shown are mean ± SEM (n=3 slices); *P < 0.05. Scale bars, 1 mm. f adapted from ref. 9, Springer Nature. All animal procedures in this figure were carried out following the Public Health Service Policy on Humane Care of Laboratory Animals and approved by the Institutional Animal Care and Use Committee of Massachusetts General Hospital.

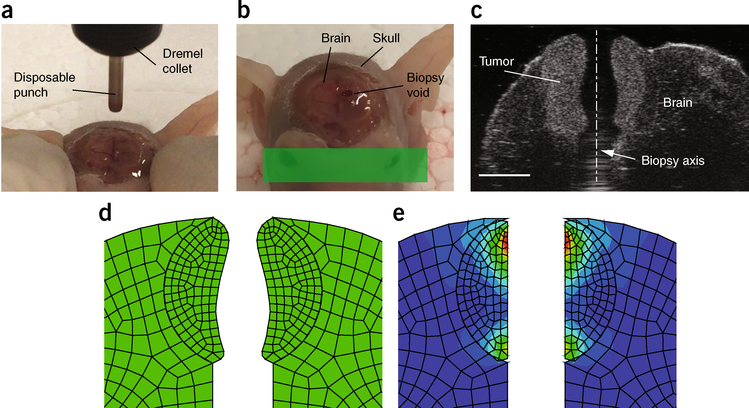
Figure 4 |.

Needle-biopsy method. (a) The tissue of interest, here a brain tumor surrounded by the brain and skull, is punched with a spinning needle. (b) The solid stress is relaxed along the axis of a cylindrical void created by the punch. (c) The ultrasound image of the cylindrical void that passes through the brain tumor and its surrounding brain. Using a mathematical model that incorporates the stress-induced deformation and the material properties of the tissue, the radial component of the solid stress is estimated. Scale bar, 2 mm. (d) The deformed (stress-released) geometry of the brain tumor. (e) The radial solid stress is estimated by returning the deformed geometry to the geometry before the stress relaxation. d,e adapted from ref. 9, Springer Nature. All animal procedures in this figure were carried out following the Public Health Service Policy on Humane Care of Laboratory Animals and approved by the Institutional Animal Care and Use Committee of Massachusetts General Hospital.

The three techniques can be used on normal host tissues (including negative controls, e.g., kidney, which showed no deformation in all three methods, and positive controls, e.g., heart), resected tumors of any size and geometry (e.g., primary versus metastatic), or host organs bearing tumors (e.g., a primary brain tumor encapsulated in an intact resected brain; a lymph node bearing breast cancer metastasis; or a liver bearing multiple metastases from pancreatic or colorectal cancers) (Fig. 1). We use our rigorously developed, well-characterized, murine orthotopic models that recapitulate human disease (Table 2) to demonstrate the effectiveness of these methods and draw biological conclusions; however, these protocols, especially the needle-biopsy method, are adaptable to human tumors as well.

TABLE 2 |.

Examples of clinically relevant orthotopic murine models of cancer for solid-stress measurements⁹.

Cell line	Site of implantation	Cancer type	Host species	Site(s) of metastasis	References
4T1	Mammary fat pad	Breast cancer—triple negative	Murine—Balb/c	Lymph node, liver, and lung	9,27,28
AK4.4	Pancreas	Pancreatic ductal adenocarcinoma	Murine—FVB	Liver	4,9,29
MCa-M3C	Mammary fat pad	Breast cancer (HER2+)	Murine—FVB	Lung	9
SL4	Cecum (for primary); spleen (for liver metastasis)	Colorectal cancer	Murine—C57BL/6	Liver	9,30
U87	Brain	Glioblastoma	Human	-	9,31

Measurement of material properties

The methods described here provide estimations of stress-induced deformation only. To estimate solid stress, the material properties (Young’s modulus and Poisson’s ratio) of the tumor—and the surrounding tissue in the case of in situ stress estimation via the needle-biopsy method—must be determined. Young’s modulus is obtained from unconfined compression tests (in the macroscale; Step 6B) or via AFM (at the microscale; Step 6A)⁹. For tissue samples that are very small or that feature high heterogeneity in material properties, microscale mapping of the stiffness via AFM is more sensitive and applicable. More recently, optical methods based on laser speckle rheology¹⁶ and Brillouin scattering¹⁵ have been developed with the potential to map the heterogeneity of material properties at high resolution. To acquire a 3D map of material properties, methods such as magnetic resonance or ultrasound elastography can be used. Poisson’s ratio is assumed to be υ=0.1, as in other soft tissues^17,18. Although stress relaxation is a time-dependent behavior that follows linear poroelasticity theory^19,20, we assume constant material properties, as both the stressed and stress-released conditions are at equilibrium.

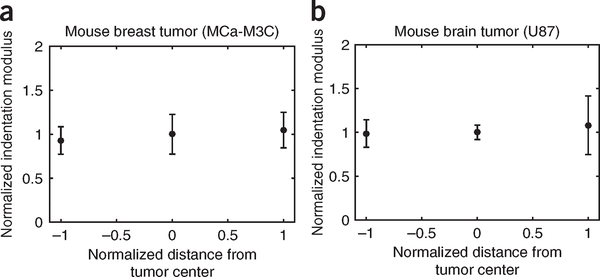
In this work, we assumed a single value for the Young’s modulus of the tumors because we did not observe substantial variability in the indentation modulus measured at the periphery versus the core of the murine breast and brain tumors that we tested (Fig. 5). In tumors that feature highly heterogeneous material properties (as is often the case in human tumors), a 3D map of material properties must be incorporated into the mathematical model. This process, required for more accurate predication of solid-stress heterogeneity, is feasible with the mathematical model that we developed in the commercially available software ABAQUS.

Figure 5 |.

Indentation modulus at the tumor periphery versus the core. (a,b) Comparison of the indentation modulus in the periphery versus the core of the breast tumor model MCa-M3C (a) and the brain tumor model U87 (b). The data shown are mean ± SEM (each data point represents the average value in n=3 mice). Owing to the lack of substantial variability in the indentation modulus at these two sites, we assumed uniform value material properties in the mathematical modeling. In highly heterogeneous tumors, a 3D map of material properties can be incorporated into the mathematical model.

Methods for imaging solid stress

Stress-induced deformation can be imaged with any 3D imaging modalities. We use high-resolution ultrasound (20-μm resolution) and optical frequency domain imaging^9,21 (OFDI, a variation of optical coherence tomography (OCT)) (1-μm resolution) to quantify stress-induced deformation (Steps 7 and 8).

Mathematical modeling of solid stress and elastic energy

Mathematical models (Step 9) are used to convert the stress-induced deformation field to the 2D solid-stress field. For simple geometries such as a sphere with a symmetric deformation field, analytical models might be available to convert strain measurements to a stress field. However, to estimate solid stress in tumors with arbitrary geometries and deformation fields, we use finite-element modeling in ABAQUS. The model that is developed in ABAQUS incorporates the stress-induced strain ε_ij (strain is derived from the deformation field u_i from ε_ij = 1/2(∂u_i/∂x_j + ∂u_j/∂x_i)), the geometry of the sample, the boundary conditions, the material properties of the sample, and estimates the stress field σ_ij based on the linear constitutive equation²²:

$${\sigma }_{ij}=\frac{E}{(1+v)}[{\epsilon }_{ij}+\frac{v}{(1-2v)}{\epsilon }_{kk}{\delta }_{ij}]-{\delta }_{ij}p$$

where E is Young’s modulus (stiffness), v is the Poisson’s ratio of the tissue (based on linear isotropic assumption), δ_ij is the Kronecker delta, and p accounts for pressurization of the fluid phase under nonequilibrium conditions. In all experiments performed for this study, the tumor is excised (planar-cut and slicing methods), or the mouse is sacrificed (needle-biopsy method) before measurement; therefore, the fluid pressure goes to zero, and we can neglect the last term in the above equation. In the in vivo condition, however, the fluid pressure in most tumors is elevated as compared with that of the normal tissue²³. The effect of elevated fluid pressure and fluid flow on the solid-stress field is an interesting problem, which can be answered by developing methods to measure solid stress in vivo, or by mathematical modeling—similar to that performed for tumor spheroids in vitro^24,25. This fluid pressure originates from the blood pressure and abnormalities of vasculature in tumors²³. Another potential effect is the cell death long after the resection of the tumors. Death of cancer cells and fibroblasts in tumors has been shown to reduce solid stress³. To avoid any artifact due to cell death in this study, we performed all measurements within 20 min after the tumor resection.

The assumption of the linear constitutive equations is based on the stress-strain analysis performed on most of the tumors involved in this study (Supplementary Fig. S8 in ref. 9; unconfined compression test). However, at high strain values, and particularly in regions with high collagen density, the tissue may not follow the above linear constitutive equations. In these cases, the appropriate stress-strain relationship, obtained by the applicable mechanical properties assay, e.g., unconfined compression or AFM indentation, must be incorporated into the mathematical model. Our mathematical model, developed in the commercial software ABAQUS, can be simply modified to incorporate any changes in the constitutive equations.

The mathematical model estimates the perpendicular (normal) stress component for the planar-cut method and the radial stress component for the needle-biopsy method. In the planar-cut method, the in-plane stresses are also partially released after the incision. This results in lateral (in-plane) displacement, which is taken into account in the finite-element model and can be reported (Supplementary Fig. S3 in ref. 9). However, because the in-plane stresses (unlike the perpendicular stresses) were not fully relaxed by the incision, we did not report the estimated in-plane stresses.

MATERIALS

REAGENTS

• Tumors from patients or orthotopic mouse models (see Table 2 for references to cell-line culture and implantation techniques) in various strains of mice, or human clinical samples either in situ, or resected

  ! CAUTION Studies on human samples must be conducted in accordance with protocols approved by the relevant institutional review boards. Human samples for this work were collected under a protocol approved by the Institutional Review Board of the Dana-Farber/Harvard Cancer Center. The subjects gave written informed consent to participate in the study and to have their resected tissue used for research.

  ! CAUTION All animal studies must be reviewed and approved by the relevant institutional animal care and use committees and must conform to all relevant ethics regulations. All animal procedures in this work were carried out following the Public Health Service Policy on Humane Care of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee of Massachusetts General Hospital. ▲ CRITICAL For solid-stress experiments on preclinical models, we highly recommend using orthotopic or genetic tumor models instead of subcutaneous or ectopic models, as these will not recapitulate the correct host organ and tumor microenvironmental conditions that contribute to solid stress.

• Isoflurane (gas anesthesia system) ! CAUTION Isoflurane is an anesthetic. Use a commercial system with a carbon-recovery chamber (e.g., VetEquip inhalation anesthesia systems) to avoid exposure to fumes.

• Ketamine (Ketaset; Patterson Veterinary, cat. no. 07–803-6637)

• Xylazine (Anased; Patterson Veterinary, cat. no. 07–808-1039)

• PBS (1× CellGro; Corning, cat. no. 20–031-CV)

• Low-gelation temperature agarose (Sigma-Aldrich, cat. no. A9414)

EQUIPMENT

Surgical equipment for tumor excision

• Syringe for anesthesia (1 ml; BD, cat. no. 309659)

• Sterile Petri dishes (Falcon, various sizes)

• Shallow container

• Tweezers (Roboz Surgical, cat. no. RS-5112)

• Curved forceps (Roboz Surgical, cat. no. RS-5135)

• Straight forceps with teeth (Roboz Surgical, cat. no. RS-5132)

• Straight Iris scissors (Bonn, cat. no. RS-5840)

• Scalpel

• Sterile gauze

Equipment for tumor embedding

• Heated magnetic stir plate

• Magnetic stir bar

• Glass Erlenmeyer flask or beaker, 100 ml or larger

• Sterile Petri dishes (35 × 10 mm; Falcon)

• Mold assembly: aluminum cast (McMaster-Carr, cat. no. 6945T811), plastic base (McMaster-Carr, cat. no. 8536K164), and clips (Staples, cat. no. 831610) (Fig. 2)

Equipment for planar-cut method

• Straight razor (Scalpel Klingen)

• Pliers

Equipment for slicing method

• Vibratome setup: equipment (e.g., Precisionary, model no. Compresstome VF-300)

• Stainless-steel specimen tube

• Syringe tube

• Chilling block

• PBS bath (or similar)

• Insulin syringe, 0.5 ml with 26 gauge × 5/7-inch needle (BD, cat. no. 309597)

Equipment for needle-biopsy method

• Disposal biopsy punch, 1–4 mm in diameter (Integra-Miltex or similar, e.g., 33–31)

• Electric drill mounted vertically with a drill press and accompanying collets/drill bits (Dremel, cat. no. 4300)

Equipment for microscale measurement of Young’s modulus

• Atomic force microscope (Asylum Research, model no. MFP3D)

• Colloidal particle (radius ~12.5 μm; Polysciences)

• AFM tipless cantilever (with spring constant ~0.12 N/m for tissues with Young’s modulus in the range of 0.3–3 kPa; Bruker, cat. no. NP-O10)

• Glue (M-Bond-610; Structure Probe Supplies)

• Super Glue

• 10 × 10-mm Glass coverslip

• Heating/drying oven

Equipment for macroscale measurement of Young’s modulus

• Unconfined compression setup, or any conventional rheometer (e.g., Electropuls, Instron)

• Brain slicer (Zivic Instruments, cat. no. BSMAS005–1)

• Disposable biopsy punch, 2 mm in diameter (Integra-Miltex, e.g., 33–31)

• Caliper

Equipment for imaging

• Ultrasound machine (e.g., Visualsonics, model no. Vevo-2100)

• Optical scattering-based equipment (e.g., OCT)

Software for mathematical modeling

• MATLAB (MathWorks, http://www.mathworks.com)

• Custom MATLAB codes, available from

• https://images.nature.com/original/nature-assets/natbiomedeng/2016/s41551–016-0004/extref/s41551–016-0004-s2.zip

• ABAQUS (Dassault Systems;

• http://www.3ds.com/products-services/simulia/products/abaqus)

• SolidWorks (Dassault Systems; http://www.solidworks.com)

REAGENT SETUP

Ketamine-xylazine solution

This 10:1 ratio cocktail is made by adding 3 ml of ketamine (Ketaset, 100 mg/ml), diluted 10 times, and 0.3 ml of xylazine (Anased, 100 mg/ml), diluted 100 times, to 27 ml of sterile saline (PBS) using aseptic techniques. The mixture can be stored at room temperature (25° C) for 7 d or at 4° C for 30 d. The administration is carried out via i.p. injection at a dose of 1 ml per 100 g of body weight.

Agarose solution

The low-gelation agarose assumes a liquid form in solution at ~40 °C. Prepare a 2% (wt/vol) agarose-PBS solution (e.g., 2 g of agarose in 100 ml of PBS). In a heated, stirring solution of PBS at 80 °C in a glass beaker or Erlenmeyer flask, add the agarose powder slowly over time to ensure uniform dissolution. Once dissolved, reduce the temperature to ~40 °C. ! CAUTION Be careful when handling the 80 °C agarose to avoid potential burns. ▲ CRITICAL Be sure to reduce the temperature and to not attempt tissue embedding with the 80 °C agarose solution. This reduced temperature will ensure that the agarose solution remains a liquid, but will not damage the tissue upon embedding. The agarose solution can be allowed to cool to form a gel within the flask/beaker with the magnetic stir bar and stored for several weeks at 4 °C for reuse.

EQUIPMENT SETUP

Planar-cut and slicing methods: assembly of the embedding mold

Center the precooled aluminum mold on top of the plastic-bottom plate with the smaller plug opening facing downward and secure it with binder clips as shown in Figure 2. ▲ CRITICAL As an efficient conductor, cooling of the aluminum mold will speed up the gelation of the agarose solution during the embedding process.

Planar-cut method: preparation of the incision razor

Using pliers, remove the handle from the razor so that you have a squared, smooth razor with which to incise the embedded tissue. ! CAUTION Take care when manipulating the razor to remove the handle so as not to harm yourself, and be sure not to bend or deform the razor while removing the handle, or you will not be able to achieve a straight, smooth incision. Alternatively, razor blades without handles could be bought.

Slicing method: preparation of the vibratome

A vibratome is used on agarose-embedded tissues in the slicing method to ensure uniform thin (100–500 μm) tissue sections, which results in relaxation of in-plane solid stresses. The VF-300 Compresstome comes with a stainless-steel specimen tube cast that is used for tumor embedding and slicing (as described in Step 5B in the PROCEDURE). Prepare the vibratome by setting the desired thickness of the sample, attaching the razor blade to the razor holder, cooling the chilling block on ice, and positioning a shallow PBS bath below the sample-cutting site so that the slices may fall into the solution as they are cut.

Needle-biopsy method: preparation of the biopsy needle and mechanical drill

Using a razor, detach the metallic cylindrical blade (hereafter referred to as the ‘punch’) from the plastic biopsy holder. ! CAUTION Take care when manipulating the razor to remove the punch so as not to harm yourself.

▲ CRITICAL Be careful not to deform the shape of the punch during this step or it will not enter the drill in an aligned orientation, nor will it provide a uniform cylindrical tissue core for analyses. Insert the punch into a collet (drill bit) of appropriate size in relation to the punch diameter, and affix it to the drill so that the punch is centered. ▲ CRITICAL Test the rotation of the drill to be sure that the punch is centered and is rotating smoothly (not wobbling in the angular directions), or else you will not be able to produce a straight punch.

Microscale measurement of Young’s modulus

Attach the colloidal particle to the tipless AFM cantilever: place a dot of glue on the tipless cantilever by dipping the cantilever into a thin layer of glue (1 μl) spread over a 10 × 10-mm glass coverslip. Immediately make contact between the tip of the cantilever and a colloidal particle resting on a glass slide and wait for 1 min with the cantilever pushing against the colloidal particle. Heat-cure the glue for 2 h at 150 °C. After tip attachment, measure the exact spring constant of the AFM tip by the thermal calibration method (built-in the AFM software), and perform calibration of the AFM system.

Macroscale measurement of Young’s modulus

A standard rheometer (here a custom-made dynastat) is used to measure Young’s modulus via the unconfined compression test.

PROCEDURE

Ex vivo tumor preparation • TIMING 5 min

▲ CRITICAL For murine tumors, follow Steps 1–4. For human tumors, proceed directly to Step 4.

• 1For ex vivo measurements (planar-cut or slicing methods), anesthetize the mouse with 1 ml per 100 g of body weight of the ketamine and xylazine cocktail. Test that the mouse is fully anesthetized via pedal reflex and respiration monitoring.

  ▲ CRITICAL STEP If it is desired to have in vivo measurement of blood perfusion in the tumor before resection, anesthetize the mouse with the isoflurane gas anesthesia system (following the approved associated animal protocol), and image the tumor via microultrasound through the skin or a transparent window, if available.

• 2Remove the tumor with the surgical supplies listed in the MATERIALS section per the standard surgical techniques warranted by the anatomical location of the tumor and the approved associated animal protocol.
• 3(Optional) If the mouse is to be sacrificed at the time of tumor excision, then follow standard institutional euthanasia steps (e.g., cervical dislocation) and perform solid-stress experiments at necropsy.

  ! CAUTION All experiments with mice must be performed under institutional and national regulations and guidelines. All animal procedures in this work were carried out following the Public Health Service Policy on Humane Care of Laboratory Animals and approved by the Institutional Animal Care and Use Committee of Massachusetts General Hospital.

• 4Submerge the excised fresh tumor (human or murine) in PBS in a Petri dish at room temperature during the preparation of the embedding mold and agarose solution.

  ▲ CRITICAL STEP Avoid freezing or fixing the tumors post excision, as any chemical and/or physical processing of the tumors will alter the solid-stress field and elastic energy. The tumor/tissue is now ready for the planar-cut method (Step 5A), the slicing method (Step 5B), or the needle-biopsy method (Step 5C) as differential methods to release solid stress.

Methods to release solid stress • TIMING 10–15 min

• 5Release the solid stress. Follow option A for the planar-cut method, option B for the slicing method, or option C for the needle-biopsy method.

(A). Planar-cut method • TIMING 15 min

▲ CRITICAL Supplementary Video 1 shows how to perform Step 5A(ii-iv).

• iGently holding one end of the tissue with tweezers, remove it from the PBS, place it inside the mold, and pour the still liquid 40 °C agarose solution (see the Reagent Setup section) on top of the sample until it is submerged.

  ! CAUTION Proceed with this embedding step and gelation at room temperature, not over ice, so as not to affect deformation and material properties (Fig. 2). Full gelation takes ~5 min.

  ▲ CRITICAL STEP To ensure that the sample is oriented as desired in the gel, be sure to remain holding the tumor with the tweezers for the period of time (within a minute) until the agarose partially gels, and the tissue is held in place if it is released and does not sink to the bottom of the mold.

• iiOnce fully gelled, disassemble the embedding apparatus and gently push the agarose-embedded tissue out of the mold.

  ? TROUBLESHOOTING

• iiiCut the extra agarose surrounding the tissue to produce flat edges for ease of handling/imaging at later steps.

  ! CAUTION Do not cut the tissue when ‘trimming’ the excess agarose, and be sure to leave enough surrounding agarose for weighing down the submerged sample during imaging (Steps 7 and 8).

• ivPlace the embedded tumor on a flat surface. Using the razor prepared as directed in the Equipment Setup section, gently and slowly slice the tissue vertically, across the largest diameter of the sample (or other plane of interest) using a smooth, sawing motion. Plate the two hemispheres of the gel-tumor construct cut side up in a Petri dish and submerge them in PBS at room temperature.

  ▲ CRITICAL STEP Allow the submerged cut tumors to remain cut side up in solution for at least 10 min to ensure that the tissue can relax and deform due to release of solid stress and elastic energy.

  ? TROUBLESHOOTING

• vAt this point, dedicate one hemisphere to solid-stress measurements (imaging and other steps below), and remove the other hemisphere from the agarose gel (using tweezers) and use it for tissue-matched histology (e.g., paraffin or frozen embedding); alternatively, you can use both hemispheres for both solid-stress measurements and histology.

  ▲ CRITICAL STEP It is recommended that a small mark or cut be placed on the tissue as a hemisphere identifier for subsequent spatial referencing of the two hemisphere tissue samples.

(B). Slicing method • TIMING 15 min

1. Perform Step 5A(i), with the exception that the stainless-steel cast accompanying the vibratome is used instead of the custom aluminum mold (Fig. 3 and Supplementary Videos 2 and 3).

2. Using the vibratome set at the desired slice thickness (100–500 μm; 200 μm is recommended as a starting thickness for initial studies), gently and slowly push the agarose gel-tissue cylindrical construct out of the cast with the provided fitted interior plug for the cast until the edge of the agarose reaches the vibratome blade. Allow the blade to cut through the excess agarose surrounding the tissue before slicing through the encased tissue.

   ? TROUBLESHOOTING

3. The tissue slices should fall into the PBS bath placed below the vibrating plate. Note that the tissues may spontaneously detach from the surrounding agarose; otherwise, manually remove the tissue from the agarose using tweezers.

   ! CAUTION Be sure not to cut the tissue when removing it from the agarose.

   ▲ CRITICAL STEP Do not damage or discard the agarose ‘blank’ left behind when the embedded tissue falls out or is removed; this blank area represents the tumor area before stress relaxation by slicing and is therefore useful for calculating indirect solid-stress measurements.

   ▲ CRITICAL STEP Allow the tissue slices to deform while submerged in PBS at room temperature for at least 10 min.

(C). Needle-biopsy method • TIMING 10 min

▲ CRITICAL Supplementary Video 4 shows how to perform Step 5C(i-iii).

1. Place the tissue sample of interest (whether ex vivo, or in situ in an anesthetized or euthanized animal) on a stage under the drill. A Styrofoam block is recommended so that, if needed, the biopsy needle can pass 100% of the way through the tissue (Fig. 4).

   ? TROUBLESHOOTING

2. Hold the tissue sample with tweezers before punching.

   ! CAUTION Do not squeeze or push on the sample when holding it or the deformation will be affected.

   ? TROUBLESHOOTING

3. Slowly lower the handle on the drill press to lower the drill and biopsy punch through the tissue sample of interest, and then raise the handle to extract the core from the tissue.

   ? TROUBLESHOOTING

4. Submerge both the punched tissue and the punch in PBS in a Petri dish; remove the core gently from the punch with tweezers, or flush it out with a syringe.

   ▲ CRITICAL STEP Allow both the punched tissue and the biopsy core to mechanically relax for at least 10 min.

(Optional) Measurement of the material properties (Young’s modulus) • TIMING 30 min

▲ CRITICAL This section describes optional procedures for determining the material properties in order to define the solid-stress fields. If the simple stress-induced deformation measurements are sufficient, then proceed to imaging in Step 7.

• 6Follow option A to determine material properties via the AFM indentation test (microscale) or option B to do so via the unconfined compression test (macroscale).

(A). AFM indentation test (microscale) • TIMING 30 min

1. Perform Step 5A to create a flat cut surface of the tissue sample; the sample thickness should be 0.5–2 mm (a thinner sample results in a more even surface, but if a sample is too thin, the substrate effect may affect the readout; 1 mm is recommended as a starting thickness.).

2. Use cyanoacrylate (‘super’) glue to attach the bottom of the agarose/sample construct to a glass slide.

3. Let the glue dry for 2 min, and add PBS to cover the top surface plane so that the AFM tip is submerged in PBS during indentation.

4. Engage the AFM tip with the sample, and obtain force-displacement curves from at least ten indentation sites.

5. Estimate the indentation modulus from the force-displacement curves, using the Hertzian contact model:

   $$F=\frac{4}{3}\frac{E_{\text{ind }}}{{(1-v)}^2}{R}^{1/2}{D}^{3/2}$$

   where F is the indentation force, D is the indentation depth, and õ is Poisson’s ratio (we assumed õ=0.1, as measured in other soft tissues^17,26).

6. Estimate the average indentation modulus of the tumor tissue as the mean of the modulus at each indentation site.

(B). Unconfined compression test (macroscale) • TIMING 30 min

1. Use a disposable biopsy punch to cut a cylindrical plug from the tissue sample from Step 4 that is 3 mm in diameter.

2. Using a brain slicer, cut the two edges of the plug to obtain flat end surfaces. The approximate height of the tissue plug should be 2 mm. Use a caliper to measure the exact height of the plug.

3. Place the plug on the unconfined compression stage, and apply four strain steps, each 5% of the total height of the plug. After each step, apply a hold (constant displacement) with a duration of 20 min to reach to the equilibrium force, and measure the equilibrium force at the end of each step.

4. Plot the equilibrium stress (the equilibrium force normalized by the area of the plug) versus the sequential strains (5, 10, 15, and 20%). Estimate the Young’s modulus as the slope of the linear fit of the stress-strain plot.

Imaging • TIMING 5 min

• 6Once the tumor solid stress has been released using one of the three methods in Step 6, submerge the sample(s) of interest in PBS at room temperature in a shallow container that allows for at least a 1-cm column of solution above the sample. For small samples and small deformations (<2 mm), optical methods, such as OCT or confocal microscopy can be used.

  ? TROUBLESHOOTING

• 7Perform the imaging in 3D using the motorized stages of the ultrasound machine for large samples (>2-mm diameter) or an optical microscope for small samples (<2-mm diameter).

  ? TROUBLESHOOTING

Postprocessing and mathematical modeling • TIMING 30–60 min

• 6Postprocess the measurements and perform mathematical modeling. Follow option A for data acquired via the planar-cut method, option B for slicing-method data, or option C for needle-biopsy data.

(A). Planar-cut method • TIMING 60 min

1. Export the 3D images of the deformed tumor from ultrasound or optical imaging into a stack of MATLAB images, using the MATLAB script load_v3.m (the codes are available at the link in the MATERIALS section). Apply appropriate thresholds and segment each image such that noise signals (e.g., during ultrasound imaging, from air bubbles within the PBS-submerged tissues, or from reflections from the bottom of the housing container during imaging) are excluded from the image of the tumor. Obtain the profile of the top surface of the tumor (the deformed surface after stress relaxation), and bottom surface of the tumor separately for each image by using the script plot_v3.m. Save the top and bottom surfaces as a set of lines in an array in an .xyz text file.

2. Import each of the profile lines of the top and bottom surfaces into the SolidWorks software. Simply use the open command to open each .xyz profile, and then save each profile as a part in SolidWorks. After importing all the line profiles of the top or bottom surfaces, open a new file in SolidWorks, and insert all the lines that were saved as a part. Construct top- and bottom-surface geometries from the sequential profiles by using the ‘Lofted Surface’ command. Save each surface as a separate part. Once the surfaces are constructed, merge them into a solid geometry by using the command Knit Surface. Make sure the option ‘Try to Form Solid’ is checked. Save the final solid object as a .STEP file in SolidWorks.

3. Import the solid geometry in .STEP format into the ABAQUS software by using the command ‘Import Part’, making sure to choose ‘*.STEP’ as the file filter. In ‘ABAQUS CAE’, mesh the geometry by first assigning the ‘Approximate Global Size’ of the mesh in the ‘Seed’ option. The appropriate mesh size is required to be substantially smaller than the characteristic geometrical variation; an appropriate check is the smoothness of the final stress results. Then choose ‘Quadratic Tet Elements (C3D10)’ from the ‘Mesh Control’ menu, and mesh the part. Next, assign material properties by using the ‘Materials’ and ‘Section Assignment’ options.

4. Apply the appropriate boundary conditions: use the spatial coordinates of the top surface to ‘undo’ the deformation to generate a representation of the originally flat surface (that existed before the cut) from the deformed top surface. The deformation boundary condition is assigned only to the perpendicular direction on each node at the top surface, and its value for each node is the negative of the z-coordinate of the node. There is no condition assigned to the lateral coordinate of the nodes.

5. Create a job using the ‘Jobs’ option in the ‘Analysis’ section, and run the ‘ABAQUS solver. Read the stress values perpendicular to the cut surface for each node, or visualize the stress map by clicking on the ODB file that is created after running the ‘ABAQUS solver’. The normal stress in this direction is the only component that fully relaxes to zero from the cut method; therefore, this is the only stress component that can be reported. The lateral stress components can be reported only as stresses that are partially released from the planar-cut method.

(B). Slicing method • TIMING 30 min

1. Export the 3D images of the deformed slice and the agarose blank (footprint) from ultrasound or optical imaging into a stack of MATLAB images. Apply appropriate thresholds and segment each image such that the noise signals (as described in Step 9A(i)) are excluded from the image of the tumor and agarose slices. Obtain the profile of the surface of the slice and the blank. As in Step 9A(i), save the profile as a set of line arrays.

2. From the profiles of each image, construct the separate geometries of the slice and blank, and estimate the surface areas in MATLAB. Estimate the area of the slice, decomposed into an array of strips, as the length of each strip multiplied by the distance between each line (the width of the strip). The surface area of the agarose blank (the agarose slice that surrounded the tumor slice before the relaxation) represents the original surface area of the tumor before the relaxation.

3. Estimate the expansion ratio I_ER as the ratio of the surface area of the slice after deformation (stress-free slice), A_tumor, to the surface area of the agarose blank, A_blank, which represents the surface area of the slice before stress relaxation:

   $$I_{\text{ER}}=\frac{A_{\text{tumor }}-A_{\text{blank }}}{A_{\text{blank }}}$$

   The expansion ratio I_ER, is an index of the strain induced by the in-plane stress components. An average in-plane stress value can potentially be estimated by multiplying the expansion ratio by the average Young’s modulus of the slice.

(C). Needle-biopsy method • TIMING 60 min

1. Export the 3D images of the deformed tumor from ultrasound or optical imaging into a stack of MATLAB images. Apply appropriate thresholds and segment each image such that the noise signals (as described in Step 9A(i)) are excluded from the image of the tumor. Obtain the diameter profile of the punch void and biopsy core along the axis of the punch. If both the tumor geometry and biopsy void deformation are symmetric with respect to the axis of the punch, an axisymmetric model can be constructed instead of a 3D model. The axisymmetric model substantially lowers the computational cost of the model.

2. Export the profile of the biopsy void and tumor geometry from MATLAB into ABAQUS. This can be done by discretizing the profile of the biopsy void (e.g., to ten segments) and tumor geometry, and inserting the xyz-coordinate of each segment manually into ‘ABAQUS CAE. An alternative approach is to use SolidWorks as explained in Step 9A(ii). After the geometry is either made or imported into ABAQUS, mesh the geometry, and assign material properties. Mesh the geometry by first assigning the ‘Approximate Global Size’ of the mesh in the ‘Seed’ option. The appropriate mesh size is required to be substantially smaller than the characteristic geometrical variation; an appropriate check is the smoothness of the final stress results. Then choose the ‘Quadratic Tet Elements (C3D10)’ from the ‘Mesh Control’ menu for a 3D model, and choose the 3D quadratic element for an axisymmetric model. Next, assign material properties by using the ‘Materials’ and ‘Section Assignment’ options.

3. Apply the appropriate boundary condition by returning the deformed geometry of the biopsy void to the original geometry of the void before the stress relaxation. The nodes on the boundary of the void are the only nodes for which the boundary conditions are assigned. The original geometry of the void before stress relaxation is a uniform cylinder with the uniform diameter of the biopsy punch that was used. Therefore, the boundary condition of each node is calculated as the radial distance that the node must travel to reach to the original uniform cylindrical geometry. The radial distance is entered manually in ‘ABAQUS CAE’ or the input file (*.inp) that can be generated in ‘ABAQUS CAE’.

4. Create a job using the ‘Jobs’ option in ‘Analysis’ section, and run the ‘ABAQUS solver. Read the radial stress values perpendicular to the surface of the cylindrical void, or visualize the stress map by clicking on the ODB file that is created after running the ‘ABAQUS solver. The radial stresses are the only component that fully relaxes to zero from the needle-biopsy method; therefore, this is the only stress component that can be reported. The axial and tangential stress components, which are accounted for in the mathematical model, can be reported only as stresses that are partially released from the needle-biopsy method.

   ? TROUBLESHOOTING

Troubleshooting advice can be found in Table 3.

TABLE 3 |.

Troubleshooting table.

Step	Problem	Possible reason	Solution
5A(ii)	Gel-tissue construct falls apart as it is being pushed out of the aluminum mold	Agarose not allowed enough time to gel fully	Using tweezers, remove the tissue from the surrounding gel carefully and repeat the embedding process
5A(iv)	The tumor is displaced during cutting	The cutting was not performed with a proper sawing motion	For tumors that are not fully adherent to the agarose cast, or tumors with surrounding fatty or connective tissues (that are difficult to cut through), a manual sawing motion with a higher amplitude and lower feed rate is required
5B(ii)	The slice is not cut through all the way and is semi-attached to the rest of the tissue bulk	Connective or fatty tissue surrounding the tumor may impede even slicing and separation	Ensure that the tumor (in particular, breast tumors) is devoid of any surrounding tissue, including fat and connective tissue. If the slice is not fully cut and separated from the bulk of the tissue, perform a second round of slicing. If the problem persists, use tweezers to extract the tissue carefully from the agarose gel, remove any surrounding fatty/ connective tissue from the sample, and then repeat the embedding and slicing process
5C(i)	Obstruction of tissue before needle-biopsy method	Transparent window was implanted into the mouse being used for needle-biopsy method	The rotary punch can be used even in the case of an in situ tumor/tissue located under a transparent window for imaging (e.g., a cranial window made from a plastic coverslip for breast cancer brain metastases). In this case, a biopsy punch with a slightly larger diameter (e.g., 0.5-mm larger) than the desired biopsy core diameter can be used to drill through the coverslip without disturbing the tissue beneath. Then, through this hole, a second, smaller biopsy punch can be used to punch the tissue in situ
5C(ii)	Uneven tissue from biopsy punch	Destabilization of tissue during punching	As an alternative approach, an ex vivo sample can be temporarily embedded in agarose to ensure its stability during punching, rather than holding the sample in place manually with tweezers
5C(iii)	Uneven tissue from biopsy punch	The biopsy needle is not centered	If the biopsy needle is off-center, the spinning vibration disturbs the tissue and results in an uneven biopsy punch. Perform the following to center the biopsy needle: (i) place the biopsy needle in a loose drill collet, (ii) turn on the drill, (iii) use the end of a pair of tweezers to gently tap the biopsy needle until the biopsy needle is centered, and (iv) tighten the drill collet
7	Gel-tissue construct moves in solution; unable to image	Gel-tissue construct is less dense than PBS and floats	Weigh down the sides of the agarose gel surrounding the tissue (either on the sides or on top) with small weights, e.g., nuts or washers, to ensure that the construct does not float or move during imaging. Be sure not to disrupt or touch the tissue with these weights, or the deformation will be affected
8	Horizontal lines obscure part of the ultrasound image	Reflection off the bottom of the container housing the PBS-submerged sample	Sterile gauze or a layer of liquid agarose solution (subsequently allowed to gel) can be placed on the bottom of the container to disperse the sound waves and avoid reflection. The sample can be placed on top of this layer
	Bright spots obscure part of the ultrasound image in a sample that has undergone the needle-biopsy method	Air bubbles in or around the biopsy hole interfere with imaging	Fill an insulin needle with PBS and gently flush the biopsy hole to remove air bubbles. Be careful not to touch the tissue or flush with extreme force so as not to affect the deformation

• TIMING

Steps 1–4, tissue preparation: 5 min per sample

Step 5, releasing solid stress: 10–15 min per sample

Step 6, measurement of material properties: 30 min per sample

Steps 7 and 8: imaging: 5 min per sample

Step 9, postprocessing and mathematical modeling: 30–60 min per sample

ANTICIPATED RESULTS

From our application of these methods to a variety of tumor types and host tissues, we were able to make important conclusions about this abnormal force in tumors, including that (i) the magnitude and distribution of solid stress are dictated not only by the cancer cells but also by the local host microenvironment, (ii) solid stress—and not stiffness—increases with tumor size, and (iii) the mechanical confinement of a tumor by the surrounding host tissue can significantly contribute to intratumoral solid-stress levels⁹.

The planar-cut method provides a 2D map of the solid-stress component normal to the cut surface (Fig. 2). From the 2D imaging, either the full range or a single average value of solid stress in the tumor can be reported as desired (in units of kPa), as can the elastic energy (in units of J/m³). Non-tumor-bearing negative-control tissues or organs (e.g., liver and kidney) that undergo negligible deformation after solid-stress release result in insignificant values of calculated solid stress or elastic energy that are close to zero. Solid-stress measurements in murine solid tumors (such as those outlined in Table 2 and ref. 9) using the planar-cut method vary in magnitude from roughly 0.1 to 10 kPa (as shown in Fig. 2e), calculated from tissue deformations typically <1 mm in 1D (for tumors <1 cm in diameter, as seen in Fig. 2d), with corresponding elastic energy magnitude ranges of 1–100 J/m³ (ref. 9).

The slicing method provides a bulk but sensitive estimate of the solid stress. The readout of the slicing method is the expansion ratio of the slice after relaxation of stress (Fig. 3). As with the planar-cut method, the expansion ratio for non-tumor-bearing control tissues is negligible (<5%, e.g., the kidney in Figure 4f). Conversely, releasing solid stress in murine tumors via the slicing method can result in tissue area expansion ratios of >30% (e.g., breast and pancreatic tumors in Figure 4f). We have also found that the expansion ratio is directly proportional to the size of the tumor; for example, breast cancer macrometastases (>1-mm diameter) in lymph nodes can have expansion ratios that are several times higher than micrometastases (<1 mm in diameter) from the same primary tumor in the same lymph node⁹. Furthermore, unlike the planar-cut method, the slicing method not only fully releases the out-of-plane stresses (σ_zz) but also partially releases the in-plane stresses (σ_xx and σ_yy).

The needle-biopsy method provides the in situ estimate of the radial stress component along the axis of the biopsy punch (Fig. 4). We found that the stress profiles in brain tumors provided by the planar-cut versus the needle-biopsy method were tightly correlated in both trend and magnitude (Fig. 6). Therefore, the needle-biopsy method provides a robust and accurate calculation of solid stress in scenarios in which the planar-cut method is not a viable option. Importantly, this method of solid-stress measurement is sensitive enough to determine the contribution of the surrounding tissue on intratumoral solid stress. Using the needle-biopsy punch on murine brain tumors, we found that solid-stress values were on the order of 0.1 kPa (ref. 9). Armed with the methods described here, preclinical and clinical researchers can readily and reproducibly measure solid stress and elastic energy in a multitude of contexts for mechanopathology.

Figure 6 |.

Comparison between planar-cut and needle-biopsy methods. The stress profile across the tumor diameter estimated via the planar-cut method (solid black line) and the needle-biopsy method (dashed red line) in two different mice with size-matched brain tumors (U87). The values, signs, and variation of the solid stress are comparable in the two methods.