BatchI: Batch effect Identification in high-throughput screening data using a dynamic programming algorithm

Abstract

Motivation

In contemporary biological experiments, bias, which interferes with the measurements, requires attentive processing. Important sources of bias in high-throughput biological experiments are batch effects and diverse methods towards removal of batch effects have been established. These include various normalization techniques, yet many require knowledge on the number of batches and assignment of samples to batches. Only few can deal with the problem of identification of batch effect of unknown structure. For this reason, an original batch identification algorithm through dynamical programming is introduced for omics data that may be sorted on a timescale.

Results

BatchI algorithm is based on partitioning a series of high-throughput experiment samples into sub-series corresponding to estimated batches. The dynamic programming method is used for splitting data with maximal dispersion between batches, while maintaining minimal within batch dispersion. The procedure has been tested on a number of available datasets with and without prior information about batch partitioning. Datasets with a priori identified batches have been split accordingly, measured with weighted average Dice Index. Batch effect correction is justified by higher intra-group correlation. In the blank datasets, identified batch divisions lead to improvement of parameters and quality of biological information, shown by literature study and Information Content. The outcome of the algorithm serves as a starting point for correction methods. It has been demonstrated that omitting the essential step of batch effect control may lead to waste of valuable potential discoveries.

Availability and implementation

The implementation is available within the BatchI R package at http://zaed.aei.polsl.pl/index.php/pl/111-software.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Batch effect is systematic error seen in a variety of high-dimensional molecular biology experiments, related to the existence of groups in the analyzed dataset called batches (Scherer, 2009). Often batches are defined as groups of samples processed together in an experiment and their sizes are defined by the capacity of a machine. Other common sources of batch effect biases are uncontrollable changes of some of the experimental conditions over time and using data obtained with different machines, at different places (Leek et al., 2010). In high-throughput experiments batch effect bias is unavoidable, occurs with different experimental platforms, survives standard normalization and correction procedures and leads to significant errors in data analyses, like the decrease of sensitivity or increased number of false discoveries (Chen et al., 2011; Luo et al., 2010). Developing procedures for batch effect identification and correction is therefore an important issue in high-throughput molecular experimental data analysis. It has been demonstrated by several studies that identification and correction of batch effects can substantially improve results of data analyses (Auer and Doerge, 2010; Sims et al., 2008; Sun et al., 2011).

Diverse techniques have been developed for the purpose of detecting existence of batch effects, estimating the proportion of variation in the data resulting from batch effects, and for batch effect correction. Alter et al. (2000) apply PCA to genome-wide expression data and propose removal of noisy components (eigengenes) corresponding to low singular values. Under the assumption that one (some) of the noisy eigengenes corresponds to batch effect the use of the method by Alter et al. leads to batch effect correction. Reese et al. (2013) present an extension of PCA to quantify the existence of batch effects, called guided PCA (gPCA). They derived a test statistic, based on the traditional PCA and gPCA, for detecting batch effects. The test statistic, δ, quantifies the proportion of variance owing to batch effects. Benito et al. (2004) developed a method called distance-weighted discrimination, based on support vector machines (SVM) classification algorithm for detecting and removing batch biases. SVM algorithm is used for computing a separating hyperplane between data points corresponding to different batches. Then the obtained parameters are used to remove batch bias. Bylesjö et al. (2007) use a multivariate regression model with hidden elements, called orthogonal projections to latent structures (Trygg and Wold, 2002) for identification and correction of batch biases. The case of gene expression data in microarray experiments enabled the creation of a family of RUV (Remove Unwanted Variation) methods, specifically for the purpose of handling these data, based on applying negative control genes for batch effect adjustment (Gagnon-Bartsch and Speed, 2012). This knowledge driven approach, however, limits the usability to a narrow group of experimental techniques where such negative control features are possible to describe. A method named ComBat (Combating Batch Effects When Combining Batches) for removing batch effects in DNA microarray data, based on using empirical Bayes approach, was proposed by Johnson et al. (2007). They define and estimate additive and multiplicative batch bias parameters and then use them to modify distributions of gene expressions. The approach was proven reliable, useful for datasets with multiple batches and robust to small sample sizes and may be extended to other experimental techniques (RNA-seq, genomics, proteomics) and shown to outperform the above mentioned methods for batch effect correction Chen et al. (2011). Surrogate variable analysis (SVA) (Leek and Storey, 2007) is an algorithm for combined batch effect identification and correction by means of effect estimation. Yi et al. (2018) proposed another approach for hidden batch effect identification based on data-adaptive shrinkage, coupled with a regularization technique of non-negative matrix factorization for batch effect correction. The most commonly used tools (SVA, ComBat) have been incorporated into the BatchQC software package (Manimaran et al., 2016).

Various methods of evaluating and comparing efficiency of batch effect correction for different algorithms are possible. There are studies in the literature focused on comparing different algorithms for batch effect correction (Chen et al., 2011; Luo et al., 2010), based on large sets of DNA microarray data either of spike-in type or obtained in clinical experiments. In the case of spike-in datasets direct comparisons between true and estimated levels of gene expressions are possible to apply (Chen et al., 2011). For clinical data coming from case–control comparisons, influence of batch bias removal on efficiency of case versus control discrimination can be used, formulated as cross-batch, group prediction performance index (Luo et al., 2010), or by area under the curve (AUC) of the receiver operator characteristic (ROC) of true versus false positive rates (Chen et al., 2011). Measures of sensitivity (true positive rate) and specificity (true negative rate) or measures of intragroup correlations can also be used as tools for measuring quality of batch correction. It is also possible to use biological consistency measures obtained from gene ontology (GO) annotations of detected differentially expressed genes.

In this paper we address the problem of detection of batch bias of unknown structure, i.e. such that assignment of samples to different batches is not known a priori for correction methods that require such information. Such problems are encountered in analyses of high throughput experimental data of molecular biology in at least two (quite common) situations, when batches in experimental results were not recorded and when some uncontrolled parameters influence experiments performed over a period of time. Motivation for researching the problem is that, as it follows from the reviewed literature, reliable and efficient methods for batch effect removal, such as ComBat (Johnson et al., 2007) require prior knowledge on assignment of samples into batches. Methods, which do not require the prior knowledge of batch [SVA by Leek and Storey (2007)] do not rely on explicitly indicating the batch structure, i.e. which samples belong to which batches but rather estimate the size of a batch effect and correct the data accordingly. In this sense, we propose a new method for assignment of samples to batches without prior knowledge, which uses the assumption that the analyzed data are sorted on a time scale. This condition naturally leads to utility of the method for samples processed in different laboratories and conditions, but also enables the identification of batch effects for data produced in one laboratory in seemingly identical conditions. As presented below, the usual sources of bioinformatics data for validation purposes—public repositories—have strict policies regarding submission file formats and that includes raw experimental data with timestamps. This fact opens a wide range of sets to choose from enabling the incorporation of numerous existing data to currently ongoing analyses by means of batch effect processing. Batches are identified by partitioning the time range of the whole experiment into segments, such that an appropriately defined quality index is optimized. We propose a dynamical programming (DP) approach that allows for finding the optimal partition without information about the batch groups. We also use the previously published guided PCA method (Reese et al., 2013) to construct a test statistic for estimating existence of batch bias in the dataset and for estimating the number of batches. The proposed method has been tested on a number of microarray gene expression, RNA-seq deep sequencing and proteomics mass spectrometry experiments, where we have demonstrated that without prior knowledge of batch structure we were, nevertheless, able to obtain accurate batch effect identification inducing valid correction.

2 Materials and methods

2.1 Dynamic programming batch identification

The experiments analyzed in this paper include series of DNA microarray, mass spectrometry (MS) and RNA-seq measurements. To each of the microarray samples a quality index (QI) is assigned, defined by the average intensities among all features. For the MS data the Total Ion Current (TIC) for each sample is applied and for the RNA-seq data the median number of counts is considered as the quality index. The quality index may be any of the aforementioned statistics, moreover, any statistic chosen by the user representing a single sample. However, bearing in mind that the goal is to account for sources of technical variation, it is important to note that the summarizing quality index should be calculated on data at as early a stage of processing as possible. The problem of batch identification treated here involves partitioning the series of samples into a number of batches, such that a sum of absolute deviations of the quality indexes within batches, is minimized. Batch identification is done by partitioning the range of indexes of samples into subranges (batches) with use of the dynamic programming algorithm (Bellman, 1961; Jackson et al., 2005).

Indexes of samples in the experiment are $i=1,2,\dots N$. Partitioning involves defining K batches, $B_1,B_2,\dots B_K$, where the kth batch is the range of indexes $B_k=B(i,i+1,\dots j)=i,i+1,\dots j$. The quality index is denoted by QI_i. Absolute deviation of the QI within batch B_k is:

$$AbsDev(B_k)=\sum _{l\in B_k}|Q{I}_l-{\overline{QI}}_{B_k}|$$ (1)

The minimization index for the dynamic programming partitioning algorithm is the sum of absolute deviations

$$I(K)=\sum _{k=1}^{K}AbsDev(B_k)$$ (2)

Optimal partition $B_1^{opt},B_2^{opt},\dots B_K^{opt}$ leads to a minimal value of the sum of absolute deviation indexes corresponding to all batches:

$$I_{1\dots N}^{opt}(K)=mi{n}_{partitions}^{1\dots N}[\sum _{k=1}^{K}AbsDev(B_k)]$$ (3)

The upper index of the minimization operator in the above, $1\dots N$, stands for the range of time indexes of samples, while the lower one indicates that minimization is over all possible partitions. In order to formulate dynamic programming recursion an optimal partial cumulative index for the range of samples $1,2\dots ,j$ is calculated:

$$OC{I}_{1\dots j}(k)=mi{n}_{partitions}^{1\dots j}[\sum _{\chi =1}^{K}AbsDev(B_{\chi })]$$ (4)

Dynamic programming recursive procedure, called Bellman equation, can be written in the following form:

$$\begin{array}{c}OC{I}_{1\dots j}(k+1)=mi{n}_{i=1\dots j-1}[OC{I}_{1\dots i-1}(k)\hfill \\ +AbsDev(B(i,i+1,\dots ,j))]\hfill \end{array}$$ (5)

Iterating the above Bellman equation leads to obtaining the optimal partition $B_1^{opt},B_2^{opt},\dots B_K^{opt}$ and to optimal (minimal) value of the sum of absolute deviations index $I_{1\dots N}^{opt}(K)$. The algorithm is designed so as to secure the fulfillment of the condition that one batch cannot contain less than three samples. This is necessary in order to calculate statistics such as the variance in subsequent stages of analysis. This parameter is also modifiable by the user if for any reason more samples are needed.

2.2 Choosing number of batches

In the proposed algorithm the parameter that remains to be determined is the number of batches present in the data. This is performed by dividing the data into a number of batches from 1 to K and in each case calculating the δ gPCA statistic as described in Reese et al. (2013), which is the proportion of total variance due to batch and may be calculated as the ratio of variance of the first principal component from guided PCA to the variance of the first principal component from unguided PCA. To estimate the sampling distribution of the δ statistic we create M permuted datasets by randomly shuffling the assignment of samples to batches and for each of them we perform calculation of δ_PERM permuted gPCA statistic. The ranking of the real test statistic δ among the shuffled δ_PERM test statistics gives an appropriate P-value, which indicates if δ is significantly larger than would be obtained by chance. There is an option, when the statistic does not appear to be significant, it may be assumed that batch effect is negligible and batch division is not performed. Otherwise, the division with the lowest P-value is chosen as the optimal number of batches. The maximal number of investigated batches corresponds to the number of samples, while abiding the rule of at least three samples per batch to enable dispersion estimation. However, in most cases it is not feasible to expect many more than a dozen batches that introduce significant batch effects. This may be observed by calculating the average U-Mann-Whitney test statistic for pairs of adjoining batches in divisions with increasing batch number. As illustrated in the Supplementary Material, even though the δ P-values decrease at high numbers of batches, the better partitioning indicated by the U-Mann-Whitney statistic average level occurs with low batch numbers.

In our experiments, when we set the value of M to 1000, which was the default value recommended by Reese et al. (2013), we do not get any δ_PERM greater than δ. In that case it is impossible to choose a suitable number of batches in the dataset. Increasing the number of permutations M leads to a drastic increase in computing time. Moreover, the distribution of δ statistic is different for each dataset, number of batches and can take multimodal shapes. As a solution to this problem we propose to use a kernel density estimation that might provide a reasonable approximation of δ statistic distribution. Given a permuted gPCA statistic δ_PERM the underlying probability density function f used to generate this sample, can be approximated by the kernel density estimator given by:

$$\widehat{f}(\delta )=\frac{1}{K}\sum _{i=1}^{k}kernel(\delta ,{\delta }_i)$$ (6)

where kernel is a kernel function. In our application kernel is chosen to be a standard Gaussian function:

$$kernel(\delta ,{\delta }_i)=\frac{1}{\sqrt{2\pi }}{e}^{\frac{-{(\delta -{\delta }_i)}^2}{2h^2}}$$ (7)

where h is the bandwidth that controls the degree of smoothness of $\widehat{f}(\delta )$. When h is small, the resulting estimate is usually over-fitted to the actual samples available. When h is too large, the computed density will be over-smoothed, but its variance across different samples is reduced. To select the bandwidth parameter we use a rule-of-thumb method available in the R stats package (Silverman, 2018). Final P-value is found by calculating the area under the estimated distribution to the right of the observed δ statistic value (Table 2). This approach used for estimation provokes a small portion of the estimated distribution to fall below zero. The issue was investigated on three exemplary datasets and it was demonstrated that the problem is marginally small compared to the resulting P-values, and therefore, may be considered negligible. The summarizing table for this issue is presented in the Supplementary Material.

Table 2.

Values of the gPCA δ statistic for different numbers of batches in the unlabeled datasets

Breast cancer
	2 batches	3 batches	4 batches	5 batches	6 batches	7 batches	8 batches
Tot. Var [%]	88.63	86.69	85.31	85.83	84.10	81.09	81.90
δ	0.45	0.43	0.44	0.53	0.56	0.56	0.51
P-value	6.89E-02	9.95E-02	1.05E-01	7.18E-02	6.59E-02	8.33E-02	1.48E-01
Colon cancer
	2 batches	3 batches	4 batches	5 batches	6 batches	7 batches	8 batches
Tot. Var [%]	80.24	64.51	61.63	55.13	54.42	50.76	37.30
δ	0.49	0.39	0.56	0.58	0.64	0.68	0.60
P-value	2.42E-01	6.27E-01	3.63E-01	4.37E-01	3.97E-01	3.71E-01	7.02E-01
Adrenocortical carcinoma
	2 batches	3 batches	4 batches	5 batches	6 batches	7 batches	8 batches
Tot. Var [%]	82.48	79.04	74.09	69.26	66.41	54.73	37.13
δ	0.45	0.56	0.57	0.56	0.54	0.51	0.62
P-value	1.46E-01	7.61E-02	1.60E-01	2.47E-01	2.28E-01	4.09E-01	3.40E-01

Note: The optimal number of batches is chosen with the minimum P-value principle (numbers in bold).

2.3 Data

The developed method for batch identification was tested for performance on various datasets acquired through the ArrayExpress (Kolesnikov et al., 2014) repository for microarray and RNA-seq data and an MS dataset acquired from the Center of Oncology—Maria Sklodowska-Curie Memorial Institute in Gliwice.

Initially, two sets of microarray data with known batch structure were investigated, E-GEOD-19419 (Walter et al., 2010) including gene expression profiles from peripheral blood of patients affected by neurological movement disorder DYT1 dystonia, and E-GEOD-36398 (Rahimov et al., 2012) including gene expression profiles of tissues of two distinct muscles in patients suffering from facioscapulohumeral muscular dystrophy and their unaffected first degree relatives. The former contains 60 samples: 15 controls, 23 symptomatic and 22 carriers. The latter contains 50 samples: 24 controls and 26 FSHD. Both experiments were performed on HuGene 1.0 ST microarrays with 32321 measured probes. In the datasets E-GEOD-19419 and E-GEOD-36398 all samples were assigned to batches due to the differences in time of sample processing. They include, respectively, three (E-GEOD-19419) and five batches (E-GEOD-36398).

The set of RNA-seq measurements was obtained under the E-GEOD-65683 identifier and produced in an experiment involving sperm from male partners of couples undergoing fertility treatment. The study contained 72 samples divided into 3 groups: 7 in group I, 56 in group II and 9 in group III. The metadata contained dates of the sequencing run performances, which pointed to a division of the data into three batches.

The MS data was collected in a study examining pulmonary cancer among smokers and due to an unfortunate design of experiment where the samples were processed in three distinct batches according to date (Pietrowska et al., 2012). The data consisted of 377 samples: 282 controls and 95 cancer and a total of 700 proteins was identified.

Afterward, studies without the information about batch assignment were investigated. Experiments chosen for the analysis, E-GEOD-2034, E-GEOD-4183 and E-GEOD-10927, have been described as demonstrating a high proportion of variance due to batch effects in Parker et al. (2014). The experimental study E-GEOD-2034 (Wang et al., 2005) concerned prediction of distant metastasis in patients suffering from lymph-node-negative primary breast cancer based on gene expression profiles obtained from frozen tumor samples. Experimental data E-GEOD-4183 (Galamb et al., 2008) included gene expression profiles measured for samples of colon biopsies using high-density oligonucleotide microarrays in order to predict local pathophysiological alterations and functional classification of adenoma, colorectal carcinomas and inflammatory bowel diseases. Dataset E-GEOD-10927 (Giordano et al., 2009) was collected in the clinical study on molecular classification and prognostication of adrenocortical tumors by gene expression profiling. For all three of these datasets, the timestamps were available and served as an ordering factor.

3 Results and discussion

In this section we first present results of batch structure identification obtained using the dynamic programming algorithm. We also present results of batch effect correction based on combining our algorithm of batch effect identification with an algorithm for batch bias removal. On the basis of summarizing results of comparisons studies (Chen et al., 2011; Luo et al., 2010) we concluded that the ComBat algorithm (Johnson et al., 2007) is a reliable, state-of-the-art method for batch effect removal and we use it in combination with our method of batch identification, as a tool for batch effect correction. For all DNA microarray datasets we used RMA normalization algorithm (Irizarry et al., 2003) as the preprocessing step. The RNA-seq data was aligned and counts were obtained using STAR (Dobin et al., 2013). The MS data serum samples were analyzed using MALDI-ToF mass spectrometer in the mass range between 1, 000 and 14, 000 Da. Data pre-processing included outlier spectra detection, global linear alignment, baseline correction, normalization and spectra alignment (Pietrowska et al., 2012). To identify peptide ions present in the spectra and calculate their relative abundances a Gaussian mixture model based algorithm was used (Polanski et al., 2015).

The experimental data with known status of batches, E-GEOD-19419 and E-GEOD-36398, RNA-seq and proteomics, were first investigated in terms of estimation accuracy of the known, true structure of batches obtained by application of the dynamic programming algorithm described in Section 2. Further, for these datasets, we also compared qualities of batch effect removal in terms of intragroup correlation.

Next, DNA microarray datasets E-GEOD-2034, E-GEOD-4183 and E-GEOD-10927, with unknown batch structure were analyzed. In each set, the date of the experiment was known and used for sorting. For evaluating results of batch effect correction we used the index of intragroup correlation and the Information Content of gene ontology terms for differentially expressed genes.

3.1 Known structure of batches

3.1.1 Batch division reproducing

The division into batches using dynamical programming was juxtaposed against the original batch grouping. Weighted average pairwise Dice-Sorensen Index (Dice, 1945) was used in order to measure the efficiency of batch effect identification. Comparisons of true and estimated batch structures are also shown graphically, in Figure 1. True batches are shown by using different symbols, while the structure of estimated batches is represented by vertical lines, which partition samples.

Fig. 1.

Division of the datasets into batches with the a priori defined groups and determined with the dynamical programming approach: (a) Set E-GEOD-19419, (b) Set E-GEOD-36398, (c) RNA-seq data, (d) Proteomics data. Different markers show the original batch structure, the vertical lines present divisions found using the dynamic programming algorithm

• Microarray data

In the first experiment the reproduction of batches is identical to the original division. In the second experiment the batch assignment reconstruction is also at a highly satisfactory level (weighted average Dice Index: 94.05%). Only three samples belonging to the third batch fell into the fourth.

• RNA-seq data

In case of the sequencing data the original batches are sufficiently well reconstructed with the value of a weighted average Dice Index of 93.02%. Two samples from batch 2 were assigned to batch 1 and three samples from batch 3 to batch 2.

• Mass spectrometry data

The mass spectrometry data batches were mapped with a weighted average Dice Index value of 99.78%. One of the samples from batch 1 and five from batch 3 were classified as batch 2.

3.1.2 Batch effect correction

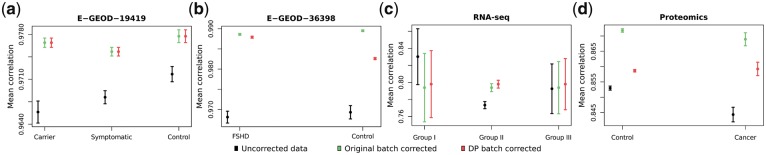
The studies examined in terms of algorithm performance where the batch effect was previously identified and on record were assessed in two steps. Firstly, correlation was measured within groups of subjects belonging to one biological condition investigated in the study. 95% confidence intervals for mean Spearman’s correlation coefficients were calculated. The results are present in Figure 2. In case of both examined microarray experiments there may be observed a significant increase in intragroup correlation after batch effect removal. The RNA-seq experiment had a strongly imbalanced design in terms of the number of samples, however, it may be observed that even in the less numerous groups mean correlation within groups does not deteriorate significantly. In the proteomics data, which in contrast to the previous experiments was obtained by means of quantitative MALDI-ToF measurements, there is a clear increase in within group correlation, though larger differences may be observed.

Fig. 2.

95% confidence intervals for mean intragroup correlation coefficients in known batch structure datasets: (a) Set E-GEOD-19419 (60 samples), (b) Set E-GEOD-36398 (50 samples), (c) RNA-seq data (72 samples), (d) Proteomics data (373 samples)

Moreover, as another qualitative measure of change between data with handled batch effects versus no correction, the δ gPCA statistic was calculated. Its significance with relation to no batch correction was assessed using P-values obtained in the course of permutation tests (Table 1). In the microarray experiments, the change of δ gPCA statistic is significant in both cases when applying batch effect correction based on identified batches. When considering RNA-seq data the change after correction becomes significant due to the use of partitioning information from the dynamic programming algorithm. In proteomics data as the samples are numerous and the overall variation observed is weak, there is not a visible difference after batch effect correction neither with the original batch label, nor the ones assigned using dynamic programming.

Table 1.

Percent of variation induced by batch effect with regard to total variation, the corresponding gPCA δ statistics and the P-values for testing the significance against no batch effect correction for two microarray, an RNA-seq and a proteomics datasets

E-GEOD-19419	Original batch corrected	DP batch corrected	E-GEOD-36398	Original batch corrected	DP batch corrected
Tot. var. [%]	69.23	69.23	Tot. var. [%]	48.15	50.14
δ	0.9271	0.9271	δ	0.9991	0.9989
P-value	4.69E-08	4.78E-08	P-value	2.24E-07	2.90E-07
RNA-seq	Original batch corrected	DP batch corrected	Proteomics	Original batch corrected	DP batch corrected
Tot. var. [%]	65.12	67.23	Tot. var. [%]	23.82	24.56
δ	0.2765	0.6175	δ	0.6645	0.6671
P-value	4.87E-01	9.38E-02	P-value	7.32E-01	7.15E-01

3.2 Detecting and correcting batch effect of unknown structure

The three experiments chosen for batch effect identification without prior knowledge of the division were examined qualitatively in the same manner as the studies with predefined batches of samples. This included investigating intragroup mean correlation within case/control subgroups. The results shown in Figure 3 demonstrate that data integrity within the subgroups is indeed enhanced with batch effect detection and correction. Analogously to Figure 2, plots are obtained by computing mean correlations and using U-Mann-Whitney test. In all nine different groups of samples, in the three datasets E-GEOD-2034, E-GEOD-4183 and E-GEOD-10927, the use of batch effect correction based on combining dynamic programming algorithm with ComBat algorithm leads to the increase of the intragroup mean correlation. In three of nine groups of samples, the increase is highly statistically significant. Furthermore, the proportion of variance explained by batch effects is diminished which may be seen while analyzing the values of the δ gPCA statistic (Table 2). In the breast cancer experiment, six batches have been identified as the optimal number by the dynamic programming algorithm. For the colon cancer experiment: two batches, and for adrenocortical carcinoma: three batches.

Fig. 3.

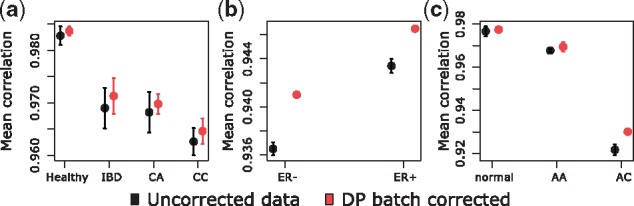
95% confidence intervals for mean intragroup correlation coefficients in unknown batch structure datasets: (a) Set E-GEOD-4183 (53 samples), (b) Set E-GEOD-2034 (286 samples), (c) Set E-GEOD-10927 (65 samples)

The E-GEOD-2034 dataset, having a large number of samples (286), was monitored additionally for the purpose of measuring algorithm runtimes. Firstly, the BatchI algorithm was run to scan for the optimal number of batches between 2 and 10 on the entire dataset, and afterwards on subsets consisting of 80, 60, 40 and 20% of the samples. This approach was re-iterated five times. Results, presented in the Supplementary Material, show that the method requires linearly increasing times with increased sample size, with an overall runtime reasonably small, even on a personal computer.

3.2.1 Functional gene ontology analysis

The experiments were then subjected to functional analysis using GO terms in order to prove the relevance of biological conclusions that may be drawn from the studies. The differentially expressed genes found in the case of no batch effect correction and comprising batch effect correction were used to find significant GO terms using the hypergeometric test. The resulting lists of terms were then compared and terms unique to both ways of analysis were thoroughly investigated.

In the case of experiment E-GEOD-10927 which is a study on adrenocortical carcinoma and adenoma the terms were matched with literature knowledge on these processes. The findings reveal that the GO terms eliminated when discarding the lack of batch effect handling approach show little relevance to the studied medical case, whereas a majority of the GO terms gained with batch effect removal has previously proven links to processes related with adrenocortical carcinoma and adenoma (Full list in Supplementary File S1).

As the remaining two studies concerned more well-defined biomedical problems such as breast and colon cancer, the resulting GO term lists were large and therefore, instead of literature studies the biological value of the findings is demonstrated with the use of the Information Content (IC) measure (Resnik, 1995). This shows that, when batch effect correction is performed, a more detailed representation of the studied process is obtained as the IC value increases (Fig. 4).

Fig. 4.

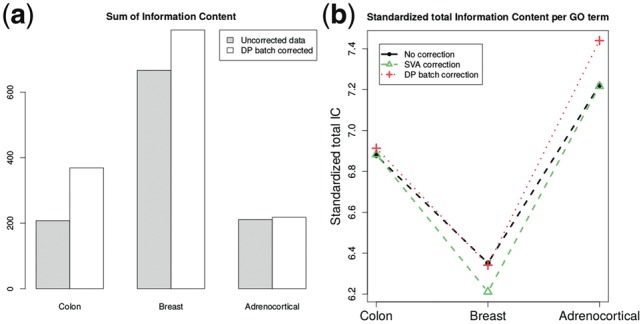
Comparison of Information Content for three studies. (a) Total Information Content of ontologies for genes unique for data without batch processing and including batch effect identification with dynamic programming and correction. (b) Standardized Information Content per GO term of ontologies for genes unique for data without batch processing and including batch effect identification and correction

Furthermore, the dynamic programming functional analysis results have been compared with ontologies obtained with data corrected using the SVA approach (Leek and Storey, 2007). The total IC measure was standardized per GO term and the outcome demonstrates that when it comes to common well described diseases, such as breast cancer [incidence rate $200-900$ cases per million (Ferlay et al., 2015)] or colon cancer [incidence rate $50-400$ per million (Haggar and Boushey, 2009)], preprocessing data with the dynamic programming approach does not lead to an important gain in quality of the information (represented by standardized total IC). This shows that though preprocessing methods, including batch effect identification and correction, are essential for careful data analyses, they alone are not sufficient to enhance the biological knowledge available in bioinformatics data bases for well described diseases. However, when we study the less prevalent case of adrenocortical carcinoma [$0.5-2.0$ cases per million (Kerkhofs et al., 2013)] data from the dynamic programming pipeline provides superior results, which increases the chance of finding potential new mechanisms of disease. Moreover, in each case the dynamic programming approach gives higher standardized total IC values than SVA and the results are no worse compared to the uncorrected data (Fig. 4).

4 Conclusions

Identifying and handling batch effects is an essential step of high-throughput molecular biology data preprocessing. We propose an efficient and unique method of batch effect identification. It allows for splitting data into corresponding batches before processing together with any correction tools requiring prior knowledge of batch structure, such as ComBat. The algorithm is based on a dynamic programming approach and relies on the choice of the number of batches using the δ gPCA statistic.

The algorithm’s performance on recovering previously known batch divisions proved to have a high level of efficacy in the case of four assessed experiments with the use of average Dice Index as a similarity measure. Moreover, when identifying and removing batch effects in data with no such a priori knowledge, it was shown with correlation investigation that in a majority of cases data integrity increases within groups formed by the studied biological processes (case/control). This also carries out a significant change in the proportion of total variance present in the data explained by batch effects.

Finally, literature and Gene Ontology term study implies that careful and apt batch effect managing leads to potential new discoveries of knowledge relevant to the studied biomedical issue. On the other hand, failing to consider batch effect when its portion in the total variation is large may lead to insignificant conclusions and inhibit the development of a studied problem, by omission of important findings resulting from carried out experiments.

Acknowledgements

We would like to thank the researchers from the Center of Oncology—Maria Sklodowska-Curie Memorial Institute in Gliwice, especially Monika Pietrowska, for kindly providing data and assistance for the proteomics analysis.

Author’s contributions

APa performed functional analysis, created the R package and wrote the manuscript, MM performed permutation tests and statistical analysis, APo conceived the algorithm, designed the implementation and helped in writing the manuscript and JP outlined the research. All authors read and approved the final manuscript.

Funding

This work was funded by Silesian University of Technology grant BK-200/RAU1/2018/8 (AP), National Science Center OPUS grant no. UMO-2015/19/B/ST6/01736 (JP), Harmonia grant no. DEC-2013/08/M/ST6/00924 (MM), National Science Center OPUS grant no. 2016/21/B/ST6/02153 (APo). All calculations were carried out using GeCONiI computational infrastructure, grant no. POIG.02.03.01-24-099/13.

Availability of data and material

The datasets supporting the conclusions of this article are available in the ArrayExpress database, http://www.ebi.ac.uk/arrayexpress/. The subsequent entry identifiers are E-GEOD-19419, E-GEOD-36398, E-GEOD-2034, E-GEOD-4183, E-GEOD-10927, E-GEOD-65683. The proteomics data is available upon request from the authors of Pietrowska et al. (2012).

Conflict of Interest: none declared.