Automatic Graph-based Modeling of Brain Microvessels Captured with Two-Photon Microscopy

Abstract

Graph models of cerebral vasculature derived from 2-photon microscopy have shown to be relevant to study brain microphysiology. Automatic graphing of these microvessels remain problematic due to the vascular network complexity and 2-photon sensitivity limitations with depth. In this work, we propose a fully automatic processing pipeline to address this issue. The modeling scheme consists of a fully-convolution neural network to segment microvessels, a 3D surface model generator and a geometry contraction algorithm to produce graphical models with a single connected component. Quantitative assessment using NetMets metrics, at a tolerance of 60 μm, false negative and false positive geometric error rates are 3.8% and 4.2%, respectively, whereas false negative and false positive topological error rates are 6.1% and 4.5%, respectively. Our qualitative evaluation confirms the efficiency of our scheme in generating useful and accurate graphical models.

I. Introduction

WITH the emergence of two-photon microscopy (2PM), it has become feasible to obtain microscopic measurements of the cerebral vascular geometry and, more recently, of associated oxygen distributions [1], [2]. Such investigations of cerebral microvasculature is essential to understand brain neurovascular coupling and neuro-metabolic activity [3]. It can also help in underpinning neurological pathologies associated with microvascular ischemic changes [4]. Furthermore, microscopic studies can be scaled: quantitative analysis of cerebral microvasculature has recently been used to establish a link between the microscopic vascular phenomena and the macroscopic (voxel size) observations found in the blood oxygenation level-dependent (BOLD) response [5], [6]. A key problem encountered in the efforts of [5] and [6] to model cerebral microvasculature is the construction of a sufficiently complete and detailed vascular network from noisy 2PM data. Physiological simulations were based on vascular connectivity which in turn required extensive manual annotations to reconstruct the microvascular topology of each dataset. This human interaction limits the applicability of such simulation frameworks in further neurological studies that would require scaling to large datasets.

Imaging brain tissue using 2PM is associated with high absorption and scattering of the emitted photons with depth leading to image degradation and intensity changes as laser power and detector gains are dynamically adjusted with depth. Also, scattering of excited photons by red blood cells degrades their focus and leads to shadows underneath large pial vessels. These deteriorations in the excited and emitted photons yields volumetric image intensity variations such that automatic processing of two-photon microscopic data is tedious and even problematic [1]. Modeling of angiographic information from 2PM includes segmentation of captured microvessels [7], [8], computation of the microvasculature network shape and topology [9], [10] and anatomical labeling of the extracted components (e.g. arterioles, venules and capillaries). Until recently, some work has been done to automate the processing of these microscopic datasets. However, the developed techniques were not sufficient to avoid significant manual corrections. With the emergence of sophisticated microvascular modeling, the design of a fully-automated scheme that is capable of generating topological models for vasculature in microscopy data is required to scale previous studies. This is the goal of this research work.

Numerous schemes for vascular segmentation have been proposed in the literature exploiting various image properties, such as the Hessian matrix [11], [12], moments of inertia [13], geometrical flux flow [14] and image gradient flux [15]. These schemes also vary in their segmentation strategies, e.g., vessellike prior modeling [11], [12], [15], tracing [16], evolution of deformable models [14] and deep learning [7], [17]–[19]. Applications to automatically segment microvessels captured with 2PM are further limited due to the very large number of segments, uneven intensities associated with optical imaging and shadowing effects. Previous studies have heavily relied on manual interactions to obtain satisfactory segmentations [5]. In recent works, models inspired by the success of ConvNets have been proposed to provide very good vascular segmentation [7], [17]–[19] with some applied to segmentation of microvessels in 2PM [7], [18]. In [7], the authors implemented a recursive architecture composed of 3D convolution blocks. However, their shallow model provides poor pixel-wise segmentation and is computationally demanding. In [18], the proposed scheme was not targeted to label the vascular space, but rather to provide a skeleton-like version of it. Other recent work, based on FC-ConvNets [20], performed end-to-end vessel segmentation using images from volumetric magnetic resonance angiography [19]. However, the proposed scheme is patch-based, which makes it hard to apply when there is significant variation in local features as observed in 2PM.

Automated representations of data topology has been of importance in many research disciplines: aerial remote sensing [21], [22], neuroinformatics [23]–[26], and vascular imaging [9], [27], [28]. Some techniques [24]–[26] target the reconstruction of tree-like structures, by first generating seed points based on probabilistic measurements to then apply algorithms, such as Shortest Path Tree [24], Minimum Spanning Tree (MST) [25] or kMST [24], to extract an optimal graph. On the other hand, modeling loopy curvilinear structures has been investigated in [9], [21]–[23], [28]. The problem we aim to solve in this paper resembles that investigated in the latter work since 2PM angiograms capture capillaries connecting the arteries to the veins which together also form a topology that is not tree-like. In [21], intensities in road images are clustered into superpixels. The shortest path algorithm is then used to assign connections between superpixels based on road likelihood. Optimal subsets of the connections are finally processed in a framework of conditional random fields. In [22], a thinned version of segmented road maps is simplified and then passed through a shortest path algorithm [22] to generate an undirected graph for road networks. The works in [21], [22], are designed only for two dimensional natural images that have low scale variability and semi-constant luminosity, and which have few disconnected components. In [27], automatic topological annotation of macroscopic cerebral arteries forming the circle of Willis was achieved. However, the task was performed with a predefined knowledge about the topological structure of the annotated object. In [9], [23], [28] different schemes have been developed to extract graphs from more complex three dimensional images (microscopy data) by optimizing a designed objective function. These schemes first attempt at building an overcomplete weighted connections between seed points, which are detected based on tabularity [9] or bifurcation [23], [28] measures. They then search for optimal subgraph representations by solving a linear integer programming (LIP) problem with specific constraints.

In [9], [23], [28], pre-processing steps to provide preliminary weighted graphs, forming the basis of a LIP solution, are designed for less-noisy datasets containing tubular structures of high size uniformity. High noise level and variation in tubular sizes are exhibited across microscopic angiograms acquired with two-photon fluorescence scanning. Moreover, despite the cautious problem formulation in the mentioned works designed to approach a near-optimal solution, LIP is theoretically a non-deterministic polynomial-time hard (NP-hard) problem. The hardness of the problem increases for applications on scalable datasets, which results in more decision variables. Lastly, practical solutions of LIP do not necessarily provide consistent output at different runs.

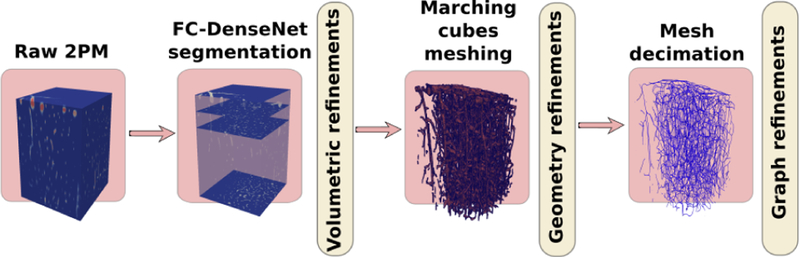
Our work below addresses the issue of extracting topological models from scalable and complex datasets, i.e. 2PM angiograms. We propose a fully-automated solution that provides a unique output for the same input data, in practical computational time. The proposed graph extraction scheme consists of 3 main stages, described in Figure 1. First, we take advantage of a recent development in deep learning semantic segmentation [20], [29] employing a fully convolution (FC) network based on the DenseNet architecture to segment potential microvessels [29]. A new well-labeled 2PM dataset is manually prepared to train our segmentation model. The volumetric output of the segmentation model is processed by 3D morphological filters to omit small isolated segments and improve the connectivity pattern of microvessels. Second, we propose a data processing flow to generate a polygonal closed-manifold geometry for the microvasculature from its volumetric mask obtained in the first stage. Finally, we exploite the 3D geometric skeletonization [30] to generate a direct representation of the microvessel network.

Fig. 1:

A schematic diagram describing the proposed multistage graph extraction scheme.

The paper is organized as follows. In the Methods Sections II–IV, we describe each phase of the graph extraction scheme: Section II details the proposed deep learning architecture for microvessels segmentation and explains the subsequent morphological refinements, Section III describes the techniques used to generate and post-process the polygonal mesh to represent the shape of the microvasculature, and Section IV provides the formalism of the 3D skeletonization to produce a final graph-based model of the microvascular network. The Results Section V demonstrates the validity of the proposed modeling scheme. A discussion and concluding remarks are provided in Section VI.

II. Deep Segmentation of Microvessels

In this section, various versions of the recently developed FC-DenseNets [29] are employed to address the problem of microvessel segmentation in large-scale 2PM images. Our use of the FC-DenseNets architectures is inspired by their success in achieving the state-of-the-art performance in semantic segmentation in natural images. We prove that applying this data-driven solution to segment microvessels in 2PM volumes can induce a substantially improved performance compared to that of other hand-crafted schemes. Below we discuss the architectures of the neural networks that were devised, data preparation and training procedure. Let $\mathcal{I}:P\to ℝ|P\subset {ℝ}^3$ be the 3D image representing the observed microscopic measurements. The aim is to create a binary mask ${\mathcal{I}}_{mask}:P\to \left\{1,0\right\}|{\mathcal{I}}_{mask}(p)=1\forall p\in \mathcal{O}$ and ${\mathcal{I}}_{mask}(p)=0$ otherwise, where $\mathcal{O}\subset {ℝ}^3$ is the object that represents the vasculature.

A. Networks Architecture

Generally, in a neural network with layers l_n, n = 0,1,2,…, N, each layer l_n performs a non-linear transformation H_n(·) that might include several operations, e.g. batch normalization, rectified linear units (ReLUs), convolutions or pooling. Let x_n denote the output of the layer l_n. In DenseNets [31], consisting of building units called dense blocks, the output x_n of the layer l_n is connected to its previous layers contained in the same dense block [31] by cascading operations. The layer transition is therefore described by the following formula:

$$x_n=H_n\left(\left[x_{n-m-1},\dots ,x_{n-2},x_{n-1}\right]\right)$$ (1)

where [·] operation denotes the concatenation process and m denotes the number subsequent layers contained in a dense block.

DenseNets are extended to a fully convolution scheme [29], analogous to that proposed in [20], comprising down- and up-sampling paths. The down-sampling pattern is composed of dense blocks and transition-down (T-down) layers, where T-down layers consist of three operations: batch normalization, convolution and max-pooling. Alongside the down-sampling path, the up-sampling path is inserted to recover the input spatial resolution. It is composed of dense blocks, transition-up (T-up) layers and skip connections where T-up layers are built of transposed convolution operations. To avoid the increase in the number of feature-maps in the up-sampling path, the input of dense blocks in this path is not concatenated with its output. Henceforth, we refer to dense blocks in the down-sampling path as type A, and that of the up-sampling path as type B. As in typical fully convolution networks [20], skip connections – from the down-sampling path to the up-sampling one – have been introduced to allow the network to compensate for the loss of information due to the pooling operations in the T-down layers.

In this work, to perform the segmentation task, we investigate three different architectures of FC-DenseNets varying in their deepness, namely, Net71, Net97 and Net127. Our architectures consist of 71, 97 and 127 convolution layers, respectively, with an input size of 256×256×1 for each. The detailed specifications for implemented convolution and pooling layers, with their number of feature-maps, in each architecture are listed in Table I. The down-sampling and up-sampling paths have 36 convolution layers each, whereas the networks bottlenecks have 11, 13 and 15, respectively. The down-sampling path is composed of dense blocks type A, that have input-output concatenation. This concatenation is omitted in the dense blocks type B forming the up-sampling path. Each T-down block is composed of one convolution layer followed by dropout [32] with p =0.2 and non-overlapping max-pooling. Each T-up block is a transposed-convolution layer with stride =2. The growth rate of feature maps in each dense block is set to k =18 and a dropout of p =0.2 is applied in all contained layers. In each architecture, one convolution layer is applied on the input and another is placed before the last (softmax) layer that provides the bi-class predictions.

TABLE I:

The various FC-DenseNet architectures tested to perform the segmentation task. At each component, we report the number of convolution layers followed by the number of feature maps.

	Architecture
Component	Net71	Net97	Netl27
Input	-; 1	-; 1	-; 1
3×3 Convolution	1; 48	1; 48	1; 48
Dense block type A	4; 120	4; 120	4; 120
T-down layer	1; 120	1; 120	1; 120
Dense block type A	5; 210	5; 210	5; 210
T-down layer	1; 210	1; 210	1; 210
Dense block type A	7; 336	7; 336	7; 336
T-down layer	1; 336	1; 336	1; 336
Dense block type A	9; 498	9; 498	9; 498
T-down layer	1; 498	1; 498	1; 498
Dense block type A	-	11; 696	11; 696
T-down layer	-	1; 696	1; 696
Dense block type A	-	-	13; 930
T-down layer	-	-	1; 930
Bottleneck	11; 198	13; 234	15; 270
T-up layer + concatenation	-	-	1; 1200
Dense block type B	-	-	13; 234
T-up layer + concatenation	-	1; 930	1; 930
Dense block type B	-	11; 198	11; 198
T-up layer + concatenation	1; 696	1; 696	1; 696
Dense block type B	9; 162	9; 162	9; 162
T-up layer + concatenation	1; 498	1; 498	1; 498
Dense block type B	7; 126	7; 126	7; 126
T-up layer + concatenation	1; 336	1; 336	1; 336
Dense block type B	5; 90	5; 90	5; 90
T-up layer + concatenation	1; 210	1; 210	1; 210
Dense block type B	4; 72	4; 72	4; 72
1×1 Convolution	1; 2	l; 2	1; 2
Softmax	-; 2	-; 2	-; 2
Convolution layer	Transition-down layer (T-down)	Transition-up layer (T-up)
Batch Normalization	Batch Normalization	3×3 Transposed convolution, stride = 2
ReLu	ReLu
3×3 Convolution Dropout p = 0.2	1×1 Convolution Dropout p = 0.2 2×2 Max-pooling

B. Data Collection

To train our segmentation networks, manual annotations were performed to create a ground truth labeling of mice cerebral microvessels captured using our custom-built two-photon laser scanning microscope. To image microvessels, 200 μL 2MDa dextran-FITC (50 mg/ml in saline, Sigma) was injected through the tail vein of mice. Due to the injected fluorescent dye, the plasma appeared bright in the images while red blood cells (RBCs) appeared as dark shadows. Acquisition was performed using 820 nm, 80 MHz, 150 fs pulses from MaiTai-BB laser oscillator (Newport corporation, USA) through an electro-optic modulator (ConOptics, USA) to adjust the gain. The optical beam was scanned in the x-y plane by galvanometric mirrors (Thorlabs, USA). Reflected light was collected by a 20× objective (Olympus XLUMPLFLNW, NA=1). Fluorescent photons were separated by dichroic mirrors, passed through a filter centered at 520 nm and relayed to a photomultiplier tube (PMT, R3896, Hamamatsu Photonics, Japan) for detection of the dextran-FITC. Manual annotations from the 3D microscopic measurements were done slice-by-slice. The annotation process was carried out with the assistance of MayaVi visualization tool to consider the final 3D structure of the microvessel network. Eight angiograms were labeled to produce a training dataset of images $T=\left\{\left(I^{(q)},I_{mask}^{(q)}\right)|q\in Q=[1,2,3,\dots ,396]\right\}$, each of size 256 × 256. Next we omit the superscript q for notational simplicity.

C. Networks Objective & Training

Let $p_x,p_y,p_z\in ℝ$ define the dimensions of one of our networks output F(I; θ_F), where θ_F is vector containing the model parameters. The model was trained to minimize the following cross-entropy loss function [33]:

$$\begin{gathered} \mathrm{\Psi }(F)=-[{\Sigma }_{p_x,p_y}{I}_{mask}\text{ log}\left(F\left(I;{\theta }_F\right)|p_z=0\right) \\ +{\Sigma }_{p_x,p_y}\left(1-I_{mask}\right)\text{ log}\left(F\left(I;{\theta }_F\right)|p_z=1\right)]. \end{gathered}$$ (2)

The stochastic RMSprop gradient descend algorithm was employed to solve our model parameters based on backpropagation [33]. Given an initial learning rate ρ and a decay parameter γ, model parameters were updated as follows:

$$\begin{gathered} {\theta }_{F_{(t+1)}}={\theta }_{F_{(t)}}-\frac{\rho }{\sqrt{{\zeta }_{(t)}}}{\nabla }_{{\theta }_F}\mathrm{\Psi }\left(F\left(I;{\theta }_F\right)\right),\text{\hspace{0.17em}where\hspace{0.17em}} \\ \zeta (t)=(1-\gamma ){\left[{\nabla }_{{\theta }_F}\mathrm{\Psi }\left(F\left(I;{\theta }_F\right)\right)\right]}^2+\gamma {\zeta }_{(t-1)}. \end{gathered}$$ (3)

The training procedure is described in Algorithm 1. In each training iteration, a set of samples from our dataset (“mini-batch”) was processed by the network models with their current parameters. Then, the gradient of the loss function Ψ was computed with respect to θ_F and parameters were updated by stepping in the descending direction of the gradient as stated in (3). In the algorithm, the training process was early-stopped if no minimization of the loss function Ψ was achieved after a certain number of consecutive training epochs, denoted as the patience period λ.

D. Morphological Post-Processing

The trained segmentation models can accept a 2D input I of an arbitrary size and produce an output F(I) of the same size. To segment microvessels in a 3D two-photon angiogram and obtain $I_{mask}$, we first stacked the outputs of the trained neural networks applied to each slice in the z-direction. Morphological 3D closing and opening filtering was then applied on the resultant image stack with a spherical shape filter of radius=8 to refine the stacked segmentation outputs. It has been found that by applying this 3D morphological processing to obtain $I_{mask}$, a reduction in false positive structures emerging after the 2D segmentation is achieved.

III. Surface Modeling

This section describes the process used to construct a triangulated mesh $\mathcal{M}=(V,C)$ representing the shape of microvasculature, where $V={\left[v_1^T,v_2^T,\dots ,v_d^T\right]}^T$ are the vertices positions, $v\in {ℝ}^3$, and $C={\left\{c_i\right\}}_{i=1,\dots ,l},c\in v\times v$, are the edges connecting the vertices of the mesh. The extracted mesh should form a 2D manifold to allow successful geometrical contraction and convergence towards a curve skeleton formulation. Many computational paradigms have been proposed to provide isosurface representations of the binary output ${\mathcal{I}}_{mask}$ obtained in the previous section. Examples are those based on the concepts of Marching Cubes (MC) [34]–[36], dual contouring [37] and advancing-front construction [38]. The MC algorithm [34] is arguably the most widely used due to its robustness and speed, however it has an ambiguity problem in its classical formulation due to lookup table redundancy. MC with asymptotic decider [35] was proposed to give better, topologically consistent, surface models. In [36], an interior ambiguity test was added to the scheme of [35] to achieve even higher topological correctness. A modified version of [36], introduced by Liener et. al.[39], was utilized to generate an initial triangulated mesh model for the microvessels surface.

The output from the MC algorithm is a polygonal mesh with a high level of triangulation redundancy. The algorithm produces a large number of small coplanar triangles resulting in a big size model. Direct processing of this raw 3D model to generate a curve skeleton abstraction would be computationally expensive. Also, the MC process introduces excessive roughness with stair-step effects that need to be removed. We applied a polygonal simplification procedure to circumvent these concerns. Many mesh simplification approaches have been developed in the literature [40]–[44] with varied characteristics: topological invariance, view-dependency – based on objects location, illumination and motion in the scene – and the polygonal removal mechanism. The vertex clustering technique in [40] works by superimposing a grid with a predetermined resolution to the cells resulting after clustering the original meshes vertices. The resampling technique [41] is based on performing low-pass filtering of the original volumetric data. These approaches are topology insensitive and provide a drastic reduction in the number of elements of the original geometry. Other simplification approaches [42], [43] have been developed to ensure appearance/rendering quality in complex scenes that hinder the rendering process by assuming different levels of detail for the discovered objects. The vertex merging technique proposed by Garland et al. [44] gives an accurate geometry for the simplified model and works on non-manifold inputs that could result from the MC process [39]. We used these features of the vertex merging technique [45] to simplify our surface model.

The process undertaken to create a surface model is not guaranteed to be a manifold and even less a closed manifold [46]. Further processing was used to eliminate possible non-manifold local defects such as self-intersections based on the work done in [47]. Lastly, the hole filling algorithm illustrated in [48] was used to ensure a watertight surface model that can be further used in the next stage of our modeling pipeline.

IV. Graph Extraction

Various definitions have been suggested as a basis to compute formal skeletons (also called medial axes) [49]. These definitions emerged from conceptualizing the skeleton based on maximally-inscribed balls, Grassfire Analogy, Maxwell Set or Symmetry Set [50]. Let $\mathcal{S}=d\mathcal{O}$ be the 2D-manifold surface of the 3D-manifold volume $\mathcal{O}$ of interest. The idea of maximally-inscribed balls defines the skeleton of $\mathcal{O}$ to be the locus of the centers of maximally inscribed balls in $\mathcal{O}$. Extension to the Medial Axis transform is done by associating the radii of these balls to their center locations. The Grassfire analogy defines the skeleton as the locations inside $\mathcal{O}$ where quenching happens if we let the surface $\mathcal{S}$ propagate isotropically toward the interior of $\mathcal{O}$. The Maxwell Set definition captures the curve skeleton as an extension of the Voronoi diagram by encoding the loci that are equidistant from at least two points on the surface $\mathcal{S}$. In the Symmetry Set definition, a curve skeleton is regarded as the infinitesimal symmetry axes generated by first linking each pair-point on the surface to calculate their symmetry centers and then combine these centers to form a curvilinear infinitesimal axis. In all definitions, skeletonization depends only on the shape of $\mathcal{O}$ rather than its position or size in its embedding space.

In this study, the target is to generate a graphed form of 1D curve skeletons that capture the topology of the microvasculature. In general, the medial axes for 3D objects are 2D [49]. Therefore, two main solutions have been proposed, following the procedures to either simplify the 2D medial axes [51], [52] or to calculate the curve skeletons directly from 3D objects [30], [53], [54]. The techniques in [51], [52] are computationally expensive and very dependent on the quality of the associated surface skeletonization. From a geometric perspective, the techniques that are based on shape contraction [30], [54] are proven to be the most successful in extracting accurate and yet smooth curve skeletons from a variety of different shapes. Moreover, such techniques provide skeletonization embedded in the geometrical space, and thus it coincides with our goal in generating a graph-based representation of microvessel networks. Therefore, we adapt the work proposed in [30] to perform graph extraction in our last stage of the designed pipeline.

A. Geometric Contraction

Based on the triangulated mesh $\mathcal{M}=(V,C)$ generated in the previous section, our goal is to extract a geometric graph $\mathcal{G}$ with node positions $N={\left[n_1^T,n_2^T,\dots ,n_m^T\right]}^T,n\in {ℝ}^3$, and edges (connections) E = {e_i}_i=1,…,h, e ∊ n × n. We follow the geometrical contraction technique in [30] to achieve our goal by iteratively moving the vertices of $\mathcal{M}$ along the corresponding curvature normal directions. At iteration t, we minimize the constrained energy function:

$$\begin{gathered} \mathcal{E}={\Vert W_{S}L{V}^{t+1}\Vert }^2+ \\ \sum _{i=1}^d{W}_{V,i}^2{\Vert v_i^{t+1}-v_i^t\Vert }^2+ \\ \sum _{i=1}^d{W}_{M,i}^2{\Vert v_i^{t+1}-\xi \left(v_i\right)\Vert }^2 \end{gathered}$$ (4)

where W_S, W_V and W_M are diagonal matrices of size d × d that impose constraints on the geometrical contraction process, such that for the ith diagonal element: W_S,_i = w_S, W_{V ,i} = w_V and W_{M ,i} = w_M·w_S, w_V and w_M serve as tuning parameters to control the smoothness, velocity and mediality of the contraction process at each iteration. In (4), the function ξ(·) maps the vertex v_i to the corresponding Voronoi pole calculated before the iteration process [30], and L is the d × d curvature-flow Laplace operator with its elements obtained as:

$${}_{\mathbf{L}ij}=\{\begin{array}{ll}{w}_{ij}=\text{cot}\left({\alpha }_{ij}\right)+\text{cot}\left({\beta }_{ij}\right)\hfill & i,j\in C\hfill \\ -{\sum }_{(i,k)\in \mathbf{C}}^k{w}_{i,k}\hfill & i=j\hfill \\ 0\hfill & otherwise\text{, }\hfill \end{array}$$ (5)

where α_ij and β_ij are the angles opposite to the edge (i, j) in the two triangles which have this edge in common [55].

B. Geometric Decimation

At each iteration step in the geometric contraction process, higher levels of local anisotropy is introduced in the processed mesh. We follow the procedure described in [54] to reduce the mesh at each contraction step maintaining a water-tight manifold structure. After completing the iteration process, the degenerated surface mesh is reduced to form a graph model by applying a series of shortest edge-collapses [54] until all mesh faces have been removed. Lastly, to ensure that the output of our modeling framework is valid for running physiological simulations, we extract the largest single connected component (LSCC) of the resulting graph to be our final graphical model.

V. Validation Experiments

In this section, we carry out various experimentations to evaluate the designed pipeline in producing graph-based representation for microvessels captured with 2PM. First, we describe the parametric settings used to train the segmentation model, extract 3D surface models and generate final geometric graphs. We illustrate the manual procedure followed to prepare a graph-based ground truth baseline. Next, we discuss the validation mechanism and the metrics used to study the performance of the designed pipeline. Lastly, based on these metrics, we present a comprehensive evaluation of our proposed modeling scheme.

A. Baseline, Parameters and Implementation

Here we discuss the issue of finding a baseline performance for the purpose of validation and the parametric setup of the model used to generate results. Also we describe implementation details.

1). Baseline:

To study the segmentation performance of the our deep segmentation models before and after applying the 3D morphological processing (3DM). Segmentation results were compared with that of manual segmentation (gold-standard), optimally oriented flux method [15] (OOF) and the hessian-based method in [12], which are state-of-the techniques used in 3D vascular segmentation.

To our knowledge, this work is the first fully automatic scheme designed to extract graph-based representation from sizable 3D 2PM datasets. Other baseline methods in the literature applicable to similar datasets rely on human interaction. Hence, in order to validate the correctness of our graphing scheme, we compare our results with manually prepared graphs recently utilized in [5], [56]. To create the manually-graphed datasets in [5], [56], manual annotations were performed on contrast-enhanced structural images of the cortical vasculature which were then skeletonized using erosion. Ensuing graphs were hand-corrected and verified by visual inspection to generate a single connected component. Datasets of six graphs (from six different mice) were prepared from angiograms with 1.2 × 1.2 × 2.0 μm voxel sizes acquired with a 20X Olympus objective (NA= 0.95). To illustrate our choice of the surface modeling and mesh contraction processes in the proposed pipeline, we compare our graph outputs with that resulting from applying the widely used 3D Thinning method [57] on the same binary masks.

2). Training the Segmentation Model:

Implementation of the deep-learning portion of the pipeline was done in Python under the Theano framework. We ran the experiments on two 12GB NVIDIA TITAN X GPUs. The model was initialized using the HeUniform method as in [29]. The training was performed by setting ρ = 10⁻³ and γ = 0.995 in (3) for all epochs of training. To monitor the training process, we randomly selected 25% of the training data as a validation set. The selection of the validation set was performed by randomly picking several 2D slices after grouping all the slices forming the 2PM stacks in one pile. The validation set was used to early-stop the training based on the acquired accuracy, with a patience of 25 epochs. The model was regularized with a weight decay of 10⁻⁵.

3). 3D Modeling and Contraction Process:

We have followed a brute-force selection of parameters used in the processes of creating 3D surface and carrying out geometric contraction, based on the quality of the generated graphs. To reduce the 3D model using the vertex merging technique in [44], we set the target number of faces in the reduced model to be half of that of the original one. Our code for generating and processing the 3D surface model was based on the VTK Python library. The parameters w_S, w_V and w_M were set to 1, 20 and 35, with ∊_vol = 10⁻⁶. We built Python bindings using SWIG to call the C++ API, CGAL, containing the implementation of the geometric contraction algorithm.

B. Metrics

To quantify the performance of the various segmentation methods, the metrics of sensitivity = TN/(TN + FP), specificity= TP/(TP+FN), accuracy = (TP+TN)/(FP+ FN) and Intersection Over Union (IoU) = TP/(TP + FP + FN), were used. The terms TP and FP denote respectively the positive predictions (vessel) with true and false ground truth, whereas TN and FN denote respectively the negative predictions (not vessel) with true and false ground truth. It is to be noted that to generate binary masks using the methods in [15] and [12], empirical thresholding is performed to achieve the highest IOU value.

For the quantification and visualization of errors incurred by our graphing scheme, we used the NetMets metrics proposed in [58]: four measures were computed to compare both the geometry and connectivity between two interconnected graphs. Namely, the Graph False Negative/Positive Rate metrics GFNR and GFPR reflected the false negative rate and the false positive rate, respectively, in the geometry of the extracted graph while the metrics CFNR and CFPR provided measures about the false negative rate and the false positive rate in the topology of the graph.

Let us define ${\mathcal{G}}_r$ and ${\mathcal{G}}_e$ as the ground truth and experimentally generated graphs. In the validation process using NetMets, we first performed a two-way matching between the junction nodes in both graphs. These nodes, denoted as J_r and J_e for ${\mathcal{G}}_r$ and ${\mathcal{G}}_e$, respectively, were those representing bifurcations in the vascular network or terminals of vessel pathways. Graph paths between junction nodes were referred to as graph branches $\mathcal{B}$. Junction node mappings J_r to J_e were denoted as J_r → J_e, whereas J_e → J_r denoted the opposite matching processes. In the matching process, we assigned each junction node in the first graph with one in the second graph based on the shortest Euclidean distance measured. GFNR was computed as $1/n_{J_r}{\sum }_{i\in J_r}1-e^{D{\left(i,{\mathcal{G}}_e\right)}^2/2{\delta }^2}$ and that of GFPR as $1/n_{J_e}{\sum }_{i\in J_r}1-e^{D{\left(i,{\mathcal{G}}_r\right)}^2/2{\delta }^2}$, where $n_{J_r}$ and $n_{Je}$ are the number of junction nodes in ${\mathcal{G}}_r$ and ${\mathcal{G}}_e$, respectively, $D(i,\mathcal{G})$ is the Euclidean distance between a node i and its matched node in $\mathcal{G}$, and δ is a sensitivity parameter.

Now, to compute CFNR and CFPR as described in [58], core graphs ${\check{\mathcal{G}}}_r$ and ${\check{\mathcal{G}}}_e$ were extracted from ${\mathcal{G}}_r$ and ${\mathcal{G}}_e$. Core graphs were obtained by first reducing both graphs, ${\mathcal{G}}_r$ and ${\mathcal{G}}_e$, by eliminating each junction node and its immediate branches if the distance D from the corresponding nodes was greater than δ. Then, in the reduced graphs of ${\mathcal{G}}_r$ and ${\mathcal{G}}_e$, we further eliminated junction nodes, and their corresponding branches, that did not form the same matching pair in the two-way matching process. Lastly, we compared the reduced ${\check{\mathcal{G}}}_r$ and ${\check{\mathcal{G}}}_e$ to calculate the following: ${\mathcal{B}}_{TP}$ = number of graph branches in ${\check{\mathcal{G}}}_r$ or ${\check{\mathcal{G}}}_e$; ${\mathcal{B}}_{FN}$ = number of graph branches in ${\mathcal{G}}_r$ but not in ${\check{\mathcal{G}}}_e$; ${\mathcal{B}}_{FN}$ = number of graph branches in ${\mathcal{G}}_e$ but not in ${\check{\mathcal{G}}}_e$. CFNR and CFPR were calculated as ${\mathcal{B}}_{FN}/\left({\mathcal{B}}_{FN}+{\mathcal{B}}_{TP}\right)$, and ${\mathcal{B}}_{FP}/\left({\mathcal{B}}_{FP}+{\mathcal{B}}_{TP}\right)$, respectively.

C. Results

1). Microvessels Segmentation:

In this section, we study the performances of the various segmentation schemes used to generate microvessels binary masks. Table II provides the averaged quantitative results obtained after applying the various segmentation schemes on the 2PM slices in our validation set. From the table, despite the slight degradation in sensitivity scores, one can notice that carrying out the 3DM post-processing on the FC-DenseNets outputs substantially improves the measures of accuracy, specificity and IOU. The table obviously shows that the method in [15] is not a suitable choice for extracting microvessel maps. The highest sensitivity value of 98.9% ± 0.01 was achieved by the Net71 architecture but at the expense of very poor specificity. The method in [12] achieved the highest specificity value of 57.33% ± 2.20. However, it produces vessel masks with poor IOU scores. The table proves that the Net97+3DM architecture achieves the best accuracy and IOU values, 92.3% ± 0.1 and 41.1% ± 0.4, respectively, with comparable values of sensitivity and specificity corresponding to the schemes of Net97 and that in [12], respectively.

TABLE II:

Quantitative performance evaluation of the various segmentation schemes.

	Method in [15]	Method in [12]	Net71	Net71+3DM	Net97	Net97+3DM	Net127	Net127+3DM
Accuracy(%)	85.3 ± 0.6	92.1 ± 0.1	82.7 ± 0.3	88.3 ± 0.2	90.3 ± 0.1	92.3 ± 0.1	88.8 ± 0.3	91.1 ± 0.1
Sensitivity(%)	95.1 ± 0.1	94.64 ± 0.1	98.9 ± 0.01	97.1 ± 0.06	97.7 ± 0.1	96.74 ± 0.1	98.7 ± 0.1	97.17 ± 0.2
Specificily(%)	31.0 ± 2.3	57.33 ± 2.20	31.2 ± 0.9	36.2 ± 1.3	51.3 ± 1.9	56.5 ± 2.1	46.8 ± 1.6	50.8 ± 1.8
IOU(%)	28.9 ± 0.4	34.4 ± 0.4	30.9 ± 0.4	34.2 ± 0.3	40.2 ± 0.4	41.1 ± 0.4	38.9 ± 0.4	40.2 ± 0.4

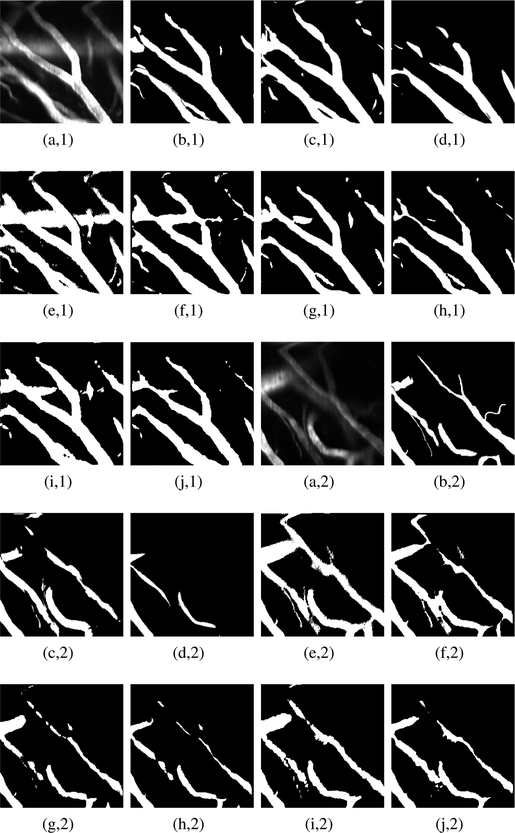
To qualitatively assess the segmentation performances, Fig. 2 depicts two raw 2PM slices, obtained from our validation set, with their binary masks counterparts generated by applying the various segmentation schemes. It is clearly seen that the scheme in [15] and those of Net71, Net71+3DM, Net127 and Net127+3DM, produce microvessel mappings that suffer from over-segmentation. On the other hand, the scheme in [12] is highly specific in a way that generates outputs with large portion of false negatives, thus missing important vesselness structures. This observation coincides the low IOU measure of this scheme reported in Table II. From the figure, one can see that the schemes of Net97, Net97+3DM exhibit better segmentation results with superiority of the Net97+3DM scheme in providing less over-segmentation. Hence, based on the previous experimental demonstration, in our study, we choose the scheme Net97+3DM to generate binary maps needed for extracting graph-based models of microvessels.

Fig. 2:

Examples of microvessel masks obtained after applying the various segmentation schemes: (a,1–2) Raw 2PM, (b,1–2) true label, (c,1–2) OOF method [15], (d,1–2) Hessian-based method [12], (e,1–2) Net71, (f,1–2) net71+3DM , (g,1–2) Net97, (h,1–2) Net97+3DM, (i,1–2) Net127 and (j,1–2) Net127+3DM.

2). Graph Modeling:

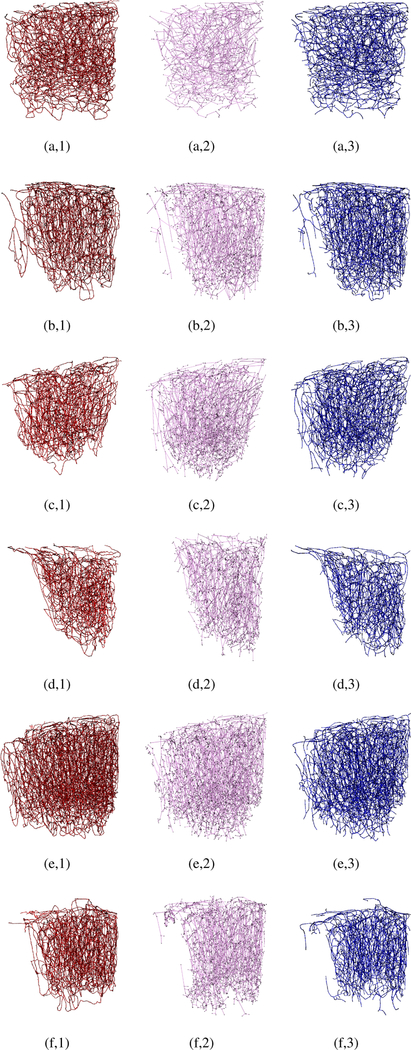
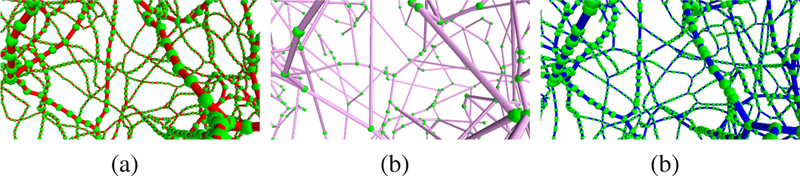
The six ground-truth graph datasets were carefully annotated, ensuring a fully interconnected topology for the captured micro vessel networks. Each graph provides a model for descending arterioles, capillary bed, and then ascending venules. These graphical models have been employed in [5] to simulate oxygen-dependent quantities across the network, and then generate synthetic MRI signals based on these measurements. Fig. 3 shows the six maximum intensity projections of the raw cerebral micro vascular spaces captured with 2PM, with their corresponding ground truth and experimental graphical modelings depicted in Fig. 4. The reader is also referred to Supplemental Fig. 1 in the supplementary material for assessing the proposed graph models based on visualizing only thin slices (10–30 μm thick) of the stack in Fig. 1 (a,1) at various depth levels. Empirical visual inspection shows that the outputs of our graph modeling scheme are significantly superior to that of the 3D Thinning method and are globally comparable to the ground-truth annotations. However, some defects are present for some boundary parts of the vascular networks, especially the capillary bed where one can observe that microvessel terminals are present for the experimentally generated models but not in the manually prepared ones. It is to be noted that the experimental models in Fig. 4 are fully interconnected graphs obtained after attaining the LSCC from the raw graph outputs. The ratio of these LSCCs to the original models generated from the first-sixth 2PM datasets, respectively, are listed in Table III. The table demonstrate that the proposed scheme generates less disconnected components compared to that produced by the 3D Thinning method.

Fig. 3:

Maximum intensity projections of raw angiograms used to validate the proposed graph extraction scheme.

Fig. 4:

Visual assessment of our graph modeling scheme applied on the six raw 2PM datasets. For all datasets (1–6), manually processed graphs (ground-truth) are depicted in the left column (a-f,1); the graphs generated based on 3D Thinning are depicted in the middle column (a-f,2); the graphs generated using our scheme are depicted in the right column.

TABLE III:

Number of nodes in the ground-truth graphs and in those generated by the 3D Thinning method and the proposed scheme. The generated graphs are obtained after extracting the LSCC from their original version.

	Ratio of LSCC to origional models		Number of all nodes			Number of junction nodes
	${\mathcal{G}}_e$ (3D thining)	${\mathcal{G}}_e$ (Proposed)	${\mathcal{G}}_r$	${\mathcal{G}}_e$ (3D thining)	${\mathcal{G}}_e$ (Proposed)	${\mathcal{G}}_r$	${\mathcal{G}}_e$ (3D thining)	${\mathcal{G}}_e$ (Proposed)
Dataset 1	95.5%	99.5%	18624	1670	15902	1496	1371	1289
Dataset 2	86.6%	99.0%	16122	3292	17524	827	1890	906
Dataset 3	91.6%	99.0%	12301	4989	16843	782	2638	876
Dataset 4	87.4%	98.5%	9678	3239	10127	640	1668	718
Dataset 5	89.3%	99.0%	27745	6619	23307	1843	3615	1783
Dataset 6	87.2%	97.5%	13723	4527	11871	841	2377	894

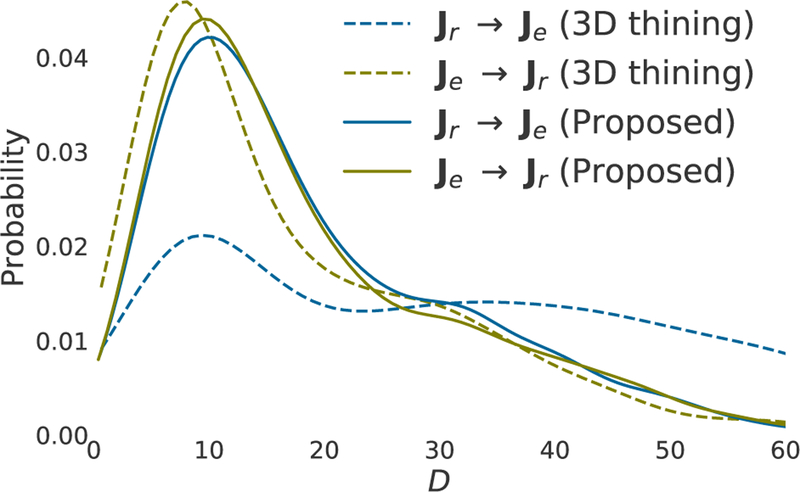
As previously mentioned, in order to quantify the performance of the modeling schemes, we performed a two-way matching, based on the shortest Euclidean distance, between junction nodes in the ground truth graphs and those in the generated ones. Fig. 5 plots the estimated probability distribution, using a Gaussian kernel, of the mapping distances D obtained after performing the matching process. It is seen that, in the case of the proposed graph modeling, the J_e → J_r matching process produced D mappings similar to that resulting from the J_e → J_r process. This implies that the localization of junction nodes coincides in both manual and experimental modelings, thus resulting a negligible difference between the statistics obtained from the two matching processes. On the other hand, the figure shows a big statistical difference between J_e → J_r and J_e → J_r calculated based on the graphs extracted by the 3D Thinning method.

Fig. 5:

Experimental probability distributions of mapping distances D for the two-way matchings between the ground-truth and experimental graphs.

Table III shows the number of nodes in the graphs generated manually, by the 3D Thinning method and by our automatic processing. It is seen from the table that, in all cases, the 3D Thinning method produces sparser models having dramatically fewer nodes than that in the ground truth ones. Our modeling scheme produces fewer nodes in some cases (datasets 1, 5 and 6), whereas the opposite was observed in the other cases. To interpret this, Fig. 6 depicts magnified versions of the dataset 1 graph. It is clearly seen that manually processed graphs are composed of nodes with almost uniform Euclidean distances between all nodes and their neighboring ones. This is due to regraphing procedures [56]. In contrast, our automatic graphing results in non-regularized placement of nodes due to the dependency of the geometric contraction process on the complexity and tortuosity of the surface modeling for microvessels. However, the figure explains the superiority of the proposed modeling scheme compared to the 3D Thinning method in extracting more accurate graphs. Also from Table III, one can note a variation in the number of junction nodes observed in the ground-truth and the experimental models generated by the proposed scheme. Hence, our modeling produces either denser or sparser interconnections than that of the manually processed graphs when applied to different raw 2PM angiographies.

Fig. 6:

Magnified perspective view of Fig. 4 (a,1): (a), Fig. 4 (a,2): (b) and Fig. 4 (a,3): (c) with enlarged and recolored graph nodes.

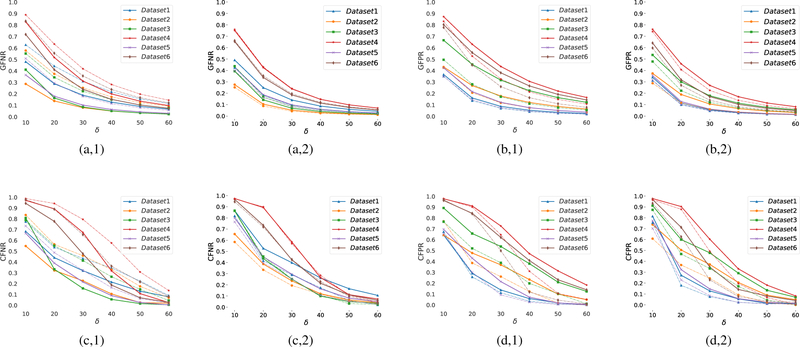
Fig. 7 plots the measurements of the GFNR, GFPR, CFNR, CFPR metrics obtained for the various datasets at different tolerance values δ. It is noted that these measurements are bounded between zero and one; the lower the value the better the performance. The figure illustrates that in all cases, the proposed modeling achieves lower geometrical and topological error rates than that of the 3D Thinning method. At the highest tolerance, δ = 60, our scheme achieves an average of 3.8 ± 2.1% and 4.2 ± 2.6% of false negative and false positive error rates, respectively, in modeling the geometry of the vascular networks. These error rates decrease to 3.5±2.6% and 3.0 ± 1.9% respectively, when excluding boundary microvessels (≈ 25 % of the angiograms) from our assessment. At the same value of δ, our scheme is able to capture the topology of the vascular networks with an average false negative and false positive error rates of 6.1 ± 2.6% and 4.5 ± 2.9%, respectively. When excluding the boundary microvessels, the average error rates decrease to 4.4 ± 2.8% and 1.5 ± 0.9%, respectively. It is to be noted the 3D Thinning method achieves even higher false negative rates when excluding the boundary microvessles, thus proving that this method is poor in capturing the geometrical and topological details from the segmented angiograms. We provide a visual illustration in Fig. 8 to interpret the improved performance when excluding the boundary vascular structures in the experimental graphs generated by the proposed scheme. The figure shows the false positive and false negative edges obtained at δ = 60 to compute the corresponding CFNR, CFPR values. One can inspect that a large portion of the mismodeled edges are those located at the boundary of the angiograms. As a result, a better performance of our modeling is achieved at the center of the angiograms, due to 2-photon sensitivity limitations. One goal of our proposed scheme is to generate topological models of microvessel networks that can be used for calculating physiological quantities. Towards that goal, we study the propagation of microvessels in the modeled networks. Fig. 9 depicts examples of ground-truth and experimental sub-graphs generated by propagating through the microvessel networks, beginning with nodes at the start pf a penetrating arteriole and ending with bifurcation nodes after 5 levels of consecutive branching. Despite some few mismodeled network branches, propagation through our experimental networks is very similar to that achieved in ground-truth ones.

Fig. 7:

Quantitative assessment of the 3D Thinning method (a-d, 1) and the proposed graphing scheme (a-d,2), as a function of the δ parameter based on (a,1–2) GFNR, (b,1–2) GFPR, (c,1–2) CFNR and (d,1–2) CFPR metrics. Dashed lines quantify the performance excluding the graphs boundary parts from the assessment process.

Fig. 8:

Visual illustration of mismodeled edges (blue-colored) for all datasets: false negative edges in (a-f,1); false positive edges in (a-f,2).

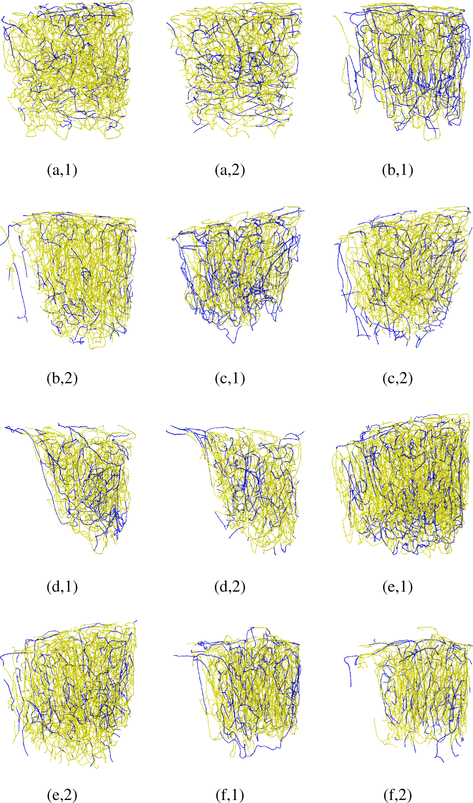
Fig. 9:

Propagating through the various microvessel networks for five consecutive branching levels beginning at the start of a penetrating arteriole (represented by white spheres), ground-truth (a-f,1) and automatically modeled (a-f,2). Each branching level is assigned a different colour.

3). Computational Complexity:

To provide a comprehensive performance evaluation of the proposed graphing scheme, analysis of its complexity in terms of computational time is necessary. We have run the experiments on a 3.0 GHz Rayzen AMD processor (8 cores, 16 threads in each) with 64 GB of RAM. Segmentation of microvessels has been carried out on a 12GB NVIDIA TITAN X GPU. The times required to perform the computations in each stage of our modeling pipeline are reported in Table IV. It is noted that most of the computation times (≈ 91.8%) is used for segmenting microvessels and contracting the generated mesh-based models. From the table, the averaged calculation time for processing one 2PM angiogram, begining with the segmentation of microvessels and ending with the extraction of their graphed networks, reaches 53 minutes. Hence, our fully automatic scheme is proved to provide a very reliable solution when applied to study cerebral microvasculature in large cohorts and can save weeks of manual labor.

TABLE IV:

Computational times (in seconds) required by each processing stage in our modeling pipeline.

	Dataset
	1	2	3	4	5	6
Segmentation/ morphology	1053/37	1183/43	1059/42	1111/44	1262/43	1113/40
Surface Modeling	177	206	204	250	291	195
Graph Extraction	1981	2463	2210	1524	2930	1860

VI. Conclusion and Future Work

In this work, we have proposed a novel fully-automatic processing pipeline to produce graphical models for cerebral microvasculature captured with 2-photon microscopy. Our scheme is composed of three main processing blocks. First, a 3D binary mapping of microvasculature is obtained using a fully-convolution deep learning model. Then, a surface mesh is computed using a variant of the marching cube algorithm. Lastly, a reduced version of the generated surface model is contracted toward the 1D medial axis of the enclosed vasculature. The contracted mesh is post-processed to generate a final graphical model with a single connected component. We used a set of manually processed graphing of 6 angiograms to validate our graphs. From the quantitative validation based on NetMet measures, our model was able to produce accurate graphs with low geometrical and topological error rates, especially at a tolerance > 30μm. Further qualitative assessment has shown that automatic processing generates realistic models of the underlying microvascular networks having accurate propagation through the modeled vessels. One important issue that could be addressed in a future work is related to the difficulty in generating watertight surface models. The employed contraction algorithm is not applicable to surfaces lacking such characteristics. Introducing a geometric contraction not restricted to such conditions on the obtained surface model could be an area of further investigation.