Bayesian hierarchical classification and information sharing for clinical trials with subgroups and binary outcomes

Abstract

Bayesian hierarchical models have been applied in clinical trials to allow for information sharing across subgroups. Traditional Bayesian hierarchical models do not have subgroup classifications; thus, information is shared across all subgroups. When the difference between subgroups is large, it suggests that the subgroups belong to different clusters. In that case, placing all subgroups in one pool and borrowing information across all subgroups can result in substantial bias for the subgroups with strong borrowing, or a lack of efficiency gain with weak borrowing. To resolve this difficulty, we propose a hierarchical Bayesian classification and information sharing (BaCIS) model for the design of multi-group phase II clinical trials with binary outcomes. We introduce subgroup classification into the hierarchical model. Subgroups are classified into two clusters on the basis of their outcomes mimicking the hypothesis testing framework. Subsequently, information sharing takes place within subgroups in the same cluster, rather than across all subgroups. This method can be applied to the design and analysis of multi-group clinical trials with binary outcomes. Compared to the traditional hierarchical models, better operating characteristics are obtained with the BaCIS model under various scenarios.

1. Introduction

Bayesian hierarchical models have been successfully applied in many research areas and play important roles in a wide variety of studies. (Blei, Ng, & Jordan, 2003; Broet, Richardson, & Radvanyi, 2002; Li & Perona, 2005; Rossi, Gilula, & Allenby, 2001) With progress in the application of Bayesian methods in clinical trials(D. A. Berry, 2006; S. Berry, Carlin, Lee, & Muller, 2010; Biswas, Liu, Lee, & Berry, 2009; Lee & Chu, 2012; Zhou, Liu, Kim, Herbst, & Lee, 2008), Bayesian hierarchical models have been used in a variety of applications of trial design and data analysis. For example, the posterior distributions of subset-specific treatment effects were studied based on Bayesian hierarchical models. (Dixon & Simon, 1991) A semiparametric Bayesian hierarchical model to combine longitudinal and survival data was proposed for HIV and cancer vaccine clinical trials. (Brown & Ibrahim, 2003) The commensurate prior in hierarchical models was derived to borrow information from historical data and reduce the overall sample size in clinical trials. (Hobbs, Carlin, Mandrekar, & Sargent, 2011) The use of Bayesian hierarchical models to study the shrinkage estimation of subgroup effects in drug development was thoroughly reviewed. (Jones, Ohlssen, Neuenschwander, Racine, & Branson, 2011) Efficient designs for Phase II studies by applying Bayesian hierarchical models were developed to borrow information among patient subgroups. (S. M. Berry, Broglio, Groshen, & Berry, 2013)

In the traditional Bayesian hierarchical model with binary outcomes, a fixed variance is applied to the response rates to control the amount of borrowing across subgroups; thus, borrowing is independent of the observed data. For example, Chugh and collaborators conducted a phase II trial to access the efficacy of imatinib on 10 different subtypes of advanced sarcoma and analyzed the results using the traditional Bayesian hierarchical model (Chugh R, 2009). There are 10 subgroups, including Angiosarcoma, Ewing, Fibrosarcoma, Leiomyosarcoma, Liposarcoma, MFH, Osteosarcoma, MPNST, Rhabdomyosarcoma, and Synovial subtypes. The number of response over the total number of patients in these subgroups are 2/15, 0/3, 1/12, 6/28, 7/29, 3/29, 5/26, 1/5, 0/2, 3/20, respectively. The observed response rates of these 10 subgroups ranges from 0 % to 24.1%. In a traditional hierarchical Bayesian model, information is shared between all subgroups, despite a wide range of observed response rates. In our paper, we address this issue by performing Bayesian hierarchical classification first followed by information sharing among the subgroups within the same cluster. We will use this study as a motivating example. More detailed discussion and analysis of this data will be presented later.

In some hierarchical models proposed to improve upon the traditional method, the borrowing strength is dynamically controlled by the data through an outcome-dependent variance across the subgroups. (S. Berry et al., 2010; Kass & Steffey, 1989; Lindley & AF, 1972; Thall et al., 2003) When the observed data from the subgroups are close in value, the data shrink more to the overall mean across subgroups and the borrowing strength is strong. However, when the outcomes of subgroups are significantly different, the borrowing strength becomes weak and borrowing information offers limited gain in efficiency.

A fundamental presumption when using a hierarchical model for information sharing across subgroups is that all subgroups must demonstrate similarity with respect to the outcomes of interest, i.e., there is exchangeability under a certain statistical distribution. (S. Berry et al., 2010) The exchangeability assumption is essential for borrowing across subgroups. For clinical trials, such similarities should be evaluated and justified under guidance from clinicians and statisticians. In practice, however, it may be difficult to make such a determination. In particular, the exchangeability assumption across subgroups often cannot be made with certainty for new treatments. Some undiscovered mechanisms or unobserved covariates may have remarkable influence on the efficacy of the drug, and those influences are difficult to identify at the trial design stage.

Sharing information across subgroups when significant differences exist may lead to biased results. For instance, suppose a drug is tested in a trial with 10 subgroups in which there are 5 subgroups with a response rate of 0.2 and 5 subgroups with a response rate of 0.4. If we place all 10 subgroups in one cluster and allow for sharing information among them, the hierarchical model shrinks the test response rates towards the overall mean response rate, which lowers the statistical power for identifying the efficacy of the drug in the high-response subgroups and increases the type I error of the low-response subgroups. (Freidlin & Korn, 2013)

Our approach to this problem is based on dynamic clustering and information sharing. It does not place all subgroups into one cluster for information sharing. Instead, subgroups are classified into different clusters on the basis of their response outcomes, and information is shared only within the same cluster, not across different clusters. Using this concept, we propose a clustered hierarchical model that combines both group classification and information sharing across subgroups. We refer to it as the Bayesian classification and information sharing (BaCIS) model. Following the simple hypothesis testing paradigm, which is to determine whether the drug works or not, the model classifies the subgroups into one or two clusters on the basis of the outcome of each subgroup. Information sharing occurs only among subgroups that belong to the same cluster. Using the aforementioned example (5 subgroups with a mediocre response rate of 0.2 and 5 subgroups with a good response rate of 0.4), the model classifies the 5 mediocre drugs and 5 good drugs into two different clusters (low-response and high-response clusters). Information borrowing takes place among either the low-response cluster or among the high response cluster, which prevents borrowing information across dissimilar subgroups.

Recent progress on genomic technology such as next generation sequencing reveals that tumors originating from the same organ or tissue can be genetically heterogeneous. On the other hand, similar genomic alterations may be found in the tumors from different tissues of origin (Ciriello et al., 2013; Kandoth et al., 2013). The use of the genomic biomarker to categorize the treatments becomes more important in specific subset of patients. Such changes in the clinic treatments lead to a new type of trial design: basket trial design (Lopez-Chavez et al., 2015; Sleijfer, Bogaerts, & LL, 2013; Trippa & Alexander, 2017; Ventz, Barry, Parmigiani, & Trippa, 2017). In this type of clinical trial design, patients with certain genomic alterations across different histologic subtypes are treated with the same targeted therapy to evaluate in which histologic types of the tumors the targeted therapy are effective. In the basket trial design, the same treatment is applied to the patients with certain genomic alterations, therefore information borrowing should be considered across different histologic types. The responses from different histologic types can be similar or very different under different situations. Therefore, the global borrowing may be not suitable to this design and the method based on the BaCIS model can be a good solution in this setting.

The subsequent sections of the paper are organized as follows: In Section 2, we introduce the details of the hierarchical model and present the subgroup classification based on the response outcome. In Section 3, we compute the operating characteristics of the new design based on the BaCIS model and compare it with the results of traditional hierarchical models. In Section 4, we conduct sensitivity analyses with different parameters. We discuss the clinical trial design based on the BaCIS model and present a clinical trial application of this hierarchical model in Section 5. The application of the BaCIS model on basket trial design is presented in Section 6. Our discussion and conclusion are in Section 7. Additional results can be found in the online Supplementary Material.

2. Hierarchical Bayesian subgroup classification and information sharing (BaCIS) model

We assume that a clinical trial includes k subgroups of patients with a binary outcome as the primary endpoint. These subgroups can be considered as different disease entities or different drugs. After the trial is completed, each of the k subgroups is classified into one of two response clusters (high or low-response clusters). The subgroups within the same response cluster share information through a hierarchical model. Let n_i denote the number of patients, Y_i denote the number of patients with a positive response, and p_i denote the response rate in subgroup i (i=1,…,k). The BaCIS method has two steps. In the first step, we apply the Bayesian hierarchical model (Model 1) to classify subgroups into two clusters. In the second step, we apply another Bayesian hierarchical model (Model 2) for information borrowing within each cluster.

The classification model (Model 1) is

$$\begin{gathered} Y_i\sim \mathit{Binomial}(n_i,p_i) \\ \mathit{logit}(p_i)={\eta }_i \\ {\eta }_i\sim \mathit{Normal}({\gamma }_{I_i},{\tau }_1) \\ {I}_i=1,\mathit{if}{\theta }_i<0 \\ {I}_i=2,\mathit{if}{\theta }_i\ge 0 \\ {\theta }_i\sim \mathit{Normal}(0,{\tau }_2),i=1,\dots ,k \\ {\gamma }_j=\mathit{logit}({\varphi }_j),j=1,2, \end{gathered}$$ (1)

where the indicators I_i and θ_i are the latent variables introduced for subgroup classification (O'Hara & Sillanpää, 2009); τ₁ is the precision parameter for each response cluster; τ₂ is the precision parameter for the latent variable θ_i; γ_j are the centers of the two response clusters; and (ϕ₁, ϕ₂) are the prespecified low and high response rates for the two response clusters. Subgroup i is classified into the cluster 1 (low-response) if Prob(θ_i > 0) > θ_c or the cluster 2 (high-response) otherwise. The threshold value θ_c for classification can be set at 0.5 or adaptively, which will be described later. We use the convention that the standard treatment yields a low response rate. The new treatments are evaluated and classified into either low or high-response clusters. There are 4 user input hyperparameters τ₁, τ₂, ϕ₁, and ϕ₂ in Model 1. The default values of ${\tau }_1=\frac{1}{{\mathit{sd}}^2}$, where $\mathit{sd}=\frac{\mathit{logit}({\varphi }_2)-\mathit{logit}({\varphi }_1)}{6}$ and τ₂=0.001. More details of parameter settings will be discussed in the Section 4 on parameter sensitivity analyses.

Based on the results of Model 1, for the subgroups in each cluster, we perform the computation of subgroup borrowing using Model 2. The Bayesian hierarchical model (Model 2) only allows for borrowing information within each respective cluster. We note that Model 2 is applied twice, once for the low-response cluster and again for the high-response cluster:

$$\begin{gathered} Y_i\sim \mathit{Binomial}(n_i,p_i) \\ \mathit{logit}(p_i)={\eta }_i \\ {\eta }_i\sim \mathit{Normal}(\mu ,{\tau }_3) \\ \mu \sim \mathit{Normal}({\mu }_0,{\tau }_4) \\ {\tau }_3\sim \text{Gamma}(\alpha ,\beta ) \\ {\mu }_0=\mathit{logit}(\varphi ) \end{gathered}$$ (2)

where τ₃ is the precision controlling the borrowing strength of each response cluster; and (α, β) are the hyperprior parameters of τ₃. The effects of the values of (α, β) on the operating characteristics are presented in Section 4. We set ϕ with ϕ₁ and ϕ₂ for the low and high-response clusters, respectively. The parameter τ₄ is the prior for the precision of the center of cluster. Typically we select a small value and the by default it is 0.1 in this study. In this study, the parameter are selected with the default values unless specified otherwise. The computation for the posterior distributions of the parameters of the two models is carried out using R and JAGS (Plummer, 2003). An R package bacistool can be downloaded from CRAN. (Chen & Lee, 2018)

Note that the number of response of each subgroup is from a binomial distribution Binomial(n_i, p_i). The response rate of the standard treatment is set as ϕ₁. The setup of the BaCIS model mimics the hypothesis testing of H₀: p_i ≤ ϕ₁ vs H₁: p_i > ϕ₁ and evaluates the statistical power at p_i = ϕ₂ where ϕ₂ > ϕ₁. After running the first model (Model 1), if the posterior probability is Prob(θ_i > 0) > θ_c (where θ_c is the threshold value for the classification), we claim that the treatment of subgroup i is classified into the high-response cluster. Otherwise, it is classified into the low-response cluster. We can determine the classification threshold value θ_c adaptively based on the response outcome: ${\theta }_c=1-\frac{1}{1+\text{exp}\left\{-\frac{2{\Delta }_r}{{\varphi }_2-{\varphi }_1}\right\}}$, where ${\Delta }_{\mathrm{r}}=(\frac{\Sigma Y_i}{\Sigma n_i}-\frac{{\varphi }_1+{\varphi }_2}{2})$. For example, when the mean response rate of all subgroups is large, Δ_r is large, and the threshold value θ_c is small. The threshold value is adaptively shifted to make more subgroups classified into the high-response cluster and vice versa. Subsequently, within the each cluster, we perform Model 2 respectively. If the posterior probability is Prob(p_i > ϕ₁) > θ_t, (where θ_t is the threshold value for the decision inference), we claim that the treatment in subgroup i is efficacious and the null hypothesis (p_i ≤ ϕ₁) is rejected. Otherwise, we claim that the treatment is no better than the standard treatment. Under the alternative or the null scenario, the rejection probability of each subgroup with high response rate is claimed as power or type I error rate, respectively. Under the global null hypothesis, the true response rates of all subgroups are low, where the probability of any one subgroup being rejected is claimed as the familywise type I error rate.

We use an example to illustrate subgroup classification in the BaCIS model. Suppose there are 5 subgroups (or arms) in the trial and the number of patients in each subgroup is 25. The pre-specified low and high response rates (indicated as ϕ₁, ϕ₂ in the model) for the two response clusters are 0.1 and 0.3, respectively. The outcome of the observed responses in the 5 subgroups is (2/25, 3/25, 1/25, 7/25, 8/25). We set α = 50, β = 10 in Model 2.

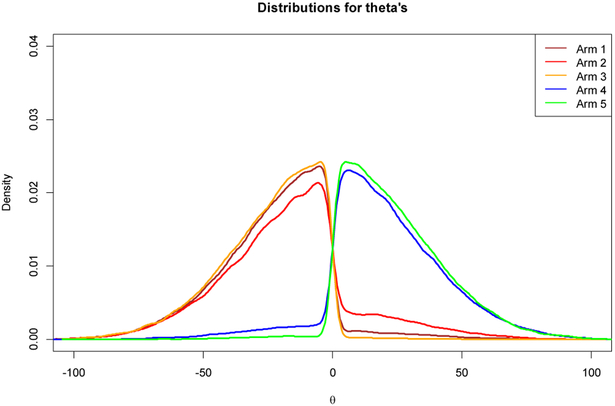
The posterior distributions of θ₁ to θ₅ are presented in Figure 1. Clearly the outcomes of subgroups 1, 2, and 3 are closer to that of the low-response cluster (response rate = 0.1) and the outcomes of subgroups 4 and 5 are closer to that of the high-response cluster (response rate = 0.3). The classification threshold θ_c = 0.58. Hence, subgroups 1, 2, and 3 are classified into the low-response cluster. In contrast, subgroups 4 and 5 are classified into the high-response cluster. The posterior distributions of response rates p₁ to p₅ are presented in Figure 2a, and the posterior response rates of the two clusters are shown in Figure 2b. From Figure 2, it can be seen that the posterior response rates of subgroups 1, 2, and 3 are pulled together, which implies borrowing of information from one another within the low-response cluster. We observe a similar phenomenon in subgroups 4 and 5 of the high-response cluster.

Figure 1.

Posterior distributions of θ₁ to θ₅ in a simulated trial with outcomes of (2/25, 3/25, 1/25, 7/25, 8/25) using the BaCIS model with parameters ϕ₁ = 0.1, ϕ₂ = 0.3.

Figure 2.

Posterior distributions of (a) response rates of all treatment arms, and (b) response rates of two clusters with outcomes of (2/25, 3/25, 1/25, 7/25, 8/25). Triangles and circles in panel (a) indicate the observed response rates of treatments within the low and high-response cluster, respectively. Computation is based on the BaCIS model with parameters: α = 50, β = 10, ϕ₁ = 0.1, ϕ₂ = 0.3.

3. Operating characteristics based on the BaCIS model

In this section, we calculate the operating characteristics based on the BaCIS model. As an illustration, we assume that there are 5 subgroups in the trial and the number of patients in each subgroup is 25. The pre-specified low and high response rates (indicated as ϕ₁, ϕ₂ in the model) for the two response clusters are 0.1 and 0.3, respectively. We choose the parameter values for the model as follows: α = 50, β = 2. We perform simulations and calculate the type I error and power with different scenarios. Using this scheme we calibrate the threshold value θ_t = 0.92 to yield a 10% type I error rate and 90% power for the frequentist operating characteristics. The calibration is carried out with θ_c = 0.5 to make the classification threshold value unchanged with different outcome scenarios.

Under the above setting, the operating characteristics of six scenarios with different low and high response rates are evaluated. The scenarios are chosen according to the settings of Freidlin and Korn (FK). (Freidlin & Korn, 2013) For each scenario, 5000 simulated trials are performed.

The probabilities of classifying the test treatments to the high-response cluster are presented in Table 1. Under all six scenarios, most subgroups are classified into the correct response clusters on the basis of the subgroup outcomes using the BaCIS model. In Scenarios 5 and 6 (global null and alternative scenarios) the classification performs the best and the false classification rates are less than 8%. In Scenarios 2 and 3, classification of all subgroups performs well and the false classification rates close to 10%. In Scenarios 1 and 4, the false classification rates of most the subgroups are lower than 10% except for Subgroup 1 of Scenario 1 (15.9%) and Subgroup 5 of Scenario 4 (100%-83.2%=16.8%) having relatively high false classification rates as a result of borrowing because all other subgroups have very different response rates than that respective subgroup.

Table 1.

Probabilities of subgroups being classified into the high-response cluster using the BaCIS model. The parameter values for the BaCIS model are ϕ₁ = 0.1, ϕ₂ = 0.3.

Scenario	Response rate in each subgroup
Scenario 1	.1	.3	.3	.3	.3
	0.159	0.917	0.906	0.904	0.921
Scenario 2	.1	.1	.3	.3	.3
	0.113	0.115	0.885	0.891	0.914
Scenario 3	.1	.1	.1	.3	.3
	0.085	0.09	0.083	0.862	0.878
Scenario 4	.1	.1	.1	.1	.3
	0.062	0.067	0.053	0.058	0.832
Scenario 5	.1	.1	.1	.1	.1
	0.039	0.04	0.03	0.032	0.047
Scenario 6	.3	.3	.3	.3	.3
	0.937	0.946	0.924	0.935	0.937

The power values for testing subgroups under different scenarios using the BaCIS model are presented in Table 2. The null hypothesis is set as H₀: p_i ≤ 0.1. For comparison, we perform a similar calculation using the traditional hierarchical model (S. Berry et al., 2010). The traditional hierarchical model does not include the subgroup classification and applies information borrowing across all subgroups. Under the traditional hierarchical model, we provide two threshold calibration settings. The first calibration is based on strong control of the type I error rate in the FK setting to prevent inflating the type I error rates in all scenarios. However, the strong control of the FK setting also decreases the power value of each subgroup with high response rates in all settings. Hence, strong control of the type I error rate is too strict and too conservative in most settings. For instance, in Scenario 1 only 1 in 5 subgroups has low response rate and the other 4 subgroups have high response rates, the traditional hierarchical model with the FK setting preserves the type I error rate of the only low-response subgroup at the cost of lowering the power of all the remaining high-response subgroups. The power of the high-response subgroups is reduced from 0.90 in Scenario 1 to 0.85, 0.82, and 0.79 in Scenarios 2, 3, and 4, respectively. The type I error rate is also reduced to 0.03 from the target value of 0.10 for each subgroup in Scenario 5. The reduced power increases the potential of failing to identify the promising treatments in the phase II evaluation.

Table 2.

Statistical power values (rejecting the null hypothesis of H₀: p_i ≤ 0.1 of subgroups using the BaCIS model and the traditional hierarchical model with (α = 50, β = 2, θ_t = 0.92, ϕ₁ = 0.1, ϕ₂ = 0.3). Two threshold calibration settings are applied for the traditional hierarchical model: The calibration based on Freidlin and Korn (FK) and the weak control (WC) of the type I error rate. Under the BaCIS model, the method described in Section 3 is used to calculate the power values.

Scenario and calibration method	Response rate in each subgroup					Familywise Type I error rate	Single Cluster %
Scenario 1	.1	.3	.3	.3	.3
BaCIS	0.159	0.917	0.907	0.904	0.921		13.3
FK	0.096	0.900	0.898	0.896	0.899
WC	0.237	0.962	0.966	0.962	0.961
Scenario 2	.1	.1	.3	.3	.3
BaCIS	0.113	0.116	0.886	0.891	0.914		2.6
FK	0.091	0.091	0.853	0.855	0.858
WC	0.225	0.229	0.951	0.939	0.941
Scenario 3	.1	.1	.1	.3	.3
BaCIS	0.086	0.091	0.084	0.862	0.878		2.9
FK	0.067	0.065	0.062	0.817	0.820
WC	0.173	0.184	0.180	0.920	0.921
Scenario 4	.1	.1	.1	.1	.3
BaCIS	0.064	0.069	0.055	0.060	0.833		15.1
FK	0.041	0.041	0.036	0.043	0.791
WC	0.119	0.126	0.123	0.120	0.905
Scenario 5	.1	.1	.1	.1	.1
BaCIS	0.044	0.043	0.035	0.035	0.050	0.171	83.4
FK	0.032	0.033	0.030	0.030	0.033	0.114
WC	0.099	0.097	0.092	0.095	0.094	0.336
Scenario 6	.3	.3	.3	.3	.3
BaCIS	0.938	0.946	0.925	0.936	0.937		74.6
FK	0.911	0.908	0.912	0.910	0.913
WC	0.987	0.968	0.969	0.967	0.967

From another point of view, the traditional hierarchical model can be applied with another calibration setting (the weak control [WC] setting) in which the nominal type I error rate constraint is satisfied only in the pure null scenario (Scenario 5 in Table 2), but not in other scenarios with some promising subgroups. The traditional hierarchical model with the WC setting works well with the pure null (Scenario 5) and the pure alternative (Scenario 6). However, in cases with mixed high and low-response subgroups, the WC setting can result in high type I error rates of 0.12, 0.18, 0.23, and 0.24 in Scenarios 4, 3, 2, and 1, respectively. The tradeoff is that strong or weak control of the type I error can result in lower or higher statistical power. In the traditional hierarchical model, information borrowing takes place across all subgroups. When the outcomes of all subgroups are similar, borrowing information from different subgroups improves the operating characteristics (reducing type I error and increasing statistical power). However, under the scenarios with mixed outcomes, information borrowing pulls the posterior response rates of subgroups towards the overall mean response rate of all subgroups. It can lead to biased results for all the subgroups. The type I error rate under the WC setting in Scenario 1 is inflated to 23.7%, which is higher than the nominal 10% type I error rate. In Scenario 4, the power value under the FK setting is reduced to 79%, which is lower than the targeted 90%. Neither strong nor weak control of the type I error rate is satisfactory in the cases with mixed response rates.

The BaCIS model presents more consistent operating characteristics under all scenarios compared to the results of the traditional hierarchical model. As we discussed, the power value of the FK calibration is lower than the targeted 90% power in mixed response scenarios, while the power value of the BaCIS model is consistently higher than those from the FK calibration and close to 90%. For the WC calibration setting, the type I error rates of the traditional hierarchical model are substantially higher than the nominal 10% level for the mixed response scenarios. The BaCIS model provides lower type I error rates than those from the WC calibration in different scenarios. In Scenarios 5 and 6, the BaCIS model presents very good operating characteristics. The type I error rates are maintained at the level of 3–5% while the power values are in the range of 92.5–94.6%. In Scenarios 2 and 3, the BaCIS still maintains relatively consistent power and type I error rates weighting in the different composition of subgroups. In the BaCIS model, subgroup classification ensures that the subgroups share information only when they belong to the same response cluster, which reduces the inconsistency in operating characteristics under different scenarios. In Scenarios 1 and 4, the BaCIS model provides good results for most subgroups. The information borrowing between subgroups makes the operating characteristics of few subgroups in mixed scenarios (Subgroup 1 in Scenario 1 and Subgroup 5 in Scenario 4) have high type I error rates or low power values. However, even for those subgroups the BaCIS model performs better than the traditional hierarchical model. For the BaCIS model, the probability of classifying a subgroup into the high-response cluster (Table 1) is close to the statistical power (Table 2). They are generally consistent but do not need to be exactly the same.

Table 2 shows that the familywise type I error rate (11.4%) of the hierarchical model with the FK setting is close to the target 10% due to the strong type I error rate control. However, it also results in generally low power values in all scenarios, especially in Scenario 4 Subgroup 5 (79.1%). With the BaCIS model, the familywise type I error rates of Scenario 5 is 17.1%, which is higher than that of the FK setting and much lower than that of the WC setting (33.6%). The subgroup type I error of the BaCIS method is comparable to the FK method in Scenario 5, but the power in Scenario 4 Subgroup 5 is higher (83.3%).

We also checked the percentage of the single cluster occurring with different scenarios and the results are presented in Table 2. When we use the BaCIS model with Scenarios 5 and 6 (all true response rates are the same), the single cluster percentages are 83.4% and 74.6%, respectively. When the true response rate of one subgroup is different from all other 4 subgroups (Scenarios 1 and 4), the single cluster percentage is about 13-15%. When the true response rates of two subgroups are different from other 3 subgroups (Scenarios 2 and 3), the single cluster percentage is only about 3%. As the sample size increases, the single cluster percentage is more consistent with the simulated truth (data not shown).

In addition, we calculate the effective sample size (ESS) of a posterior response rate distribution by matching its mean and variance values with those from a beta distribution with known parameters (Morita, Thall, & Muller, 2008). The ESS values for all subgroups under different scenarios obtained from the BaCIS model are presented in Table 3. The ESS values are more than the original sample size (25) of each subgroup with information borrowing, which demonstrates that within the same cluster, information is borrowed from different subgroups to increase the ESS values. In addition, the ESS is higher when the subgroups are more similar and lower when the subgroups are more different. Higher ESS values provide more information for posterior inference and further analyses. The magnitude of borrowing within a cluster is controlled by the hyperprior parameters (α, β). More details about the effects of hyperprior parameters on borrowing are given in the next section.

Table 3.

Effective sample sizes of all subgroups under different scenarios using the BaCIS model. Parameter values for the models: (ϕ₁ = 0.1, ϕ₂ = 0.3, α = 50, β = 2, θ_t = 0.92).

Scenario	Response rate in each subgroup
Scenario 1	.1	.3	.3	.3	.3
	28.32	43.65	43.72	43.76	43.73
Scenario 2	.1	.1	.3	.3	.3
	37.2	37.08	41.83	41.78	41.1
Scenario 3	.1	.1	.1	.3	.3
	42.86	43.28	42.99	38.34	37.67
Scenario 4	.1	.1	.1	.1	.3
	47.36	47.43	47.6	47.77	33.62
Scenario 5	.1	.1	.1	.1	.1
	51.89	52.34	51.88	51.37	50.88
Scenario 6	.3	.3	.3	.3	.3
	45.21	45.57	45.23	45.35	45.28

4. Parameter sensitivity analyses

Generally in this study we choose the default values of τ₁ as described in Section 2. More details on the sensitivity analyses of τ₁ can be found in the Supplementary Material, Section 1, Table S1. The result shows that the default value of τ₁ yields sensible classification of subgroups. However, values far from the default value can lead to unreasonable classifications, To examine the effects of the precision parameter τ₂ on the subgroup classification, a sensitivity analysis was reported in the Supplementary Material, Section 2, Table S2. The results show that the classification probabilities are not sensitive to the value of τ₂ in the range of (0.0001, 10). When there is no prior information for subgroup classification, a noninformative prior with low precision of τ₂ = 0.001 is recommended. The sensitivity analysis on the parameter of τ₄ can be found in the Supplementary Material, Section 3, Table S3. Larger value of the precision parameter τ₄ leads to strong borrowing. While the posterior means of response rates of subgroups maintain relatively stable, larger τ₄ results in larger posterior probability the subgroup response rates being greater than ϕ₁ and the increase of effective sample sizes. In general, strong borrowing should be avoided. The default value of τ₄ =0.1 seems reasonable.

In Table 4, we present the effects of hyperprior parameters α and β on the operating characteristics of the design. In Model 2, hyperprior parameters α and β control the borrowing strength through the gamma prior to the precision τ₃ with the mean being α/β. With a higher value of τ₃ (higher α or lower β), information borrowing within the cluster becomes stronger and leads to larger ESS values. We vary the values of α from 1 to 50 and β from 1 to 10 while fixing the other parameters, and θ_t = 0.92. The posterior probabilities of subgroups vary with different α and β values and stronger priors (higher α values or lower β values) pull different subgroups more together within each clusters. The ESS values vary from 30 to 45 for Subgroups 1 and 2 in the low-response cluster and from 26 to 43 for Subgroups 3, 4, and 5 in the high-response cluster with different α and β values. With higher α values, the ESS values increase; with higher β values, the ESS values decrease. The amount of borrowing within each cluster can be seen by Prob(p_i < ϕ₁) and Prob(p_i ≤ ϕ₂) for each subgroup. With more borrowing, the posterior probability of response rate for each subgroup is pooled more toward to the cluster mean. As a result, Prob(p_i > ϕ₁) and Prob(p_i > ϕ₂) are more similar for subgroups within the same cluster. With less borrowing, these results are more different between subgroups which reflect the response rate of each individual subgroup. Additional analyses with a variety of different outcomes are presented in the Supplemental Material, Section 4, Tables S4 and S5.

Table 4.

Sensitivity analyses of hyperprior parameters α, β on the operating characteristics of the BaCIS model: Posterior probability and the effective sample size (ESS) with different priors of τ₃ (θ_t = 0.92, ϕ₁ = 0.1, ϕ₂ = 0.3) using the same outcomes of (1/25, 3/25, 6/25, 7/25, 9/25).

Priors	Subgroups
Subgroups	1	2	3	4	5
Observed Response Rates	1/25	3/25	6/25	7/25	9/25
Classification	L	L	H	H	H
α = 50, β = 2	1	2	3	4	5
Prob(pi > ϕ1)	0.251	0.299	1	1	1
Prob(pi > ϕ2)	0	0	0.381	0.422	0.517
Effective sample size (ESS)	33.62	45.07	38.21	40.01	43.24
α = 50, β = 10	1	2	3	4	5
Prob(pi > ϕ1)	0.198	0.364	0.998	0.999	1
Prob(pi > ϕ2)	0	0.001	0.304	0.408	0.62
Effective sample size (ESS)	32.54	37.95	30.88	31.44	32.21
α = 10, β = 2	1	2	3	4	5
Prob(pi > ϕ1)	0.194	0.361	0.998	0.999	1
Prob(pi > ϕ2)	0	0.001	0.303	0.405	0.619
Effective sample size (ESS)	32.76	37.91	30.89	31.57	32.16
α = 5, β = 2	1	2	3	4	5
Prob(pi > ϕ1)	0.162	0.412	0.995	0.998	1
Prob(pi > ϕ2)	0	0.003	0.279	0.398	0.656
Effective sample size (ESS)	32.31	34.11	28.29	28.92	28.93
α = 2, β = 2	1	2	3	4	5
Prob(pi > ϕ1)	0.13	0.474	0.988	0.997	1
Prob(pi > ϕ1)	0	0.006	0.256	0.395	0.688
Effective sample size (ESS)	31.98	30.57	26.76	26.78	26.70
α = 1, β = 1	1	2	3	4	5
Prob(pi > ϕ1)	0.131	0.473	0.989	0.996	1
Prob(pi > ϕ2)	0	0.005	0.260	0.395	0.677
Effective sample size (ESS)	31.69	30.72	26.94	27.17	27.00

5. Clinical trial design and an example based on the BaCIS model

The BaCIS model can be applied to clinical trial designs for making inference of multi-subgroup treatments based on the subgroup classification and information sharing within a cluster. Multiple iterations of trial simulations are needed to determine the sample size and design parameters. The steps are described as follows. With a pre-specified number of subgroups, we first carry out trial simulations to determine the sample size in each subgroup to satisfy the type I error and power constraints. After the sample size is determined, we need to run multiple simulations with different parameters to derive the operating characteristics and evaluate parameter sensitivities. In this step, we may vary the values of parameters and compare the resulting operating characteristics. For example, we may apply α = 50, β = 1 and α = 50, β = 20 for strong borrowing and weak borrowing, respectively. The threshold value θ_t is calibrated based on the pre-specified type I error and power. Following this strategy, as an illustration, we calibrate the design parameters for 3-arm, 5-arm, and 10-arm trials with 10% type I error rates and 90% power using the BaCIS model. We find that the parameters calibrated for the 5-arm trial still can make the 3-arm and 10-arm trials satisfy the type I error rates and power constraints. The computation results based on the BaCIS model include the classification results for each subgroup, the posterior response rates for each subgroups, the posterior probabilities of subgroup response rates being greater than ϕ₁ and ϕ₂, and the final inference results of each subgroups.

When applying the BaCIS model in a clinical trial, specific parameters can be chosen per trial’s specifications. Extensive simulation studies should be conducted to study the operating characteristics of the design. Sensitive analysis can be performed to ensure that the choices of the design parameters are sensible and robust. All the important and relevant information should be included in the statistical considerations of the study protocol.

We go back to the motivating example of the sarcoma study presented in the introduction section. (Chugh R, 2009). When the observed response rates of different subgroups vary in a large range (0% - 24.1%), assigning all subgroups in one cluster is too aggressive for information sharing. Here we use the BaCIS model to analyze the data and the following parameter values are applied: α = 50, β = 10, ϕ₁ = 0.1, ϕ₂ = 0.3. Subgroups 4, 5 are classified into the high-response cluster and other subgroups are classified into the low-response cluster. The posterior mean response rates of 10 subgroups are (12.3%, 9.7%, 11.4%, 22.2%, 23.6%, 11.3%, 14.6%, 13.0%, 11.8%, 12.8%) which show the value of information borrowing. Although the posterior probability of response rates greater than the 30% target are low for all subgroups (0.002, 0.001, 0.003, 0.127, 0.170, 0.001, 0.006, 0.012, 0.009, 0.004), the probability of response rates greater than 15% are substantially high in some subgroups (subgroups 4 and 5) (0.259, 0.113, 0.203, 0.863, 0.905, 0.175, 0.420, 0.310, 0.240, 0.289). If we use the traditional hierarchical model from the reference (Chugh R, 2009), the probability of response rates greater than 15% are (0.356, 0.066, 0.228, 0.739, 0.844, 0.200, 0.634, 0.482, 0.308, 0.423). Comparing the results of subgroups 4 and 5 from two methods, it is clear that the probability of response rates greater than 15% from the BaCIS method are higher than that from the traditional hierarchical model. In the traditional model, when global borrowing is applied, the response rates of the high-response subgroups 4 and 5 are pull down by the other low-response subgroups while the response rate of the low-response subgroups are pull up, which limits the capability of identifying differential treatment effects. In the BaCIS model, only the subgroup 4 and 5 are classified into the high-response cluster and their posterior inference is not affected by the other low-response subgroups.

In addition, the BaCIS model can be extended to incorporate multi-stage designs. At any point of the study conduct, an interim analysis can be performed by computing the posterior probability that a subgroup is likely to be efficacious or not. If not, early stopping for futility can be implement to suspend or stop the enrollment of patients into those subgroups. Early stopping for efficacy can also be constructed to allow the highly effective subgroups to “graduate” from the trial. With early stopping in the interim analysis, the design can increase homogeneity among the remaining subgroups to allow for more information borrowing across subgroups.

6. Basket trial design

Simon et al. proposed a Bayesian basket design for genome variant-driven phase II trial to deal with the clinical trials with a population of humans with tumors of different histologic types (Simon, Geyer, Subramanian, & Roychowdhury, 2016). One parameter is applied in the method to specify the borrowing magnitude between subgroups. However, the borrowing in this method is essentially a global borrowing. The parameter adjusts the information borrowing magnitude from the hypothesis of “all subgroups are identical” to “all subgroups are independent” and the method does not include the subgroup borrowing within clusters. Liu et al. proposed a Bayesian hierarchical mixture model to assess the homogeneity of the response rates of different subgroups (Liu, Liu, Ghadessi, & Vonk, 2017). Similar to the method proposed by Simon et al., a type of global borrowing is applied and information borrowing within clusters is not used in this method.

The method we proposed in this study provides a flexible solution to the basket trial design. It incorporates the subgroup clustering and subgroup borrowing in one framework, and the information borrowing occurs within each cluster, not globally. In a basket trial design, patients are categorized into subgroups based on their histologic types and the number of patients in each subgroups usually is low. If we analyze each subgroup individually, it is difficult to make clear decisions due to the small sample size in each subgroup. With the method we proposed in this study, sharing information within the cluster leads to smaller posterior variances of each subgroup and better decisions can be made based on the posterior distributions with the reduced variance. In Figure 3 we present a basket design example. The trial has 5 subgroups and the outcomes of 5 subgroups are (1/8, 1/10, 2/8, 2/5, 6/15). In the left panel of the figure, each subgroup is analyzed using a beta distribution and in the right panel, the posterior distribution of each subgroups is calculated using the BaCIS model. The parameters used in the BaCIS model are (α = 5, β = 2, θ_t = 0.92, ϕ₁ = 0.1, ϕ₂ = 0.3). The standard deviation values of each subgroups are (0.086, 0.077, 0.138, 0.175, 0.116) for the individual analysis and (0.085, 0.077, 0.120, 0.141, 0.107) for the BaCIS model. In the BaCIS model, Subgroup 1 and 2 are classified into the low-response cluster and all other subgroups are classified into the high-response cluster. The standard deviations of subgroups of the BaCIS model are smaller than those from the individual analysis, which provides higher precision for further analyses.

Figure 3.

Posterior distribution of 5 subgroups (1/8, 1/10, 2/8, 2/5, 6/15) using (a) individual analysis and (b) BaCIS model. The parameter values for the BaCIS model are (α = 5, β = 2, θ_t = 0.92, ϕ₁ = 0.1, ϕ₂ = 0.3).

We have also compared the performance of BaCIS with the two-stage basket design proposed by Liu et al. (Liu et al., 2017). The BaCIS design provides comparable or slightly better performance than the BHMM design in the setting of two-stage basket designs. Detailed results are given in the Supplementary Material, Section 5, Table S6.

7. Discussion and conclusion

There are two extremes for information borrowing across subgroups. In the first extreme, in which the outcomes from the different subgroups are very similar, we place the outcomes of all subgroups into one pool (simple pooling) and apply full borrowing of information. In the other extreme, in which the outcomes from different subgroups are very different, we analyze each subgroup separately without any information borrowing (individual subgroup analysis). In real life, however, most applications are in between these two extremes. In these situations, subgroups may have some magnitude of similarity, but each subgroup still has its own characteristics. The appropriate magnitude of information borrowing between subgroups should be determined by the prior parameters and observed data to best utilize the information of all subgroups.

The hierarchical model provides a controllable way of sharing information across subgroups, and the magnitude of borrowing between subgroups is adjusted using different hyperprior parameters. However, the application of the traditional hierarchical model to share information between subgroups must be carefully evaluated on the basis of the exchangeability assumption between subgroups. When large differences exist between subgroups, the exchangeability assumption may not hold and strong borrowing across all subgroups can lead to biased results. Hence, it is reasonable to allow information borrowing to occur only among subgroups that share similarity and thus are exchangeable. The BaCIS model combines subgroup classification and information borrowing to first determine the cluster membership, then, to borrow information within a cluster. Subgroup classification, implemented in the model through latent variables with non-informative priors, plays an important role in finding the proper subsets for information borrowing. Informative prior can be added when such information is available.

The proposed BaCIS model provides a flexible approach to deal with two response clusters in multiple subgroups. It incorporates the subgroup classification as well as the posterior inference of the parameters of interest under the hierarchical model. This setting mimics the hypothesis testing framework in which the null hypothesis is either rejected or not rejected. However, for more complex cases such as the observed outcomes forming more than two clusters, the proposed model needs to be extended to incorporate multiple clusters in the inherent hierarchical structure. Non-parametric Bayesian approach was proposed with nonexchangeable priors for analyzing data from multiple clusters. (Leon-Novelo, Bekele, Müller, Quintana, & Wathen, 2012) Complex data outcomes with multiple clusters can be analyzed in detail and information borrowing within a cluster can be implemented. However, with the multiple cluster structure, the uncertainty of the number of the clusters become a problem. We are working on this topic to extend the current model based on the non-parametric Bayesian method. Robust exchangeability designs were proposed for Phase I and Phase II studies with multiple strata. (Neuenschwander, Wandel, Roychoudhury, & Bailey, 2016) Statistical clustering methods and unsupervised learning methods can also be applied to construct more flexible models in more complex settings (Hastie, R, & J, 2008; Vapnik, 1998). Finally, BaCIS model can also be extended to the multi-stage design setting to allow interim efficacy monitoring. The study efficiency can be improved by terminating the underperforming subgroups and graduating effective subgroups early. Further research is required to construct optimal designs in such settings.