Abstract
Radiation therapy of thoracic and abdominal tumors requires incorporating the respiratory motion into treatments. To precisely account for the patient’s respiratory motions and predict the respiratory signals, a generalized model for predictions of different types of patients’ respiratory motions is desired. The aim of this study is to explore the feasibility of developing a long short-term memory (LSTM)-based generalized model for the respiratory signal prediction. To achieve that, 1703 sets of real-time position management (RPM) data were collected from retrospective studies across three clinical institutions. These datasets were separated as the training, internal validity and external validity groups. Among all the datasets, 1187 datasets were used for model development and the remaining 516 datasets were used to test the model’s generality power. Furthermore, an exhaustive grid search was implemented to find the optimal hyper-parameters of the LSTM model. The hyper-parameters are the number of LSTM layers, the number of hidden units, the optimizer, the learning rate, the number of epochs, and the length of time lags. The obtained model achieved superior accuracy over conventional artificial neural network (ANN) models: with the prediction window equaling to 500 ms, the LSTM model achieved an average relative mean absolute error (MAE) of 0.037, an average root mean square error (RMSE) of 0.048, and a maximum error (ME) of 1.687 in the internal validity data, and an average relative MAE of 0.112, an average RMSE of 0.139 and an ME of 1.811 in the external validity data. Compared to the LSTM model trained with default hyper-parameters, the MAE of the optimized model results decreased by 20%, indicating the importance of tuning the hyper-parameters of LSTM models to obtain superior accuracies. This study demonstrates the potential of deep LSTM models for the respiratory signal prediction and illustrates the impacts of major hyper-parameters in LSTM models.
Keywords: deep learning, long short-term memory networks, hyper-parameter tuning, motion tracking and prediction, radiation therapy
1. Introduction
The precision of radiotherapy at specific sites, such as lung, liver, breast, and pancreatic, can be greatly influenced by the respiratory motion of a patient. A modern radiotherapy system is expected to (1) detect and predict the patient-specific respiratory motions ahead of time and (2) accommodate the radiotherapy planning and delivery to the breathing-induced motion patterns. A number of motion management methods have been investigated: breathing-hold (Murphy et al 2002, Nelson et al 2005, Petralia et al 2012, Chen et al 2015) and gating method (Shirato et al 2000, Berbeco et al 2005, Yan et al 2005) are employed to reduce the treatment field and minimize the overdose to surrounding organs at risk (OAR); multileaf collimator (MLC)- and robotic couch-based (D’Souza et al 2005, Jiang 2006, Yi et al 2008, Sawant et al 2009, Han-Oh et al 2010, Buzurovic et al 2011, Hansen et al 2016) dynamic tracking methods have been explored for real-time target tracking to improve the delivery efficiency. When respiratory motion is incorporated into the delivery strategy, target motion needs to be predicted ahead of time by a certain amount in order to compensate the latency of beam and field adjustments (Shepard et al 2018).
Existing prediction methods of respiratory motion fall into two major categories: model-based and learning-based. Model-based methods estimate predictions of respiratory motion by linear or non-linear functions and predictor coefficients. Existing model-based methods include autoregressive moving average model (ARIMA) (Makridakis and Hibon 1997, McCall and Jeraj 2007), sinusoidal model (Vedam et al 2004, Wu et al 2004) and kalman filter (Wang and Balakrishnan 2003, Putra et al 2006). Learning-based methods employ neural networks or adaptive filters with higher complexity compared to the model-based methods, thus providing greater adapt-ability and nonlinearity to predict respiratory motion of patients, especially when the breathing pattern is irregular and fuzzy. Artificial neural network (ANN) and recurrent neural network (RNN) are two commonly used learning-based methods. ANN usually consists of one input layer, two to five hidden layers and one output layer. The input layer takes in the respiratory curves and passes them to hidden layers, which are composed of neurons with adjustable weights and biases. These weights and biases are iteratively trained with the back propagation method until the threshold of the cost function is hit. The output layer finally outputs the prediction of future respiratory amplitudes. Previous studies (Isaksson et al 2005, Tsai and Li 2008, Sun et al 2017) have demonstrated the superiority of ANN or its variant architectures in the breathing motion prediction especially for patients with nonlinear breathing curves. The major limitation of ANN is the ignorance of temporal dependency of previous inputs. RNN, on the other hand, is designed to process temporal data, and a feedback architecture is utilized to allow signals from previous hidden and output layers to feed back to current hidden and input layers. In this way, signals from very irregular breathing patterns can be supplemented by filtered data from the outputs and the response of the network becomes smooth. Lee et al (2012) have explored the usage of RNN as the predictor of respiratory curves and encountered a problem regarding the expensive gradient descent calculations. As a result, they employed the extend kalman filter (EKF) (Puskorius and Feldkamp 1994) as the corrector of the RNN predictor. Although the architecture of RNN is shown to be a better fit for temporal data, in practice, it is hard to train it properly. The widely known issue is the exploding and vanishing gradient problem. Due to the long-term temporal contributions, the norm of the gradients either explodes to infinity or shrinks to zero, making it impossible to learn from timely distant events. As a result, a variant architecture of deep neural networks called long short-term memory (LSTM) (Hochreiter and Schmidhuber 1997) was developed to address the problem of exploding and vanishing gradient in conventional RNN, achieving superior performance in many sequential data tasks such as speech recognitions (Graves et al 2013, Graves and Jaitly 2014) and machine translations (Cho et al 2014, Sutskever et al 2014).
In the previous studies of predictive model development, one generally used clinical data from limited number of patients to train the model. The models can provide accurate predictions for the same patients whose respiratory curve data were used to develop the model (Murphy and Pokhrel 2009, Sun et al 2017, Teo et al 2018). However, limited results were presented when the model was applied to new patients, whose data were never used for model development. Large amount of clinical investigations have shown that the respiratory pattern can vary significantly from patient to patient (Chen and Kuo 1989, Braun 1990, Ozhasoglu and Murphy 2002, Parameswaran et al 2006), and even for the same patient under different physical conditions (e.g. overweight or underweight, before or after surgery). Therefore, it will be more clinically practical if a generalized model (for example in Teo et al (2018)) is developed to predict respiratory signals for different patients. To develop such a generalized model, respiratory data from a large number of patients with considerably different breathing features are needed. Moreover, a powerful neural network that can ‘remember’ and ‘resolve’ tremendous amount of different data patterns needs to be constructed.
In this study, a novel LSTM-based approach was proposed to exploit recent developments in deep learning and its power in providing superior predictions of patient respiratory curves. The proposed deep learning neural network was trained using real-time position management (RPM) data from 1187 sets of respiratory signals, and the effectiveness of the network was first self-validated using the validation data that came from the same 1187 respiratory curves. This validation process is called internal validity, as the patterns of these validation data were learned during the training process, while the internal validity data remained untouched in the training process. Data sets from additional 516 breathing curves were then used as the external validity data to test the generality of the developed model. These data were not utilized until the LSTM model had been trained and validated across the internal validity data. To our knowledge, this is the first time that a deep LSTM method has been developed as a generalized model for patient RPM predictions and with by far the largest amount of data employed for model training and validation (1703 RPM data from 985 patients in total).
2. Methods and materials
2.1. Data acquisition
The respiratory data (in total 1703 sets) were collected from 985 patients across three institutions by the real-time position management (RPM; Varian Medical Systems, Palo Alto, CA) system. Patients were not subject to any active breathing motion management techniques (such as coaching or breath hold) during the data acquisition process, therefore the breathing curve can be considered as the record of each patient’s free breathing pattern. The average frequency of the data is 30 Hz, and the recorded length ranged two to five minutes.
2.2. LSTM networks
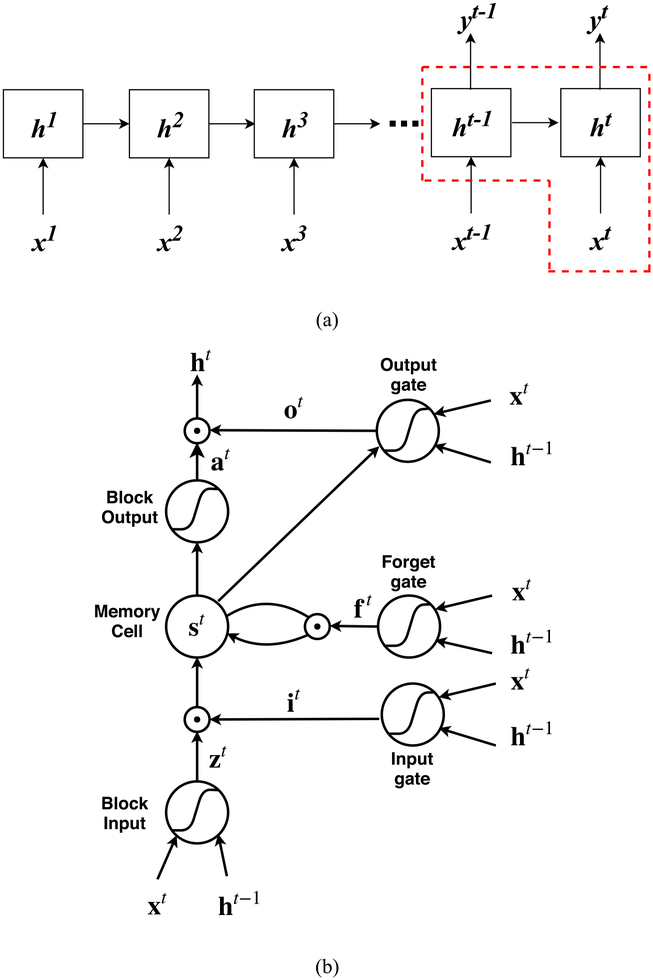
Long short-term memory (LSTM) is one of the most effective sequential models that can overcome the vanishing and exploding gradient problem during the long-term sequence learning compared to conventional RNN. The core idea of LSTM (Hochreiter and Schmidhuber 1997) is to introduce a memory cell that enforces constant errors flowing through non-linear gating units and can truncate the gradient at some point. The decision of when to open the gating unit, close the gating unit, or delete the gating unit’s access to the data is learned through an iterative process. The basic structure of an LSTM block is illustrated in figure 1. The LSTM block can be simply decomposed into four major parts: a memory cell st, an input gate it, a forget gate ft, and an output gate ot. To train an LSTM model consisting of multiple LSTM blocks, at a specific time step t, the core step is to update the memory cell state st by a self-loop. The control of the input, forget, and output gates of LSTM are achieved by specific weight and bias matrices. The details of updating the memory cell and each gate are illustrated as follows:
Figure 1.
(a) The LSTM many-to-many architecture for respiratory sequence prediction. The input vector is denoted by xt, the hidden layer vector is denoted by ht, and the output vector is denoted by yt. (b) A schematic diagram of a basic LSTM block as delineated in (a) by the red dash lines. The LSTM block consists of four parts: a memory cell st, an input gate it, a forget gate ft and an output gate ot. The updates of each part and the output of the LSTM block are illustrated in equations (1)–(6).
Let the input vector be denoted by xt and the current hidden layer vector be denoted by ht. Vectors b, U, and W denote the biases, input weights and recurrent weights respectively, and the subscripts z, i, f and o denote the block input, the input gate, the forget gate and the output gate. ⊙ denotes the element-wise multiplication. The logistic sigmoid function was employed as the activation function of gates, and the hyperbolic tangent function was usually used in the block input and block output.
The input gate it is responsible for filtering the information (from the input vector and the previous hidden layer vector) that can be transferred to the memory cell. it is updated by:
| (1) |
The forget gate ft controls the self-loop of the memory cell and decides which information from the previous memory cell state needs to be neglected. ft is updated by:
| (2) |
The memory cell controls the update of cell state from st−1 to st, and is updated with the use of block input zt:
| (3) |
| (4) |
The output gate ot is responsible for generating the output and updating the current hidden layer vector ht with the use of block output at:
| (5) |
| (6) |
| (7) |
The predictive model was built with three LSTM layers, each with fifteen hidden layer units. The output layer was a fully connected layer with fifteen units, designed to output the predicted sequence of respiratory signals. The optimization of hyper-parameters such as the number of hidden layer units and the number of LSTM layers will be illustrated in section 2.5.
2.3. Data partitioning
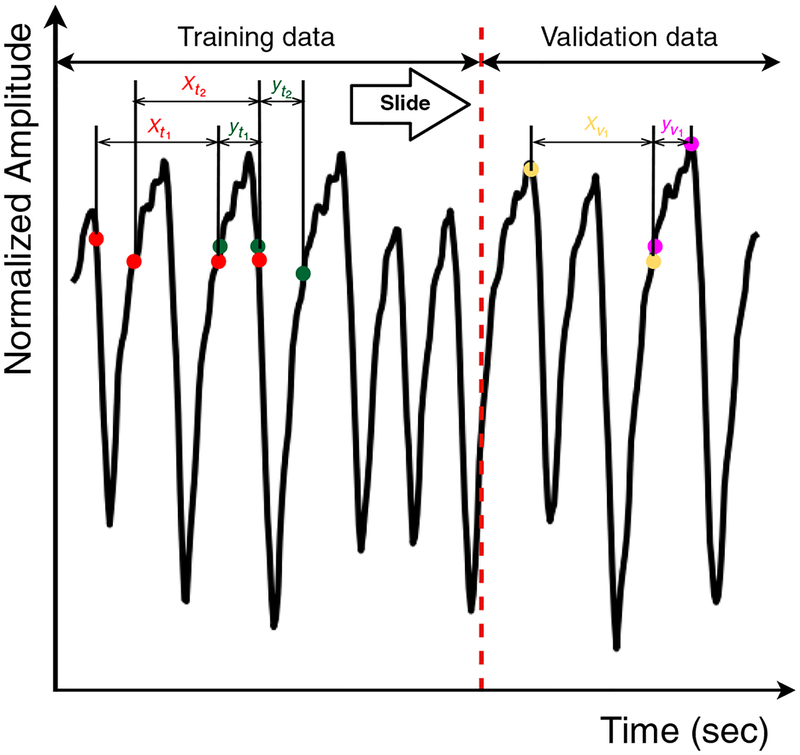
As the starting point, the offset of each breathing curve was removed and the curves were normalized to −1 to 1. The general scheme of data partitioning is outlined in figure 2. Each training dataset was separated into a training part and an internal validity part. The input of the LSTM model was denoted as xi, a vector that contains m data points and represents a segment of the breathing signal. The aim of training was to provide predictions of next n data points (n represents the size of the output window) right after xi, denoted as yi. The training inputs and outputs were sampled in a sliding window fashion, in which a moving window consisting of one pair of input and output data (xi and yi) were extracted from the signal and slid along the time axis in order to train the LSTM model. The successive input xi+1 was generated by moving the sliding window by n data points in order to continuously predict every data point right after the training input. We continued moving the sliding window until the last available observation in the training part was hit. Owing to the fact that the frequency of respiration signal is about 30 Hz, the length of n = 15 corresponded to the prediction window of 500 ms. The input length m, also known as the length of time lags, is an important hyper-parameter in an LSTM architecture, so the value of m was optimized. The details of this optimization are illustrated in section 2.5.
Figure 2.
Data partitioning of the respiratory breathing signal. The breathing curves in the training dataset were first divided into the training part and the validation part. The training inputs (xti) and outputs (yti) of LSTM networks were generated via the sliding window technique. xvi and yvi represent the inputs and outputs of a pair set of internal validity data.
2.4. Model training and evaluation process
In the model training process, online learning was performed, which means the batch size was set to one and the network weights were updated after each training pattern. The m data points within the training sample window were provided as LSTM inputs. Predictions of the following n output data points were generated, and the errors were calculated. The sliding window was moved forward, and the weights and biases of the LSTM model were updated after each epoch. The model was trained for a fixed number of epochs, where a single epoch is a complete pass over the training set. After each epoch, we evaluate the model’s mean absolute error (MAE) using the output data in the training set. The network parameters for the next training epoch were inherited from the preceding training epoch, where the inherited parameters served as the initialization and regularization for the subsequent training epoch. The LSTM model was trained with the breathing signals in the training dataset, and the model evaluation was two-fold: first, the pre-trained model was evaluated using the internal validity data, where MAE, root mean square error (RMSE) and ME were used as the model performance metrics; and second, as an external validity dataset, an additional 516 sets of breathing signals, which were not ever used or ‘seen’ through the model training process, were employed to assess the generality of the LSTM model.
2.5. Hyper-parameter optimization
Hyper-parameter selection and optimization play an important role in obtaining superior accuracy with LSTM networks (Greff et al 2017, Reimers and Gurevych 2017). Although there are other methods (Bergstra and Bengio 2012) that can efficiently obtain good hyper-parameters for complex networks, we chose to use the grid search method as it is easy to implement and parallelize. In the grid search, exhaustive searching was performed through the hyper-parameter space that consists of manually specified parameter subsets. Specifically, we performed 44 100 random searches, one for each combination of the six variants and each encompassing ten trials. Since the training for the LSTM model is time-consuming, the performance of the model with each parameter combination was evaluated by MAEs using a forward out-of-sample validation instead of cross-validation. For this LSTM network, we have investigated the following hyper-parameters.
2.5.1. Number of LSTM layers
Networks with a 1, 2, 3, 5 or 10 stacked LSTM layers were investigated.
2.5.2. Number of hidden units per layer
The number of hidden units per LSTM layer was selected from the set {3, 5, 10, 15, 20, 30, 40}. In case of multiple layers, we assigned the same value for each LSTM layer.
2.5.3. Optimizer
The optimizer is responsible to minimize the objective function of the LSTM networks. In this study we investigated the performance of seven optimizers, including stochastic gradient descent (SGD) (Robbins and Monro 1985), Adam and Adamax (Kingma and Ba 2014) and Nesterov Adam (Nadam) (Dozat 2016), Adagrad (Duchi et al 2011), Adadelta (Zeiler 2012) and RMSprop (Tieleman and Hinton 2012).
2.5.4. Learning rate
The optimizer performance is affected by the learning rate. If the learning rate is too small, the training time will be very long; on the other hand, if the learning rate is too big, it may oscillate around the global optimum instead of converging to it. The learning rate was sampled from {0.0001, 0.001, 0.005, 0.01, 0.1}.
2.5.5. Number of epochs
The number of epochs is a hyper-parameter that defines the number of times that the LSTM networks passes through the entire training dataset. One epoch means that each sample in the training dataset has had an opportunity to update the internal model parameters. An epoch is comprised of one or more batches. The number of epochs is traditionally large, allowing the learning algorithm to run until the error from the model has been sufficiently minimized. In this study, the number of epochs was selected from the set {10, 20, 30, 50, 100, 500}.
2.5.6. Length of time lags
Time lag refers to a sequence of the respiration signal acting as the LSTM model’s input. The length of time lag represents the amount of intakes to make prediction, and different length of time lag may cause different prediction results. The length of time lag was sampled from the set {1, 5, 15, 20, 50, 100}.
2.6. Evaluation of predictive accuracy
MAE, RMSE and ME were used to evaluate the respiratory signal predictions generated by the LSTM model. The evaluation criteria indicated the overall prediction ability of the model by comparing (1) the internal validity dataset and (2) the external validity dataset with their corresponding predicted values.
MAE is a measure of the magnitude of errors, and can be calculated by
| (8) |
where yi is the actual respiratory data point, ŷi is the predicted respiratory data point, and N is the number of investigated points.
RMSE is calculated by taking the square root of the mean of the square of all the errors. The RMSE represents the sample standard deviation of the differences between predicted values and ground truth values. The effect of each error on RMSE is proportional to the size of the squared error. Consequently, RMSE is sensitive to outliers. RMSE can be expressed by:
| (9) |
ME represents the ME occurred in the predicted breathing sequence compared to the true sequence, and is calculated by:
| (10) |
2.7. Experiment details
The LSTM model construction, training, and evaluation were implemented in the high-level neural networks API Keras version 2.0.4 (Chollet 2015) in the Python 3.6 environment (Van Rossum and Drake 1995), and the backend engine is TensorFlow 1.4 (Abadi et al 2016), where low-level tensor manipulations such as the convolution and tensor products were handled. An Ubuntu server with Xeon E5–2697 CPU and one Nvidia Quadro P6000 (8 GB RAM, 64 GB memory) was used to perform all the calculations. The model training time was 25.6 h.
3. Results
3.1. Hyper-parameter tuning in LSTM
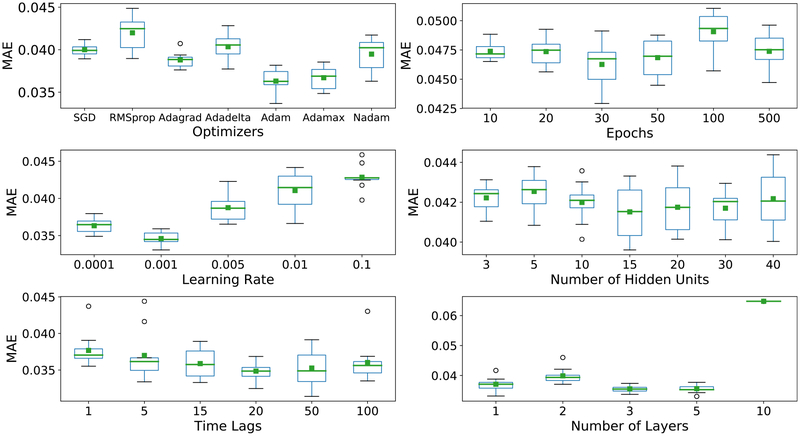
Figure 3 depicted the MAE (in a relative unit) as a function of the optimizers, the number of epochs, the learning rates, the number of hidden units, the length of time lags, and the number of LSTM layers. Table 1 summarizes the best hyper-parameter values and their importance levels affecting the MAE. Among them, the number of LSTM layers has the greatest impact on the model. The best performance was from a three-layer LSTM model and the worst was from a ten-layer model, causing up to 0.03 difference in relative MAE. In comparison, the type of optimizers and the learning rate demonstrated only a modest impact on the predictive performance of the model, where the MAE difference varied from 0.006 to 0.0075. The number of hidden units, the number of epochs, and the length of time lags showed little impact on the predictive accuracy, leading to small MAE differences from 0.003 75 to 0.007.
Figure 3.
The MAE of predicted signals (mean value in green) with different values of different optimizers, the number of epochs, learning rates, the number of hidden units, lengths of time lags, and the number of LSTM layers. The MAEs were calculated in the internal validity dataset. The box plot indicates the standard deviation between the predicted marginal and thus the reliability of the predicted mean performance.
Table 1.
The summary of LSTM hyper-parameters investigated in this study, the recommended configurations, and the impact level of each parameter.
| Hyper-parameter | Range | Recommended configuration | Impact |
|---|---|---|---|
| Number of layers | {1, 2, 3, 5, 10} | 3 | High |
| Number of hidden units per layer | {3, 5, 10, 15, 20, 30, 40} | 15 | Low |
| Learning rate | {0.0001, 0.001, 0.005,0.01,0.1} | 0.001 | Intermediate |
| Number of epochs | {10, 20, 30, 50, 100, 500} | 30 | Low |
| Length of time lags | {1, 5, 15, 20, 50, 100} | 20 | Low |
| Optimizer | {SGD,RMSprop,Adagrad,Adadelta,Adam,Adamax,Nadam} | Adam | Intermediate |
3.2. Predictive performance evaluation
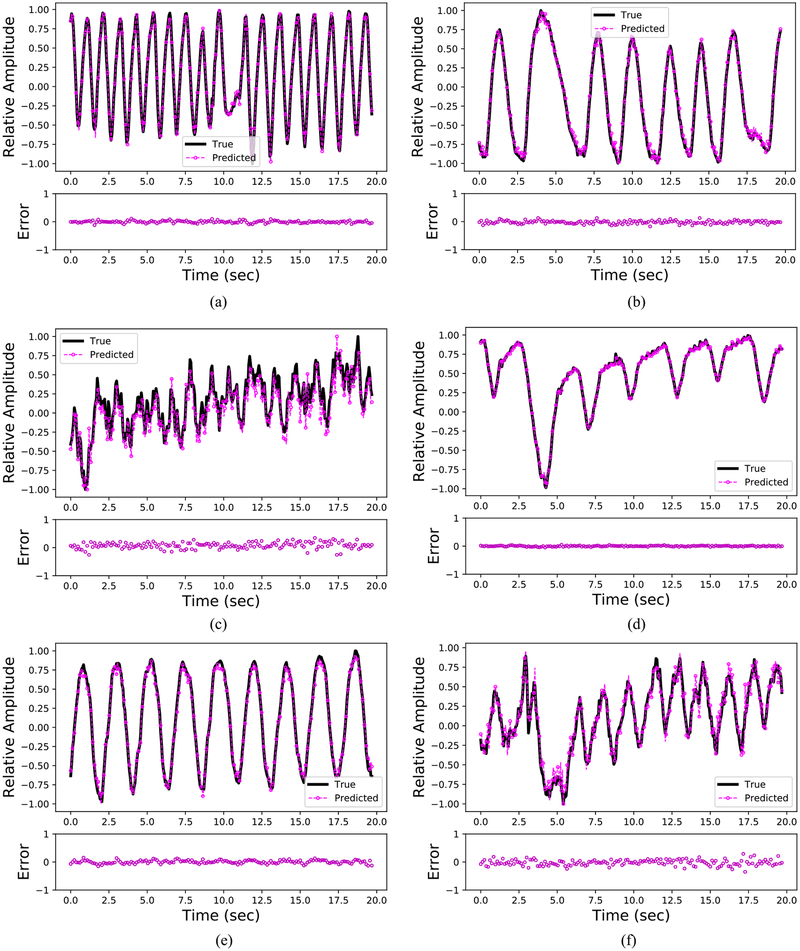
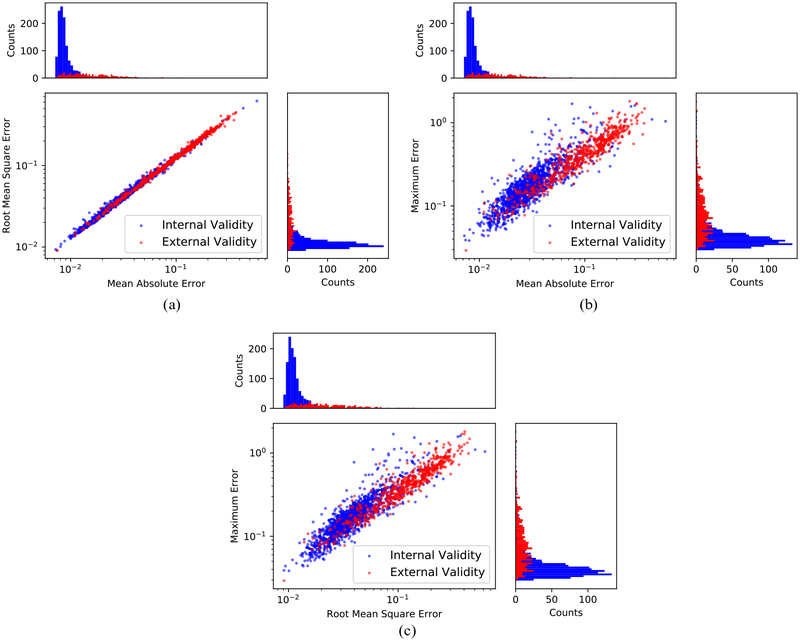
Figure 4 depicts six representative cases of ground truth versus predicted respiratory curves using the generalized LSTM model. For trajectories a, b, d, and e, no drastic prediction errors were observed. Most of the errors occurred near the peaks (transitions from inhale to exhale) and troughs (transitions from exhale to inhale) of respirations. Figure 5 provides a summary of the predictive performance on respiratory signals that are used for the model’s internal validation and external validation. The MAE, RMSE, and ME of the internal validity dataset and external validity dataset are averaged and summarized in table 2. Results in figure 5 and table 2 indicate that the LSTM model can provide accurate predictions of respiratory signal of patients even if the dataset was not used to establish the parameters for the LSTM model. On the other hand, the model errors (MAE and RMSE) on the external validity dataset are about three times greater compared to the internal validity dataset. This is reasonable since the LSTM model captured the respiratory patterns of the internal validity dataset during the training process.
Figure 4.
Predicted respiratory signals benchmarked against the ground truth signals (selected from six patients with different breathing frequencies and amplitudes). The ground truth signals are depicted in black, and the predicted signals are depicted in magenta. The error plot is attached below each subplot. Note time = 0 in each subplot stands for the initial starting point of the testing part. (a) Patient pattern 1: deep in depth and fast. (b) Patient pattern 2: deep in depth and slow. (c) Patient pattern 3: shallow in depth and fast. (d) Patient pattern 4: shallow in depth and slow. (e) Patient pattern 5: deep in depth and with a normal speed. (f) Patient pattern 6: shallow in depth and with a normal speed.
Figure 5.
Illustration of the LSTM model’s predictive performance on the internal validity dataset and the external validity dataset using MAEs, RMSEs and MEs metrics. The histograms of each metric were inserted next to the axes of each subplot. The internal validity patient data was plotted in blue, and the external validity patient data was plotted in red. (a) Distributions and histograms of MAE and RMSE values for all patients. (b) Distributions and histograms of MAE and ME values for all patients. (c) Distributions and histograms of RMSE and ME values for all patients.
Table 2.
The mean and standard deviation of MAEs, RMSEs and MEs in predicting patient respiratory signals for the internal validity patient set (includes 1187 sets of breathing curves) and the external validity set (includes 516 sets of breathing curves).
| MAE | RMSE | ME | |
|---|---|---|---|
| Internal validity data (1187 breathing curves) | 0.037 ± 0.034 | 0.048 ± 0.040 | 1.687 ± 0.177 |
| External validity data (516 breathing curves) | 0.112 ± 0.070 | 0.139 ± 0.085 | 1.811 ± 0.285 |
4. Discussion
4.1. Impact of Hyper-parameters
4.1.1. Number of LSTM layers
As expected, the number of LSTM layers played the key role in the network performance—the deeper the LSTM model went, the better the prediction performance, with the law of diminishing returns applied. In fact, the MAE of the five-layer model was only slightly better than the three-layer model, with the price of an over-fitting issue and slower convergence speed. Therefore, we decided to choose the three-layer structure. It can also be seen in figure 3 that the MAE increased significantly when the number of LSTM layers was ten, which may be caused by the over-fitting of the model.
4.1.2. Number of hidden units per layer
As the number of LSTM layers determined the depth of an LSTM model, the width of an LSTM model was determined by the number of hidden units per layer. Finding the optimal number of hidden units was not straightforward due to its dependency on different inputs and the number of LSTM layers. The optimal value in our case was found to be 15. However, as table 1 reveals, the number of hidden units had a small impact on the results. Adding or removing ten hidden units from a three-layer LSTM model only changed the performance by roughly 2%.
4.1.3. Optimizers and learning rates
Learning rate is the most important hyper-parameter for the optimization process. As shown in figure 3, the model performance was sensitive to the change of learning rates. We observed that the variances for SGD and Adagrad were much smaller in comparison to other optimizers. We also measured the time an optimizer took to converge. According to our measurements, Adam (optimization) converged first and required the least number of training epochs to obtain a good performance, while SGD took the longest time to converge.
4.1.4. Length of time lags
The decision of the length of time lags depends on the periodic characteristics of the training data. Using many lagged values can enhance the probability of capturing time-dependent features, while at the same time increasing the dimensionality of the convergence, leading to over-fitting as well as difficulties in training the model. The LSTM model performed poorly when using a smaller number of time lags compared to the case in which it was trained with a large number of time lags.
4.1.5. Number of epochs
It was observed that the MAE increased significantly beyond a certain number of epochs. This phenomenon may be due to the over-fitting when the model was trained with too many epochs. In that case, the LSTM model did not learn the data pattern but only memorized the data.
4.2. Performance comparison with other architectures
The superiority of neural network architectures in internal and external respiratory motion predictions has been demonstrated in previous studies (Yun et al 2012, Sun et al 2017, Teo et al 2018, Wang et al 2018). To our knowledge, this study is the first to implement a multi-layer LSTM architecture for external respiratory signal prediction utilizing over 1000 patient datasets. We have illustrated the pipeline to build up the LSTM model and approaches to tune the hyper-parameters of the model. The advantage of optimizing the hyper-parameters has also been investigated. The results demonstrated that tuning the hyper-parameters led to approximately a 20% increase in predictive accuracy and up to more than 80% improvements for certain parameters, in comparison to utilizing the default hyper-parameters. Thus, our study proves that tuning the hyper-parameters is vitally important to obtain good results using a deep LSTM model for respiratory motion prediction.
Compared to previous studies that mainly focused on investigating the power of ANNs (Murphy and Dieterich 2006, Murphy and Pokhrel 2009, Sun et al 2017, Teo et al 2018), our LSTM model allowed connections through time and provided a mechanism to feed the hidden layers from previous steps (long-term and short-term) as additional inputs of the next step. Since our datasets were collected from multiple institutions with different amplitude calibrations (such as the RPM camera angle, the location of the reflector box and the distance to the marker), the absolute amplitudes of RPM signals were significantly distinct from one to the other. Therefore, data normalization was employed in this study to enable a fair comparison of respiratory signals within the dataset and with previous studies. Comparisons with the results presented in this study can be achieved by either normalizing the data to the same range as used in this study, or scale the MAE and RMSE with a multiplication factor, which equals to the new normalization range divided by the old normalization range (which is two in our case). The derivation of the multiplication factor was illustrated as follows:
The minimum and maximum absolute amplitude of a respiratory signal are denoted as rmin and rmax. Assume the lower bound of the old normalization range is aold, the upper bound of the old normalization is bold, and the lower bound of the new normalization is anew and the upper bound of the new normalization is bnew. For a given data point y, its normalized value is denoted as n(y), which equals to
| (11) |
Note that rmin and rmax remain unchanged for the old and new normalization processes. According to the MAE definition as shown in equation (8), MAE of the old normalization range [aold, bold] equals to
| (12) |
Similarly, MAE of the new normalization range [anew, bnew] can be calculated by
| (13) |
The relationship between the new MAE and old MAE is
| (14) |
In the same manner, the relationship between the new RMSE and old RMSE can be derived as
| (15) |
Compared to previous studies utilizing the multiplication factor shown above, our results display a great accuracy in terms of the MAE and RMSE, both in the internal validity and external validity scenarios. As for the calculation speed, although the training of our deep LSTM model took over 20 h to finish, it is a one-time effort. Once the model was trained, it took only 5 ms to deploy the pre-trained model to make predictions per prediction window (500 ms), thus making it possible to perform the real-time respiratory signal predictions in the clinic.
4.3. Limitations and future work
There are some limitations of the current study. The first is due to the current method of hyper-parameter tuning. Although the grid search can mostly cover the search space, the uniformity of each hyper-parameter is limited and the exhaustive search process is very time-consuming. In addition, some hyper-parameters correlate with each other, and can result in different performances when optimized simultaneously rather than tuned individually. For future work, we will explore some emerging parameter optimization methods such as the random search (Bergstra and Bengio 2012) and the Bayesian optimization (Snoek et al 2012) that can efficiently search through the parameter space and incorporate the parameter interactions.
The second limitation involves the unknown correlations between internal and external respiratory motion patterns. As expected, there are non-negligible differences between the external respiratory signals and internal tumor motions, thus to make our LSTM model clinically useful, we need to fill in the gap between external respiration prediction and internal tumor motion prediction. This can be achieved by developing another model to learn the correlations between external and internal respiratory motions, which is beyond the scope of this study.
5. Conclusion
A deep LSTM model was developed for the external respiration signal prediction for radiotherapy and has demonstrated the superior performance compared to optimized conventional neural networks. A total of 1703 sets of breathing curves collected from 985 patients across three institutions were used for the model training and validation, and the internal and external validity results have shown that the developed model can be generalized and applied to predict respiratory motions for patients over a wide range of conditions. This study is one of the first few attempts to develop and evaluate a single generalized model for respiratory prediction. In addition, a large-scale study on the impacts of LSTM hyper-parameters was investigated and reported, illustrating the necessity of hyper-parameter tuning to boost the model performance and providing insights on the relative importance of these hyper-parameters. This study has demonstrated the feasibility of utilizing the deep LSTM model for external respiratory signal predictions, which can be further extended to track the dynamic tumor motions during the treatment delivery in the future.
Acknowledgments
This research was funded in part through the NIH/NCI Cancer Center Support Grant P30 CA008748. This study was originated from an independent study with Dr Wei Ji and accomplished by Dr Hui Lin while completing her dissertation at RPI under the research support by Dr X George Xu.
Footnotes
Disclosure of conflict of interest
The authors have no relevant conflicts of interest to disclose.
References
- Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G and Isard M 2016. TensorFlow: A system for large-scale machine learning OSDI 2016 (Berkeley: USENIX Association; ) pp 265–83 [Google Scholar]
- Berbeco RI, Nishioka S, Shirato H, Chen GT and Jiang SB 2005. Residual motion of lung tumours in gated radiotherapy with external respiratory surrogates Phys. Med. Biol 50 3655. [DOI] [PubMed] [Google Scholar]
- Bergstra J and Bengio Y 2012. Random search for hyper-parameter optimization J. Mach. Learn. Res 13 281–305 [Google Scholar]
- Braun SR 1990. Respiratory rate and pattern Clinical Methods: The History, Physical, and Laboratory Examinations 3rd edn (Boston: Butterworths; ) ch 43 [PubMed] [Google Scholar]
- Buzurovic I, Huang K, Yu Y and Podder T 2011. A robotic approach to 4D real-time tumor tracking for radiotherapy Phys. Med. Biol 56 1299. [DOI] [PubMed] [Google Scholar]
- Chen H and Kuo C-S 1989. Relationship between respiratory muscle function and age, sex, and other factors J. Appl. Physiol 66 943–8 [DOI] [PubMed] [Google Scholar]
- Chen Z-G, Xu L, Zhang S-W, Huang Y and Pan R-H 2015. Lesion discrimination with breath-hold hepatic diffusion-weighted imaging: a meta-analysis World J. Gastroenterol 21 1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho K, Van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H and Bengio Y 2014. Learning phrase representations using RNN encoder-decoder for statistical machine translation Proc. Conf. on Empirical Methods in Natural Language Processing (Stroudsburg: ACL; ) pp 1724–34 (arXiv:1406.1078) [Google Scholar]
- Chollet F 2015. Keras (https://github.com/keras-team/keras)
- D’Souza WD, Naqvi SA and Cedric XY 2005. Real-time intra-fraction-motion tracking using the treatment couch: a feasibility study Phys. Med. Biol 50 4021. [DOI] [PubMed] [Google Scholar]
- Dozat T 2015. Incorporating Nesterov momentum into Adam Technical Report (Stanford, CA: Stanford University; ) [Google Scholar]
- Duchi J, Hazan E and Singer Y 2011. Adaptive subgradient methods for online learning and stochastic optimization J. Mach. Learn. Res 12 2121–59 [Google Scholar]
- Graves A and Jaitly N 2014. Proc. of the 31st Int. Conf. on Machine Learning (ICML-14) pp 1764–72 (vol Series) [Google Scholar]
- Graves A, Mohamed A-R and Hinton G 2013. 2013 IEEE Int. Conf. on Acoustics, Speech and Signal Processing (IEEE; ) pp 6645–9 (vol Series) [Google Scholar]
- Greff K, Srivastava RK, Koutník J, Steunebrink BR and Schmidhuber J 2017. LSTM: A search space odyssey IEEE Trans. Neural Netw. Learn. Syst 28 2222–32 [DOI] [PubMed] [Google Scholar]
- Han-Oh S, Yi BY, Lerma F, Berman BL, Gui M and Yu C 2010. Verification of MLC based real-time tumor tracking using an electronic portal imaging device Med. Phys 37 2435–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen R, Ravkilde T, Worm ES, Toftegaard J, Grau C, Macek K and Poulsen PR 2016. Electromagnetic guided couch and multileaf collimator tracking on a TrueBeam accelerator Med. Phys 43 2387–98 [DOI] [PubMed] [Google Scholar]
- Hochreiter S and Schmidhuber J 1997. Long short-term memory Neural Comput 9 1735–80 [DOI] [PubMed] [Google Scholar]
- Isaksson M, Jalden J and Murphy MJ 2005. On using an adaptive neural network to predict lung tumor motion during respiration for radiotherapy applications Med. Phys 32 3801–9 [DOI] [PubMed] [Google Scholar]
- Jiang SB 2006. Seminars in Radiation Oncology (Amsterdam: Elsevier; ) pp 239–48 (vol Series 16) [Google Scholar]
- Kingma DP and Ba J 2014. Adam: a method for stochastic optimization (arXiv:1412.6980)
- Lee SJ, Motai Y and Murphy M 2012. Respiratory motion estimation with hybrid implementation of extended Kalman filter IEEE Trans. Ind. Electron 59 4421–32 [Google Scholar]
- Makridakis S and Hibon M 1997. ARMA models and the Box–Jenkins methodology J. Forecast 16 147–63 [Google Scholar]
- McCall K and Jeraj R 2007. Dual-component model of respiratory motion based on the periodic autoregressive moving average (periodic ARMA) method Phys. Med. Biol 52 3455. [DOI] [PubMed] [Google Scholar]
- Murphy MJ and Dieterich S 2006. Comparative performance of linear and nonlinear neural networks to predict irregular breathing Phys. Med. Biol 51 5903. [DOI] [PubMed] [Google Scholar]
- Murphy MJ and Pokhrel D 2009. Optimization of an adaptive neural network to predict breathing Med. Phys 36 40–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy MJ, Martin D, Whyte R, Hai J, Ozhasoglu C and Le Q-T 2002. The effectiveness of breath-holding to stabilize lung and pancreas tumors during radiosurgery Int. J. Radiat. Oncol. Biol. Phys 53 475–82 [DOI] [PubMed] [Google Scholar]
- Nelson C, Starkschall G, Balter P, Fitzpatrick MJ, Antolak JA, Tolani N and Prado K 2005. Respiration-correlated treatment delivery using feedback-guided breath hold: a technical study Med. Phys 32 175–81 [DOI] [PubMed] [Google Scholar]
- Ozhasoglu C and Murphy MJ 2002. Issues in respiratory motion compensation during external-beam radiotherapy Int. J. Radiat. Oncol. Biol. Phys 52 1389–99 [DOI] [PubMed] [Google Scholar]
- Parameswaran K, Todd DC and Soth M 2006. Altered respiratory physiology in obesity Can. Respir. J 13 203–10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petralia G, Summers P, Viotti S, Montefrancesco R, Raimondi S and Bellomi M 2012. Quantification of variability in breath-hold perfusion CT of hepatocellular carcinoma: a step toward clinical use Radiology 265 448–56 [DOI] [PubMed] [Google Scholar]
- Puskorius GV and Feldkamp LA 1994. Neurocontrol of nonlinear dynamical systems with Kalman filter trained recurrent networks IEEE Trans. Neural Netw 5 279–97 [DOI] [PubMed] [Google Scholar]
- Putra D, Haas O, Mills J and Bumham K 2006. Predication of tumor motion using interacting multiple model filter 3rd Int. Conf. on Advances in Medical, Signal and Information Processing (New York: Curran; ) pp 1–4 [Google Scholar]
- Reimers N and Gurevych I 2017. Optimal hyperparameters for deep lstm-networks for sequence labeling tasks (arXiv:1707.06799)
- Robbins H and Monro S 1985. Herbert Robbins Selected Papers (Berlin: Springer; ) pp 102–9 [Google Scholar]
- Sawant A, Smith RL, Venkat RB, Santanam L, Cho B, Poulsen P, Cattell H, Newell LJ, Parikh P and Keall PJ 2009. Toward submillimeter accuracy in the management of intrafraction motion: the integration of real-time internal position monitoring and multileaf collimator target tracking Int. J. Radiat. Oncol. Biol. Phys 74 575–82 [DOI] [PubMed] [Google Scholar]
- Shepard AJ, Matrosic CK, Radtke JL, Jupitz SA, Culberson WS and Bednarz BP 2018. Characterization of clinical linear accelerator triggering latency for motion management system development Med. Phys 45 4816–21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirato H, Shimizu S, Kunieda T, Kitamura K, van Herk M, Kagei K, Nishioka T, Hashimoto S, Fujita K and Aoyama H 2000. Physical aspects of a real-time tumor-tracking system for gated radiotherapy Int. J. Radiat. Oncol. Biol. Phys 48 1187–95 [DOI] [PubMed] [Google Scholar]
- Snoek J, Larochelle H and Adams RP 2012. Practical Bayesian optimization of machine learning algorithms Adv. Neural Inf. Process. Syst (New York: Curran; ) pp 2951–9 [Google Scholar]
- Sun W, Jiang M, Ren L, Dang J, You T and Yin F 2017. Respiratory signal prediction based on adaptive boosting and multi-layer perceptron neural network Phys. Med. Biol 62 6822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutskever I, Vinyals O and Le QV 2014. Sequence to sequence learning with neural networks Adv. Neural Inf. Process (New York: Curran; ) pp 3104–12 [Google Scholar]
- Teo TP, Ahmed SB, Kawalec P, Alayoubi N, Bruce N, Lyn E and Pistorius S 2018. Feasibility of predicting tumor motion using online data acquired during treatment and a generalized neural network optimized with offline patient tumor trajectories Med. Phys 45 830–45 [DOI] [PubMed] [Google Scholar]
- Tieleman T and Hinton G 2012. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude COURSERA: Neural Networks For Machine Learning vol 4 pp 26–31 [Google Scholar]
- Tsai T-I and Li D-C 2008. Approximate modeling for high order non-linear functions using small sample sets Expert Syst. Appl 34 564–9 [Google Scholar]
- Van Rossum G and Drake FL Jr 1995. Python tutorial Technical Report CS-R9526 (Amsterdam: Centrum voor Wiskunde en Informatica; ) [Google Scholar]
- Vedam S, Keall P, Docef A, Todor D, Kini V and Mohan R 2004. Predicting respiratory motion for four-dimensional radiotherapy Med. Phys 31 2274–83 [DOI] [PubMed] [Google Scholar]
- Wang F and Balakrishnan V 2003. Robust steady-state filtering for systems with deterministic and stochastic uncertainties IEEE Trans. Signal Process 51 2550–8 [Google Scholar]
- Wang R, Liang X, Zhu X and Xie Y 2018. A feasibility of respiration prediction based on deep Bi-LSTM for real-time tumor tracking IEEE Access 6 51262–8 [Google Scholar]
- Wu H, Sharp GC, Salzberg B, Kaeli D, Shirato H and Jiang SB 2004. A finite state model for respiratory motion analysis in image guided radiation therapy Phys. Med. Biol 49 5357. [DOI] [PubMed] [Google Scholar]
- Yan H, Yin F-F, Zhu G-P, Ajlouni M and Kim JH 2005. Adaptive prediction of internal target motion using external marker motion: a technical study Phys. Med. Biol 51 31. [DOI] [PubMed] [Google Scholar]
- Yi BY, Han-Oh S, Lerma F, Berman BL and Yu C 2008. Real-time tumor tracking with preprogrammed dynamic multileaf-collimator motion and adaptive dose-rate regulation Med. Phys 35 3955–62 [DOI] [PubMed] [Google Scholar]
- Yun J, Mackenzie M, Rathee S, Robinson D and Fallone B 2012. An artificial neural network (ANN)-based lung-tumor motion predictor for intrafractional MR tumor tracking Med. Phys 39 4423–33 [DOI] [PubMed] [Google Scholar]
- Zeiler MD. Adadelta: an adaptive learning rate method (arXiv:1212.5701) 2012.