Hyperspectral Tissue Image Segmentation using Semi-Supervised NMF and Hierarchical Clustering

Abstract

Hyperspectral imaging (HSI) of tissue samples in the mid-infrared (mid-IR) range provides spectro-chemical and tissue structure information at sub-cellular spatial resolution. Disease-states can be directly assessed by analyzing the mid-IR spectra of different cell-types (e.g. epithelial cells) and subcellular components (e.g. nuclei), provided we can accurately classify the pixels belonging to these components. The challenge is to extract information from hundreds of noisy mid-IR bands at each pixel, where each band is not very informative in itself, making annotations of unstained tissue HSI images particularly tricky. Because the tissue structure is not necessarily identical between the two sections, only a few regions in unstained HSI image can be annotated with high confidence, even when serial (or adjacent) H&E stained section is used as a visual guide. In order to completely use both labeled and unlabeled pixels in training images, we have developed an HSI pixel classification method that uses semi-supervised learning for both spectral dimension reduction and hierarchical pixel clustering. Compared to supervised classifiers, the proposed method was able to account for the vast differences in spectra of sub-cellular components of the same cell-type and achieve an F1-score of 71.18% on twofold cross-validation across 20 tissue images. To generate further interest in this promising modality we have released our source code and also showed that disease classification is straightforward after HSI image segmentation.

I. Introduction

Microspectroscopy based on vibrational hyperspectral imaging (HSI) in the mid-infrared (mid-IR) band is a powerful imaging modality to assess the chemical composition of materials, which can be applied to tissue samples for understanding pathology. With sub-cellular resolution and information from hundreds of mid-IR bands at each pixel, modern HSI systems can be used for the identification of different cell-types and their sub-cellular components without the use of contrast-enhancing or protein-targeting stains commonly used in pathology [1]–[3]. Although the spatial resolution of IR microspectroscopic systems is still coarser by about an order of magnitude than that of brightfield microscopy (which is the mainstay of pathology), but it has the potential advantage to facilitate the identification of disease-states of tissue samples for diagnosis and prognosis. For instance, HSI has shown to accurately predict renal treatment failure or transplant rejection by uncovering rich biochemical information from tissue images [4]. Thus, HSI can function complementary to traditional histopathology by providing access to chemical information that is not otherwise available.

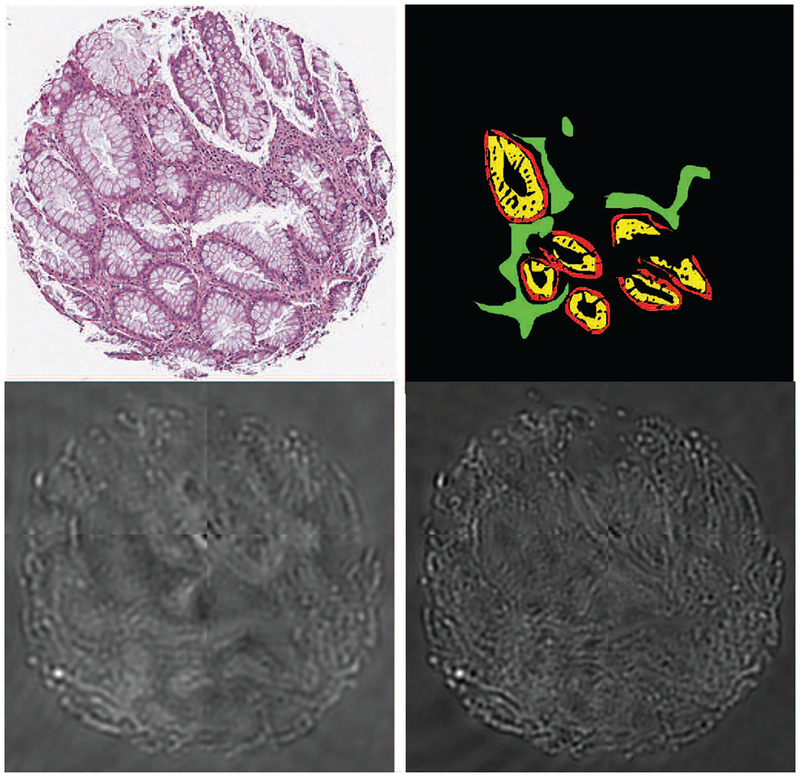
The main challenges in working with unstained tissue HSI images are the cost of the imaging equipment, lack of visibly discernible features in individual bands, and the lack of available software for visualization and analysis. The latter two aspects make annotating these images for supervised training of segmentation and pixel classification methods quite tedious. Typically, annotations have to be done by examining a serial (or adjacent) H&E-stained tissue section in which different cell-types can be readily identified. Even then annotations can only be done confidently for a small subset of pixels due to the change in tissue structure across the two serial sections. These challenges are illustrated in Figure 1, where an H&E stained tissue microarray (TMA) core of a human colon tissue sample is shown along with raw spectra of two IR wavenumbers and those regions of absorptive, goblet, and stromal cells that could be confidently annotated. The visual differences in the three types of cells are somewhat evident to the naked eye in the H&E section but not in the IR bands.

Fig. 1:

Top row: An H&E stained section of a colon tissue TMA core (left) with annotations on its serial HSI image (right) represented by red for epithelial absorptive cells, yellow for epithelial goblet cells, green for stroma, and black for un-annotated regions that include the previous three categories as well as non-tissue background. Bottom row: IR bands at 1,080 cm⁻¹ (left) and 1,545 cm⁻¹ (right) of its serial (adjacent) section. (Best viewed on a color monitor)

We present a method to classify pixels of a test HSI image according to their cell-type for image segmentation. Our algorithm is unique in the following aspects. Firstly, our method generalizes well and it does not require any annotations of cell types on the test images unlike even some recent studies that use at least a few labeled pixels from test images [5]. Secondly, because annotation of even training HSI images is tedious and uncertain, we designed our technique to require only a subset of pixels from the training images to be labeled by using semi-supervised learning for both spectral dimension reduction as well as pixel classification. Semi-supervised learning allows more complete use of all the given data that includes rich spectral data for all pixels and labels for a subset of pixels in the training images. By contrast, supervised techniques neglect the subspace structure of the unlabeled data, while the unsupervised techniques neglect the labels. Thirdly, for pixel classification, we propose using a semi-supervised hierarchical clustering (SSHC [6]) method that can model each class of cells as a collection of a few clusters such that intra-class variation due to differences in spectra of sub-cellular components (e.g. nuclei and cytoplasm) can easily be modeled. Finally, we also reduced the number of data-points sent to the computationally expensive SSHC by using a unique pre-clustering approach.

We demonstrate the advantages of our method through extensive experiments and visualization. Our method was trained and cross-validated on a dataset that contains IR images of colon TMA of 20 patients divided evenly among normal and hyperplasia disease classes. Each patient contributed one image, and the images were partially annotated for three types of constituent cells — absorptive, goblet, and stromal. We did not come across any prior work on semi-supervised segmentation of tissue HSI images to do a direct comparison. Therefore, we coded and compared with some alternatives ourselves. We show that image-level disease classification becomes very easy after accurate pixel cell-type classification. Although we are unable to release the data due to our agreement with the equipment manufacturer, we hope that our released code will be useful for benchmarking HSI image segmentation algorithms in the future.

In the rest of the paper, we introduce the reader to hyper-spectral imaging, its segmentation challenges, and previous techniques in Section II. The dataset and segmentation objectives are described in Section III. We give details of our proposed method in Section IV, followed by experimental results in Section V. We conclude in Section VI.

II. Background and Related Work

In this section, we review the current capabilities of IR microspectroscopy and its challenges. We also review HSI segmentation techniques from both biomedical and geospatial domains due to the similarities between the two and the abundance of research done on the latter.

A. Infrared microspectroscopy and its challenges

When light from a source such as an IR lamp or a laser is shone on a tissue sample, many of its constituent biomolecular functional groups that have resonant frequencies in the mid-IR range modify the signal sent to the photosensor to yield rich chemical information. Instead of just three channels captured by brightfield scanners, HSI captures hundreds of channels, although its SNR and spatial resolution are lower than those of the former.

Although vibrational spectroscopy, especially Fourier transform infrared spectroscopy (FTIR), became a well-recognized imaging modality by the 1950’s and 1960’s, its spatial resolution was too coarse to study tissue structure [7], [8]. FTIR optics, controls, and sensors have advanced significantly over the last two decades. Quantum cascade lasers (QCL) have also emerged as a light source. These advances have enabled the acquisition of microspectroscopic images with spatial resolution of a few microns (sub-nuclear) and a spectral resolution that divided the IR band into hundreds of sub-bands. It is now possible to study human tissues using this modality in multiple areas of medical research including cancers, osteoporosis and osteoarthritis, myopathies, dermopathies, liver fibrosis and degenerative diseases, without employing any contrast-enhancing stains [9]–[17]. Thus, compared to brightfield microscopy, HSI can give a rich chemical map of a tissue without requiring a large laboratory with specialized chemicals.

There are several reasons why FTIR and QCL based microspectroscopic equipment is not widely used in spite of its current physical capabilities. Firstly, it is still relatively expensive. Additionally, there is a dearth of computational tools required to extract meaningful information from tissue HSI images for visualization, segmentation, and classification. Traditional image processing pipelines cannot be applied directly to these images because IR bands can appear as noisy greyscale images due to the inherent lack of energy used to illuminate the tissue without destroying it [10]. Such greyscale images of each band often lack contrast and discernible visual features to delineate tissue compartments such as nuclei, cytoplasm, epithelium, and stroma. Although modern QCL systems have a higher signal-to-noise ratio and faster scan times [15]–[17], they also often introduce coherence artifacts wherein the captured microspectrcopic images have fringing patterns (see Figure 1).

Availability of public datasets, annotations, and codes can play an important role in the development of algorithms and software for microspectroscopy, as it has been done for other domains and medical imaging modalities. Annotating HSI images is not straightforward as already explained in Section I. Additionally, to our knowledge, there are no public microspectroscopic datasets of acceptable quality available due to agreements between researchers and private equipment manufacturers in a nascent competitive industry. The next best thing would be to publicly release codes that can be compared on private datasets till the time the datasets themselves can be made public.

B. Segmentation techniques for hyperspectral images

Most of the previous approaches for segmenting micro-spectroscopic images relied on domain knowledge such as the application of chemometric methods based on the knowledge of tissue biochemistry and exploited the chemical differences in tissue components indicated by spectral peaks and band shapes [8], [10], [18], [19]. For example, the ratio of absorbance of the phosphodiester with a peak at 1,080 cm⁻¹ to that of amide II at 1,545 cm⁻¹ can be used for segmenting various tissue components [10]. Thus, the performance of these approaches depended heavily on the ability of the user to define useful spectral features. Without advanced machine learning techniques, these methods fail to extract data-dependent features, and thus generalize poorly across multiple tissue samples of normal and diseased patients.

Subsequently, another set of approaches emerged that used unsupervised learning for both dimension reduction (e.g. principal component analysis) and clustering (e.g. k-means or hierarchical clustering) of spectral values at each pixel to improve the segmentation performance [14], [20]. However, such techniques often fail to generalize due to the lack of biological concordance and intra-class variance across samples. As a result, there is an increasing interest and need for developing supervised learning algorithms to improve the segmentation performance and subsequently establish the clinical utility of HSI images [14], [20], [21].

Unlike tissue HSI, satellite (remote sensing) HSI images have seen a lot more research primarily due to the wider availability of datasets such as AVIRIS [22], ROSIS [23], and HYDICE [24], [25]. Most early stage satellite HSI segmentation techniques used band selection algorithms (similar to chemometrics for biological samples) to first reduce the spectral dimensions of the data before using supervised machine learning approaches such as support vector machines, random forests, Bayesian classifiers, or multinomial logistic regression for segmentation [23], [26]–[30]. However, in addition to having high dimensionality, HSI pixels can also be mixtures of heterogeneous spectra when they cover the spatial boundaries of the underlying classes (for example, forest, road and water). Sub-space analysis techniques such as singular value decomposition, noise adjusted principal component analysis, non-negative matrix factorization, manifold learning and Bayesian inference based methods have significantly improved the segmentation performance by simultaneously reducing dimensionality and unmixing such mixed spectra [31]–[34].

The latest HSI segmentation techniques incorporate spatial context into segmentation algorithms by using graph regularization or statistical methods such as Markov or conditional random fields [35]–[37]. Recently, a few deep learning-based techniques using convolutional neural networks or stacked denoising autencoders have also been proposed [38]–[40]. Deep learning, however, requires lots of labeled data for effective generalization. Since the number of HSI samples available for training is generally limited, semi-supervised variants of the aforementioned segmentation techniques are becoming increasingly popular [29], [41]. More importantly, publicly available codes¹ of satellite HSI segmentation algorithms continuously drive the technical innovations in this field.

Direct adaptation of HSI segmentation techniques from satellite images to microspectroscopic ones is not advisable. This is because microspectrscopic images have subtle intra- and inter-class spectral variations due to minute biochemical changes across tissue components unlike high spectral differences among land cover classes seen in remote sensing images.

III. Dataset and Segmentation Task

In this section, we describe the dataset, how it was prepared, its disease-class labels, its cell-type annotations, and its analysis objectives for which algorithms can be developed.

A. Dataset preparation

Four formalin-fixed paraffin-embedded unstained colon biopsy TMAs were acquired from the University of Illinois at Chicago tissue bank. These samples were sectioned at 4μm thickness onto BaF2 slides (International Crystal Laboratories, Garfield, NJ) for infrared HSI imaging. These samples were dewaxed by rinsing in hexane as per established protocols [14]. Serial (adjacent) sections were cut onto standard glass slides for hematoxylin and eosin (H&E) staining.

The unstained IR samples were then imaged using the Daylight Solutions Spero QCL IR imaging system (San Diego, CA) in transmission mode, with the 12.5× objective (pixel size 1.4μm × 1.4μm). The system’s spectral range of 900cm⁻¹ to 1800cm⁻¹ with 4cm⁻¹ spectral step size was used to yield 226 spectral bands. The spatial dimensions of each TMA core varied between 480 × 450 to 779 × 652 pixels.

The H&E-stained serial sections were imaged on an Aperio ScanScope CS (Leica Biosystems, Nussloch, Germany) system. The cores were independently examined by three pathology residents and classified by consensus into two disease-states – normal or hyperplasia (pre-cancer). Twenty TMA core images divided evenly between the two disease-states were selected, such that each image came from a different patient. Having two different disease classes and taking only one image per patient allowed us to test the generalization of our segmentation technique to unseen cases with unknown disease-state. For instance, goblet cells become very thin in hyperplasia, and we were able to verify that in the test images from which we did not use any pixel labels for training.

Based on these diagnoses and by visual comparison to the serial (adjacent) H&E sections, regions of interest were drawn on the unstained IR images corresponding to three cell-types – epithelial absorptive cells, epithelial goblet cells, and stroma – as shown in Figure 1. The high confidence annotations were performed by consensus among three pathology residents. Only those regions that could be confidently marked were annotated covering on an average only 12, 500 pixels per image. Any region for which the cell-type could not be confidently identified was left unannotated. If the patient was a part of the training set then its unannotated pixels were used as unlabeled data for semi-supervised learning.

B. Dataset analysis objectives

There are two objectives that can be defined on this dataset. The first one is semi-supervised image segmentation, and the second one is identification of the patient disease-state. We cast the first objective as a pixel classification problem, which is our main result. Furthermore, we demonstrate that disease classification at image level becomes much easier after the pixel-level image segmentation.

We divided the images (patients) into two folds to cross-validate both pixel-level tissue structure segmentation and image-level disease classification results. That is, no pixels (not even a subset of labeled or unlabeled pixels) from the test images (patients) were included in the training set for either objective. This allowed us to test whether our methods would generalize across patients. Eight images in each fold were used for training and the other two were used for validation (hyper-parameter tuning). Rest of the ten images in the other fold formed the test set. In each fold, there were ten images for testing disease classification and more than 100,000 labeled pixels for testing pixel classification (segmentation).

To measure and compare pixel-level classification performance we used F1-score on labeled pixels from test images. Since F1-score is a metric for binary classification, we used a one-vs.-all F1-score for each of the three classes and took their average weighted by the number of labeled pixels in each class for a given test image. To measure the performance of image-level disease classification, we computed the average (across 10 test images) accuracy through majority voting among the disease classification obtained from individual pixels in an image

IV. Proposed Technique

Our technique was designed to generalize from partially annotated training images to unannotated test images across two disease-states (normal and hyperplasia) in colon tissue. Insights about the tissue structure and the image formation process informed the choices of our pixel dimension reduction and classification methods. The challenges faced included unexpected negative pixel values (arising due to pre-processing methods such as baseline corrections applied to raw spectra), a large number of background pixels with no tissue or annotations, imbalance in the number of pixels representing each cell-type, a large number of spectral bands, a large number of unlabeled pixels, and a large intra-class variation due to different sub-cellular components being part of the same class. In this section we describe the steps of our segmentation method that were designed to overcome these challenges.

A. Pre-processing

Although IR absorption values cannot be negative, the data had a significant proportion of negative values due to a log transformation of the type, f₂(i, x, y, s) = a_i log f₁(i, x, y, s) + b_i, applied to the raw absorbance f₁, at location (x, y) for spectral band s in image i to get the pixel value f₂ using image-specific constants a_i and b_i. To make all pixel values non-negative we subtracted a constant corresponding to the minimum value across all pixel locations and bands for a given image.

The background regions without any tissue have nearly zero spectral energy, which can make spectral unmixing ill-conditioned. Such points were in abundance in our data. To identify and exclude the background pixels we exploited the knowledge that these were not annotated and were more likely to have low spectral energy than the tissue foreground. To find a common threshold of spectral energy to identify background pixels, we examined two cumulative distribution functions (CDF) – one of all pixels and another of only the labeled pixels from the training images.

B. Dimension reduction using semi-supervised NMF

To model a generative process in which different groups of biomolecules additively contribute to the absorption spectra, we found non-negative matrix factorization (NMF) to be a natural choice for dimension reduction. We thought that a semi-supervised variant of NMF (SSNMF) [42] would be a better choice compared to vanilla (unsupervised) NMF, because SSNMF tries to select basis that are discriminative among different classes of labeled data samples, such as the partially annotated pixels. To do so, in addition to the Frobenius norm of the data reconstruction error, SSNMF also minimizes data label estimation error. The latter part of the loss function is based on the assumption that the labels can be computed using the same linear combination (mixing coefficients) but with a different basis matrix. This cost function is shown below [42]:

$$\left(W\odot \Vert X-AS{\Vert }^2\right)+\mathrm{\lambda }\left(L\odot \Vert Y-BS{\Vert }^2\right)$$ (1)

where ʘ is element-wise product, $X\in {ℝ}_{+}^{m\times n}$ is the data matrix with n data points of m-dimensions each, $Y\in {ℝ}_{+}^{c\times n}$ is a label matrix for c classes that includes dummy labels for unlabeled points, $S\in {ℝ}_{+}^{r\times n}$ is the mixing coefficient (or feature) matrix that is common to both data and label reconstruction, $A\in {ℝ}_{+}^{m\times r}$ is the basis matrix for reconstructing the data, $B\in {ℝ}_{+}^{c\times r}$ is the basis matrix for linear reconstruction of labels, r is the factorization rank, $W\in {ℝ}_{+}^{m\times n}$ is a weight matrix whose elements can be varied to put different emphases on fidelity of reconstruction of different data points, $L\in {ℝ}_{+}^{c\times n}$ is the weight matrix whose elements can be varied to put different emphases on label reconstruction of different data points (and set to zero corresponding to unlabeled data with dummy labels in Y), and λ is a trade-off parameter which emphasizes label reconstruction accuracy over data reconstruction fidelity for larger values.

The original SSNMF technique was intended to be a standalone technique for both dimension reduction and classification [42]. The label matrix Y comprised one-hot-bit vectors to code a label for each data point (including dummy labels for unlabeled points whose corresponding weights in L were set to zero). So long as the element corresponding to the correct label was maximum in a column representing a data point in BS, the classification of that point was considered to be correct. This required that for columns corresponding to labeled points in BS, the other elements be driven close to zero using a relatively higher weight, while the element corresponding to the correct class be greater than 0 under the constraint that all elements of BS are non-negative. Therefore, L_ij was set to zero for all elements corresponding to columns of unlabeled data. For the columns corresponding to the labeled points, it was set to 1 for those elements where the datum was not from i^th-th class (Y_ij = 0, background), and it was set to a small positive value (e.g. 0.001) when Y_ij = 1 (i.e. datum was from i^th class).

In our modified implementation, the classification error in SSNMF for each class was weighted by the inverse of the number of pixels from that class to account for class imbalance. From each of the training images, the set of all unlabeled samples was randomly subsampled to 100, 000 pixels and all labeled pixels of the three annotated classes from the eight training images were included in the training set.

We selected the hyper-parameters of SSNMF – rank r, classification weight λ, and labeled point weight L_ij (for Y_ij = 1) – based on the classification accuracy of labeled pixels in the two validation images of the training fold. Features for pixels of the test images were computed afterwards by projecting the shifted pixel values to the SSNMF basis found using the training set.

C. Semi-supervised hierarchical clustering of pixels

We observed that there is a wide variation in pixel spectra within each cell-type due to differences in sub-cellular components such as nuclei and cytoplasm. In fact, similar subcellular components of different cell-types (e.g. stromal and epithelial nuclei) can be closer to each other than two different sub-cellular components of the same cell-type (e.g. epithelial nuclei and stroma), even in features spaces learned in a semi-supervised manner. Without using label information, features of similar sub-cellular components across cell-types can turn out to be the same. We reasoned that pixels in each cell-type class must be modeled as collection of clusters that may be far away from each other as these may correspond to different sub-cellular components. To use the partially labeled data to guide this over-clustering process we used semi-supervised hierarchical clustering (SSHC) method [6] whose performance was compared with popular supervised classifiers.

1) Pre-clustering to reduce the number of data points: The time complexity of SSHC scales quadratically with the number of data points (pixels) [6]. So, we reduced the data fed to it by pre-clustering the pixels represented in SSNMF space into a large number of clusters and used SSHC only on the resultant centroids. We selected the minimum number of clusters K for which the training data gave the highest weighted average cluster purity. We define purity p_k of cluster number k as the proportion of the most representative class of labeled samples among all labeled samples in the cluster. We computed average cluster purity by weighing the purity of each cluster by the number of labeled pixels in that cluster as follows:

$$p_k={\text{max}}_{c\in [C]}\frac{\left|\left\{y_i=c,x_i\in k\right\}\right|}{{\sum }_{\omega \in [C]}\left|\left\{y_i=\omega ,x_i\in k\right\}\right|}$$ (2)

$$A_K=\sum _{k\in [K]}\left|\left\{x_i\in k\right\}\right|p_k$$ (3)

where k is the cluster number ranging from 1 to K, p_k is purity of cluster k, A_K is the weighted average cluster purity of all K clusters, c and ω are class indices ranging from 1 to C, i is pixel index, y_i is its label, x_i is its spectral (or feature) value, and |.| is set cardinality operator. Cluster purity p_k can range from 1/C (most impure) to 1 (most pure), or can be indeterminate (with a weight of 0). The maximum value for weighted average cluster purity is also 1, for which a trivial case is that of maximal over-clustering when the number of clusters is equal to the number of samples. We found the minimal K for which A_K = 1. Henceforth, we refer to these K-clusters as pre-clusters.

2) Semi-supervised hierarchical clustering: We next performed hierarchical clustering of the pre-cluster centroids using SSHC [6]. SSHC algorithm allows specifying constraints on triplets of data samples [6]. These triplets can code class information of labeled pixels from training images. Two samples in the triplet are chosen from the same class, while the third one is from another class. The training algorithm tries to assign a smaller ultra-metric distance to the pair from the same class compared to a pair from different classes in each triplet. The ultra-metric distance matrix between all pairs of points has a one-to-one correspondence with the dendogram of hierarchical clustering [6].

Specifically, if two pre-cluster x_i and x_j belong to class c while another pre-cluster x_k that belongs to a different class ω such that labels y_i = y_j = c ≠ ω = y_k, where c, ω ∈ {1; 2; 3} and the class indices represent absorptive, goblet, and stroma cell-types, then we represent a triple-wise relative constraint C_ijk as follows [6]:

$$C_{ijk}=\left\{\left(x_i,x_j,x_k\right)|d\left(x_i,x_j\right)<d\left(x_i,x_k\right)\right\}$$ (4)

where, d(.; .) represents an appropriate pairwise dissimilarity metric such Euclidean distance used in the proposed algorithm. We created a set of constraints for SSHC algorithm by considering all possible triplets of labeled pre-clusters while leaving the unlabeled pre-clusters unconstrained.² The pixels of the test image were simply assigned to the pre-clusters by comparing their Euclidean distances to the pre-cluster centroids computed using the training data.

3) Finding the optimal number of clusters: We reasoned that as per Occam’s razor principle if the hierarchical clustering dendogram was cut higher up where it had fewer clusters, then it would lead to better generalization. On the other hand, reducing the number of clusters too much would lead to poor accuracy due to the intra-class variance as described above. To balance these two goals (generalization and accuracy), we decided on the number of clusters based on weighted average cluster purity once again as defined in Equations 2 and 3. This over-clustering assumes that it is easier to recognize clusters corresponding to a particular sub-cellular component (e.g.nucleus) of a cell-type rather than the cell-type itself. The task of cell-type classification is then to club together the disparate clusters belonging to different sub-cellular components of the same cell-type into the same class. We propose to do this by majority voting among the labeled pixels within the disparate clusters during training.

V. Experiments and Results

We conducted experiments to test the utility of the proposed steps in our pipeline. For example, we compared NMF-based dimension reduction, which is widely used in chemometrics, with the SSNMF-based dimension reduction. We assessed the importance of k-means pre-clustering in reducing the overall computational complexity of the proposed approach. Additionally, we compared our SSHC-based classification method with popular alternatives such as support vector machines and random forests to ascertain the efficacy of the proposed algorithm.

A. Background pixel identification

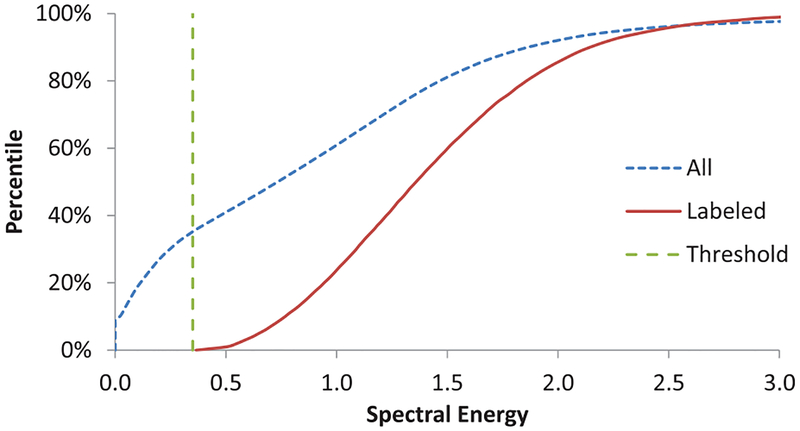
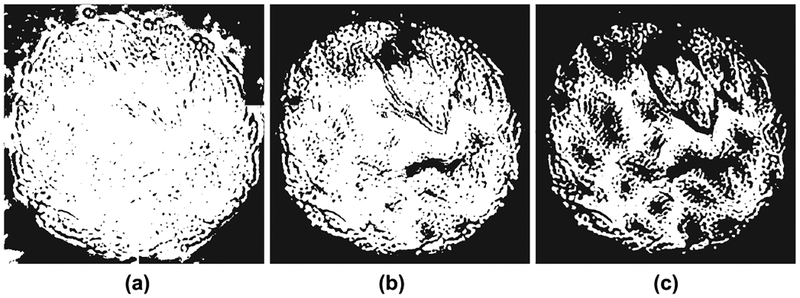
To select the spectral energy threshold for background pixels as described in Section IV-A, we examined the cumulative distribution function (CDF) of the spectral energy of all pixels along with the CDF of annotated pixels. As shown in Figure 2, the CDF of all pixels seems to have a large constant slope till about 0.35 value and there were no annotated pixels with spectral energy below this value. Values below this threshold led to inclusion of background pixels into the foreground and vice versa, as shown in Figure 3.

Fig. 2:

Cumulative distribution of spectral energy of all pixels (blue dotted) and labeled pixels (red solid) show that a threshold of 0.35 (green dashed) will exclude labeled (subset of foreground) pixels.

Fig. 3:

Background subtraction for various spectral energy thresholds: (a) 0.1, (b) 0.35, and (c) 0.7. A small threshold counts some background pixels as tissue (white), and a large threshold marks some tissue pixels as background (black). Compare to Figure 1.

B. Spectral dimensionality reduction using SSNMF

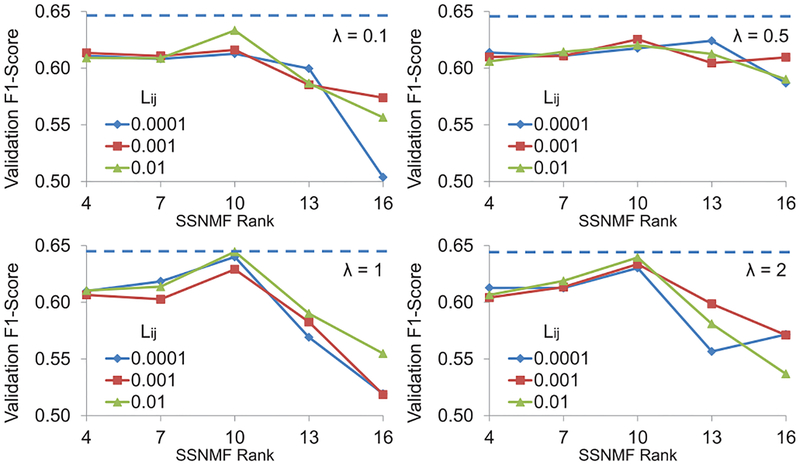
We validated various values of the three hyper-parameters for SSNMF – r (rank of NMF), λ (relative emphasis on label reconstruction), and L_ij (weight for label reconstruction for the correct class). Because our goal was to classify unseen pixels, we propose that a principled criterion to optimize the hyper-parameters is to maximize the classification accuracy on the labeled pixels in the validation set. If we had optimized data reconstruction error itself, then there was no need for λ > 0 and the rank r could have been increased to simply improve data reconstruction accuracy in Equation 1. Similarly, if we had optimized classification accuracy on labeled pixels from the training images alone, then λ could have been increased in an unrestricted way. Instead, validation accuracy was calculated as one-vs.-all F1 score for each of the three classes of pixels weighted by class membership. Classification results from SSNMF were obtained by taking arg max_i(BS)_ij of each column j of matrix BS obtained by optimizing the expression in Equation 1.

Figure 5 shows average F1 score for labeled pixels from the validation set averaged across the two folds for various combinations of hyper-parameters. It is clear that there is an optimal value for each of the hyper-parameters below or above which the validation accuracy suffered. These results confirm our understanding of the hyper-parameters explained above. We selected r = 10, λ = 1, and L_ij = 0.01 when the j^th data element was from the i^th class as this combination gave the maximum classification accuracy of 64.46%.

Fig. 5:

Label reconstruction accuracy for the validation set using combinations of three SSNMF hyper-parameters. Dotted line indicates the maximum accuracy (64:46%) obtained for r = 10; L_ij = 0.01; and λ = 1.

We also noted that the use of raw spectral pixels without SSNMF-based spectral dimensionality reduction quadruples the training and testing time of the subsequent computation in the proposed algorithm.

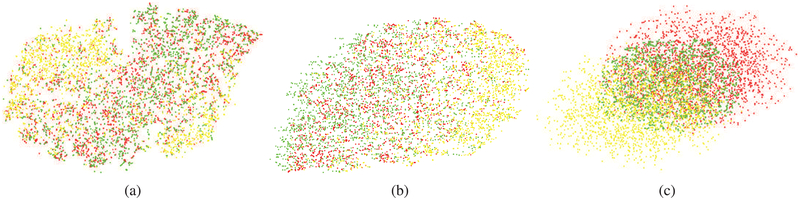
We used visualization techniques to confirm that SSNMF leads to better separation of the target classes. As shown in Figure 4 using t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm [43], the raw pixels of the three types of cells formed overlapping classes (see supplementary Figure S1 for raw pixel spectra). Unsupervised NMF was able to separate three classes to some extent. Using SSNMF, the three classes were further separated, although significant overlap remained. We attribute the remaining overlap to the confusion between similar sub-cellular components (e.g. nuclei) across different cell types, which we counter using SSHC [6].

Fig. 4:

t-SNE plots [43] of randomly selected spectral pixels from absorptive (red), goblet (yellow), and stromal (green) classes show high intra-class variance (large clusters for each class) and low inter-class variance (high inter-cluster overlap) in (a) the raw spectral pixel space and (b) the NMF feature space while (c) SSNMF features show some separation of classes. (Best viewed on a color monitor)

C. Data reduction using pre-clustering

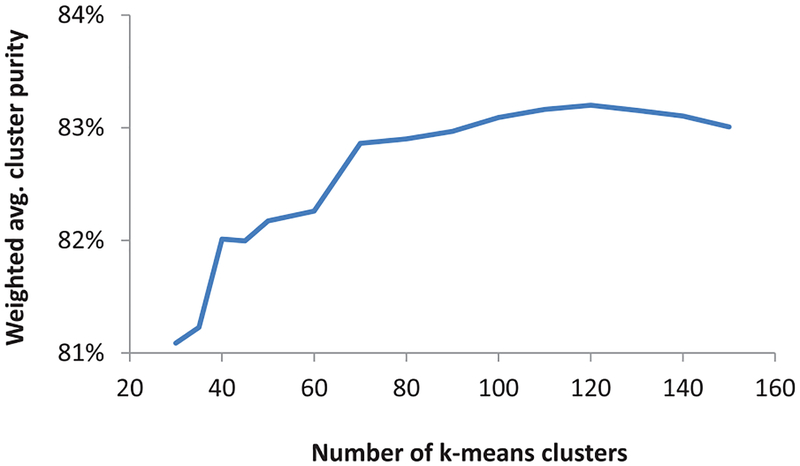
To select the right number of pre-clusters as a proxy for the data points (to speed up SSHC), we analyzed the average cluster purity of clusters found using k-means for different number of clusters. As shown in Figure 6, 120 was the smallest number of clusters with maximum purity. These cluster centroids were used for SSHC in the next step to represent about 200,000 pixels present in the training set. Because SSHC’s time complexity scales as O(n²) with respect to the number of data points n, the reduced number of data points (120 k-means centroids in SSNMF feature space instead of 200,000 data points) allowed the proposed algorithm to train efficiently in just 4.5 hrs. Similarly, the testing time was reduced from 1.4 hours to six minutes using pre-clusters.

Fig. 6:

Cluster purity vs. number of pre-clusters

D. Semi-supervised hierarchical clustering of pixels

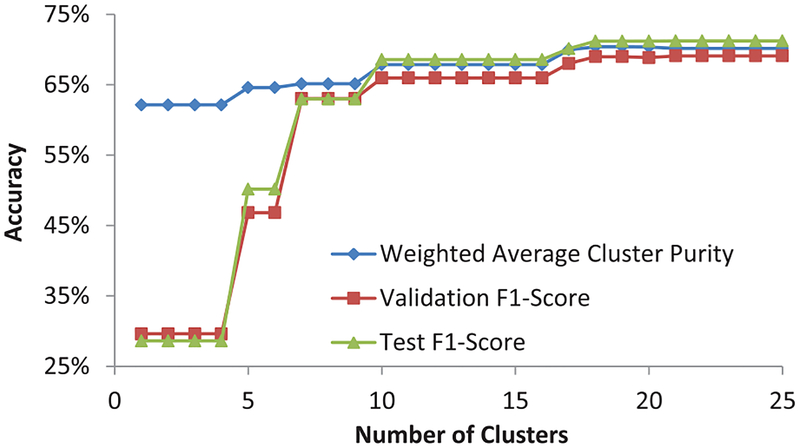
The number of unique triplet constraints that could be formed using n training data points can be as high as $\left(\begin{array}{c}n\\ 3\end{array}\right)$. Even with 120 pre-cluster centers obtained after k-means, the number of triplets can be unmanageable. Therefore, we randomly selected only 10,000 triplet constraints to train the SSHC model. Increasing the number of constraints beyond 10,000 only increased the training time of the algorithm without any significant gains in the classification performance, while reducing the number of constraints decreased the weighted average cluster purity. The dendogram of SSHC was then cut at a level where the clusters were optimally pure in labeled samples of validation set. We expected that although we will end up with more clusters than the number of classes (three) due to intra-class variance arising out of differences in spectra of sub-cellular components, each class will span only a few clusters. Figure 7 shows that our intuition was confirmed. Validation F1-score was near optimal with just 18 clusters.

Fig. 7:

Accuracy vs. number of clusters using SSHC [6]

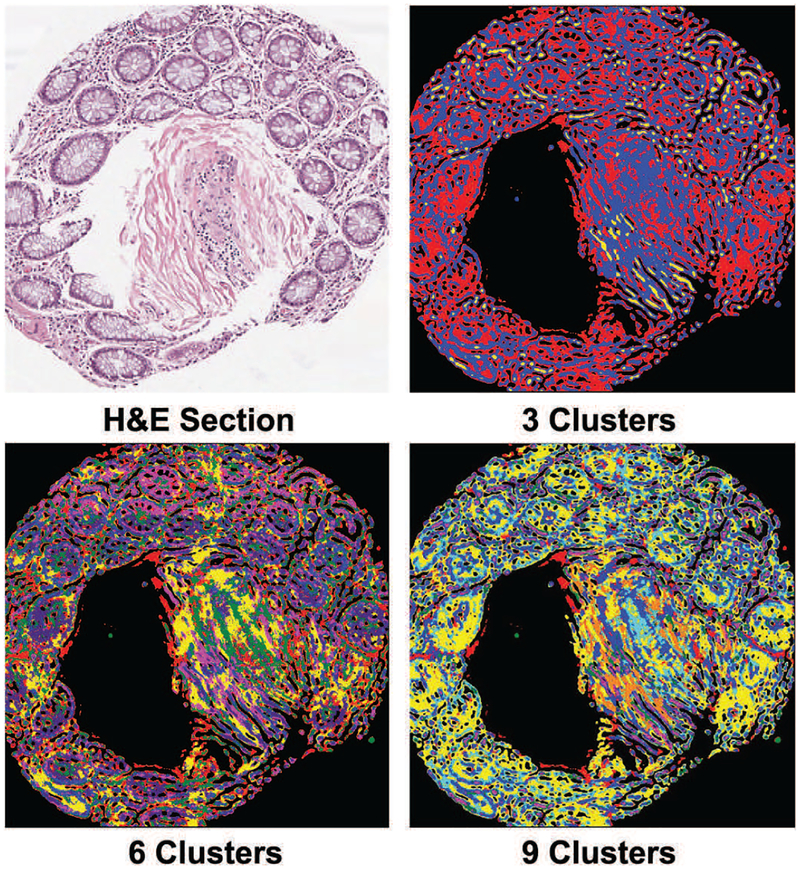
To verify that finding more clusters than the number of cell-types leads to separation of nuclei and cytoplasm of the same cell-type into different clusters, we visualized the cluster membership maps of the pixels of a few images. As shown in Figure 8, this indeed was the case. What is also satisfactory is the fact that the number of clusters can be reduced to a small multiple of number of classes without compromising classification accuracy by much as shown in Figure 7. For a small number of clusters (e.g. 9) individual nuclei and cytoplasm of a particular cell-type do not seem to be fragmented in Figure 8. To further illustrate that overclustering leads to separation of sub-cellular components into different clusters we plotted SSNMF features of pixels using SSHC assigned class labels by t-SNE algorithm [43] in Figure 9. This confirms the understanding that there is relative uniformity in spectral signatures within the main sub-cellular components,i.e. nuclei or cytoplasm. But, if we used any smaller number of clusters (e.g. 3 or 6), then the boundary between cytoplasm of different cell-types disappears, which is even more undesirable than mild over-fragmentation.

Fig. 8:

Using a serial H&E stained section as a visual reference it becomes apparent that sub-cellular components such as cytoplasm of neighboring cells of different types (glandular and stromal) merge when the number of clusters is low (3 or 6). Glandular shapes start to stand out with an appropriately large number of clusters (9). (Best viewed on a color monitor)

Fig. 9:

t-SNE plots [43] of pixels in SSNMF feature space illustrates that using only a few clusters (e.g. 3) in SSHC leads to high inter-cluster overlap. Over-clustering improves class separation by assigning different regions of a class into different clusters. (Best viewed on a color monitor)

E. Comparison between different pixel classification methods

SSNMF itself can be used for pixel classification by examining arg max_i(BS)_ij after optimizing the expression in Equation 1. To improve the classification further, various classifiers such as support vector machines (SVM), Gaussian naive Bayes (GNB), random forests (RF), can be applied to the SSNMF and NMF features, including the SSHC-based classification described in this work. Classification metric (F1-score on labeled pixels of the ten test images) for the best hyper-parameter settings of these classifiers are shown in Table I, which gives the following insights. Firstly, SSNMF by itself does not give the best pixel classification results; other classifiers in combination with dimension reduction by SSNMF give better results by introducing nonlinear functions. Secondly, using SSNMF as opposed to NMF for dimension reduction gives better results for each tested classifier because the former uses the partial labels for learning appropriate basis. Finally, the use of SSHC gives better results than using popular classifiers based on both NMF and SSNMF. This is because other classifiers were unable to make use of the unlabeled data leading to poor generalization (across test cases spanning two disease-states) performance for micro-spectroscopic image segmentation.

TABLE I:

Pixel classification accuracy (averaged over 2-folds) of the proposed and alternative techniques on test images.

Features+classifier	Optimal settings	F1-score (%)
SSNMF+ArgMax	SSNMF: r = 10, λ = 1, Lij = 0.01	55.92
NMF+SVM	NMF: r = 10; SVM: RBF kernel, σ=0.2, C=10	62.81
NMF+GNB	NMF: r = 10	64.32
NMF+RF	NMF: r = 10; Number of trees = 500, Number of variables per split = 5	66.75
NMF+SSHC	NMF: r = 10; SSHC: Number of clusters = 24	69.02
SSNMF+SVM	SSNMF: r = 10, λ = 1, Lij = 0.01; SVM: RBF kernel, σ=0.2, C=10	64.93
SSNMF+GNB	SSNMF: r = 10, λ = 1, Lij = 0.01	65.71
SSNMF+RF	SSNMF: r = 10, λ = 1, Lij = 0.01; Number of trees=500, Number of variables per split=5	67.84
SSNMF+SSHC	SSNMF: r = 10, λ = 1, Lij = 0.01; SSHC: Number of clusters = 21	71.18

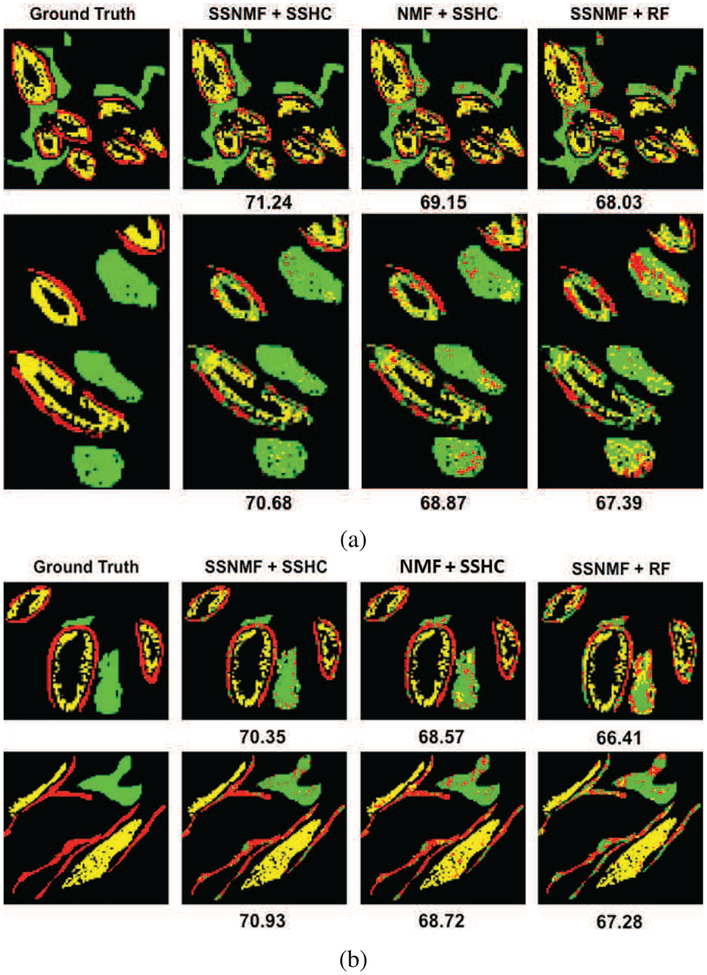
We also compared the segmentation results qualitatively by examining the resultant class maps for test images. Please note that the ground truth and estimated labels for only annotated pixels are shown for quantitative and qualitative assessment in Table I and Figure 10, respectively. It is clear that the proposed SSNMF+SSHC based HSI segmentation gives smooth and natural looking gland shapes and layers of epithelial goblet cells even without using any spatial priors. In comparison, SSNMF+RF, whose quantitative accuracy is slightly lower, shows some obvious pixel misclassification within various tissue regions. Other techniques performed even worse.

Fig. 10:

Examples of partially annotated ground truth (left), and corresponding pixel classifications by the best (SSNMF+SSHC, middle) and the second best (SSHC+RF, right) performing methods on two normal and two hyperplasia test images. Numbers under the images indicate F1-score (%) for the respective image. Red, yellow and green maps represent absorptive cells, goblet cells and stroma respectively. Black pixels were not annotated and their classification results are also not shown to facilitate comparison with the ground truth. (Best viewed on a color monitor). (a) Normal samples 1 (top) and 2 (bottom). (b) Hyperplaslia samples 1 (top) and 2 (bottom).

F. Disease classification

Using labeled pixels from training images, we trained and validated three single hidden layer neural networks - one for each type of cell - that took SSNMF features as input and computed the probability of the pixel being from normal or hyperplasia. For each test image, we routed each pixel to one of the neural networks based on its cell-type label computed by the proposed segmentation technique (SSNMF+SSHC)³. The pixel-level disease class accuracy thus calculated was 97.5% , 98.2% and 98.4% for pixels identified as absorptive, goblet and stroma, respectively when averaged over test images across 2-folds. Combining the individual pixel-level disease-state estimates through majority voting for each test image resulted in 100% image-level disease-state estimation across the two folds. We also evaluated the utility of raw pixel spectra in disease-state estimation by training a single neural network that took raw pixel spectra as input and computed the probability of the pixel being from normal or hyperplasia. The raw pixel-level disease class accuracy was 74.8%, which yielded 80% image-level disease-state identification after majority voting. This confirms that the spectral information available exclusively in micro-spectroscopic image is highly disease-specific and can be used directly for disease-state estimation, provided the pixels are first classified by cell-type.

G. Training and testing time

All our algorithms were implemented in python and executed on a computer with a six core processor running at 2.3GHz with a 32GB RAM. Our algorithm took 4.5 hours to train and produced segmentation results on a hyperspectral image in 6 minutes on average. The most computationally expensive step during training was pre-clustering with k-means that was used to reduce the spatial dimensions for further processing with SSHC. However, this step was crucial as it reduced the number of data points sent to SSHC (Section V-C).

VI. Conclusion and Discussion

Our main conclusion is that semi-supervised classification techniques such as SSHC [6] outperform supervised ones such as random forests and support vector machines when there is a large intra-class variation and the proportion of labeled samples is much smaller than that of unlabeled samples. We confirmed that when at least a few labeled samples are available, semi-supervised dimension reduction techniques such as SSNMF [42] better aid classification as compared to the unsupervised ones. And, although SSNMF itself can yield classification results with a built-in linear classifier, the results of non-linear classifiers were better. Our SSNMF+SSHC based method was able to achieve an F1-score of 71.18% on two-fold cross-validation across 20 tissue images.

We also demonstrated that the spectral information available exclusively in mid-IR micro-spectroscopic images makes disease-state classification at the image or patient level fairly straightforward once the tissue components (cell-types) are accurately segmented at the pixel level.

Our work can be extended and improved in several ways. We think that HSI segmentation accuracy can be further improved by incorporating a spatial prior, for example by using a Markov or conditional random field [35]–[37]. It will be interesting to see how deep learning based techniques can be adapted and perform on HSI data with hundreds of channels and the paucity of labeled pixels such as the one used in this paper. To develop deep learning based algorithms we will annotate more HSI images of colon tumors by including disease-states such as dysplasia and carcinoma in addition to normal (benign) and hyperplasia samples in a separate study. Additionally, HSI datasets have the potential to solve important problems of histological HSI analysis, such as disease classification, genomic class identification, and treatment outcome prediction. For reaching its potential, we hope that additional HSI analysis studies will be done accompanied with release of corresponding software and datasets.