Mapping a Systematic Ribozyme Fitness Landscape Reveals a Frustrated Evolutionary Network for Self-Aminoacylating RNA

Abstract

Molecular evolution can be conceptualized as a walk over a “fitness landscape”, or the function of fitness (e.g., catalytic activity) over the space of all possible sequences. Understanding evolution requires knowing the structure of the fitness landscape and identifying the viable evolutionary pathways through the landscape. However, the fitness landscape for any catalytic biomolecule is largely unknown. The evolution of catalytic RNA is of special interest because RNA is believed to have been foundational to early life. In particular, an essential activity leading to the genetic code would be the reaction of ribozymes with activated amino acids, such as 5(4H)-oxazolones, to form aminoacyl-RNA. Here we combine in vitro selection with a massively parallel kinetic assay to map a fitness landscape for self-aminoacylating RNA, with nearly complete coverage of sequence space in a central 21-nucleotide region. The method (SCAPE: sequencing to measure catalytic activity paired with in vitro evolution) shows that the landscape contains three major ribozyme families (landscape peaks). An analysis of evolutionary pathways shows that, while local optimization within a ribozyme family would be possible, optimization of activity over the entire landscape would be frustrated by large valleys of low activity. The sequence motifs associated with each peak represent different solutions to the problem of catalysis, so the inability to traverse the landscape globally corresponds to an inability to restructure the ribozyme without losing activity. The frustrated nature of the evolutionary network suggests that chance emergence of a ribozyme motif would be more important than optimization by natural selection.

Introduction

Molecular evolution is largely governed by the function of fitness in the space of all possible sequences, known as the “fitness landscape”.^1,2 Evolution corresponds to a biased random walk on this landscape, in which mutation enables exploration of neighboring points in sequence space, and natural (or artificial) selection favors hill-climbing toward higher fitness. Therefore, knowledge of the fitness landscape is necessary for a systematic, quantitative understanding of molecular evolution.³⁻⁵ For example, a deep question is whether the landscape allows selection to optimize biochemical activity. If the topography of the fitness landscape is relatively smooth, optimization by selection can occur readily through hill-climbing. However, if the landscape is riddled with low-fitness valleys between local fitness optima, then many potential evolutionary pathways through sequence space will be inaccessible, inhibiting global optimization of activity. A comprehensive map of the fitness landscape would enable understanding of such fundamental issues.

Fitness landscapes of ribozymes are of special interest because RNA may have been the first evolving molecule during an “RNA World” at the time of the origin of life.⁶⁻¹² In addition, ribozymes have been proposed as the genetic and catalytic basis for a minimal synthetic cell.¹³ On the practical side, ribozymes can be relatively short in length (L),¹⁴ so it is possible to interrogate the entirety of sequence space in a laboratory setting (e.g., for L = 21, 4²¹ ≈ 4 × 10¹² possible sequences). Recent studies have emphasized the importance of comprehensive coverage vs sparse sampling of sequence space for understanding evolutionary pathways. For example, sparse sampling (e.g., based on known genotypes) can miss viable evolutionary pathways and create a biased view of the fitness landscape.^15,16 Exhaustive data could also aid computational efforts to explore larger sequence spaces.^17,18 Therefore, mapping the comprehensive fitness landscape for ribozymes is an important goal.

We previously developed a method for mapping the comprehensive fitness landscape of an RNA aptamer by in vitro selection,¹⁹ with abundance used as a proxy for fitness. However, binding is qualitatively different from catalysis,²⁰ which involves a reaction pathway, often including covalent modification of the ribozyme, in addition to binding of the substrate and stabilization of the transition state. Furthermore, work by us and others has established methods for measuring affinity constants, ribozyme reaction rates, and RNA processing and thermodynamic stability by high-throughput sequencing, raising the prospect of mapping the landscape in terms of affinity or activity.²¹⁻²⁹ Although prior studies measuring chemical activity were applied to small populations or sparse samples of sequence space, these studies, combined with the ability to map a comprehensive fitness landscape, point toward the possibility of mapping the comprehensive chemical activity landscape for ribozymes.

In the current work, we use this combined approach, termed SCAPE (sequencing to measure catalytic activity paired with in vitro evolution), to map a comprehensive ribozyme activity landscape. We focus on an activity that would be foundational to protein translation, perhaps the most impressive invention of the RNA World. Despite its importance, the emergence of protein translation is poorly understood. A key activity is the covalent attachment of specific amino acids to specific tRNAs, which establishes the biophysical information content of the “second genetic code”.³⁰ In modern biology, this attachment is catalyzed by aminoacyl-tRNA synthetases, but self-aminoacylating ribozymes could have been the original basis of the tRNA/synthetase system. Ribozymes that react with aminoacyl adenylates or other activated substrates have been discovered,³¹⁻³⁵ illustrating the ability of ribozymes to catalyze formation of aminoacyl-RNAs, although the substrates studied previously are prebiotically implausible or highly unstable. In contrast, N-carboxyanhydrides (NCAs) and the related 5(4H)-oxazolones can be produced from amino acids (or peptides) by multiple prebiotically plausible reaction pathways (e.g., with carbonyl sulfide,³⁶ cyanate,³⁷ or cyanamide³⁸ as activating agents). These compounds react with amino acids to form peptides,³⁹ and therefore have been proposed as a prebiotic form of chemically activated amino acids. At high concentration, NCAs and 5(4H)-oxazolones react with phosphate esters, including nucleotides, to form aminoacyl-RNA mixed anhydrides in low yield,⁴⁰⁻⁴⁴ suggesting this reaction as a candidate for ribozyme catalysis. Use of 5(4H)-oxazolones avoids uncontrolled polymerization in comparison to NCAs, making oxazolones a practical and prebiotically relevant substrate for in vitro selection. Thus, we apply SCAPE to map the catalytic activity landscape for ribozymes that self-aminoacylate using a prebiotically plausible form of chemical activation, and we analyze the evolutionary and mechanistic implications of the empirically determined ribozyme landscape.

Results

The SCAPE strategy begins with a population of molecules containing a randomized central region of 21 nt flanked by two constant regions used for PCR amplification (total length = 71 nt). In a first step, this library is subjected to in vitro selection for aminoacylation activity to isolate the ribozymes. In a second step to assay the ribozymes’ activities, a pool of the selected molecules that includes many (∼10⁴ to 10⁵) different active sequences is allowed to react with various concentrations of substrate, and the products are isolated and sequenced on the Illumina platform. The sequencing output is used to quantify reaction products²⁸ and thereby measure the catalytic rates of potentially hundreds of thousands of sequences in parallel. We refer to this second step as kinetic sequencing (k-Seq).

Selection of Aminoacylation Ribozymes

Beginning with a pool of random-sequence RNAs (central random region length L = 21) with high coverage of sequence space (∼70–99.99% coverage; Supporting Text S1), six rounds of in vitro selection for aminoacylation activity were conducted (Figure 1A). In each round, the RNA pool was reacted with a biotinylated tyrosine analog, biotinyl-Tyr(Me)-oxazolone (BYO). RNAs that react with BYO become covalently attached to the biotin tag, allowing their isolation by binding to streptavidin beads. These RNAs are reverse-transcribed and amplified by PCR, providing templates for the next round of selection and amplification. The progress of the selection was followed by high-throughput sequencing, which yielded 2 × 10⁶ to 1 × 10⁷ sequence reads per round of selection. Two replicates of the selection were performed (RS1 and RS2). Analysis was conducted using RS1, with data from RS2 used to confirm reproducibility of the selection.

Figure 1.

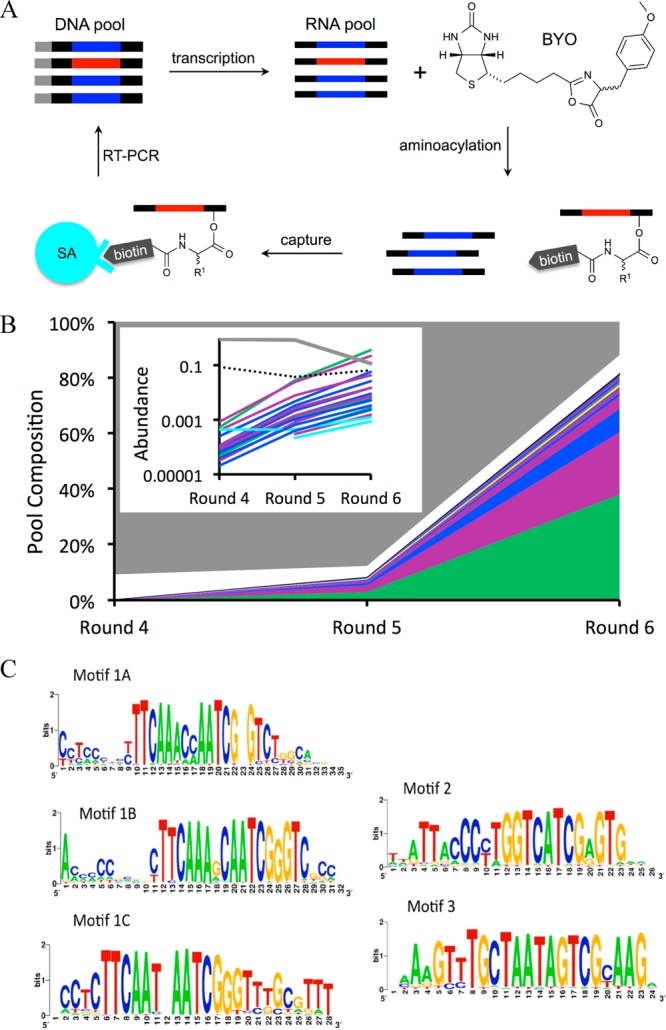
In vitro selection for aminoacylation ribozymes. (A) Selection began with DNA templates containing a transcription promoter (gray) and a central region of 21 random-sequence residues (red or blue) flanked by constant regions (black). These templates were transcribed into RNA and incubated with BYO. Aminoacylated RNAs (red) were isolated using streptavidin beads and amplified by RT-PCR for the next round of selection. (B) Pool composition over Rounds 4–6 after clustering. The top 20 families are indicated in non-neutral colors; gray corresponds to unclustered sequences; white corresponds to families with rank by abundance >20. Multiple families from submotif 1A (purple), 1B (dark blue), 1C (cyan), Motif 2 (green), and Motif 3 (yellow) are shown. Inset: Abundance of the top 20 families in Rounds 4–6 (same color scheme, except that the dotted black line corresponds to families of rank >20). (C) SeqLogo representations of the motifs.

For each round, sequences were first clustered into families using a maximum edit distance of 3 mutations (substitutions, insertions, or deletions) from the center sequence, which was defined as the sequence of highest abundance in the family. Sequence families could be identified starting in Round 4 (Figure 1B, Supporting Figure S1A). The 20 ribozyme families of highest center abundance identified in the RS1, Round 5 pool were compared manually to identify conserved sequence motifs. The top 20 families comprised 80% of sequence reads by Round 6 and were consistent in RS1 and RS2 (Supporting Figure S1B). These 20 families could be characterized by one of three distinct motifs, numbered as Motif 1, 2, and 3. Motif 1 contained the shortest conserved region (Figure 1C, Supporting Figure S1C) and the greatest number of unique sequences contained Motif 1. This motif could be further categorized into three submotifs (1A, 1B, 1C) based on differences in the conserved region, with 14 of the top 20 families containing Motifs 1A or 1B. Motif 2 characterized fewer unique sequences than Motif 1, but more than Motifs 1A, 1B, or 1C. Motif 2 also characterized Family 2.1, the most abundant family in the pool. Of Motifs 1−3, Motif 3 was found in the smallest fraction of the pool and characterized the fewest unique sequences.

Kinetic Sequencing (k-Seq)

We determined the rate constants of the selected ribozymes by a massively parallel assay (kinetic sequencing, or k-Seq; Figure 2A). In a gel-based assay to measure the rate constant of aminoacylation, a single RNA sequence was mixed with BYO and product formation was monitored by gel shift of the RNA in the presence of streptavidin. In the k-Seq assay, we reacted a heterogeneous pool obtained from in vitro selection, which contained many different RNA sequences, with BYO and isolated the aminoacylated RNAs using streptavidin beads. These RNAs were analyzed by high-throughput sequencing (HTS), yielding the relative abundance of each sequence in the products, which were converted to absolute concentrations by comparison to a standard of known concentration in the product pool. Rate constants (k_s for sequence s) and maximum amplitude of reaction (A_s) in both assays were obtained from the dependence of product formation on the concentration of BYO. k-Seq estimates for activity could be obtained for 8.9 × 10⁶ sequences, but the majority of sequences were present at low abundance and correspond to low activity (Supporting Figure S2). ∼10⁵ unique sequences, out of ∼4²¹ possibilities, were found to have activity >10-fold above the noncatalytic background rate (i.e., catalytic enhancement r_s > 10, where r_s = k_sA_s/k₀A₀, and k₀ and A₀ are the rate constant and amplitude of reaction of the noncatalyzed reaction, measured in the randomized RNA pool).

Figure 2.

Emergence of ribozymes and kinetic characteristics. (A) In k-Seq, an RNA pool enriched for active ribozymes is reacted at multiple BYO concentrations, in triplicate. Captured RNA is then reverse-transcribed and sequenced. Activity curves are constructed for sequences detected in the enriched pool. (B) Aminoacylation at various [BYO] for ribozyme S-2.1-a observed by both gel shift and k-Seq Data for all other measured ribozymes are shown in Supporting Figure S3. Error bars correspond to standard deviation among triplicates. (C) Correlation between catalytic enhancement of ten ribozymes, measured by gel shift assay and k-Seq Error bars correspond to standard deviation among triplicates (k-Seq) or 2–3 replicates (gel assay) (R² = 0.87; Supporting Table S1). Dotted orange line indicates line of unity.

To determine how well k-Seq results corresponded to results of the standard assay, we chose ten sequences that are close to the consensus sequences of the high- or medium-activity families (with all five motifs and submotifs represented) and measured aminoacylation activity by the gel-shift assay.⁴⁵ Rate constants determined from k-Seq matched well with gel-shift measurements (Figure 2B,C, Supporting Table S1). All k-Seq and gel-shift measurements were performed in triplicate and the standard error was similar between k-Seq and gel-shift measurements (Supporting Figure S1A). Measurement error during k-Seq decreased as sequence read abundance increased, as expected for stochastic noise. For most sequences with count >10, and nearly all sequences with count >100, the noise of k-Seq measurements appeared to be within a factor of 2 (Supporting Figure S4).

High-activity sequences (e.g., the center of Family 2.1, with r_S-2.1-a = 1010 and k_s = 779 ± 21 min^–1 M^–1) exhibit saturating kinetics from k-Seq, providing both the rate constant (k_s) and the maximum amplitude of reaction (A_s). However, the reaction for lower activity sequences (approximately k_s < 20 min^–1 M^–1) appears linear under the conditions tested, so that k_s and A_s are difficult to estimate separately using these data; instead the combined parameter k_sA_s can be estimated (Supporting Figure S5A).

Aminoacylation Site and True Catalytic Enhancement

The most highly abundant sequences from each major motif were chosen (S-1A.1-a, S-1B.1-a, S-2.1-a, S-3.1-a; see Methods for sequence nomenclature) for characterization of the reactive site. Identification of the reactive site was performed in two steps. First, reverse transcription is known to be sensitive to 2′ adducts, such that stalled products can be used to identify the sites of 2′ acylation.^46,47 The putative ribozymes were ligated to a 3′ adapter to test for stalling of reverse transcription along the entire length of the ribozyme. Stalling resulted in a truncated product whose length, determined by gel electrophoresis, suggested a likely site of aminoacylation (Figure 3A; Supporting Figure S10). Second, the nucleophilic importance of the 2′-OH at the candidate site was verified by testing the activity of a synthetic RNA modified at this position by 2′-O-methylation. In each case, a control synthetic RNA that was instead modified at an adjacent position was also tested. Blocking of the candidate site (but not the control sites) by O-methylation is expected to abolish the reaction. For all sequences tested, the results were consistent with aminoacylation at a specific internal 2′-OH position within the 3′ constant region of the sequence (Figure 3B; Supporting Figure S6). While the reactive site was conserved for sequences from the same major motif (e.g., S-1A.1-a and S-1B.1-a, both from Motif 1), the site differed among sequences from the three major motifs, indicating that ribozymes with different motifs utilize different detailed reaction mechanisms.

Figure 3.

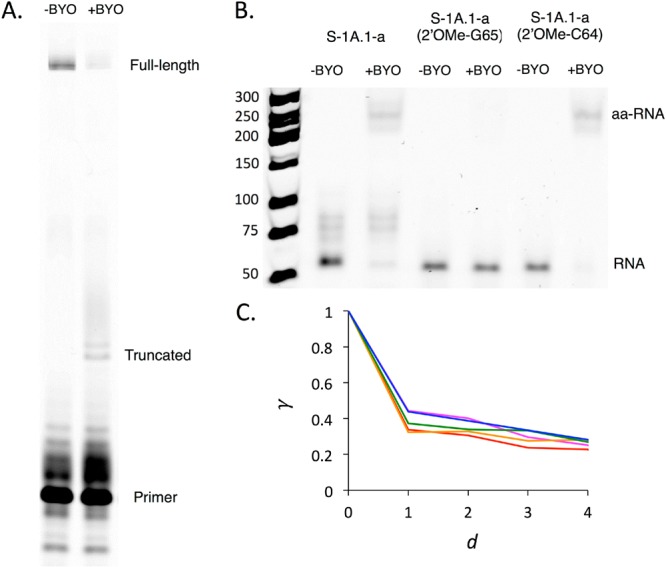
Aminoacylation site and landscape ruggedness. The likely site of BYO modification on ribozyme S-1A.1-a was identified by stalling of reverse transcription, resulting in a truncated product (A). The site, G65, was verified by loss of activity upon 2′-O-methylation, assayed by streptavidin gel shift after BYO reaction (B). 2′-O-Methylation of an adjacent site (C64) did not show loss of activity. (C) Average correlation of fitness effects γ_d as a function of edit distance d, shown for the sequence families around the five most abundant centers: 2.1 (magenta), 1A.1 (red), 1B.1 (orange), 1B.2 (green), 1A.2 (blue).

Note that the catalytic enhancement r_s calculated here underestimates the true catalytic enhancement at the modified site. The potential nucleophilic sites include 70 internal 2′-OH groups, the vicinal diol at the 3′ end, and the 5′-triphosphate. Thus, the uncatalyzed reaction rate at a particular site is at least 73-fold lower than k₀A₀, which we measured for the entire RNA. In addition, previous work on oxazolone modification of small RNA oligonucleotide models indicates that the vicinal diol and terminal phosphates (2′, 3′, or 5′) are strongly preferred as nucleophiles, with no detectable reactivity at internal 2′-OH sites.^43,44 In contrast, we found that all ribozymes tested, representing each motif (1A, 1B, 2, 3), were modified at an internal 2′-OH. Therefore, the true catalytic enhancement provided by these ribozymes at a specific internal 2′-OH is likely to be at least 700-fold greater (Supporting Text S2) than the r_s as reported here.

Frequency Distribution of Catalytic Activity

The log-normal shape of the frequency distribution of catalytic activity k_sA_s, is consistent with prior findings.^24,48 Because the rate constant scales exponentially with the activation energy, it was of interest to determine the distribution of k_s alone. For the highest activity family (2.1), many ribozymes could be characterized by k_s and A_s separately. k_s was observed to fit a log-normal distribution, indicating that activation energies are normally distributed for a ribozyme family (Supporting Figure S5B,C). The distribution of A_s, which represents the maximum extent of reaction and may indicate the fraction of RNA that is well-folded, also fit well to a log-normal distribution, suggesting that folding energies may also be normally distributed for a ribozyme family. For the regime in which k_s and A_s could be determined separately, these parameters are not well-correlated with each other (Supporting Figure S5A), suggesting no relationship between the catalytic rate and fraction folded.

Ruggedness of Chemical Activity Peaks

To understand how the overall character of the ribozyme fitness landscape compares with well-known theoretical models, we characterized the ruggedness of the ribozyme peaks. Generally, the fitness of close relatives is highly correlated to each other, but the fitness of more distant relatives is less correlated. A simple measure of ruggedness is the fitness correlation γ_d for a ribozyme family, which is the average correlation of activity effects of single mutations between sequences at evolutionary distance d of each other⁴⁹ (d is the Levenshtein edit distance, i.e., the number of substitutions, insertions or deletions between two related sequences). γ_d = 1 indicates a perfectly smooth landscape and γ_d = 0 indicates a highly rugged, completely uncorrelated landscape. γ₁ was approximately 0.3–0.4 for all families analyzed, i.e., the typical effect of a particular mutation is 30–40% correlated across all single mutant backgrounds (Figure 3C, Supporting Figure S7), indicating substantial ruggedness of the fitness peaks. Interestingly, as the neighborhood size increased up to d = 4, γ_d dropped only slightly (Figure 3C), indicating that activity remained similarly correlated at longer evolutionary distances within the peaks. The relative constancy of γ_d over a range of d indicates an underlying smoothness that is felt throughout the peak.

Evolutionary Pathways between Ribozyme Motifs

A series of single mutations defines an evolutionary pathway between two sequences. Although there are very many conceivable pathways, many of these include intermediate sequences of low fitness. Under selection, such fitness valleys represent dead ends that effectively block evolution. An open question is whether viable evolutionary pathways exist between different sequences that catalyze the same reaction. Using the chemical activity data from k-Seq, we searched for viable evolutionary pathways between center sequences of the major ribozyme families (Figure 4, Supporting Table S2).

Figure 4.

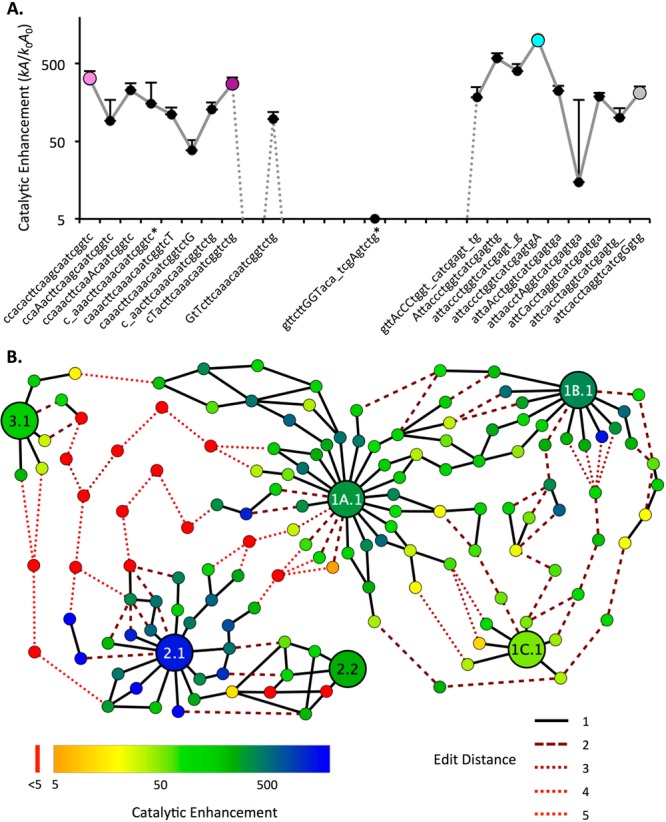
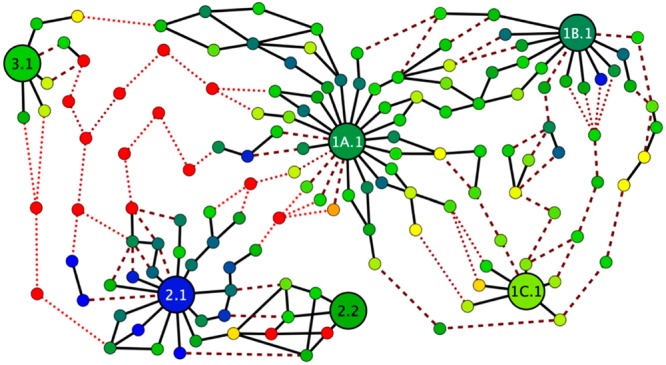
Evolutionary pathways for aminoacylation ribozymes. (A) Catalytic enhancement along a best pathway discovered from the center of Family 1B.1 (pink, S-1B.1-a), to 1A.1 (purple, S-1A.1-a), to 2.1 (cyan, S-2.1-a), to 2.2 (gray, S-2.2-a). Capital letters denote sequence positions changing at each step; underscore indicates a deletion. A large drop in activity is required for several mutations between Motif 1 and Motif 2. Error bars are standard deviation from triplicate measurements (only top bar is shown). Also see Supporting Figure S11. Asterisk (*) indicates a sequence that was found in only one replicate (RS1). (B) Evolutionary network displaying the 10 best pathways discovered between the centers of six key families (1A.1, 1B.1, 1C.1, 2.1, 2.2, and 3.1) representing each motif and submotif and the two most active centers from Motif 2. Each node is an individual sequence with activity measured by k-Seq indicated by color (see legend; red indicates activity at or below the baseline rate). The lines indicate mutational distance between sequences (solid black line = 1 mutation). Dotted lines indicate sequences at baseline activity (see legend). The majority (67%) of the edits along these pathways are substitutions; the remainder are indels.

A broad network of pathways was found among Families 1A.1, 1B.1, and 1C.1, with a <10-fold catalytic rate decrement at the lowest point of the best pathways. Thus, the families of Motif 1 form a “plateau” in the chemical activity landscape, corresponding to the small size of Motif 1. Similarly, viable pathways exist between the top two families of Motif 2. Although Motif 2 encompasses a smaller region of sequence space compared to Motif 1 due to a larger conserved region, Motif 2 contains the global optimum of the landscape. Viable pathways were not found between families of Motif 3, likely due to the small number of unique sequences in this motif. Within Motifs 1 and 2, the number of viable pathways was relatively small, suggesting that evolution within a motif would be fairly reproducible.

However, evolutionary pathways between motifs appeared strikingly different. The only pathways that could be constructed between different motifs contain fitness losses down to baseline activity, with multiple mutational steps occurring at near baseline activity. The closest apposition of motifs was a pathway between Family 3.1 and Family 1A.1, which involves 5 consecutive intermediates expected to have baseline activity (i.e., r ∼ 10³-fold less than r_S-2.1-a). The global optimum (Family 2.1) is especially isolated, with >10 mutations at baseline activity required along any pathway toward a different motif. These pathways would not be viable under selection, indicating that optimization of activity over the global fitness landscape would be frustrated.

Discussion

In the SCAPE method, a ribozyme fitness landscape can be mapped in two steps. First, the vast majority of inactive sequences are removed from the pool through in vitro selection. Second, the catalytic activities of the remaining sequences are directly assayed by kinetic sequencing (k-Seq). In this case, k-Seq yielded estimates for ∼10⁵ unique sequences (a number that in general depends on pool diversity, activity distribution, and sequencing depth). Using SCAPE, we mapped the first comprehensive fitness landscape for catalytic activity, subject to the following caveats. First, in order to survive the selection, sequences must be both catalytically active and replicable (by transcription and RT-PCR). Because RT stalls at the aminoacylated site, ribozymes that aminoacylate within the randomized region are presumably disfavored. Consistent with this, all of the ribozymes tested here react within the 3′ constant region, as modification does not preclude primer binding. Sequences may also have been lost during selection for other reasons (e.g., transcription or RT-PCR bias, and genetic drift in early rounds). While such occasional losses might affect the details of evolutionary pathways, they would likely not affect the overall findings given the extensive fitness valleys found. Alternatively, if the starting library were relatively small (∼10⁶ sequences), k-Seq alone (without selection) could be used to build a comprehensive map of the library; advances in sequencing technologies may push this bound further. Second, fitness is measured in the specific environment applied, in this case for aminoacylation activity under the chemical conditions of the selection. How the environment would affect the fitness landscape, and how aminoacylation activity might relate to the replicative fitness of an RNA World organism (a variety of relationships are possible⁵⁰⁻⁵⁴), are difficult to address at present.

We discovered ribozymes that self-aminoacylate using a 5(4H)-oxazolone, a key step toward the genetic code. The best ribozyme found here has a rate constant comparable to that of ribozymes obtained using a biologically derived aminoacyl adenylate,^31,32 indicating that these reactions could proceed efficiently even with only prebiotic substrates. Interestingly, all ribozyme families discovered here react at an internal 2′-OH of the RNA. These sites stand in contrast to the modification of modern tRNAs at the vicinal diol (3′ terminus), which is also found to be more reactive in model oligonucleotides.^43,44 It is possible that an internal reaction site facilitates establishment of multiple contacts with BYO, and the rate acceleration caused by these structural features outweighs the intrinsic reactivity of the vicinal diol. Similarly, it is unknown whether the identity of the 3′ terminal sequence (CUG in this study, compared to CCA in tRNAs) may contribute to this finding. This difference raises the interesting question of whether ribozymes such as those discovered in this model system could be on the pathway toward the modern implementation of the genetic code; whether they have the evolutionary capacity to adopt a mechanism more similar to the aminoacyl-tRNA synthetase system is currently unknown.

Analysis of individual ribozyme families indicates that the overall topography of each peak can be described as a combination of two components: a “smooth” component (∼40%) in which mutations have additive effects on catalytic activity, and a “rough” component (∼60%) that represents deviations from additivity (i.e., epistasis). This combination resembles the so-called “Rough Mt. Fuji” model, which consists of a perfectly smooth peak overlaid by uncorrelated ruggedness^4,56−59 (Supporting Figure S7; also see discussion below).

In addition to discovering novel ribozymes, a primary motivation for SCAPE analysis is to learn about molecular evolution by exhaustively determining the viable evolutionary pathways and networks through sequence space. We found that, while some viable pathways exist locally around an optimum, most conceivable pathways toward the global fitness optimum (Family 2.1) are blocked by extensive fitness valleys. The likely reason is that the three major motifs differ substantially in structure, as indicated by their different aminoacylation sites. It appears that the ribozyme structure cannot be changed without essentially destroying the structure of one ribozyme and building another, requiring extensive mutations at negligible activity. Such evolutionary walks would be essentially impossible while under selection for catalytic activity, frustrating optimization over the network.

This landscape can be compared to other landscapes and evolutionary pathways that have been described for functional RNA. Extensive work on in silico folding of RNA sequences has predicted the existence of large neutral networks for secondary structure, in which evolutionary walks over long distances could maintain a given structure.⁶⁰⁻⁶² Such neutral networks would permit facile exploration of sequence space through evolution. In addition, multiple examples of ribozymes evolving to perform different functions are known.⁶³⁻⁶⁶ In contrast, the previously described landscape for RNAs selected to bind GTP (based on sequence abundance rather than activity measurement; see Supporting Figures S3F and S8) showed that the landscape consisted of several evolutionarily isolated peaks.¹⁹ Thus, it appears that, although preservation of secondary structure could occur over a neutral network, the additional tertiary structural requirements of a functional RNA leads to a qualitative change in the nature of the evolutionary network. Such a change is analogous to the phase transition-like behavior of percolation through a network;⁶⁷ as the frequency of active nodes decreases, the network suddenly switches from highly connected, as in the case of neutral networks of RNA secondary structure, to essentially impermeable, as observed for evolutionary networks of functional RNAs. An important caveat is that the landscape reported here was mapped under constant selection for a single catalytic activity and cannot be directly compared to evolutionary pathways leading to new functions; changing environments⁶⁸ or selection pressures may significantly alter this picture.

The phenomenon of frustration arises when competing interactions prevent overall optimization of a system, resulting in a large number of local maxima. A classic illustration of frustration is the antiferromagnetic spin glass, in which energy would be minimized by antiparallel placement of neighboring electronic spins. In certain configurations (e.g., a triangular lattice), no placement of spins can satisfy all desired constraints, leading to rugged energy landscapes.⁶⁹ The analogy to frustrated spin glasses has been explored theoretically to understand fitness landscapes.^3,59,70−72 For example, the NK model of fitness landscapes, in which there are N sites and the fitness contribution of each site is influenced by K other sites, is equivalent to a form of spin glass, with the ruggedness of the landscape tuned by the epistatic parameter K.^74,75 At an extreme, when K = N – 1, the fitness of similar genotypes is completely uncorrelated. This regime is similar to the “House-of-Cards” landscape generated when fitness values are randomly assigned, giving a maximally rugged, degenerate landscape with a very large number of local optima.^3,76,77 The House-of-Cards landscape is also equivalent to the random energy model approximation for a disordered spin glass.⁷⁸ These theoretical models of maximally rugged energy or fitness landscapes are characterized by frustration: no configuration (i.e., sequence) can simultaneously satisfy all desirable interactions. The ruggedness of the empirically determined ribozyme fitness landscape reported here can be described by the Rough Mt. Fuji model, which is a combination of a smooth “Mt. Fuji” landscape and the random House-of-Cards landscape,^57,79 with the weighting of this combination reflected by the fitness correlation γ_d.⁴⁹ Our analysis of γ_d showed that the rugged House-of-Cards component dominated the shape of the major peaks of the landscape, with ∼60% of the variance of fitness being attributable to random contributions. (Note that this ruggedness is not fully represented in Figure 4, which only illustrates the best evolutionary pathways found between peaks.) Thus, while the fitness landscape observed here is not entirely uncorrelated, we suggest that the major House-of-Cards character found implies a substantial level of frustration, consistent with the lack of viable evolutionary pathways among the major optima.

Frustration in biological systems has also been invoked to understand the folding energy landscape of proteins,⁸¹⁻⁸³ where individual local molecular arrangements that minimize energy may be mutually incompatible, resulting in rugged energy landscapes and misfolded states. Other systems that may exhibit some frustration include gene expression networks,⁸⁴ morphological innovation,⁸⁵ and even the evolution of biological complexity.⁸⁶ Our results show that the experimentally determined ribozyme activity landscape exhibits a degree of frustration, as individually beneficial mutations are often mutually incompatible, leading to ruggedness on the fitness landscape.^72,87 Walks on such energy or evolutionary landscapes are characterized by sensitivity to initial conditions, difficult optimization, and multiple possible outcomes. It should be noted that mechanisms that favor greater genetic diversity, such as recombination, gene duplication, or epistasis among genes, could enable crossing of fitness valleys.^88,89 Recent work suggests that recombination, in particular, can occur spontaneously in pools of RNA.^90,91 The quantitative effect of such mechanisms on traversal of the fitness landscape is unknown at present. Nevertheless, in the absence of such mechanisms, the emergence of a globally optimal sequence is likely to result from chance events rather than natural selection.

Methods

Synthesis of Biotinyl-Tyr(Me)-Oxazolone (BYO)

General Synthetic Procedures

Reagents and solvents were obtained from Fluka, Sigma-Aldrich or Bachem, and were used without further purification. NMR spectra in either CDCl₃, DMSO-d₆ or D₂O solution were recorded on a Bruker DPX 300 spectrometer (300 MHz) or on a Bruker Avance 400 spectrometer (400 MHz); chemical shifts δ_H are reported in ppm with reference to the solvent resonance (CDCl₃: δ_H = 7.26 ppm; DMSO: δ_H = 2.50 ppm; H₂O: δ_H = 4.79 ppm); coupling constants J are reported in Hz. UHPLC analyses were carried out on a Thermo Scientific Dionex UltiMate 3000 Standard system including an autosampler unit, a thermostated column compartment and a photodiode array detector, using UV absorbance detection at λ = 273 nm. HPLC/ESI-MS analyses were carried out on a Waters UPLC Acquity H-Class system including a photodiode array detector (acquisition in the 200–400 nm range), coupled to a Waters Synapt G2-S mass spectrometer, with capillary and cone voltage of 30 kV and 30 V, respectively, source and desolvation temperature of 140 and 450 °C, respectively. ESI⁺ and ESI^– refer to electrospray ionization in positive and negative mode, respectively. HRMS spectra were recorded on the same spectrometer, using the same source settings as above.

Preparation of N-tert-Butoxycarbonyl-O-methyl-tyrosine methyl ester (Boc-Tyr(Me)-OMe)

Synthesis of Boc-Tyr(Me)-OMe was carried out according to a published procedure.^92,93 A solution of Boc-Tyr-OH (7.0 mmol, 2.0 g; Bachem) in dimethylformamide (DMF, 20 mL) was cooled using an ice bath and treated with freshly ground KOH (7.7 mmol, 0.43 g). A cooled solution of CH₃I (7.7 mmol, 0.49 mL) in DMF (5 mL) was added dropwise over 1 min. The mixture was stirred at room temperature for 30 min, then cooled using an ice bath, and additional KOH (7.7 mmol, 0.43 g) and a cooled solution of CH₃I (7.7 mmol, 0.49 mL) in DMF (5 mL) were added dropwise over 1 min. The mixture was stirred for 3 h at room temperature, poured onto ice (40 g), and extracted with ethyl acetate (3 × 20 mL). The organic layers were washed with water (3 × 13 mL), brine (2 × 13 mL), and dried over Na₂SO₄. The solvent was removed under reduced pressure to afford a colorless oily residue. Then the oil was purified by preparative silica gel chromatography (mobile phase: ethyl acetate–hexane, 3:7 v/v) (yield: 1.4 g, 63.6%). ¹H NMR (400 MHz, DMSO-d6) δ 7.14 (d, J = 8.5 Hz, 2H), 6.84 (d, J = 8.6 Hz, 2H), 4.11 (ddd, J = 10.0, 8.1, 5.3 Hz, 1H), 3.72 (s, 3H), 3.61 (s, 3H), 2.99–2.72 (m, 2H), 1.33 (s, 9H).

Preparation of Biotinylated O-Methyl-Tyrosine (Biotin-Tyr(Me)-OH)

This compound was prepared in three steps. In the first stage, Boc-Tyr(Me)-OMe (1.0 g) was treated by trifluoroacetic acid (TFA)/water solution (9:1 v/v, 2 mL) for 30 min. TFA was removed by evaporation in vacuo, the residue was poured into diethyl ether, the TFA salt of H-Tyr(Me)-OMe was collected by filtration as a white precipitate (yield: 0.88 g, 84%). ¹H NMR (400 MHz, CDCl₃) δ 7.14 (d, J = 8.1 Hz, 2H), 6.88 (d, J = 7.9 Hz, 2H), 4.23 (t, J = 6.4 Hz, 1H), 3.80 (s, 3H), 3.78 (s, 3H), 3.24 (qd, J = 14.6, 6.2 Hz, 2H).

In the second stage, biotin (345 mg, 1.41 mmol), was activated with 1-ethyl-3-(3-(dimethylamino)propyl)carbodiimide (EDC, 293 mg, 1.55 mmol) and hydroxybenzotriazole monohydrate (HOBt, 242 mg, 1.55 mmol) in a mixture of CH₂Cl₂ (7 mL) and DMF (7 mL). The mixture was stirred for 5 h. Then the TFA salt of H-Tyr(Me)-OMe (500 mg, 1.55 mmol) was added with N-ethyl-N,N-diisopropylamine (DIEA, 531 μL, 3 mmol), and the mixture stirred overnight. DMF was removed under reduced pressure, and the residue redissolved in ethyl acetate (100 mL), washed with water (30 mL), 1 M KHSO₄ (10 mL), NaHCO₃ (saturated solution, 10 mL), and brine (10 mL), consecutively. The solution was dried over anhydrous Na₂SO₄ and concentrated under reduced pressure. Residual DMF was removed by dissolving the residue in ethyl acetate (20 mL) and precipitation with hexane (5 mL). The solid was recovered by filtration, washed with hexane, and dried in vacuo (300 mg, 46%).

The methyl ester biotinyl-Tyr(Me)-OMe (270 mg, 0.62 mmol) was then dissolved in iPrOH:H₂O (7:3 v/v) (minimum volume), treated with 1 N NaOH (0.93 mL). The mixture was stirred at room temperature overnight. The solvent was removed under reduced pressure, and the product was precipitated upon addition of water and acidification with 1 M HCl. The free acid biotinyl-Tyr(Me)-OH was recovered by filtration as a white solid, washed with water, and then dried under reduced pressure (yield: 226 mg, 86%). ¹H NMR (300 MHz, DMSO-d₆) δ 8.05 (d, J = 8.1 Hz, 1H), 7.13 (d, J = 8.5 Hz, 2H), 6.83 (d, J = 8.5 Hz, 2H), 6.37 (d, J = 9.9 Hz, 2H), 4.45–4.24 (m, 2H), 4.19–4.06 (m, 1H), 3.71 (s, 3H), 3.09–2.90 (m, 2H), 2.80 (ddd, J = 20.9, 13.2, 7.3 Hz, 2H), 2.05 (t, J = 7.1 Hz, 2H), 1.69–1.08 (m, 6H). HRMS (ESI+) m/z calcd for C₂₀H₂₈N₃O₅S [M + H]⁺ 422.1750, found 422.1747.

Preparation of Biotinyl-Tyr(Me)-Oxazolone (BYO)

In a typical experiment, biotinyl-Tyr(Me)-OH (42 mg, 0.1 mmol) was mixed with CH₂Cl₂ (3 mL) and then EDC (21.9 mg, 0.12 mmol) was added. After stirring by magnetic stirrer for 1 h, all the starting material was dissolved. Additional CH₂Cl₂ (3 mL) was added, then the mixture was washed by H₂O (5 mL) twice and saturated brine (5 mL) once. The organic layer was dried by anhydrous Na₂SO₄ and concentrated under reduced pressure. The residue was dried in vacuum in the presence of P₂O₅ for 1 h. The product was stored under −20 °C, or kept in a solution of CH₃CN under −20 °C. HRMS (ESI+) m/z calcd for C₂₀H₂₆N₃O₄S [M + H]⁺ 404.1644, found 404.1644. See Supporting Figure S9 for NMR data.

Ribozyme Selection and Sequencing

Chemical synthesis (IDT, PAGE purification) was used to obtain a library of DNA molecules having the sequence 5′-GATAATACGACTCACTATAGGGAATGGATCCACATCTACGAATTC-N21-TTCACTGCAGACTTGACGAAGCTG-3′, where N21 denotes 21 consecutive random positions and nucleotides upstream of the transcription start site are underlined. Two replicates of the selection were performed (RS1 and RS2), beginning with 9.1 (coverage ≈ 1.3-fold) and 145 pmol (coverage ≈ 20-fold) of DNA for RS1 and RS2, respectively. RNA was transcribed using HiScribe T7 polymerase (New England Biolabs) and purified by denaturing polyacrylamide gel electrophoresis (PAGE). In the first round of selection, 3.4 × 10¹⁴ or 1.9 × 10¹⁵ RNA sequences (RS1 and RS2, respectively) were incubated with 50 μM BYO in the aminoacylation selection buffer (100 mM HEPES (pH 6.95), 100 mM NaCl, 100 mM KCl, 5 mM MgCl₂, 5 mM CaCl₂) for 90 min, at an RNA concentration of 1.4–3.2 μM. The reaction was stopped by removing unreacted substrate using Bio-Spin P-30 Tris desalting columns (Bio-Rad). Streptavidin MagneSphere paramagnetic beads (Promega) were used to isolate reacted sequences at a volume ratio of 1:4, which were then eluted with a 5 min incubation at 65 °C in a solution containing 95% formamide and 10 mM EDTA. Sequences were prepared for the next round of selection by reverse transcription and PCR (RT-PCR), with primers complementary to the fixed sequence shown above. Five additional rounds of selection were performed using the same procedure, with ∼400 pmol (∼2 × 10¹⁴ molecules; 2 μM) of RNA in each round. DNA samples from each round were barcoded and pooled for sequencing by Illumina NextSeq 500 (Biological Nanostructures Laboratory, California NanoSystems Institute at UCSB).

Identification of Ribozyme Families and Motifs

Clustering was performed on the Galaxy platform⁹⁴ for sequences in Rounds 4–6. Multiple families containing the same motif were designated as 1A.1, 1A.2, etc., or 2.1, 2.2, etc. Center sequences were used to assign each family to a motif. SeqLogo plots⁹⁵ representing motifs were generated from all sequences identified among every family grouped into that motif. Sequences are named according to the convention: S-Motif.family rank-sequence rank, where rank is determined by relative abundance in Round 6. For example, S-1B.1-a is the top-ranked sequence from the top-ranked family of Motif 1B.

Kinetic Sequencing (k-Seq)

Two μg of RNA from Round 5 (RS1) were incubated with BYO substrate at various concentrations (2, 10, 50, and 250 μM), under buffer conditions and reaction time otherwise identical to those during selection. Streptavidin beads were added at a volume ratio of 1:1, and bound RNA was eluted as described above. To enable absolute quantitation of the products, 4, 12, 17, and 42 fmol, respectively, of a control RNA sequence were spiked into the RNA eluted from each concentration point. The spike-in control sequence was transcribed by T7 RNA polymerase from a DNA oligonucleotide (IDT) having the sequence 5′-GATAATACGACTCACTATAGGGAATGGATCCACATCTACGAATTCAAAAACAAAAACAAAAACAAATTCACTGCAGACTTGACGAAGCTG-3′ (promoter underlined). The k-Seq reactions were performed in triplicate, barcoded, and sequenced as described above.

Every unique sequence detected in Round 5 was tracked across all 12 k-Seq samples. The absolute concentration of each sequence was calculated as (n_s/n_spike)[spike], where n_s and n_spike are the number of reads found for sequence s or the spike-in sequence, respectively, and [spike] is the known concentration of the spike-in sequence in the sample. Concentrations were averaged across triplicates and fit to the first-order rate equation 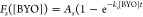), where F_s is the measured fraction of sequence s reacted, A_s is the maximum reacted fraction, t is the incubation time of 90 min, and k_s is the effective rate constant of the reaction catalyzed by sequence s (see Supporting Text S3). To obtain an estimate of error, each set of 12 observations was randomly grouped into three series of four concentrations, k_s and A_s were fit individually for each set, and the standard deviation among the three series was calculated.

For sequences of low activity, the parameter A_s could not be accurately estimated over the concentrations tested, leading to a fitting artifact with A_s = 1 and underestimation of k_s (Supporting Figure S5A). However, while A_s and k_s are poorly estimated individually, the combined chemical activity parameter k_sA_s is estimated more accurately. Thus, k_sA_s was used to compare catalytic activity across the broad range of observed activity. The ratio of k_sA_s to k₀A₀ (the uncatalyzed activity, see below) is defined as the catalytic enhancement of sequence s (r_s).

Determination of Aminoacylation Rate by Gel Shift Assay

Ten sequences were chosen from among the top 20 peaks for experimental testing (Supporting Table S1). The corresponding DNA oligonucleotides were obtained from IDT (HPLC-purified) and RNA was transcribed using T7 RNA polymerase. In addition, a control sample of random pool sequences was used to determine baseline uncatalyzed activity (k₀A₀, measured as a combined parameter). RNA was labeled using a 5′ EndTag Labeling Kit (Vector Laboratories) with Alexa 488 (Fisher), and purified by phenol-chloroform extraction. Labeled RNA sequences were then incubated (RNA concentration of 100 nM) with BYO for 90 min under conditions described as above for k-Seq. Following desalting, samples were incubated with 2 μM streptavidin for 15 min in 10 mM Tris (pH 7.0), then analyzed by native PAGE. Gels were scanned and fluorescence was quantified with ImageQuant software on an Amersham Typhoon 5 Biomolecular Imager. Bands corresponding to the streptavidin complex and the free RNA band were quantified to calculate the fraction of each sequence that had undergone aminoacylation. Values determined by k-Seq were compared to gel shift percentages (Supporting Figure S3A) to determine the average fraction loss l during streptavidin bead pull-down. This value of l was used as a correction factor when calculating catalytic enhancements using k-Seq data, as k₀A₀ was measured by gel-shift assay (also see Supporting Table S1).

Identification of the Reactive Nucleotide

Ribozyme aminoacylation reactions were performed in selection buffer containing 1 μM RNA and 500 μM BYO and incubated with gentle agitation for 90 min. RNA was concentrated using Amicon Ultracel-3 filters (EMD Millipore) and an adapter oligo having the sequence 5′-AACCTGCTGTCATCGTCGTCCCTATAGTGAGC-3′ was adenylated using a 5′ adenylation kit (NEB) and ligated to the 3′ end using T4 RNA Ligase 2, truncated KQ (New England BioLabs) (see exception noted below). The ligated products were gel purified and reverse transcribed using a 5′ Rhodamine Green-X-tagged reverse primer complementary to a region of the adapter sequence (5′-CTCACTATAGGGACGACGATGACAGCAGG-3′) and SuperScript III Reverse Transcriptase (Thermo Fisher), with a 10 min extension at 55 °C. Reverse transcripts were run on a 12% denaturing sequencing gel, scanned on an Amersham Typhoon 5 Biomolecular Imager. The likely site of truncation was identified by gel position from the primer (bands at single nucleotide resolution could be visualized at high contrast; see Supporting Figure S10). To verify specific 2′-OH positions, RNA sequences containing 2′-O-methyl modifications were obtained from IDT and tested for aminoacylation activity by streptavidin gel shift (described above).

Sequences from families 1A.1 and 1B.1 were ligated to an alternative adapter oligo (5′-AAAACGGGCTTCGGTCCGGTTC-3′), as ligation to the original adapter oligo (listed above) was noted to interfere with folding of these sequences. The corresponding RT primer was 5′-GAACCGGACCGAAGCCCG-3′.

Degradation Rate of BYO

RNA sequence S-1A.1-a (Supporting Table S1) was added to 250 μM BYO that was preincubated with reaction buffer for 5–180 min. The initial rate of the reaction was compared to the reaction kinetics for this sequence determined without preincubation of BYO (see above). The effective concentration of BYO at the start of reaction was calculated assuming a first-order reaction (i.e., effective [BYO] = (250 μM × initial rate)/(k_sA_s), where k_sA_s is the activity of the ribozyme without preincubation of BYO), giving a half-life for BYO of 36.5 min. Reaction rates for ribozymes were adjusted accordingly to account for lower effective substrate concentrations (Supporting Text S3).

Ruggedness of Chemical Activity Peaks

We compute the d-dependent epistatic correlation γ_d.⁴⁹ This parameter measures the correlation between the effect of a certain mutation at locus j in sequence s, Δ_j(s), and the effect of the same mutation in a d mutant background (i.e., all sequence pairs separated by a distance d), 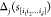, averaged over all possible sequences s, mutations j, and d mutant backgrounds :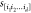

The effect of a mutation at locus j is measured as the change in (log-scale) activity of sequence s, as . For each pair of sequences having a certain mutation at a certain locus j, we identify all possible d mutant backgrounds by finding every other pair of sequences in the pool (Round 5, RS1) that (i) are at an edit distance d + 1 from each other, and (ii) differ by the same mutation at the same locus j. Data values from k-Seq with k_sA_s < baseline activity were assigned the baseline value.

Evolutionary Pathways between Ribozymes

Evolutionary pathways between two sequences (s₁ and s₂) were determined by applying a modified A* search algorithm.⁹⁶ The activity landscape determined by k-Seq can be considered a graph of nodes (sequences) connected by edges with weights equal to the edit distance between two nodes. In general, the A* algorithm is an established search method to find the lowest cost path from a starting node to the target node. Sequences present in Round 5 with absolute sequencing count ≥2 were used as the set of possible node sequences. Beginning at the starting sequence s₁, paths were chosen for extension according to minimization of the cost function f(s) = g(s) + h(s), where g(s) is the mutational distance traveled along the path from s₁ to sequence s and h(s) is the edit distance from s to the target sequence s₂. If more than one sequence gave the minimum f(s) value, these sequences were prioritized according to the following criteria in order of decreasing importance: (1) shortest average step distance, and (2) highest minimum sequence abundance along the pathway. The best five pathways from s₁ to s₂ were built with the shortest possible maximum step distance (i.e., edit distance for one step). Five additional pathways were built by allowing a step distance up to the previous maximum +1. To decrease runtime in practice, the algorithm kept an updated queue of sequences within a maximum edit distance of the last node(s). Initially, this maximum edit distance was set at 1, but if no pathway was found, this edit distance was increased by 1 until the desired number of pathways was found. To prevent unreasonably long search times, the search was terminated if f(s) > 42 (i.e., each nucleotide being mutated more than twice on average). The algorithm was implemented in Python. Pathway searches were conducted between family centers of the top two families of motif 2, among the top families of motifs 1A, 1B, and 1C, and among the top families of each of the three motifs (Supporting Table S2). Cytoscape⁹⁷ was used to generate a landscape overview from pathway data.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b13298.

• Supporting Text S1–S4, Supporting Tables S1–S3, Supporting Figures SS1–S11, Supporting References (PDF)

The authors declare no competing financial interest.

Notes

Galaxy computer code used is available as previously reported.⁹⁴ Additional scripts, HTS data, and related files are archived at the Dryad Digital Repository: https://doi.org/10.5061/dryad.nm1189t. Scripts are also  available on GitHub (https://github.com/ichen-lab-ucsb/SCAPE-BYO).