The Different Interactions of Lysine and Arginine Side Chains with Lipid Membranes

Abstract

The basic amino acids lysine (Lys) and arginine (Arg) play important roles in membrane protein activity, the sensing of membrane voltages, and in the actions of antimicrobial, toxin and cell-penetrating peptides. These roles are thought to stem from the strong interactions and disruptive influences of these amino acids on lipid membranes. In this study we employ fully atomistic molecular dynamics simulations to observe, quantify and compare the interactions of Lys and Arg with saturated phosphatidylcholine membranes of different thickness. We make use of both charged (methylammonium and methylguanidinium) and neutral (methylamine and methylguanidine) analog molecules, as well as Lys and Arg side chains on transmembrane helix models. We find that the free energy barrier experienced by a charged Lys crossing the membrane is strikingly similar to that of a charged Arg (to within around 2 kcal/mol), despite the two having different chemistries, H-bonding capability, and hydration free energies that differ by ~10 kcal/mol. In comparison, the barrier for neutral Arg is higher than that for neutral Lys by around 5 kcal/mol, being more selective than for the charged species. This can be explained by the different transport mechanisms for charged or neutral amino acid side chains in the membrane; involving membrane deformations or simple dehydration, respectively. As a consequence, we demonstrate that Lys would be deprotonated in the membrane, whereas Arg would maintain its charge. Our simulations also reveal that Arg attracts more phosphate and water in the membrane, and can form extensive H-bonding with its five H-bond donors to stabilize Arg-phosphate clusters. This leads to enhanced interfacial binding and membrane perturbations, including the appearance of a trans-membrane pore in a thinner membrane. These results highlight the special role played by Arg as an amino acid to bind to, disrupt and pemeabilize lipid membranes, as well as to sense voltages for a range of peptide and protein activities in nature and in engineered bionanodevices.

1 Introduction

Charged amino acids are essential for various biological phenomena, as they can provide both short-range and long-range interactions for protein folding ¹, helix aggregation ², membrane protein anchoring ³, the sensing of membrane potentials ^4–5, and the deformations of phospholipid bilayers by cell penetrating peptides (CPP) ^6–9 and antimicrobial peptides (AMP) ^10–12. In this study we explore the origins, strengths, structural perturbations and thermodynamics of charged amino acid interactions with membranes.

Lysine (Lys) and arginine (Arg) have been suggested to play similar roles in various membrane proteins, as they are both basic amino acids with high aqueous pK_a values (12–13.7 for Arg ^13–14 and ~10.5 for Lys ¹⁵) that enable them to carry charge in most circumstances, and give rise to strong electrostatic interactions. Yet, the occurrence of these two amino acids in naturally occurring proteins is highly dependent on the particular biological function ¹⁶, likely owing to their differing chemical properties which determine their abilities to interact with other amino acids and biomolecules. As a good example, Arg appears much more frequently in ion channel voltage sensors.^{4, 17} In addition, poly-Arg enters cells more efficiently than other oligomers of Lys, ornithine, or histidine.¹⁸ Substitution of Arg by Lys has been shown to decrease the translocation efficiency of CPP’s (e.g. penetratin ¹⁹), while increased Arg content has been shown to significantly improve cellular uptake^20–21 (e.g. for HIV1 Trans-Activator of Transcription protein fragment, Tat_49–57; RKKRRQRRR). Also, studies have shown that a high (9:1) Arg:Lys molar ratio in mammalian α-defensins, a family of AMPs, is essential for their bactericidal activity.^22–23 This prevalence of Arg in comparison to Lys is striking, given that the amino acid sequences of α-defensins are so diverse.²⁴. Arg also brings about key interactions associated with protein folding and ligand binding (e.g. in stabilization of protein structures²⁵, RNA binding²⁶ and heparin binding²⁷). The need for Arg to carry out so many functions is in spite of the fact that Arg is actually less abundant than Lys in living organisms (e.g. Archaea, bacteria, and eukaryotes).¹⁶ We question why Arg is so important in these cases, and explore the possible origins of the disparity between Arg and Lys in membrane proteins and membrane-active peptides, for which underlying differences in the chemistry may explain their contributions to biological function.

A range of experiments have been carried out in the past to elucidate or to infer the energetics of charged amino acid side chains interacting with membranes. However, difficulties are faced when attempting to obtain the thermodynamics of charged amino acids as a function of their depth in a membrane, needed to understand their interactions with membrane components. The cell biology experiments by Hessa et al.^28–29 were interpreted to suggest small energetic costs for inserting charged side chains at the center of a trans-membrane (TM) helix ^{28, 30}, challenging the long-held view that membranes act as barriers to the passage of charged molecules. Yet, due to the complexity of the translocon machinery of protein synthesis, and the challenges in creating a construct that is able to localize charged amino acids deep within the membrane,³¹ we remain without any direct measurements of spatially resolved studies of Arg and Lys interactions with membranes.

Free energies for transferring side chains from water to cyclohexane, a mimic for the membrane hydrophobic interior, were measured by Radzicka et al.³² In this study, however, the free energies for ionizable side chains were only measured for their neutral states (although corrected for the distribution of protonation states within the aqueous phase), because the energy cost for partitioning the charge into hydrocarbon is so high. As a result, no experimental measures for the movement of charged side chains into the hydrocarbon core exist, although it is well established via theoretical^{31, 33} and MD simulations^{31, 34–36} that the costs are prohibitively high. However, experimental measures do exist for the thermodynamics of interactions with the membrane interface, based on partitioning of host-guest peptides to 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC) bilayer interfaces³⁷, as well as through studies of partitioning into water-saturated n-octanol,³⁸ long considered to be a good mimic of the water/membrane interface.^{31, 35, 39–40}

In contrast, MD simulations can provide spatial variations in energetics, not limited to the membrane interface, and reveal the origins of protein-lipid interactions and subsequent membrane deformations. Simulations of Arg^{31, 36, 41–46}, in particular, have already revealed membrane perturbations associated with entry into a lipid bilayer, as well as the associated thermodynamics. In these simulations, the energy cost to deform the membrane has been shown to be critical in determining the free energy of the charged side chain’s movement in the membrane. These outcomes are in stark contrast to previous theoretical models that assume a uniform low dielectric slab membrane and neglect the deformability of the lipid bilayer. Also, these MD studies have hypothesized a special role for Arg due to its ability to maintain its protonated form, even deep inside the membrane.^{34, 41–42} Furthermore, the guanidinium group on Arg possesses a fairly unique ability to hydrogen-bond (H-bond) to multiple species in water and within the membrane. It can form 5 H-bonds with its 5 donors. This could lead to various Arg-phosphate complexes, such as the “arginine fork”,²⁶ “arginine claw”,⁴⁷ “Arg-Arg ion pair”,^48–49 “2:1 guanidinium/phosphate complex”⁵⁰ and “cyclic water-phosphate-guanidinium”⁵¹, especially in Arg-rich molecules. These H-bonding networks have significant implications for many other biological phenomena, such as in stabilizing protein structures,²⁵ phosphorylation,^{47, 52} phase transfer of oligo-arginine,^{50, 53} membrane perturbation by antimicrobial peptides,²² RNA/DNA binding²⁶ and molecular recognition.⁵⁴

In this study, Lys is compared with Arg through detailed analysis of their membrane-perturbing capabilities, their spatially resolved solvation and H-bonding, and through contributions that determine the free energies of these side chains entering a membrane, including their abilities to maintain charge. We will show that Arg possesses a unique ability to form extensive H-bonds with phosphate groups of lipids, which leads to enhanced membrane interfacial binding and membrane perturbation. We will show that the free energy barriers for charged Arg and Lys to cross the membrane are remarkably similar, and provide an explanation for why this is the case, despite their vastly differing properties, including the fact that the hydration free energy for methylguanidinium is −62 kcal/mol, and that for methylammonium is −72 kcal/mol (Table S1). We will show that Arg is the only amino acid side chain that can maintain a positive charge in the hostile membrane environment. These findings help understand the mechanisms of a range of membrane phenomena, providing a deeper understanding of the chemically-specific interactions amino acids have with lipid components, and enabling rational design of membrane-active peptides for biosensing,⁵⁵ therapeutics and drug delivery.^56–57

2 Methods

2.1 Molecular Dynamics Models

Two different models have been constructed to explore the interactions of peptides containing Lys and Arg with membranes. We first considered the simple analog molecules methylguanidine (Mguan⁰, and its protonated form is methylguanidinium, MguanH⁺; studied previously ^41–42) for Arg and methylamine (Mam⁰, and its protonated form is methylammonium, MamH⁺) for Lys. We have chosen Mam⁰/MamH⁺, as opposed to the full side chain analog, butylamine, to better isolate the influence of the amine functional group while maintaining a similar charge distribution, as well as to provide the most straight-forward comparison with the Arg analogs Mguan⁰/MguanH⁺. The second model studied is a long α-helix (poly-Leu) that passes through the membrane, and provides a suitable TM host for each side chain, despite small artifacts owing to the passing through the lipid bilayer interface.⁵⁸ In this case, the Lys or Arg side chain was placed at the middle of the helix and translocated across the lipid bilayer. While various sequences and structures for TM membranes exist in nature, this uniform poly-Leu helix was chosen because it provides a translationally invariant background, which permits us to focus on the interactions between Arg/Lys and the membrane. The comparison of Arg with Lys as simple analogs will provide easily interpretable findings, whereas the role of the host helix in modulating the interactions, including the ability of the side chain to snorkel within the membrane, will be captured by the TM helix model.

Both charged/protonated and neutral/deprotonated side chains have been simulated as analog and helix models, corresponding to a total of 8 systems (MamH⁺, LysH⁺; Mam⁰ and Lys⁰; MguanH⁺, ArgH⁺; Mguan⁰ and Arg⁰, see Fig. 1). An 80-residue α-helical TM helix, with the 40^th residue mutated to Arg or Lys, was built in an ideal conformation (Ф = −57°, ψ = −47°) and placed at a desired position, then a hydrated membrane was built around it by methods described elsewhere⁵⁹. These helices were long enough (~120 Å) such that the terminus-interface interaction was avoided for translations up to ± 30 Å. The C and N termini were kept neutral by using acetyl and ethanolamine groups, respectively. Dihedral constraints of 0.030 kcal/mol/deg² were applied to approximately maintain their α-helical conformation, so that sampling unfolding/folding of these hydrophobic helices outside the membrane was avoided.³¹ To keep the peptide vertical, a cylindrical constraint of 5 kcal/mol/Ų was applied to the centers of mass (COM) of each residue backbone.

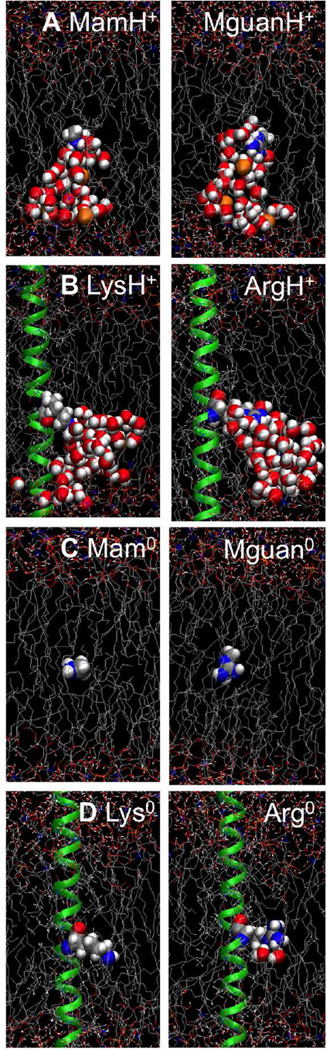
Figure 1.

Equilibrated MD systems for charged methylammonium analog (MamH⁺,A), charged Lys side chain (LysH⁺,B), neutral methylamine analog (Mam⁰,C), and neutral Lys side chain (Lys⁰,D), with the protein/analog molecule held near the center of the DPPC bilayer. The Lys side chain/analog molecule is drawn as blue N, gray C, and white H atoms; the TM helix, as a green ribbon; and the hydrated DPPC bilayer with gray C atoms, orange P, red O, and blue N atoms, and red/white water molecules. Lipid phosphate and water atoms that have been pulled into the bilayer core (|z|≤13Å) are drawn as balls. Corresponding Arg systems are in the right column.

Dipalmitoylphosphatidylcholine (DPPC; 16 carbon saturated tails) lipid bilayers consisting of 48 lipids were studied, were chosen to provide a reasonable model for a biological membrane^60–62 To explore the role of membrane thinning, we carried out additional simulations in bilayers of dilauroylphosphatidylcholine (DLPC; 12 carbon saturated tails). For the TM helix systems, hexagonal periodic boundaries with an xy-translation length of ~44 Å (based on an experimental area/lipid of 64 Å^{2 63} and a protein cross-sectional area of ~180 Ų) and mean height of ~190 Å, maintained with 1 atm pressure coupling in the z direction, were used. To neutralize the net charge on the protein/analog and to sample the movement of ions thoroughly, a 0.5 M KCl solution was used (corresponding to 7,896 or 7,895 water molecules, 72 K⁺ and 72 or 73 Cl⁻ ions for the neutral or charged side chains, respectively). The TM helix – DPPC systems contained 31,592–31,593 atoms in total. Left column in Figure 1B (LysH⁺) and D (Lys⁰) show equilibrated structures from a simulation with Lys near the center of the bilayer. Analog – DPPC systems were smaller than the TM helix systems, with lateral box dimension of ~42.6 Å and average height of ~80 Å, and consisted of 12,852–12,853 atoms, including 2,186–2,187 water molecules, 20 K⁺ ions and 20 or 21 Cl⁻ ions for neutral and charged side chain analog models, respectively (with the same numbers of water and ions, and 11,695–11,696 atoms in DLPC membrane systems). Figure 1A (MamH⁺) and C (Mam⁰), left column show sample coordinates from simulations with charged or neutral Lys analog molecules, respectively. Figures in the right column of Fig. 1 show the corresponding systems for Arg side chain models.

2.2 MD Simulations

Simulations of these four Lys systems: MamH⁺, LysH⁺, Mam⁰ and Lys⁰ (Fig. 1A to 1D, left column) were carried out with the following free energy protocols, whereas Arg helix and Mguan analog systems (Fig. 1A to 1D, right column) have been simulated previously.^{31, 41–42} For each system, 61 simulations were carried out, with simulation time of ~10 ns each. Simulations were performed with the program CHARMM^64–65 (version 32), the C27 force field^66–67 and TIP3P water ⁶⁸, shown to give similar results (within 0.5 kcal/mol for free energy profiles)⁶⁹ to the more recent C36 lipid force field.⁷⁰ Electrostatics were calculated by the particle-mesh Ewald (PME) method,⁷¹ and covalent bonds to H atoms were constrained using the SHAKE algorithm.⁷² Pressure along the z direction and temperature were coupled to 1 atm and 330K (above the gel-phase transition temperature for a pure DPPC membrane⁷³), respectively, by the Langevin piston and Nose-Hoover methods.⁷⁴ For Lys analog simulations in the thinner DLPC membrane, we used the more recent C36 lipid force field,⁷⁰ a temperature of 318 K due to the lower gel-phase transition temperature for this lipid (see Ref ⁶⁹. for discussion), and 1 atm pressure with the semi-isotropic pressure coupling in z and xy directions.

2.3 Structural and Energetic Analysis

The numbers of polar molecules (water O atoms, lipid head group P and N atoms) that penetrated into the membrane were calculated by summing their distributions along the z axis in membrane hydrocarbon core (|z|≤13Å for a DPPC membrane). Solvation numbers were the average number of atomic species within the first solvation shells defined by radii 3.50, 3.20, and 3.65 Å for water oxygen (determined as a position of the 1^st minimum on the corresponding radial distribution functions for representative windows), phosphate oxygen, and carbonyl oxygen, respectively, relative to the nitrogen atom of the Lys side chain or analog. Arg solvation numbers have been calculated either as the average number of atomic species within the first solvation shell around the central guanidine C, as we have done previously ⁴¹, or for better comparison to Lys, as the corresponding average numbers of O atoms in the first solvation shells relative to the guanidine nitrogen atoms. See Supporting Information (Fig. S7) for a more detailed description. Interaction energies were obtained using long (20 Å) non-bond cutoffs previously shown to have similar results to using PME electrostatics ⁴¹ and avoiding net charge artifacts⁷⁵.

H-bond numbers were calculated with the criteria that the distance H⋯O < 2.5 Å, and the angle N-H ⋯ O>120° ⁷⁶. The relative free energy of H-bonding clusters (MguanH⁺ /MamH⁺)(PO₄−)_x(H₂O)_y (phosphate and water H-bonded to a charged analog) was calculated by

$$w(x,y)=-k_{B}T\mathrm{l}\mathrm{n}\rho (x,y)$$ (1)

where w(x, y) is the relative free energy, and ρ(x, y) is the normalized population calculated in different regions (Outer interface: |z|>22 Å; Interface: 22Å≥|z|>13Å; Interior: 13Å≥|z|>4Å; Central core: |z|≤4Å).

2.4 Potential of Mean Force and pK_a Shift Calculations

Umbrella sampling (US)⁷⁷ was used to calculate the free energy profile, or Potential of Mean Force (PMF) from 61 independent simulations (windows) in 1 Å steps spanning −30≤z≤30 Å, where z was the helix’s or the analog’s COM position relative to the bilayer COM, maintained by a harmonic constraint of 2.5 kcal/mol/Ų. Each system was simulated for about 8 ns following a 2–4 ns equilibrium period (see Fig. S1 for PMF convergence), and free energy profiles were then obtained using the weighted histogram analysis method.⁷⁸

In simulations of charged MamH⁺ or LysH⁺, the membrane was deformed when water molecules and lipid head groups entered the bilayer to solvate the charge, and such interfacial connections required an additional procedure to sample the equilibrium distribution of configurations,⁴¹ requiring simulations that sample connections between the charged analog and either the “near” or “far” (beyond the center of the membrane) interface when close to the center of the membrane (within ~1Å for DPPC, Fig. S2)⁶⁹. All 4 PMFs for Lys models in this study converged to within 0.5 kcal/mol (Fig. S1) with error bars less than 1 kcal/mol (Fig. S3, see Fig. S4 for convergence and error bars of Mam/DLPC simulations). In addition, the C27 force field used has been shown to yield free energies accurate to 1–2 kcal/mol for charged Arg models.⁷⁵ The lack of explicit treatment of polarizability in this force field, crucial for accurate ion solvation in non-polar solvents, does not affect charged Arg energetics due to membrane deformations ^75,79. For neutral Arg, water-alkane partitioning free energies (which dominate membrane partitioning energetics for neutral solutes) have been shown to be within 1 kcal/mol of both experimental and polarizable model values, with similar accuracy expected for Lys. The lack of effect of explicit polarizability for neutral solutes has also been seen in our studies of the general anesthetic chloroform ⁸⁰ Free energy contributions from different components (e.g. water, ion, lipid head groups) were calculated by integrating the negative of the mean force originating from those interactions,^31,41 using the same non-bond scheme and PME electrostatics as used in the MD simulations.

In order to investigate the protonation states of the side chains in the membrane, their pK_a shifts were calculated from the difference between the PMFs for neutral and charged species via a thermodynamic cycle ⁴¹:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{deprot}}}(z\text{'}\to z)=W_0(z\text{'}\to z)-W_{H^{+}}(z\text{'}\to z)$$ (2)

$$\mathrm{\Delta }p{K}_a=\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{deprot}}}/2.3k_{B}T,$$ (3)

where z is the analog or side chain position in the membrane, z' is its reference position in bulk water, W₀(z' → z) is the reversible work associated with moving the neutral form (e.g. Lys ⁰) from position z' to z, and W_H⁺ (z' → z) is that associated with moving the charged form (e.g. LysH⁺).

3 Results and Discussion

3.1 Comparison of Membrane Deformations

Equilibrated MamH⁺, LysH⁺, Mam⁰ and Lys⁰ systems (Fig. 1A to D) are compared to those of MguanH⁺, ArgH⁺, Mguan⁰ and Arg⁰ (right column) in Fig. 1, showing only the case where the side chain or analog was residing near the center of the lipid bilayer (where maximal membrane deformation has occurred). It can be seen that both charged Lys and charged Arg pulled extensive numbers of water molecules, as well as lipid head groups, into the bilayer, leading to similar local membrane perturbations. However, the neutral species did not cause such membrane deformations, because their interactions with water or lipid head groups were much weaker (see below).

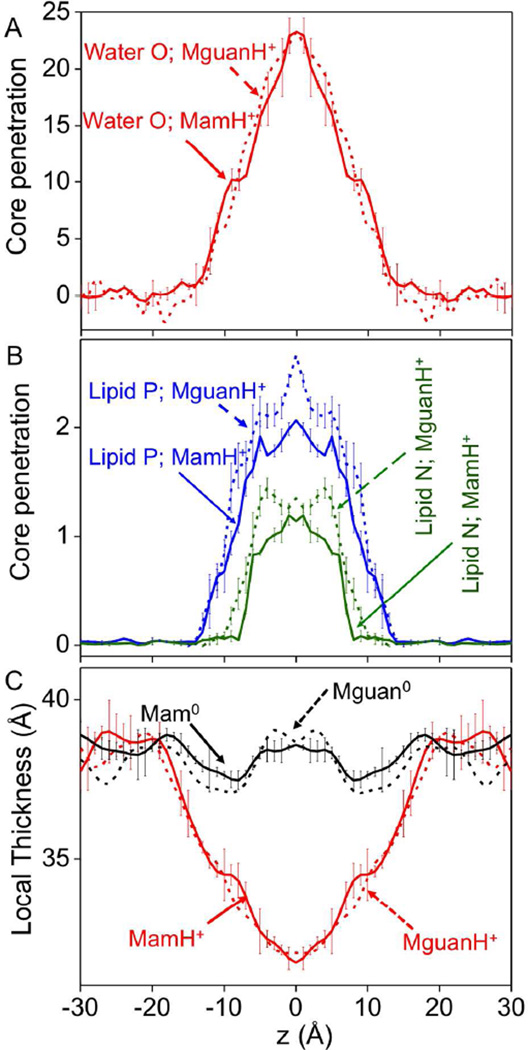
To quantify these membrane deformations, the penetration of polar species into the bilayer core is shown in Fig. 2A and B (only charged analogs MamH⁺ (solid) and MguanH⁺ (dashed) are shown). When MamH⁺ was at the membrane center, ~23 water molecules (solid red), ~2 lipid P atoms (solid blue) and ~1 lipid N (solid green) atom were pulled into the core. While core penetration of water due to MguanH⁺ was similar to MamH⁺, MguanH⁺ led to greater displacement of lipid head groups (dashed blue and dashed green), especially at greater depths (as illustrated by greater numbers of phosphate P atoms entering the membrane; Fig. 2B). We remark that this increased lipid phosphate penetration for Arg may become significant for a polypeptide containing multiple Arg side chains. Overall, however, the perturbations due to Lys and Arg analogs were broadly similar. This is further demonstrated by the changes in the local thickness of the membrane shown in Fig. 2C; both MamH⁺ and MguanH⁺ reduce the local membrane thickness by up to 7 Å.

Figure 2.

(A, B) Penetration of molecules into the bilayer hydrocarbon core (defined as |z|≤13Å) due to the insertion of MamH⁺ (solid) or MguanH⁺ (dashed): for water (red), lipid phosphate (blue), and choline groups (olive green). The number of core-located water molecules is calculated with respect to those in an unperturbed bilayer. (C) Local membrane thickness as a function of MamH⁺ (red) or Mam^0,s (black) z position. The local membrane thickness is defined as a vertical distance (along z axis) between P atoms on both sides of the membrane averaged over the centremost 4 P atoms in each leaflet. Corresponding thicknesses of MguanH⁺ Mguan⁰ systems are plotted as dashed lines. Error bars are based on asymmetries across the membrane center. Previously reported error bars for MguanH⁺/Mguan⁰, similar to MamH⁺/Mam⁰, are not shown for clarity.

The core penetration of water by the side chain on the TM helix, LysH⁺, was fairly similar to that by MamH⁺ (Fig. S5A), although there was a slight increase for the analog model, simply because the reaction coordinate chosen is the position of the MamH⁺ group itself, which passed through the bilayer center, whereas the Lys model on the TM helix may snorkel, by ~5 Å (data not shown), such that its ammonium group never resided right at the center of the bilayer (see e.g. Fig. 1B). As a result, the deformations due to LysH⁺ on the helix were smaller than those for MamH⁺. The effects of the helix on the core penetration of lipid P and N atoms were similar (Fig. S5B).

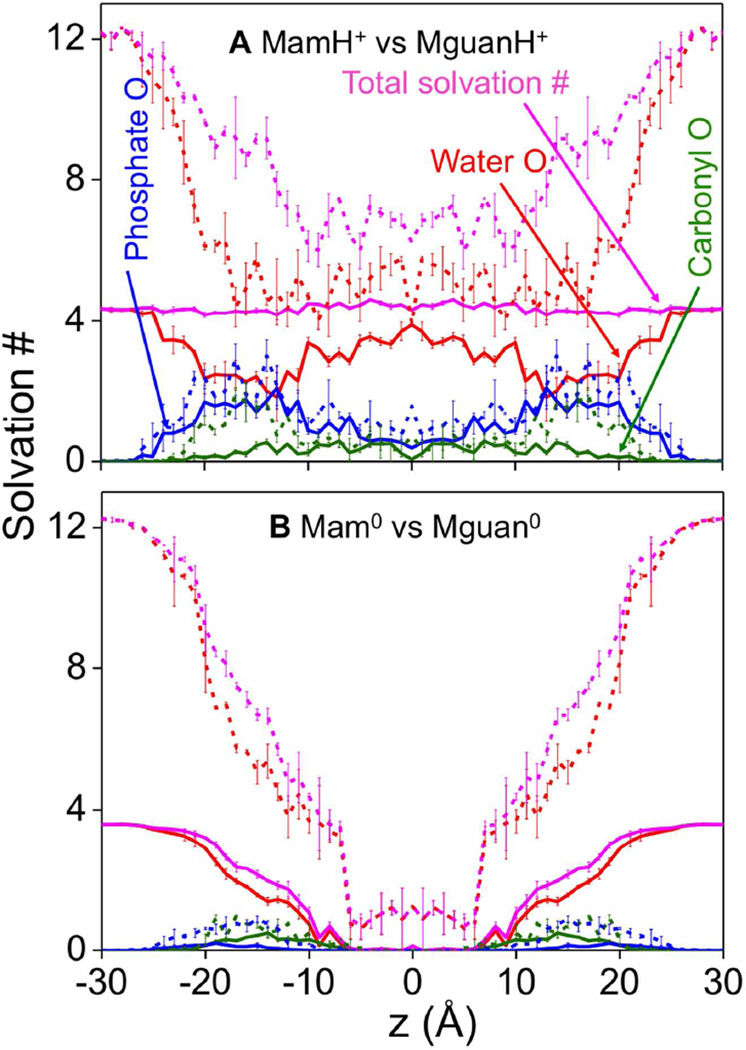
3.2 Side Chain Solvation within the Membrane

Solvation numbers for the Lys analog are compared to those for the Arg analog in Fig. 3A. Even at the center of the membrane, MamH⁺ (solid) was solvated by 3–4 water molecules (solid red) and about 1 lipid head group phosphate oxygen (solid blue; being higher near the interface). Although the LysH⁺ side-chain (shown in Fig. S6A) had similar coordination numbers to the analog MamH⁺, the presence of the host helix tended to decrease solvation by phosphate oxygen (solid blue) and carbonyl groups (solid green) in the interfacial region. We note that the host helix also led to reduced hydration in bulk water (especially for Arg), although the TM helix model was not designed for the aqueous phase.⁴¹

Figure 3.

Solvation analysis. Mean first-shell solvation numbers of MamH⁺ (A) and Mam⁰ (B) for water oxygen (red), lipid phosphate oxygen (blue), lipid carbonyl oxygen (olive green), and their sums, (i.e. total oxygen solvation numbers, pink) are shown as solid lines. Solvation numbers are the average number of atomic species within the first solvation shells defined by radii 3.50, 3.20, and 3.65 Å for water oxygen, phosphate oxygen, and carbonyl oxygen, respectively, relative to nitrogen atom of the Lys side chain analog. The corresponding numbers for MguanH⁺ (A) and Mguan⁰ (B) analogs are shown as dashed lines, with 1^st solvation shells defined by radii 4.85, 4.55, and 5.00 Å for water oxygen, phosphate oxygen, and carbonyl oxygen, respectively, relative to the central carbon atom of guanidine/guanidinium. Error bars have been calculated from asymmetries.

Arg analog or side chain’s solvation numbers were higher than those for Lys. For instance, MguanH⁺ or ArgH⁺ were bound to approximately one additional lipid phosphate oxygen atom at most positions across the bilayer (dashed blue curves in Figs.3A and S6A; being especially noticeable near the interface), ~1 additional glycerol ester carbonyl oxygen (dashed green curves) when near the interface, and ~2 additional water molecules (dashed red) throughout the membrane. This is to be expected because the guanidinium group has 3 amine groups (2 -NH₂ and 1 -NH-) to attract and form H-bonds with oxygen atoms, while MamH⁺ only has 1 such group (−NH₃). We remark that MguanH⁺’s solvation numbers in Fig. 3 were calculated in a way different from MamH⁺: they were computed around the guanidine C atom for MguanH⁺, compared to the ammonium N atom of MamH⁺. If we instead calculate MguanH⁺’s solvation numbers around each N atom (Fig. S7A), much more similar results for MguanH⁺ and MamH⁺ are obtained. The total solvation number of MamH⁺ was fairly constant (Fig. 3A, solid pink). For MguanH⁺, provided we compute solvation around the guanidinium N atoms, we also obtain well-defined first hydration shells with a fairly constant total coordination throughout the membrane (solid pink, Fig. S7A). However, using the central C selection (Fig. 3A, dashed pink), there was a large drop, because this central atom selection includes a broad and weakly interacting solvation shell, consistent with neutron diffraction experiments that have suggested guanidinium has no recognizable hydration shell. ⁸¹

In contrast, the neutral analogs (Mam⁰ and Mguan⁰; Fig. 3B) and side chains (Lys⁰ and Arg⁰; Fig. S6B) lost most of their coordination by lipid head groups and water in the middle of the membrane, due to weaker interactions. While Mam⁰ and Lys⁰ lost almost all of their coordinating oxygens, Mguan⁰ and Arg⁰ can occasionally maintain one or two water molecule in the first shell. The convergence analysis of Fig.S1D indicates that ~8 ns sampling time per umbrella sampling window was sufficient for neutral side chain models. While longer simulation times have been suggested for an Arg dipeptide⁸², using far more challenging free energy perturbation (involving partially charged intermediates⁴¹) in mixed lipid bilayers,⁸² we have observed frequent exchange of hydration water molecules with the bulk (typically occurring in a few hundred ps; not shown), and consistent analysis of hydration spanning 15 independent umbrella sampling simulations within the bilayer core, where dehydration had plateaued (Fig. 3B) for Mam⁰ or Mguan⁰. However, the near-complete dehydration suggests energetics for the neutral species will be determined by hydration energetics and not by membrane deformations, in stark contrast to the charged species.

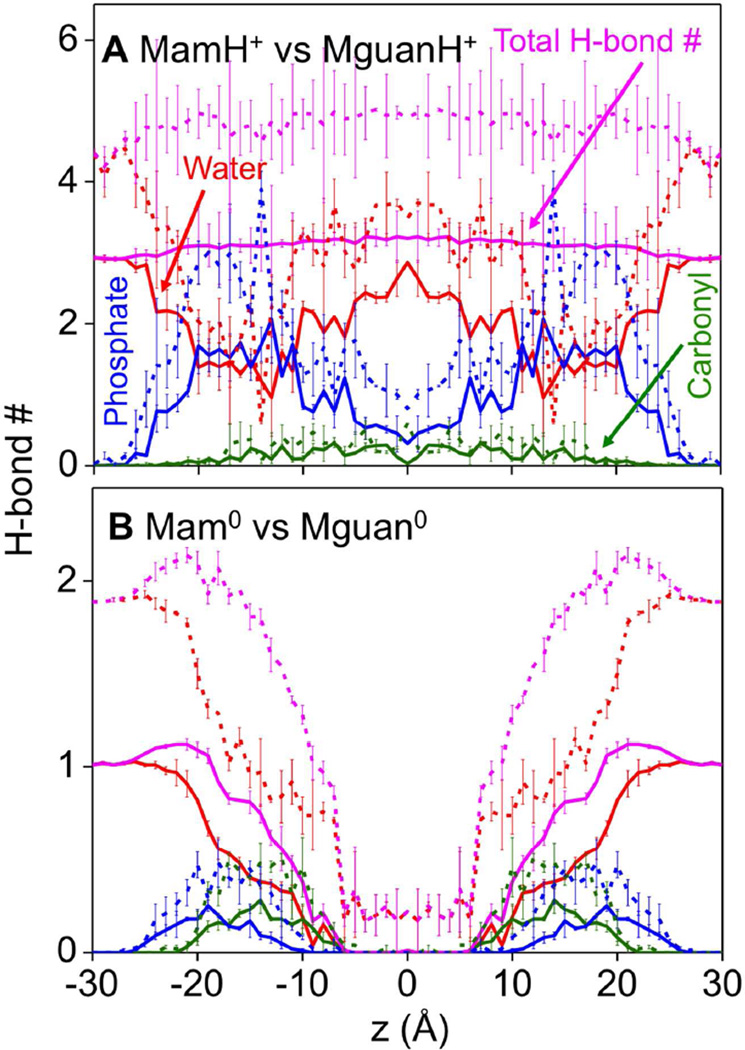
3.3 Hydrogen Bonds and Interaction Strengths within the Membrane

Among the oxygen atoms within the Lys or Arg solvation shells, we are particularly interested in those that formed H-bonds, shown in Fig. 4. The total number of H-bonds for MamH⁺ (solid pink in Fig. 4A) is fairly constant throughout the membrane, although individual terms vary with position: H-bonds mainly come from water in the core of the membrane or in bulk water, while about half of the H-bonds originate from lipids at the interface. H-bond numbers by phosphate for MamH⁺ are close to their solvation numbers, suggesting almost all 1st solvation shell phosphate O atoms form H-bonds with the ion, leading to well defined peaks in their radial distribution functions (Fig. S8). In the case of LysH⁺ (Fig. S9A), the helix has the effect of reducing H-bonding to lipids (Fig. S9A; phosphate-blue, carbonyl-green), but H-bonding to water (solid red) increases, so that the total H-bond number (solid pink) is still constant, around 3 corresponding to the number of H-bond donors in a charged Lys side chain or analog. Mam⁰ (Fig. 4B) and Lys⁰ (Fig. S9B) are very different; forming many fewer H-bonds (substantially less than their H-bonding capacity), and lose almost all of them in the membrane core due to dehydration.

Figure 4.

Hydrogen bond analysis. The numbers of hydrogen bonds of MamH⁺ (A) and Mam⁰ (B) by water (red), lipid phosphate (blue), and lipid carbonyl (olive green). The total hydrogen bond numbers are shown as pink lines. The corresponding numbers of MguanH⁺ and Mguan⁰ analogs are shown as dashed lines. Hydrogen bond D-H⋯A is defined when the distance H⋯A < 2.5 Å, and angle D-H⋯A >120°. Error bars have been calculated from asymmetries.

The H-bond plots for the Arg models share some similar characteristics to the Lys models. The total H-bond number for MguanH⁺ (dashed pink in Fig. 4A) is almost constant (around 4 – 5 with 5 H-bond donors in MguanH⁺), though individual components change. Also, Mguan⁰ forms fewer H-bonds (Fig. 4B), which disappear in the membrane core. In fact, the ratio of their total H-bond numbers is 5:3 for charged (MguanH⁺:MamH⁺) (Fig. 4A), and 2:1 for neutral (Mguan⁰:Mam⁰) (Fig. 4B, when |z|>15 Å) analogs, in line with their numbers of H-bond donors. We note that for both charged Arg and Lys analogs, the number of H-bonds to lipid carbonyl O atoms is substantially smaller than those for phosphate oxygens, but shows similar relative trends (see olive green curves in Fig. 4). We therefore focus most analysis on phosphate oxygen atoms, which are key to the differences in membrane interactions.

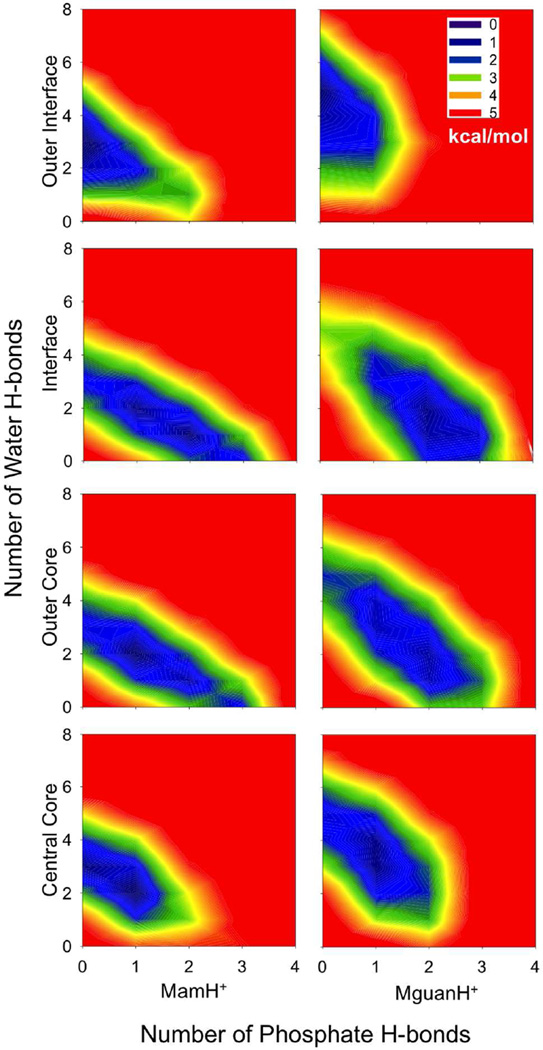
To quantify the relative stability of these H-bonding clusters (MguanH⁺/MamH⁺)(PO₄⁻)_x(H₂O)_y, a 2-D free energy map is shown in Fig. 5. In the outer interfacial region, the free energy basins are confined around clusters (MguanH⁺)(H₂O)₅ or (MamH⁺)(H₂O)₃, as their H-bonds mainly come from water. In the interfacial or outer core regions, the free energy basins are elongated along lines x+y=5 (MguanH⁺) or x+y=3 (MamH⁺), which indicates that the total H-bond numbers of MguanH⁺ or MamH⁺ are constant, because phosphate groups take the place of water molecules. In the central core of the membrane, the basins move back toward the y axis, as water molecules are contributing more to the total H-bonding for each analog. In all situations, the free energy rises sharply outside the basin. This tells us that MguanH⁺ and MamH⁺ must fulfill all of their H-bond capabilities.

Figure 5.

2-dimensional relative free energy map of hydrogen-bonding clusters, (MamH⁺ MguanH⁺PO₄⁻)_x(H₂O)_y (lipid phosphate and water forming hydrogen bonds with the charged analog), in different regions (Outer interface: |z|>22 Å; Interface: 22Å≥|z|>13Å; Outer core: 13Å≥|z|>4Å; Central core: |z|≤4Å).

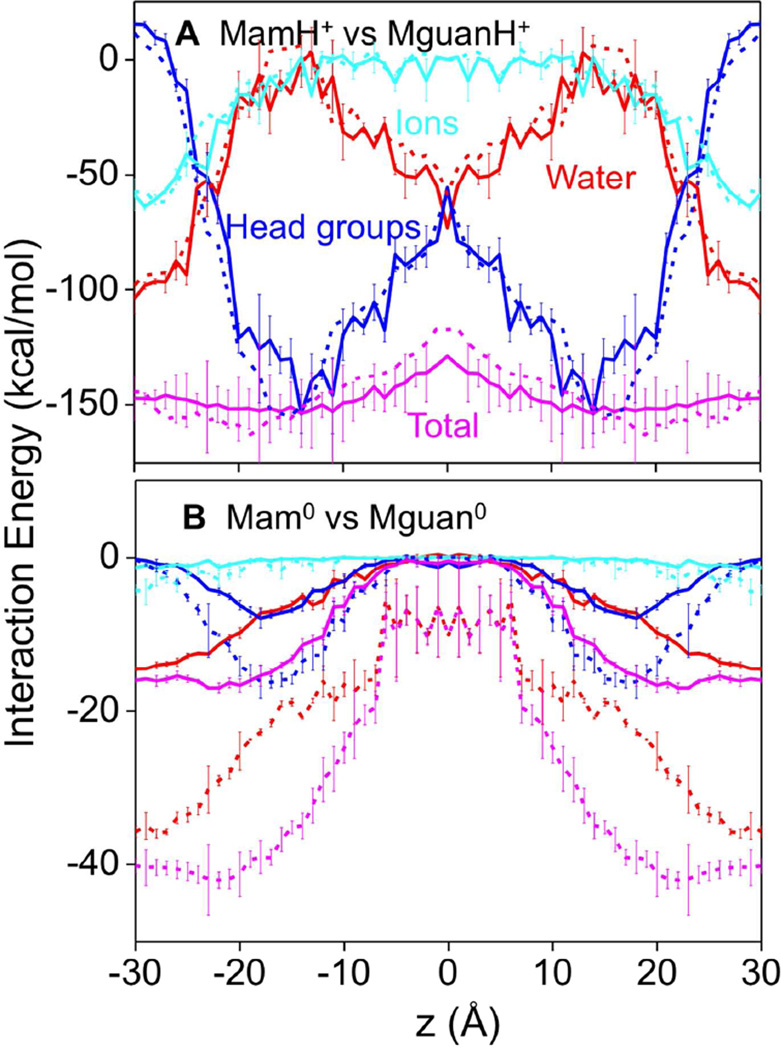
Interaction energies for the Lys analog (or side chain) with lipid head groups (sum of both phosphocholine and glycerol ester contributions, with the former being dominant), water and ions are illustrated in Fig. 6 (and Fig. S10). MamH⁺ (Fig. 6A) interacts with head groups (solid blue) or water (solid red) strongly throughout the membrane, with typical numbers near the interface of −100 kcal/mol or −150 kcal/mol respectively. LysH⁺’s interactions (Fig. S10A) are of a similar magnitude, but with smaller variations. MguanH⁺ and ArgH⁺ (dashed lines in Fig. 6A and Fig. S10A) have similar interaction energies to their Lys counterparts, despite the fact that MguanH⁺ and ArgH⁺ attract more polar molecules (especially water), and form more H-bonds. This similarity may result from the fact that the guanidinium group interacts weakly with many of its solvated polar molecules due to its delocalized charge, except for those that form H-bonds. Total interaction energies with polar components (Fig. 6A, pink curves) show much less z dependence for both MamH⁺ and MguanH⁺ throughout the membrane.

Figure 6.

Average side chain interaction energies of MamH⁺ (A) and Mam⁰ (B) with components: water (red); lipid head groups including carbonyl moieties (blue) and K⁺ & Cl⁻ ions (cyan), and total polar (pink). The corresponding numbers of MguanH⁺ and Mguan⁰ analogs are shown as dashed lines for comparison. Error bars have been calculated from asymmetries. Error bars for MguanH⁺/Mguan⁰, previously reported, are similar to MamH⁺/Mam⁰ and have not been shown for clarity.

As expected, interaction energies for Mam⁰ and Lys⁰ (Fig. 6B and S10B) are much weaker than those of charged species. For the neutral side chain models we see clear differences between Arg and Lys models. Charge delocalization, together with increased dipole moment (Mguan⁰ 2.2 D ⁴² and Mam⁰ 1.6 D ⁸³), leads to stronger interactions with neutral Arg compared to neutral Lys; e.g. the interaction energy between neutral Mguan⁰ and head groups (Fig. 6B; dashed blue) in the interfacial region is −15 kcal/mol, while that for neutral Mam⁰ (Fig. 6B; solid blue) is −8 kcal/mol. Another contributor to neutral Arg’s stronger interactions is its ability to form a greater number of H-bonds (Fig. 4B). Total interaction energies show similar trends (Fig. 6B, pink curves), with Mguan⁰ being more than twice that for Mam⁰. Because Mguan⁰ is coordinated by 1–2 water molecules near the membrane center (Fig. 3B), its energy of interaction with polar membrane components does not vanish, unlike that for Mam⁰, which is completely dehydrated.

3.4 H-bonding Clusters

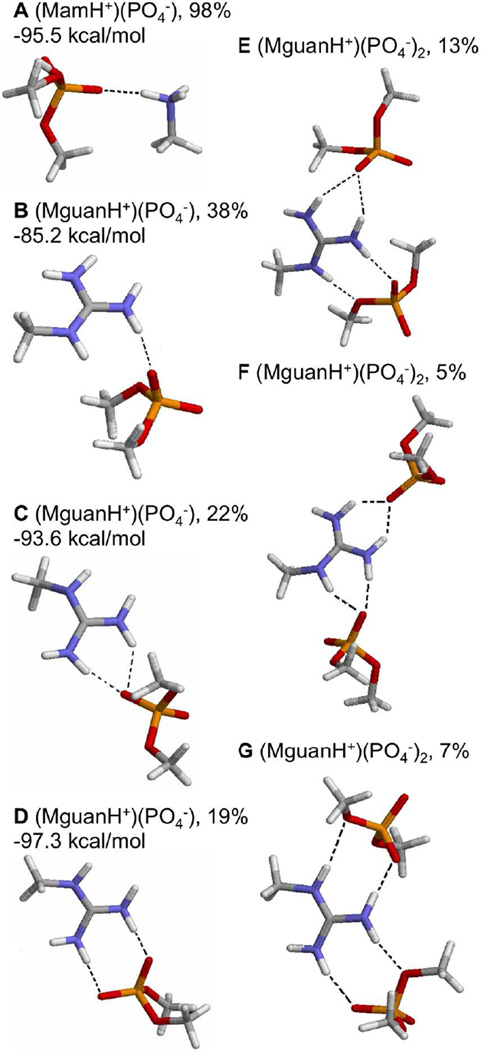
The H-bonding clusters that phosphate groups form with MamH⁺ or MguanH⁺ are shown in Fig. 7. In our simulations, when an oxygen atom of a phosphate group fell within the 1^st solvation shell of MamH⁺, that PO₄⁻ group almost always (98% of the time) formed 1 H-bond with the ammonium group in a ‘co-linear’ configuration (Fig. 7A), where the angle N-H…O and the angle between N-H and P-O vectors were greater than 130° (Fig. S11). In contrast, when a single phosphate group coordinated MguanH⁺, it formed a single oxygen-single amine H-bond (Fig. 7B) only 38% of the time, preferring to form multiple H-bonds 41% of the time (over-coordinated oxygen (OCO), Fig. 7C, 22%, and bidentate H-bond, Fig. 7D, 19%).

Figure 7.

Representative H-bonding configurations of cluster (MamH⁺)(PO₄⁻) (A), (MguanH⁺)(PO₄⁻) (B, C, D), (MguanH⁺)(PO₄⁻)₂(E, F, G). Hydrogen bonds are shown as dashed lines. C shows an “OCO (overcoordinated O) H-bond”, D shows a “bidentate H-bond”. E shows MguanH⁺ forming an OCO H-bond with one phosphate group and a bidentate H-bond with the other. F shows MguanH⁺ forming 2 OCO H-bonds with 2 phosphate groups. G shows MguanH⁺ forming 2 bidentate H-bonds with 2 phosphate groups, called “Arg-fork”. Their percentage and the associated average interaction energy between the charged analog and phosphates are also shown. The percentage in (A) was calculated as the number of PO₄⁻ forming H-bonds with MamH⁺ / the number of PO₄⁻ coordinating with MamH⁺ in all simulations; The percentages in (B,C,D) were calculated as the number of that configuration / the number of (MguanH⁺)(PO₄⁻) clusters, where at least 1 oxygen of PO₄⁻ fell in the 1^st solvation shell of MguanH⁺, in all simulations; The percentages in (E,F,G) were calculated separately as the number of that configuration / the number of (MguanH⁺)(PO₄⁻)₂ clusters.

Average interaction energies for a single H-bonded PO₄⁻ with MamH⁺ or MguanH⁺ are also given in Fig. 7. When there is only 1 H-bond to a lipid phosphate, MguanH⁺ interacted more weakly than MamH⁺ (the mean interaction energies for MguanH⁺ and MamH⁺ are −85.2 kcal/mol and −95.5 kcal/mol, respectively), probably because the charge in the Lys analog is more localized ⁵². However, when there are 2 H-bonds between MguanH⁺ and a phosphate group, the interaction energy strengthens to ~-95 kcal/mol (Fig. 7C & D), close to that for MamH⁺. This indicates that the (MguanH⁺)(PO₄⁻) complex gains stability from multiple H-bonds, and agrees with a recent computational study that showed bidentate H-bond between Arg and phosphate yielded a low H-bonding free energy in solution,⁵² as observed in recent NMR studies.⁸⁴

When coordinating more than 1 phosphate, MguanH⁺ can form multiple H-bonds with each of them (Fig. 7E, F, G). Phosphate groups are more likely to form multiple H-bonds in (MguanH⁺)(PO₄⁻)₂ clusters (52% of the time) than in (MguanH⁺)(PO₄⁻) (41% of the time), as fewer water molecules are competing for H-bonds in (MguanH⁺)(PO₄⁻)₂ clusters. When both phosphates coordinate the guanidinium group by bidentate H-bonds, this is called an “arginine-fork” (Fig. 7G). This configuration is assumed by 7% of (MguanH⁺)(PO₄⁻)₂ complexes and has been previously reported to play important roles in biological functions such as DNA/RNA binding,^85,26 and is expected to be an important contributor to lipid bilayer perturbations.

3.5 TM Pores Stabilized by Arg

We propose that the extensive H-bond capabilities of the guanidinium group of Arg are responsible for promoting membrane deformations. While complete defect formation may be rare in bilayers such as DPPC, they may occur much more frequently in bilayers of other compositions. To better illustrate the differences between Arg and Lys, we now explore their interactions with a thinner DLPC lipid bilayers, since the local thinning of the membrane is involved in many membrane biological processes, such as in CPP activity.⁶

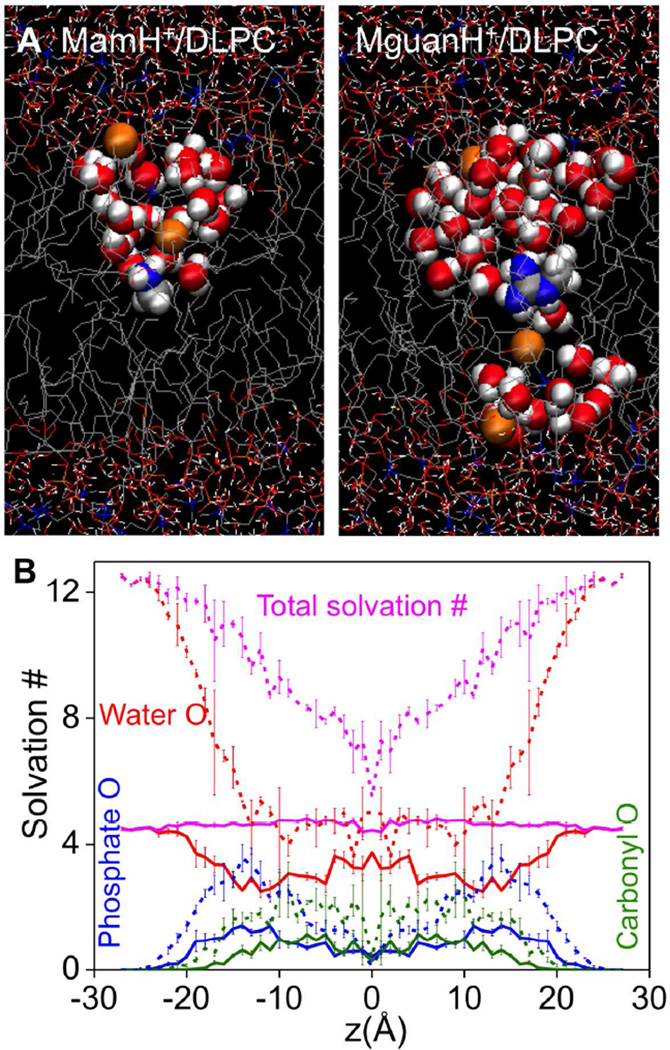
As illustrated in Fig. 8A (right), in the case of DLPC, MguanH⁺ can pull in water and head groups from both sides of the membrane, leading to a transmembrane defect that is stable during the whole simulation of more than 20ns. This was seen independently in simulations of DLPC with the analog COM positioned at z=0 and ±1Ǻ (as well as in dimyristoylphosphatidylcholine, DMPC, with 14 C-long saturated tails at z=0 ⁶⁹). In addition, when we moved MguanH⁺ from z= ±2 to ±1 Ǻ in DLPC simulations, the TM pores occurred within a few ns, indicating the TM pore does not depend on the initial condition of MD simulations. While Fig. 8B shows MguanH⁺’s solvation numbers are largely the same as they were in DPPC, the occurrence of a TM pore means that MguanH⁺ pulls in water and head groups from both sides of the membrane, as illustrated by the distribution of lipid P and water O atoms along z-axis (Fig. S12). In MamH⁺ simulations (Fig. 8A left), however, such TM pores occurred only briefly in DLPC membranes (z=–1, 0 Ǻ), but disappeared quickly (in 0.5ns) and never returned in 20ns.

Figure 8.

(A) Equilibrated MD systems for charged methyl-ammonium analog (MamH⁺,left), charged methyl-guanidinium analog (MguanH⁺, right) near the center of the DLPC bilayer. The style and color scheme is the same as that in Fig.1. Lipid phosphate and water atoms that have been pulled into the bilayer core (|z|≤11Å) are drawn as balls. (B) Mean first-shell solvation numbers of MamH⁺ in DLPC, calculated in the same way as those in Fig. 3, for water oxygen (red), phosphate oxygen (blue), and lipid carbonyl oxygen (olive) are shown. Total solvation numbers are drawn as pink lines. Corresponding numbers for MguanH⁺ analog are shown as dashed lines. Error bars have been calculated from asymmetries.

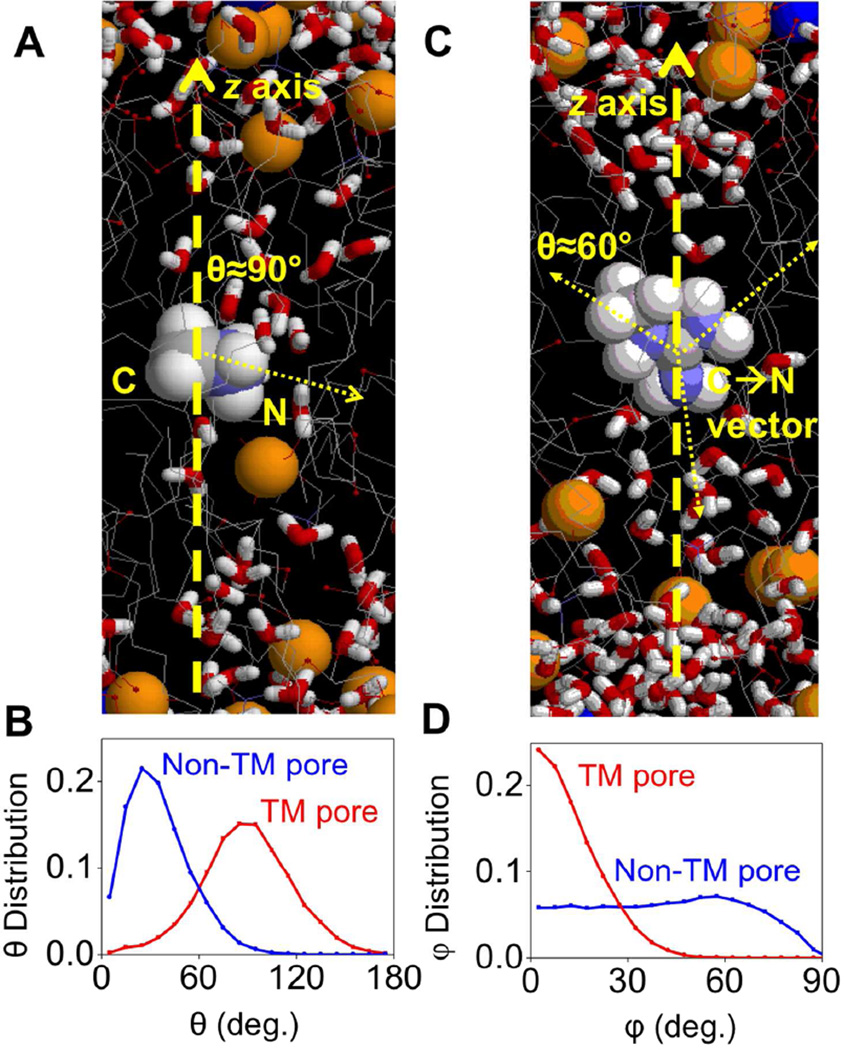
A closer look at the trajectory of MamH⁺ simulations reveals that, when a TM pore occurs transiently, MamH⁺ is attempting to stabilize it with its 3 H-bond donors so that the C-N vector lies in the xy plane most of the time (Fig. 9A,B). However, this configuration is not stable, and MamH⁺ will re-orient to point its C-N vector to the nearest interface, and the TM pore disappears quickly. For MguanH⁺, when a TM pore forms, it recruits polar species from both sides of the membrane with its 5 H-bond donors. This aligns its molecular plane almost parallel to the z-axis (Fig. 9C,D), so that H-bonds can form, with favorable interactions (e.g. with proper D-H⋯A angle and H⋯A distance). Stabilization of the TM pore by H-bonds also leads to preferred orientation of C-N vectors in MguanH⁺, as shown in Fig. 9C: one C-N vector would be parallel to the z-axis while the other two would form angles of about ±60° with the z-axis (Fig. S13).

Figure 9.

(A) A snapshot taken from MamH⁺/DLPC simulations when a TM Pore occurs in the very beginning. Yellow spheres represent phosphorus atoms; gray lines represent hydrocarbon tails of lipids; Water molecules are shown as red and white sticks. Refer to Fig. 8A for Mam⁺/DLPC simulation snapshot without a TM pore. (B) The normalized distribution of angles between C-N vector and z-axis in MamH⁺/DLPC simulations (z=0), when TM pores occur (red) or do not (blue). (C) A snapshot of MguanH⁺/DLPC simulation with a TM pore, where the 2 upward C-N vectors of MguanH⁺ form angles around ±60° with the z-axis, and the downward one forms an angle of about 180°. (D) The normalized distribution of angles between the MguanH⁺ molecular plane (defined by the 3 N atoms) and the z-axis in MguanH⁺/DLPC simulations, when TM pores occur (red) or do not (blue).

All of these findings highlight the significance of the H-bonding capacity of the guanidinium group and its geometry. We predict that Arg can induce pores in lipid bilayers by attracting water or head groups from both sides with multiple H-bonds, and thus can cause greater membrane deformations.

3.6 Membrane Binding and Translocation Thermodynamics

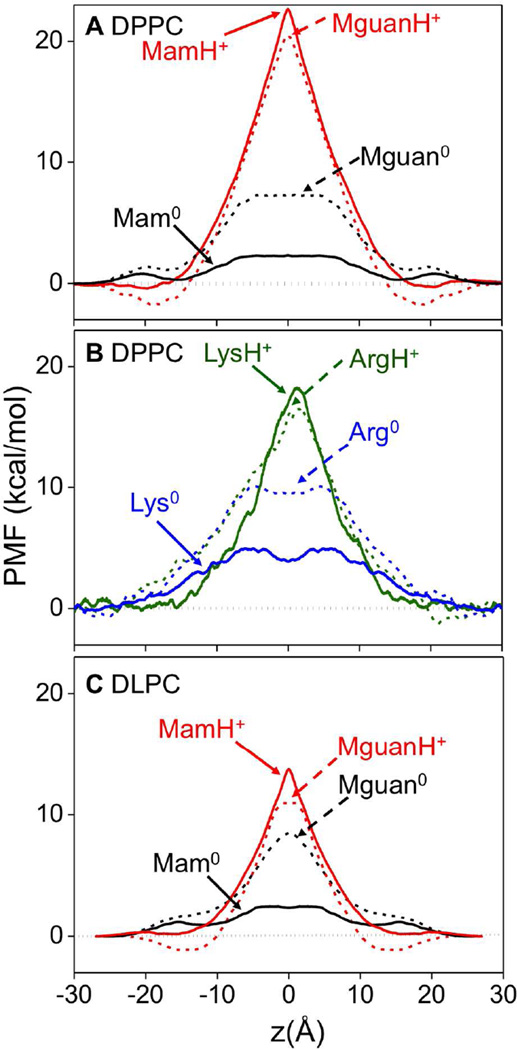
We now reveal the free energies that govern the partitioning and thermodynamic stability of Lys and Arg side chains in the membrane, as shown in Fig. 10. All charged Arg and Lys side chain and analog models show “Λ” (or inverse “V”) shaped free energy profiles. The free energy barrier for MamH⁺ (solid red, Fig. 10A&S3A) to cross the membrane is high, at 22.5±0.2 kcal/mol, as it is for MguanH⁺ at 21.6±0.1 kcal/mol (dashed red, Fig. 10A), both exhibiting a very similar slope that is steeper than a typical dielectric barrier for a model membrane.⁷⁵ We attribute this to the strongly repulsive forces as the charge enters the bilayer and causes significant membrane deformations. The PMFs of LysH⁺ and ArgH⁺ attached to TM helices are compared in Fig. 10B; solid and dashed green curves, respectively). The helix introduces various influences on the PMF.⁴¹ On one hand, it lowers the free energy barrier by artificially reducing side chain hydration in bulk water, while also raising the local dielectric response within the membrane interior. We also note that the side chains (butylammonium and propylguanidinium) are bigger and more hydrophobic than the chosen analog molecules (methylammonium and methylguanidinium). In addition, the poly-Leu helix increases the barrier because it also excludes a non-polar Leu residue from the membrane when Lys or Arg enters. Finally, and importantly, the ammonium group on the Lys side chain and guanidinium group on the Lys side chain can snorkel to approach the interface (see Fig. 1B), reducing the free energy cost, which cannot occur for the analog molecules.

Figure 10.

(A) Symmetrized PMFs for analogs, MamH⁺ (solid red), Mam⁰ (solid black), MguanH⁺ (dashed red) and Mguan⁰ (dashed black) in DPPC. (B) PMFs for side chains LysH⁺ (solid olive green), Lys⁰ (solid blue), ArgH⁺ (dashed olive green) and Arg⁰ (dashed blue) in DPPC. (C) Symmetrized PMFs for analogs, MamH⁺ (solid red), Mam⁰ (solid black), MguanH⁺ (dashed red) and Mguan⁰ (dashed black) in DLPC. See Figs. S1, S3, S4, and Supporting Text for PMF convergence and error bars.

The MguanH⁺ (Fig. 10A, dashed red) and ArgH⁺ (Fig. 10B, dashed green) free energy barriers are remarkably similar to those of their corresponding LysH⁺ and MamH⁺ models. The one difference is that only the Arg side chain models experience interfacial binding (with wells of ~-1.5 kcal/mol located around |z|=18 Å for the analog MguanH⁺). This reveals a preference for guanidinium to bind at the interface, which can be explained by its greater coordination and extensive H-bonding with lipid head groups. This preferential binding is consistent with recent studies on CPP’s,^86–87 and may help explain a preference for Arg in these membrane-perturbing peptides.^{6, 19–20}

If one removes the difference in free energy at the interface, the PMFs for MamH⁺ and MguanH⁺ are almost identical (not shown). This outcome is surprising, given that these analogs are so different in terms of size, hydration free energy (−62 kcal/mol for MguanH⁺, and −72 kcal/mol for MamH^+, see Table S1) and H-bonding capacity. The similarity is also clearly evident in the work decomposition analysis reported in Fig. S14. The MamH⁺ and MguanH⁺ PMFs are also very similar to those for other charged molecules with various chemistries and hydration free energies.⁷⁹ We attribute this to the consequences of the membrane deformations; when a charged molecule crosses the membrane, it remains coordinated by water molecules and lipid head groups pulled into the membrane. It thus continually reforms the interface, such that it never partitions from water to the hydrophobic core, and therefore it is the cost to deform the membrane instead of their hydration energies that determines these PMFs.^{79, 89} This is in stark contrast to standard models⁹⁰ that would estimate very different energetics according to hydration free energies.

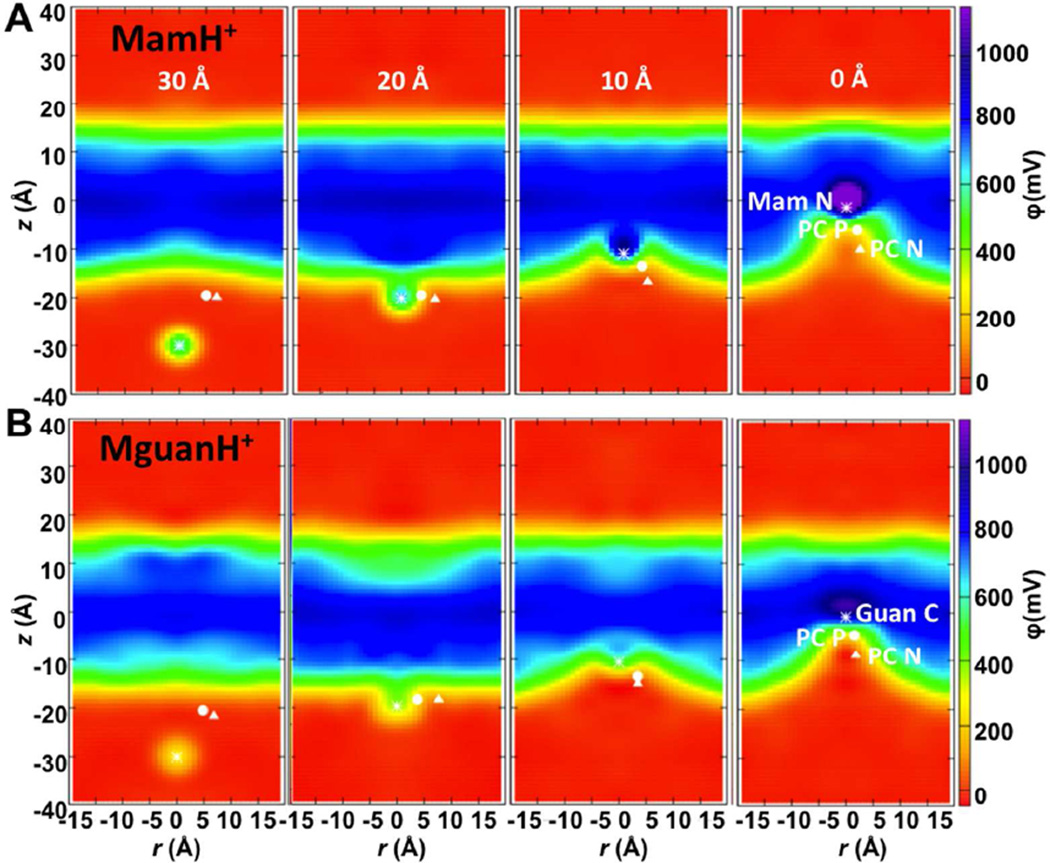
To assist in explaining the origin of the similar PMF profiles for charged Arg and Lys side chains, we have computed electrostatic potential maps for several MguanH⁺ and MamH⁺ umbrella sampling windows, shown in Fig. 11. As a translocating charged species (white asterisk) moves across the membrane, it is always located at the interface between regions of a low potential (red; bulk aqueous solution) and high potential (blue; hydrophobic membrane interior), and never crosses it.⁷⁹ Each charged molecule experiences a high and nearly constant force pushing it back to the aqueous solution, being similar for both MguanH⁺ and MamH⁺ (see 1D potential profiles in Fig. S16); presumably because the costs involved are those for deforming the membrane and are similar for each translocating charge. The fact that the ion is always located at the deformed interface and senses a fairly constant opposing force explains the “Λ” shaped profiles.⁷⁹ The side chain analogs do, however, lead to differing results in the thinner DLPC membrane, where MguanH⁺ can form a TM pore (Fig. 9C), leading to a lower-potential region extending across a membrane (Fig. S17), with MguanH⁺ experiencing no electric field at the membrane center (Fig. S18), corresponding to the plateau in the PMF (dashed red line in Fig. 10C).

Figure 11.

Electrostatics of the deformable DPPC membrane: 2D electrostatic potential maps along the z axis and distance r from the z axis when the MamH⁺ (A) or MguanH⁺ (B) ion is located in outer interface region (<z(ion)>≈−30Å), membrane interface (<z(ion)>≈−20Å), outer membrane core (<z(ion)>≈−10Å), and around the membrane center (<z(ion)>≈0Å). The average positions of the ion (N for MamH⁺ and guanidinium C for MguanH⁺) and its closest DPPC P and N atoms are shown as asterisk, circle and triangle, respectively. The corresponding system snapshots for <z(ion)>≈0 Å are shown in Fig. 1 and 1D electrostatic profiles are shown in Fig. S16.

The PMF’s of the neutral Mam⁰ (Fig. 10A, solid black) and Lys⁰ (Fig. 10B, solid blue) exhibit lower free energy barriers (~2.5 kcal/mol for Mam⁰, and ~4 kcal/mol for Lys⁰, respectively), determined by simple dehydration. The free energy barriers for Mguan⁰ and Arg⁰ are considerably higher than for the Lys counterparts, due to their higher dipole moments and because they break more H-bonds when entering the membrane. As a result, we anticipate a lower free energy barrier for Mam⁰ to cross the membrane, simply based on hydration free energies (Mguan⁰: −11.2 kcal/mol,⁹¹ Mam⁰: −4.6kcal/mol,⁹² see also Table S1).

3.7 Comparison of Lys and Arg pK_a Profiles

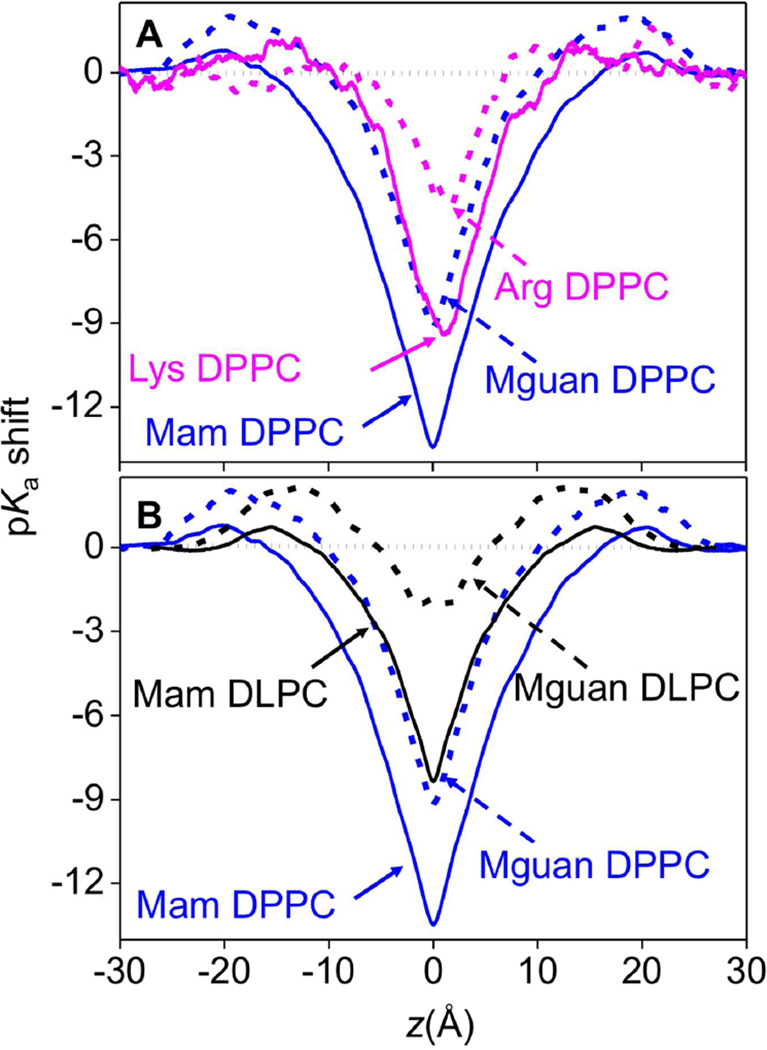
The ability of Lys and Arg to carry charge is essential for numerous membrane biological processes. While these 2 amino acid side chains are protonated in water at pH 7 (the pK_a of Arg is 12–13.7,^13–14 and that of Lys is ~10.5 ¹⁵), it is possible that they may take neutral forms in the membrane core because the PMFs of charged Lys and Arg exhibit high barriers. As shown in Fig. 12A&S19, the pK_a shifts for the Lys analog and side chain near the membrane center reach up to −13.5±0.2 and −9.5±0.3, respectively (solid lines); both of which are significantly (~4–5 units) greater than that experienced by Arg (−9.2±0.1 for analog and ~ −4.5 for side chain, dashed lines in Fig. 12A). Because the free energies of LysH⁺ and ArgH⁺, as well as those for corresponding analogs, are roughly similar inside the membrane (Fig. 10), this difference is caused primarily by the difference in free energies of their neutral states: with that of neutral Arg being higher due to its higher dipole moment and greater extent of dehydration in the membrane relative to bulk water.

Figure 12.

(A) pK_a shift profiles for the Mam analog (solid blue), Lys side chain (solid pink), Mguan analog (dashed blue) and Arg side chain (dashed pink) in DPPC. (B) pK_a shift profiles for Mam analog (solid black), Mguan analog (dashed black) in DLPC, corresponding Mam/Mguan pK_a shift profiles in DPPC are plotted as solid/dashed blue lines. See Fig. S19 and Supporting Text for pK_a shift profile error bars.

Perhaps this outcome is not altogether surprising, given that the partitioning free energy from water to cyclohexane for the neutral Lys side chain analog is much lower than that for neutral Arg (Table S1), explained in terms of both H-bonding capacity and dipole moment (e.g. see ³²). Considering the pK_a for Lys is ~10.5 in aqueous solution, it will decrease to −3 or 1, for Mam and Lys, respectively, in the center of the membrane. In fact, when the Lys analog and side chain are still quite far from the membrane center, |z|~9Å for the analog and |z|~5Å for the side chain, their pK_a will drop below 7, which means they will very likely take neutral forms anywhere inside the membrane core under physiological conditions. In contrast, Arg has a higher aqueous pK_a of 12–13.7,^13–14 but a smaller pK_a shift. The pK_a of methylguanidinium will drop below 7 only when within ~2 Å from the membrane center, while that of Arg side chain remains above 7 throughout the membrane, as shown in Fig. 12. This makes Arg a unique amino acid to maintain charge, even in the seemingly hostile environment of the core of a lipid membrane.^41–42 Importantly, Fig. 12B shows that, even at the center of a thinner DLPC membrane, Lys will deprotonate, whereas Arg will suffer little pK_a shift, demonstrating a clear difference in the charge carrying abilities of Arg and Lys. This is in agreement with recent experimental results suggesting deprotonation of a Lys but not Arg side chain located in the middle of trans-membrane GWALP peptide. ⁹³

4 Conclusions

Atomistic simulations on Lys have been carried out with both simple side chain analogs and a TM helix model to provide a detailed comparison to Arg in its ability to interact with and deform lipid membranes. When a charged Arg or Lys side chain entered a DPPC membrane, it deformed the bilayer by pulling up to ~23 water molecules and ~2 lipid head groups into the hydrocarbon core due to their strong interactions. Charged Lys experienced total solvation that was fairly constant throughout the membrane, but individual components changed with depth. The free energy barriers for charged analog MamH⁺ or side chain LysH⁺ to cross the membrane were about 22.5 kcal/mol or 18.0 kcal/mol respectively.

Charged Arg causes very similar membrane deformations to Lys, but can pull in more lipid head groups. This difference is small, but significant, and is expected to play an important role when multiple basic side chains are present (e.g. in CPPs and AMPs). Charged Arg is solvated by more oxygen atoms and can form more H-bonds than Lys, but interacts with individual polar molecules more weakly due to its delocalized charge. We have demonstrated that Arg can form multiple H-bonds and lead to more dramatic membrane deformations, including the pulling in of polar species from both sides of the bilayer to form a TM defect in a thinner DLPC membrane. The free energy barriers for charged Arg and Lys are surprisingly similar, because they cause similar perturbations to the bilayer. The only difference is the more significant binding of Arg to the interfaces, as a result of Arg’s greater solvation and H-bonding with lipid head groups.

Neutral Lys interactions with water or lipid head groups are weaker and thus do not deform the membrane significantly. They lose almost all H-bonds when in the hydrophobic core. The free energy barriers for neutral analog Mam⁰ and side chain Lys⁰ are ~2.5 and ~4 kcal/mol, governed by simple dehydration energies. These low free energies lead to large pK_a shifts of up to −13.5 for the analog and −9.5 for the side chain, suggesting Lys will very likely be deprotonated in the membrane. In contrast, the neutral Arg analog or side chain interacts with water or lipid head groups more strongly, due to their larger dipole moments, and experience greater dehydration relative to bulk water, which leads to higher free energy barriers. These higher free energy barriers for neutral Arg result in moderately small pK_a shifts and indicate that Arg will most likely retain its charge in the hydrophobic core of the membrane.

We expect similar Arg and Lys translocation free energies and pK_a shifts for a range of lipid membrane compositions, including membranes containing anionic lipids. We have previously shown that the free energy cost for charged Arg translocation drops by 2–3 kcal/mol in the presence of phosphatidylglycerol lipids. This effect is primarily due to increased interfacial binding, with the actual forces felt by the side chain across the bilayer being largely unchanged as a result of membrane deformations.⁹⁴ For Lys, this effect is expected to be even smaller due to weaker interfacial binding.

These findings have implications for a range of membrane protein and membrane-active peptide phenomena, where interactions between protein and lipids play important roles. For instance, our observations can explain why Arg-rich CPPs perform better than Lys-rich CPPs ¹⁸ via a direct membrane-penetrating mechanism (e.g.^{6, 86}). First, the guanidinium group of Arg can bind to the interface more favorably, and due to its more extensive H-bonding to lipids, is more likely to cause local thinning of the bilayer. The guanidinium group is then better at inducing a TM pore due to its capacity to attract more head groups and form multiple H-bonds, including ones from both interfaces of the lipid bilayer. Furthermore, Arg’s ability to retain its charge, even within the hostile environments of a membrane, is not only a prerequisite for causing cell-perturbations, but helps explain why it appears more frequently in the voltage sensor domains of ion channels,⁴ for example. In fact, the existence of Arg in voltage sensors is suggested to be an adaptation to the phospholipid composition of cell membranes.⁹⁵ These findings help us understand a broad range of biological phenomena, including the actions of antimicrobial, toxin and cell penetrating peptides, and a diverse range of membrane protein functions involving charged protein domains.