Abstract
Cervical cancer is a leading cause of cancer mortality in women worldwide. Human papillomavirus (HPV) types 16 and 18 cause about 70% of all cervical cancers. Clinical trials have demonstrated that three doses of either commercially available HPV vaccine, Cervarix ® or Gardasil ®, prevent most new HPV 16/18 infections and associated precancerous lesions. Based on evidence of immunological non-inferiority, 2-dose regimens have been licensed for adolescents in the United States, European Union, and elsewhere. However, if a single dose were effective, vaccine costs would be reduced substantially and the logistics of vaccination would be greatly simplified, enabling vaccination programs in developing countries. The National Cancer Institute (NCI) and the Agencia Costarricense de Investigaciones Biomédicas (ACIB) are conducting, with support from the Bill & Melinda Gates Foundation and the International Agency for Research on Cancer (IARC), a large 24,000 girl study to evaluate the efficacy of a 1-dose regimen. The first component of the study is a four-year non-inferiority trial comparing 1- to 2-dose regimens of the two licensed vaccines. The second component is an observational study that estimates the vaccine efficacy (VE) of each regimen by comparing the HPV infection rates in the trial arms to those in a contemporaneous survey group of unvaccinated girls. In this paper, we describe the design and statistical analysis for this study. We explain the advantage of defining non-inferiority on the absolute risk scale when the expected event rate is near 0 and, given this definition, suggest an approach to account for missing clinic visits. We then describe the problem of estimating VE in the absence of a randomized placebo arm and offer our solution.
Keywords: Human papillomavirus, HPV, Non-inferiority trial, Vaccine efficacy, Clinical trial
1. Introduction
Cervical cancer is a leading cause of cancer mortality in women worldwide. Human papillomavirus (HPV) types 16 and 18 cause about 50% and 20% of cervical cancers respectively; the remaining 30% are caused mainly by ten other carcinogenic types. Therefore, HPV vaccines directed at these types have the potential to substantially reduce cervical cancer incidence and subsequent mortality.
Clinical trials [1–4] have demonstrated that three doses of either of the two commercially available HPV vaccines, Cervarix or Gardasil, prevent most new HPV 16/18 infections and associated precancerous lesions. These trials have resulted in their 3-dose regimens being approved in the United States and elsewhere. Later, based on the evidence of immunological non-inferiority, 2-dose regimens have been licensed for adolescents in several countries. However, if a single dose were effective, vaccine costs would be reduced substantially and the logistics of vaccination would be greatly simplified, enabling vaccination programs in developing countries. Two lines of evidence already support the efficacy of one dose. A single dose induces a persistent [5] immunological response exceeding that produced by natural infection. Moreover, the small number of women who received only a single dose in previous trials had high protection against HPV16/18 infection and related diseases [5–8]. Nevertheless, more data are needed to determine the efficacy of one dose.
The National Cancer Institute (NCI) and the Agencia Costarricense de Investigaciones Biomédicas (ACIB) are conducting, with support from the Bill & Melinda Gates Foundation and IARC, a large 24,000 girl study to evaluate the efficacy of a one-dose regimen. The first component of the study is a four-year non-inferiority trial comparing a 1-dose regimen and the currently recommended 2-dose regimen of each of the licensed vaccines. The second component is an observational study that estimates the vaccine efficacy (VE) of each regimen by comparing the HPV infection rates in the trial arms to those in a contemporaneous group of girls, referred to as the “survey cohort”, who had not been vaccinated at an earlier age. This study, for the reasons discussed below, poses special challenges and requires novel approaches in design and analysis.
The challenge in the non-inferiority trial is to choose a meaningful definition for non-inferiority. Letting π1 and π2 be the risk of infection in the 1- and 2-dose arms respectively, we could either define non-inferiority as π1 − π2 < tAR (i.e. on the risk difference scale) or π1/π2 < tRR (i.e. on the relative risk scale), where tAR and tRR are appropriately chosen thresholds. We chose the nontraditional option, de-fining non-inferiority on the risk difference scale [9], for the reasons fully explained in the Discussion. In brief, because we expect an extremely low event rate in the two dose arm, we believe there is no meaningful threshold (tRR) for defining non-inferiority on the relative risk scale and furthermore we can show that tests of non-inferiority on the relative risk scale will have low power. Moreover, the risk difference better captures the effect on public health from choosing a 1-dose regimen. This decision requires us to use nontraditional statistical tools, designed for testing the risk difference [10–14], and to modify these tools to account for missing data.
The challenge in estimating vaccine efficacy (VE), where VE = 100(1 − RR) and the relative risk (RR) compares vaccinated to unvaccinated girls, is the lack of a placebo-controlled trial arm. An ideal statistical design for estimating vaccine efficacy would have been to compare the cumulative rate of incident HPV 16/18 infections during the study in each trial arm to the rate of incident infections in a concurrently randomized placebo control arm. However, given the high vaccine efficacy, a placebo arm was judged to be unethical. Therefore, instead of a placebo controlled trial, we consider the number of incident infections present at the end of the trial and the number of prevalent infections in the unvaccinated observational survey cohort. To adjust for these design features, we: (i) estimate and subtract off the number of preexisting infections from the number of prevalent infections in the survey cohort and (ii) use propensity scores [15] to adjust for potential confounders such as age, region, years of sexual activity and number of sexual partners.
The Methods section describes the design and proposed analysis for the study. The Results section describes the statistical power and the properties of the analytic procedures. The Discussion summarizes our results and reviews key assumptions underlying the proposed design and analysis.
2. Methods
2.1. Study population
Costa Rica is administratively divided into seven provinces that are subdivided into districts and then into minimal geo-statistical units (MGUs), which are roughly equivalent to one city block. The study source population resides in six provinces (Guanacaste, Puntarenas, Alajuela, Hererdia, San Jose, Cartago) and, so long as recruitment goals are met, will include 174 districts containing 17,202 MGU’s. In total, this region includes approximately 79,877 girls between 12 and 16 years old in 2017, and a similar number between the ages of 17 and 21. We also defined 64 District Units (DU). A DU combined neighboring districts when necessary so each DU contained at least 800 girls between 12 and 16 years old.
The study population for the randomized trial includes about 20,000 girls meeting the eligibility criteria defined in Section 2.2. The study population will be recruited from the source population in multiple phases as follows. In the first recruitment phase, to begin in the fall of 2017, we will randomly select 35% of all eligible MGUs within each district. Every house in each selected MGU will be contacted to obtain consent for participation and to identify all girls aged 12 to 16. We chose an age range that balances the desire to vaccinate prior to sexual debut with the knowledge that the trial can only produce useful results if cohort members are sexually active. Every such girl will be invited to an initial visit to determine eligibility and receive an initial vaccination if eligible. Based on participation and eligibility rates in the first phase, which was designed to recruit about 10,000 girls, we will initiate one or more additional phases of recruitment within different sets of randomly selected MGUs to attain the final recruitment goal of 20,000 girls. To minimize the possible effects of herd immunity and the potential for 1-dose trial participants to have a reduced infection rate from the corresponding decrease in the population prevalence of HPV, we plan to vaccinate at most 33% of the population in a district and only 25% of the eligible population, overall.
To estimate vaccine efficacy, we must compare the infection rate in a vaccinated population to the rate in an unvaccinated population. We estimate the infection rate in a vaccinated population by looking at the proportion of trial participants who are infected at their final two visits, which are scheduled to occur between the years 2020 and 2023. However, we still need to estimate the infection rate in an unvaccinated population. Therefore, while recruiting the 20,000 trial participants, we concurrently recruit 4000 girls between the ages of 17–20 from the same households. We combine these 4000 girls with the 15.5–17 year olds recruited for the trial to create a population that spans15.5–20 years old (i.e. same ages as the trial participants during their final two visits) and that had not been previously vaccinated. We then estimate the infection rate in this combined “survey cohort” during their first two visits, scheduled to occur between 2017 and 2019. Note, if infection rates do not fluxuate over calendar time, comparing the estimated rates in these two groups, as described below, will provide an unbiased estimate of vaccine efficacy. The 4000 girls specifically recruited for the survey will attend only the first two visits.
2.2. Non-inferiority trial eligibility
Girls will be potentially eligible for the non-inferiority trial if they are female, 12 to 16 years old, live in the selected region, and have not previously received an HPV vaccination. Other requirements are good general health and informed consent by a parent or guardian. Exclusion criteria are defined in detail in the protocol, including allergies to vaccine components or latex, pregnancy, and certain autoimmune, degenerative, and genetic diseases. Although all women will be followed, those given a vaccine at the first visit who do not return for a potential revaccination after 6 months will not be included in the analytic trial cohort (see Section 2.3). Thus, the first six months of the trial can be considered to be a run-in phase that determines eligibility for the analytic cohort in the trial.
2.3. Non-inferiority trial randomization to treatments
Approximately 20,000 girls will be enrolled into this study (Section2.1). The randomization will then proceed in two phases. At the baseline visit, we will use blocked randomization (in blocks of four) within strata defined by DU and age group (12–14, 15–16 years old) to assign 10,000 eligible girls to receive Cervarix ® and 10,000 eligible girls to receive Gardasil-9 ®. At the 6-month visit, we will use blocked randomization (in blocks of 4) within strata defined by DU, age-group, and vaccine type to assign girls to either a second vaccination of the same type or an active control vaccine placebo (i.e. diphtheria/pertussis/tetanus vaccine). For purposes of the statistical analysis, we only include a girl in the non-inferiority trial if she returned and received a 6-month vaccination (or placebo). The investigational team and trial participants will not be informed of the treatment assignments.
2.4. Non-inferiority trial follow-up and endpoint
Each girl is scheduled to attend nine clinic visits. After her baseline and 6-month visit, she will return to the clinic for seven follow-up visits at six month intervals (i.e. at months 12, 18, …, 48). At each visit, all participants will collect urine and participants at least 15 years old will also self-collect a cervicovaginal specimen for HPV DNA testing.
The primary end-point is an incident persistent HPV16 or an incident persistent HPV18 infection during the follow-up visits, defined by: (i) two same-type HPV positive test results at consecutive visits; and(ii) type-specific HPV negative test results from baseline and 6-month visits. For example, a girl who tested negative for HPV16 at the 0 and 6 month visit but who tested HPV16-positive at the18- and 24-month visits had an incident persistent HPV16 infection, regardless of any other test results. If she was HPV16-positive at the 18- and 30-month visits, but not at other times (including the 24-month visit), she did not have an incident persistent HPV16 infection. A woman had an incident persistent infection if she had either an HPV16 or HPV18 incident persistent infection. Note, if cervicovaginal samples are not available at either baseline or 6 month visits, HPV infection status will be assessed using a urine specimen. We chose persistent infection, spanning two visits, as the endpoint to avoid counting incidents where HPV is present from a recent sexual encounter but is cleared prior to integration.
2.5. Non-inferiority trial analysis
2.5.1. General description
We estimate the probabilities, π1 and π2, that a girl qualifying for the trial and attending all scheduled visits will have an incident persistent infection when enrolled in the 1- and 2-dose arms, respectively. We then estimate the risk difference, Δ = π1 − π2 and test the null hypothesis H0 : Δ ≥ ΔN, where ΔN is a pre-specified value, 0.00986. For the reasons discussed in Appendix A, we believe that the statement that the risk difference does not exceed 0.00986 is approximately equivalent to the statement that the VE of the 1-dose regimen is not below 80%. Furthermore, we believe that a vaccine with an efficacy exceeding 80% would have significant public health utility.
In the absence of missing data, estimation and inference is simple. Let there be m1 girls with an incident persistent infection among the n1 girls enrolled in the 1-dose arm, and the let there be m2 girls with an incident persistent infection among the n2 girls enrolled in the 2-dose arm. Then we estimate πk by (where superscript “nm” abbreviates “non-missing”), estimate Δ by , and test H0 : Δ ≥ ΔN using Farrington and Manning’s (FM) approach [13] (see their Method 3 and their Appendix). The FM approach defines Z(Δ0)
| (1) |
where and are the MLE under the restriction that , and then defines the corresponding p-value to be min, where ΔN = 0.00986 and is the (1 − α)th quantile of a standard normal distribution. The FM method similarly defines the upper and lower bounds, ΔUB and ΔLB, for the 95% confidence interval of Δ by
| (2) |
However, given that some girls will miss visits, we must modify this approach.
2.5.2. Missing data
We let be the number of girls in the k-dose arm with an observed incident persistent infection and we let be the number of girls in the k-dose arm expected to have had an incident persistent infection given the observed data. For example, if half the girls attended all follow-up visits and half the girls attended no follow-up visits, then if the data can be considered missing at random. We offer a full description on how to calculate in the next paragraph. Given and , we modify the above approach by defining an effective sample size as and proceed with the previously described approach replacing nk with (i.e. ).
To describe our approach for obtaining , we need to introduce some notation. The observed data over the 9 visits can be summarized by the nk × 9 matrices, Uk16, Uk18, Sk, and Vk where.
Uk16[j, t] = 1 (Uk18[j, t] = 1) if the jth girl in the k-dose arm attended visit t and had an HPV-16 (HPV-18) infection at visit t, 0 otherwise.
Sk[j, t] = 1 if the jth girl in the k-dose arm was sexually active at visit t, 0 otherwise.
Vk[j, t] = 1 if the jth girl in the k-dose arm attended visit t, 0 otherwise.
We also define the nk-vector, Yk* (which includes unobserved values) by.
Yk*[j] = 1 if the jth girl in the k-dose arm has an incident persistent infection, 0 otherwise.
We then define
| (3) |
where
| (4) |
if the girl is not observed to have an incident persistent infection (otherwise clearly E[Yk*[j]|Uk16,Uk18,Vk,Sk] = 1), with and being the probabilities that the girl had an incident persistent HPV-16 or HPV-18 infection during the gth gap of missing visits and are defined as follows. For the jth girl of the k-dose arm, we first identify the Gkj gaps of missing values (i.e. a girl with Vk[j,] = [1, 1, 1, 0, 1, 1, 0, 0, 1] has two gaps spanning visits 4 and visits 7/8 so Gkj = 2). For each gap g, we then identify the two adjacent attended visits, tkjgB and tkjgA (i.e. for the visit 4 gap, the adjacent visits would be tkj1B = 3 and tkj1A = 5; for the visit 7/8 gap, the adjacent visits would be tkj2B = 6 and tkj2A = 9). After identifying these adjacent visits for each gap, we identify two sets of girls, Ωkjg16, Ωkjg18. We let girl l be in Ωkjg16 (Ωkjg18) if she (i) has the same HPV-16 (HPV-18) infection status at visits tkjgB and tkjgA as girl j (i.e. Uk16 [l, tkjg•] = Uk16 [j, tkjg•]), (ii) has the same sexual activity status at visits tkjgB and tkjgA (i.e. Sk[l, tkjg•] = Sk[j, tkjg•]), and (iii) attended all visits between tkjgB and tkjgA (i.e. Vk[l,(tkjgB,…,tkjgA)] = [1,..,1]). Finally, we estimate the probability, , that the girl had an incident persistent HPV-16 (HPV-18) infection during the gap by the proportion of women in Ωkjg16 (Ωkjg18) who had an incident persistent infection between tkjgB and tkjgA. Simulations demonstrate that this method of handling missing data yields near nominal coverage of confidence intervals on the risk difference (Section 3.1). We are assuming that the data are missing at random, or that missingness does not depend on the unobserved infection status conditional on the sexual status. We will evaluate whether other covariates were associated with missingness and perform sensitivity analyses to evaluate the effect of violations in our assumptions. All simulations and analysis were performed using the R software [16].
2.6. Vaccine efficacy study population, eligibility and recruitment for the survey cohort
As described in Section 2.1, approximately 4000 unvaccinated girls aged 17–20 will be specifically enrolled into the survey cohort. Recall that the survey cohort is recruited from the identical set of households as the non-inferiority trial, and with the exception of the age range, will have the same eligibility criteria apply as the non-inferiority trial (Section 2.2). All girls specifically recruited for the survey cohort will receive HPV vaccination (either Cervarix or Gardasil) at their first and only two visits. For a given analysis (i.e. estimating VE for 1-dose of Cervarix), the survey cohort will be expanded to include girls aged 15–16 who were enrolled into one of the other three arms of the non-inferiority trial (i.e. any trial participant not receiving 1-dose of Cervarix). The age range of the entire survey cohort spans 15.5–20 years old at recruitment. Note, at the 42 month visit, which will occur between 42 and 48 months after the initial visit, girls in the non-inferiority trial will be similarly aged 15–20.
2.7. Vaccine efficacy study endpoints
Each girl enrolled into only the survey cohort will have two visits at the clinic to determine whether or not a prevalent persistent HPV16/18 infection is present. Survey cohort participants who are not in the non-inferiority trial will self-collect a cervicovaginal specimen for HPV testing at her baseline and 6-month visit and will be offered a vaccination at each visit. Vaccination does not affect the persistence of existing HPV infections [17,18]. Prevalent persistence for 15 and 16 year old girls in the non-inferiority trial will likewise be based on cervicovaginal specimens at their baseline and 6-month visits.
While the end-point for girls in the survey cohort will be a prevalent persistent HPV 16/18 infection, the end-point for girls in the non-inferiority trial arm will be an incident persistent infection spanning the 42- and 48-month visits. The analysis will account for this difference in endpoint definitions. We note that, at the time of writing, there is still the possibility of using information from the 36- and 42-month visits as well.
2.8. Vaccine efficacy study analysis
2.8.1. General description
As stated in the previous section, we measure the incident persistent infection rate in a group of 15–20 year old trial participants who received a vaccination 3–4 years earlier. We also measure the prevalent persistent infection rate in a group of 15–20 year old girls who had received no prior vaccination (i.e. the survey cohort). Because these rates are fundamentally different (i.e. incident vs prevalent) and are measured in two distinct populations with potentially different characteristics, we need to adjust the estimate of the infection rate in the survey cohort. We first correct the prevalence in the survey cohort by subtracting an estimate of the proportion who were already infected 3–4 years earlier. We then adjust, via propensity scores, for risk factors of infection, such as age, province, urban/rural status of DU, and years of sexual activity. All trial participants who would not have qualified for the survey (e.g. due to pregnancy) will be omitted from the analysis.
We describe the analysis plan to compare a single trial arm, arbitrarily chosen to be the 1-dose Cervarix arm, with the survey cohort. Other arms are treated similarly. Let μ1 be the probability that a girl eligible for the trial has an incident persistent infection spanning the 42- and 48-month visits given that she receives 1-dose of Cervarix, and let μ0 be the probability that the same girl has an incident persistent infection spanning the 42- and 48-month visits given that she receives no vaccine. We define the relative risk of a new infection to be Φ = μ1/μ0. The corresponding vaccine efficacy is VE = 100(1 − Φ). Our objectives are to estimate the VE and to test the hypothesis that VE < 80%.
We start by introducing notation. Let Ω0 be the set of girls in the survey cohort, and let Ω1 be the set of trial participants who received 1-dose of Cervarix and attended either the 42 or the 48 month follow-up visits. To adjust for imbalances in the K risk factors {Xj1,Xj2,…,XjK} recorded for individual j at time 0 for the survey cohort and at 42 months in the 1-dose Cervarix arm, we use logistic regression to estimate the probability (propensity) pj that individual j is in the 1-dose arm of the combined population, Ω = Ω0 ∪ Ω1. The propensity estimate is defined by
| (5) |
We further define, for trial subjects, Yj = 1 if subject j has a persistent HPV16 or persistent HPV18 infection at the 42- and 48-month visits, 0 otherwise. For survey subjects, Yj = 1 if subject j has a persistent HPV16 or persistent HPV18 infection at the 0- and 6-month visits, 0 otherwise. Furthermore, for trial subjects, we define Wj = 1 if subject j has the same type of HPV infection, either HPV16 or HPV18, at visits 0, 42- and 48-months, 0 otherwise. With the above notation and in the absence of missing data, we define our estimate for the relative risk at time t to be
| (6) |
The term reweights the number of infections in the survey cohort to reflect the characteristics and the total sample size of the trial population, and if the covariates were discrete, would be equivalent to direct standardization. From the (weighted) total number of infections, we then subtract off an estimate of the number of women who were positive four years earlier, namely .
We then estimate vaccine efficacy by .
We calculate the 95% confidence interval for VE using the bias-corrected and accelerated, BCa, bootstrap procedure [19]. Briefly, the α-level endpoint of the BCa interval is given by
| (7) |
Where is the cumulative distribution function of the bootstrap replications of , F is the cumulative distribution function of the standard normal distribution, is the 100αth percentile of a standard normal distribution, and and are the bias and acceleration ad-justments,
| (8) |
| (9) |
Here is the estimate after leaving out the jth individual and is the average value across all leave-one-out estimates. We use a non-parametric bootstrap procedure, where we randomly sample individuals [20], as we find its performance to be slightly better than bootstrapping DUs in the expected scenario where there is no significant variation in VEs across DUs. We can then define the corresponding p-value, by .
2.8.2. Missing data
For some girls in the 1-dose arm, we may not observe Yj and Wj because they are missing either their 42 and 48 month visit and had an infection at their non-missing visit. For these girls, we will replace Yj and Wj with their expected values conditional on the observed data using a method similar to the one described in Section 2.5.1 for the non-inferiority trial. Assume the jth girl is missing her infection status, , at the 42-month visit. In order for Yj and Wj to be missing, her infection status, , at 48 months must be positive (i.e. ); otherwise Yj = Wj = 0. Recall, we exclude girls who are missing both visits. Let be her type-specific infection status at baseline. Furthermore, let and be the number of girls in Ωj. Then, the expected value of Yj for this girl would be the proportion of girls in Ωj with Yl = 1 (i.e. ) and the expected value Wj would be the proportion of girls in Ωj with Wl = 1 (i.e. ). We can similarly define the expected value for those girls missing the visit at 48 months. We are assuming that data are missing at random conditional on HPV status at the non-missing visits.
2.9. Estimating key parameters needed to evaluate the analytic procedures
Certain key parameters are needed in simulations to evaluate the operating characteristics of the methods used for the non-inferiority trial and for the vaccine efficacy study. The justification for our estimates, based on relevant epidemiological data and an extensive microsimulation, are presented in Appendix A. The parameters needed are:
πj: Probability a trial participant would acquire an incident persistent HPV 16/18 infection during the follow-up visits had she received j-doses of the vaccine, j ∈ {0,1,2}. We estimate π0 = 0.0725 and π2 = 0.0725(1 − VE2/100) = 0.00464.
δj: Probability an initially uninfected trial participant would acquire an incident persistent HPV 16/18 infection that is still present during the final two trial visits (t = 8 and 9) had she received j-doses of the vaccine, j ∈ {0,1,2}. We estimate δ0 = 0.0407 and δ2 = 0.0407(1 − VE2/100) = 0.00260.
po: Probability a trial participant has an HPV 16/18 infection at her initial visit. We estimated po = 0.013.
pp: Probability a baseline HPV 16/18 infection persists from the 0-month to 48-month visit. We estimated pp = 0.6668 = 0.039.
3. Results
We have defined methods to estimate incident infection rates, and their differences, for the non-inferiority trial and we have defined methods to estimate vaccine efficacy using our survey cohort. We will now discuss the operating characteristics, including test power and validity of confidence intervals, using simulations.
3.1. Results for the non-inferiority trial
3.1.1. Coverage of confidence intervals
We evaluated the actual coverage of the nominal 95% confidence interval for Δ = π1 − π2 by simulating 20,000 data sets and estimating the coverage by the proportion of simulations in which Δ was included in the confidence interval (Table 1). We set π2 = 0.00464, as stated in Section 2.9, and let π1 be 0.00464, 0.00928 or 0.0145, corresponding to VEs of 93.6, 87.3 and 80.0%. For simplicity, we assumed a single infection type (i.e. HPV16 or 18) accounted for all infections. We assumed that there were 5000 subjects in each study arm, each subject was scheduled for 9 clinical visits (months 0, 6, 12, 18,…, 48), and each subject could be diagnosed with a persistent infection at any of the last 6 visits. Furthermore, each subject belonged to one of 100 DUs (50 subjects per DU). To allow for heterogeneity of rates among DUs, we set the overall risk of infection for a girl in the 2-dose arm from cluster i to π2i = 0.00464 × Ci, where Ci is a DU-specific multiplier 2i/101. Hence the average risk, π2, over DUs is 0.00464, as stated above. Risk in the 1-dose arm is distributed across DUs in the same way. The distribution of disease across the 6 time points was similar to that observed in the simulations described in Appendix A. Finally, we allowed for missing data. We allowed either 0%, 10%, or 30% of the subjects to be lost to follow-up, with the loss to follow-up date distributed at random with equal probability over the third through ninth visit. We additionally allowed subjects to miss a randomly selected subset of either 0%, 10%, or 30% of their visits. Given the simulated data, we were then able to estimate for each treatment arm and construct the resulting confidence intervals based on the methods in Section 2.5.
Table 1.
The coverage probabilities for 95% confidence intervals of Δ = π1 − π2. We let the true difference (Δ) be either 0, 0.00464, or 0.00986; the percentage of subjects lost to follow-up (LF) be either 0%, 10%, or 30%; the percentage of visits missed (MV) be either 0%, 10%, or 30%. For each scenario, we simulated 20,000 studies with 5000 individuals from 100 clusters. We report the mean estimate of Δ across simulations, the proportion, P (Δ < UB), where Δ was smaller than the lower bound (LB), and, the proportion, P (Δ > UB), of the simulations where Δ was larger than the upper bound (UB) of the 95% confidence interval. The average incident infection rate in the 2-dose arm is π2 = 0.00464. The cluster-specific infection rates vary from 0% to twice the average (Section 3.1).
| Δ | LF | MV | Mean | P(Δ < LB) | P(Δ > UB) |
|---|---|---|---|---|---|
| 0 | 0% | 0% | 0 | 0.0246 | 0.0246 |
| 0 | 0% | 10% | 0 | 0.0182 | 0.018 |
| 0 | 0% | 30% | 1.00E-05 | 0.0104 | 0.0084 |
| 0 | 10% | 0% | 0 | 0.0224 | 0.0222 |
| 0 | 10% | 10% | − 1.00E – 05 | 0.0175 | 0.0185 |
| 0 | 10% | 30% | 0 | 0.011 | 0.0106 |
| 0 | 30% | 0% | 1.00E – 05 | 0.0234 | 0.022 |
| 0 | 30% | 10% | 1.00E – 05 | 0.0175 | 0.0177 |
| 0 | 30% | 30% | 0 | 0.0209 | 0.0209 |
| 0.00464 | 0% | 0% | 0.00463 | 0.0244 | 0.0226 |
| 0.00464 | 0% | 10% | 0.00466 | 0.0201 | 0.0161 |
| 0.00464 | 0% | 30% | 0.00465 | 0.0102 | 0.0097 |
| 0.00464 | 10% | 0% | 0.00464 | 0.0251 | 0.022 |
| 0.00464 | 10% | 10% | 0.00463 | 0.019 | 0.0168 |
| 0.00464 | 10% | 30% | 0.00461 | 0.0117 | 0.0122 |
| 0.00464 | 30% | 0% | 0.00466 | 0.0252 | 0.0215 |
| 0.00464 | 30% | 10% | 0.00465 | 0.0206 | 0.017 |
| 0.00464 | 30% | 30% | 0.00463 | 0.0226 | 0.0216 |
| 0.00986 | 0% | 0% | 0.00987 | 0.0266 | 0.0245 |
| 0.00986 | 0% | 10% | 0.00987 | 0.0222 | 0.0185 |
| 0.00986 | 0% | 30% | 0.00987 | 0.0119 | 0.0096 |
| 0.00986 | 10% | 0% | 0.00986 | 0.0268 | 0.023 |
| 0.00986 | 10% | 10% | 0.00989 | 0.0214 | 0.015 |
| 0.00986 | 10% | 30% | 0.00987 | 0.015 | 0.0099 |
| 0.00986 | 30% | 0% | 0.00986 | 0.0239 | 0.0221 |
| 0.00986 | 30% | 10% | 0.00985 | 0.0202 | 0.0175 |
| 0.00986 | 30% | 30% | 0.00989 | 0.0216 | 0.0208 |
These simulations show that the non-coverage tail probabilities, or the proportion of simulations where Δ was either above or below the estimated 95% confidence interval, were very near the nominal 2.5% levels when there was no missing data and slightly below 2.5% when some subjects were missing data (Table 1). In the absence of missing data, Farrington and Manning [5] showed that the original FM procedure had nominal size even for very small numbers of binomial events and we expect at least 0.7 × 0.9 × 5000 × 0.00464 = 14.6 events in the 2-dose arm, and more events in the 1-dose arm. Our data confirmed that the FM procedure performed well in the absence of missing data. Our simulations further demonstrate that the coverage of the entire procedure, including the substitution of the effective sample size for the true sample size with missing data, is nominal or slightly above nominal.
3.1.2. Power to reject the null hypothesis of inferiority
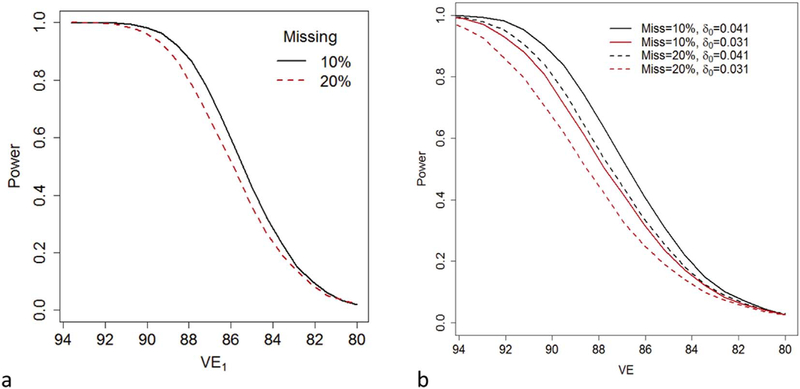
In Fig. 1a, we plot power to reject the inferiority null hypothesis Δ ≥ 0.00986 as a function of VE1 (Fig. 1a), as VE1 decreases from93.6% to 80%. Recall, if π2 = 0.00464, the chosen value for the power calculations, then Δ ≥ 0.00986 implies π1 > 0.0145 which is the expected rate if VE1 = 80%. Separate lines are shown for different combinations of patterns of missingness. We allowed either 10% or 20% of the subjects to be lost to follow-up, with the loss to follow-up date distributed equally across the 7 follow-up visits. We additionally allowed subjects to miss a randomly selected subset of either 10% or 20% of their visits. We based our power calculations on simulations similar to those described for evaluating our confidence interval for Δ. Even if 10% of the girls are lost to follow-up and 10% of all visits are missed, the power exceeds 90% if VE1 is 88.2% or greater (Fig. 1a). If 20% of the girls are lost to follow-up and 20% of all visits are missed, power exceeds 90% only if VE1 is 89.1% or greater (Fig. 1a).
Fig. 1.
(a) The power to test the null hypothesis that the difference, Δ = π1 − π2, in incident infection rates between a 1-dose and 2-dose arm exceeds 0.00987 as a function of the vaccine efficacy, VE1, of the 1-dose regimen with a one-sided α = 0.025. Each arm of the trial initially contains 5000 individuals. Among the 5000 girls in each arm, either 10% of girls are lost to follow-up and 10% of visits are not attended (Missing = 10%; black/solid) or 20% of girls are lost to follow-up and 20% of visits are not attended (Missing = 20%; red/dashed). We assumed that the probability, π0, that a trial participant would acquire an incident persistent infection is 0.0725 had they not been vaccinated and that vaccine efficacy of the 2-dose regimen is 93.6%. (b) The power to reject the null hypothesis VE < 80% as a function of the VE of the tested regimen at a one-sided α = 0.025. We assume that the survey arm and trial arm start with 5000 individuals. We assume that the risk of an incident infection, in the absence of vaccination, spanning the last two trial visits would be either δ0 = 0.041 (black) or δ0 = 0.031 (red). Among the 5000 girls in the trial arm, either 10% of girls are lost to follow-up and 10% (among those girls not lost to follow-up) of each of the final two visits are not attended (Miss = 10%; solid) or 20% of girls are lost to follow-up and 20% of visits are not attended (Miss = 20%; dashed). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
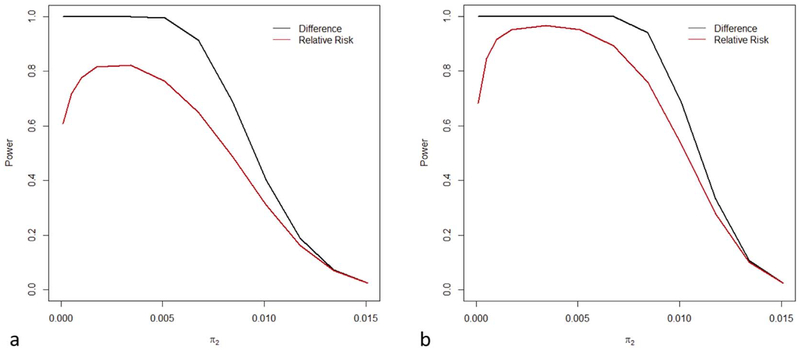
We compared the power to reject inferiority on the risk difference scale and on the relative risk scale. The corresponding statements of non-inferiority are π1 − π2 < ΔN and π1/π2 < RRN. We considered the alternative hypothesis π1 = π2 and a sequence of null hypotheses ΔN = 0.0145 − π2 and RRN = 0.0145/π2 as π2 ranges from 0 to 0.0145 (Fig. 2a and b). In Fig. 2a and b we assumed 2500 and 5000 girls in each study arm respectively. Fig. 2a therefore corresponds to 50% immediate censoring. The power on the risk difference scale exceeds that on the relative risk scale, especially as π2 tends to zero (Fig. 2).
Fig. 2.
The power to reject inferiority when non-inferiority is defined in terms of a risk difference (black) or in terms of the relative risk risk (red). We assumed that the underlying objective is to show that, for a 1-dose regimen, the VE > 0.80. Therefore, for various infection rates, π2, in the 2-dose arm (0 < π2 < 0.0145), we calculated the power to reject the null hypothesis that Δ > 0.0145 − π2 (black) or RR > 0.0145/π2 (red) under the alternative that π1 = π2. (a) The number of subjects in each arm is 2500. (b) The number of subjects in each arm is 5000. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.2. Results for the vaccine efficacy study
3.2.1. Coverage of confidence intervals on vaccine efficacy
We evaluated the actual coverage of the nominal 95% confidence interval for VE by simulating 20,000 data sets and estimating the coverage by the proportion of simulations in which VE was included in the confidence interval. For concreteness, we assumed that this was a 1-dose arm. We assumed that 5000 girls were recruited into this 1-dose arm and, although a slight simplification, that 5000 girls were recruited into the comparable survey cohort, with the latter group including the 4000 17–20 year olds specifically recruited for the survey and approximately 1000 15–16 year old trial participants. We assumed that the 1-dose arm sampling fraction (propensity) is known to be pj = 0.5 and that a single type (i.e. HPV16 or 18) accounted for all infections. We assumed these girls come from 100 district units (DUs) or clusters, i = 1, 2, …, 100, each containing the same number of girls. The baseline risk of infection for a girl enrolled in the trial was po = 0.013, and the chance that such an infection persisted throughout the trial was pp= 0.039. We assumed that the overall probability that an initially uninfected girl would acquire an incident persistent infection that existed at the end of the trial was δ0 = 0.0407 in the absence of vaccination and 0.0407 × RR in an arm with relative risk RR. We allowed two types of heterogeneity. To allow for heterogeneity in baseline risk for unvaccinated women, we multiplied δ0 = 0.0407 by the DU-specific random variable C1i which is assumed to be uniformly distributed on [0, 2], so that the DU-specific incident persistent infection rate in the survey arm is δ0i = 0.0407 × C1i. To allow for variation in relative risks over DUs, we multiplied by another independently distributed factor, C2i, also uniform on [0,2] so that the DU-specific incident persistent infection rate in the 1-dose arm is δ1i = 0.0407 × RR × C1i × C2i. We assumed that either 10% or 30% of the subjects were missing each of the last two visits, but show only results for 10%, as both sets of results were similar.
We studied the coverage of a 95% confidence interval for vaccine efficacy, VE, based on the bootstrap (Section 2.8). Specifically, we used the BCa bootstrap and resampled individuals. For comparison, we also consider the bootstrap procedure where (i) DUs, not individuals, are resampled and (ii) the confidence intervals are based on the 0.025 and 0.0975 quintiles of the bootstrap distribution.
The mean estimated VE was very close to the true VE for the range of VE values studied, 50% to 99% (Table 2). The BCa tail probabilities were very close to the nominal 0.025 values when individuals are re-sampled so long as the relative risk does not vary across DU’s. Confidence intervals based on bootstrap distribution quantiles had less than nominal lower tail probability and above nominal upper tail probability, but the overall coverage was also near the nominal 0.95 level. Confidence intervals based on BCa, but with resampled DU’s, provided < 95% coverage. On the basis of these simulations and the assumption that VE will not significantly vary across DU’s, we recommend the BCa confidence intervals with resampling of individuals.
Table 2.
The coverage probabilities for our 95% confidence intervals for VE. We let the true VE be either 0.99, 0.95, 0.90, 0.80, 0.60, or 0.50 and we let either the baseline infection rate (cluster = “Baseline”), the relative risk (cluster = “Relative Risk”), neither (cluster = “None”), or both (cluster = “Both”) vary across cluster. For each scenario, we simulated 20,000 studies in which the trial arm and survey cohort each contain 5000 individuals from 100 clusters. We report the mean and the proportions, P(VE > UB) and P(VE < LB), of simulations where VE was outside the the upper and lower bounds of the 95% confidence interval. Bootstrapped confidence intervals were based on either the bias-corrected and accelerated (BCa) procedure with resampled individuals, bootstrap distribution quantiles (BC-Q) with resampled individuals, or the BCa procedure with resampled DU’s. For our simulations, we assumed that without vaccination, the expected rate of incident infections that would be detectable in the last two visits is 0.0407, the rate of baseline infections is 0.013, the proportion of baseline infections that persist throughout the trial is 0.039, and 10% of trial participants miss each of the last two visits. The VE is estimated based on the methods described in Section 2.8, with the vaccinated arm sampling fraction (propensity) assumed to be known as 0.5.
| Cluster | VE | BCa confidence intervals (resampled individuals) | BC-Q confidence intervals (resampled individuals | BCa confidence intervals (resampled DU’s) | ||||
|---|---|---|---|---|---|---|---|---|
| P(VE < LB) | P(VE > UB) | P(VE < LB) | P(VE > UB) | P(VE < LB) | P(VE > UB) | |||
| None | 0.99 | 0.99 | 0 | 0.018 | 0 | 0.008 | 0 | 0.019 |
| None | 0.95 | 0.95 | 0.022 | 0.021 | 0.048 | 0.014 | 0.023 | 0.023 |
| None | 0.90 | 0.899 | 0.026 | 0.024 | 0.039 | 0.019 | 0.027 | 0.025 |
| None | 0.80 | 0.799 | 0.026 | 0.024 | 0.034 | 0.021 | 0.028 | 0.026 |
| None | 0.60 | 0.598 | 0.026 | 0.024 | 0.03 | 0.023 | 0.029 | 0.026 |
| None | 0.50 | 0.497 | 0.027 | 0.025 | 0.03 | 0.023 | 0.029 | 0.027 |
| Baseline | 0.99 | 0.99 | 0 | 0.019 | 0 | 0.008 | 0 | 0.02 |
| Baseline | 0.95 | 0.95 | 0.023 | 0.022 | 0.046 | 0.014 | 0.026 | 0.023 |
| Baseline | 0.90 | 0.899 | 0.026 | 0.024 | 0.04 | 0.018 | 0.029 | 0.025 |
| Baseline | 0.80 | 0.799 | 0.025 | 0.024 | 0.031 | 0.021 | 0.028 | 0.027 |
| Baseline | 0.60 | 0.598 | 0.025 | 0.023 | 0.028 | 0.021 | 0.028 | 0.026 |
| Baseline | 0.50 | 0.498 | 0.026 | 0.024 | 0.028 | 0.023 | 0.029 | 0.026 |
| RR | 0.99 | 0.99 | 0 | 0.019 | 0 | 0.008 | 0 | 0.02 |
| RR | 0.95 | 0.95 | 0.024 | 0.022 | 0.046 | 0.015 | 0.025 | 0.021 |
| RR | 0.90 | 0.899 | 0.028 | 0.027 | 0.04 | 0.021 | 0.028 | 0.024 |
| RR | 0.80 | 0.799 | 0.032 | 0.03 | 0.04 | 0.025 | 0.03 | 0.025 |
| RR | 0.60 | 0.597 | 0.036 | 0.036 | 0.041 | 0.033 | 0.03 | 0.025 |
| RR | 0.50 | 0.497 | 0.036 | 0.036 | 0.038 | 0.035 | 0.027 | 0.025 |
| Both | 0.99 | 0.99 | 0 | 0.018 | 0 | 0.008 | 0 | 0.018 |
| Both | 0.95 | 0.95 | 0.025 | 0.024 | 0.05 | 0.015 | 0.028 | 0.022 |
| Both | 0.90 | 0.899 | 0.028 | 0.028 | 0.043 | 0.022 | 0.031 | 0.026 |
| Both | 0.80 | 0.799 | 0.036 | 0.031 | 0.045 | 0.026 | 0.033 | 0.023 |
| Both | 0.60 | 0.598 | 0.038 | 0.036 | 0.043 | 0.034 | 0.029 | 0.025 |
| Both | 0.50 | 0.497 | 0.039 | 0.042 | 0.043 | 0.04 | 0.029 | 0.027 |
3.2.2. Power to reject vaccine efficacy < 80%
We used simulations to estimate the power to reject the null hypothesis that the VE of a 1-dose regimen, compared to the survey cohort, was below 80%. We assumed that uninfected girls enrolled in a trial arm, had they not been vaccinated, would have had an incident persistent infection rate of 4.07% (i.e. δ0 = 0.0407) at the 42- and 48-month visits (Appendix A). We simulated a 1-dose trial arm with 5000 women and a survey cohort with 5000 women. Additionally, for the trial arm we allowed either 10% or 20% of the girls to be lost to follow-up (i.e. missing both the 42- and 48-month visits) and either 10% or 20% of the remaining girls to be missing each of their last two visits. In the 1-dose trial arm, 1.3% were initially infected, 3.9% of the initially infected girls had a persistent infection at their last two visits, and RR × 4.07% of the initially uninfected girls had a persistent infection at the last two visits. In the survey cohort, 4.07% had a persistent infection at their first two visits. We calculated the test statistic assuming the propensity was known to be 0.5 for all individuals. We repeated this simulation 2500 times and estimated the power as the proportion of simulations where the p-value was below 0.025. Fig. 1b shows that power is 90% or more if the true VE of the 1-dose regimen is 90.3% or greater, 10% of all girls are lost to follow-up, and 10% of all visits among remaining girls are missing. Fig. 1b also shows good power for other combinations of VE, loss to-follow-up, percentage of missing visits, and unvaccinated infection rates.
We used similar simulations to estimate the expected length of the 95% CI for VE. In the scenario where 10% of girls are lost to follow-up and an additional 10% of the remaining girls are missing one of their last two visits, the expected length of the 95% CI is 0.072, 0.10, 0.15, and 0.26 when the true VE is 0.95, 0.90, 0.80, and 0.50. The length of the confidence interval was only minimally affected by changing the rate of missingness over plausible values.
3.2.3. Effect of ignoring infections prevalent at baseline in Eq. 6
Eq. 6 subtracts off infections prevalent at baseline (about 4 years earlier) in order to compare the incident infection rates in the vaccinated and unvaccinated groups. If one ignores these prevalent infections, one could use the simpler estimate
| (10) |
Ignoring prevalent infection biases towards 1.0, leading to an underestimate of . For our study, we expect the bias, defined as , to be relatively small, but non-negligable. For estimating bias, we consider the following expected values: 1.3% of individuals have a baseline infection; 3.9% of baseline infections persist throughout the trial; 4.1% of the baseline-uninfected individuals, in the absence of vaccination, would have an infection at the end of the trial; and the true VE against new infections is 93.6%. The expectation of is then approximately
| (11) |
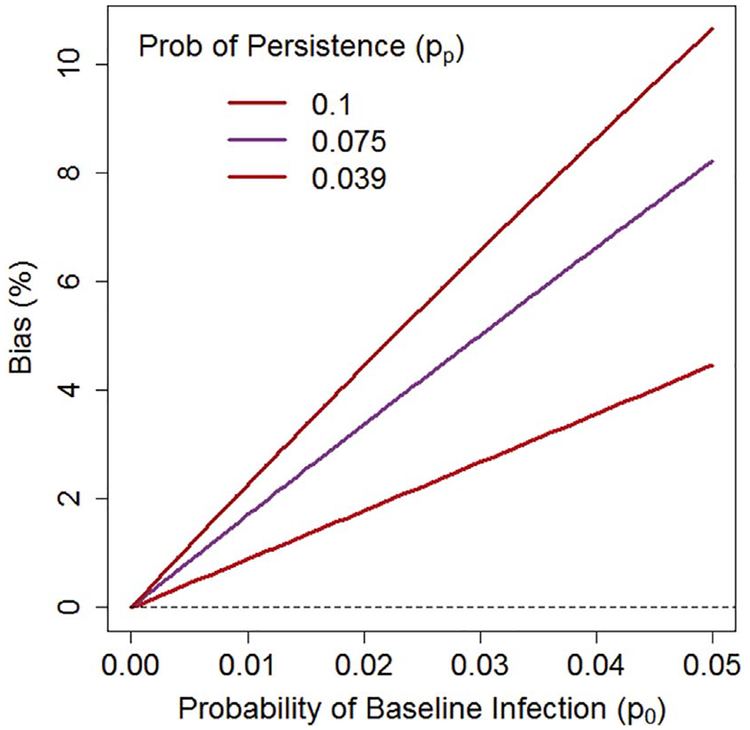
Thus the simple estimate in Eq. (10) has a bias of 93.6%–92.4% = 1.2%. The bias can be larger for other choices of these parameters (Fig. 3). Therefore, we recommend Eq. (6), which subtracts off prevalent infections.
Fig. 3.
A comparison of true vaccine efficacy (VE) and the estimated vaccine efficacy (), when the estimate does not properly account for infections prevalent at baseline. The bias, , depends on the probability of a baseline infection po (x-axis) and the probability of a baseline infection persisting throughout the study pp (red = 0.039; purple = 0.075; brown = 0.1). Calculations assume VE = 93.6%, with other details described in the text. In our study, if the probability of a baseline infection is 0.013 and the probability of persistence is 0.039, we expect and bias = 93.6%–92.4% = 1.2%, but the bias can be much larger for other combinations of parameters. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
4. Discussion
In this paper we have discussed two objectives of the proposed study to evaluate the ability of one dose of a vaccine to protect against incident HPV 16/18 infection lasting six months or longer. The first objective is to demonstrate that a 1-dose regimen is non-inferior to a 2-dose regimen. One key feature of this analysis is that we chose to define non-inferiority in terms of the risk difference instead of the relative risk. We made this choice so that we could translate our statement of non-inferiority into a clear statement about the VE of a 1-dose regimen. Had we used a RR scale, this translation would have depended too strongly on VE2, a quantity that can only be roughly estimated. For example, if VE2 = 94%, then a RR = 3.24 would translate to a VE1 = 80% (100 × (1–3.24(1–0.94))). If VE2 = 99%, then a RR = 3.24 would translate to a VE1 = 96.7%. Therefore, a definition of non-inferiority on the RR scale would be less interpretable for public health decisions. Another advantage of using the risk difference scale is that tests for non-inferiority had greater power than tests on the RR scale for this study with rare outcomes in the control arm (2-dose arm in this study), as our simulations demonstrated. A second key feature of our trial analysis is that we modified standard methods to account for missing values and we showed, by simulation, that the resulting confidence intervals yielded accurate coverage levels. Our simulations allowed for heterogeneity in infection rates across district units, and yielded results in line with previous work [21] that suggested that this heterogeneity should not affect randomized comparisons.
Another objective is to determine the vaccine efficacy compared to no vaccination. Because it was not considered ethical to randomize girls to a placebo arm in this trial, we had to estimate the vaccine efficacy by comparing the rate of infection in each trial arm to the prevalent infection in a contemporaneous survey of unvaccinated women. Both of these rates were corrected for an estimate of prevalent infection at baseline in the trial. Furthermore, infection counts in the survey were standardized (via a propensity-type adjustment) to the distribution of risk factors in the trial arm. Bias-corrected and accelerated bootstrap confidence intervals yielded nominal coverage in simulations. Although we have demonstrated good statistical properties of these procedures, inference on the efficacy of the 1-dose arm is based on observational data, not a randomized experiment. We assumed that the demographics of HPV infection did not change with calendar year, and that the behavior and characteristics between girls in the trial and survey cohort were comparable. Although the latter assumptions can be weakened by using the propensity score to adjust for observable risk factors such as age, region and sexual activity, one needs to be aware that estimates of vaccine efficacy may be affected by unmeasured confounders or by incomplete adjustment for measured confounders. Despite these limitations, the ability to estimate vaccine efficacy is an important objective, because a 1-dose regimen with < 80% vaccine efficacy may be very useful in developing countries, even if one cannot demonstrate non-inferiority to the 2-dose regimen.
Although others have proposed non-inferiority trials based on risk differences [22–24], as far as we know this is the first time that this approach has been advocated for prevention trials with rare outcomes, for which non-inferiority on the risk difference scale has both public health justification and statistical power advantages.
These methods and design considerations have informed the development of the protocol for the upcoming study to evaluate the ef-ficacy of a single dose of the HPV vaccine. Evidence for non-inferiority compared to two doses and evidence of adequate vaccine efficacy compared to the survey arm could provide policy makers with information that could justify comparatively inexpensive and logistically feasible 1-dose vaccination programs in developing countries.
Acknowledgements
This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov).
Funding
This work was supported by the intramural program at the NIH.
Appendix A. Appendix
A1Estimating key parameters
For the purposes of calculating power, assessing the performance of our test statistics, and providing a meaningful definition of non-inferiority, we need to have estimates of the following parameters.
πj: Probability a trial participant acquires an incident persistent HPV 16/18 infection during the follow-up visits had she received j-doses of the vaccine, j ∈ {0,1,2}.
δj: Probability an initially HPV negative trial participant acquired an incident persistent HPV 16/18 infection and is HPV 16/18-positive during the final two trial visits (t = 8 and 9) had she received j-doses of the vaccine, j ∈ {0,1,2}.
po: Probability a trial participant has an HPV 16/18 infection at her initial visit.
pp: Probability a baseline HPV 16/18 infection persists throughout the trial.
We can use these parameters to define our non-inferiority threshold. We define our goal to be showing that the VE of a 1-dose regimen exceeds 80%. Given that the expected VE of a 2-dose regimen is 93.6%, we define our non-inferiority threshold, ΔN by
We estimated these parameters based on quantities derived from reported data and a simulated study. We estimate the proportion of women who are sexually active at various ages using data from a nationally representative survey conducted in Costa Rica in 2010. The proportion of girls who are sexually active at ages 12, 13, 14, 15, 16, 17, 18, 19, and 20 years are 0.009, 0.04, 0.12, 0.28, 0.46, 0.64, 0.80, 0.88, and 0.93 respectively. We estimated the proportion of uninfected sexually active women who will have an infection 6 months later using results from the original Costa Rica Vaccine Trial (CVT) [1–3]. The CVT recorded that 9.00%, 7.02%, and 5.93% of sexually active girls who were 18, 19, and 20 years old respectively acquired a new infection within 1 year. We used the approach described below to convert 1-year incidence rates to 6 month incidence rates. We estimated the proportion of infected women who will clear their infection within 6 months to be 0.333 based on previously reported results from the CVT(65,66). We estimated pp by 0.6668 = 0.039.
We calculated the cumulative probability of infection in 6 months as follow. Assume the time to infection is exponentially distributed with hazard η. We assume that the rate of clearance following infection is λ = −2log(0.666) = 0.405. Then the proportion, p(T), of women who have a new infection at time T is given by the convolution
| (A1) |
Using p(1) = 0.073, the weighted 1-year incidence rate across the age groups, we solved Eq. (A1) for η = 0.11. We then estimated p(0.5) as 0.0453.
Given these parameters estimated from epidemiological data, we next estimated the desired parameters δ0 = 0.0407, π0 = 0.0725 and po = 0.013 from a large simulated cohort. We simulated a cohort of 2,000,000 12-year old girls and recorded their HPV infection status at visits spaced 6 months apart until they were age 20. Each woman was assigned an age of sexual debut based on the national survey. A woman was recorded as infected at her nth visit with probability 0.0453 if her current age equaled or exceeded her age of sexual debut and she was uninfected at her n-1th visit, 0.666 if she was infected at her n-1th visit, and 0 otherwise. All women were assumed uninfected at their 0th (i.e. age = 11.5) visit. These 2,000,000 girls were then randomly divided into 5 groups, corresponding to ages at entry into the study of 12,13,14,15 and 16 years, and their infection status was observed for up to 9 visits beginning at their age of entry or at 15 years old. Based on the resulting large simulated study population, we estimated the desired parameters.
Finally, using π0 = 0.0725, we can define ΔN = ((1 − 0.064) − (1 − 0.2))π0 = 0.00986.
References
- [1].Herrero R, Hildesheim A, Rodriguez AC, Wacholder S, Bratti C, Solomon D,Gonzalez P, Porras C, Jimenez S, Guillen D, Morales J, Alfaro M, Cyr J,Morrisey K, Estrada Y, Cortes B, Morera LA, Freer E, Schussler J, Schiller J,Lowy D, Schiffman M, Costa Rica Vaccine Trial G, Rationale and design of a community-based double-blind randomized clinical trial of an HPV 16 and 18 vaccine in Guanacaste, Costa Rica, Vaccine 26 (2008) 4795–4808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Herrero R, Wacholder S, Rodriguez AC, Solomon D, Gonzalez P, Kreimer AR,Porras C, Schussler J, Jimenez S, Sherman ME, Quint W, Schiller JT,Lowy DR, Schiffman M, Hildesheim A, Costa Rica Vaccine Trial G, Prevention of persistent human papillomavirus infection by an HPV16/18 vaccine: a community-based randomized clinical trial in Guanacaste, Costa Rica, Cancer Discov. 1 (2011) 408–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Hildesheim A, Wacholder S, Catteau G, Struyf F, Dubin G, Herrero R, Group CVT, Efficacy of the HPV-16/18 vaccine: final according to protocol results from the blinded phase of the randomized Costa Rica HPV-16/18 vaccine trial, Vaccine 32 (2014) 5087–5097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Apter D, Wheeler CM, Paavonen J, Castellsague X, Garland SM, Skinner SR,Naud P, Salmeron J, Chow SN, Kitchener HC, Teixeira JC, Jaisamram U,Limson G, Szarewski A, Romanowski B, Aoki FY, Schwarz TF, Poppe WAJ, Bosch FX, Mindel A, De Sutter P, Hardt K, Zahaf T, Descamps D, Struyf F,Lehtinen M, Dubin G, Grp HPS, Efficacy of human papillomavirus 16 and 18 (HPV-16/18) AS04-adjuvanted vaccine against cervical infection and Precancer in young women: final event-driven analysis of the randomized, double-blind PATRICIA trial, Clin. Vaccine Immunol. 22 (2015) 361–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Safaeian M, Porras C, Pan Y, Kreimer A, Schiller JT, Gonzalez P, Lowy DR,Wacholder S, Schiffman M, Rodriguez AC, Herrero R, Kemp T, Shelton G,Quint W, van Doorn LJ, Hildesheim A, Pinto LA, Group CVT, Durable antibody responses following one dose of the bivalent human papillomavirus L1 virus-like particle vaccine in the Costa Rica Vaccine Trial, Cancer Prev. Res. (Phila.) 6 (2013) 1242–1250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kreimer AR, Struyf F, Del Rosario-Raymundo MR, Hildeshim A, Skinner SR,Wacholder S, Garland SM, Herrero R, David MP, Mfeeler CM,PATRICIA CRVT, Efficacy of fewer than three doses of an HPV-16/18 AS04-adjuvanted vaccine: combined analysis of data from the Costa Rica Vaccine and PATRICIA trials, Lancet Oncol. 16 (2015) 775–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Sankaranarayanan R, Prabhu PR, Pawlita M, Gheit T, Bhatla N, Muwonge R, Nene BM, Esmy PO, Joshi S, Poli UR, Jivarajani P, Verma Y, Zomawia E,Siddiqi M, Shastri SS, Jayant K, Malvi SG, Lucas E, Michel A, Butt J, Vijayamma JM, Sankaran S, Kannan TP, Varghese R, Divate U, Thomas S,Joshi G, Willhauck-Fleckenstein M, Waterboer T, Muller M, Sehr P, Hingmire S,Kriplani A, Mishra G, Pimple S, Jadhav R, Sauvaget C, Tommasino M,Pillai MR, Indian HPVVSG, Immunogenicity and HPV infection after one, two, and three doses of quadrivalent HPV vaccine in girls in India: a multicentre prospective cohort study, Lancet Oncol. 17 (2016) 67–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Kreimer AR, Rodriguez AC, Hildesheim A, Herrero R, Porras C, Schiffman M,Gonzalez P, Solomon D, Jimenez S, Schiller JT, Lowy DR, Quint W,Sherman ME, Schussler J, Wacholder S, Grp CV, Proof-of-principle evaluation of the efficacy of fewer than three doses of a bivalent HPV16/18 vaccine, J. Natl. Cancer Inst. 103 (2011) 1444–1451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Uno H, Wittes J, Fu HD, Solomon SD, Claggett B, Tian L, Cai TX, Pfeffer MA, Evans SR, Wei LJ, Alternatives to hazard ratios for comparing the efficacy or safety of therapies in noninferiority studies, Ann. Intern. Med 163 (2015) 127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Studio Cytel, Corporation Cytel, (2015).
- [11].Chan ISF, Zhang ZX, Test-based exact confidence intervals for the difference of two binomial proportions, Biometrics 55 (1999) 1202–1209. [DOI] [PubMed] [Google Scholar]
- [12].PASS 14 Power Analysis and Sample Size Software, NCSS, LLC, Kaysville, UT, USA, 2015. [Google Scholar]
- [13].Farrington CP, Manning G, Test statistics and sample-size formulas for comparative binomial trials with null hypothesis of nonzero risk difference or non-unity relative risk, Stat. Med 9 (1990) 1447–1454. [DOI] [PubMed] [Google Scholar]
- [14].Miettinen O, Nurminen M, Comparative-analysis of 2 rates, Stat. Med 4 (1985) 213–226. [DOI] [PubMed] [Google Scholar]
- [15].Austin PC, An introduction to propensity score methods for reducing the effects of confounding in observational studies, Multivar. Behav. Res 46 (2011) 399–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, 2017. [Google Scholar]
- [17].Hildesheim A, Gonzalez P, Kreimer AR, Wacholder S, Schussler J,Rodriguez AC, Porras C, Schiffman M, Sidawy M, Schiller JT, Lowy DR,Herrero R, C.R.H.V.T. CVT, Impact of human papillomavirus (HPV) 16 and 18 vaccination on prevalent infections and rates of cervical lesions after excisional treatment, Am. J. Obstet. Gynecol 215 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Hildesheim A, Herrero R, Wacholder S, Rodriguez AC, Solomon D, Bratti MC, Schiller JT, Gonzalez P, Dubin G, Porras C, Jimenez SE, Lowy DR, Effect of human papillomavirus 16/18 L1 viruslike particle vaccine among young women with preexisting infection - a randomized trial, JAMA 298 (2007) 743–753. [DOI] [PubMed] [Google Scholar]
- [19].Efron B, Better bootstrap confidence-intervals, J. Am. Stat. Assoc 82 (1987) 171–185. [Google Scholar]
- [20].Field CA, Welsh AH, Bootstrapping clustered data, J. R. Stat. Soc. Ser. B Stat. Methodol 69 (2007) 369–390. [Google Scholar]
- [21].Proschan M, Follmann D, Cluster without fluster: the effect of correlated outcomes on inference in randomized clinical trials, Stat. Med 27 (2008) 795–809. [DOI] [PubMed] [Google Scholar]
- [22].Blum J, Winikoff B, Raghavan S, Dabash R, Ramadan MC, Dilbaz B, Dao B,Durocher J, Yalvac S, Diop A, Dzuba IG, Ngoc NTN, Treatment of post-partum haemorrhage with sublingual misoprostol versus oxytocin in women receiving prophylactic oxytocin: a double-blind, randomised, non-inferiority trial, Lancet 375 (2010) 217–223. [DOI] [PubMed] [Google Scholar]
- [23].Turpie AGG, Lassen MR, Davidson BL, Bauer KA, Gent M, Kwong LM, Cushner FD, Lotke PA, Berkowitz SD, Bandel TJ, Benson A, Misselwitz F, Fisher WD, Investigators R, Rivaroxaban versus enoxaparin for thromboprophylaxis after total knee arthroplasty (RECORD4): a randomised trial, Lancet 373 (2009) 1673–1680. [DOI] [PubMed] [Google Scholar]
- [24].Windecker S, Serruys PW, Wandel S, Buszman P, Trznadel S, Linke A, Lenk K,Ischinger T, Klauss V, Eberli F, Corti R, Wijns W, Morice MC, di Mario C,Davies S, van Geuns RJ, Eerdmans P, van Es GA, Meier B, Juni P, Biolimuseluting stent with biodegradable polymer versus sirolimus-eluting stent with durable polymer for coronary revascularisation (LEADERS): a randomised non-inferiority trial, Lancet 372 (2008) 1163–1173. [DOI] [PubMed] [Google Scholar]