Abstract
In our recent efforts to map protein surfaces using mixed-solvent molecular dynamics (MixMD),1 we were able to successfully capture active sites and allosteric sites within the top-four most occupied hotspots. In this study, we describe our approach for estimating the thermodynamic profile of the binding sites identified by MixMD. First, we establish a framework for calculating free energies from MixMD simulations, and we compare our approach to alternative methods. Second, we present a means to obtain a relative ranking of the binding sites by their configurational entropy. The theoretical maximum and minimum free energy and entropy values achievable under such a framework along with the limitations of the techniques are discussed. Using this approach, the free energy and relative entropy ranking of the top-four MixMD binding sites were computed and analyzed across our allosteric protein targets: Abl Kinase, Androgen Receptor, Pdk1 Kinase, Farnesyl Pyrophosphate Synthase, Chk1 Kinase, Glucokinase, and Protein Tyrosine Phosphatase 1B.
Graphical Abstract
Introduction
Using cosolvent simulations to map protein surfaces and identify binding hotspots has gained increasing prominence with the advancements in computing power.2 Several such techniques have been reported in the literature.3–8 The ability to incorporate full protein flexibility and direct competition of organic compounds with water make these molecular dynamics (MD) methods an attractive alternative to existing approaches. For instance, docking ignores such contributions or incorporates them only to a limited extent.9 Our MixMD approach uses binary-solvent simulations of water and water-miscible, organic probes.1, 5, 10–12 Recently, we have applied MixMD on a test set of allosteric proteins.1 The application of MixMD on this test set demonstrated that the active sites and allosteric sites were captured within the top-four most occupied hotspots. The success of the technique certainly suggests that MixMD holds great promise as a tool for druggability assessment. Identifying druggable binding sites is an important first step in choosing which sites on a protein surface to target. Additional information detailing each binding site would allow one to make a more informed decision on which sites to target. Thermodynamic measures such as free energy and entropy values fall in this important category. It is more straightforward to optimize enthalpy-driven binding affinity with typical scoring functions for structure-based drug discovery. Such considerations merit the development of techniques that can be used to obtain additional data on local thermodynamic properties. Techniques that estimate free energies from mixed-solvent simulations have been reported by several groups.3,4,6,13 All of the methods decompose the free energy of organic probes onto a sub-atomic grid. In this study, we use those grids in a slightly different way and propose an alternate framework for the calculation of free energies. Furthermore, efforts are made to obtain a relative ranking in terms of configurational entropies of probe molecules, using the well-established concept of entropy as a measure of the density of states. Such measures allow one to examine the interplay of binding site and probe structures on each other. Taken together, these studies construct and demonstrate the utility of a suite of computational techniques that one can use to characterize binding sites obtained from MixMD simulations.
It should be noted that Raman and MacKerell14 have previously reported free energies and enthalpies of probe molecules based on a rigorous approach, Grid Inhomogeneous Solvation Theory (GIST).15 The model systems were propane and methanol binding to multiple, diverse pockets on the proteins Factor Xa and p38 MAP kinase. In that study, they calculated detailed contributions of the ligand and water degrees of freedom to understand the different thermodynamic driving forces. The drawback to their approach is that after the hotspots are located with a cosolvent simulation, individual MD simulations must be run of a single probe alone with the protein. Calculating each hotspot requires a separate simulation. Here, we seek to estimate thermodynamic properties directly from the cosolvent simulations themselves. Furthermore, Raman and MacKerell’s approach constrained the protein heavy atoms, so the protein was unable to adapt its conformation in response to the presence of the probe molecules. Our approach uses free, unconstrained proteins.
Methods
Simulation of 5% box of MixMD probes to obtain expected occupancies (no proteins present)
Simulations of TIP3P water16 and 5% v/v boxes of acetonitrile, isopropanol, and pyrimidine were performed. These simulations were setup in a similar manner outlined in our earlier work on validating probe parameters.11 The 5% boxes of probes and water were prepared to be ~ 50Å × 50 Å × 50 Å size. The boxes were simulated in AMBER1617 using SHAKE18 and a time step of 1fs. Following an initial minimization, the system was gradually heated to 300K at constant volume. An initial 2ns equilibration run was followed by 20ns of constant-pressure simulation. The center of mass (CoM) of each probe’s location in the last 5 ns of 10 runs were binned onto a grid of 0.5 Å spacing, using an in-house modified version of cpptraj from AmberTools1419. If there were no bias by a protein, the expected occupancy per grid point is simply the number of probe molecules divided by the number of grid points. The expected occupancies for a grid point and the volume of a probe for a 5% simulation are presented in Table 1.
Table 1.
The expected occupancy for a grid point and the volume of a probe are presented for the MixMD probes acetonitrile, isopropanol, and pyrimidine. Note that these values are for a 0.5-Å grid and a 5% concentration of probes.
| Probe | Expected Occupancy per grid point | Probe radius | Probe volume (no. of grid points) | Expected Occupancy for volume of probe |
|---|---|---|---|---|
| Acetonitrile | 0.00007109 | 2.24 Å | 47.16 Å3 (389) | 0.002346102 |
| Isopropanol | 0.00005108 | 2.54 Å | 68.74 Å3 (515) | 0.002911845 |
| Pyrimidine | 0.00004683 | 2.62 Å | 75.28 Å3 (619) | 0.002669823 |
Estimating free energies from MixMD simulations
The proteins used in this study were Abl Kinase (PDBid: 3KFA)20, Androgen Receptor (2AM9)21, Pdk1 Kinase (3RCJ)22, Farnesyl Pyrophosphate Synthase (4DEM)23, Chk1 Kinase (1ZYS)24, Glucokinase (3IDH)25, and Protein Tyrosine Phosphatase 1B (2CMB)26. Ten independent MixMD simulations were performed for each probe solvent with each protein. Detailed methods for the MixMD simulation of our allosteric proteins in 5% probe solvent have been given previously.1 Free energies from those MixMD simulations were derived using a process illustrated in Figure 1. Initially, using an in-house modified version of the cpptraj module in AmberTools14, the CoMs of all the probes from the MixMD simulations were “binned” onto a grid of 0.5 Å spacing. MixMD simulation data from the last 5ns of all 10 runs were used to perform the binning for each probe. These raw bin counts reflect the number of snapshots (amount of time) a probe molecule has spent at a particular location. The raw bin counts are then converted to occupancies by dividing the bin count at each grid point with the number of MixMD simulation snapshots that were used to obtain the initial raw bin counts.
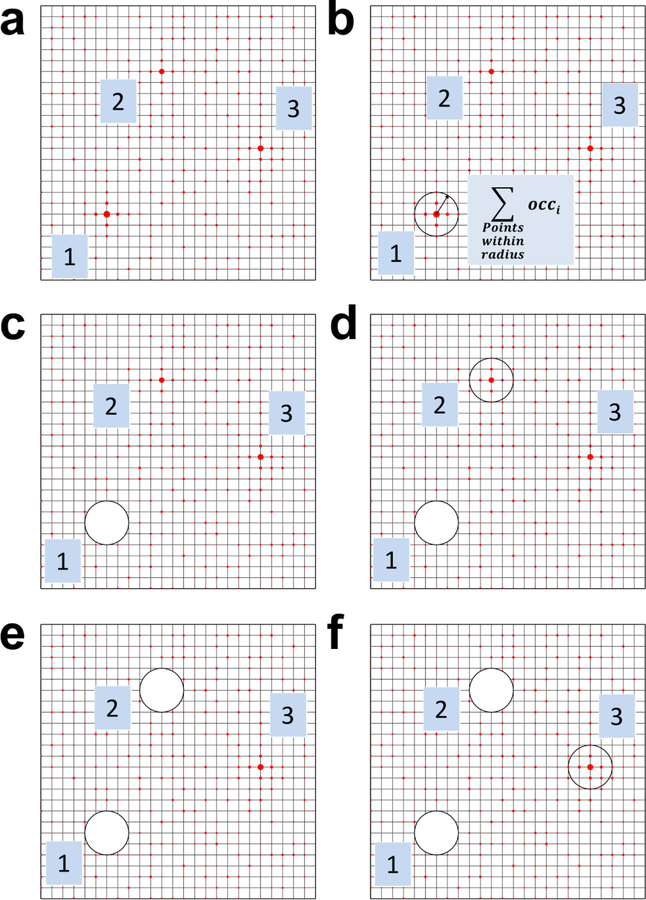
Figure 1.
The process of obtaining observed occupancies and free energies from MixMD simulations is depicted in subfigures a-f. a) The grid points are sorted from highest to lowest occupancy, based on the counts of the probe’s CoM. The size of the red circles on the grid indicates high vs low occupancies. The top-three grid points with the highest occupancies are shown for the purpose of demonstration. b) The grid point with the highest occupancy is taken to be the center of the first probe. All grid points enclosed within the spherical volume of a probe are added to obtain its observed occupancy. c) After processing a given probe location, the grid points associated with this probe are removed from the search process. d) The observed occupancy is calculated for the second probe centered on the next grid point with the highest occupancy. e) Upon obtaining the occupancy of the probe at this second grid point, it is removed from the search process. f) This process is continued until all the grid points are exhaustively searched and assigned to a probe location.
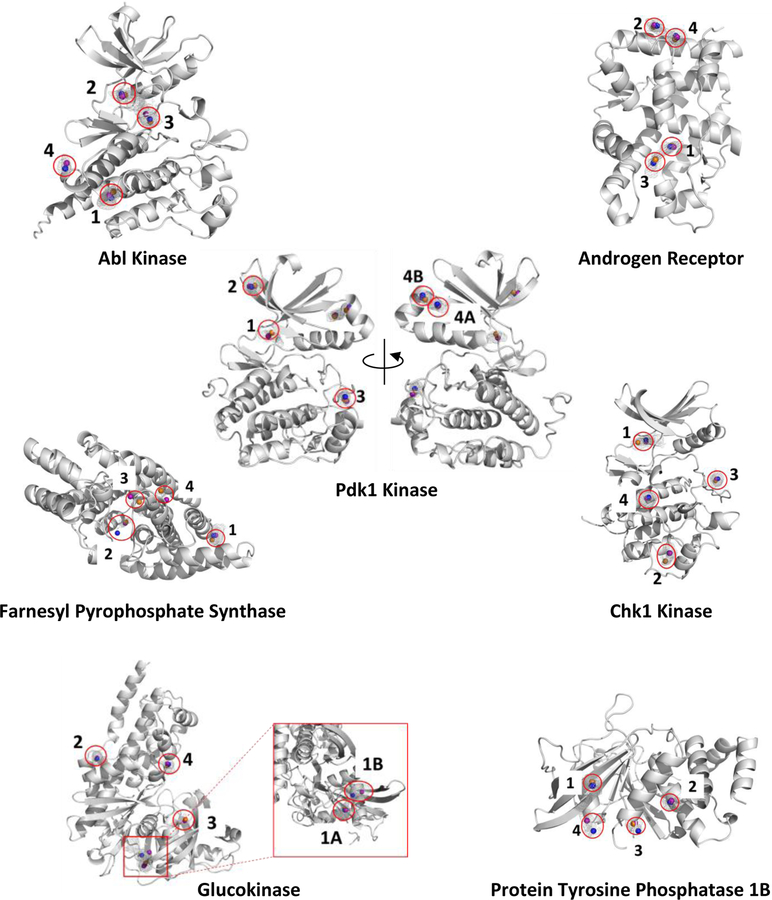
The grid point with the highest occupancy is taken to be the center of the first probe site. The occupancy of all grid points within an enclosing sphere of the volume of the probe, centered on this grid point, are summed to determine the observed occupancy for this probe location (Figure 1B). In a similar manner, the next grid point with the second highest grid occupancy is taken to be the center of the second probe site. Again, the occupancy of the second site is calculated summing the grid points within the volume of the probe sphere. (Figure 1D). This process is iteratively repeated until all grid points are assigned to probe locations. We do recognize that using spherical sites is an approximation of the actual location of the CoM of the probe in the hotspot. In our analysis of the MixMD grids, we again focused on the top-four binding sites in each protein as reported in the previous study. Within those binding sites, our MixMD simulations revealed 82 probe-binding hotspots across all seven proteins, see Figure 2.
Figure 2.
The probes acetonitrile (orange spheres), isopropanol (blue spheres), and pyrimidine (purple spheres) are bound within the top-four MixMD binding sites (as identified using our previous all-atom binning method in reference 1). On rare occasions, the binding site identified by MixMD accommodated more than one probe-binding hotspot. These sites were further divided in to subsites A and B, see Pdk1 Kinase and Glucokinase. There are a total of 82 probe hotspots across all seven proteins.
In order to calculate the free energies from these observed occupancies, one needs to compare them to expected occupancies in Table 1, using equation (1):
| (1) |
where i is every grid point in the probe’s volume and the expected occupancy is constant. The free energy value from equation (1) estimates the change in free energy of moving a probe molecule from the bulk into the binding-site location. A negative value for this free energy change indicates a binding site that is more occupied and more favorable for the probe molecule compared to the bulk. Good convergence of these free energy values is shown in the supplemental information.
Our use of equation (1) is analogous to the approach pioneered by Seco et al.3:
| (2) |
for each grid point i. However, there is a difference in how other groups generate and use the grid values. Rather than CoM grids, others have computed grids for each atom type and then used those atomic grids to estimate free energies of a drug-like molecule docked into a protein pocket.4, 27 The exact approaches of each group are outlined further below.
To compare our CoM-sphere approach for estimating free energies of binding to other approaches based on atomic grid free energies (AGFE), we also calculated free energies based on summing the atomic positions. Each atom type was binned on the 0.5-Å grid, rather than the CoM for this approach. The resulting atomic grids are used to score docked poses. We obtained these poses by placing a probe molecule at the center of each identified hotspot and energy minimizing it to the closest local minimum on the surface of the crystal structures (using the prepped proteins that initiated the setup of the MD simulations, 500 steps of conjugant gradient followed by 2500 steps of steepest descent). The contribution of each atom of the probe is estimated by the closest grid point on the appropriate atomic grid. The contribution of each atom is then summed to give a free energy estimate of the whole molecule.
Comparing our free energies to the Linear Interaction Energy (LIE) method
The most rigorous approach for calculating the free energies of binding is to use Free Energy Perturbation (FEP) methods. The problem is that it is prohibitively expensive to perform 85 disappear-a-molecule FEPs to evaluate all of our MixMD-identified binding hotspots. Instead, we turned to the LIE method.28 LIE estimates the free energies of binding by comparing the interaction energies of the probe in the bound state to the unbound, free state:
| (3) |
Where <> denotes the average electrostatic (elec) and Van der Waals (vdw) energies of the ligand with its surrounding environment, bound to the protein versus alone in water.
The method required 85 independent MD simulations of a single probe molecule, 82 cases with a probe bound to each hotspot in the protein complexes and 3 of each probe alone in water. The MD simulations were conducted similarly to the previous study of the allosteric proteins with the exception that a 1-fs timestep was used and 50 ns of production run were conducted. The probe was constrained to remain in its hotspot using a soft harmonic potential of 5 kcal/mol·Å. The energies for equation 3 were averaged over the full 50 ns.
Results and Discussion
The maximum free energy of a probe is dictated by system setup
The oversimplification of obtaining free energy values using equation (1) or (2) does come with its own set of limitations which have not been highlighted in previous studies. Free energies obtained from calculations such as these are subject to the concentration of probe molecules used in the cosolvent simulation. The limitation can be best illustrated by deriving the maximum free energy values achievable under such a framework, . At best, a probe molecule can occupy a given probe volume for the entire simulation, so the maximum occupancy at any particular site cannot exceed 1. Using a maximum observable occupancy of 1 and the expected occupancies for our 5% MixMD simulations (Table 1), one arrives at −2.14 kcal/mol, −2.17 kcal/mol, and −2.11 kcal/mol as the for acetonitrile, isopropanol, and pyrimidine, respectively. This corresponds to Kd(max) of 27.7 mM, 26.3 mM, and 29.0 mM, respectively. Using a lower concentration of probe molecules within the same volume of a simulation would result in lower expected occupancies and more favorable free energies for the maximum occupancy state. Conversely, using a higher concentration of probe molecules would result in higher expected occupancies and poorer . It should be noted that MacKerell and coworkers address this issue by using 1M concentrations of the probe molecules, the standard reference concentration.4, 27
Free energy calculations using similar cosolvent simulations have been used by other groups to propose upper limits on the maximum achievable affinity possible for any/all drug-like molecules at a given site.3, 6 Our findings call in to question the rationale for setting an upper limit on the binding free energy for drug molecules, particularly when the values are inherently dictated by the system setup and the concentration of probes used to perform the simulations. A more appropriate use for such free energy estimates lie in relative ranking. Even as expected occupancies increase or decrease, the relative ranking between the sites remains the same.
Free energy calculations from cosolvent simulations
Several groups have used similar approaches for obtaining free energy changes with grids and a ratio of observed and expected occupancies. However, the approach adopted differs from one group to another.
Barril and coworkers, in their use of isopropanol-based binary solvent simulations, calculate the binding free energy for the methyl and oxygen atoms of isopropanol separately.3 Volumes of the size of typical drug-like molecules are then created using clustering techniques by combining grid maps of the free energies for methyl and oxygen atoms of isopropanol. Using the argument that ligands of the size of drug molecules are not only involved in achieving binding affinity but also serve as a framework for the atoms to interact with the protein, the sum of the free energies of all the grid points within these drug molecule sized volumes is considered to be the maximal affinity achievable within that site/volume. Interestingly, the authors reveal that the free energy per heavy atom (HA) for the methyl and oxygen groups of isopropanol frequently surpassed the limit of −1.5 kcal/mol per non-hydrogen atom observed by Kuntz and coworkers.29 However, we show below that our method for calculating free energies gives ligand efficiencies (LE) values that never exceeded the Kuntz limit. The maximum LE we found was for acetonitrile molecules at −0.65 kcal/mol·HA. The binding affinity of organic solvents to the protein surface is very weak, mM level,30–32 so a value like ours appears more reasonable. Acetonitrile’s LE is in keeping with values desired from fragment screening.
Similarly, Mackerel and coworkers have developed “Site-Identification by Ligand Competitive Saturation” (SILCS), a cosolvent simulation technique that originally involved performing ternary solvent simulations of 1M benzene, 1M propane, and water.4 Free energies for each atom type in SILCS were calculated separately for the benzene carbons, propane carbons, water hydrogens and oxygens, using equation (2). The authors describe these free energies as Grid Free Energies (GFE). The GFE values obtained from benzene carbons correspond to interaction energies of aromatic atoms. Similarly, propane carbons, water hydrogens and oxygens correspond to aliphatic, donor, and acceptor atoms, respectively. Using these GFE values, the authors assign atom types to drug-like ligands and estimate its free energy by first bringing the ligand from a crystal structure into the frame of reference of a grid with these GFE values. The free energies of ligands were then computed by summing up the GFE values based on the atom types in the ligand and the corresponding GFE values on the grid. Our use of AGFE is meant to approximate this method for estimating the free energies for the probes themselves.
Bakan et al. have also performed cosolvent simulations using a mixture of isopropanol, isopropyl amine, acetic acid, and acetamide. Free energies were derived from the maximum occupancy of grid points within the volume of a probe.6 Our approach for calculating free energies from MixMD simulations is along similar lines in that free energies should be calculated by taking into consideration the entire volume of a probe.
Free energies of MixMD hotspots from sphere occupancies compared to AGFE and LIE
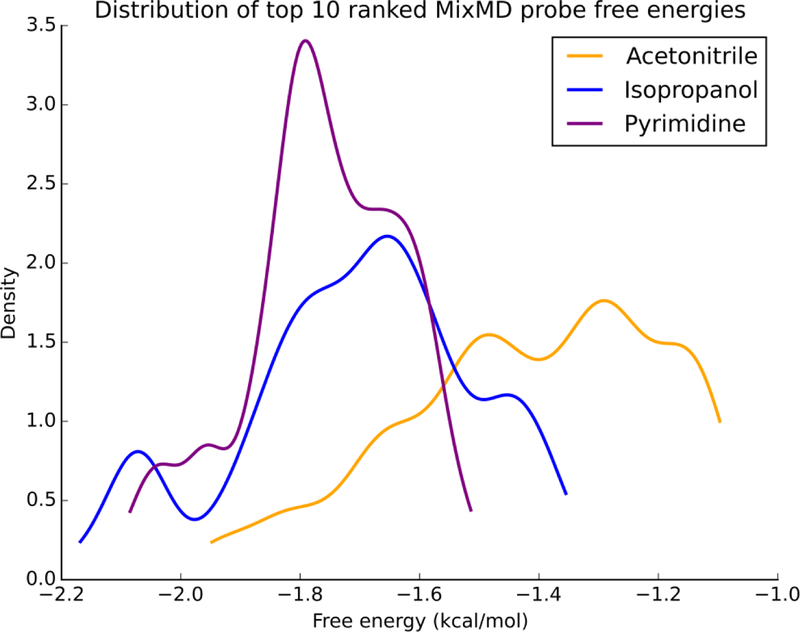
In our MixMD simulations, the free energies for acetonitrile, isopropanol, and pyrimidine were calculated using the aforementioned summation of occupancies at all points within a probe sphere (Figure 1). Across all the protein targets, for acetonitrile were lower compared to isopropanol and pyrimidine. Figure 3 shows the distribution of for the top-10 probes from each binary simulation across all the protein targets. Interestingly, LE for these same probes were flipped; acetonitrile probes had higher LE (Figure 4). The LE for all these sites were well within the −1.5 kcal/mol limit established in a study by Kuntz and coworkers29 and the −1.75 kcal/mol observed in our previous work.33 Using our approach, we have calculated of the probe molecules within the active and allosteric binding sites on our test proteins. Their locations on the protein surface are shown in Figure 2, and their free energies are presented in Table 2. Previously, we visualized the MixMD hotspots using all-atom binned occupancy maps; this revealed the full volume of the binding site mapped by MixMD probes. These MixMD maps allow one to understand the all atom contacts of the probe molecules with the protein. However, our current free energy calculations were performed on CoM binning. Thus, we found instances where our previous binding-site volumes accommodated multiple probe locations. For example in Pdk1 Kinase, site 4 (allosteric site) can be seen to bind two probes in distinct sub-sites, so it was subdivided into 4A and 4B. Similar observations were made for site 1 (the allosteric site) in Glucokinase where two subsites (site 1A and 1B) could be seen.
Figure 3.
The normalized distribution profile of ΔGbind for the top-10 MixMD probes is shown. Across the seven protein targets studied, binding free energies for isopropanol and pyrimidine were found to be more favorable than acetonitrile. Acetonitrile distribution is colored yellow, isopropanol distribution is colored purple, and pyrimidine distribution is colored purple.
Figure 4.
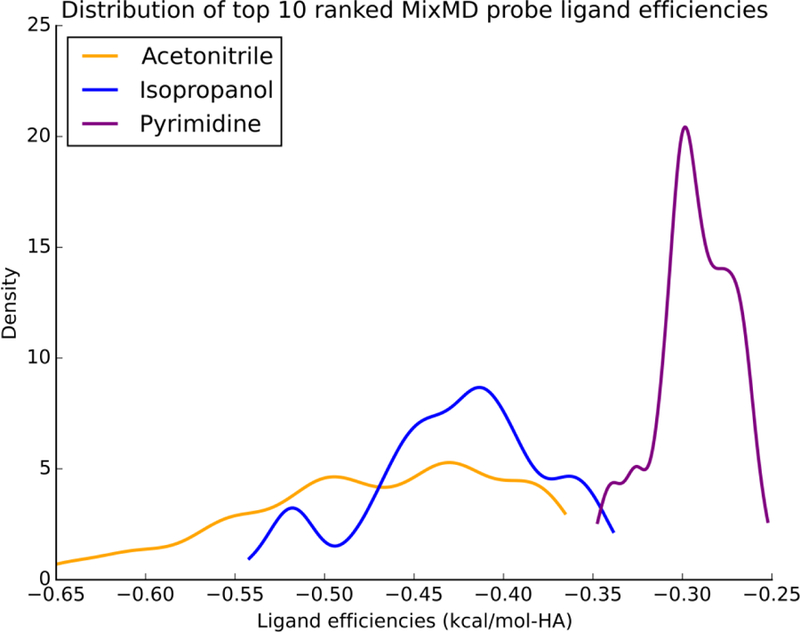
The ligand efficiencies for the top-10 probes from MixMD simulations of seven protein systems are presented in the units kcal/mol-HA. Across the seven protein targets studied, ligand efficiencies for acetonitrile were more favorable than isopropanol and pyrimidine. Acetonitrile distribution is colored yellow, isopropanol distribution is colored purple, and pyrimidine distribution is colored purple.
Table 2.
For each estimation method, the ΔGbind (kcal/mol) of the probes acetonitrile (ACN), isopropanol (IPA), and pyrimidine (PYR) are given for the hotspots within the top-four MixMD sites shown in Figure 2. Not all probes mapped into every site (--).
| Protein (PDB ID) Binding Site | Sphere Occupancy | LIE | AGFE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ABL(3KFA) | ACN | IPA | PYR | ACN | IPA | PYR | ACN | IPA | PYR |
| 1 | −1.94 | −1.92 | −1.69 | −2.06 | −3.50 | −2.14 | −2.64 | −2.60 | −1.90 |
| 2 | −1.12 | −1.55 | −1.96 | −1.89 | −2.29 | −1.86 | −2.87 | −2.27 | −1.93 |
| 3 | −1.78 | −2.07 | −2.02 | −2.15 | −0.15 | −1.20 | −2.14 | −2.03 | −2.13 |
| 4 | -- | −1.74 | −1.82 | -- | −1.15 | −2.12 | -- | −1.93 | −1.84 |
| AR(2AM9) | |||||||||
| 1 | −1.68 | −1.36 | −1.65 | −2.04 | −0.07 | −1.55 | −1.51 | −1.94 | −1.87 |
| 2 | −1.47 | −1.63 | −1.95 | −0.89 | −2.88 | −1.70 | −1.49 | −1.76 | −1.31 |
| 3 | −1.46 | −1.84 | −1.37 | −1.63 | 0.01 | −2.23 | −1.61 | −1.73 | −1.98 |
| 4 | −1.46 | −1.23 | −1.80 | −1.53 | −2.32 | −1.48 | −1.14 | −1.06 | −1.93 |
| PDK1(3RCJ) | |||||||||
| 1 | −0.85 | -- | −2.01 | −1.43 | -- | −1.62 | −1.00 | -- | −2.44 |
| 2 | −1.69 | −2.08 | −1.86 | −1.82 | −0.78 | −1.13 | −1.84 | −2.17 | −2.75 |
| 3 | −1.16 | −1.75 | −1.59 | −1.34 | −0.71 | −2.81 | −1.45 | −1.97 | −2.64 |
| 4A | −1.53 | −1.51 | −1.75 | −1.44 | −0.11 | −2.22 | −1.73 | −2.11 | −2.50 |
| 4B | −1.42 | −1.78 | −1.70 | −1.73 | −1.72 | −0.76 | −1.48 | −1.86 | −2.25 |
| FPPS(4DEM) | |||||||||
| 1 | −1.53 | −1.81 | −1.95 | −0.57 | −1.58 | -2.28 | −2.28 | −2.26 | −1.94 |
| 2 | −1.43 | −0.90 | −1.28 | −1.58 | −1.34 | −1.01 | −2.06 | −1.52 | −1.28 |
| 3 | −1.24 | -- | −1.17 | −1.03 | -- | −1.11 | −1.70 | -- | −1.79 |
| 4 | −1.48 | -- | −0.78 | −1.30 | -- | −0.90 | −2.00 | -- | −1.63 |
| CHK1(1ZYS) | |||||||||
| 1 | −1.80 | −1.62 | −1.81 | −1.70 | −4.38 | −1.55 | −1.70 | −2.28 | −2.98 |
| 2 | −1.41 | −1.95 | −1.96 | −0.40 | −4.91 | −1.65 | −1.82 | −2.29 | −2.25 |
| 3 | −1.62 | −1.76 | −2.05 | −1.45 | −3.33 | −1.54 | −1.54 | −1.93 | −2.52 |
| 4 | −1.85 | −2.08 | −2.05 | −0.67 | −2.89 | −1.37 | −1.67 | −2.03 | −2.67 |
| Glucokinase(3IDH) | |||||||||
| 1A | −1.65 | −1.86 | −1.87 | -1.50 | −1.90 | −1.64 | −1.79 | −1.96 | −2.37 |
| 1B | -- | −2.04 | −1.62 | -- | −1.02 | −2.30 | -- | −2.19 | −1.98 |
| 2 | −1.82 | −1.78 | −1.80 | −1.69 | −0.01 | −1.40 | −1.62 | −1.89 | −1.95 |
| 3 | −1.19 | -- | −0.87 | −1.24 | -- | −1.71 | −1.52 | -- | −1.32 |
| 4 | −1.19 | −1.49 | −1.60 | −1.12 | −1.40 | −2.05 | −1.63 | −2.13 | −2.14 |
| PTP1B(2CMB) | |||||||||
| 1 | −1.66 | −2.07 | −2.08 | −1.11 | −2.12 | −2.06 | −0.58 | −2.03 | −1.85 |
| 2 | -- | −1.65 | −1.83 | -- | −1.02 | −1.80 | -- | −2.09 | −1.89 |
| 3 | −1.09 | −1.22 | −1.57 | −0.76 | −1.22 | −1.09 | −1.15 | −1.91 | −1.75 |
| 4 | -- | −1.47 | −1.82 | -- | −1.38 | −0.62 | -- | −1.85 | −1.82 |
When proposing an alternate approach for estimating free energies, it is important to compare the results to other similar techniques. For this work, we compared our sphere occupancy method to the use of AGFE and LIE. Table 2 presents the values for the three methods. Good agreement is seen between all three. estimated by sphere occupancy is very similar to AGFE with a mean unsigned difference (MUD) of only 0.37 kcal/mol and RMSD of 0.49 kcal/mol. In comparison to LIE, the sphere occupancy method is slightly closer (MUD = 0.60 kcal/mol, RMSD = 0.85 kcal/mol) than the AGFE method (MUD = 0.71 kcal/mol, RMSD = 0.93 kcal/mol).
Ranking MixMD binding sites based on configurational entropy
The entropy of a probe in a site can be partitioned into
| (4) |
where reflects the behavior of the probe within the site and is the entropy of taking a probe from the freedom of occupying anywhere in the simulation box to occupying a site identified by the volume of the probe. As noted earlier, we define that site by a sphere centered at each high-occupancy point. That sphere definition is the same anywhere on the protein surface, so the translational entropy is the same for all sites in the same MixMD simulation. It simply reflects the difference in the volume of the sphere vs the volume of the box: = k × ln(number of grid points in sphere) – k × ln (total number of grid points in the box). This dependence upon the box highlights that is defined by the system setup, just like . However, the value is basically the same for all probes to the same protein because it just reflects translation of the CoM.
In calculating the difference in entropy between the sites , the term cancels. The interesting comparison lies in the other degrees of freedom sampled by the probe’s atoms. While molecules in the bulk rotate freely, interactions with the protein impart a level of structure, limiting the probe’s freedom. is the difference between a probe evenly and freely sampling the sphere, Sprobe(max), to the actual translational and rotational behavior of the probe seen during the simulations, Sprobe. Here, we draw upon the concept of entropy as the density of states and use our grid points as shown in Figure 5. To simplify the analysis, we decomposed the probe into its non-hydrogen atoms and used the same binning routine from calculating free energies to count the atomic occupancies on the grid points in the sphere. Entropy of the probe is calculated using the Gibbs-Shannon equation,34 shown in equation (5). The probability of finding an atom at a particular grid point is determined by equation (6). The entropy measures obtained for each heavy atom are then combined as shown in equations (7) and (8) to approximate Sprobe.
Figure 5.
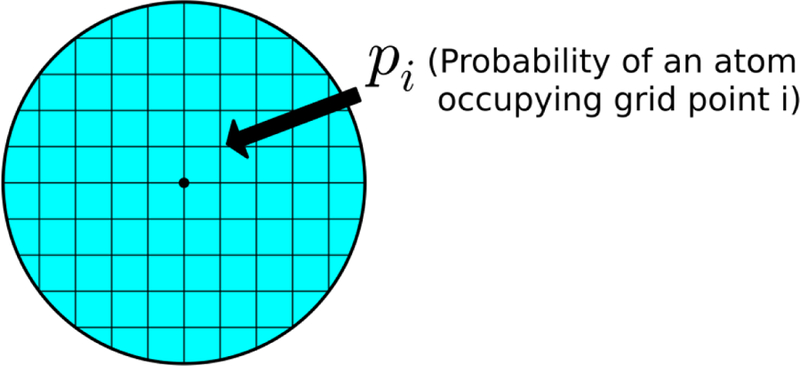
The concept of entropy as the density of states is applied within the volume of a probe sphere. Each grid point within the volume is considered a state. The probability of each state (pi) for each heavy atom is calculated using equation (6).
| (5) |
| (6) |
| (7) |
| (8) |
Under no constraint while freely exploring the box in the bulk solvent, each grid point is equally occupied, and one can establish an upper limit of entropy achievable within the volume of a probe. The Sprobe(max) values possible under our framework are presented in equations (9) and (10) and listed for acetonitrile, isopropanol, and pyrimidine in Table 3. This maximal value is an over-estimate because the chemical structure of the probe imparts an inherent bias to sampling the grid. However, this inherent bias is the same in all sites; furthermore, Sprobe(max) representing the free bulk behavior drops out when calculating the difference between the sites,. Of course, this only cancels when comparing the same type of probe molecules in different locations, not necessarily across different probe types.
Table 3.
Maximum entropy at 300K (in kcal/mol) for a freely rotating and translating probe molecule is calculated. Under such conditions every grid point within the volume of a probe will be occupied with equal probability (pbulk).
| Probe | No. of grid points in volume of probe (gpt) | pbulk 1/(gpt) | –TSprobe(max) (kcal/mol at 300K) |
|---|---|---|---|
| Acetonitrile | 389 | 0.0025706940874 | 11.497 |
| Isopropanol | 515 | 0.00194174757282 | 15.329 |
| Pyrimidine | 619 | 0.0016155088853 | 22.993 |
| (9) |
| (10) |
Entropies across MixMD binding sites
In order to compare the configurational entropy of MixMD binding sites, we have computed the change in entropy of moving a probe molecule from the bulk into each binding-site sphere. As one would expect, moving a freely rotating probe in the bulk to a binding site decreases the entropy and thus one should observe that such a change is unfavorable (but compensated by enthalpic gain). We have confirmed this behavior by computing the for the top-50 probe sites ranked by free energy in all the allosteric protein systems which we simulated in MixMD. The distribution of for the probes acetonitrile, isopropanol, and pyrimidine are shown in Figure 6. The high peaks close to zero show that many probe molecules tumble close to the bulk behavior. Most importantly, none of the entropy changes are less than zero; this confirms our assumption that none of the probe molecules exceed the maximal entropy we have calculated in previous sections (Table 3).
Figure 6.
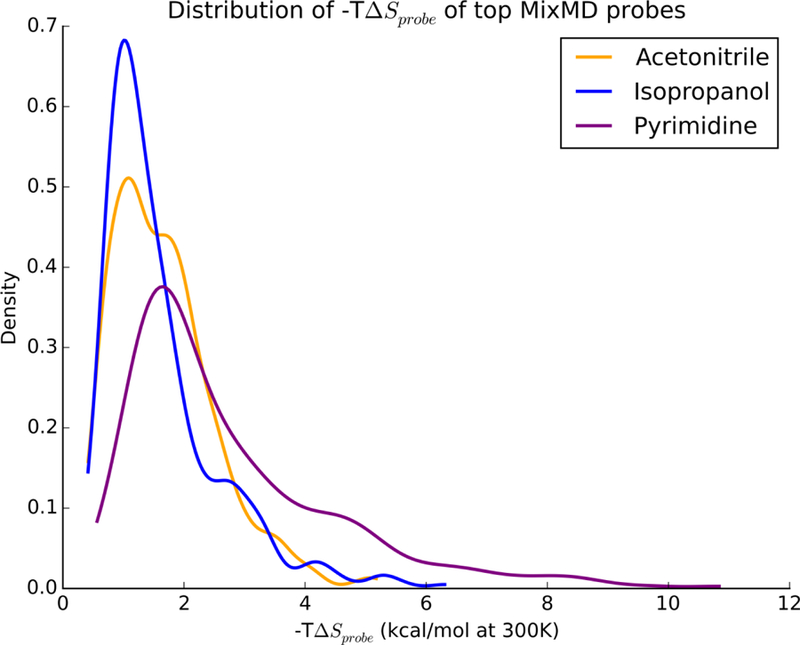
The distribution of –TΔSprobe for the top-50 MixMD probes ranked by free energy are presented for acetonitrile (orange), isopropanol (blue), and pyrimidine (purple). As expected, moving from the bulk into the binding site where the probes are restricted is unfavorable, thus –TΔSprobe values are positive.
Interpreting configurational entropies obtained from MixMD binding sites
Entropies measured using our approach report upon the local thermodynamic environment of an individual probe molecule and as such cannot be verified using experiments. It is important to note that an experimental measure of a binding event also reflects the entropic costs paid by the protein and the reordering of the water around the binding site.15 While the effect on the protein may be partially observed from the order seen for the probes, the effects on water are very hard to estimate. More importantly, very subtle changes to ligands can result in significant and unexpected changes in water as the work of Klebe shows.35 It is unreasonable to assume that the water’s behavior around the solvent probes is a good estimate of their behavior in the presence of a drug-like ligand.
Despite these limitations, these measures describe the structure/order of the probe’s conformational sampling within the binding site, and one can in principle visualize the occupancies of the HA of the probe molecules to validate these findings. When visualizing the occupancies of the probe’s HA, it is important to normalize the HA density within the volume of the probe, as we do in equation (6). This is necessary because, raw bin counts not only reflect upon the positional preference of a probe, but also on the duration a probe molecule has spent its time at a given location. By normalizing the occupancies to give densities of HA within the binding site sphere, one can separate the information needed for to reflect each HA’s contribution to and analyze the density for any probe’s configurational sampling within their binding site sphere. We have assessed this important metric using calculated for all the systems and MixMD probes used on our earlier study. The minimum, median, and maximum are presented for the probes acetonitrile, isopropanol, and pyrimidine in Table 4.
Table 4.
The change in configurational entropy when moving a cosolvent from the bulk to the protein binding site were calculated using the top-fifty MixMD probes ranked by free energy from all seven allosteric systems. The minimum, median and maximum –TΔSprobe in this dataset was reported for each probe at 300K. The proteins to which these values belong along with the rank of the probe according to free energy are provided in brackets. FPPS is an abbreviation for Farnesyl Pyrophosphate Synthase.
| Probe | Minimum –TΔSprobe (kcal/mol at 300K) | Median –TΔSprobe (kcal/mol at 300K) | Maximum –TΔSprobe (kcal/mol at 300K) |
|---|---|---|---|
| Acetonitrile | 0.42 (Abl Kinase, rank 19) |
1.56 (Pdk1 Kinase, rank 43) |
5.18 (Glucokinase, rank 32) |
| Isopropanol | 0.42 (FPPS, rank 3) |
1.3 (Androgen Receptor, rank 38) |
6.31 (Glucokinase, rank 31) |
| Pyrimidine | 0.57 (FPPS, rank 4) |
2.18 (Androgen Receptor, rank 32) |
10.84 (FPPS, rank 43) |
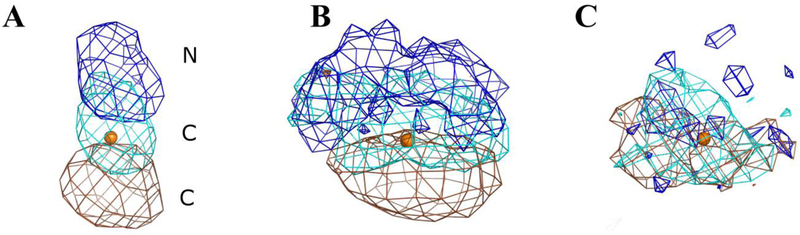
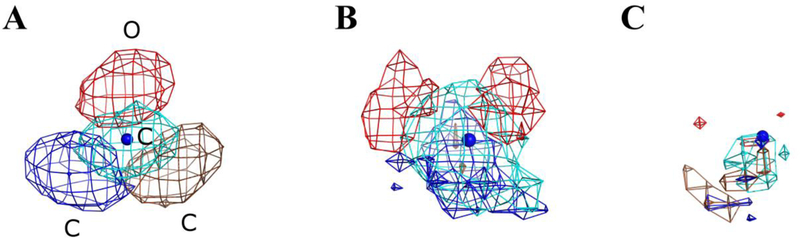
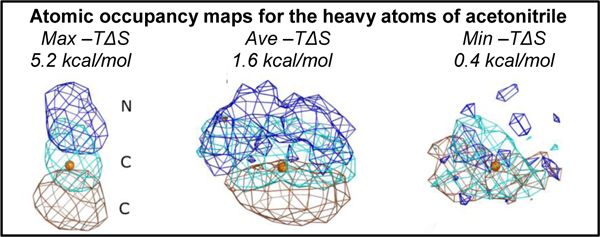
In order to make a proper comparison across the minimum, median, and maximum , we have visualized the population density of each HA in the probe molecule at a contour level of 0.5% of the population in the binding site. In the case of acetonitrile, these densities are show in Figure 7. The density of the nitrogen atom of acetonitrile is colored blue, whereas the densities of the central and terminal carbons of acetonitrile are colored cyan and brown. The CoM that defines the binding site of the probe molecule is shown as an orange colored sphere for reference. The maximum represents the most unfavorable transfer from the bulk to the protein binding site. As expected, in Figure 7A, the densities of the three atoms within the acetonitrile probe molecule are clearly visible at the atomic level. This demonstrates the restriction on the probe when bound to the site. When the density of the probe with the median is visualized in Figure 7B, one sees a lesser degree of structure. Clearly, the acetonitrile molecule is oriented with its nitrogen pointing up like the example in Figure 7A, but some freedom is seen in the lateral movement. Figure 7C shows the probe with the minimum observed for acetonitrile, where the HA density around the CoM is disperse and overlapping. This is consistent with the idea that a low probe in this location is similar to the bulk environment and thus is freely rotating. In going from maximum to minimum , there is a trend of decreasing structure/order of the probe molecules seen when visualizing the HA density. This is consistent with our theoretical framework.
Figure 7.
Acetonitrile HA densities are presented for the maximum, median, and minimum entropies reported in Table 4. The CoM that defines the binding site of the acetonitrile probe is shown as an orange sphere for reference. The normalized occupancies of all the atoms in A, B, and C are contoured at 0.005. The density of nitrogen atoms is colored blue, the density of the carbon atom in the middle of acetonitrile is colored cyan, and the density of the terminal carbon is colored brown. A) The –TΔSprobe is at a maximum, making this the most constrained probe in our dataset. Consequently, all atoms of the acetonitrile probe can be clearly seen in this case. B) The acetonitrile with the median –TΔSprobe shows some structure in the configurational sampling but also some latitude. C) Density for the case of minimum –TΔSprobe shows that the probe molecule at this location is freely rotating and is close to the entropy of the bulk. As a result, the density is smeared out and overlapping.
Similar trends were observed for isopropanol. When the density of the probe molecule with the maximum (Figure 8A) was visualized clear, structured density could be seen. The densities at the median (Figure 8B) clearly show two conformations with the hydroxyl oxygen sampling between two hydrogen-bonding interactions. The minimum (Figure 8C) follows similar trends as seen for acetonitrile. The same results were obtained for pyrimidine, where visualization of the densities for the maximum, median, and minimum followed the established trend of decreasing structure/order in the probe molecules (Figure 9). Probe entropies calculated for our sites across the seven allosteric protein systems are given in Table 5.
Figure 8.
Normalized HA occupancies of isopropanol are presented for the maximum, median, and minimum entropies reported in Table 4. The CoM that defines the binding site of the isopropanol probe is shown as a blue sphere for reference. The density of all the atoms in A, B, and C are contoured at 0.005. The density of oxygen atoms is colored red, the density of the central carbon is colored cyan, and the two terminal carbons are colored blue and brown. A) The maximum –TΔSprobe example is the most constrained probe in our dataset. Consequently, all atoms of the isopropanol probe can be clearly seen in this case. B) The –TΔSprobe in this case is at the median of all processed sites, there is some structure in the probe molecule. Notably, the hydroxyl oxygen is sampling two hydrogen-bonding interactions. C) For the case of minimum –TΔSprobe, the molecule at this location is freely rotating, and is close to the entropy of the bulk. As a result, the density is smeared out and can only be seen partly.
Figure 9.
Pyrimidine per probe normalized density is presented for the maximum, median, and minimum entropies reported in Table 4. The CoM that defines the binding site of the pyrimidine probe is shown as a purple sphere for reference. The normalized occupancies of all the atoms in A, B, and C are contoured at 0.005. The density of two nitrogen atoms are blue and green, whereas the density of carbon atoms is colored brown, purple, yellow, and orange. A) In the maximum –TΔSprobe case, the molecule is very constrained. Consequently, all atoms of the pyrimidine probe can be clearly seen in this case. B) The –TΔSprobe in this case is at the median of all processed sites, there is some structure in the probe molecule. Notably, the molecule is rotating and giving HA densities with a torus shape. It appears that the nitrogens are sampling three locations, separated by roughly 120°. C) For the minimum –TΔSprobe case, the probe molecule at this location is freely rotating, and is close to the entropy of the bulk. As a result, the density is smeared out and cannot be seen.
Table 5.
The entropic penalties (-TΔSprobe in kcal/mol) of the MixMD binding sites are computed at 300K and are presented for the top-four sites. Each probe solvent is presented for the hotspots within sites as shown in Figure 2: acetonitrile (ACN), isopropanol (IPA), and pyrimidine (PYR). Not all probes mapped into every hotspot (--).
| Protein (PDB ID) Binding Site | Entropic Penalties (kcal/mol) | ||
|---|---|---|---|
| ABL(3KFA) | ACN | IPA | PYR |
| 1 | 1.47 | 1.58 | 3.12 |
| 2 | 2.45 | 2.91 | 3.72 |
| 3 | 0.95 | 1.39 | 1.89 |
| 4 | -- | 1.07 | 1.74 |
| AR(2AM9) | |||
| 1 | 1.99 | 2.66 | 4.54 |
| 2 | 1.36 | 0.97 | 2.65 |
| 3 | 1.68 | 2.58 | 3.95 |
| 4 | 2.0 | 2.2 | 4.12 |
| PDK1(3RCJ) | |||
| 1 | 3.4 | -- | 5.39 |
| 2 | 0.64 | 1.09 | 1.45 |
| 3 | 1.45 | 1.8 | 2.86 |
| 4A | 0.92 | 0.93 | 1.19 |
| 4B | 0.69 | 0.75 | 1.04 |
| FPPS(4DEM) | |||
| 1 | 1.3 | 1.85 | 1.73 |
| 2 | 2.0 | 2.66 | 4.58 |
| 3 | 2.09 | -- | 8.14 |
| 4 | 1.61 | -- | 5.4 |
| CHK1(1ZYS) | |||
| 1 | 2.01 | 1.76 | 3.61 |
| 2 | 2.53 | 4.08 | 3.44 |
| 3 | 1.31 | 1.11 | 1.87 |
| 4 | 1.03 | 1.15 | 1.38 |
| Glucokinase(3IDH) | |||
| 1A | 1.66 | 2.22 | 2.95 |
| 1B | -- | 1.71 | 1.72 |
| 2 | 1.72 | 1.6 | 2.29 |
| 3 | 3.74 | -- | 6.49 |
| 4 | 1.87 | 1.67 | 3.99 |
| PTP1B(2CMB) | |||
| 1 | 1.68 | 1.82 | 2.46 |
| 2 | -- | 2.44 | 3.15 |
| 3 | 2.79 | 2.39 | 8.3 |
| 4 | -- | 2.78 | 4.64 |
Conclusion
We have established a means of obtaining the free energy and entropy rankings based on MixMD simulations. The limitations of the free energy calculations were demonstrated. These limitations are universal to cosolvent MD simulations, and they call in to question other groups’ rationale for trying to use cosolvent grids to establish a maximal free energy achievable for any/all drug-like molecules.3, 6 Furthermore, a framework for calculating entropies is proposed and validated. In particular, we note that the entropies are only for the probe, not the whole system. The entropic effects on reordering water around protein-ligand complexes are very hard to estimate, and very subtle changes to ligands can result in significant and unexpected changes in water. It is unreasonable to assume that the water’s behavior around the solvent probes is a good estimate of their behavior in the presence of a drug-like ligand. Despite these limitations, estimating the entropy of the probe molecules in the binding hotspots yields information about the conformational flexibility that may be useful when designing drug-like molecules to complement a binding site.
Supplementary Material
Acknowledgements
We thank Dr. Charles L. Brooks III for providing access to the Gollum clusters at the University of Michigan. We also thank the IBM Matching Grants Program for granting the GPU units for high-performance MD simulations. We greatly appreciate the generous donation of the MOE software from Chemical Computing Group. This work has been supported by the National Institutes of Health (R01 GM065372).
Footnotes
Supplemental Information
Data showing convergence of the sphere-occupancy free energies is given.
References
- 1.Ghanakota P; Carlson HA, Moving Beyond Active-Site Detection: MixMD Applied to Allosteric Systems. J. Phys. Chem. B 2016, 120, 8685–8695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ghanakota P; Carlson HA, Driving Structure-Based Drug Discovery through Cosolvent Molecular Dynamics. J. Med. Chem 2016, 59, 10383–10399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Seco J; Luque FJ; Barril X, Binding Site Detection and Druggability Index from First Principles. J. Med. Chem 2009, 52, 2363–2371. [DOI] [PubMed] [Google Scholar]
- 4.Raman EP; Yu W; Guvench O; MacKerell AD Jr., Reproducing Crystal Binding Modes of Ligand Functional Groups Using Site-Identification by Ligand Competitive Saturation (SILCS) Simulations. J. Chem. Info. Model 2011, 51, 877–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lexa KW; Carlson HA, Full Protein Flexibility Is Essential for Proper Hot-Spot Mapping. J. Am. Chem. Soc 2011, 133, 200–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bakan A; Nevins N; Lakdawala AS; Bahar I, Druggability Assessment of Allosteric Proteins by Dynamics Simulations in the Presence of Probe Molecules. J. Chem. Theory Comput 2012, 8, 2435–2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tan YS; Spring DR; Abell C; Verma C, The Use of Chlorobenzene as a Probe Molecule in Molecular Dynamics Simulations. J. Chem. Info. Model 2014, 54, 1821–1827. [DOI] [PubMed] [Google Scholar]
- 8.Oleinikovas V; Saladino G; Cossins BP; Gervasio FL, Understanding Cryptic Pocket Formation in Protein Targets by Enhanced Sampling Simulations. J. Am. Chem. Soc 2016, 138, 14257–14263. [DOI] [PubMed] [Google Scholar]
- 9.Lexa KW; Carlson HA, Protein Flexibility in Docking and Surface Mapping. Q. Rev. Biophys 2012, 45, 301–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lexa KW; Carlson HA, Improving Protocols for Protein Mapping through Proper Comparison to Crystallography Data. J. Chem. Info. Model 2013, 53, 391–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lexa KW; Goh GB; Carlson HA, Parameter Choice Matters: Validating Probe Parameters for Use in Mixed-Solvent Simulations. J. Chem. Info. Model 2014, 54, 2190–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ung PMU; Ghanakota P; Graham SE; Lexa KW; Carlson HA, Identifying Binding Hot Spots on Protein Surfaces by Mixed-Solvent Molecular Dynamics: HIV-1 Protease as a Test Case. Biopolymers 2016, 105, 21–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alvarez-Garcia D; Barril X, Relationship between Protein Flexibility and Binding: Lessons for Structure-Based Drug Design. J. Chem. Theory Comput 2014, 10, 2608–2614. [DOI] [PubMed] [Google Scholar]
- 14.Raman EP; MacKerell AD Jr., Spatial Analysis and Quantification of the Thermodynamic Driving Forces in Protein-Ligand Binding: Binding Site Variability. J. Am. Chem. Soc 2015, 137, 2608–2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nguyen CN; Young TK; Gilson MK, Grid Inhomogeneous Solvation Theory: Hydration Structure and Thermodynamics of the Miniature Receptor Cucurbit[7]uril. J. Chem. Phys 2012, 137, 044101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML, Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- 17.Case DA; Betz RM; Botello-Smith W; Cerutti DS; Cheatham TE III; Darden TA; Duke RE; Giese TJ; Gohlke H; Goetz AW; Homeyer N; Izadi S; Janowski P; Kaus J; Kovalenko A; Lee TS; LeGrand S; Li P; Lin C; Luchko T; Luo R; Madej B; Mermelstein D; Merz KM; Monard G; Nguyen H; Nguyen HT; Omelyan I; Onufriev A; Roe DR; Roitberg A; Sagui C; Simmerling CL; Swails J; Walker RC; Wang J; Wolf RM; Wu X; Xiao L; York DM; Kollman PA AMBER 2016. University of California, San Francisco 2016.
- 18.Ryckaert JP; Ciccotti G; Berendsen HJ, Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of N-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- 19.Roe DR; Cheatham TE III, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput 2013, 9, 3084–3095. [DOI] [PubMed] [Google Scholar]
- 20.Zhou T; Commodore L; Huang WS; Wang Y; Sawyer TK; Shakespeare WC; Clackson T; Zhu X; Dalgarno DC, Structural Analysis of DFG-in and DFG-out Dual Src-Abl Inhibitors Sharing a Common Vinyl Purine Template. Chem. Biol. Drug Des 2010, 75, 18. [DOI] [PubMed] [Google Scholar]
- 21.Pereira de Jésus-Tran K; Côté PL; Cantin L; Blanchet J; Labrie F; Breton R, Comparison of Crystal Structures of Human Androgen Receptor Ligand-Binding Domain Complexed with Various Agonists Reveals Molecular Determinants Responsible for Binding Affinity. Protein Sci 2006, 15, 987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Merkul E; Klukas F; Dorsch D; Grädler U; Greiner HE; Müller TJJ, Rapid Preparation of Triazolyl Substituted NH-Heterocyclic Kinase Inhibitors via One-Pot Sonogashira Coupling–TMS-Deprotection–CuAAC Sequence. Org. Biomol. Chem 2011, 9, 5129. [DOI] [PubMed] [Google Scholar]
- 23.Lin YS; Park J; De Schutter JW; Huang XF; Berghuis AM; Sebag M; Tsantrizos YS, Design and Synthesis of Active Site Inhibitors of the Human Farnesyl Pyrophosphate Synthase: Apoptosis and Inhibition of ERK Phosphorylation in Multiple Myeloma Cells. J. Med. Chem 2012, 55, 3201. [DOI] [PubMed] [Google Scholar]
- 24.Stavenger RA; Zhao B; Zhou B-BS; Brown MJ; Lee D; Holt DA The citation for structure 1ZYS at the PDB is listed as “To be published” (Pyrrolo[2,3-B]pyridines Inhibit the Checkpoint Kinase Chk1.) http://www.rcsb.org/pdb/explore/explore.do?structureId=1zys, accessed May 27, 2016.
- 25.Petit P; Antoine M; Ferry G; Boutin JA; Lagarde A; Gluais L; Vincentelli R; Vuillard L, The Active Conformation of Human Glucokinase Is Not Altered by Allosteric Activators. Acta Crystallogr., Sect. D: Biol. Crystallogr 2011, 67, 929. [DOI] [PubMed] [Google Scholar]
- 26.Ala PJ; Gonneville L; Hillman MC; Becker-Pasha M; Wei M; Reid BG; Klabe R; Yue EW; Wayland B; Douty B, Structural Basis for Inhibition of Protein-Tyrosine Phosphatase 1B by Isothiazolidinone Heterocyclic Phosphonate Mimetics. J. Biol. Chem 2006, 281, 32784. [DOI] [PubMed] [Google Scholar]
- 27.Faller CE; Raman EP; MacKerell AD Jr.; Guvench O, Site Identification by Ligand Competitive Saturation (SILCS) simulations for fragment-based drug design. Methods Mol. Biol 2015, 1289, 75–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Åqvist J; Luzhkov VB; Brandsal BO, Ligand Binding Affinities from MD Simulations. Acc. Chem. Res 2002, 35, 358–365. [DOI] [PubMed] [Google Scholar]
- 29.Kuntz ID; Chen K; Sharp KA; Kollman PA, The Maximal Affinity of Ligands. Proc. Natl. Acad. Sci. U. S. A 1999, 96, 9997–10002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Huang D; Caflisch A, Small Molecule Binding to Proteins: Affinity and Binding/Unbinding Dynamics from Atomistic Simulations. Chemmedchem 2011, 6, 1578–1580. [DOI] [PubMed] [Google Scholar]
- 31.Huang D; Rossini E; Steiner S; Caflisch A, Structured Water Molecules in the Binding Site of Bromodomains Can Be Displaced by Cosolvent. Chemmedchem 2014, 9, 573–579. [DOI] [PubMed] [Google Scholar]
- 32.Erlanson DA; Fesik SW; Hubbard RE; Jahnke W; Jhoti H, Twenty Years on: The Impact of Fragments on Drug Discovery. Nat. Rev. Drug Discov 2016, 15, 605–619. [DOI] [PubMed] [Google Scholar]
- 33.Smith RD; Engdahl AL; Dunbar JB Jr.; Carlson HA, Biophysical Limits of Protein-Ligand Binding. J. Chem. Info. Model 2012, 52, 2098–2106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Suárez D; Díaz N, Direct Methods for Computing Single-Molecule Entropies from Molecular Simulations. WIREs Comput. Mol. Sci 2015, 5, 1–26. [Google Scholar]
- 35.Klebe G, Applying Thermodynamic Profiling in Lead Finding and Optimization. Nat Rev Drug Discov 2015, 14, 95–110. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.