Microalgae and cyanobacteria modeling in water resource recovery facilities: A critical review

Abstract

Microalgal and cyanobacterial resource recovery systems could significantly advance nutrient recovery from wastewater by achieving effluent nitrogen (N) and phosphorus (P) levels below the current limit of technology. The successful implementation of phytoplankton, however, requires the formulation of process models that balance fidelity and simplicity to accurately simulate dynamic performance in response to environmental conditions. This work synthesizes the range of model structures that have been leveraged for algae and cyanobacteria modeling and core model features that are required to enable reliable process modeling in the context of water resource recovery facilities. Results from an extensive literature review of over 300 published phytoplankton models are presented, with particular attention to similarities with and differences from existing strategies to model chemotrophic wastewater treatment processes (e.g., via the Activated Sludge Models, ASMs). Building on published process models, the core requirements of a model structure for algal and cyanobacterial processes are presented, including detailed recommendations for the prediction of growth (under phototrophic, heterotrophic, and mixotrophic conditions), nutrient uptake, carbon uptake and storage, and respiration.

Graphical abstract

Highlights

• •A critical review of 324 peer-reviewed phytoplankton models was conducted.
• •Modeling approaches for pseudo-mechanistic processes are synthesized.
• •Key factors (e.g., C, P, temperature) were only included in ∼25% of models.
• •Core model structure for wastewater treatment is proposed to advance model utility.
• •Future efforts should build on existing IWA models for transparency and usability.

Abbreviations

ADM1

Anaerobic Digestion Model 1

ASMs

Activated Sludge Models (1, 2, 2d, 3)

BNR

Biological nutrient removal

COD

Chemical oxygen demand

CTMI

Cardinal temperature model with inflection

DO

Dissolved oxygen

HRAP

High-rate algal pond

IWA

International Water Association

N

Nitrogen

P

Phosphorus

PBR

Photobioreactor

PI

Photosynthesis-Irradiance

S

Model state variable representing a soluble component

S_NO

Soluble nitrate and nitrite

S_S

Readily biodegradable soluble COD

T_max

Maximum temperature at which growth can occur

T_min

Minimum temperature at which growth can occur

T_opt

Optimal temperature which results in the highest growth rate

WRRF

Water resource recovery facility

WWTP

Wastewater treatment plant

X

Model state variable representing a particulate component

X_B,A

Active autotrophic biomass

X_B,H

Active heterotrophic biomass

X_I

Inert suspended solids

Y_H

Yield of heterotrophic biomass on COD

Introduction

Nutrient removal requirements for water resource recovery facilities (WRRFs) are nearing the limit of current technologies (e.g., the limit of biological nutrient removal (BNR) is roughly 3 mg N·L^-1 for total nitrogen and 0.1 mg P·L^-1 for total phosphorus (USEPA, 2007)). As effluent requirements become more stringent, removal of both nitrogen and phosphorus past the current limit of technology requires the development of new technologies capable of reliably scavenging all forms of nutrients, including dissolved organic nitrogen and dissolved organic phosphorus (Bott and Parker, 2011). Microalgal resource recovery systems could significantly advance nutrient management of wastewaters by simultaneously achieving effluent concentrations of nitrogen and phosphorus below the current limit of technology and allowing for nutrient reuse (e.g., as fertilizer (Leow et al., 2015; Metting, 1996)). Although technical and economical bottlenecks still exist, the broad and sustained adoption of algal and cyanobacterial treatment processes is contingent upon the ability to reliably and accurately simulate full-scale performance in response to reactor and process design, influent composition, and environmental conditions. This ability is hindered by a lack of model fidelity and transparency regarding model structure and underlying science.

Some microalgae and cyanobacteria have the ability to utilize phototrophic, heterotrophic, or mixotrophic (i.e., phototrophic and heterotrophic simultaneously) metabolisms (e.g., Chlorella vulgaris (Adesanya et al., 2014), Spirulina platensis (Zhang et al., 1998), and Synechocystis sp. (Lopo et al., 2012)). The metabolism being used depends on environmental conditions, such as substrate availability and lighting. Additionally, the presence or absence of nutrients (both currently and in the cell’s recent past) can affect carbon uptake and partitioning (e.g., as biomass or storage compounds). These complex processes are frequently handled by formulating models with either (i) more variables (i.e., compared to most models of heterotrophic bacteria) or (ii) incorrect simplifying assumptions that diminish model accuracy. These contrasting approaches have resulted in hundreds of models for algae, indicating a lack of clear direction for this field.

Initial modeling efforts sought to understand phytoplankton behavior in natural ecosystems (e.g., (Jørgensen, 1976; Steele, 1962)), but translation of empirically derived models from nature to engineered systems requires verification and possibly modification. Additionally, disparate approaches to algal and cyanobacterial process modeling, highly variable experimental conditions (for model calibration and validation), and a lack of regard for existing chemotrophic model structures (e.g., ASMs, ADM1) have also impeded the development of generalizable model structures and well-defined parameters relevant to WRRFs (a.k.a. wastewater treatment plants, WWTPs). Recent review articles have summarized the breadth of models available to simulate algal growth (e.g., (Darvehei et al., 2018; Lee et al., 2015)), but there is no clear indication of when subcomponents should be considered or excluded (e.g., simulate organic carbon uptake or not) nor is there a rationale or guidance for choosing any particular equation to simulate each subcomponent. Recent process models developed by the authors (Baroukh et al., 2014; Guest et al., 2013; Wágner et al., 2016) have attempted to reconcile these differences, but an industry-wide, harmonized consensus is still lacking. To advance the broader implementation of algae and cyanobacteria process models by researchers and practitioners, it is critical to establish a unified modeling framework that is capable of accounting for relevant process and environmental conditions while simultaneously avoiding unnecessary complexity.

The objective of this work was to critically review approaches to algae and cyanobacteria modeling and propose a unified framework for phytoplankton process modeling in the context of WRRFs. As researchers attempt to balance model complexity with accuracy, the range of disparate phytoplankton wastewater treatment models continues to grow. To gain a better understanding of current approaches to modeling, a critical literature review was performed to characterize core components of modeling algal and cyanobacterial bioprocesses and elucidate their relative importance to the overall accuracy and complexity of wastewater models. Based on the available information, a modeling framework is proposed that can be used for future research and development in order to advance phytoplankton model fidelity and transparency as well as allow for its integration with current International Water Association (IWA) models (e.g., (Batstone et al., 2002; Henze et al., 2000)). This work synthesizes the findings and recommendations from an international collaboration of phytoplankton modelers working toward the development of a unified modeling framework for microalgal and cyanobacterial process models. Building on recent process models developed by the authors and on recent reviews, the results from an extensive critical literature review of 324 articles and conference proceedings presenting algae/cyanobacteria models is presented to identify state variables and processes that can serve as the core, unified modeling framework for phytoplankton-based bioprocesses.

Methods

A comprehensive review of algal and cyanobacterial modeling literature was conducted through Scopus based on the presence of search terms in the title, abstract, or keywords of research articles. The search terms for this review utilized “wildcards” to efficiently search for multiple variants of a word at once (e.g., model, modeling, and models are all found using the term “model*”) as well as a proximity search to ensure the word “model*” was within 10 words of “grow*” or “metabol*”(i.e., “w/10”). The specific search used was: “title-abs-key((alga* or cyanobact* or phytoplank*) and (grow* or metabol*) w/10 model*) which yielded 2,402 research articles on January 26, 2018. Each paper was then screened to determine if it met any of the following exclusion criteria: (i) it did not model growth, (ii) it did not pertain to cyanobacteria or eukaryotic algae, (iii) there was no new or updated model presented, (iv) the model presented was a simple regression of experimental data, or (v) the paper was a review. Following screening, citations as well as citing papers were examined for each included paper in order to capture any research articles that may have been excluded from the Scopus search; these papers were included if they did not meet any of the exclusion criteria. The literature review yielded a total of 324 articles and conference proceedings that met the inclusion criteria (i.e., 2,078 did not meet inclusion criteria; a full list of the included papers can be found in Listing S1 of the supplementary information, SI).

For each research article included in this review, model components were extracted and classified based on the processes being simulated – including the process rate equations for growth, nutrient uptake, and storage – as well as state variables (e.g., inorganic carbon, ammonium, nitrate, phosphate), main forcing variables (incident irradiance, temperature, background turbidity), metabolisms considered (phototrophic, heterotrophic, and/or mixotrophic), inclusion of photoacclimation, and how the photosynthesis-irradiance (PI) relationship was modeled. Finally, approaches to explicitly model pH, irradiance within the reactor, gas transfer, and other supporting processes were also evaluated to identify paths forward.

Mechanistic modeling of phytoplankton

Energy sources

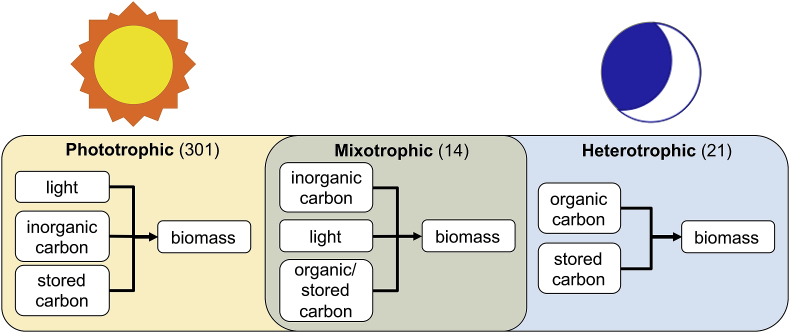
Photoautotrophic growth of microalgae and cyanobacteria is the most frequently modeled metabolism (included in 93% of articles). Broadly speaking, phytoplankton photosynthesize CO₂ into organic carbon using the energy garnered from light (Blankenship, 2002). Given this ability to convert inorganic carbon to organic carbon, phytoplankton are considered to be primary producers (Falkowski and Raven, 2007). As a result of their dependence on light, accurately simulating lighting conditions (e.g., continuous vs. diurnal, light intensity) and the response of phytoplankton to light (e.g., increased/decreased growth rate) is of utmost importance, which is rarely included as a consideration in other WRRF processes. In addition to light and inorganic carbon, photoautotrophic growth requires nutrients (namely nitrogen and phosphorus). In the absence of nutrients, algae produce storage compounds that can later be metabolized once nutrients are available ((Guest et al., 2013), Fig. 1). Discussions on how to model light, carbon, and nutrients can be found below.

Fig. 1.

Energy and carbon sources that are used by algae in each of the three metabolisms. Numbers in parentheses are manuscripts in the literature review that utilized that metabolism. Specific citations can be found in Listing S1 of the SI.

Modeling heterotrophic or mixotrophic growth of microalgae has recently received increased attention due to the higher productivities and lower operational costs associated with these growth regimes compared to photoautotrophic growth (Abreu et al., 2012; Adesanya et al., 2014; Liang et al., 2009). While photoautotrophic growth primarily utilizes CO₂ as the carbon source, heterotrophic growth involves organic carbon and mixotrophic growth can utilize both sources ((Adesanya et al., 2014; Lowrey et al., 2015); Fig. 1). Experimental studies have shown that mixotrophic growth rates of some microalgae are the sum of autotrophic and heterotrophic growth rates operated independently (Adesanya et al., 2014; Lee, 2001), but autotrophic activity can affect heterotrophic activity (Chojnacka and Noworyta, 2004) and vice-versa (Nieva and Valiente, 1996). While mixotrophic growth does increase the number of uncertain parameters requiring calibration, this metabolism has the potential to improve algal productivity at WRRFs, lowering effluent nutrient concentrations and decreasing costs. Though interest in these growth conditions has increased, only 9.6% of models reviewed considered non-photoautotrophic metabolism. Initial heterotrophic and mixotrophic modeling efforts were developed to describe the production of specific molecules (e.g., astaxanthin (Zhang et al., 2016), phycocyanin (Zhang et al., 1998), and lutein (Zhang et al., 1999b)) or simulate high density monocultures (e.g., Haematococcus sp. (Barbera and Mestre, 2002; García-Malea et al., 2005; Moya et al., 1997; Zhang et al., 2016), Chlamydomonas reinhardtii (Zhang et al., 1999a), Chlorella protothecoides (Zhang et al., 1999b), or Spirulina platensis (Zhang et al., 1998)) and often relied on mass balances coupled with a growth model. More recent models have focused on specific growth rates, yields, and productivities as functions of carbon (e.g., glucose, acetate (Turon et al., 2015), or glycerol (Villanova et al., 2017)) or nutrients (e.g., nitrogen and phosphorus (Palabhanvi et al., 2014)) as well as pH, O₂, and irradiance (i.e., for mixotrophic conditions (Bose and Chakraborty, 2016)). When modeling either of these growth regimes, the implications on dissolved oxygen (DO) need to be considered (e.g., produced during photoautotrophic growth and consumed during heterotrophic growth).

General model structures

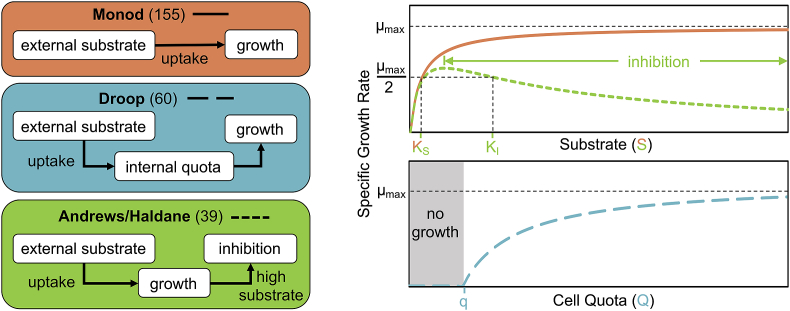
When attempting to simulate growth in silico, models must possess adequate accuracy to represent the processes that are occurring while simultaneously minimizing complexity. The simplest way to simulate growth is with a logistic model ((Verhulst, 1838); Table 1), which does not explicitly represent the interactions between an organism and its internal or external environment; growth is solely dependent on population. However, growth of microorganisms has long been observed to be affected by environmental conditions surrounding the cell, especially regarding substrate and nutrient concentrations (Monod, 1949). Though using the logistic model is not computationally intensive, its insensitivity to environmental conditions limits is applicability to wastewater treatment. Nonetheless, 5.6% of papers reviewed used this model. The empirically-based Monod model ((Monod, 1949); Table 1) – which is structurally the same as the mathematically-derived Michaelis-Menten model (Michaelis and Menten, 1913) – approximates kinetics as a hyperbolic relationship between growth and an external factor (e.g., organic carbon, nutrients, oxygen, irradiance). This relationship is defined by the maximum specific growth rate and half-saturation constant (i.e., the concentration at which the growth rate is half the maximum rate; Fig. 2). The Monod model is widely used in the wastewater industry because it can be calibrated easily (due to having two parameters), closely approximates reality for many chemotrophic prokaryotes, and is accurate across a wide range of conditions for bacteria and archaea when substrate concentrations are below inhibitory levels. As a result, Monod has been adapted for use in the ASM models (Henze et al., 2000), ADM1 (Batstone et al., 2002), and number of custom models embedded in simulation platforms (e.g., GPS-X^TM (Hydromantis, 2017), BioWin (EnviroSim, 2017), and Sumo^© (Dynamita, 2017)); of the phytoplankton models reviewed, 48% used a Monod equation.

Table 1.

Growth models with associated equations, citations, and a list of parameters.

Model	Equation	Parameters	Citation
Logistic	$\text{μ}={\text{μ}}_{\max }\left(1-\frac{\text{X}}{{\text{X}}_{\max }}\right)$	μ ≡ specific growth rate [d-1] μmax ≡ maximum specific growth rate [d-1] X ≡ biomass concentration [g·m-3] Xmax ≡ maximum biomass concentration [g·m-3]	Verhulst (1838)
Monod	$\text{μ}={\text{μ}}_{\max }\left(\frac{\text{S}}{{\text{K}}_{\text{S}}+\text{S}}\right)$	Ks ≡ half-saturation constant [g·m-3] S ≡ substrate concentration [g·m-3]	Monod (1949)
Droop	$\text{μ}={\text{μ}}_{\max }\left(1-\frac{\text{q}}{\text{Q}}\right)$	q ≡ subsistence quota [g·cell-1] Q ≡ cell quota [g·cell-1]	Droop (1968)
Haldane/Andrews	$\text{μ}={\text{μ}}_{\max }\left(\frac{\text{S}}{{\text{K}}_{\text{S}}+\text{S}+\frac{{\text{S}}^2}{{\text{K}}_{\text{I}}}}\right)$	KI ≡ inhibition constant [g·m-3]	(Andrews, 1968; Haldane, 1930)

Fig. 2.

Conceptual representation of three most common growth rate equations used in algae modeling detailing how external substrate concentrations influence growth rates. Numbers in parentheses are the number of manuscripts that used that equation to model growth. If an article used multiple formulations, all were counted. Specific citations can be found in Listing S1 of the SI. Parameter definitions can be found in Table 1.

A layer of complexity was added to the substrate-growth relationship when microalgae were observed to exhibit a notable lag between nutrient uptake and growth (Ketchum, 1939), suggesting these two processes may be partially decoupled (Droop, 2009, 1968). Further, microalgae were found to take-up and store nutrients (notably nitrogen and phosphorus) in excess of what was needed for growth (Ketchum, 1939). In configurations or process designs in which algae are exposed to fluctuating nutrient concentrations, the Droop model formulation ((Droop, 1968); Table 1) is better positioned to simulate the lag that occurs between uptake and growth due to luxury nutrient uptake and internal nutrient stores ((Stevenson et al., 1996); Fig. 2). This model – which is based on phenomena observed in both batch and continuous cultures (Droop, 1975, 1974) – utilizes maximum specific growth rate at high concentrations of internal stores (similar to, but different from, Monod), but also includes a subsistence quota parameter (i.e., the minimum internal concentration of a nutrient or substrate needed for growth to occur). Correlating the growth rate to internal substrate/nutrient content – the amount of which is determined by uptake and consumption – allows this model to decouple nutrient uptake and growth (Cunningham and Maas, 1978; Droop, 2009, 1968; Flynn, 2008; Stevenson et al., 1996; Sunda et al., 2009). Though this formulation is more appropriate for modeling phytoplankton growth, only 19% of the articles reviewed used a Droop equation.

Excessively high nutrient (e.g., ammonia) or substrate (e.g., acetate) concentrations have, at times, been shown to decrease growth rates due to inhibition (e.g., through ammonia toxicity or increased maintenance energy requirements (Chen and Johns, 1996)). High oxygen concentrations can also inhibit photosynthesis (Blankenship, 2002). Component concentrations that could be inhibitory may be modeled via the empirical Haldane model for enzymatic reactions ((Haldane, 1930); Table 1) – also referred to as the Andrews equation given that it was first used for growth of microorganisms based on observations by Andrews (1968) and confirmed for phytoplankton in laboratory experiments by (Aiba, 1982) – which is formulated similarly to the Monod model but includes an inhibition parameter (12% of models reviewed; Fig. 2).

When light reaches the cell, phytoplankton can grow photoautotrophically as defined by the relationship between photosynthesis and irradiance (PI). The simplest way to achieve this is with a Monod expression (18% of articles; e.g., (Béchet et al., 2015; Concas et al., 2012)). Slightly more intricate models have been developed and implemented for engineered systems, including the Poisson single-hit model (5.0%; (Sakshaug et al., 1989; Skjelbred et al., 2012)), the Smith model (1.6%; (Broekhuizen et al., 2012; Kenny and Flynn, 2016; Smith, 1936)), and the Jassby-Platt model (3.7%; (Breuer et al., 2015; Jassby and Platt, 1976; Van Wagenen et al., 2014); Table 2). While more complex than Monod, these models do not account for the potential inhibitory effects of prolonged light exposure. The Steele model (10%; (Drewry et al., 2015; Gonçalves et al., 2016; Steele, 1962; Wágner et al., 2016)) and the Eilers and Peeters model (11%; (Guest et al., 2013; Ketheesan and Nirmalakhandan, 2013; Peeters and Eilers, 1978)) – similar in structure to (Andrews, 1968) – are able to account for photoinhibition. A further discussion of photoinhibition is included below.

Table 2.

Models of photosynthesis-irradiance response with associated equations, citations, and a list of parameters.

Model	Equation	Parameters	Citation
Eilers and Peeters	$\text{μ}=\frac{2\cdot {\text{μ}}_{\max }\left(1+\text{β}\right)\frac{\text{I}}{{\text{I}}_{\text{S}}}}{{\left(\frac{\text{I}}{{\text{I}}_{\text{S}}}\right)}^2+2\cdot \frac{\text{I}}{{\text{I}}_{\text{S}}}\cdot \text{β}+1}$	μ ≡ specific growth rate [d-1] I ≡ light intensity [μE·m-2·s-1] μmax ≡ maximum specific growth rate [d-1] Is ≡ optimum irradiance [μE·m-2·s-1] β ≡ attenuation coefficient [-]	Peeters and Eilers (1978)
Monod	$\text{μ}={\text{μ}}_{\text{max}}\frac{\text{I}}{{\text{K}}_{\text{I}}+\text{I}}$	KI ≡ half saturation intensity [μE·m-2·s-1]	Monod (1949)
Platt and Jassby	$\text{μ}{=\text{μ}}_{\max }\cdot \tanh \left(\frac{\text{αI}}{{\text{μ}}_{\max }}\right)$	α ≡ initial slope of PI curve [m2·μE-1]	Jassby and Platt (1976)
Poisson single hit model	$\text{μ}{=\text{μ}}_{\max }\left(1-{\text{e}}^{-\frac{\text{I}}{{\text{K}}_{\text{I}}}}\right)$	KI ≡ light saturation [μE·m-2·s-1]	(Poisson, 1837)
Smith	$\text{μ}={\text{μ}}_{\text{max}}\frac{\text{αI}}{\sqrt{{\text{μ}}_{\max }^2+{\left(\text{αI}\right)}^2}}$	α ≡ initial slope of PI curve [m2·μE-1]	Smith (1936)
Steele	$\text{μ}={\text{μ}}_{\text{max}}\text{αI}\cdot {\text{e}}^{\left(1-\text{αI}\right)}$	α ≡ initial slope of PI curve [m2·μE-1·s]	Steele (1962)

When formulating a growth equation, these models can be multiplied (e.g., Droop for phosphorus multiplied by Andrews for nitrogen. Multiplication was first postulated by (Baule, 1917) and used in 44% of papers) or combined through a threshold formulation, where growth rates are only impacted by the most limited nutrient or substrate ((von Liebig, 1841); used in 11% of papers). However, the multiplicative approach is only applicable when model components (e.g., light, nutrients, carbon, etc.) are independent, indicating that multiplying model components is overused. Thus, the threshold formulation should be used to account for scenarios where growth is dependent on multiple components (e.g., limitation by N and P). More complex relationships must be accounted for when the two compounds interact nonlinearly in the cell. For example, a phosphorus limitation reduces the nitrogen uptake efficiency (Bougaran et al., 2010).

Nutrient uptake, storage, and mobilization

In scenarios where phytoplankton are used for secondary or tertiary treatment of municipal wastewaters (i.e., when treating waters with dilute nutrient concentrations), phytoplankton growth can be dependent on either external or internal nutrients. In terms of macronutrients, phytoplankton are unique in their ability to metabolize multiple forms of nutrients (e.g., NO₃^-, NH₄⁺, NO₂^-, and DON for nitrogen (Dortch, 1990; Flynn et al., 1997; Liu et al., 2012): PO₄^3- and DOP for phosphorus (Brown and Shilton, 2014; Liu et al., 2012)). The respective rates of N and P uptake are not independent: rather, algae can modify their N:P ratio via growth rate (typically between 2.3:1 to 23:1 on a mass basis) in response to fluctuating nutrient concentrations, which commonly occur at WRRFs (Gardner-Dale et al., 2017; Geider and La Roche, 2002). The form of nitrogen that is being taken up affects growth rate as well as pH. Specifically, nitrate or nitrite must be reduced to be metabolized, which results in slower growth due to expending reducing equivalents toward nitrogen (Fuggi et al., 1981; Sanz-Luque et al., 2013). Ammonia does not require reduction, but its uptake lowers pH (Fuggi et al., 1981). Therefore, the pH implications of the form of nitrogen being taken up should be considered when creating a model. In addition to macronutrients, micronutrients (e.g., zinc, manganese, etc.) are necessary for growth (Kropat et al., 2011) and can limit productivity if lacking (Carvalho et al., 2006; Singh et al., 2016). Micronutrients have been shown to be present in wastewaters (Westerhoff et al., 2015) and, in many cases, can be sufficient to support growth (Daneshvar et al., 2018).

The simplest way to predict nutrient uptake rate is by making substrate a linear function of biomass growth rate with a yield coefficient (e.g., Y_H (Henze et al., 2000); 16% of papers reviewed). When modeling nutrient dynamics of phytoplankton, however, the decoupling between uptake and growth necessitates the two processes to be modeled separately (Droop, 2009; Ketchum, 1939). In the case of microalgae, it is not uncommon to expect nutrient uptake to tend to increase with nutrient concentration following Michaelis-Menten kinetics (Michaelis and Menten, 1913) – which is structurally similar to the Monod model – and be down-regulated by the corresponding internal nutrient quota ((Bougaran et al., 2010; Droop, 1968); used in 39% of papers reviewed). In non-inhibitory, nutrient-replete conditions, some phytoplankton will take-up nutrients in excess of that required for growth. This luxury uptake of nutrients will continue until the maximum internal quota is reached (Brown and Shilton, 2014; Carey et al., 2012; Elrifi and Turpin, 1985). If nutrient concentrations become inhibitory (e.g., free ammonia above 35 mg-N·L^-1 (Abeliovich and Azov, 1976)), Haldane kinetics should be used. In nutrient-deplete conditions, however, growth does not simply cease; though biomass growth rates decrease, algae will continue to metabolize organic or inorganic carbon and will instead produce carbon-storage compounds (e.g., carbohydrates, lipids, or a combination of the two) so that growth can resume when nutrients become available in the future (see below (Ball et al., 1990; Guest et al., 2013; Guschina and Harwood, 2006)). While Michaelis-Menten kinetics are necessary to model nutrient uptake, the model requires two calibrated parameters (rather than one when utilizing a yield coefficient). This equation can be simplified if nutrient concentration is several orders of magnitude greater than the half saturation coefficient (e.g., when growing cultures on WRRF sidestreams such as anaerobic digester centrate). In this case, the uptake rate for that nutrient will be so close to the maximum specific uptake rate that the half-saturation coefficient can be considered negligible, simplifying the model.

Following uptake, nitrogen and phosphorus are metabolized to form intermediate biomass compounds when carbon is available (Blankenship, 2002). When luxury uptake occurs, algae have been shown to store phosphorus as polyphosphate (Brown and Shilton, 2014). Additionally, nitrogen may be stored either as intracellular pools (Coppens et al., 2014; Thoresen et al., 1982) or as amino acids, though not as readily as phosphorus (Elrifi and Turpin, 1985). These nutrient stores will then be utilized during nutrient deplete conditions, if carbon is available. As a result, careful consideration must be taken when deciding how to incorporate the effect of nutrients on algal metabolism.

Carbon uptake, storage, and mobilization

In addition to nutrients, the uptake of organic and/or inorganic carbon should also be considered carefully (included in 26% of articles). Carbon uptake is commonly modeled using Michaelis-Menten or Haldane kinetics, depending on whether or not the compound can be inhibitory at higher concentrations (Baroukh et al., 2017) and on the amount of existing internal carbon stores (Concas et al., 2016; Guest et al., 2013). Apart from uptake, carbon utilization is dependent on several interrelated factors that must be considered concurrently. For example, under low light or dark conditions, algae cannot photosynthesize enough to meet maintenance requirements, so they will consume either external organic carbon (i.e., mixotrophic or heterotrophic metabolism) or stored carbohydrates/lipids (Baroukh et al., 2017; Guest et al., 2013). As a result, carbon usage should be modeled with switching functions (introduced in ASM1 (Henze et al., 1987)) to account for these factors.

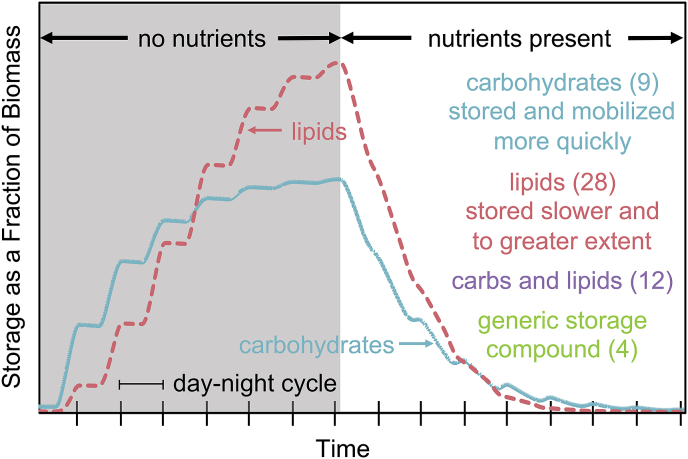
In many algal species (e.g., Chlorella sorokiniana, Chlamydomonas reinhardtii, and Scenedesmus obliquus (Guschina and Harwood, 2006; Harwood and Guschina, 2009; Subramanian et al., 2013; Vitova et al., 2015)), carbon storage compounds (e.g., carbohydrates and lipids) accumulate in the cell in response to nutrient-deplete conditions (Fig. 3). Broadly, these two compounds have been modeled in numerous ways, most consistently as a function of biomass concentration using a yield coefficient (4.6% of articles; e.g., (Dillschneider and Posten, 2013; Mohammad Mirzaie et al., 2016)). More complex models for these compounds involve switching functions dependent on nutrient availability as well as the relative concentrations of each storage compound; these models do not have a consistent structure (7.1 % of articles (Baroukh et al., 2014; Guest et al., 2013; Mairet et al., 2011)). Given the relatively limited knowledge of storage compound dynamics in the timescale of dynamic wastewater processes, there is no clear model that is optimal, but in general, carbohydrates and lipids should both be modeled separately (2.8% model carbohydrates only, 8.7% model lipids only, 3.7% model both together as a generic storage compound, 1.2% model both separately). Additionally, carbohydrates typically are produced and consumed faster than lipids, but also reach the maximum internal concentration sooner (Davis et al., 2016; Laurens et al., 2014). Lipids, conversely, are produced at a slower rate, but accumulate to a greater extent in many species of algae (Davis et al., 2016; Laurens et al., 2014). As an added layer of complexity, biomass composition can change both over diel cycles and also in response to design decisions (e.g., SRT (Gardner-Dale et al., 2017)), necessitating more mechanistic modeling of these metabolic processes. Oxygen consumption should also be accounted for using Monod kinetics when modeling stored carbon usage. In addition to this, stored carbohydrates have been shown to be interconverted to lipids, further increasing the potential intricacy of this sub-process (Pick and Avidan, 2017). Given the complexity of modeling carbohydrate and lipid accumulation, carbon storage should only be considered if nutrient-deplete conditions are expected to exist or if the cells are exposed to fluctuating lighting conditions (e.g., diel, natural lighting) in the scenario being modeled.

Fig. 3.

Simulation of accumulation of carbohydrates and lipids in phytoplankton using the PPM model from Guest et al. (2013). Storage compounds are formed in nutrient deplete conditions and are consumed in nutrient replete conditions. Numbers in parentheses are manuscripts that modeled carbohydrates only, lipids only, both carbohydrates and lipids (not shown), or a generic storage compound (not shown in the line plot). One day-night cycle is equivalent to 24 h (i.e., 14 h of day and 10 h of night). Specific citations can be found in Listing S1 of the SI.

Light

Irradiance and dissipation

Light is an energy source during photoautotrophic and mixotrophic algal growth for photosynthesis. Accurately predicting light distribution is essential for modeling algal growth and metabolism. Photosynthetically active radiation (PAR) – the spectral range of radiation that photosynthetic cells can use – occurs between wavelengths of 400-750 nm (Wilhelm and Jakob, 2011). Three types of irradiance models were identified in (Béchet et al., 2013): type I models which use incident or average irradiance to predict the rate of photosynthesis for the entire culture, type II models which estimate overall reactor productivity as the sum of depth-resolved productivities within the system, and type III models which account for both light gradients and short light cycles for individual cells. Type I models are simplest, but type II models tend to exhibit greater accuracy for a small increase in complexity. Type III models are likely to be too complex for WRRFs given the need for individual-based (a.k.a. microscopic) models (Gujer, 2002). As light penetrates a phytoplankton cultivation system, it can be attenuated through absorption or scattering by cells or by the reactor itself ((Posten, 2009; Wágner et al., 2018; Wang et al., 2014); Fig. 4). Light extinction can be exacerbated by high concentrations of highly diffusive particulate matter (Borowitzka, 1998). The Beer-Lambert law (Table 3) is widely used in phytoplankton modeling (35% of articles) and accounts for light extinction due to absorption by pigments and scattering by the cells as well as absorption and diffusion due to non-cellular components (Martínez et al., 2018). Often, the extinction coefficient is taken as the absorption rate (Koller et al., 2017). For dilute cultures, the attenuation coefficient has been proposed to be expressed as a nonlinear function of absorption and scattering coefficients (Kirk, 1984; Morel, 1988). Modifications to this equation may be required to simulate the effects of multiple scattering, when applicable (e.g., (Tam and Zardecki, 1982)), or to account for the disparity in coefficient values between natural and engineered systems.

Fig. 4.

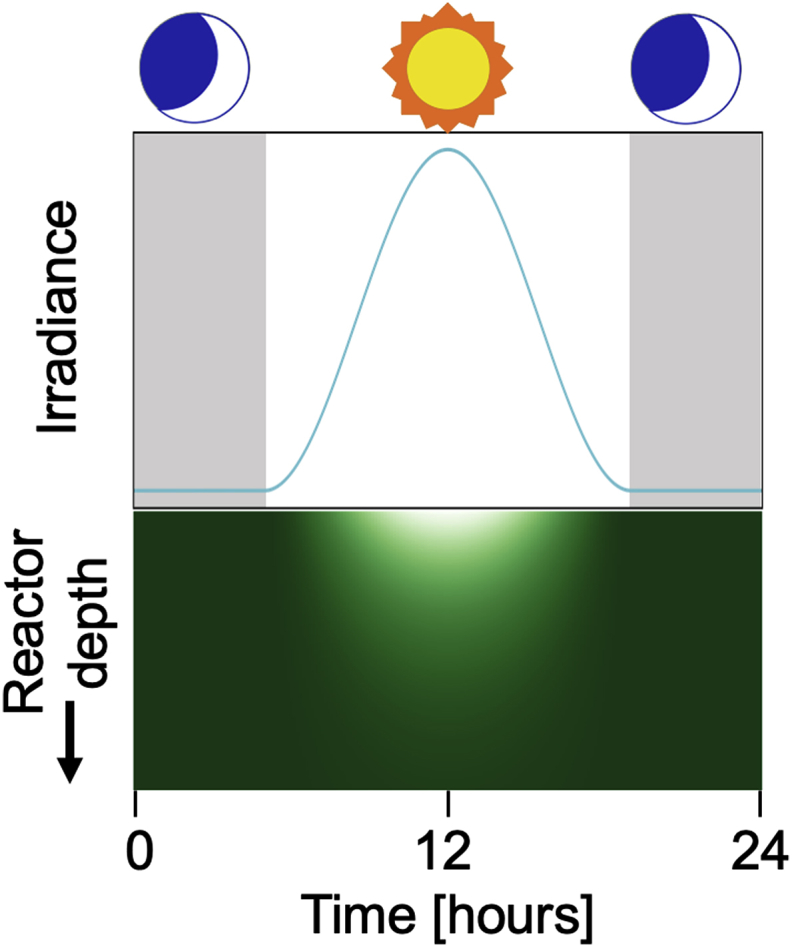
Simulation of light penetration into reactor (lower graphic) using Beer-Lambert as a function of irradiance (upper graphic, y-axis) and time (x-axis). Light is simulated using a 14-hour sinusoidal wave. Green shading represents light in reactor (i.e., darker colors correspond to lower light). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Table 3.

Model of light penetration with associated equation and a list of parameters.

Model	Equation	Parameters	Citation
Beer-Lambert	${\text{I}=\text{I}}_0\cdot {\text{e}}^{-{\text{k}}_{\text{a}}\cdot \left(\text{X}+{\text{k}}_{\text{bg}}\right)\cdot \text{z}}$	I ≡ light intensity [μE·m-2·s-1] z ≡ depth [m] I0 ≡ incident light intensity [μE·m-2·s-1] X ≡ biomass concentration [g·m-3] kbg ≡ background turbidity [g·m-3] ka ≡ attenuation coefficient [m2·g-1]	(Beer, 1852)

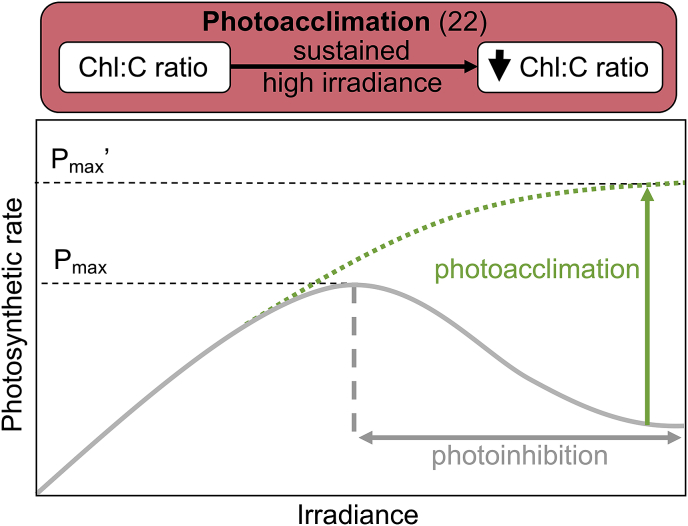
Photoinhibition and photoacclimation

When modeling the effects of irradiance in engineered systems, temporal changes in light intensity need to be considered, especially in naturally lit scenarios which will follow a diel cycle. Some algae have developed the ability to adapt in response to changing lighting conditions (Carvalho et al., 2011). Photoinhibition (i.e., the reduction in growth due to exposure to excess light) can begin affecting growth within 1 min if irradiance is high enough ((Béchet et al., 2013); Fig. 5). Under high light intensities, photoacclimation processes are used to mitigate photoinhibition, whereby the chlorophyll production is suppressed and carotenoids (i.e., photo-protective pigments) are synthesized (Aburai et al., 2015; Anning et al., 2000; García-Camacho et al., 2012; Guihéneuf and Stengel, 2015; Koller et al., 2017; MacIntyre et al., 2002; Safafar et al., 2015; Vaquero et al., 2014; Xie et al., 2016). This photoacclimation strategy takes place at a time-scale of days or weeks (Combe et al., 2015) and contributes to chlorophyll:carbon mass ratio variations typically within a factor of five (Falkowski, 1983). (Anning et al., 2000) studied the PI response curves of microalgae cultures pre-acclimated at different light irradiances and showed 65% higher growth rates and higher chlorophyll content for the cells pre-acclimated in the dark. (Bouterfas et al., 2002) compared multiple PI models and found that the Eilers and Peeters model is the most accurate when simulating growth in response to high irradiance. This phenomenon is of utmost importance for wastewater treatment given that particulate and dissolved materials increase medium turbidity, reducing the light penetration and maintaining a low average light in the water. On top of this, pigment synthesis can be strongly impacted by nitrogen limitation as the pigment content is related to the protein content, which is itself related to the nitrogen status (represented by the quota q in the Droop model (Griffiths et al., 2014)). Nitrogen limitation has also been shown to strongly reduce chlorophyll content (Breuer et al., 2015; Geider et al., 1993).

Fig. 5.

Conceptual representation of photoacclimation. Numbers in parentheses are manuscripts that included this process. Specific citations can be found in Listing S1 of the SI.

(Geider et al., 1998) were among the first to introduce chlorophyll as a state variable in their models, in addition to the carbon and nitrogen contents. They expressed the rate of pigment synthesis per carbon unit as proportional to the product between the rates of photosynthesis and nitrogen uptake. More recently (Bernard et al., 2015), proposed a model whereby chlorophyll is proportional to the cellular nitrogen content. Beyond nitrogen, temperature also has a strong effect on photoacclimation (Geider, 1987), which has been represented by a model relating the chlorophyll quota to the current light irradiance and temperature. More complex models exist (Flynn, 2001; García-Camacho et al., 2012; Nikolaou et al., 2016), but the computational intensity of these models relative to the increase in fidelity precludes their use in the context of modeling WRRFs. Accounting for photoacclimation in model development is crucial to represent successive phases with low turbidity (where cells are subjected to high light) and growth periods in a highly turbid medium (for which average light is low); only 6.8% of models reviewed included this process. For studies focusing on growth in a permanently turbid medium, cells will be mostly dark acclimated, and photoacclimation can be neglected. However, growth model calibration must be carried out in low light conditions (or equivalently in a very turbid medium) in order to ensure sufficient accuracy.

Temperature

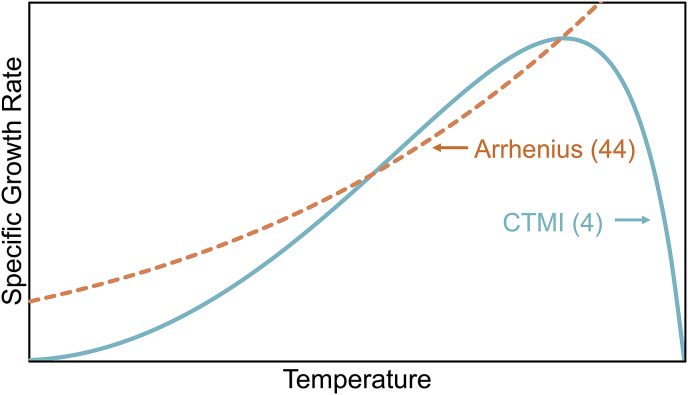
The influence of temperature on process dynamics can be tantamount to that of light ((Ras et al., 2013); 34% of articles included temperature). Wastewater treatment processes cultivating phytoplankton typically have reduced depths (i.e., less than 0.5 m), and therefore lower thermal inertia than deeper, in-ground reactors. When subjected to the solar irradiance, temperatures within the reactor can vary from 5 ˚C to as high as 56 ˚C (De-Luca et al., 2017; Dermoun et al., 1992; Talbot et al., 1991; Tredici and Materassi, 1992). Microalgae and cyanobacteria can be particularly sensitive to environmental temperatures in engineered systems due to its effect on enzymatic activity and stability (Béchet et al., 2011; Bernard and Rémond, 2012). The impact of temperature on metabolism can be represented in mechanistic models accurately predicting the temperature dynamics over the course of the day (Béchet et al., 2011, 2010), but its effect has commonly been neglected or minimized in biological models, often by using an Arrhenius formulation ((Arrhenius, 1889); 40% of models considering temperature; Fig. 6 and Table 4).

Fig. 6.

Conceptual representation of response of growth to temperature. Numbers in parentheses are manuscripts that included this process. Specific citations can be found in Listing S1 of the SI.

Table 4.

Models of temperature impacts on growth with associated equations and a list of parameters.

Model	Equation	Parameters	Citation
Arrhenius	${\text{μ}}_{\text{max}}\left(\text{T}\right)={\text{μ}}_{\text{max}}{\text{e}}^{-\frac{{\text{E}}_{\text{a}}}{\text{kT}}}$	Ea ≡ activation energy [m2·kg·s-2] k ≡ Boltzmann constant [m2·kg·s-2·K-1] T ≡ absolute temperature [K]	(Arrhenius, 1889)
CTMI	$\begin{array}{l}{\text{μ}}_{\text{max}}\left(\text{T}\right)={\text{μ}}_{\max }\frac{\left(\text{T}-{\text{T}}_{\max }\right)}{\left({\text{T}}_{\text{opt}}-{\text{T}}_{\min }\right)}\times \\ \frac{{\left(\text{T}-{\text{T}}_{\min }\right)}^2}{\left[\left({\text{T}}_{\text{opt}}-{\text{T}}_{\min }\right)\left(\text{T}-{\text{T}}_{\text{opt}}\right)-\left({\text{T}}_{\text{opt}}-{\text{T}}_{\max }\right)\left({\text{T}}_{\text{opt}}{+\text{T}}_{\min }-2\text{T}\right)\right]}\end{array}$	T ≡ temperature [˚C] Topt ≡ optimum temperature [˚C] Tmin ≡ minimum temperature [˚C] Tmax ≡ maximum temperature [˚C]	Rosso et al., (1993)

The response of growth rate to temperature has been proposed to follow an asymmetric curve for most microorganisms ((Rosso et al., 1993); 3.6% of articles that included temperature; Fig. 6 and Table 4). This response is defined by three cardinal temperatures: T_min, the minimum temperature that will support growth; T_max, the maximum temperature that will support growth; and T_opt, the optimum temperature for growth. The asymmetry of the growth curve results from differential effects on cellular physiology at temperatures lower or higher than T_opt. At low temperatures, the rates of enzymatic biochemical reactions are affected (Blankenship, 2002). At high temperatures, structure and stability of some cellular components, such as key enzymes or membrane compounds (mainly lipids or proteins), are denatured (Ras et al., 2013; Salvucci and Crafts-Brandner, 2004). The consequences on cell metabolism and integrity lead to an increase in mortality (Serra-Maia et al., 2016). Growth rates at temperatures greater than T_max or less than T_min are considered to be zero. The deleterious effects of high temperature exposure are also temporally dependent, and the concept of thermal dose has been used to quantify the damages at high temperature (Béchet et al., 2017; Holcomb et al., 1999). Given the potential impacts that temperature can have on biomass, a temperature model should be carefully chosen and calibrated (a more detailed review of temperature models can be found in (Grimaud et al., 2017)).

Respiration and maintenance

While the main focus of this critical review is on phytoplankton growth and related processes, carbon loss through endogenous respiration and maintenance should not be neglected when constructing a model (included in 57% of models reviewed). These processes are often considered to occur at a constant rate (e.g., (Decostere et al., 2013); 47% of the models that included respiration); this assumption is valid for maintenance energy requirements, but endogenous respiration is impacted by multiple factors (e.g., light, temperature, pH, etc. (Béchet et al., 2017; Ippoliti et al., 2016)). Maintenance energy is dependent on the ATP requirements of the organism and, as such, does not change (Beeftink et al., 1990). The ATP demand can be met through multiple routes, depending on the situation being modeled (i.e., if carbon storage products are being formed or not). For instance, cells can meet maintenance requirements first through storage products and only rely on endogenous respiration in the absence of these internal stores (Beeftink et al., 1990). In addition to reducing biomass concentrations, respiration can also lead to DO consumption, which can have an impact on any aerobic chemotrophic organisms in the system. As such, incorporation of maintenance and endogenous respiration (as one mechanism to meet maintenance ATP demands (Guest et al., 2013)) is advisable.

Lumped pathway metabolic modeling

Metabolic modeling uses biochemical data representing a species’ or community’s metabolism to develop stoichiometric parameters for cellular operations (e.g., yield coefficients for substrates; 3.4% of the papers utilized metabolic reconstructions). Metabolic models can incorporate different energy sources (e.g., photoautotrophic, mixotrophic, and heterotrophic growth (Juneja et al., 2016; Yang et al., 2000)), different metabolic pathways leveraged under a given set of environmental conditions (e.g., nutrient replete and deplete), and the accumulation of storage compounds (Guest et al., 2013; Radakovits et al., 2012). Full metabolic models typically involve entire genome reconstructions, comprised of individual reactions (i.e., between 200-3,000) and metabolic flux analyses (Baroukh et al., 2015; Chang et al., 2011). Although metabolic reconstructions provide a very thorough view of phytoplankton metabolism, the complexity hinders process engineers from implementing metabolic models of phototrophic technologies at WRRFs. Several models build upon the concept of metabolic reconstructions while taking a simpler approach that may be considered more accessible and valuable for developing processing parameters at WRRFs through metabolic modeling. In WRRF modeling of chemotrophic processes (e.g., enhanced biological phosphorus removal, EBPR), the concept of “lumped pathway metabolic modeling” has been applied (e.g., (Smolders et al., 1994)), which groups reactions based on whether intermediate compounds accumulate. These grouped (or “lumped”) reactions are assumed to occur simultaneously and are modeled as a function of one parameter (Roels, 1983). As such, lumped pathway metabolic modeling has the potential to simplify metabolic reconstructions, given that they have on the order of 10 reaction equations as opposed to >100 equations present in some reconstructions ((Filipe and Daigger, 1999; Guest et al., 2013); Fig. 7).

Fig. 7.

Conceptual representation of model complexity by type. Empirical models convert substrate to biomass through the use of yield coefficients. Lumped pathway models use simplified metabolic reactions to simulate growth. Metabolic flux models track individual metabolites as they are consumed and converted in the cell. Numbers in parentheses are manuscripts that included this process. Specific citations can be found in Listing S1 of the SI.

WRRF modeling platforms typically use empirical yield coefficients for the ASMs to help describe sludge accumulation within the system ((Figueroa-Torres et al., 2017; Henze et al., 2007); Fig. 7), with the general recommendation to conduct experiments to develop yield coefficients for a specific WRRF (Henze et al., 2007; Rieger et al., 2012). Any variation in yield coefficients between WRRFs is generally believed to be caused solely by environmental influences such as pH, temperature, and fluctuating substrate concentrations (Henze et al., 2007). However, yield coefficients have a foundation in the metabolic pathways an organism is using (e.g., glycolysis, pentose phosphate pathway, etc.), indicating that values for these coefficients can be theoretically grounded. If metabolic pathways are conserved, derived theoretical values can then be used regardless of situation being modeled. Variability in terms of growth rate will still exist due to environmental conditions, but this variation can be accounted for in associated subprocesses (e.g., maintenance) rather than by yield coefficients.

Lumped pathway metabolic models allow stoichiometric parameters to be based on phytoplankton metabolism while simultaneously reducing complexity (relative to metabolic models) and increasing reproducibility (relative to empirical models). Using lumped pathways also grounds many parameters (e.g., P/O ratio) in fundamental, well-established ranges while decreasing the number of unknown stoichiometric parameters in the model, thus increasing the model’s innate mechanistic friction, lowering the degrees of freedom, and simplifying the final model structure (Baroukh et al., 2014; Guest et al., 2013; van Aalst-van Leeuwen et al., 1997). While there are many benefits to using full metabolic models, the additional complexity often precludes their inclusion in algal models.

Inclusion of other organisms

In the context of wastewater treatment, maintaining a community of one type of organism is challenging, if not entirely unrealistic. In the context of algae and cyanobacteria, chemotrophic bacteria (e.g., heterotrophic bacteria, nitrifiers) and predatory organisms (e.g., zooplankton) can be present, which impact the dynamics of the entire system being modeled ((Mehrabadi et al., 2016; Wolf et al., 2007); other organisms were included in 21% of models). The relationship between heterotrophic bacteria and photoautotrophic phytoplankton has long been known to be symbiotic, where bacteria and phytoplankton exchange products: chemotrophic bacteria produce CO₂ and consume DO while phytoplankton take-up CO₂ and produce DO (Rich, 1963). This interaction can be particularly beneficial for photoautotrophic phytoplankton because high DO concentrations can inhibit photosynthesis (Kaplan and Reinhold, 1999). However, higher biomass concentrations (stemming from chemotrophic organism growth) can also limit photosynthesis by reducing light to suboptimal levels. Additionally, phytoplankton and chemotrophs (including autotrophs) will be competing for substrates (N, P, inorganic carbon, etc.). If the phytoplankton are utilizing mixotrophy or heterotrophy, they will be competing with the chemotrophic bacteria for organic resources, which can impact system performance (Grover, 2000; Thingstad et al., 1998). Predators and grazers commonly have much more detrimental impacts on algal performance, which is primarily a result of algal biomass being directly reduced (Baird et al., 2003). Depending on the conditions, predators can result in frequent turnover of algal communities, preventing the system from treating the water as anticipated (Sutherland et al., 2017). Whether including bacteria, predators, or both, considering other organisms can quickly increase the complexity of a model due to the need to account for all the parameters the organism can affect (e.g., oxygen, CO₂, organic carbon, pH, light penetration, etc. (Solimeno et al., 2017; Zambrano et al., 2016)). However, if phytoplankton are in a closed system (e.g., a closed photobioreactor), invasive organisms can be assumed to be negligible if not present in the influent.

Physico-chemical processes

Gas-liquid mass transfer

Gas-liquid mass transfer was included in 17% of reviewed articles. The most important dissolved gases in phytoplankton processes are oxygen (O₂), carbon dioxide (CO₂), and ammonia (NH₃); depending on their concentration, they can either promote or inhibit growth. Generally speaking, algae require 1.8–2.4 g CO₂ for each gram of biomass grown, which results in a N demand of 0.02-0.25 g per gram of algae (given that the C:N ratio can vary from roughly 2.6–32 g C·g N^-1 (Geider and La Roche, 2002; Leow et al., 2015; Li et al., 2017)). Microalgae also produce approximately 1.5–1.92 g O₂·g biomass^-1 (Grobbelaar et al., 1988; Muñoz and Guieysse, 2006). Moreover, CO₂ and NH₃ can significantly impact pH (see below). CO₂ and NH₃ are also involved in bacterial processes and consequently play an important role in algal-bacterial interactions, necessitating their accurate simulation in WRRF process models (Solimeno et al., 2017, 2015).

In the case of gas-liquid system with a relatively dilute liquid phase, Henry’s law is generally used to describe the equilibrium relationship (Eq. 1 in Table 5). Due to the continuous production and/or consumption of gaseous components by biological processes, however, gas-liquid mass transfers occur continuously. The driving force of gas-liquid mass transfer is therefore the difference between the saturation concentration and the real concentration in the liquid phase (Eq. 2 in Table 5). The local mass transfer coefficient represents the resistance of the interface to transfer. For gases with low solubility (e.g., O₂ and CO₂), dissolution into the liquid phase is more challenging, while more soluble gases (e.g., NH₃) are more difficult to remove from solution. The mass transfer rate depends on gas and liquid physico-chemical properties, temperature, and turbulence of the medium.

Table 5.

Equations for modeling gas-liquid mass transfer.

Equation	Parameters	Eq. No.
${\text{K}}_{\text{Hi}}=\frac{{\text{C}}_{\text{s,i}}}{{\text{p}}_{\text{i}}}$	KHi ≡ Henry’s law coefficient [mol·L-1·atm-1] Cs,i ≡ concentration of i in the liquid phase under equilibrium conditions (i.e., saturation concentration) [mol·L-1] pi ≡ partial pressure of i in the gas phase [atm]	1
${\text{ρ}}_{\text{i}}={\text{k}}_{\text{L/Gi}}\cdot \text{a}\cdot \left({\text{C}}_{\text{s,i}}-{\text{C}}_{\text{i}}\right)$	ρi ≡ mass transfer rate [mol·s-1] Ci ≡ concentration of i in the liquid phase [mol·L-1] a ≡ interfacial area between liquid and gas [m2] kL/Gi ≡ local mass transfer coefficient [m·s-1]	2
$\frac{{\text{k}}_{\text{L}}{\text{a}}_{{\text{O}}_2}}{{\text{k}}_{\text{L}}{\text{a}}_{\text{i}}}=\sqrt{\frac{{\text{D}}_{{\text{O}}_2}}{{\text{D}}_{\text{i}}}}$	kLaO2 ≡ overall mass transfer coefficient for O2 [m·s-1] kLai ≡ overall mass transfer coefficient gas i [m·s-1] DO2 ≡ O2 diffusivity in liquid [m2·s-1] Di ≡ diffusivity in liquid of gas I [m2·s-1]	3

Several models exist to describe this mass transfer rate, including Higbie's penetration theory (Higbie, 1935) or the double layer model (Lewis and Whitman, 1924). However, both the local mass-transfer coefficient and the interfacial area require calibration, and determining these parameters is challenging. Therefore, the combination of both parameters (i.e., the local mass transfer coefficient and the interfacial area) is often considered; this combined coefficient is typically referred to as k_L/Ga. The prevalence of aeration in the activated sludge process has resulted in extensive in situ determination of the oxygen-specific k_La value (i.e., k_La_O2) (Amaral et al., 2017; Kayser, 1979) as well as models to describe it (Gillot et al., 2005). Overall mass transfer coefficients for other gases with low solubility (e.g., CO₂) are usually calculated from the oxygen transfer rate using Higbie's penetration theory (Eq. 3 in Table 5). In order to determine the effect that these gaseous compounds can have, gas-liquid mass transfer should be considered when constructing a WRRF model.

pH/acid-base equilibrium

Acid-base equilibrium considers the change in concentration of one or several compounds of interest (e.g., CO_2,aq, HCO₃^-, and CO₃^2-) in aqueous phase and the subsequent effect it has on pH and therefore microalgal processes ((Brönsted, 1923; Lowry, 1923); 13% of models). Similar to compounds involved in liquid-gas transfer, these compounds are continuously produced or consumed by biological processes. Contrary to liquid-gas transfer, however, acid-base equilibrium occurs rapidly compared to biological processes. As a result, equilibrium is often assumed to be established instantaneously (i.e., on the order of 10⁴ and 10⁵ d^-1 (Jupsin et al., 2003; Reichert et al., 2001; Solimeno et al., 2015)). The direct impact of pH on algal growth (included in 16% of models) is rather limited when pH is between 5-8.5, depending on the algal species and other operational parameters such as temperature (Benemann et al., 1987; Berge et al., 2012; Mayo, 1997). Algal growth can affect pH by consuming CO₂ during photosynthesis, resulting in a net increase in pH as protons are consumed to maintain chemical equilibrium (Berenguel et al., 2004). In addition to the bicarbonate system, the nitrogen species present in solution have an impact on pH. If ammonium is applied as the nitrogen source, pH drops due to the release of protons during assimilation; conversely, pH can rise when nitrate is used due to the consumption of protons needed to assimilate nitrate (Nguyen and Rittmann, 2015). Most phytoplankton models for municipal wastewater treatment exclude pH dependence for algal growth (Broekhuizen et al., 2012; James et al., 2013; Mayo, 1997), but pH indirectly affects algal growth by changing the relative concentrations of substrates such as CO₂ (Decostere et al., 2016; Wolf et al., 2007). Additionally, high pH (i.e., above 9) may induce inhibition of algal growth by free ammonia (Abeliovich and Azov, 1976; Konig et al., 1987).

Some models simulate pH as a function of the bicarbonate system (Decostere et al., 2016; Fernández et al., 2010; Liehr et al., 1988), but the simplicity of these models results in inaccuracy when other pH-altering components are present. The River Water Quality Model 1 (RWQM1 (Reichert et al., 2001)) introduced a set of differential equations to model the acid-base equilibria for inorganic carbon, ammonia, and phosphate, as well as the water acid-base equilibrium. This approach was later modified to a system of differential (for biological process rates) and algebraic (for fast chemical reactions) equations (DAE), where pH is numerically estimated by closing the charge balance (i.e., mono-dimensional numerical methods) in the system (Broekhuizen et al., 2012; Gehring et al., 2010; Wolf et al., 2007). The application of DAE systems to predict pH is commonly used to model other wastewater systems, as it reduces the stiffness of the model compared to differential equation systems (Batstone et al., 2012, 2002; Hellinga et al., 1999). This approach has been improved by (Vangsgaard et al., 2013) by formulating a set of equations describing the mass balances and equilibrium equations of weak acids and bases and a charge balance, which are solved using a multidimensional Newton-Raphson method. During the last few years, the acid-base system has been better described by including the effect of ionic strength, ion pairing, and developing improved numeric solvers to ensure robustness in the calculations (Flores-Alsina et al., 2015; Lizarralde et al., 2015; Solon et al., 2015). Other common ways to estimate pH changes in water systems are by closing proton or alkalinity balances (Luff et al., 2001; Serralta et al., 2004).

Calibration/validation and uncertainty/sensitivity analyses

Whether constructing a new model or tailoring an existing one to a specific scenario, a model should always be calibrated and validated (to the degree possible) prior to use (69% of models were calibrated, but only 36% were validated). Calibration involves adjusting parameter values to fit the model to collected and reconciled data (i.e., data that have been cleaned and ensured are accurate (Hauduc et al., 2010)); validation ensures that the model also matches data from a different set of conditions (distinct from the calibration dataset) by comparing the calibrated model to another set of data (Rieger et al., 2012). This step in building a model is important because it ensures that model outputs are both reliable and reproducible; in the context of wastewater treatment, a model that can accurately predict performance can mean the difference between meeting discharge requirements or not. Calibration of WRRF models is often performed manually, which frequently results in unreliable output values (Sin et al., 2005). Though calibration protocols have been proposed (e.g., BIOMATH (Vanrolleghem et al., 2003), STOWA (Hulsbeek et al., 2002), and the IWA Unified Protocol (Rieger et al., 2012)), there is no consensus on calibration methodology, making the comparison and evaluation of calibration across models incredibly challenging. While calibrating all parameters is extremely difficult and prone to errors – particularly for complex models with many parameters (e.g., RWQM1 and ADM1 with 24 and 45 parameters, respectively) – most of the variability in a model is often due to a subset of parameters. This subset can be determined through a sensitivity analysis (Sin et al., 2005). Ensuring that these parameters are calibrated carefully is essential; other parameters do not need to be calibrated as carefully or standard values can be sourced from previously published articles. Model prediction quality can be evaluated in relation to quality of fit (e.g., through the use of Akaike or Bayesian Information Criterion (Grimaud et al., 2017)) or by examining the percentage of experimental data falling within the confidence interval of the model output (Ramin et al., 2017; Wágner et al., 2018).

Uncertainty and sensitivity analyses can be used in tandem to determine how parameter variations affect output variability as well as which parameters affect model outputs the most. Broadly, uncertainty analyses in WRRF modeling pass randomly chosen input values through the model and record the outputs to determine either the range of potential outputs or estimate the likelihood of meeting a target value (e.g., discharge requirements (Loucks et al., 2005)). Uncertainty analyses can be conducted with Monte Carlo simulation, wherein probability density functions are assigned to inputs and are randomly sampled tens of thousands of times (Saltelli et al., 2006; Sin et al., 2009). To reduce the computational burden of characterizing uncertainty around WRRF process model results, Latin hypercube sampling (LHS) can be used to reduce the required number of simulations in a Monte Carlo analysis by discretizing probability density functions into equal probability portions (Helton and Davis, 2003; McKay et al., 1979; Shoener et al., 2016).

Following the uncertainty analysis, model inputs and outputs can be compared to determine parameter sensitivity. Similar to calibration procedures, there is no universal sensitivity analysis procedure, though sensitivity analyses can be broadly categorized as local or global. Morris one-factor-at-a-time (Morris, 1991) and Markov-Chain Monte Carlo (Sharifi et al., 2014) are examples of global sensitivity analyses, whereas differential analysis (Brun et al., 2002) is local. Sensitivity metrics can be used to concisely compare sensitivities of model outputs to individual inputs (e.g., Spearman’s rank correlation coefficient (Iman and Conover, 1982; Marino et al., 2008; Wang et al., 2015)). When evaluating a model, the analysis chosen should depend on the core objective (e.g., reducing model structural uncertainty or input uncertainty) which should be explicitly stated when describing the model (only 30% of models utilized sensitivity analyses, 26% of which did not describe the procedure used). Rigorously performing uncertainty and sensitivity analyses will not only simplify model calibration and validation, but will also help to inform future experimentation by identifying critical information needs for model application and development. For instance, if a particular model output is very sensitive to a highly uncertain parameter, extensive experimentation could be conducted to ensure the parameter is accurately calibrated and the model can be validated.

Integration with existing WRRF models

Standard wastewater modeling nomenclature

As we seek to develop phytoplankton-based processes for wastewater treatment, the likelihood of broad adoption of developed models will be directly influenced by their alignment with existing WRRF modeling structure and nomenclature. To the degree possible, any phytoplankton models developed should be able to be integrated with the IWA’s Activated Sludge Models (e.g., ASM2d and ADM3) and Anaerobic Digestion Model 1 (ADM1). There may be circumstances or applications of phytoplankton modeling that necessitate or warrant alternative model structures, but it should be recognized that any deviations will reduce transparency and the likelihood of adoption by industry.

The original IWA ASM1 publication popularized a standard approach to naming the state variables upon which pseudo-mechanistic model structures are built (Henze et al., 1987). Each state variable defines one fundamental component around which a dynamic mass balance is determined. The ASM1 state variable structure allows for grouping of different sets of variables by their fundamental composition (e.g., chemical oxygen demand, nitrogen, phosphorus), and by the processes which act upon them (e.g., biomass state variables undergo growth and decay) through rate equations. In addition to establishing a straightforward nomenclature (discussed below), the ASM1 also used a Petersen matrix (Petersen, 1965), which concisely displays an entire model (both kinetics and stoichiometry) and helps ensure the maintenance of mass balances.

The original ASM1 (Henze et al., 1987) sets out a nomenclature that specifies attributes of the state variables, and allows straightforward grouping of the state variables based on inherent characteristics and the processes acting on them (46% of articles focusing solely on wastewater; 5.0% of all articles). A capital letter specifies the component category (“S” for soluble and “X” for slowly biodegradable or particulate) and subscripts are then used to uniquely identify the component. Subscripts may specify if a component is readily biodegradable (e.g., S_S) or inert (e.g., X_I) or can identify the short-form chemical composition (e.g., S_NO for soluble nitrate and nitrite). Biomass components typically use the nomenclature X_B followed by a second subscript to distinguish between biomass types (e.g., X_B,H for heterotrophs, X_B,A for autotrophs). The subsequent IWA models ASM2 (Henze et al., 1995), ASM2d (Henze et al., 1999), ASM3 (Gujer et al., 1999), and ADM1 (Batstone et al., 2002) maintained this nomenclature structure, adhering to the S and X prefixes for soluble and particulate components. The ASM2 model report also explicitly states that the X components must be electrically neutral (no ionic charges) whereas the soluble components may carry charges.

Further model development by academic researchers and commercial simulation companies has generally followed the established IWA nomenclature, but diversity in model complexity and approach to naming state variables has led to some confusion and inconsistency across the wastewater modeling industry. (Corominas et al., 2010) summarized many of the issues faced with conflicting variable names, including consistency of variable names and meanings (e.g., “b” has been used to stand for “biomass” or “biodegradable”), usage of upper or lower cases, and different units associated with the same variable (e.g., biomass has been represented by g COD·m^-3, g-C·m^-3, or mol-C·m^-3). Additionally, state variable definitions should incorporate the processes which act upon them; this aspect is often disregarded when identifying variables. (Corominas et al., 2010) proposed a structured methodology for setting names for state variables and model parameters, using a series of subscripts to represent biodegradability, organic/inorganic nature, organism name (if relevant) and any other distinguishing characteristics. This standardized nomenclature has not been broadly adopted, however. To the degree possible, developers of new models should also use existing ASM and ADM variables (e.g., X_LI for stored lipids, X_CH for stored carbohydrates (Guest et al., 2013)) and only focus on adapting variables that are not already represented (e.g., X_ALG for algae biomass). Ultimately, nomenclature congruent with IWA naming conventions must be adhered to if phytoplankton pseudo-mechanistic models are to be usable by the wastewater industry.

Integration approaches

In order to develop plant-wide models that include phytoplankton-based processes alongside activated sludge or anaerobic digestion processes, existing integration techniques for ASMs and ADM1 can be leveraged. At present, there are three main approaches to plant-wide dynamic WRRF modeling: (i) the interfaces approach (Nopens et al., 2009; Vanrolleghem et al., 2005; Volcke et al., 2006; Zaher et al., 2007); (ii) the standard supermodel approach (Jones et al., 2007; Seco et al., 2004); and (iii) the tailored supermodel approach (Grau et al., 2007). A summary of these approaches can be found in (Grau et al., 2009). A number of software packages are commercially available for whole-plant simulations (e.g., GPS-X™, BioWin, WEST^®, and Sumo^©), taking advantage of both the interface and supermodel (e.g., GPS-X™, BioWin) approaches for whole-plant modeling. Although the interface approach can use state variable transformers to add new unit processes to models, developing these transformers is typically difficult (Grau et al., 2009). The supermodel approach requires the development of new state variables and processes, but allows for greater flexibility in terms of model development and is therefore more frequently used in practice (e.g., used in GPS-X^TM, BioWin, and Sumo^©). Additionally, when integrating models, a continuity check should be performed to avoid inconsistencies in mass balances (see (Rieger et al., 2012) for details).

Path forward

Model development

Algae modeling needs in wastewater treatment

Accurately modeling full-scale phytoplankton treatment systems – accounting for reactor design, influent composition, algal-bacterial interactions, and environmental conditions – is essential. Models should be able to accommodate different reactor types (e.g., HRAPs, raceway ponds, PBRs, etc. (Shoener et al., 2014)) as well as influents (e.g., raw sewage, primary or secondary effluent, etc.). In order for a model to be useful, an objective should be established prior to model construction (e.g., prediction, control, monitoring, etc.) which will help practitioners navigate tradeoffs between complexity and accuracy (Bernard et al., 2015). A model should also be as simple as possible while maintaining the ability to assist with decision-making (Daigger, 2011).

Key factors in model development

The number of disparate models uncovered during this review and the absence of critical model components (e.g., calibration and validation methodology) in many papers underscore the need for more rigorous phytoplankton model formulation procedures. Before constructing a model, researchers must first consider environmental and reactor conditions to determine which processes to include and which equations can best simulate that process (Table 6). This consideration is of particular importance given that several influential components are frequently omitted from published models (e.g., carbon, phosphorus, and temperature were only included in 27%, 26%, and 24% of reviewed articles, respectively). When considering growth, Monod kinetics are adequate in circumstances with stable nutrient conditions (e.g., chemostats with fixed environmental conditions) and substrate concentrations below inhibitory values. In configurations or process designs in which algae are exposed to fluctuating nutrient concentrations, Droop model formulation should be used to decouple nutrient uptake and growth. Additionally, high ammonia or substrate (e.g., acetate) concentrations that could be inhibitory may be modeled via Haldane/Andrews (Andrews, 1968; Haldane, 1930); similarly, inhibition from high irradiance can be modeled via the Eilers and Peeters or Steele expressions (Eilers and Peeters, 1988; Steele, 1962). Given that the choice of a PI sub-model will only have an impact at high light intensities (where photoinhibition and photoacclimation may occur (Eilers and Peeters, 1988)), if only non-photoinhibitory situations are being considered, the simplest model that can still accurately simulate the process may be chosen. For substrate uptake and utilization, given the dynamicity of WRRFs, organisms must be modeled with their history in mind. For example, if the organism was previously in N-replete conditions but then experiences N-deplete conditions, it will continue growing off internal reserves before forming storage compounds. Additionally, the impacts of changing environmental conditions on phytoplankton processes should be assessed (e.g., temperature changes across seasons); excluding environmental history or dynamic conditions will limit the accuracy of a model.

Table 6.

Summary of recommendations for model construction, components, and assessment including relative importance and additional information regarding recommendation. An X denotes the recommended frequency with which to consider a given topic. If a different letter is used (e.g., M), a specific equation(s) is recommended for use when modeling that component (e.g., Monod; see definitions at bottom of table). Percentages listed are the number of articles that included that particular component in the presented model (this percentage did not influence the subsequent recommendations).

	Topic	Percent Used	When to Consider			Details
			Frequently	Sometimes	Rarely
Model Construction	Threshold formulation	11%	X			Use if at least one factor is potentially limiting.
	Multiplicative formulation	44%			X	Only applicable when growth components are independent.
Model Component	Carbon	27%	M			Inorganic carbon if only considering photoautotrophic; Organic carbon if only considering heterotrophic; Organic and inorganic carbon if considering mixotrophic.
	Nitrogen	53%	D or A			Include if concentration fluctuates, if modeling nutrient recovery, or if potentially inhibitory; Consider impacts on growth and pH.
	Phosphorus	26%	D			Include if concentration fluctuates or if modeling nutrient recovery.
	Light	66%	M or E&P			Consider light penetration into reactor and scattering; If potentially inhibitory, include impacts of photoacclimation.
	Temperature	24%	X			Include to assess impact on algal growth kinetics; Consider model choice if potentially inhibitory.
	Carbon storage	16%		X		Include if nutrient-deplete conditions or other accumulation triggers (e.g., thermal stress or high light intensity) exist, or if subjected to fluctuating lighting conditions.
	Respiration	57%	X			Maintenance energy requirements are constant, but endogenous respiration rates are not.
	Other organisms	16%		X		Consider if not growing algae in pure culture.
	Mass transfer	17%		X		Consider if CO2 can be limiting, or if NH3 or O2 can be inhibitory.
	pH	16%		X		Consider if system is not well-buffered or can cause inhibition.

M ≡ Monod; D ≡ Droop; A ≡ Andrews; E&P ≡ Eilers and Peeters; X – no specific model recommended.

In addition to selecting model components carefully, the model foundation should be built upon a mechanistic understanding of phenomena. This will not only improve the generalizability and accuracy of the model, but may also reduce the number of calibrated parameters, provide a theoretically grounded range for biochemical model parameters, and increase model transparency by reducing the number of empirical parameters. This comprehensive understanding will also enable the integration of separate, but related models (e.g., hydrodynamics), which will be critical to translate laboratory-scale data into predictions of full-scale performance. Also, when gathering experimental data, it should be noted that diel cycles will often necessitate frequent sampling (multiple times per day) to enable model validation. High-resolution models require multiple measurements each day (or even each hour) in order to capture diel variability; this is crucial during model calibration and validation. More broadly, the lack of clearly defined calibration and validation procedures is a serious shortcoming in many of the papers reviewed (17% of papers that calibrated their models did not specify a procedure). Calibration and validation need to be conducted to assess the accuracy and precision of a model appropriately and ensure the fidelity of a model is upheld. If a model cannot be calibrated and validated reliably, it cannot be utilized for a full-scale reactor, let alone as a component of a WRRF model.

Broader context

WRRF practitioners are tasked with protecting the health of the public and the aquatic environment, and an inaccurate model could have serious deleterious effects on WRRF investment, design, and performance. When proposing a model, the phytoplankton process should be considered as part of an entire WRRF, not just an independent unit. Promising model structures should be able to handle the frequent changes that occur at WRRFs. In order to ensure models are accessible to the broadest possible audience and can be compared easily, IWA nomenclature should be used more frequently to increase WRRF model inter-compatibility. The ASMs proposed the use of a stoichiometric matrix to quickly and efficiently display the model structure. However, only 6.2% of papers reviewed used a stoichiometric matrix. This approach should be used to make models simpler to interpret and to implement in simulation software, thus widening the user base of phytoplankton models and accelerating their broader adoption at full-scale WRRFs. Microalgal resource recovery systems have tremendous potential to improve WRRF function achieving effluent nutrient concentrations below the current limit of technology. In order to realize this potential, however, WRRF practitioners must first believe that the tools available to them are accurate and reliable. This trust can only be attained if algae process models adhere to the same level of rigor and transparency as current IWA models.

Conclusion

• •Algal and cyanobacterial technologies have the potential to achieve effluent nutrient concentrations below existing biological nutrient removal systems, but there is no established modeling framework for engineered phytoplankton treatment systems.
• •In the context of wastewater treatment, a Droop formulation for nutrient uptake and an Eilers and Peeters formulation for irradiance response can accurately simulate external and internal conditions.
• •The effects of temperature fluctuations on phytoplankton growth rates should be assessed with either an Arrhenius or CTMI formulation.
• •Lumped pathway metabolic models rooted in a mechanistic understanding of biochemical processes can simplify model structure and reduce parameter uncertainty.
• •Calibration and validation should be rigorous and clearly defined.

Appendix A. Supplementary data

The following is the Supplementary data to this article: