Anterior insular cortex is a bottleneck of cognitive control

Abstract

Cognitive control, with a limited capacity, is a core process in human cognition for the coordination of thoughts and actions. Although the regions involved in cognitive control have been identified as the cognitive control network (CCN), it is still unclear whether a specific region of the CCN serves as a bottleneck limiting the capacity of cognitive control (CCC). Here, we used a perceptual decision-making task with conditions of high cognitive load to challenge the CCN and to assess the CCC in a functional magnetic resonance imaging (fMRI) study. We found that the activation of the right anterior insular cortex (AIC) of the CCN increased monotonically as a function of cognitive load and showed a significant correlation to the CCC. In a subsequent study of patients with unilateral lesions of the AIC, we found that lesions of the AIC were associated with a significant impairment of the CCC. Simulated lesions of the AIC resulted in a reduction of the global efficiency of the CCN in a network analysis. Altogether, these findings suggest that the AIC, as a critical hub in the CCN, is a bottleneck of cognitive control.

Introduction

Cognitive control, which coordinates mental operations under conditions of uncertainty at perceptual or higher levels so that decisions can be made (Fan et al., 2014), is supported by the cognitive control network (CCN) in the brain (Fan et al., 2014; Niendam et al., 2012; Wu et al., 2018). The CCN is a large-scale network composed of two sub-networks: (1) the frontoparietal network (FPN), including the frontal eye field (FEF) and supplementary eye field, mid frontal gyrus (MFG), areas near and along the intraparietal sulcus (IPS) and superior parietal lobule (Corbetta, 1998; Fan et al., 2014); (2) the cingulo-opercular network (CON), including the anterior cingulate cortex (ACC) and anterior insular cortex (AIC) (Dosenbach et al., 2008; Dosenbach et al., 2007); and subcortical structures, including the thalamus and basal ganglia (Fan et al., 2014; Koziol, 2014; Rossi et al., 2009). It is known that the cognitive control system has a severely low upper limit (Posner and Snyder, 1975). According to the information theory (Shannon and Weaver, 1949), this upper limit can be quantified as the capacity of an information processing channel, i.e., the maximal amount of information that can be processed during a certain period of time. Under this framework, we have recently quantified the capacity of cognitive control (CCC) as approximately 3 to 4 bits per second (bps) (Fan, 2014; Wu et al., 2016). However, the neural mechanisms limiting the CCC remain unclear.

A potential mechanism of this capacity limit could be the existence of a single bottleneck region/sub-network of the CCN exerting a heavy working load due to its concurrent involvement in multiple processes during cognitive control (i.e., an integrative hub) (De Baar, 1994; Gorban et al., 2011; Watanabe and Funahashi, 2014). The AIC appears to be best candidate for a bottleneck region that determines the CCC. It receives information from multiple modalities (e.g., visual, auditory, somatosensory, motor, and autonomic nervous systems) and domains (e.g., cognitive control, interoception, emotion, and language) (Ackermann and Riecker, 2004; Augustine, 1996; Bamiou et al., 2003; Chang et al., 2012; Critchley et al., 2004), and re-represents the vast information to generate higher-level abstract and subjective information that are considered as “thoughts”, “feelings”, and “awareness” (Brass and Haggard, 2010; Craig, 2009, 2011; Gu et al., 2013; Nelson et al., 2010; Singer et al., 2009). The AIC has abundant anatomical connections with diverse parts of the brain (Augustine, 1996; Cauda et al., 2012; Cauda et al., 2011; Cauda and Vercelli, 2012; Eckert et al., 2009; Flynn, 1999; Kelly et al., 2012; Spagna et al., 2018a), which may support dynamic coordination among information processes in different large-scale brain networks (Cocchi et al., 2013; Menon and Uddin, 2010; Sridharan et al., 2008). Each of the functions of the AIC (e.g., encoding, integrating, switching, and controlling) requires and competes for the limited neural resources of this region. Inefficient information processing in such a brain hub should significantly impair global communication (Albert et al., 2000; Power et al., 2013), and consequently, damage of the AIC may significantly impact the CCC.

Here we employed a perceptual decision-making task, the backward masking majority function task (MFT-M) (Wu et al., 2016), to challenge cognitive control by manipulating both information amount (measured as information entropy), which depends on both uncertainty of inputs at perceptual level and higher-level mental algorithms to make the decision, and the exposure time (ET) of the stimuli so that the amount of to-be-controlled information during a unit of time (i.e., information rate, referred as cognitive load in this study) could be varied within a wide range, and therefore the CCC of each participant could be estimated based on the relationship between cognitive load and response accuracy. We tested the role of the AIC as a bottleneck of cognitive control by examining (1) the relationship between its activity and the cognitive load and the relationship between its activity and CCC in a functional magnetic resonance imaging (fMRI) study, and (2) the necessity of the AIC in supporting the CCC in a human lesion study. The mechanism of the AIC, in comparison to the ACC, in relation to the CCC was further explored by combining complex network analyses with lesion simulations.

Materials and Methods

Participants

Adults with no history of head injury, psychiatric, and neurological disorders (n = 32) participated in the fMRI study. All participants were right-handed and had normal or corrected-to-normal vision. We excluded one participant for poor image quality and an additional four participants because of high percentage (> 5%) of missing responses. The final sample size was 27 (15 females and 12 males; mean ± standard deviation [SD] age, 25.6 ± 4.6 years). The Institutional Review Boards (IRB) of The City University of New York (CUNY) and of the Icahn School of Medicine at Mount Sinai (ISMMS) approved the protocol and written informed consent was obtained from each participant before participation.

In the lesion study, we recruited patients with a focal lesion of the AIC (AIC group, n = 8), patients with a focal lesion of the ACC (ACC group, n = 7), and patients with a focal lesion outside the CCN regions as brain damage controls (BDC group, n = 9, eight with a lesion in the temporal pole, and one with a lesion in the frontal pole) from the Patient’s Registry of Tiantan Hospital, Beijing, China. All lesions were unilateral. We also recruited participants with no history of head injury, psychiatric, and neurological disorders as neurologically intact controls (NIC group, n = 27) from local Beijing communities. All participants were right-handed and had normal or corrected-to-normal vision. The demographic information (including gender, age, and education) was matched across groups. All participants completed the Mini-Mental State Examination (MMSE) (Cockrell and Folstein, 2002) and the Beck Depression Inventory (BDI) (Schwab et al., 1967) questionnaires for assessment of cognitive ability and mood state, respectively (see Supplementary Material and Supplementary Table 1 for details). One patient in the ACC group and one patient in the BDC group were excluded from further analyses because they did not follow the instruction to make a response in at least 95% of the trials. The IRB of Tiantan Hospital of the Capital Medical University in Beijing approved the protocol and written informed consent was obtained from each participant.

The backward masking majority function task

To make a decision under conditions of uncertainty at either perceptual or higher-levels, cognitive control is employed to coordinate the mental operations needed for the decision-making. The majority function task (MFT) requires participants to indicate the direction majority of a set of left and right-pointing arrows displayed on the screen (e.g., with 2 left-pointing arrows and 3 right-pointing arrows). In our previous studies using the MFT, we have demonstrated that a sophisticated algorithm that consists of a series of binary decision-making processes has to be adopted to reach the final decision of the majority (which is right-pointing for this case) (Fan et al., 2008; Wang et al., 2011). The information amount, determined by both inputs (the ratio of left- and right-pointing arrows and the set size) and mental algorithms, estimated under the framework of information theory as information entropy in unit of bit, varied from 0 to 4.91 bits. This range is much wider than in the flanker task (Eriksen and Eriksen, 1974) and the color-word Stroop task (Stroop, 1935), which are classical cognitive control tasks that only require a single binary decision-making process that ranges from 0 to less than or equal to 1 bit in terms of information entropy (Fan, 2014; Mackie et al., 2013).Therefore, cognitive control will be more challenged in the MFT, compared to in the flanker task.

According to the information theory (Shannon and Weaver, 1949), when the amount of information to-be-processed during a unit of time (information rate in bps) exceeds capacity, the communication accuracy starts to reduce and eventually reaches the chance level when the information rate is too high. In the MFT, the exposure time (ET) of the arrow sets was fixed to 2500 ms and a relative high accuracy (about 75%, much higher than chance level of 50%), was observed under the condition with the highest cognitive load (Fan 2008; Mackie et al., 2013), indicating that the cognitive load in this task was not high enough to challenge the CCC. To further challenge cognitive control, we additionally manipulated the ET using a backward masking approach (i.e., following the presentation of a target set for a duration of time, which is the ET, a mask set was displayed to prevent further visual processing of the target) so that the time given for cognitive control in a trial was constrained from long to short. The cognitive load in this MFT-M task varied between 0.79 and 19.64 bps (see below). When the cognitive load is higher than the capacity (i.e., the CCC), it would lead to a drop in response accuracy (Wu et al., 2016). This relationship can be used to estimate the CCC of each participant (also see below). The MFT-M has a test-retest reliability of 0.86 in assessing participants’ CCC (Wu et al., 2016).

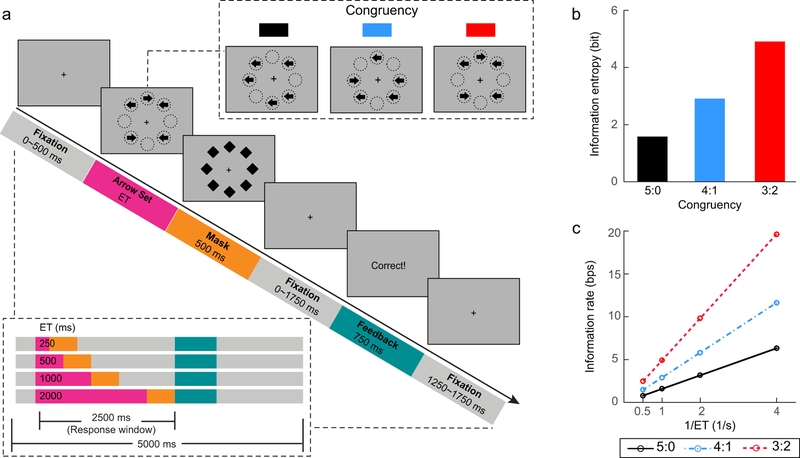
To increase both detection and estimation power for this fMRI study, the task was modified by reducing the number of task conditions with increased number of trials in each task condition, and by adding null trials with no visual stimuli presented (see below for details). Other parameters were identical to the full version of the MFT-M (Wu et al., 2016) (see Fig. 1a for an illustration of this task). At the beginning of each trial, there was a fixation period for 0 to 500 ms, followed by five arrows presented simultaneously lasting for a variable ET. Each arrow pointed either to the left or to the right. The length of each arrow was 0.37° of visual angle. These arrows were randomly presented at eight possible locations arranged as an octagon that subtended approximately 1.5° from the fixation cross. Following this arrow set, a mask consisting of eight diamond shapes at the same eight positions was presented for 500 ms, and was replaced by a fixation period of 0 to 1750 ms. The diameter of each diamond shape was identical to the length of each arrow. Participants were required to indicate the direction in which the majority of the arrows pointed by pressing a corresponding button as accurately and quickly as possible. Response accuracy was emphasized over RT. Responses had to be made within a 2500 ms window starting from the onset of the arrow set. Participants were instructed to make a response in every trial and to guess when they failed to find the majority direction. Participants with a response rate lower than 95% were excluded from analyses. Following the 2500 ms trial period, a feedback was presented for 750 ms to inform the participants whether their response in the current trial was correct. At the end of each trial, there was a variable post-feedback fixation period for 1250 to 1750 ms. Each trial was 5000 ms in duration. This trial structure ended with a 2500 ms jittered design for stimulus onset with a range of 3250 to 5750 ms, in addition to null trials (see below).

Figure 1. The backward masking majority function task (MFT-M).

(a) Schematic of the MFT-M. Participants were required to report the majority of arrow directions in each trial. Upper right panel: possible congruency ratios (majority : minority) of arrow sets. Lower left panel: timeline of the stimuli in one trial under different stimulus exposure time (ET, in ms) conditions. Events in a trial of sequence are indicated by the color-coded blocks. Duration of each stimulus is illustrated by the length of each color bar. Responses had to be made with the 2500 ms response window and the total length of each trial was 5000 ms. (b) Information entropy as an index of information amount in each congruency condition, regardless of the ET. (c) Information rate as an index of cognitive load in each task condition. The information rate increases as a function of both information entropy and the reciprocal of ET (1/ET), and shows a super-additive interaction between information entropy and 1/ET.

The cognitive load (in information rate) of each condition was manipulated by varying both congruency and ET in a 3 (congruency) × 4 (ET) factorial design. The congruency refers to the ratio between the majority and minority direction of arrows, which could be 5:0 (5 left or 5 right), 4:1 (4 left with 1 right or 4 right with 1 left), or 3:2 (3 left with 2 right or 3 right with 2 left). The ET could be 250, 500, 1000, or 2000 ms. Table 1 provides the estimates of information amount (measured as information entropy), the reciprocal of ET (i.e., 1/ET), and cognitive load (measures as information rate, which can be computed as entropy/ET) in each task condition. Fig. 1b and 1c show the information entropy in each congruency condition and the information rate in each task condition, respectively. The information rate increases as a function of both information entropy and the reciprocal of ET with a super-additive effect. In the fMRI study, there were 12 null trials as a 5000-ms fixation period, in addition to 36 test trials in each run. The congruency was varied within each run with 12 trials under each congruency condition. The ET was varied between runs with three runs for each ET, and there were 12 runs in total. For each participant, the presentation of the trials within each run was in a random order across all levels of congruency, and the presentation of runs was also in a random order across all ETs. The exposure time was manipulated between blocks to avoid speed-accuracy trade-off, and the congruency was manipulated within block to keep participants’ attention on the task. At the beginning and end of each run, there was a 30 s fixation period in the fMRI study and a 3 s fixation period in the lesion study. In the fMRI study, each run was composed by 48 trials (36 task trials and 12 null trials) and lasted 300 s. In total, 432 task trials were presented, and the task took approximately 68 minutes to be completed. In the lesion study, each run was composed by 36 task trials without any null trial and lasted 213 s. In total, there were 432 task trials presented and the task took approximately 43 minutes. Additional information about the testing procedure can be found in the Supplementary Methods.

Table 1.

Estimates of information amount and information rate in each task condition, and the contrast vectors of each effect.

		ET (ms)
	Congruency	250	500	1000	2000
Estimates
Information entropy (bit)	5:0	1.58	1.58	1.58	1.58
	4:1	2.91	2.91	2.91	2.91
	3:2	4.91	4.91	4.91	4.91
1/ET (1/s)	5:0	4	2	1	0.5
	4:1	4	2	1	0.5
	3:2	4	2	1	0.5
Information rate (bps)	5:0	6.32	3.16	1.58	0.79
	4:1	11.64	5.82	2.91	1.46
	3:2	19.64	9.82	4.91	2.46
Contrast vectors	5:0	−0.87	−0.87	−0.87	−0.87
Information entropy	4:1	−0.13	−0.13	−0.13	−0.13
	3:2	1.00	1.00	1.00	1.00
1/ET	5:0	1	0.06	−0.41	−0.65
	4:1	1	0.06	−0.41	−0.65
	3:2	1	0.06	−0.41	−0.65
Interaction	5:0	−0.87	−0.05	0.36	0.57
	4:1	−0.13	−0.01	0.05	0.08
	3:2	1	0.06	−0.41	−0.65

Note: ET refers to exposure time. Information entropy is a measure of information amount in each congruency condition. Information rate is a measure of cognitive load, as a joint effect of both congruency and ET (information rate = entropy/ET).

Estimation of the capacity of cognitive control

For each participant, response accuracy was used to estimate the CCC (Wu et al., 2016). According to the definition of the capacity of a channel (Shannon and Weaver, 1949), we assumed that the probability of obtaining a correct response (equivalent to response accuracy) was determined by the difference between the amount of to-be-processed information and the amount that can be processed, i.e., the CCC. When the cognitive load is increased but is still lower than the CCC, the responses should be accurate. However, when the cognitive load exceeds the CCC, there should be the drop in response accuracy. The cognitive load was calculated using the congruency and ET in a grouping search model demonstrated in our previous studies (Fan et al., 2008; Wang et al., 2011; Wu et al., 2016). In this model, participants keep randomly drawing a subset of stimuli from the given stimuli set, with the sample size as the majority size (N_maj, which is 3 for the set size of 5), until a congruent sample (i.e., all arrows pointing to same direction) is obtained. The arrow direction in this congruent sample is then returned as the final response. The estimated amount of to-be-processed information (information entropy) can be estimated as the log₂ transformation of the averaged number of to-be-processed arrows to reach a congruent sample. Each participant’s CCC limits the amount of can-be-processed information under each ET. A correct response would be made if a congruent sample can be obtained within the ET, otherwise a random guessing response would be made. Therefore, the expected response accuracy (E[accuracy]) is as:

$$E\left[accuracy\right]=P_{congruent}\hspace{0.17em}\times \hspace{0.17em}{p}_0+ \hspace{0.17em}\left(1-P_{congruent}\right)\hspace{0.17em}\times \hspace{0.17em}{p}_{guess}$$

in which p₀ is the baseline response accuracy when a congruent sample is obtained, p_guess is the chance level of accuracy for guessing (50%), and P_congruent is the probability that at least one congruent sample can be obtained within a given ET. The P_congruent can be calculated as 100% minus the probability of obtaining no congruent sample within the ET, which is $P_{miss}{ }^{n_s}$, with P_miss as the probability of obtaining an incongruent sample by one attempt of search and n_s as the number of attempts. The P_miss is determined by the congruency of an arrow set (see Supplementary Materials for details), while n_s is determined by the amount of information that can be processed within a unit of time (parameter C), N_maj, and ET, expressed as n_s = 2^C × ET / N_maj. The final equation is

$$E\left[accuracy\right]=\left[1-P_{miss}{ }^{\frac{2^C\times ET}{N_{maj}}}\right]\hspace{0.17em}\times p_0+P_{miss}{ }^{\frac{2^C\times ET}{N_{maj}}}\times p_{guess}.$$

The estimated CCC is the value of C that provides the best global fitting of the predicted response accuracy to the empirical response of each participant across all conditions. A high CCC indicates that more information (in bps) can be accurately processed during a given period, leading to high response accuracy in task conditions with high information rate (as the index of cognitive load). See Supplementary Methods for details of the estimation of the CCC, as well as the computation of the mean response accuracy and reaction time (RT) in each condition. The RT was not included in the model for the estimation of the CCC. In our previous study for the task development and CCC estimation (Wu et al., 2016), we found that although including the RT had a weak improvement in model fitting compared to the model used in the current study, the reliability of the estimation was impaired.

Intelligence quotient (IQ) measurement

For the fMRI study, the IQ of each participant was measured using a short form of the Wechsler Adult Intelligence Scale – Fourth Edition (WAIS-IV), which included three subtests: Symbol Search, Vocabulary, and Figure Weight. This combination is one of the best three-subtest short-form combinations, with high reliability (.935) and validity (.915) coefficients (Sattler and Ryan, 2009). The raw score of each subtest was converted to the scaled score for the individual’s age group. The total scaled score across the three subtests was then converted to the estimated FSIQ following the Tellegen and Briggs (Tellegen and Briggs, 1967) procedure.

fMRI data acquisition

MRI acquisitions were obtained at ISMMS on a 3T Siemens Magnetom Skyra scanner with a 16-channel phase-array coil. Each scan session lasted about 1.5 hours. All images were acquired along axial planes parallel to the anterior commissure-posterior commissure (AC-PC) plane. Twelve runs of T2*-weighted images for fMRI were acquired with a gradient-echo planar imaging (GE-EPI) sequence with the following parameters: 40 axial slices of 4 mm thick, interleaved, skip = 0 mm, TR = 2000 ms, TE = 27 ms, flip angle = 77°, FOV = 240 mm, matrix size = 64 × 64, voxel size = 3.8 × 3.8 × 4 mm. Each run began with two dummy volumes before the onset of the task to allow for equilibration of T1 saturation effects, followed by the acquisition of 150 volumes. A high-resolution T1-weighted anatomical volume of the whole brain was also acquired with a magnetization-prepared rapid gradient-echo (MPRAGE) sequence with the following parameters: 176 axial slices of 0.9 mm thick, skip = 0 mm, TR = 2200 ms, TE = 2.51 ms, flip angle = 8°, FOV = 240 mm, matrix size = 256 × 256, voxel size = 0.9 × 0.9 × 0.9 mm.

fMRI data analysis

Image preprocessing.

Event-related fMRI data analysis was conducted using the Statistical Parametric Mapping package (SPM 12, RRID: SCR_007037; Welcome Trust Centre for Neuroimaging, London, UK). The T1 image and all EPI images were manually adjusted to align the AC-PC plane. For each participant, each EPI image volume was realigned to the first volume and then slice timing corrected using the first slice as the reference. The T1 image was then coregistered to the mean EPI image using normalized mutual information. The coregistered T1 image was segmented into grey matter, white matter, cerebrospinal fluid, bone, soft tissue, and air/background according to the SPM tissue probability map (Mazziotta et al., 1995), with affine regularization as ICBM space template – European brains. Realigned EPI images were then spatially normalized using the forward deformation field estimated in segmentation, resampled to a voxel size of 2 × 2 × 2 mm. Normalized EPI images were then spatially smoothed with a Gaussian kernel of 8 mm full-width half-maximum.

General linear modeling.

If a brain region is associated with the CCC, it should show the following two properties. First, the activation of this region should match the pattern of information rate (Fig. 1c). This property was examined by the conjunction of a main effect of information entropy, a main effect of the reciprocal of ET, and the super-additive interaction effect. Second, this super-additive activation should be positively correlated to the CCC across participants, because a greater super-additive interaction effect in activation of this region indicates a better response to the demand of an increase in information rate, which determines the CCC.

First-level (single-subject level) statistical analyses of the event-related BOLD signal of each participant were conducted to identify the significant relationship between the hemodynamic responses in brain regions and task events (Friston et al., 1994). For each run, three regressors were constructed based on the onset vectors of arrow sets corresponding to the three congruency conditions under each ET in trials with correct responses in each run. An additional nuisance regressor was constructed for each condition based on the onset vectors of the arrow set for trial(s) with incorrect responses in this condition if there was any (minimum 0 and maximum 3 nuisance regressors in each run). The duration of these vectors were set as the ET in the corresponding condition for the regressors mentioned above. To model out the feedback-related responses, two additional regressors were constructed for each run based on the onset vectors of feedback, with one for positive feedbacks and the other one for negative feedbacks. The durations of these vectors of feedbacks were set as 0. All of the above mentioned vectors were convolved with a standard hemodynamic response function (HRF) (Friston et al., 1998). The six motion parameters generated during realignment and sessions were entered into the model as additional nuisance covariates for each run. A high-pass filter with a 128-s cutoff was used to remove low-frequency signal drift, and serial correlation was estimated using an autoregressive AR(1) model (also for the following first-level GLM analyses). The GLM was estimated and the image of parameter estimate (β) for each regressor was obtained. For the arrow set-related regressors, the brain response to an event was modeled as the convolution of a standard HRF and a rectangular function with the ET as the duration. The parameter estimate of each regressor (i.e., the β value) represents the change of HRF amplitude, while the convoluted hemodynamic response curve represents the cumulated BOLD responses across the duration. The area under a response curve depends on two factors: HRF amplitude and duration (ET). By manipulating the information entropy and ET, we can disassociate the contributions of information rate and processing time to BOLD responses. The estimated HRF amplitude is the brain response as a function of information rate. For a given value of information entropy, a large change of HRF amplitude could be associated with a high information rate due to a short ET.

For the first-level analysis, a contrast image of all conditions versus baseline was generated by averaging the β values across the regressors for trials with correct responses. The linear main effect of information entropy was examined using the orthogonal polynomial contrast of entropy for 5:0, 4:1, and 3:2 congruency conditions, regardless of the ET, based on the information entropy estimation of each congruency condition, and this contrast vector was demeaned to remove the zero-order term and by normalizing to an absolute maximum value. The linear main effect of the reciprocal of ET was examined using the contrast based on the demeaned and normalized reciprocal of ET regardless of congruency. The information entropy × reciprocal of ET interaction was examined using the contrast as the scalar product between the contrast vectors of information entropy and the reciprocal of ET. The positive interaction effect indicates a super-additive effect between the entropy and reciprocal of ET, with stronger activation increase as entropy increases under conditions with shorter ET than under conditions with longer ET. It is worth noting that this interaction effect is statistically independent of the information rate because both entropy and the reciprocal of ET were demeaned when computing the interaction. These contrast vectors are summarized in Table 1.

Second-level group analyses were conducted to identify regions with significant activation changes across participants associated with each effect, including single condition versus baseline, all condition versus baseline (All-minus-Baseline), the main effects of information entropy and reciprocal of ET, and the information entropy × reciprocal of ET interaction. For each effect, the corresponding contrast image for each participant was entered in a random-effects statistical model that accounts for inter-subject variability and permits population-based inferences. One-sample t-test was performed for each voxel. The conjunction of the two main effects and their interaction was examined. A positive effect in this conjunction indicates that the pattern of brain activation across task conditions matches the information rate as a function of information entropy, the reciprocal of ET, and their interaction. A significance level for the height of each voxel of p < .001 (uncorrected) was used, together with a contiguous-voxel extent threshold (estimated based on the random field theory) to correct for multiple voxel comparisons resulting in cluster-level p < .05. This thresholding approach was also applied for the whole brain analyses described below.

A whole-brain voxel-wise second-level regression analysis was conducted to identify the super-additive activation regions that predict the CCC across participants. Contrast images of the information entropy × reciprocal of ET interaction effect were entered in a random-effects model, with the CCC values of participants as the regressor, to conduct a voxel-wise regression analysis between the super-additive activation and CCC.

Examination of the relationship between the neural involvement and cognitive load.

To illustrate the regional activation in each task condition, we conducted regions of interest (ROI) analyses for regions that revealed a positive effect in the conjunction analysis. Their coordinates were defined as the corresponding positive local peaks in the second-level interaction contrast image (left AIC: [−32, 22, 0], right AIC: [32, 26, −8], left ACC: [−2, 18, 50], right ACC: [8, 28, 38]), which is statistically independent to the models in following ROI analysis. For each ROI, the first eigenvariate of the β value was extracted across all voxels within a sphere with 6 mm radius around the peak, from the first-level single-condition-versus-baseline contrast map of each condition of each participant. The hemodynamic response curve within a 12 scans (24 s) window after the onset of arrows was reconstructed for each of these ROI using the MarsBaR toolbox (RRID: SCR_009605) (Brett et al., 2002).

Based on our previous studies (Wu et al., 2016), the activity of an information processing entity increases as a function of the rate of information input, and this increase is approximately linear when the information rate is lower than the capacity. The increase would start to slow down when the information rate exceeds the capacity until an activity plateau is reached (Buschman et al., 2011; Moreno-Bote et al., 2014). To test this pattern in the ROIs defined above, we adopted a non-linear capacity-limited model to fit the relationship between the regional activation (Y) of each ROI and cognitive load (i.e., information rate, I) as a logistic function: Y = Y₀ + S * (1 – e^{−K * I}), which is a typical function to describe a growth with plateau. Here Y₀ denotes the baseline activation when I is 0 bps, S denotes the span of the activity change when I rises from 0 to infinite, and K is the rate constant. The half-time of activity increase can be calculated as ln(2) / K, and the plateau of activity increase can be calculated as S + Y₀. This model was compared to a simpler linear function: Y = Y₀’ + K’ * I, where Y₀’ denotes the baseline activation and K’ denotes the rate of information processing, which indicates that no activation plateau is shown within the range of information rate in this study.

A mixed effect model with Y₀, S, and K as both fixed and random effects, and participant as the random effect was adopted to estimate parameters for each model, in which the restricted likelihood of the linear mixed-effect model (RELME) was used. The Bayesian information criterion (BIC) of each fitted mixed effect model, which takes likelihood, sample size, and number of free parameters into account, was used for the group-level model selection. For model comparison (∆BIC = BIC _linear –BIC _logistic), a ∆BIC > 2 indicates positive evidence against the model with higher BIC (∆BIC = 2–6: positive; 6–10: strong; >10: very strong). The estimated model parameters and other statistics of model fitting (e.g., log likelihood, Akaike information criterion, and root mean squared residual) were also computed.

For the regions with the logistic function as the optimal model (i.e., left and right AIC, see Results), we compared the estimated parameters (i.e., Y₀, S, and half-time) between these two regions, using one-tailed pair-wise t-tests. Each index was calculated as the sum between the estimated fixed effect as a constant across participants and the random effect varying across participants. To examine how the activation changes in the right AIC determine the CCC, a Pearson correlation analysis was conducted between the CCC and each index (i.e., Y₀, S, and half-time).

Examination of the mediative role of AIC activation for the relationship between CCC and IQ.

The relationship among the super-additive activation in the right AIC, CCC, and IQ was examined using mediation analyses (Baron and Kenny, 1986), with the CCC as the predictor (X), super-additive activation in the right AIC as the mediator (M), and IQ as the target variable (Y). We first examined the predictive effect of X to Y (path c: Y = b₁₀ + b₁₁ ∙ X) and the predictive effect of X to M (path a: Y = b₂₀ + b₂₁ ∙ X). Then a regression model with both X and M as predictors (Y = b₃₀ + b₃₁ ∙ X + b₃₂ ∙ M) was estimated if both paths a and c were significant. If the b₃₂ (path b) is significant and b₃₁ is smaller than b₁₁, M is a mediator between X and Y, with a non-significant b₃₁ indicating a full-mediation effect and a significant b₃₁ indicating a partial mediation effect. This analysis was conducted for the FSIQ and each subscale of the IQ (i.e., Symbol Search sub-index, Vocabulary sub-index, scaled Vocabulary sub-index, and Figure Weight sub-index).

Comparison of the CCC across groups in the lesion study

Justification of the inclusion of groups.

The design of the lesion study followed the logic used in our previous study (Gu et al., 2012). To examine whether a lesion in the AIC, but not in the ACC, would lead to an impaired CCC, we included patients with a unilateral focal lesion of the AIC (the AIC group) and patients with a unilateral focal lesion in the ACC (the ACC group). The ACC group also served as an active control group to test whether a lesion in any region of the CON would lead to a reduced CCC. We included a matched sample of neurologically intact controls (the NIC group) as a baseline reference of normal CCC. An additional group of patients with a lesion outside the CCN regions (brain damage controls, the BDC group) was recruited to exclude the potential explanation that the impaired CCC is due to brain surgery procedures per se, rather than the AIC or ACC lesion.

Lesion reconstruction.

For each patient, the brain regions with the lesion were identified and plotted onto an anatomical template of a normal control (ch2.nii, provided by MRIcron: RRID: SCR_002403, http://www.cabiatl.com/mricro/mricro/index.html) by a neurosurgeon (X. W.). A group overlap of multiple lesions was created for each group using the MRIcron, with all lesions mapped on the right hemisphere.

Comparison of the CCC among groups.

The estimated CCC values were compared among groups. If a region is necessary for cognitive control, the CCC in patients with a lesion in this region should be significantly lower than in both NIC and BDC groups. In addition, BDC patients should not be significantly different from the NIC participants, to demonstrate that the impaired CCC is not due to the surgery procedure per se. Therefore, for each of the AIC and ACC, we conducted three planned comparisons with Bonferroni correction applied.

For each comparison, the non-parametric bootstrapping method (Hasson et al., 2003; Mooney and Duval, 1993) was used to assess the probability of observing a between-group difference, because the current data set with a small sample size in each lesion group did not meet the assumptions of parametric statistics. This procedure was conducted with 10,000 iterations for each effect (e.g., the comparison between 8 AIC patients and 27 NIC participants). In each iteration: (i) a whole sample with all of the 35 participants from both AIC and NIC groups was created; (ii) 27 participants were randomly selected from the whole sample as the surrogate NIC sample; (iii) 8 participants were selected randomly from the whole sample as the surrogate AIC group; and (iv) the t-value (one-tailed, AIC < NIC) of the difference between the two surrogate groups was calculated. After the 10,000 iterations, the distribution of the t-values was obtained. The observed t-value of the CCC difference between the original AIC and NIC groups was calculated and compared along this t distribution. If the probability of obtaining the observed t-value along the permutated distribution of t-values was less than 5% (one-tailed), we considered the difference between the patient and control groups as significant.

Network analyses of the CCN

Single-trial brain response extraction.

To estimate the task-evoked brain connectivity, we first extract whole-brain single-trial brain responses using an “extract-one-trial-out” approach, as utilized in previous studies (Choi et al., 2012; Kinnison et al., 2012; Rissman et al., 2004; Wu et al., 2018). The single-trial responses (in β values) represent the change of brain activation associated with a specific event. Specifically, for each participant, a first-level GLM was constructed for each trial, which included (1) all regressors of the first-level GLM described in the above “General linear modeling” section for the onsets all corresponding events for each regressor convoluted with the HRF, as well as the nuisance regressors, with the onset of the event of the trial to be modeled excluded in its corresponding regressor, and (2) the regressor for this single trial to be modeled, which is the convolution of its onset vector with the HRF. The estimation of the GLM was looped trial-by-trial across all trials. The single-trial brain response is the estimated β image of the single trial modeled. The detection and estimation power of this single-trial extraction approach has been demonstrated in our previous study (Wu et al., 2018).

Bayesian network construction.

ROI-based Bayesian network analyses (Wu et al., 2018) were conducted to investigate the effective connectivity between regions of the CCN, and between the CCN and sensory regions (i.e., visual areas) for the event-related single-trial responses. Here the estimated effective connectivity can be considered as the dependence of response changes (the single-trial β values) across trials between ROIs, which reflects the modulation effects of the task on the intrinsic connectivity driven by task-irrelevant BOLD signal fluctuation across time. Although the network structure can also been discovered by the stochastic Dynamic Causal Modeling (DCM) (Friston et al., 2011), which is a more classical approach to estimate the effective connectivity, the set of our ROIs (n = 14, see below) is too large to be handled by DCM. Compared to the DCM, our Bayesian network analyses have advantages in computational efficiency.

The nodes of the networks were defined based on the conjunction between the main effect of information entropy and the main effect of the reciprocal of ET, as clusters that passed the threshold of cluster-level p < .05 for this conjunction (i.e., the height threshold p < .001 with the extent threshold k > 185, estimated based on the random field theory). Fourteen nodes were included: four CON regions (left and right AIC, left and right ACC), four FPN regions (left and right FEF, left and right IPS), four subcortical regions (left and right thalamus, left and right caudate nucleus), and left and right visual areas. For each node, the first eigenvariate β value was extracted across all voxels in the corresponding cluster of each single-trial β image. Then for each node, its trial-by-trial first eigenvariate β values were extracted for each participant with all task trials included.

At first-level (single-subject level), the connectivity between nodes was estimated, using the max-min hill-climbing (MMHC) Bayesian structure learning algorithm (Tsamardinos et al., 2006). In this algorithm, the skeleton of the network (i.e., an undirected network consisting of the connections between nodes without their directions) is first learned by the Max-Min Parents & Children (MMPC) algorithm. After the MMPC procedure, the direction of each connection in the skeleton is estimated using the hill-climbing (HC) algorithm, which is a local search method. A bootstrapping strategy was used to identify the global fitting structure (Friedman et al., 1999), in which we generated 200 random datasets with each dataset containing 432 trials randomly sampled form the original task trials with replacement, and then one MMHC learned network was contrasted for each random dataset. The bnlearn package (http://www.bnlearn.com) (Schwarz, 1978; Scutari and Nagarajan, 2011) was used to implement the MMHC algorithm. The outputs of the MMHC include the estimated strength and direction of each connection. For a connection between nodes i and j, the strength value is the frequency of the bootstrapped samples showing this connection, while the direction value is the probability of the connection from i to j. Both strength and direction values range from 0 and 1. For a pair of forward and backward connections between i and j (i.e., from i to j vs. from j to i), the strength values are identical, and the sum of the direction values is 1 if the strength value is greater than 0. The direction value is 0 if the strength value is 0. A 14 × 14 weighted directed connectivity matrix was constructed, with the connectivity value (i, j; i ≠ j) as the product of the strength value and the direction value. The values on the diagonal of this matrix were set as 0 as required by the complex network analyses.

After constructing the networks for each participant, we examined the significance of the network connections at the group level. A pairwise t-test (two-tailed) was conducted between the empirical connectivity and the baseline connectivity for each connection across participants. A significance level of p < .001 (uncorrected) was adopted. Here the baseline connectivity was estimated by 1000 permutations for each participant. In each permutation, the values within each ROI were shuffled so that the correlation between each pair of nodes would be random. Then the corresponding connectivity matrix was constructed using the same Bayesian network construction procedure described above. The 1000 connection matrixes were averaged as the baseline connection matrix for each participant.

Graph analysis.

To characterize the structure of the learned Bayesian networks, we conducted complex network analysis that measured topological properties of the networks using the Brain Connectivity Toolbox (RRID: SCR_004841; brain-connectivity-toolbox.net) (Rubinov and Sporns, 2010). The community structure of the network was constructed by subdividing it into non-overlapping groups of nodes in a data-driven manner, i.e., by maximizing the possible numbers of within-group connections and minimizing the number of between-group connections. This estimated community structure was applied to all participants in the following estimations of the functional segregation and integration, which assumes that the brain networks of all participants share a common community structure.

For each participant, we examined whether the right AIC played a more important role as a connector hub for intermodular connections compared to the ACC in the estimated network by comparing their participation coefficients, which is a measurement of the centrality of nodes that quantifies the diversity of intermodular interconnections of each node. A node with a 0% participation coefficient indicates that it connects only with regions in its own module, while a participation coefficient of 100% indicates that it evenly connects with regions in all modules. A higher value indicates the greater importance of a node in facilitating global intermodular integration. Compared to the degree-based measures of centrality (i.e., the strength and betweenness centrality), the measure of the participation coefficient is more appropriate in identifying the hubs of brain networks that are critical to the communication among multiple systems (sub-networks) (Power et al., 2013). The participation coefficients for the inward connections (i.e., connections from other nodes to a given node) and the outward connections (i.e., connections from a given node to other nodes) were measured respectively. Pairwise t-tests (one-tailed) were conducted to test whether the participation coefficient of the right AIC was significantly higher than the participation coefficients of other regions, i.e., left AIC, left ACC, and right ACC. For the outward connections, because the left ACC had the highest participation coefficient across regions of the CON, we compared its participation coefficient to other regions in the CON using pairwise t-tests (two-tailed). Bonferroni correction was applied as multiple comparison correction for each test. The computation of participation coefficient was based on the unthresholded connectivity matrix to avoid the influence of thresholding on network sparsity. The correlations between participation coefficient and the CCC across participants were examined.

Lesion simulation.

Changes in network properties and connections after simulated lesion of 14 nodes were examined with the focus on the AIC lesion. We simulated the lesion of a node by setting the trial-by-trial β values of this node as zero, and the corresponding Bayesian network was learned for each participant. Because the global fit of the network to the empirical data has been taken into consideration in the MMHC, the simulated lesion would not only set the connections of that lesioned node as 0 but also impact the overall connectivity pattern. To quantify the influence of the simulated lesion on the global communication across regions in the network, the global efficiency (E_global) of each of the 14 lesioned networks was compared to the global efficiency of the non-lesioned network using a pairwise t-test (two-tailed), with Bonferroni correction applied. To compare the influence on global efficiency caused by an AIC and ACC lesion, we conducted a 2 (Region: AIC, ACC) × 2 (Lateral: left, right) repeated measures ANOVA on the change of global efficiency [∆E_global = E_global (non-lesioned) - E_global (lesioned)]. We also explored the connections showing significant changes after simulated lesion (see Supplementary Materials for details).

Data and code availability

All of the behavioral and imaging data used in this study cannot be shared because of the lack of approval by the IRBs of a data-sharing agreement. E-Prime programs were developed for the task presentation, which are available on the authors’ personal GitHub (https://github.com/TingtingWu222/CCC). The Matlab scripts related to the estimation of CCC from behavioral data are also available in the same GitHub repository. Other Matlab, Python, and R scripts for image preprocessing and fMRI modeling, non-parametrical bootstrapping, and Bayesian network analyses are available upon request, and will be also released via our GitHub repository as soon as we have all the codes documented and organized.

Results

Results of the fMRI study

The accuracy of behavioral responses was close to 100% in the easiest condition (congruency of 5:0 and 0.25/s of reciprocal of ET, 1/ET), and declined as a function of both information entropy and the reciprocal of ET until reaching chance level (Fig. 2a and Supplementary Table 2; see Supplementary Materials for statistic details). These results indicate that the input information could be processed accurately in conditions with low information rate, but the information processing became less accurate when the information rate was increased. For each participant, the CCC was estimated based on the response accuracy, and the group mean ± standard deviation (SD) of the CCC was 4.08 ± 0.67 bps (range: 2.81 to 5.38 bps; Supplementary Fig. 1). In addition, an increase in RT was associated with an increase of both information entropy and ET, indicating that the RT increase as a monotonic function of the information entropy was constrained by ET (Fig. 2b and Supplementary Table 3; see Supplementary Materials for the statistic details).

Figure 2. Behavioral performance in the fMRI study.

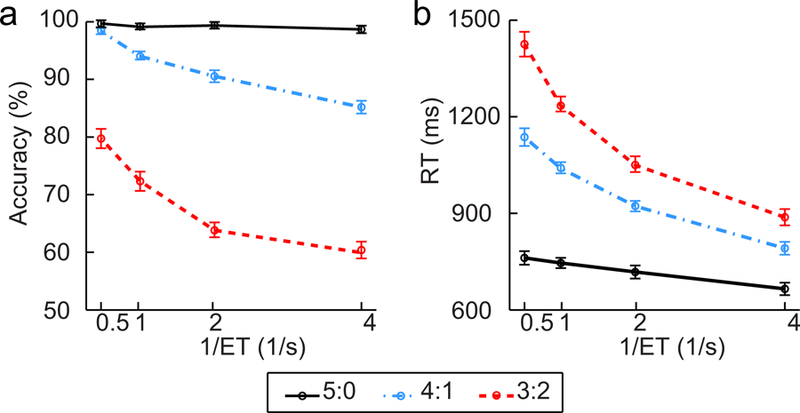
(a) Response accuracy and (b) Reaction time (RT) in each condition. Error bars indicate standard error (SE) for within-subject design.

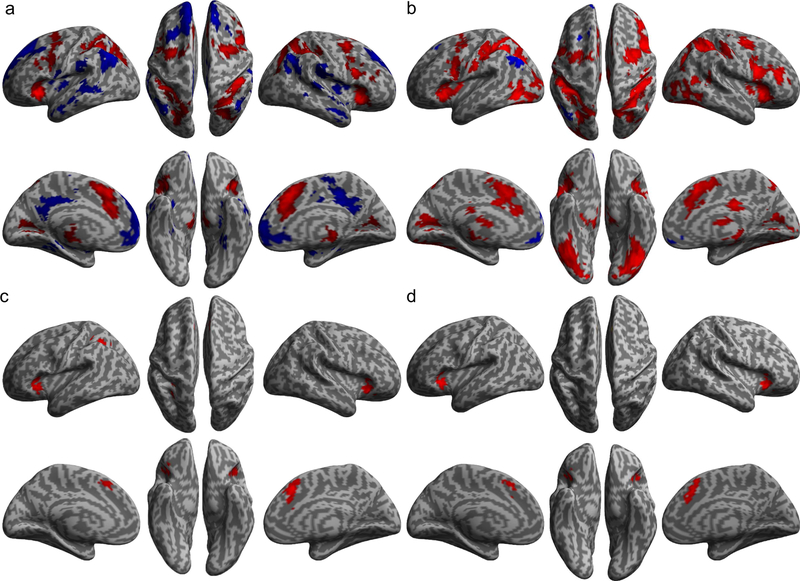
The significant positive main effects of information entropy (Fig. 3a and Supplementary Table 3) and reciprocal of ET (Fig. 3b and Supplementary Table 4) in terms of activation (i.e., the HRF amplitude rather than the convoluted hemodynamic response) were found in all core regions of the CCN and visual areas, while the significant negative main effects were observed in regions of the default mode network (DMN) (Raichle et al., 2001) (see Supplementary Materials for details). The significant positive information entropy × reciprocal of ET interaction effect was found in the left and right AIC, the left and right dorsal ACC extending to the supplementary motor area (SMA), and the left anterior IPS (Fig. 3c and Supplementary Table 5), while there was no region showing a significant negative interaction effect. The positive interaction indicates a super-additive activation in these regions of the CCN when information entropy and the reciprocal of ET were increased synergistically. The significant positive effect of the conjunction of the two main effects and their interaction effect was found in the left and right AIC, and in the left and right ACC, with no significant negative effect found (Fig. 3d and Table 2). Fig. 4a shows the pattern of the super-additive effect in terms of estimated HRF amplitude change in these regions. It is worth noting that while both RT and HRF amplitude increased as a function of information entropy, there was a dissociation of the impact of ET on RT and on HRF amplitude: the RT increased but the HRF amplitude decreased as a function of ET. Supplementary Fig. 2 shows the cumulative hemodynamic responses (not HRF) in each task condition, revealing that the area under these curves increased as a function of information entropy for all ETs.

Figure 3. Main effects of general linear modeling.

Brain regions with significantly increased (red) or decreased (blue) activation as a linear function of information entropy (a) and the reciprocal of ET (b). (c) Regions with significant positive information entropy by the reciprocal of ET interaction (super-additive effect). (d) Regions with a positive effect in the conjunction of the two main effects and the interaction effect.

Table 2.

Brain regions that showed positive effect for the conjunction the entropy by reciprocal of ET interaction.

Regions	L/R	BA	x	y	z	T	Z	K
Anterior insular cortex	R		32	26	−6	6.55	5.83	411
Anterior cingulate cortex	R	32	4	24	42	6.32	5.66	650
Anterior insular cortex	L		−32	22	0	6.19	4.81	442

Note: The threshold was p < 0.001 (T > 3.20) for the height and p < 0.008 (k > 185 of 2 × 2 × 2 mm voxels) for the extent, resulting in a corrected threshold of cluster level p < 0.05.

^aExtending to left anterior cingulate cortex.

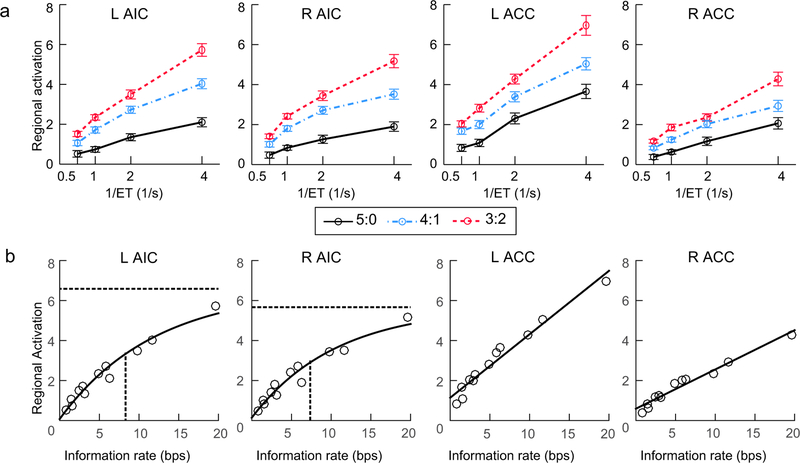
Figure 4. Activation in the anterior insular cortex (AIC) and the anterior cingulate cortex (ACC).

(a) Illustration of the super-additive activation in these regions. (b) Fitted curves (black lines) for the relationship between information rate and activation in these regions. For the left and right AIC, the horizontal dashed line and the vertical solid lines indicate the estimated plateau and half-time of the fitted logistic function, respectively. L: left, R: right.

The fitted curves for the direct relationship between information rate and activation in the AIC and ACC were shown in Fig. 4b. The capacity-limited model (logistic function) fitted the relationship between regional activation (i.e., the HRF amplitude) and the information rate better than a simpler linear model for left AIC (∆BIC = BIC _linear – BIC _logistic = 11.3) and right AIC (∆BIC = 10.0), indicating that although there was a super-additive activation in these region, the increase of activation was slower in the high information rate conditions compared to the low rate conditions. Moreover, the right AIC revealed a significantly shorter half-time (mean: 7.70) than that of the left AIC (mean ± standard errors: 8.66 ± 0.01; t₍₂₆₎ = 9.47, p < .001), indicating that the right AIC reached its activation plateau faster. It should be noted that the standard errors (SE) were not reported for the right AIC because the random effects (which represents the between-subjects difference) were not significant. The linear model was preferred for the right ACC (∆BIC = −83.0), and the fitness of capacity-limited model and of the linear model for the left ACC were not significantly different (∆BIC = 0.9 < 2), indicating that the activation increased as a linear function of information rate in the left and right ACC. Details of each fitted model are provided in the Supplementary Materials.

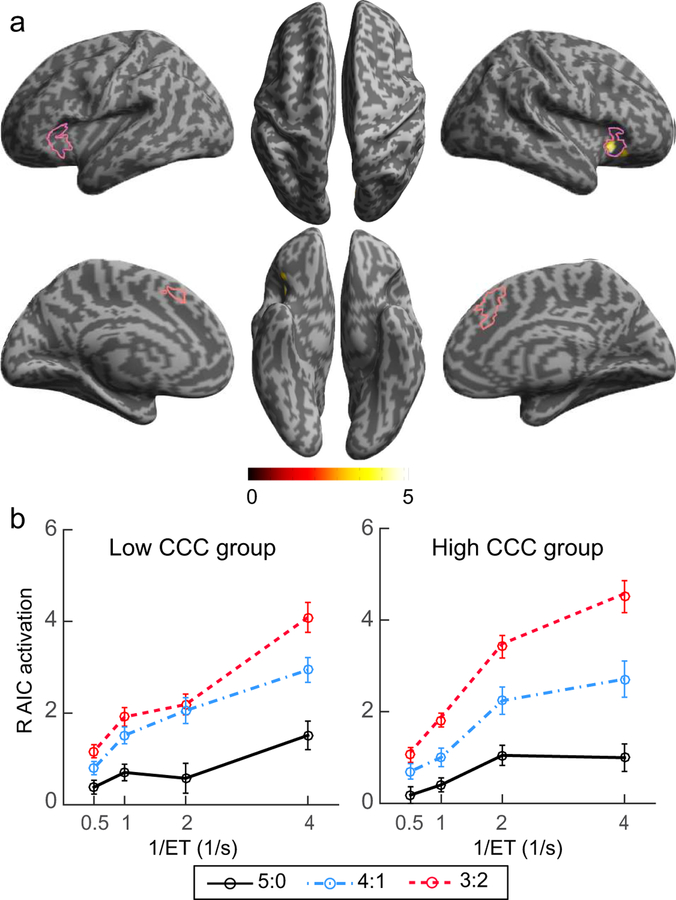
The estimates of the CCC were positively correlated to the coefficients of the information entropy × reciprocal of ET interaction contrast only in the right AIC (coordinates of the local peak: x = 30, y = 20, z = −4; T = 5.33, Z = 4.32, cluster size = 105, corrected cluster level p = 0.029; Fig. 5a), as shown by the whole-brain voxel-wise regression analysis of individual difference in CCC. No significant negative correlationeffect was found in any other voxel or region. The patterns of the super-additive activation in the right AIC separately for the median-split low CCC and high CCC participants are illustrated in Fig. 5b, which shows that the right AIC reached a higher activation in high cognitive load conditions for the high CCC participants compared to the low CCC participants. Other properties of the right AIC (i.e., parameter estimates of the capacity-limited model and the grey matter volume) were not significantly correlated to the CCC (see Supplementary Materials for details).

Figure 5. Correlation between brain activation and the CCC.

(a) The brain region showing significant positive correlation between the super-additive effect and the CCC. Areas in the pink outlines are the regions showing a significant effect in the conjunction analysis of Fig. 3d. (b) Illustration of the activation in the right AIC in the median-split low and high CCC groups.

Both super-additive activation in the right AIC and CCC significantly predicted individual’s FSIQ (super-additive activation in right AIC: R² = .37, F_{1, 25} = 14.89, B = 2.71, p = .001; CCC: R² = .30, F_{1, 25} = 10.73, B = 10.45, p = .003, path c). In the mediation model with the CCC as the predictor variable, the super-additive activation in the right AIC as the mediator, and FSIQ as the target variable (Fig. 6), the coefficient of the super-additive activation (path b) in the right AIC was significant (B = 1.97, p = .023), while the coefficient of the CCC (path c’) was not significant (B = 5.79 < 10.45, p = .110). The regression model with CCC as the predictor controlling for the super-additive activation in right AIC (path a) was significant (R² = .44, F_{2, 26} = 9.34, p = .001).These results indicate that the relationship between the CCC and the FSIQ was fully mediated by the super-additive activation in the right AIC. This mediation effect was not significant for any sub-indices of the IQ (see Supplementary Results).

Figure 6. AIC as a mediator between the CCC and IQ.

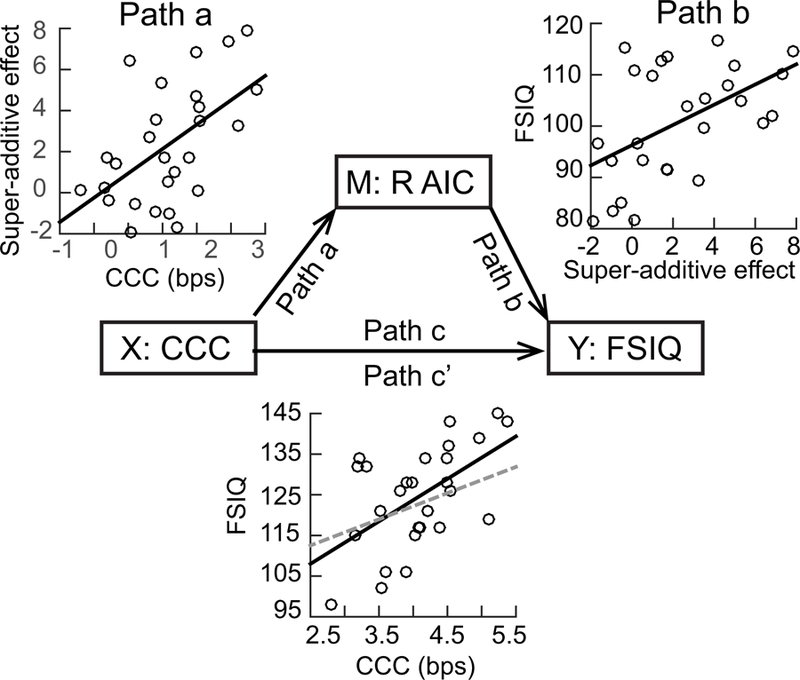
The super-additive activation in right AIC as a mediator (M) between the CCC (X) and Full-Scale IQ (FSIQ) (Y). In the scatter plot for the relationship between CCC and FSIQ, the solid black line and the dashed grey line represent the path c (correlation between X and Y) and path c’ (correlation between X and Y controlling M), respectively.

Results of the lesion study

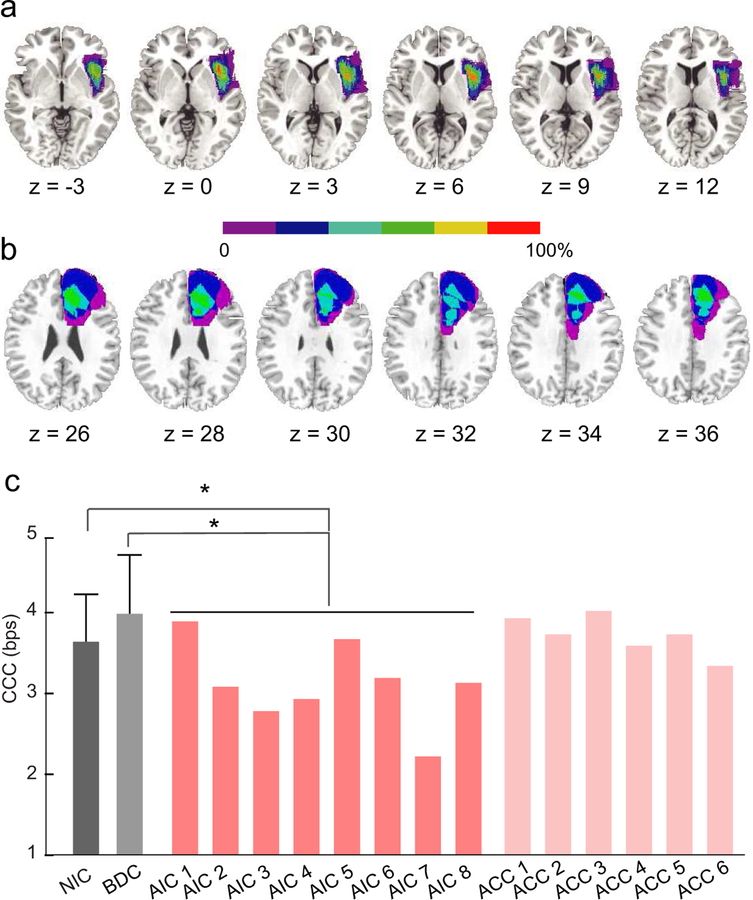
Lesion reconstruction for the AIC group and the ACC group (i.e., patients with unilateral focal lesion in the AIC and ACC, respectively) were shown in Fig. 7a and 7b. The CCC in the AIC group (3.11 bps; 95% CI: 3.10 to 3.12 bps; range: 2.20 to 3.89 bps; pink bars in Fig. 7c) was significantly lower than in the BDC group (i.e., patients with lesion in a region outside the CCN; 3.98 bps; 95% CI: 3.97 to 4.01 bps; range: 2.71 to 4.83 bps; p = .018; the light gray bar in Fig. 7c,), and in the NIC group (3.64 bps; 95% CI: 3.63 to 3.65 bps, range: 2.45 to 4.77 bps; p = .036; the dark gray bar in Fig. 7c). The difference in CCC between the BDC and NIC groups was also not significant (p = .346). These findings indicate a reduction of the CCC in the AIC group, which was not due to the surgery procedure per se. In contrast, the CCC of the ACC group (3.72 bps, 95% CI: 3.71 to 3.73 bps, range: 3.34 to 3.93 bps; light pink bars in Fig. 7c) was not significantly different from the BDC group (p = .405) and the NIC group (p = .693). These findings indicate that lesions in the ACC were not associated with any reduction in the CCC. The group-mean accuracy and RT in each condition for each group are illustrated in Supplementary Fig. 3.

Figure 7. Impaired CCC in patients with lesions in the AIC.

Lesion reconstruction for patients with unilateral lesion in anterior insular cortex (AIC group) and (b) patients with unilateral lesion in anterior cingulate cortex (ACC group). All lesions were mapped on right hemisphere. Colors indicate the percentage of the overlap of lesions across patients. (c) Estimated CCC of participants in different groups. NIC (dark grey bar): neurological intact control. BDC (light grey bar): brain damage control, referring to patients with lesion in regions outside the cognitive control network. Error bars indicate the standard deviation. Pink bar: each patient in the AIC group (left AIC lesion: 2 and 7; right AIC lesion: AIC 1, 3, 4, 5, 6, and 8). Light pink bar: each patient in the ACC group (left ACC lesion: ACC 3, 5, and 6; right ACC lesion: ACC 1, 2, and 4). *: p < .05.

Result of network analyses

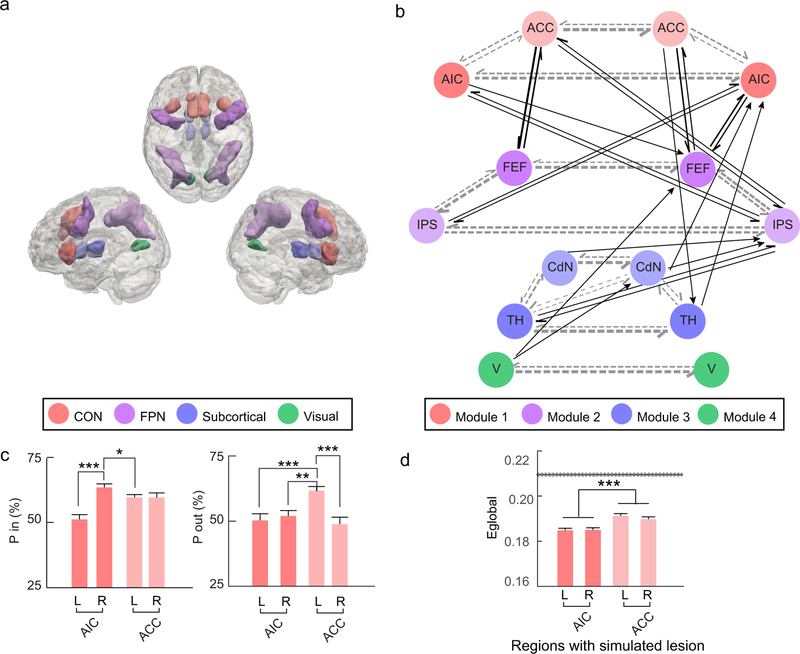
The connectivity across the regions defined by the conjunction between the main effects of entropy and the reciprocal of ET (Fig. 8a) is shown in Fig. 8b (thresholded) and Supplementary Fig. 4 (unthresholded). The estimated community structure of this network revealed four modules: Module 1, including left and right AIC together with left and right ACC; Module 2, including left and right FEF together with left and right IPS; Module 3, including left and right thalamus together with left and right caudate nuclei; and Module 4, including left and right visual areas. This data-driven structure subdivision was consistent with our definition of the sub-networks of the CCN, with Model 1 to 3 corresponding to the CON, FPN, and subcortical network, respectively.

Figure 8. Network analysis results.

(a) Regions of interest (ROI) definition. CON: cingulo-opercular network. FPN: frontoparietal network. (b) Group-averaged Bayesian network. Circles represent nodes, with their colors indicating the module they belong to. Arrows represent directional connections between nodes with their strength (indicated by the thickness of the arrow shaft) significantly higher than baseline. FEF: frontal eye field. IPS: areas around and along the intra-parietal sulcus. TH: thalamus. CdN: caudate nucleus. V: visual areas. Regions in the left and right hemisphere are presented at the left and right sides, respectively. Gray dashed arrows: intra-module connections. Black arrows: inter-module connections. (c) Participation coefficient of the inward (P in; upper-panel) and outward (P out; lower-panel) connections of the AIC and ACC. (d) Global efficiency (E_global) of networks with simulated unilateral lesion of the AIC and ACC, compared to the non-lesioned network. The grey line represents the mean (solid line) and standard error (dashed lines) of the E_global of the non-lesioned network. *: p < .05, **: p < .01, ***: p < .001. Error bars indicate the standard error for within-subject design.

Across regions of the CCN, the right AIC showed the highest participation coefficient in terms of the inward connections (i.e., connections from other regions to a given region; Supplementary Fig. 5a). Within the CON, the participation coefficient of the right AIC (63.6 ± 1.5%) was significantly higher than the left AIC (51.1 ± 2.3%, t₂₆ = 4.61, p < .001) and the left ACC (59.7 ± 1.5%, t₂₆ = 2.34, p = .041), but not significantly higher than the right AIC (59.7 ± 2.0%, t₂₆ = 1.92, p = .096; left panel of Fig. 8c). Across regions of the CCN, the left ACC showed the highest participation coefficients in terms of the outward connections (i.e., connections from a given region to other regions; Supplementary Fig. 5b). Within the CON, the participation coefficient of the left ACC (63.6 ± 1.5%) was significantly higher than the left AIC (51.1 ± 2.3%, t₂₆ = 4.51, p < .001), the right AIC (59.7 ± 1.5%, t₂₆ = 3.22, p = .006), and the right ACC (59.7 ± 2.0%, t₂₆ = 3.59, p < .001; right panel of Fig. 8c). The correlation between participation coefficient of the right AIC and CCC was not significant for the outward connections (r = −.01, p = .95) and the inward connections (r = −.28, p = .15).

Networks with a simulated unilateral lesion of the AIC and ACC showed decreased global efficiency compared to the non-lesioned network (Fig. 8d and Supplementary Table 6). The decrease in global efficiency due to the simulated lesion of the AIC (0.025 ± 0.001) was significantly greater than the decrease due to the simulated lesion of the ACC (0.019 ± 0.001), F_{1, 26} = 16.77, p < .001. The main effect of laterality and the interaction between laterality and brain region were not significant (laterality: F_{1, 26} < 1; interaction: F_{1, 26} = 2.05, p = .164). Decreased global efficiency was also found in networks with a simulated lesion of other regions of the CCN (Supplementary Fig. 7). The connections showing significant changes in connectivity after unilateral lesion of the AIC are shown in Supplementary Fig. 7 (also see Supplementary Materials for details).

Discussion

The activation of the AIC is associated with information rate

The super-additive pattern of the AIC activation demonstrates that the AIC is associated with the rate of information processing. In previous studies, we have demonstrated that the activation of regions in the CCN increases as a linear function of the information entropy, not information rate, when cognitive control is not overloaded (Fan et al., 2014; Wu et al., 2018). Regional brain response is related to the amount of information being processed (Fan et al., 2014; Harrison et al., 2006; Strange et al., 2005; Wu et al., 2018) and information is encoded by means of neural spikes of defined populations of neurons (Averbeck et al., 2006; Borst and Theunissen, 1999). If each bit of information requires a constant number of spikes to be represented, an increase in the amount of the to-be-processed information should be associated with a linear increase of neural activation. If a brain region responses to the rate of information processing, its activation should increase monotonically as a function of information rate, shown as a super-additive effect with both information entropy and ET as factors. In this study, the main effects and the super-additive activation found in both AIC and ACC indicates that these two regions are the entities responding to not only the information entropy, but also the rate of information processing under time constrain.

When a region is overloaded by the amount of information to be processed in a given period of time, the resource in terms of neural spikes saturates resulting in information loss (Buschman et al., 2011; Marois and Ivanoff, 2005; Moreno-Bote et al., 2014; Rolls et al., 1997; Todd and Marois, 2004; Watanabe and Funahashi, 2014). Therefore, the activation plateau of a region indicates that the information to be processed exceeds the maximal amount of information that can be accurately processed in that region in a period of time. Although both of AIC and ACC showed a monotonic activation increase as a function of the information rate, only the left and right AIC showed the activation plateau, suggesting that the bilateral AIC, but not the ACC, have a limited resource for cognitive control at least in the range of cognitive load tested in this study. In addition, the right AIC reached its activation plateau earlier than the left AIC, which may suggest that this region is most responsible in limiting the CCC.

The relationship between the cognitive load (measured as information rate in bps) and activation in the AIC and ACC was not confounded by the effect of RT on brain activation: the cognitive load, rather than the RT, is associated with the amplitude changes of HRF in these regions. An increase in information amount (measured as information entropy in unit of bit) is usually accompanied by prolonged RT (Attneave, 1959; Hick, 1952; Hyman, 1953). However, RT also depends on processing rate, making it difficult to dissociate the contribution of information entropy and information rate to the RT and to the brain activation when only the information entropy is manipulated (Fan et al., 2014; Wu et al., 2018). In this study, we manipulated information entropy via the congruency and manipulated information rate via the variation of both information entropy and ET. We showed that the RT decreased and the HRF amplitude in the AIC and ACC increased as a function of ET decrease (an increase in information rate) regardless of information entropy. These results suggest that the information rate is reflected by the HRF amplitude, whereas the information entropy is reflected by the area under the cumulative hemodynamic response curves, which can be modeled as the convolution between the HRF with estimated amplitude and the rectangular function with the ET as the duration representing the processing time. It is worth noting that these findings were obtained only when response accuracy was emphasized over RT. Participants may employ a different mental processing strategy if response speed is emphasized, which may be associated with different brain dynamics.

The activation of the AIC is associated with the CCC

The bottleneck role of the AIC in cognitive control is further supported by its association with individual differences in terms of CCC. Examining the association between neural responses and task manipulations is a typical approach in cognitive neuroscience to test the involvement of a specific brain region in a cognitive process. Beyond this approach, testing of the association between neural responses and behavioral outputs across individuals provides additional constraints to the model (Vogel and Awh, 2008). In this study, although both AIC and ACC were associated with information rate, the right AIC was the only region revealing a significant positive correlation between the super-additive effect and the CCC, suggesting that a person’s CCC may be determined by the AIC. The neural efficiency theory proposes that for complex tasks with a large amount of information to be processed, high cognitive ability is accompanied by greater neuronal involvement (Neubauer and Fink, 2009). We found that the activation of the AIC reached a higher level in individuals with high CCC when the information rate is high, which may indicate that individuals with high CCC have more neuronal resources to recruit from the right AIC under high cognitive load.

The AIC is necessary for cognitive control

Although the AIC and ACC constitute the CON, a sub-network of the CCN, and usually co-activate (Dosenbach et al., 2006; Medford and Critchley, 2010), the necessity of the AIC, but not the ACC, for cognitive control was demonstrated by the evidence that only the lesion of the AIC resulted in a significant reduction of CCC. Beyond demonstrating a region’s involvement in a cognitive process using fMRI, investigating whether this cognitive process is impaired in patients with a lesion in that region can inform us about its necessity (Fellows and Farah, 2005; Swick and Jovanovic, 2002). Impaired CCC in patients with an AIC lesion suggests that without the support from one lateral of this critical region, the neural resource in the contra-lesional AIC was not enough to support efficient cognitive control under high information rate. The negative finding in patients with a lesion of the ACC is consistent with previous that did not find a signficant deficit in conflict processing in patients with an ACC lesion (Fellows and Farah, 2005; Gu et al., 2012; Gu et al., 2013; Ochsner et al., 2001; Swick and Jovanovic, 2002), suggesting that the ACC may not be a critical region in supporting cognitive control. Significant reduction of CCC in patients with an AIC lesion may also suggest that other regions in the CCN cannot replace the functional role of the AIC, whereas the role of the ACC in cognitive control may be compensated by other regions of the CCN, such as the AIC and the FEF.

The AIC as a hub of the CCN

The role of the AIC as a bottleneck of cognitive control may also be related to its role as a hub of the CCN as indicated by our network analysis. The capacity of a high-level cognitive process may not only be limited by activity plateau in crucial regions (Fukuda et al., 2010), but also by the connectivity among brain regions and networks involved in this process (Gulbinaite et al., 2014; Palva et al., 2010). The “brain hubs”, which are the regions that participate in multiple modules (i.e., sub-networks), have significant contributions in facilitating network traffic (Newman, 2010; Power et al., 2013; van den Heuvel et al., 2012) and support functional integration across modules (Sporns, 2013), and may be easily overloaded (Avena-Koenigsberger et al., 2017; Misic et al., 2014). The AIC has been identified as a network hub during resting state (Power et al., 2013; Sporns, 2013; van den Heuvel and Sporns, 2011, 2013) and cognitive control (Eckert et al., 2009; Gratton et al., 2017). In addition, the AIC, especially the right AIC, plays a critical role in switching between the CON and other large-scale networks (e.g., FPN, DMN, and sensory cortices) to facilitate the access of task-relevant and salient information (Menon and Uddin, 2010; Sridharan et al., 2008). In this study, we showed that the right AIC had the highest participation coefficient across regions of the CCN for the inward connections. If the right AIC plays a central role in receiving and integrating information from other regions/sub-networks of the CCN and coordinates information from multiple regions/sub-networks simultaneously, it can be overloaded and becomes the bottleneck. The left ACC showed a higher participation coefficient compared to the AIC for the outward connections, which may suggest that the left ACC plays an important role in distributing information from the CON to the other sub-networks of the CCN. Although we found evidence suggesting that the AIC plays a role as a hub of the CCN, we did not find a significant association between the participation coefficient of the AIC and the CCC.

The simulated lesion of the AIC significantly impaired the functional integration of the CCN, indicated by the reduced network global efficiency. Global efficiency, also called “routing efficiency”, reflects the global capacity of a network to transmit information through all possible routes (Avena-Koenigsberger et al., 2017). In a network with abundant parallel pathways, a hub is the key node for a great number of shortest paths between nodes in different modules. The loss of a hub would lead to detours of information transmission between numerous pairs of nodes, and therefore has a global impact on communication in the network (Albert et al., 2000; Jeong et al., 2000; Power et al., 2013). In our simulation, we found that compared to lesions of the ACC, lesions of the AIC led to a greater reduction of the global efficiency, suggesting that the capacity of information transmission in the CCN is reduced more after the AIC lesion. These results might provide an insight to the mechanism responsible for the reduction of CCC in patients with an AIC lesion.

The functional role of the AIC in higher-level cognition

Taken together, the activation of the AIC as a function of information rate, the early plateau in responding to the high information rate, the positive correlation between the AIC activation and the CCC, the impaired CCC in patients with AIC lesion, and the role of the AIC in the CCN support the hypothesis that the AIC is a bottleneck of cognitive control. Although the AIC has been identified in this study as a bottleneck using a visual perceptual decision-making task, it may be a unified bottleneck of cognitive control in other sensory modalities (i.e., supramodal) (Spagna et al., 2018b; Spagna et al., 2015) and cognitive domains. The homeostatic model suggests that the insular cortex serves as a modality-general integrative hub that is crucial for generating all human feelings (Craig, 2011). The AIC has also been identified as one of the unified bottleneck regions based on its involvement in limiting speeded dual-task performance in both visual and auditory modalities (Tombu et al., 2011), indicating that information received concurrently from multiple sensory modality competes for resources in the AIC. Beyond receiving and integrating information inputs, the AIC, especially the right AIC, also serves as a coordinator that links the inputs to the subsequent domain-specific control processes. Studies support this proposal by showing that the right AIC plays an important role in coordinating the inputs from sensory regions and the implementation of inhibition control in domain-specific regions (Cai et al., 2017; Cai et al., 2014; Hu et al., 2015). A meta-analysis also demonstrated that the dorsal anterior part of the insular cortex is involved in more general cognitive processing rather than modality- and domain-specific processing (Chang et al., 2012).

In addition, the AIC may also play an important role in supporting human intelligence. In this study, we found that the CCC was positively correlated to an individual’s FSIQ, which has been replicated in a study with a larger sample of participants (Chen et al., In press), supporting a cognitive model of human intelligence. The result that the relationship between CCC and IQ was fully mediated by the super-additive effect in the right AIC suggests that the AIC is a core structure underlying the intellectual activity.