Extreme events reveal an alimentary limit on sustained maximal human energy expenditure

Maximum sustained energy expenditure in humans is limited by energy intake and strongly tied to event duration.

Abstract

The limits on maximum sustained energy expenditure are unclear but are of interest because they constrain reproduction, thermoregulation, and physical activity. Here, we show that sustained expenditure in humans, measured as maximum sustained metabolic scope (SusMS), is a function of event duration. We compiled measurements of total energy expenditure (TEE) and basal metabolic rate (BMR) from human endurance events and added new data from adults running ~250 km/week for 20 weeks in a transcontinental race. For events lasting 0.5 to 250+ days, SusMS decreases curvilinearly with event duration, plateauing below 3× BMR. This relationship differs from that of shorter events (e.g., marathons). Incorporating data from overfeeding studies, we find evidence for an alimentary energy supply limit in humans of ~2.5× BMR; greater expenditure requires drawing down the body’s energy stores. Transcontinental race data suggest that humans can partially reduce TEE during long events to extend endurance.

INTRODUCTION

Considerable interest has focused on the physiological limits on energy expenditure, which is often expressed as a multiple of basal metabolic rate (BMR), also called “metabolic scope,” to account for differences in body size (1–13). Seminal studies have suggested that maximum sustained metabolic scope (SusMS) is capped at ~4× to 5× BMR in humans and other endotherms (1–3), approaching ~7× BMR for some rodents under cold conditions (4, 13). The effect of event duration on SusMS has been hypothesized (3) but has never been quantified and has often been ignored. However, analogous to the relationship for short-duration events between maximum running speed and race distance (14), evidence suggests that SusMS may decrease over longer time periods. The estimated SusMS of ~4× to 5× BMR [often cited as a metabolic ceiling for humans (2–4)] came from the 23-day Tour de France, but athletes in 11-hour triathlons and 25-hour ultramarathons exhibit metabolic scopes of 9.4× and 8.5× BMR, respectively (15), and a metabolic scope of 6.6× BMR was measured over a 10-day period of arctic trekking (16). Complicating the relationship between event duration and SusMS, individuals respond to sustained increases in physical activity by reducing total energy expenditure (TEE) (17, 18). The limits and timing of this metabolic compensation are unclear, particularly under extreme workloads.

In this study, we quantified the relationship between maximum measured metabolic scope and duration of the activity using published measures of human metabolic scope for endurance activities spanning 0.5 to 95 days (e.g., triathlons, Tour de France, and arctic trekking) and measures presented here for the first time for runners in the 140-day transcontinental Race Across the USA (RAUSA) (see Materials and Methods).

RESULTS

Combining RAUSA data with published measures of metabolic scope in other long-duration, energy-intensive activities (e.g., pregnancy; table S1), we found that SusMS is not a static value but instead follows a strong (r² = 0.98, n = 11, P < 0.001) negative logarithmic relationship with event duration (Fig. 1). Limiting the analysis to competitions, where athletes are highly motivated to maximize SusMS, produces a similar curve, as does including estimated (rather than directly measured) metabolic scopes for world-record ultramarathon performances (Fig. 1 and tables S1 and S2). We can find no instance of measured or reliably estimated human metabolic scopes that exceed this curve. The relationship between SusMS and duration differs from the relationship for much shorter events (e.g., half-marathon and full marathon; Fig. 1 and table S2), suggesting different limits on expenditure for short (<0.5 days) versus long events.

Fig. 1. Metabolic scope and duration.

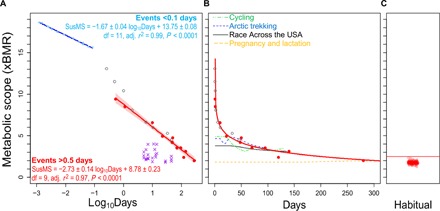
(A) Blue circles and trend line: Short events (<0.1 days; 800 m to marathon). Red circles: Events 0.5 to 95 days. Gray open circles: Estimates for ultramarathon world records and other well-documented endurance events. Purple cross: Other high metabolic scope measurements. Red trend line with 95% confidence interval (CI): SusMS versus duration limit (analysis A in table S2). Data: table S1. (B) SusMS versus duration relationship [unlogged and redrawn from (A); analysis A in table S2] flattens out at ~2.5× BMR. Cumulative average metabolic scope (see Materials and Methods) is shown for elite cyclists over a touring season, arctic trekking, RAUSA runners, and pregnancy and lactation. (C) Habitual metabolic scope (“physical activity level”) for n = 130 cohorts from a diverse global sample (29) cluster below 2.5× BMR (red line).

Metabolic data from RAUSA athletes provide a detailed examination of energy expenditure over the course of an extreme endurance event. RAUSA athletes ran approximately one marathon (42.2 km) per day, 6 days per week, for 14 to 20 weeks from the Pacific (Huntington Beach, CA) to the Atlantic coast (Washington, DC), making it the longest event to date with associated metabolic measures. Using the doubly labeled water (DLW) method, we measured TEE in six RAUSA athletes (table S2) immediately before the start of the race (Pre-Race), during the first week of the race (Week 1), and during the final week of the race. Resting metabolic rate (RMR) was measured in three of the racers at Week 1 and Week 20 via respirometry. Week 1 TEE measured during the first five consecutive days of marathon running (6202 ± 881 kcal/day) was elevated from Pre-Race, differing by only 2% from the increase predicted from running workload (table S2, Fig. 2, and fig. S1). For the three subjects with RMR measurements, mean metabolic scope (i.e., TEE/RMR) increased from 1.76 (range, 1.59 to 1.92) Pre-Race to 3.76 (range, 3.08 to 4.13) during Week 1. At Week 20, their TEE decreased by 1224 kcal/day (range, 791 to 1606 kcal/day) for these three subjects, ~20% down from Week 1 values (P = 0.02, paired t test) to 4906 ± 864 kcal/day. RMR for these three subjects was essentially unchanged (P = 0.18, paired t test), trending ~6% greater (table S1 and Fig. 2), resulting in a decreased metabolic scope (mean, 2.81; range, 2.74 to 2.89). Metabolic scope averaged across the entire 140-day transcontinental run was 3.11 (range, 2.86 to 3.28; fig. S2). The two other subjects who finished the transcontinental run on an accelerated schedule (100 days) had slightly higher estimated average metabolic scopes (3.32 and 3.56), consistent with the shorter duration of their run (table S2 and fig. S2). Water throughput for the five race finishers was high in both Week 1 (8.1 ± 2.2 liters/day) and the final week (7.7 ± 1.6 liters/day; P = 0.32, paired one-tailed t test), underscoring the importance of water balance and fluid availability in maintaining performance (15).

Fig. 2. Observed and predicted energy expenditures for RAUSA athletes.

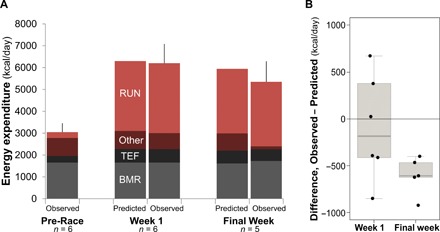
(A) Observed versus predicted TEE and its components. TEF, thermal effect of food; RUN, running expenditure. Observed columns depict means (±SD) for all subjects. (B) Differences from predicted TEE for subjects at Week 1 and the final week (see Materials and Methods and Eqs. 4 and 5).

The reduction in TEE among RAUSA subjects can be partly attributed to marginally reduced body mass and daily mileage (table S3). Still, even after accounting for these changes, Week 20 TEE was 596 kcal/day lower (range, 400 to 923 kcal/day) than expected (see Materials and Methods, table S2, and Fig. 2). The mechanisms underlying this metabolic compensation are unclear but likely include reduction in nonexercise activity and reduction of physiological activity in other organ systems (17, 18). Changes in running cost could also contribute, but evidence for training-induced improvement in running efficiency is mixed and the effect, when present, is generally modest, ~3% savings in energy per kilometer (19). Whatever the mechanisms, the reduction in TEE and metabolic scope may have been crucial in enabling them to complete the run; the relationship between SusMS and duration (Fig. 1) suggests that these runners’ Week 1 metabolic scope would have only been sustainable for ~70 days. The magnitude of metabolic response in RAUSA athletes (~600 kcal/day, ~20% TEE) is similar to the degree of adaptation reconstructed for the most physically active subjects in a recent cross-sectional study (17) and may reflect humans’ maximal capacity for metabolic compensation.

DISCUSSION

The nature of the events that fit the apparent ceiling in SusMS and event duration (Fig. 1) provides additional insight into the mechanisms that limit long-term sustained expenditure. A broad range of activities, involving different muscle groups and organ systems (e.g., running, swimming, cycling, trekking, and pregnancy), all fit the SusMS versus duration curve. Active muscle volume and maximal capacity to uptake oxygen and nutrients and expend energy vary substantially among sports (20), and the reproductive organs likely have their own different maximal capacities. The diversity of events adhering to a common metabolic ceiling (Fig. 1) makes it unlikely that limits to energy expenditure in the peripheral tissues constrain prolonged expenditure in humans. Similarly, maximal metabolic scopes measured under cold conditions (i.e., arctic trekking) were no different with respect to duration than those under warm conditions (Fig. 1 and table S1), challenging thermoregulatory explanations for SusMS.

Limits to energy expenditure could emerge from limits to oxygen and nutrient distribution. The heart, lungs, and vascular system have the capacity to bring in oxygen and distribute oxygen and nutrients at more than 10× BMR for several hours (Fig. 1). Nonetheless, humans and other animals may be sensitive to the energy required for distribution. West and colleagues (21) have argued that, across species, BMR reflects selection to minimize energy expenditure on oxygen and nutrient distribution via the vasculature. It is unclear whether these systems fatigue with prolonged expenditures above the minimal distribution energy, but additional research is warranted. Similarly, the potential for long-term fatigue in the kidneys and other organs involved in waste excretion deserves future investigation.

Limits to energy intake would implicate the alimentary system (e.g., digestive tract and liver) and would predict some maximal rate of energy intake; energy demand exceeding this maximum rate would require drawing on energy reserves and would not be sustainable indefinitely. We tested for an energy intake limit by examining two paradigms that maximally stress the alimentary system: endurance studies with ad libitum food supply (n = 23, including those in Fig. 1) and overfeeding studies (n = 6; table S1). In overfeeding studies, subjects’ energy consumption is much greater than TEE for several days, while physical activity is kept very low. Overfeeding protocols provide a measure of maximum energy uptake by the alimentary system under conditions of food energy surplus.

For each endurance and overfeeding study, we calculated energy intake per day by taking the measured metabolic scope and either subtracting the energy derived from weight loss or adding energy converted to weight gain. Precise conversion of weight change to energy requires detailed information on proportions of fat and lean mass gained or lost (22, 23) that is unavailable for many studies. As a first approximation, we assumed an equivalence of 1 kg/day to 5× BMR (approximately 7650 kcal/kg) following observations from weight loss studies (23). We found that sustained energy intake was similar across studies (2.36 ± 0.59× BMR) and independent of event duration (Fig. 3B), consistent with an alimentary mechanism limiting SusMS. Varying the kilogram per day–to–BMR ratio by ±20% only changes mean estimated sustained energy intake by 2% (fig. S3). Furthermore, we found a strong relationship between energy balance and metabolic scope for endurance and overfeeding studies (Fig. 3A and table S1). Reduced major axis regression gives a 95% confidence interval (CI) for energy balance of 2.20× to 2.35× BMR and a slope of −0.17 (95% CI, −0.13 to −0.22).

Fig. 3. Maximal energy intake.

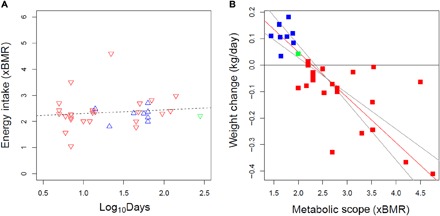
(A) Estimated energy intake, calculated from metabolic scope and weight change, is consistent across overfeeding (red inverted triangles), endurance (blue triangles), and pregnancy (green inverted triangle) studies and is unrelated to event duration (P = 0.51, r² = 0.01, least squares regression; dashed line). (B) Weight change (in kg/day) versus metabolic scope (×BMR) for endurance (red squares), pregnancy (green square), and overfeeding (blue squares) studies (table S1). Reduced major axis regression (red line) and 95% CIs (gray lines) are indicated.

The agreement of weight change data from overfeeding studies with those from endurance studies (Fig. 3) suggests that a common alimentary limit to energy uptake constrains a broad range of activity. These results also strengthen the case for an alimentary limit to SusMS because the effects of energy expenditure or distribution constraints would not be expected to persist at low (<2.0× BMR) expenditures and activity levels. Conversely, the relationship between weight change and expenditure (Fig. 3) indicates that SusMS above ~2.5× BMR generally rely on drawing down energy stores to supplement alimentary supply. The increment of expenditure above 2.5× BMR cannot be met with additional intake and therefore cannot be sustained indefinitely. Notably, metabolic scope during human pregnancy (during which weight gain is imperative) and lactation peaks at ~2.2× BMR, which might constrain gestation length and fetal growth (24, 25).

An alimentary limit of ~2.5× BMR is consistent with the SusMS versus activity duration curve, which flattens out below ~3× BMR (Fig. 1B), but raises directions for further research. First, in at least two studies (Tour de France cyclists and elite Nordic skiers; table S1), subjects maintained metabolic scopes of 3× to 5× BMR without substantial weight loss. While neither group exceeded the apparent SusMS ceiling (Fig. 1A), it is unclear whether their above-average energy intake reflects special nutritional strategies (e.g., infusing glucose intravenously) or individual biological variation. Second, the signaling mechanisms linking energy imbalance to the body’s central regulation of activity, and that ultimately prevent humans from exceeding the observed SusMS versus duration curve, remain unknown. Measurements of energy imbalance versus metabolic scope (Fig. 3B) support the hypothesis that SusMS is constrained by the alimentary system, but other systems of energy consumption and distribution warrant further investigation. As with the limits to VO₂max (26), we can expect the various organ systems that constrain prolonged SusMS to converge on a common limit (symmorphosis), making it difficult to parse their individual contributions.

The lack of a cold temperature effect is unexpected, given the strong evidence for heat dissipation limits in other mammals (5, 13). The absence of a thermoregulatory limit in this sample may be because endurance sporting events are not typically staged at high temperatures where heat dissipation might limit expenditure, reduce performance, and increase health risks. In ultramarathons staged under hot conditions (e.g., Badwater Ultra), the limits of heat dissipation and the risk of acute heat-related injury and dehydration may impose a lower limit on energy expenditure than is evident in this sample (5, 15). Humans may also have physiological adaptations that make us particularly robust to thermoregulatory constraints and vulnerable to alimentary constraints. First, humans and other primates are hypometabolic, with TEE ~50% reduced compared to nonprimate eutherian mammals (27). Reduced habitual expenditure decreases heat load and may have also selected for reduced alimentary capacity. Second, humans have evolved a remarkable capacity to dissipate heat through sweating with effectively hairless skin (28). Thus, under mild or temperate conditions, humans may reach the limits of energy supply machinery well before the limits of heat dissipation. However, under hot conditions or when water supply is limited, the reverse may be the case and heat dissipation may become the primary constraint. Future work may aim to define the conditions (and species) in which SusMS is limited by alimentary factors versus other factors such as heat dissipation.

Whatever the physiological mechanism, the strong relationship between SusMS and duration reveals a common underlying framework uniting the full range of protracted endurance endeavors among humans, from exploration (16) to sport (2) and reproduction (24, 25). The relationship between SusMS and duration flattens out at ~2.5× BMR (Fig. 1B), suggesting a metabolic ceiling for habitual metabolic scope (often termed “physical activity level”) in humans. Prolonged expenditure above this metabolic ceiling (~2.5× BMR) requires consuming energy reserves and is not sustainable indefinitely. Consistent with this hypothesis, humans around the globe display remarkably similar metabolic scopes of ≤2× BMR during daily life, regardless of differences in activity and lifestyle (Fig. 1C) (17, 18, 29).

Humans have evolved greater endurance capabilities than other apes, which has typically been ascribed to selection for increased physical activity, particularly long-distance running (14). The common metabolic limit shared among disparate physiological tasks revealed here (Fig. 1) suggests that selection for increased SusMS in one domain (e.g., running) would raise the metabolic ceiling for others (e.g., pregnancy). Humans’ greater TEE relative to other apes fuels a range of evolutionarily derived, energetically costly traits (30), making it unclear which elements of the human adaptive suite were the primary targets of selection for greater metabolic capacity. The evolution of alimentary mechanisms limiting energy supply in humans warrants further investigation, and it is notable that the gross morphology of the gastrointestinal tract and the genes involved in liver function are evolutionarily derived in humans compared to apes (31, 32). Other mammalian lineages appear to operate under different, non-alimentary constraints to SusMS (4, 5, 13). Together, the potential for variation among species in the mechanisms governing SusMS and the unified relationship between SusMS and duration (Fig. 1) suggest a previously unappreciated diversity in metabolic evolution and an unexpected physiological linkage among essential life tasks.

MATERIALS AND METHODS

Metabolic scope versus duration

We examined metabolic scope data from a recent review (33), adding other measures of SusMS from racing, trekking, farming, and pregnancy (table S1). For the determination of the SusMS versus duration curve (Fig. 1A), we first limited our analyses to studies in which TEE was measured through either DLW (34) or energy balance. For trekking and cycling subjects, we estimated BMR from weight, age, and (if available) height (35) to calculate metabolic scope. TEE was measured over three different time periods in (16), and those three measures (SusMS and duration) were included separately in tables S1 and S2 (analysis A). Pregnancy value is the maximum ratio of (TEE)/(pre-pregnancy BMR) in a review of pregnancy costs [from table 6 in (24)]. A subset of these data provides an apparent ceiling of metabolic scope versus ln duration (red circles and trend line in Fig. 1A). We searched PubMed and Google Scholar for measurements of TEE or metabolic scope that fall above this ceiling but were unable to find any that exceed the trend line in Fig. 1A. Other high metabolic scope measurements and durations are shown in Fig. 1A (purple crosses).

To determine whether any well-documented world records for ultramarathon events might represent metabolic scopes that exceed the apparent metabolic ceiling for SusMS versus duration, we examined records for events 0.5 days from an online compendium (https://en.wikipedia.org/wiki/Ultramarathon) and a recent record set for the Appalachian Trail (http://running.competitor.com/2016/09/news/meltzer-nearing-finish-appalachian-trail-record-attempt_155618). For ultramarathon records, we calculated mean running speed [i.e., (race distance/time) from] and converted this to estimated metabolic scope using the following equation:

$$\text{Metabolic scope}=-0.154 {\text{speed}}^2+3.615 \text{speed}$$ (1)

This relationship is derived by combining the equations for BMR and the rate of energy expenditure versus running speed in (14). For the Appalachian Trail record, we estimated metabolic scope from reported estimates of energy intake per day. For a case study following a subject completing 33 Ironman triathlons in 33 days (36), we estimated mean daily metabolic scope as 12 hours per day at triathlon metabolic scope (9.4; see table S1), 8 hours per day sleeping (metabolic scope = 1.0), and the remainder at a metabolic scope of 1.5. As discussed in the text and shown in table S2, inclusion of these estimates of metabolic scope does not markedly affect the relationship between SusMS and duration (Fig. 1A).

For comparison with shorter events, we examined world-record speeds and durations for foot races from 800 m to marathon distances reported in (14). Estimated metabolic scopes were calculated from running speed using Eq. 1 as for ultramarathon records.

Reconstructing cumulative average SusMS

Cumulative average SusMS for arctic trekking, elite competitive cyclists, pregnancy and lactation, and RAUSA runners (Fig. 1B) was reconstructed for every nth day of an event as a cumulative average daily metabolic scope, $\left({\displaystyle {\sum }_{i=1}^n}{\text{metabolic scope}}_i\right)/n$, where (metabolic scope_i) is the metabolic scope for each day of the event and n is the elapsed event duration. Daily metabolic scopes were calculated as follows:

1) Arctic trekking: Stroud and colleagues (16) reported mean metabolic scope for days 1 to 10, 11 to 20, 21 to 30, 41 to 50, and 50 to 95. Daily metabolic scopes were reconstructed from these records, setting daily metabolic scope to the mean value for each period.

2) Cyclists: We considered a cyclist competing in the grand tours (Giro d’Italia, Tour de France, and Vuelta a España) following the typical calendar schedule of 23 days competing (Giro d’Italia), 34 days off, 23 days competing (Tour de France), 28 days off, 22 days competing (Vuelta a España). For competition days, metabolic scope was set at 4.9 following mean measured expenditures from the Tour de France (2). For days off, we assumed a daily metabolic scope of 2.0, which is typical of elite athletes during tapering periods before a race (33).

3) Pregnancy and lactation: We used reported metabolic scopes measured at weeks 6, 24, 30, and 36 of pregnancy and during the first 3 months of lactation using the highest reported values from a review of pregnancy and lactation costs (24). Daily metabolic scope was set to the mean value for each period.

4) RAUSA runners: For runners R1, R2, R3, and R6, we reconstructed daily metabolic scope, assuming that measured metabolic scope in Week 1 persisted until day 30 and then decreased steadily (~1% per day) to achieve final week values at day 60. Final week values for metabolic scope were assumed to persist from day 60 until the end of the race (day 100 or 140). For R5, who followed an accelerated schedule and increased mileage and TEE at the end of the event, we assumed that Week 1 metabolic scope persisted until day 80 and that final week metabolic scope persisted from day 81 to day 100. Note that BMR and, hence, metabolic scope were estimated for R2 and R5 (fig. S2).

RAUSA: Subjects

We measured TEE (in kcal/day) in six adult athletes (five males, ages 34 to 73 years; one female, age 32 years), participating in the RAUSA transcontinental marathon event. This race covered 4957 km during 20 weeks of running, with subjects running approximately one marathon (42 km) per day, 6 days per week from 16 January 2015 to 2 June 2015. A written explanation of the experimental protocol and associated risks was provided to all subjects, and their written informed consent was obtained before participation in the study. Permission was obtained from the organizers of the RAUSA event, and Institutional Review Boards at Hunter College and Purdue University approved the study (IRB reference no. 398749-4).

Of the six subjects, only three completed the planned racecourse on the original schedule. One subject (RS4, female, age 32 years) dropped out of the race after 8 weeks because of running-related injuries. Two subjects decided to disassociate from the RAUSA event at week 4 and continue running their own route across the country, covering a greater daily and total distance. Of these two subjects, one (RS5, male, age 36 years) continued to run, and the other (RS2, male, age 42 years) walked while carrying a backpack. These subjects completed the transcontinental course ahead of the RAUSA team, and we therefore measured their final expenditures at Week 14 after the start of the race. For each subject, the daily running distances were recorded using wearable GPS. Daily elevation gain or loss was recorded using online course maps (e.g., www.mapmyrun.com/routes/view/389064072).

RAUSA: TEE

TEE was measured using the DLW method (34) during three periods for each subject: (i) Pre-Race [5 days before the start of RAUSA (10 to 15 January 2015)]: Subjects were preparing for RAUSA during this period but did not refrain from running, and daily running distance was 4.0 km (see table S3). (ii) Week 1: First 5 days of race running (16 to 20 January 2017). (iii) Final [last 12 days of the transcontinental run, either Week 14 (RS2 and RS5; 17 April 2015 to 5 May 2015) or Week 20 (RS1, RS3, and RS6; 24 May 2015 to 2 June 2015)]: Subjects ingested 1.2 g of DLW per kilogram of body mass, the dose material containing ~6% ²H₂O and ~10% H₂¹⁸O (Sigma-Aldrich). After consuming the dose, the dose container was rinsed twice with bottled water that was consumed to ensure total dose ingestion. A urine sample was collected 5 min before dosing to establish baseline isotope enrichment, and post-dose urine samples were collected to measure isotope elimination rates. Subjects were provided with single-use collection cups, transfer pipettes, and 4-ml screw cap vials for collecting their samples. All samples were kept frozen or stored on frozen cold packs during transport until collected by a researcher and brought to the Human Evolution & Energetics Lab at Hunter College in New York. Isotope enrichment was measured using cavity ring-down spectrometry (Picarro). All samples were either carbon-filtered or ultrafiltered by centrifuge using Vivaspin tubes (Vivaproducts) at Hunter College. Isotope enrichment analysis was performed using a Picarro Cavity Ring-Down spectrometer at the Pontzer Lab at Hunter College, NY, USA.

The first dose was administered 6 days before the start of the race and was used to calculate Pre-Race and Week 1 TEE as follows. Urine samples were collected daily for the 5 days before the race and the first 5 days of the race. For both Pre-Race and Week 1 calculations, dilution spaces for ²H and ¹⁸O (N_D and N_O, respectively) were calculated via the slope-intercept method using the least squares regressions of lnδ versus time over the first 5 days (Pre-Race) of enrichment values (fig. S1 and table S1). This regression was also used to calculate depletion rates (lnδ day⁻¹) for ²H and ¹⁸O (k_D and k_O, respectively) for the Pre-Race period. A separate regression was used to calculate depletion rates for the Week 1 samples (fig. S1 and table S3). Note that this approach assumes that the dilution spaces did not change appreciably from Pre-Race to Week l. This assumption is consistent with relatively short duration (~10 days) and the observed stability in body weight from the start of Pre-Race to the end of Week 1 (table S1).

A second dose of DLW was administered 2 weeks before the end of the race (Week 14 or Week 20). A Week 20 baseline sample was collected and used for analysis to account for changes in background isotope enrichment between Week 1 and Week 20. Furthermore, given the high rates of water throughput for these subjects (table S3), there was more than sufficient time for all of Week 1 dose to be flushed from the body before the second measurement. Three post-dose urine samples were obtained, evenly spaced over a 12-day period. Dilution spaces and depletion rates were calculated from the least squares regression of lnδ versus time as described above.

The rate of CO₂ production (in mol day⁻¹) was calculated using equation 6.6 in (34)

$${\text{rCO}}_2=0.455 \text{TBW} (1.007 k_{\mathrm{O}}–1.041 k_{\mathrm{D}})$$ (2)

where total body water, TBW = (N_O/1.007 + N_D/1.041)/2. TEE was then calculated from rCO₂ using the modified Weir equation, kcal/day = 22.4 rCO₂ (1.1 + 3.9/FQ), where the food quotient, FQ, was assumed to be 0.85. We note that, while diets were not closely monitored during the race, foods consumed did not change greatly over the course of the event. Daily water throughput (in liters/day) was calculated following equation 6.8 in (24) as rH₂O = 0.01802 N_D k_D/0.99, assuming H₂O of 0.01802 liters/mol and a fractionation correction of 0.99.

RAUSA: Respirometry, bioelectrical impedance, and body weight

Respirometry was used to measure RMR for three subjects (RS1, RS3, and RS6) using the Cosmed (Italy) Fitmate Pro (37), during 20-min trials in Week 1 and Week 20. The other subjects chose not to participate in RMR measurement. We consider these measures of RMR, rather than BMR, because while subjects were rested, fasted, and supine, we were unable to ensure the strict control of environmental conditions needed for true BMR measurement (35). For example, measures were taken in a tent outdoors (ambient temperatures were in the thermoneutral zone), and the subject did not refrain from physical activity for 24 hours before measurement. RMR trials were performed on subjects early in the morning (~06:00) after fasting overnight and at least 30 min of resting while in a supine position.

Bioelectrical impedance was used to measure fat-free mass (FFM) with a single-frequency (50 kHz) analyzer (model BIA 101Q, RJL Systems, Clinton Township, MI) for the three RAUSA subjects in January and May. This method was not available for RS2 and RS5, so their FFM was estimated using TBW data obtained from DLW and using a hydration constant of 0.732. The inability to account for fluctuations in body hydration due to the extreme physical activity of the athletes made bioelectrical impedance the preferred method of measuring FFM when possible. Note that the main effect of this preference is on calculations of predicted TEE in the final week because changes in FFM were used to calculate predicted final week TEE (see below). As discussed below, using the DLW measures of TBW and FFM does not change the results: Observed TEE in the final week was still 165 to 622 kcal/day less than predicted.

Each subject’s body weight was closely monitored and recorded throughout the study using the Tanita BC-558 Ironman Segmental Body Composition Monitor (Tanita Corporation, Arlington Heights, IL) on the athletic setting. RAUSA subjects were weighed daily. Subjects RS2 and RS5 provided their own body weight measurements at Week 14.

RAUSA: Components of TEE

To investigate metabolic changes over the course of the race, we parsed TEE measured Pre-Race, Week 1, and during the final week into four components: basal metabolism, thermic effect of food (i.e., digestion costs), running cost, and other. RMR was directly measured via respirometry (RS1, RS3, and RS6) or estimated from height, weight, and age using sex-specific equations for BMR (35). Thermic effect of food (in kcal/day) was estimated as 10% of TEE. Running cost (in kcal/day) was calculated from the “slope method” equation developed in a meta-analysis of human running cost (38), using each subject’s body mass (in kg) and distance run (in km/day), which gives kcal/day = 0.937 mass·distance. To this was added an elevation cost (in kcal/day) reflecting the energy cost of the mean net change in elevation, ΔElevation (in m/day). Following previous work on the cost of running uphill (39), we assumed that elevation was gained at 23% efficiency (i.e., energy cost of climbing equal to the change in potential energy divided by 0.23). This gives

$$\text{Elevation cost}=0.000239 (9.8 \mathrm{\Delta }\text{Elevation}·\text{mass}/0.23)$$ (3)

where 0.000239 converts joules to kilocalories. Mean ΔElevation was +207 m/day during Week 1 and −10 m/day during Week 20. Daily running cost was therefore calculated as

$$\text{Run}=0.937 \text{mass distance}+\text{elevation cost}$$ (4)

Equation 4 was modified for subject RS2, who walked with a backpack during the final week of the race (Week 14). Previous work (40) indicates that the cost of walking while carrying a load increases proportionally with the percentage increase in gross mass (i.e., body mass + load). Thus, for RS2 during Week 14, we used the walking cost equation from Rubenson and colleagues (38) and multiplied by 1.175 to account for the additional load being carried, which was equal to 17.5% of his body weight, Run_{RS2_Week14} = 1.175 (0.492 mass·distance).

The portion of TEE remaining after subtracting basal metabolism, the thermic effect of food, and running cost was denoted as “other.” This component is part of what is often termed “activity energy expenditure” and is analogous to “AEE2” described in a recent analysis of TEE and activity in a large human sample (17), that is, it is the portion of TEE that is not attributable to empirically measured activity (i.e., running), estimated dietary thermogenesis, or measured BMR.

RAUSA: Predicted TEE and metabolic adaptation

We calculated predicted TEE for Week 1 and the final week (Week 14 or Week 20) to test for metabolic adaptation in observed TEE. For Week 1, we used the Pre-Race values for RMR (RMR_PreRace) and other (Other_PreRace) components of TEE and added to them the expected running cost for Week 1 (Eq. 4). We then multiplied the sum of these three components by 1.11 to add the expected thermic effect of food (at 10% TEE) so that predicted Week 1 TEE, Week 1_pred, was given as

$$\text{Week} 1_{\text{pred}}=1.11 ({\text{RMR}}_{\text{PreRace}}+{\text{other}}_{\text{PreRace}}+{\text{Run}}_{\text{Week}1})$$ (5)

Because the thermic effect of food is generally estimated at 10% of energy intake, this approach assumes that TEE is equivalent to energy intake. This assumption is reasonable because subjects were weight stable during Week 1 (mean weight change, 0.2 kg/week; table S3). Our approach (Eq. 5) also makes the simplifying assumption that energy expended on activity not attributable to BMR, running, or digestion (i.e., the term “other” in Eq. 5) would not change from Pre-Race to Week 1. As evident from the fit between predicted and observed TEE for Week 1 (Fig. 2 and table S3), these assumptions were consistent with the results of our analyses.

We used a similar approach, with the same simplifying assumptions for digestion costs and “other” expenditure, to calculate predicted TEE in the final week, Final_pred (Week 14 or Week 20), adjusting these values to account for the change in FFM. Pre-Race measurements of TEE were correlated with FFM, increasing as 42 kcal/day per kg FFM (fig. S1), similar to that reported for a large (n = 332) adult human sample (17). Therefore, we reduced predicted final TEE, Final_pred, for each subject by 42 kcal/day per kg reduction in FFM

$${\text{Final}}_{\text{pred}}=1.11 ({\text{RMR}}_{\text{PreRace}}+{\text{other}}_{\text{PreRace}}+{\text{Run}}_{\text{Final}} – 42 \mathrm{\Delta }\text{FFM})$$ (6)

where ΔFFM was the change in FFM since Week 1. Note that Run_Final was calculated using the body mass at Week 14 or Week 20 and therefore reflects the change in body mass from Week 1. This approach to calculating predicted TEE for the final week takes into account changes in body mass, FFM, distance run, and elevation gain. Differences between observed and predicted TEE (Fig. 2) therefore reflect metabolic change that is not attributable to changes in body size, FFM, or running costs.

We prefer this approach for calculating Final_pred TEE because it follows an empirically based regression generated from a large dataset (17) and allows us to incorporate data on running distance and FFM. We note that an alternative approach, Hall’s dynamic body composition simulator (22), provides similar results. We used the simulator to calculate the difference between Week 1 TEE for each subject and their estimated weight maintenance TEE for their weight during the final week. The highest physical activity level (2.5) permitted by the simulator was used. Substituting this calculated difference for the 42 ΔFFM term in Eq. 6, we found that the observed TEE in the final week was 219 to 793 kcal/day less than expected from the simulator. Similarly, using DLW measures of TBW and FFM rather than bioimpedance measures (see above) produces similar results, with observed TEE 165 to 622 kcal/day less than predicted.

RAUSA: Daily water throughput

Daily water throughput, a critical physiological variable in endurance activities (15), did not track TEE strongly. For all six subjects, mean water throughput increased from 4.79 ± 1.57 liters/day Pre-Race to 8.41 ± 2.09 liters/day during Week 1. During the final week (Week 14 or Week 20), mean water throughput among the five remaining subjects was essentially unchanged, trending slightly down from Week 1 levels to 7.68 ± 1.60 liters/day (P = 0.32, paired t test; table S1). Of these remaining subjects, three had marginally increased water throughput at the end of the race, while the other two showed decreases (table S1).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/6/eaaw0341/DC1

Fig. S1. TEE and FFM.

Fig. S2. Cumulative average SusMS of RAUSA runners reconstructed for the duration of the event.

Fig. S3. Estimated energy intake at varying equivalencies of weight loss per BMR.

Fig. S4. Isotope enrichments for a representative subject, RS2.

Table S1. Metabolic Scope, duration, and weight loss.

Table S2. Linear regressions for SusMS versus log₁₀ duration.

Table S3. Pre-Race (Pre-), Week 1 (W1), and final week (Final) measures.

Table S4. Results of isotopic analyses.

References (41–48)